【抢分秘籍】各地区中考数学真题分类突破:选择题(二)(含答案)
文档属性
| 名称 | 【抢分秘籍】各地区中考数学真题分类突破:选择题(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:58:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【抢分秘籍】各地区中考数学真题分类突破:选择题(二)
1.(2025 开州区模拟)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是( )
A.中 B.考 C.顺 D.利
2.(2025 英德市二模)是一个很奇妙的数,在艺术、建筑中以“黄金分割”体现美感,估计的值( )
A.在0和1之间 B.在1和2之间
C.在2和3之间 D.在3和4之间
3.(2025 太康县一模)计算结果为a8的是( )
A.a2 a4 B.a14﹣a6 C.a4+a4 D.(a4)2
4.(2025 临沧模拟)如图,在平行四边形ABCD中,若AB=3,BC=5,E为AD上一点,且BE=BC,CE=CD,则DE的长为( )
A.1.8 B.1.5 C.2.5 D.2
5.(2025 裕华区校级模拟)如图,小明将等式5a﹣2b=3a﹣2b进行变形,最后得到一个错误的结论,则下列说法正确的是( )
A.第一步错误
B.第二步错误
C.第三步错误
D.三步都正确,原等式错误
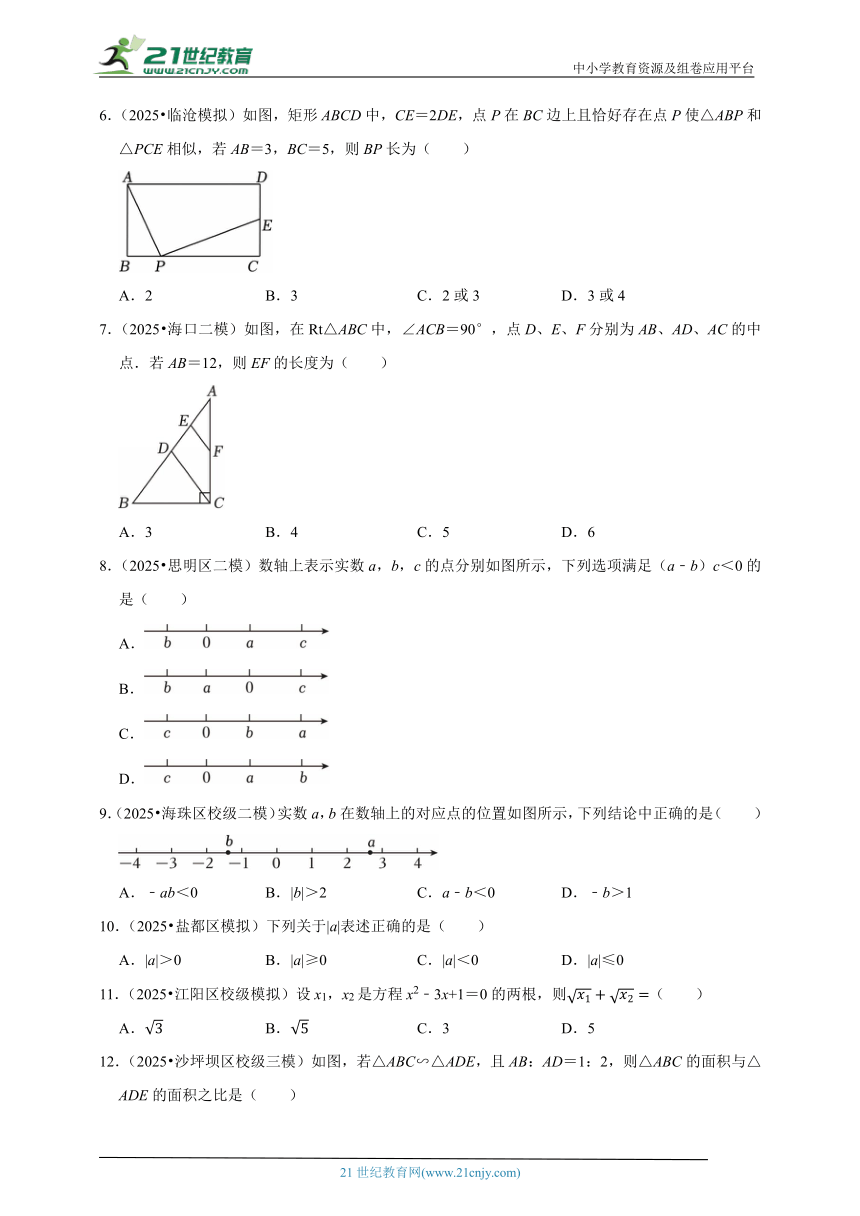
6.(2025 临沧模拟)如图,矩形ABCD中,CE=2DE,点P在BC边上且恰好存在点P使△ABP和△PCE相似,若AB=3,BC=5,则BP长为( )
A.2 B.3 C.2或3 D.3或4
7.(2025 海口二模)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别为AB、AD、AC的中点.若AB=12,则EF的长度为( )
A.3 B.4 C.5 D.6
8.(2025 思明区二模)数轴上表示实数a,b,c的点分别如图所示,下列选项满足(a﹣b)c<0的是( )
A.
B.
C.
D.
9.(2025 海珠区校级二模)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.﹣ab<0 B.|b|>2 C.a﹣b<0 D.﹣b>1
10.(2025 盐都区模拟)下列关于|a|表述正确的是( )
A.|a|>0 B.|a|≥0 C.|a|<0 D.|a|≤0
11.(2025 江阳区校级模拟)设x1,x2是方程x2﹣3x+1=0的两根,则( )
A. B. C.3 D.5
12.(2025 沙坪坝区校级三模)如图,若△ABC∽△ADE,且AB:AD=1:2,则△ABC的面积与△ADE的面积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
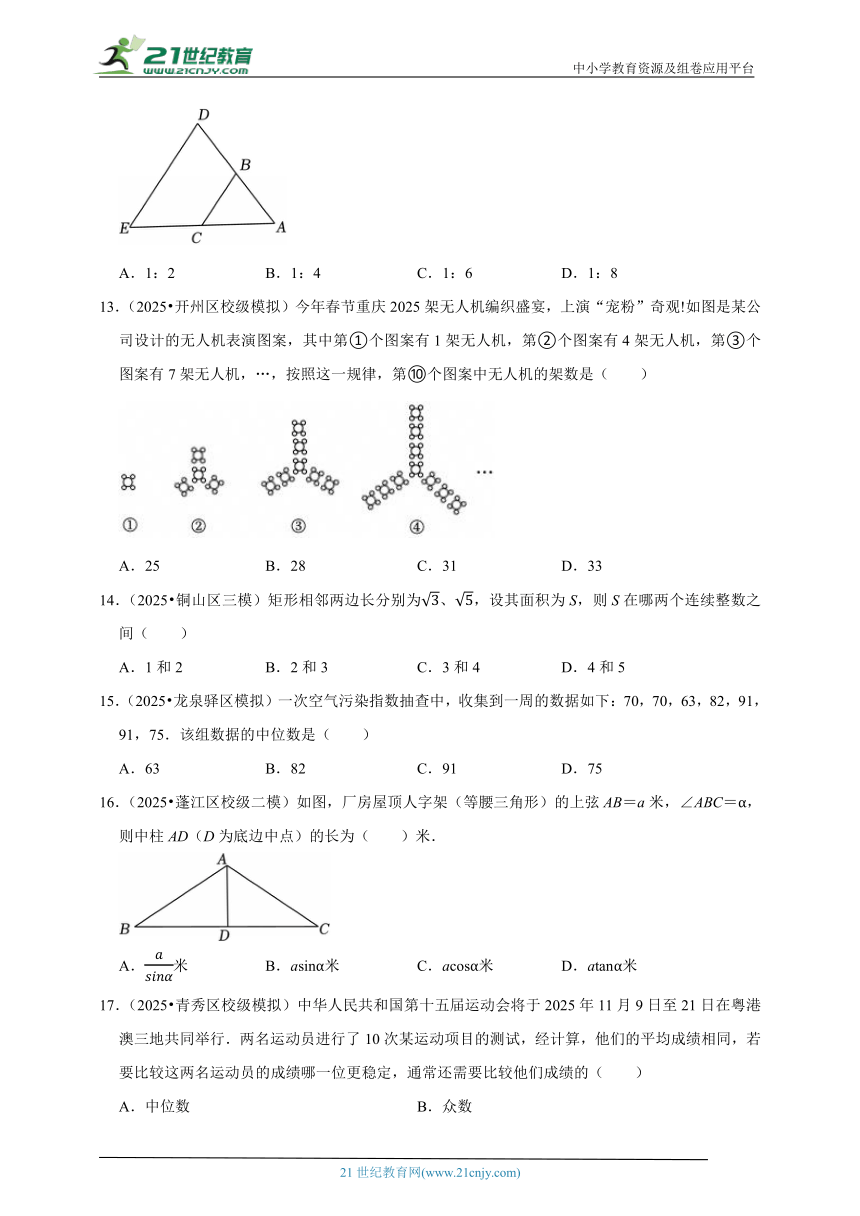
13.(2025 开州区校级模拟)今年春节重庆2025架无人机编织盛宴,上演“宠粉”奇观!如图是某公司设计的无人机表演图案,其中第①个图案有1架无人机,第②个图案有4架无人机,第③个图案有7架无人机,…,按照这一规律,第⑩个图案中无人机的架数是( )
A.25 B.28 C.31 D.33
14.(2025 铜山区三模)矩形相邻两边长分别为、,设其面积为S,则S在哪两个连续整数之间( )
A.1和2 B.2和3 C.3和4 D.4和5
15.(2025 龙泉驿区模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
16.(2025 蓬江区校级二模)如图,厂房屋顶人字架(等腰三角形)的上弦AB=a米,∠ABC=α,则中柱AD(D为底边中点)的长为( )米.
A.米 B.asinα米 C.acosα米 D.atanα米
17.(2025 青秀区校级模拟)中华人民共和国第十五届运动会将于2025年11月9日至21日在粤港澳三地共同举行.两名运动员进行了10次某运动项目的测试,经计算,他们的平均成绩相同,若要比较这两名运动员的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.中位数 B.众数
C.方差 D.以上都不对
18.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
19.(2025 思明区二模)如图,在△ABC中,∠ABC=90°,∠A=50°,将△ABC绕点C顺时针旋转到△A'B'C,当点A,C,B′在一条直线上时,△ABC旋转的度数为( )
A.40° B.50° C.130° D.140°
20.(2025 德州模拟)下面是“过直线l外一点P作直线l的垂线”的尺规作图方法.
(1)任取一点K,使得点K和点P在直线l的两旁; (2)以点P为圆心,PK长为半径作弧,交直线l于点A和点B; (3)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C; (4)作直线PC. 直线PC就是所求作的垂线.
上述方法通过构造直线l上线段AB的垂直平分线,得到直线l的垂线PC.其中判定点C在线段AB的垂直平分线上的依据可以是( )
A.点P与点C关于直线l对称
B.过直线外一点有且仅有一条直线与已知直线垂直
C.线段垂直平分线上的点与这条线段两个端点的距离相等
D.与线段两个端点距离相等的点在这条线段的垂直平分线上
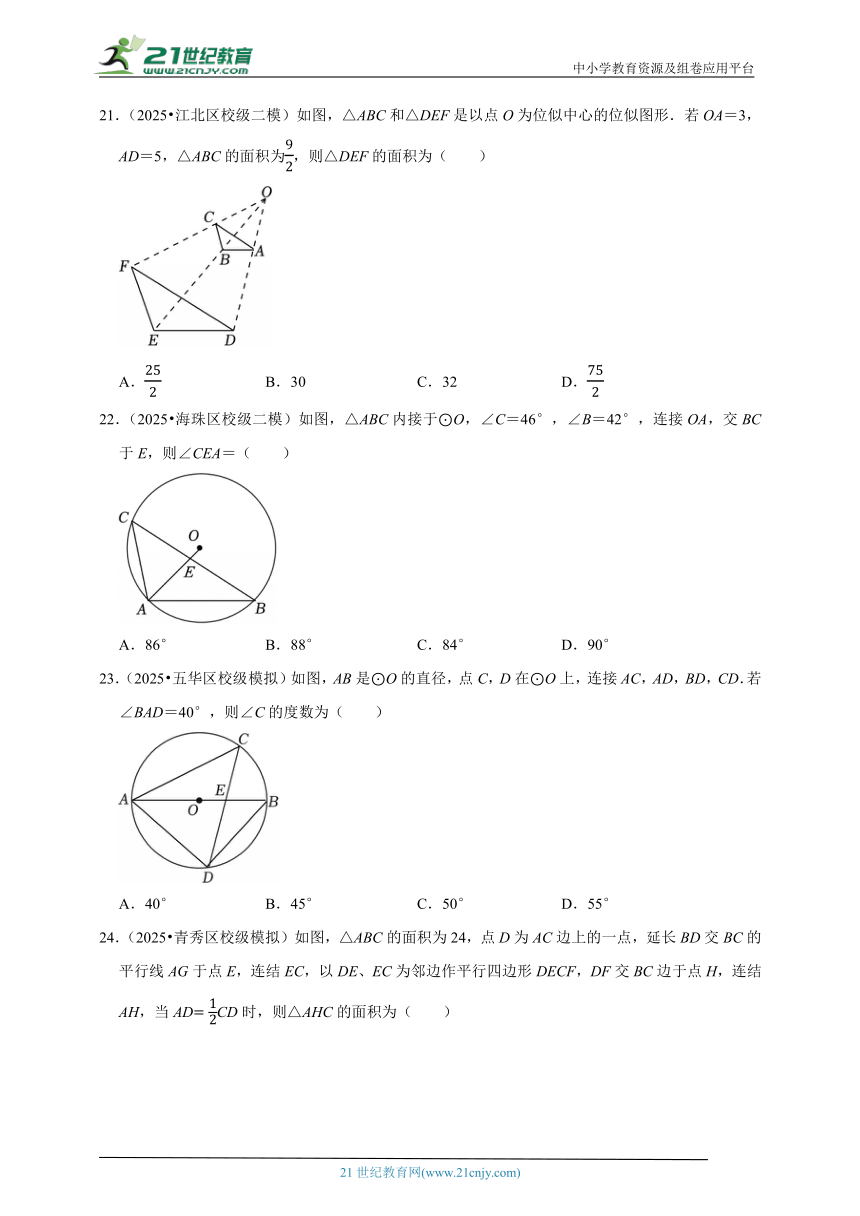
21.(2025 江北区校级二模)如图,△ABC和△DEF是以点O为位似中心的位似图形.若OA=3,AD=5,△ABC的面积为,则△DEF的面积为( )
A. B.30 C.32 D.
22.(2025 海珠区校级二模)如图,△ABC内接于⊙O,∠C=46°,∠B=42°,连接OA,交BC于E,则∠CEA=( )
A.86° B.88° C.84° D.90°
23.(2025 五华区校级模拟)如图,AB是⊙O的直径,点C,D在⊙O上,连接AC,AD,BD,CD.若∠BAD=40°,则∠C的度数为( )
A.40° B.45° C.50° D.55°
24.(2025 青秀区校级模拟)如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当ADCD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
25.(2025 大方县模拟)屏风是中国传统建筑物内部挡风用的一种家具,历史由来已久,一般陈设于室内的显著位置,起到分隔、美化、挡风、协调等作用.图①中的屏风,其中间部分是扇形的一部分,图②是整个屏风的几何示意图,则阴影部分面积与整个屏风面积的比是( )
A. B. C. D.
26.(2025 巢湖市模拟)“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
27.(2025 开封二模)如图,在平面直角坐标系中,已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,点A2025的坐标为( )
A.(1013,1012) B.(5063,1012)
C.(5065,1012) D.(5065,2025)
28.(2025 镇江模拟)如图,点O是正五边形ABCDE的中心,OH⊥CD于点H.则( )
A.OH=OC sin36° B.OH=OC sin35°
C.OH=OC cos36° D.OH=OC cos35°
29.(2025 叶县模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
30.(2025 英德市二模)代数推理是一种数学推理方法,它主要基于代数运算和代数结构的性质来进行逻辑推导和证明.
42+32>2×4×3;
32+32=2×3×3;
22+(﹣3)2>2×2×(﹣3);
(﹣4)2+(﹣4)2=2×(﹣4)×(﹣4);
观察以上各式,用含有字母a,b的式子归纳表示为:a2+b2≥2ab,当a=b时,左右两边取等号.
为了证明上述规律,下列选项做法正确的是( )
A.证明:∵a2+b2﹣2ab=(a﹣b)2≥0,∴a2+b2≥2ab
B.证明:∵a2﹣b2+2ab=(a+b)2≥0,∴a2+b2≥2ab
C.证明:∵a2+b2+2ab=(a+b)2=0,∴a2+b2=2ab
D.证明:∵a2﹣b2+2ab=(a+b)2=0,∴a2+b2=2ab
【抢分秘籍】各地区中考数学真题分类突破:选择题(二)
参考答案与试题解析
一.选择题(共30小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B A D A C C A C D B B
题号 12 13 14 15 16 17 18 19 20 21 22
答案 B B C D B C D D D C A
题号 23 24 25 26 27 28 29 30
答案 C C A D B C B A
一.选择题(共30小题)
1.(2025 开州区模拟)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是( )
A.中 B.考 C.顺 D.利
【解答】解:一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是考,
故选:B.
2.(2025 英德市二模)是一个很奇妙的数,在艺术、建筑中以“黄金分割”体现美感,估计的值( )
A.在0和1之间 B.在1和2之间
C.在2和3之间 D.在3和4之间
【解答】解:,
∵1,
∴1,
∴1,
则估计的值在0和1之间,
故选:A.
3.(2025 太康县一模)计算结果为a8的是( )
A.a2 a4 B.a14﹣a6 C.a4+a4 D.(a4)2
【解答】解:A、a2 a4=a6,a6≠a8,不符合题意;
B、a14与a6不是同类项,不能合并,不符合题意;
C、a4+a4=2a4,2a4≠a8,不符合题意;
D、(a4)2=a8,a8≠a8,符合题意.
故选:D.
4.(2025 临沧模拟)如图,在平行四边形ABCD中,若AB=3,BC=5,E为AD上一点,且BE=BC,CE=CD,则DE的长为( )
A.1.8 B.1.5 C.2.5 D.2
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=3,
∴∠CED=∠BCE,
∵BE=BC=5,CE=CD=3,
∴∠BCE=∠BEC=∠CED=∠D,
∴△BCE∽△CDE,
∴,即,
解得:DE=1.8.
故选:A.
5.(2025 裕华区校级模拟)如图,小明将等式5a﹣2b=3a﹣2b进行变形,最后得到一个错误的结论,则下列说法正确的是( )
A.第一步错误
B.第二步错误
C.第三步错误
D.三步都正确,原等式错误
【解答】解:A.由5a﹣2b=3a﹣2b,得5a﹣2b+2b=3a﹣2b+2b,故选项A说法错误;
B.第二步合并同类项,可得5a=3a,故选项B说法错误;
C.当a=0时,由5a=3a,两边同时除以a错误,故选项C说法正确;
D.第一步和第二步正确,第三步错误,故选项D说法错误.
故选:C.
6.(2025 临沧模拟)如图,矩形ABCD中,CE=2DE,点P在BC边上且恰好存在点P使△ABP和△PCE相似,若AB=3,BC=5,则BP长为( )
A.2 B.3 C.2或3 D.3或4
【解答】解:∵矩形ABCD中,CE=2DE,AB=3,BC=5,
∴AB=CD=3,∠C=∠B=90°,
∴,
设BP=x,则CP=5﹣x,
当△ABP∽△PCE时,,
∴,
解得:x1=3,x2=2,
经检验,x1=3,x2=2是分式方程的解;
当△ABP∽△ECP时,,
∴,
解得:x=3,
经检验,x=3是分式方程的解,
综上,BP长为2或3.
故选:C.
7.(2025 海口二模)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别为AB、AD、AC的中点.若AB=12,则EF的长度为( )
A.3 B.4 C.5 D.6
【解答】解:∵点D是Rt△ABC斜边上的中点,
∴CD是中线,
∴CD,
又∵点E,F分别是AD,AC的中点,
∴EF是三角形ADC的中位线,
∴EF,
故选:A.
8.(2025 思明区二模)数轴上表示实数a,b,c的点分别如图所示,下列选项满足(a﹣b)c<0的是( )
A.
B.
C.
D.
【解答】解:∵(a﹣b)c<0,
ac﹣bc<0,
∴ac<bc,
A.观察数轴可知:a>b,c>0,∴ac>bc,故此选项不符合题意;
B.观察数轴可知:a>b,c>0,∴ac>bc,故此选项不符合题意;
C.观察数轴可知:a>b,c<0,∴ac<bc,故此选项符合题意;
D.观察数轴可知:a<b,c<0,∴ac>bc,故此选项不符合题意;
故选:C.
9.(2025 海珠区校级二模)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.﹣ab<0 B.|b|>2 C.a﹣b<0 D.﹣b>1
【解答】解:观察数轴可知:b<﹣1<0<2<a,|a|>|b|,
∴﹣ab>0,|b|<2,a﹣b>0,﹣b>1,
∴A,B,C选项的结论错误,D选项的结论正确,
故选:D.
10.(2025 盐都区模拟)下列关于|a|表述正确的是( )
A.|a|>0 B.|a|≥0 C.|a|<0 D.|a|≤0
【解答】解:任何实数的绝对值都是非负数,
则|a|≥0,
故选:B.
11.(2025 江阳区校级模拟)设x1,x2是方程x2﹣3x+1=0的两根,则( )
A. B. C.3 D.5
【解答】解:∵x1,x2是方程x2﹣3x+1=0的两根,
∴x1+x2=3,x1 x2=1,
而()2=x1+x2+23+2=5,
且0,0故0,
∴,
故选:B.
12.(2025 沙坪坝区校级三模)如图,若△ABC∽△ADE,且AB:AD=1:2,则△ABC的面积与△ADE的面积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
【解答】解:∵△ABC∽△ADE,
∴()2=()2.
故选:B.
13.(2025 开州区校级模拟)今年春节重庆2025架无人机编织盛宴,上演“宠粉”奇观!如图是某公司设计的无人机表演图案,其中第①个图案有1架无人机,第②个图案有4架无人机,第③个图案有7架无人机,…,按照这一规律,第⑩个图案中无人机的架数是( )
A.25 B.28 C.31 D.33
【解答】解:第①个图案由1架无人机组成,
第②个图案由3×2﹣2=4架无人机组成,
第③个图案由3×3﹣2=7架无人机组成,
第④个图案由3×4﹣2=10架无人机组成,
……,
第n个图案由(3n﹣2)架无人机组成,
∴第⑩个图案需要无人机的数量为:3×10﹣2=28.
故选:B.
14.(2025 铜山区三模)矩形相邻两边长分别为、,设其面积为S,则S在哪两个连续整数之间( )
A.1和2 B.2和3 C.3和4 D.4和5
【解答】解:∵矩形相邻两边长分别为、,
∴S,
∵9<15<16,
∴34,
即S在3和4之间,
故选:C.
15.(2025 龙泉驿区模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
【解答】解:将这组数据重新排序为:63,70,70,75,82,91,91,则其中位数为75,
故选:D.
16.(2025 蓬江区校级二模)如图,厂房屋顶人字架(等腰三角形)的上弦AB=a米,∠ABC=α,则中柱AD(D为底边中点)的长为( )米.
A.米 B.asinα米 C.acosα米 D.atanα米
【解答】解:∵△ABC是等腰三角形,AB=a米,∠ABC=α,
∴AC=AB=a米,BD=CD,
∴AD⊥BC,即∠ADB=∠ADC=90°,
∵∠ABC=α,
∴,
∴AD=asinα米,
故选:B.
17.(2025 青秀区校级模拟)中华人民共和国第十五届运动会将于2025年11月9日至21日在粤港澳三地共同举行.两名运动员进行了10次某运动项目的测试,经计算,他们的平均成绩相同,若要比较这两名运动员的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.中位数 B.众数
C.方差 D.以上都不对
【解答】解:由于方差能反映数据的稳定性,需要比较这两名学生立定跳远成绩的方差.
故选:C.
18.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
【解答】解:如图,AE交BF于点O,连接EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线AE交BC边于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵BF⊥AE,
∴OA=OE,
∵∠FAO=∠BEO,OA=OE,∠AOF=∠EOB,
∴△AFO≌△EBO(ASA),
∴OF=OB,
在Rt△ABO中,AB=5,AOAE=2,
∴OB,
∴BF=2OB=2,
故选:D.
19.(2025 思明区二模)如图,在△ABC中,∠ABC=90°,∠A=50°,将△ABC绕点C顺时针旋转到△A'B'C,当点A,C,B′在一条直线上时,△ABC旋转的度数为( )
A.40° B.50° C.130° D.140°
【解答】解:∵∠ABC=90°,∠A=50°,
∴∠ACB=180°﹣∠ABC﹣∠A=40°.
∵点A,C,B′在一条直线上,
∴∠BCB'=180°﹣∠ACB=140°,
∴△ABC旋转的度数为140°.
故选:D.
20.(2025 德州模拟)下面是“过直线l外一点P作直线l的垂线”的尺规作图方法.
(1)任取一点K,使得点K和点P在直线l的两旁; (2)以点P为圆心,PK长为半径作弧,交直线l于点A和点B; (3)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C; (4)作直线PC. 直线PC就是所求作的垂线.
上述方法通过构造直线l上线段AB的垂直平分线,得到直线l的垂线PC.其中判定点C在线段AB的垂直平分线上的依据可以是( )
A.点P与点C关于直线l对称
B.过直线外一点有且仅有一条直线与已知直线垂直
C.线段垂直平分线上的点与这条线段两个端点的距离相等
D.与线段两个端点距离相等的点在这条线段的垂直平分线上
【解答】解:由题意得,判定点C在线段AB的垂直平分线上的依据可以是与线段两个端点距离相等的点在这条线段的垂直平分线上.
故选:D.
21.(2025 江北区校级二模)如图,△ABC和△DEF是以点O为位似中心的位似图形.若OA=3,AD=5,△ABC的面积为,则△DEF的面积为( )
A. B.30 C.32 D.
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵OA=3,AD=5,
∴OD=8,
∴OA:OD=3:8,
∴S△ABC:S△DEF=9:64,
∵S△ABC,
∴S△DEF=32,
故选:C.
22.(2025 海珠区校级二模)如图,△ABC内接于⊙O,∠C=46°,∠B=42°,连接OA,交BC于E,则∠CEA=( )
A.86° B.88° C.84° D.90°
【解答】解:如图,连接OB,
由圆周角定理得:∠AOB=2∠C=2×46°=92°,
∵OA=OB,
∴∠OAB=∠OBA(180°﹣92°)=44°,
∴∠CEA=∠OAB+∠ABC=44°+42°=86°,
故选:A.
23.(2025 五华区校级模拟)如图,AB是⊙O的直径,点C,D在⊙O上,连接AC,AD,BD,CD.若∠BAD=40°,则∠C的度数为( )
A.40° B.45° C.50° D.55°
【解答】解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=40°,
∴∠B=90°﹣∠BAD=50°,
∴∠B=∠C=50°,
故选:C.
24.(2025 青秀区校级模拟)如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当ADCD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
【解答】解:如图,连接EH,
∵△ABC的面积为24,ADCD,
∴S△BDC=16,
∵AE∥BC,
∴S△ABC=S△BCE=24,S△AHC=S△EHC,
∴S△CDE=8,
∵四边形DECF是平行四边形,
∴DF∥EC,
∴S△EHC=S△DEC=8=S△AHC,
故选C.
25.(2025 大方县模拟)屏风是中国传统建筑物内部挡风用的一种家具,历史由来已久,一般陈设于室内的显著位置,起到分隔、美化、挡风、协调等作用.图①中的屏风,其中间部分是扇形的一部分,图②是整个屏风的几何示意图,则阴影部分面积与整个屏风面积的比是( )
A. B. C. D.
【解答】解:由图可知,∠EOF=∠GOH=90°,EO=1+1=2(cm),GO=1cm,
∴S阴影=S扇形EOF﹣S扇形GOH,
;
整个屏风的面积为:AB AD=12cm2,
∴阴影部分面积与整个屏风面积的比是,
故选:A.
26.(2025 巢湖市模拟)“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
【解答】解:∵大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成,
∴AF=DE,DH=AE,∠AED=∠DEF=90°,
∴AF﹣AE=DE﹣DH,
∴EF=EH,
在直角三角形EFH中,,
由勾股定理得:EF2+EH2=HF2,
∴EF=EH=2,
在直角三角形DEF中,,
由勾股定理得:,
∴AE=AF﹣FE=5﹣2=3,
在直角三角形ADE中,由勾股定理得:,
故选:D.
27.(2025 开封二模)如图,在平面直角坐标系中,已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,点A2025的坐标为( )
A.(1013,1012) B.(5063,1012)
C.(5065,1012) D.(5065,2025)
【解答】解:已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,
可得每两个坐标一个周期,每个周期横坐标+5,纵坐标+1,
即A2n(5n,n+2),A2n+1(5n+3,n),
∴A2025(5×1012+3,1012),
即A2025(5063,1012),
故选:B.
28.(2025 镇江模拟)如图,点O是正五边形ABCDE的中心,OH⊥CD于点H.则( )
A.OH=OC sin36° B.OH=OC sin35°
C.OH=OC cos36° D.OH=OC cos35°
【解答】解:连接OD,
∵点O是正五边形ABCDE的中心,
∴OD=OC,∠COD360°=72°,
∵OH⊥CD于点H,
∴∠OHC=90°,∠COH=∠DOH∠COD72°=36°,
∵cos∠COH=cos36°,
∴OH=OC cos36°,
故选:C.
29.(2025 叶县模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
【解答】解:∵四边形ABCD是矩形,
∴AB=DC=3,∠BCD=90°,OD=OC,
∵∠ACB=30°,
∴∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=DC=3,
又∵DE∥OC,OD∥CE,
∴四边形OCED是菱形,
∴菱形OCED的周长为:3×4=12,
故选:B.
30.(2025 英德市二模)代数推理是一种数学推理方法,它主要基于代数运算和代数结构的性质来进行逻辑推导和证明.
42+32>2×4×3;
32+32=2×3×3;
22+(﹣3)2>2×2×(﹣3);
(﹣4)2+(﹣4)2=2×(﹣4)×(﹣4);
观察以上各式,用含有字母a,b的式子归纳表示为:a2+b2≥2ab,当a=b时,左右两边取等号.
为了证明上述规律,下列选项做法正确的是( )
A.证明:∵a2+b2﹣2ab=(a﹣b)2≥0,∴a2+b2≥2ab
B.证明:∵a2﹣b2+2ab=(a+b)2≥0,∴a2+b2≥2ab
C.证明:∵a2+b2+2ab=(a+b)2=0,∴a2+b2=2ab
D.证明:∵a2﹣b2+2ab=(a+b)2=0,∴a2+b2=2ab
【解答】解:由题意,∵a2+b2﹣2ab=(a﹣b)2≥0,
∴a2+b2≥2ab,故A正确,B、C、D均不正确.
故选:A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【抢分秘籍】各地区中考数学真题分类突破:选择题(二)
1.(2025 开州区模拟)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是( )
A.中 B.考 C.顺 D.利
2.(2025 英德市二模)是一个很奇妙的数,在艺术、建筑中以“黄金分割”体现美感,估计的值( )
A.在0和1之间 B.在1和2之间
C.在2和3之间 D.在3和4之间
3.(2025 太康县一模)计算结果为a8的是( )
A.a2 a4 B.a14﹣a6 C.a4+a4 D.(a4)2
4.(2025 临沧模拟)如图,在平行四边形ABCD中,若AB=3,BC=5,E为AD上一点,且BE=BC,CE=CD,则DE的长为( )
A.1.8 B.1.5 C.2.5 D.2
5.(2025 裕华区校级模拟)如图,小明将等式5a﹣2b=3a﹣2b进行变形,最后得到一个错误的结论,则下列说法正确的是( )
A.第一步错误
B.第二步错误
C.第三步错误
D.三步都正确,原等式错误
6.(2025 临沧模拟)如图,矩形ABCD中,CE=2DE,点P在BC边上且恰好存在点P使△ABP和△PCE相似,若AB=3,BC=5,则BP长为( )
A.2 B.3 C.2或3 D.3或4
7.(2025 海口二模)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别为AB、AD、AC的中点.若AB=12,则EF的长度为( )
A.3 B.4 C.5 D.6
8.(2025 思明区二模)数轴上表示实数a,b,c的点分别如图所示,下列选项满足(a﹣b)c<0的是( )
A.
B.
C.
D.
9.(2025 海珠区校级二模)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.﹣ab<0 B.|b|>2 C.a﹣b<0 D.﹣b>1
10.(2025 盐都区模拟)下列关于|a|表述正确的是( )
A.|a|>0 B.|a|≥0 C.|a|<0 D.|a|≤0
11.(2025 江阳区校级模拟)设x1,x2是方程x2﹣3x+1=0的两根,则( )
A. B. C.3 D.5
12.(2025 沙坪坝区校级三模)如图,若△ABC∽△ADE,且AB:AD=1:2,则△ABC的面积与△ADE的面积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
13.(2025 开州区校级模拟)今年春节重庆2025架无人机编织盛宴,上演“宠粉”奇观!如图是某公司设计的无人机表演图案,其中第①个图案有1架无人机,第②个图案有4架无人机,第③个图案有7架无人机,…,按照这一规律,第⑩个图案中无人机的架数是( )
A.25 B.28 C.31 D.33
14.(2025 铜山区三模)矩形相邻两边长分别为、,设其面积为S,则S在哪两个连续整数之间( )
A.1和2 B.2和3 C.3和4 D.4和5
15.(2025 龙泉驿区模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
16.(2025 蓬江区校级二模)如图,厂房屋顶人字架(等腰三角形)的上弦AB=a米,∠ABC=α,则中柱AD(D为底边中点)的长为( )米.
A.米 B.asinα米 C.acosα米 D.atanα米
17.(2025 青秀区校级模拟)中华人民共和国第十五届运动会将于2025年11月9日至21日在粤港澳三地共同举行.两名运动员进行了10次某运动项目的测试,经计算,他们的平均成绩相同,若要比较这两名运动员的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.中位数 B.众数
C.方差 D.以上都不对
18.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
19.(2025 思明区二模)如图,在△ABC中,∠ABC=90°,∠A=50°,将△ABC绕点C顺时针旋转到△A'B'C,当点A,C,B′在一条直线上时,△ABC旋转的度数为( )
A.40° B.50° C.130° D.140°
20.(2025 德州模拟)下面是“过直线l外一点P作直线l的垂线”的尺规作图方法.
(1)任取一点K,使得点K和点P在直线l的两旁; (2)以点P为圆心,PK长为半径作弧,交直线l于点A和点B; (3)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C; (4)作直线PC. 直线PC就是所求作的垂线.
上述方法通过构造直线l上线段AB的垂直平分线,得到直线l的垂线PC.其中判定点C在线段AB的垂直平分线上的依据可以是( )
A.点P与点C关于直线l对称
B.过直线外一点有且仅有一条直线与已知直线垂直
C.线段垂直平分线上的点与这条线段两个端点的距离相等
D.与线段两个端点距离相等的点在这条线段的垂直平分线上
21.(2025 江北区校级二模)如图,△ABC和△DEF是以点O为位似中心的位似图形.若OA=3,AD=5,△ABC的面积为,则△DEF的面积为( )
A. B.30 C.32 D.
22.(2025 海珠区校级二模)如图,△ABC内接于⊙O,∠C=46°,∠B=42°,连接OA,交BC于E,则∠CEA=( )
A.86° B.88° C.84° D.90°
23.(2025 五华区校级模拟)如图,AB是⊙O的直径,点C,D在⊙O上,连接AC,AD,BD,CD.若∠BAD=40°,则∠C的度数为( )
A.40° B.45° C.50° D.55°
24.(2025 青秀区校级模拟)如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当ADCD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
25.(2025 大方县模拟)屏风是中国传统建筑物内部挡风用的一种家具,历史由来已久,一般陈设于室内的显著位置,起到分隔、美化、挡风、协调等作用.图①中的屏风,其中间部分是扇形的一部分,图②是整个屏风的几何示意图,则阴影部分面积与整个屏风面积的比是( )
A. B. C. D.
26.(2025 巢湖市模拟)“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
27.(2025 开封二模)如图,在平面直角坐标系中,已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,点A2025的坐标为( )
A.(1013,1012) B.(5063,1012)
C.(5065,1012) D.(5065,2025)
28.(2025 镇江模拟)如图,点O是正五边形ABCDE的中心,OH⊥CD于点H.则( )
A.OH=OC sin36° B.OH=OC sin35°
C.OH=OC cos36° D.OH=OC cos35°
29.(2025 叶县模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
30.(2025 英德市二模)代数推理是一种数学推理方法,它主要基于代数运算和代数结构的性质来进行逻辑推导和证明.
42+32>2×4×3;
32+32=2×3×3;
22+(﹣3)2>2×2×(﹣3);
(﹣4)2+(﹣4)2=2×(﹣4)×(﹣4);
观察以上各式,用含有字母a,b的式子归纳表示为:a2+b2≥2ab,当a=b时,左右两边取等号.
为了证明上述规律,下列选项做法正确的是( )
A.证明:∵a2+b2﹣2ab=(a﹣b)2≥0,∴a2+b2≥2ab
B.证明:∵a2﹣b2+2ab=(a+b)2≥0,∴a2+b2≥2ab
C.证明:∵a2+b2+2ab=(a+b)2=0,∴a2+b2=2ab
D.证明:∵a2﹣b2+2ab=(a+b)2=0,∴a2+b2=2ab
【抢分秘籍】各地区中考数学真题分类突破:选择题(二)
参考答案与试题解析
一.选择题(共30小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B A D A C C A C D B B
题号 12 13 14 15 16 17 18 19 20 21 22
答案 B B C D B C D D D C A
题号 23 24 25 26 27 28 29 30
答案 C C A D B C B A
一.选择题(共30小题)
1.(2025 开州区模拟)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是( )
A.中 B.考 C.顺 D.利
【解答】解:一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你中考顺利”,把它折成正方体后,与“你”相对的字是考,
故选:B.
2.(2025 英德市二模)是一个很奇妙的数,在艺术、建筑中以“黄金分割”体现美感,估计的值( )
A.在0和1之间 B.在1和2之间
C.在2和3之间 D.在3和4之间
【解答】解:,
∵1,
∴1,
∴1,
则估计的值在0和1之间,
故选:A.
3.(2025 太康县一模)计算结果为a8的是( )
A.a2 a4 B.a14﹣a6 C.a4+a4 D.(a4)2
【解答】解:A、a2 a4=a6,a6≠a8,不符合题意;
B、a14与a6不是同类项,不能合并,不符合题意;
C、a4+a4=2a4,2a4≠a8,不符合题意;
D、(a4)2=a8,a8≠a8,符合题意.
故选:D.
4.(2025 临沧模拟)如图,在平行四边形ABCD中,若AB=3,BC=5,E为AD上一点,且BE=BC,CE=CD,则DE的长为( )
A.1.8 B.1.5 C.2.5 D.2
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=3,
∴∠CED=∠BCE,
∵BE=BC=5,CE=CD=3,
∴∠BCE=∠BEC=∠CED=∠D,
∴△BCE∽△CDE,
∴,即,
解得:DE=1.8.
故选:A.
5.(2025 裕华区校级模拟)如图,小明将等式5a﹣2b=3a﹣2b进行变形,最后得到一个错误的结论,则下列说法正确的是( )
A.第一步错误
B.第二步错误
C.第三步错误
D.三步都正确,原等式错误
【解答】解:A.由5a﹣2b=3a﹣2b,得5a﹣2b+2b=3a﹣2b+2b,故选项A说法错误;
B.第二步合并同类项,可得5a=3a,故选项B说法错误;
C.当a=0时,由5a=3a,两边同时除以a错误,故选项C说法正确;
D.第一步和第二步正确,第三步错误,故选项D说法错误.
故选:C.
6.(2025 临沧模拟)如图,矩形ABCD中,CE=2DE,点P在BC边上且恰好存在点P使△ABP和△PCE相似,若AB=3,BC=5,则BP长为( )
A.2 B.3 C.2或3 D.3或4
【解答】解:∵矩形ABCD中,CE=2DE,AB=3,BC=5,
∴AB=CD=3,∠C=∠B=90°,
∴,
设BP=x,则CP=5﹣x,
当△ABP∽△PCE时,,
∴,
解得:x1=3,x2=2,
经检验,x1=3,x2=2是分式方程的解;
当△ABP∽△ECP时,,
∴,
解得:x=3,
经检验,x=3是分式方程的解,
综上,BP长为2或3.
故选:C.
7.(2025 海口二模)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别为AB、AD、AC的中点.若AB=12,则EF的长度为( )
A.3 B.4 C.5 D.6
【解答】解:∵点D是Rt△ABC斜边上的中点,
∴CD是中线,
∴CD,
又∵点E,F分别是AD,AC的中点,
∴EF是三角形ADC的中位线,
∴EF,
故选:A.
8.(2025 思明区二模)数轴上表示实数a,b,c的点分别如图所示,下列选项满足(a﹣b)c<0的是( )
A.
B.
C.
D.
【解答】解:∵(a﹣b)c<0,
ac﹣bc<0,
∴ac<bc,
A.观察数轴可知:a>b,c>0,∴ac>bc,故此选项不符合题意;
B.观察数轴可知:a>b,c>0,∴ac>bc,故此选项不符合题意;
C.观察数轴可知:a>b,c<0,∴ac<bc,故此选项符合题意;
D.观察数轴可知:a<b,c<0,∴ac>bc,故此选项不符合题意;
故选:C.
9.(2025 海珠区校级二模)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.﹣ab<0 B.|b|>2 C.a﹣b<0 D.﹣b>1
【解答】解:观察数轴可知:b<﹣1<0<2<a,|a|>|b|,
∴﹣ab>0,|b|<2,a﹣b>0,﹣b>1,
∴A,B,C选项的结论错误,D选项的结论正确,
故选:D.
10.(2025 盐都区模拟)下列关于|a|表述正确的是( )
A.|a|>0 B.|a|≥0 C.|a|<0 D.|a|≤0
【解答】解:任何实数的绝对值都是非负数,
则|a|≥0,
故选:B.
11.(2025 江阳区校级模拟)设x1,x2是方程x2﹣3x+1=0的两根,则( )
A. B. C.3 D.5
【解答】解:∵x1,x2是方程x2﹣3x+1=0的两根,
∴x1+x2=3,x1 x2=1,
而()2=x1+x2+23+2=5,
且0,0故0,
∴,
故选:B.
12.(2025 沙坪坝区校级三模)如图,若△ABC∽△ADE,且AB:AD=1:2,则△ABC的面积与△ADE的面积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
【解答】解:∵△ABC∽△ADE,
∴()2=()2.
故选:B.
13.(2025 开州区校级模拟)今年春节重庆2025架无人机编织盛宴,上演“宠粉”奇观!如图是某公司设计的无人机表演图案,其中第①个图案有1架无人机,第②个图案有4架无人机,第③个图案有7架无人机,…,按照这一规律,第⑩个图案中无人机的架数是( )
A.25 B.28 C.31 D.33
【解答】解:第①个图案由1架无人机组成,
第②个图案由3×2﹣2=4架无人机组成,
第③个图案由3×3﹣2=7架无人机组成,
第④个图案由3×4﹣2=10架无人机组成,
……,
第n个图案由(3n﹣2)架无人机组成,
∴第⑩个图案需要无人机的数量为:3×10﹣2=28.
故选:B.
14.(2025 铜山区三模)矩形相邻两边长分别为、,设其面积为S,则S在哪两个连续整数之间( )
A.1和2 B.2和3 C.3和4 D.4和5
【解答】解:∵矩形相邻两边长分别为、,
∴S,
∵9<15<16,
∴34,
即S在3和4之间,
故选:C.
15.(2025 龙泉驿区模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
【解答】解:将这组数据重新排序为:63,70,70,75,82,91,91,则其中位数为75,
故选:D.
16.(2025 蓬江区校级二模)如图,厂房屋顶人字架(等腰三角形)的上弦AB=a米,∠ABC=α,则中柱AD(D为底边中点)的长为( )米.
A.米 B.asinα米 C.acosα米 D.atanα米
【解答】解:∵△ABC是等腰三角形,AB=a米,∠ABC=α,
∴AC=AB=a米,BD=CD,
∴AD⊥BC,即∠ADB=∠ADC=90°,
∵∠ABC=α,
∴,
∴AD=asinα米,
故选:B.
17.(2025 青秀区校级模拟)中华人民共和国第十五届运动会将于2025年11月9日至21日在粤港澳三地共同举行.两名运动员进行了10次某运动项目的测试,经计算,他们的平均成绩相同,若要比较这两名运动员的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.中位数 B.众数
C.方差 D.以上都不对
【解答】解:由于方差能反映数据的稳定性,需要比较这两名学生立定跳远成绩的方差.
故选:C.
18.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
【解答】解:如图,AE交BF于点O,连接EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线AE交BC边于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵BF⊥AE,
∴OA=OE,
∵∠FAO=∠BEO,OA=OE,∠AOF=∠EOB,
∴△AFO≌△EBO(ASA),
∴OF=OB,
在Rt△ABO中,AB=5,AOAE=2,
∴OB,
∴BF=2OB=2,
故选:D.
19.(2025 思明区二模)如图,在△ABC中,∠ABC=90°,∠A=50°,将△ABC绕点C顺时针旋转到△A'B'C,当点A,C,B′在一条直线上时,△ABC旋转的度数为( )
A.40° B.50° C.130° D.140°
【解答】解:∵∠ABC=90°,∠A=50°,
∴∠ACB=180°﹣∠ABC﹣∠A=40°.
∵点A,C,B′在一条直线上,
∴∠BCB'=180°﹣∠ACB=140°,
∴△ABC旋转的度数为140°.
故选:D.
20.(2025 德州模拟)下面是“过直线l外一点P作直线l的垂线”的尺规作图方法.
(1)任取一点K,使得点K和点P在直线l的两旁; (2)以点P为圆心,PK长为半径作弧,交直线l于点A和点B; (3)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C; (4)作直线PC. 直线PC就是所求作的垂线.
上述方法通过构造直线l上线段AB的垂直平分线,得到直线l的垂线PC.其中判定点C在线段AB的垂直平分线上的依据可以是( )
A.点P与点C关于直线l对称
B.过直线外一点有且仅有一条直线与已知直线垂直
C.线段垂直平分线上的点与这条线段两个端点的距离相等
D.与线段两个端点距离相等的点在这条线段的垂直平分线上
【解答】解:由题意得,判定点C在线段AB的垂直平分线上的依据可以是与线段两个端点距离相等的点在这条线段的垂直平分线上.
故选:D.
21.(2025 江北区校级二模)如图,△ABC和△DEF是以点O为位似中心的位似图形.若OA=3,AD=5,△ABC的面积为,则△DEF的面积为( )
A. B.30 C.32 D.
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵OA=3,AD=5,
∴OD=8,
∴OA:OD=3:8,
∴S△ABC:S△DEF=9:64,
∵S△ABC,
∴S△DEF=32,
故选:C.
22.(2025 海珠区校级二模)如图,△ABC内接于⊙O,∠C=46°,∠B=42°,连接OA,交BC于E,则∠CEA=( )
A.86° B.88° C.84° D.90°
【解答】解:如图,连接OB,
由圆周角定理得:∠AOB=2∠C=2×46°=92°,
∵OA=OB,
∴∠OAB=∠OBA(180°﹣92°)=44°,
∴∠CEA=∠OAB+∠ABC=44°+42°=86°,
故选:A.
23.(2025 五华区校级模拟)如图,AB是⊙O的直径,点C,D在⊙O上,连接AC,AD,BD,CD.若∠BAD=40°,则∠C的度数为( )
A.40° B.45° C.50° D.55°
【解答】解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=40°,
∴∠B=90°﹣∠BAD=50°,
∴∠B=∠C=50°,
故选:C.
24.(2025 青秀区校级模拟)如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当ADCD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
【解答】解:如图,连接EH,
∵△ABC的面积为24,ADCD,
∴S△BDC=16,
∵AE∥BC,
∴S△ABC=S△BCE=24,S△AHC=S△EHC,
∴S△CDE=8,
∵四边形DECF是平行四边形,
∴DF∥EC,
∴S△EHC=S△DEC=8=S△AHC,
故选C.
25.(2025 大方县模拟)屏风是中国传统建筑物内部挡风用的一种家具,历史由来已久,一般陈设于室内的显著位置,起到分隔、美化、挡风、协调等作用.图①中的屏风,其中间部分是扇形的一部分,图②是整个屏风的几何示意图,则阴影部分面积与整个屏风面积的比是( )
A. B. C. D.
【解答】解:由图可知,∠EOF=∠GOH=90°,EO=1+1=2(cm),GO=1cm,
∴S阴影=S扇形EOF﹣S扇形GOH,
;
整个屏风的面积为:AB AD=12cm2,
∴阴影部分面积与整个屏风面积的比是,
故选:A.
26.(2025 巢湖市模拟)“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
【解答】解:∵大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成,
∴AF=DE,DH=AE,∠AED=∠DEF=90°,
∴AF﹣AE=DE﹣DH,
∴EF=EH,
在直角三角形EFH中,,
由勾股定理得:EF2+EH2=HF2,
∴EF=EH=2,
在直角三角形DEF中,,
由勾股定理得:,
∴AE=AF﹣FE=5﹣2=3,
在直角三角形ADE中,由勾股定理得:,
故选:D.
27.(2025 开封二模)如图,在平面直角坐标系中,已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,点A2025的坐标为( )
A.(1013,1012) B.(5063,1012)
C.(5065,1012) D.(5065,2025)
【解答】解:已知A(0,2),A1(3,0),A2(5,3),A3(8,1),A4(10,4),A5(13,2), ,按照此规律,
可得每两个坐标一个周期,每个周期横坐标+5,纵坐标+1,
即A2n(5n,n+2),A2n+1(5n+3,n),
∴A2025(5×1012+3,1012),
即A2025(5063,1012),
故选:B.
28.(2025 镇江模拟)如图,点O是正五边形ABCDE的中心,OH⊥CD于点H.则( )
A.OH=OC sin36° B.OH=OC sin35°
C.OH=OC cos36° D.OH=OC cos35°
【解答】解:连接OD,
∵点O是正五边形ABCDE的中心,
∴OD=OC,∠COD360°=72°,
∵OH⊥CD于点H,
∴∠OHC=90°,∠COH=∠DOH∠COD72°=36°,
∵cos∠COH=cos36°,
∴OH=OC cos36°,
故选:C.
29.(2025 叶县模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
【解答】解:∵四边形ABCD是矩形,
∴AB=DC=3,∠BCD=90°,OD=OC,
∵∠ACB=30°,
∴∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=DC=3,
又∵DE∥OC,OD∥CE,
∴四边形OCED是菱形,
∴菱形OCED的周长为:3×4=12,
故选:B.
30.(2025 英德市二模)代数推理是一种数学推理方法,它主要基于代数运算和代数结构的性质来进行逻辑推导和证明.
42+32>2×4×3;
32+32=2×3×3;
22+(﹣3)2>2×2×(﹣3);
(﹣4)2+(﹣4)2=2×(﹣4)×(﹣4);
观察以上各式,用含有字母a,b的式子归纳表示为:a2+b2≥2ab,当a=b时,左右两边取等号.
为了证明上述规律,下列选项做法正确的是( )
A.证明:∵a2+b2﹣2ab=(a﹣b)2≥0,∴a2+b2≥2ab
B.证明:∵a2﹣b2+2ab=(a+b)2≥0,∴a2+b2≥2ab
C.证明:∵a2+b2+2ab=(a+b)2=0,∴a2+b2=2ab
D.证明:∵a2﹣b2+2ab=(a+b)2=0,∴a2+b2=2ab
【解答】解:由题意,∵a2+b2﹣2ab=(a﹣b)2≥0,
∴a2+b2≥2ab,故A正确,B、C、D均不正确.
故选:A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
