【抢分秘籍】各地区中考数学真题分类突破:解答题(含答案)
文档属性
| 名称 | 【抢分秘籍】各地区中考数学真题分类突破:解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:57:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【抢分秘籍】各地区中考数学真题分类突破:解答题
1.(2025 鼓楼区校级模拟)有三个购房者在售楼部进行抽签选房,在一个不透明的盒子中,共有标号为1至3的3个小球,除颜色外其他完全相同.买房者按照到达的先后顺序进行抽签,不放回地从盒中抽球,将球的编号作为最终选房的顺序(如抽到2号球的人第2个选房)
(1)第一个抽签的人第1个选房的概率为 .
(2)有买房者质疑这种选房规则,认为先抽签的人第一个选房的概率更大.请判断这种说法是正确?用概率知识并结合树状图说明理由.
2.(2025 思明区二模)如图,点B,C,D,E在一条直线上,∠B=∠FCE,AB=FC,BC=DE.求证:AD∥FE.
3.(2025 梁溪区校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
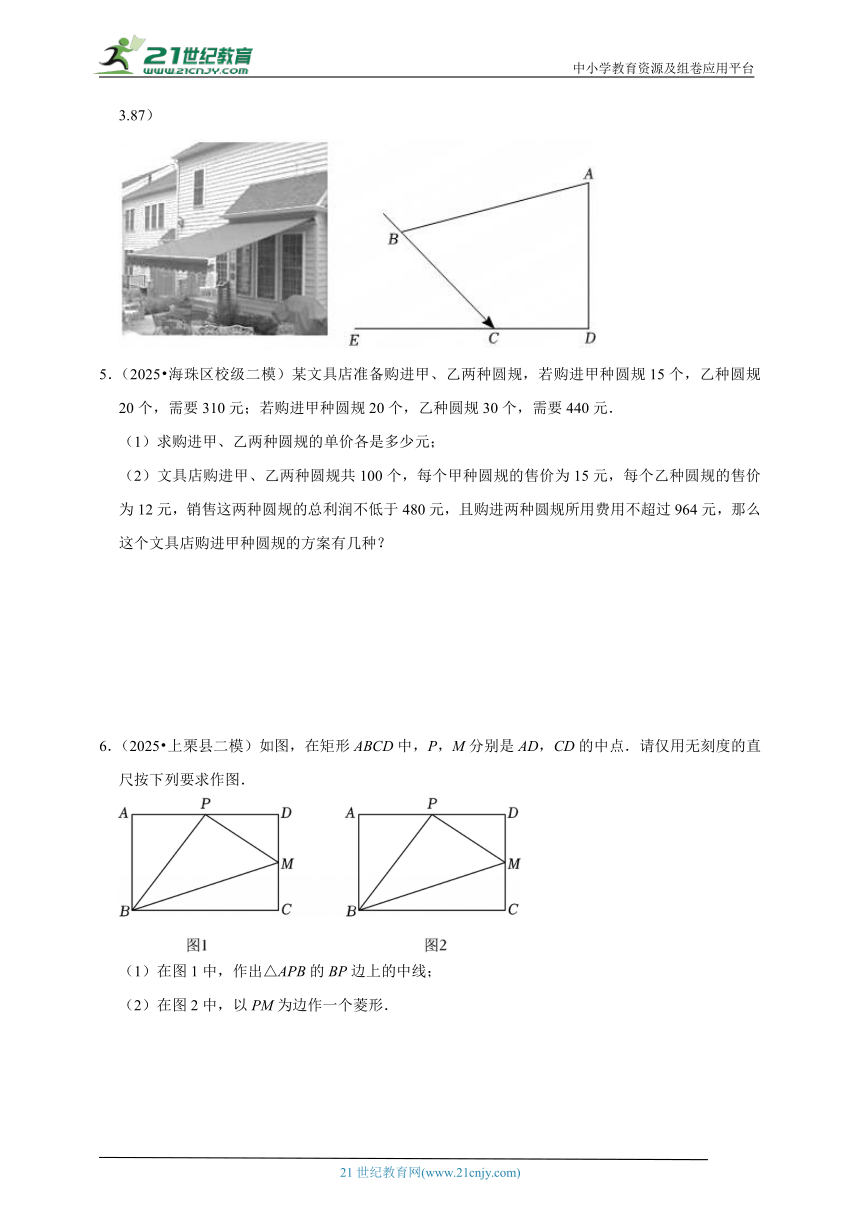
4.(2025 锦江区校级模拟)随着人民生活水平的日益提高,许多农村的房屋普遍进行了改造,小明家改造时在门前安装了一个遮阳棚,如图,在侧面示意图中,遮阳篷AB长为4米,与墙面AD的夹角∠BAD=75.5°,靠墙端A离地高AD为3米,当太阳光线BC与地面DE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据:sin75.5°≈0.97,cos75.5°≈0.25,tan75.5°≈3.87)
5.(2025 海珠区校级二模)某文具店准备购进甲、乙两种圆规,若购进甲种圆规15个,乙种圆规20个,需要310元;若购进甲种圆规20个,乙种圆规30个,需要440元.
(1)求购进甲、乙两种圆规的单价各是多少元;
(2)文具店购进甲、乙两种圆规共100个,每个甲种圆规的售价为15元,每个乙种圆规的售价为12元,销售这两种圆规的总利润不低于480元,且购进两种圆规所用费用不超过964元,那么这个文具店购进甲种圆规的方案有几种?
6.(2025 上栗县二模)如图,在矩形ABCD中,P,M分别是AD,CD的中点.请仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△APB的BP边上的中线;
(2)在图2中,以PM为边作一个菱形.
7.(2025 惠州二模)某中学举行了迎国庆中华传统文化节活动.本次文化节共有五项活动:A.书法比赛;B.国画竞技;C.诗歌朗诵;D.汉字大赛;E.古典乐器演奏.活动结束后,某数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据调查结果绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)此次随机抽取共 名学生,m= ,并补全条形统计图;
(2)若该校共有3000名学生,请估计最喜欢D活动的学生人数;
(3)该校准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用画树状图法或列表法求选出的两名选手正好是一男一女的概率.
8.(2025 开封二模)某校兴趣小组在广场进行无人机飞行表演,一架无人机的飞行线路是一条抛物线,其飞行高度y(m)与水平距离x(m)满足二次函数关系.
(1)用配方法求出抛物线的顶点坐标,并说明其顶点坐标的实际意义.
(2)若距飞行起始点正前方10m处有一个16m高的大型广告牌,请通过计算判断该无人机在飞行过程中,是否存在与广告牌发生碰撞的风险.
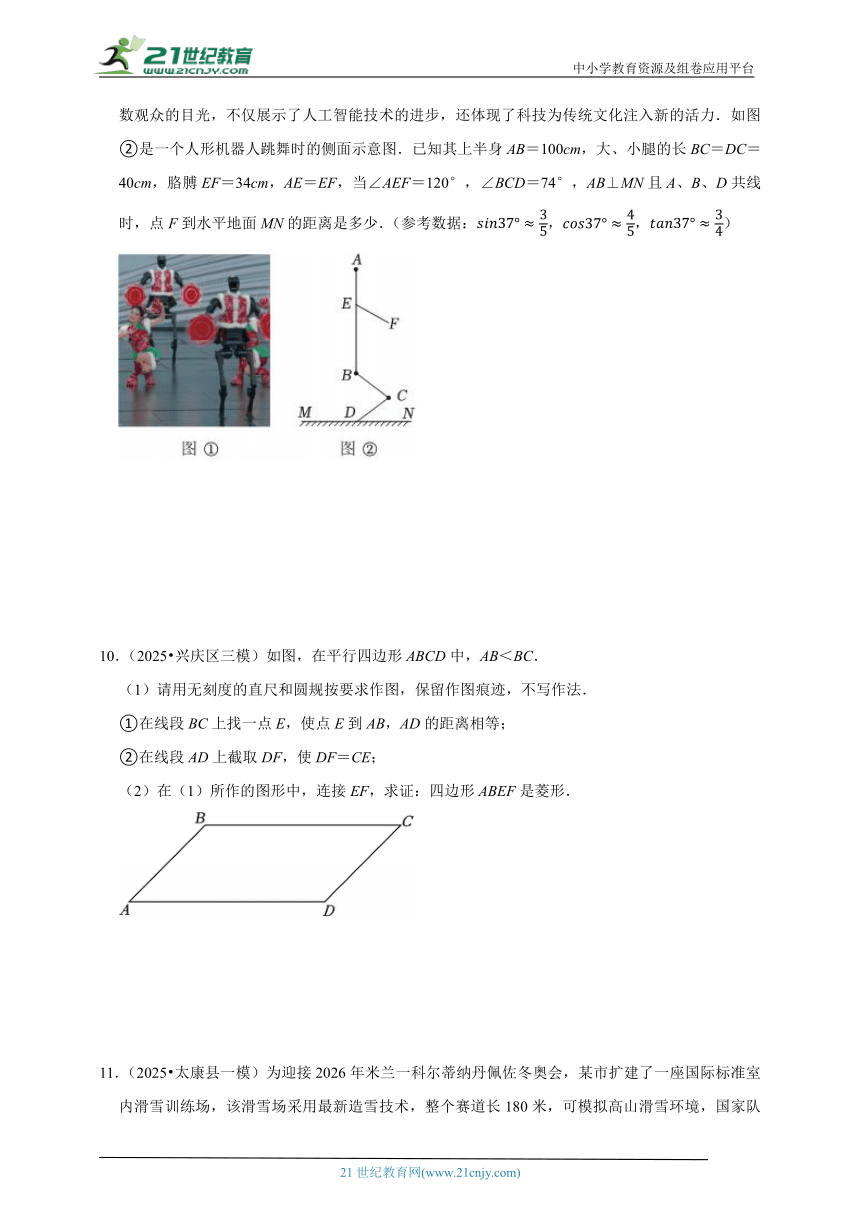
9.(2025 开封二模)如图①是2025年春晚一群活泼又喜感的人形机器人扭秧歌,该节目吸引了无数观众的目光,不仅展示了人工智能技术的进步,还体现了科技为传统文化注入新的活力.如图②是一个人形机器人跳舞时的侧面示意图.已知其上半身AB=100cm,大、小腿的长BC=DC=40cm,胳膊EF=34cm,AE=EF,当∠AEF=120°,∠BCD=74°,AB⊥MN且A、B、D共线时,点F到水平地面MN的距离是多少.(参考数据:,,)
10.(2025 兴庆区三模)如图,在平行四边形ABCD中,AB<BC.
(1)请用无刻度的直尺和圆规按要求作图,保留作图痕迹,不写作法.
①在线段BC上找一点E,使点E到AB,AD的距离相等;
②在线段AD上截取DF,使DF=CE;
(2)在(1)所作的图形中,连接EF,求证:四边形ABEF是菱形.
11.(2025 太康县一模)为迎接2026年米兰一科尔蒂纳丹佩佐冬奥会,某市扩建了一座国际标准室内滑雪训练场,该滑雪场采用最新造雪技术,整个赛道长180米,可模拟高山滑雪环境,国家队运动员小明为备战冬奥会,在此进行技术训练.如图,他从赛道顶端A处开始下滑,滑行3秒后,教练操控一台无人机从A处沿赛道方向保持安全高度跟拍训练过程(安全高度可忽略不计).训练中心记录了小明离A处的滑行距离y(单位:m)以及无人机离A处的距离s(单位:m)随滑行时间x(单位:s)的变化数据如下:
滑行时间x/s 0 1 2 3 4 5 6
滑行距离y/m 0 4 10 18 28 40 54
无人机离A处的距离s/m 0 0 0 0 12 24 36
经探究发现,y与x之间成二次函数关系,s与x(x≥3)之间成一次函数关系.
(1)直接写出y关于x的函数解析式和x关于x(x≥3)的函数解析式;(不要求写出自变量的取值范围)
(2)小明滑完整个训练赛道需要耗时多久?
(3)分析在小明到达终点前,无人机能否追上小明,若能,求出相遇时间;若不能,求出无人机与小明的最小距离.
12.(2025 上栗县二模)某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整
收集数据:七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70.
整理数据:七年级20名学生测试成绩频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的成绩范围为50≤x<60):
八年级20名学生测试成绩频数分布表:
成绩 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数 0 4 5 7 4
分析数据:两组样本数据的平均数、中位数、众数方差如表所示:
年级 平均数 中位数 众数 方差
七年级 76.9 a b 119.89
八年级 79.2 81 74 100.4
(1)补全七年级20名学生测试成绩频数分布直方图.
(2)请直接写出a,b的值.
(3)请根据抽样调查数据,估计全校七年级垃圾分类知识测试成绩在80分及以上的大约有多少人.
(4)通过以上分析,你认为哪个年级学生对垃圾分类知识掌握得更好?请说明推断的理由(两条即可).
13.(2025 天府新区模拟)如图,在△ABC中,∠BAC=90°,D为AB上一点,以AD为直径作⊙O,交BC于E,F两点,点E为BC中点,连接AE,DE.
(1)求证:AE AC=AB DE;
(2)若,,求⊙O的直径和EF的长.
14.(2025 上栗县二模)如图,在平面直角坐标系中,点B坐标为(0,1),点A(m,3)在函数y(k>0,x>0)的图象上,将线段AB向右下方平移,得到线段CD,此时点C落在函数y的图象上,点D落在x轴正半轴上,且点D坐标为(1,0).
(1)求k的值;
(2)求直线AC所对应的函数表达式.
15.(2025 铁岭模拟)某工厂加工某种型号芯片,成本价为20元/个.根据市场调查发现,销售量y(个)是关于销售单价提高x(元)的一次函数(x≥0,且x为整数),其关系如下表:
提高x元 单价(元/个) 销售量(个)
0 25 500
1 26 480
2 27 460
… … …
x 25+x
(1)求销售量y与x之间的函数关系式;
(2)由于工厂生产规模受限,每日加工该种芯片不能少于340个且不能超过620个,每日加工的芯片全部售出,该芯片销售单价定为多少元时,才能获得最大销售利润?最大销售利润是多少?
16.(2025 开封二模)如图,△ABC的顶点为网格线的交点,反比例函数的图象过格点A,B.将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′.
(1)求过点C′的反比例函数解析式,并画出其图象(x<0).
(2)在过点C′的反比例函数图象上任取一点D,过点D向y轴作垂线,交的图象于点E,连接DO,EO,△ODE的面积会发生变化吗?若不变化,求出△ODE的面积;若变化,请说明理由.
17.(2025 扬州一模)如图①,在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)如图②,连接CE,若∠FCB=90°,CE=5,求AB的长.
18.(2025 鼓楼区二模)如图①所示,沪宁高速公路可近似看作一条直线.一辆货车以80km/h的速度从南京出发匀速驶往上海;同时,一列轿车以120km/h的速度从苏州出发匀速驶往上海,停留0.5h后,按照原速度继续开往南京,最终两车同时到达目的地.设货车行驶的时间为t h,货车与南京的距离y1km,轿车与南京的距离y2km.
(1)在图2中,分别画出和补全y1、y2关于t的函数图象;
(2)分别求苏州到上海的距离,南京到上海的距离;
(3)若镇江距离南京90km,直接写出货车和轿车经过镇江的时间间隔.
19.(2025 上栗县二模)秋水广场音乐喷泉是江西省南昌市红谷滩新区赣江边上的一道亮丽风景线,它不仅是城市景观的重要组成部分,也成为了市民休闲娱乐的好去处.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)用含a,b的代数式表示抛物线y=ax2+bx的顶点坐标为(, );
(2)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a,b的值;
(3)若k=3,,则喷出的抛物线水线能否达到岸边?
20.(2025 深圳校级二模)新课标中,数学课程要培养的学生核心素养是“用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界”,这集中体现了数学课程的育人价值,也说明数学和实际生活密不可分.数学老师给小明小组布置了一项数学与实际的作业,让他们到菜市场进行调研,并利用所学的数学知识对销售提出合理化建议.小明小组经调研发现,某店铺蔬菜的售卖情况大致遵循以下规律.
规律一 当每千克蔬菜的售价为8元时,每天能销售80千克.
规律二 当每千克蔬菜的售价每降低0.5元,每天的销售量就会增加10千克.
经小组讨论,发现里面可能存在函数关系,考虑用已学的函数知识帮助店家解决问题.
【建立模型】
(1)设每天销售这种蔬菜的销售额为y元,每千克蔬菜降价x元,求y与x的函数关系式;
【设计方案】
(2)当每千克蔬菜降价多少元时,该店铺每天销售这种蔬菜的销售额最多?最多为多少元?
【实际需求】
(3)若该店铺老板希望每天销售这种蔬菜的销售额不低于540元,求这个蔬菜应参考的售价范围.
21.(2025 琼山区校级一模)在平面直角坐标系中,已知抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C.
(1)如图,若抛物线经过A(1,6),B(﹣2,3)两点,
①求抛物线的解析式;
②设抛物线顶点为D,求△ACD的面积;
③点P是抛物线对称轴上的动点,则PA+PC的最小值为 ;
(2)若抛物线经过E(2a,3),F(x1,y1),G(x2,y2)三点,对于x1=3a,3≤x2≤4,都有y1<y2,求a的取值范围.
22.(2025 张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
23.(2025 镇江模拟)如图,在平面直角坐标系中,直线yx+b经过点A(﹣6,0),与y轴交于点B,与反比例函数y(x>0)交于点C,连接OC,且S△AOB=2S△BOC.
(1)求b,k的值;
(2)若点D为反比例函数y(x>0)图象上一点,连接CD,使得CD⊥OC,求点D的坐标.
24.(2025 厦门模拟)如图1,AB为半圆O的直径,AB=4,C为半圆上的动点,连接OC,点A关于OC的对称点为点D,连接BD.(0°<∠AOC<45°)
(1)若∠AOC=40°,连接AC,AD,求∠CAD的度数;
(2)如图2,若点E在半圆O上,BE的长度为π,连接DE,F为DE中点,连接OF交BD于点M,Q为OE上一点,OQ=1.2.
①当∠AOC=30°时,判断点Q与直线BD的位置关系,并说明理由;
②如图3,连接QM,在点C运动过程中,当BQ=QM时,记α=45°﹣∠AOC,求tanα的值.
25.(2025 湖州一模)纵观古今,解码测量背后的数学智慧.
(1)【古】《周髀算经》中记载了“偃矩以望高”的方法.意思是把“矩(曲尺)”仰立放,可测物体的高度.如图,点B,D,E在同一水平线上,∠ABE=∠CDE=90°,AE与CD交于点F.测得DF=0.35米,DE=0.55米,BE=22米,求树AB的高度.
(2)【今】某综合实践活动小组,尝试通过利用无人机(无人机限高120米)测算某山体的海拔高度,设计了如下两种方案.请选择其中一种可行的测算方案,计算该山体的海拔高度(AB的长).(精确到1米)
测量示意图 方案说明
方案一
无人机位于海拔高度为60米的C处,测得与山顶A处的仰角α为45°,与山脚D处的俯角β为65°.(参考数据:sin65°≈0.90,cos65°≈0.42,tan65°≈2.14)
方案二
当无人机位于海拔高度为60米的C处时,测得与山顶A处的仰角γ为45°;当无人机垂直上升到海拔高度为113米的G处时,测得与山顶处A的仰角θ为25°.(参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47)
26.(2025 上蔡县三模)如图,正方形ABCD的两个顶点A(2,m),C(4,n)都在反比例函数y(x>0)的图象上.
(1)求这个反比例函数的表达式.
(2)反比例函数y(x>0)的图象经过点B,直线x=t(t>0)分别与反比例函数y(x>0),y(x>0)的图象交于点M,N.若1<t<6,求MN的长的取值范围.
27.(2025 雁塔区校级模拟)如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴分别相交于A,B两点,与y轴交于点C,直线y=﹣x+3经过B、C两点.
(1)求抛物线的表达式;
(2)抛物线的顶点为M,点N是y轴上一点,点Q是平面内一点,是否存在以B、M、N、Q为顶点的四边形是以BM为边的矩形?若存在,请求出点N、Q的坐标;若不存在,请说明理由.
28.(2025 思明区校级二模)研究发现人的身体每天消耗的热量主要由碳水化合物和脂肪(不考虑蛋白质及其他有机物)提供,碳水化合物和脂肪分解时所消耗的氧气、生成的二氧化碳、释放的热量三个方面的相关数据如表:
分解的营养物质 氧气消耗量/克 二氧化碳生成量/克 释放热量/千焦
1克碳水化合物 1 1.5 15
1克脂肪 3 3 45
请解答下列问题:
(1)研究人员测出小祺在某次运动中平均每分钟消耗氧气2.5克,产生二氧化碳3克,求小祺的身体平均每分钟分解碳水化合物与脂肪各多少克.
(2)已知小祺骑脚踏车每分钟消耗热量20千焦,快走每分钟消耗热量27千焦,小祺某天骑脚踏车和快走共1小时,若要消耗完40克碳水化合物与20克脂肪分解后释放的热量,小祺至少需要分配多少分钟进行快走?(精确到1分钟)
29.(2025 香坊区校级三模)在平面直角坐标系中,O为坐标原点,直线AB交x轴负半轴于点A,交y轴正半轴于点B,,AB=20.
(1)如图1,求直线AB的解析式;
(2)如图2,P为x轴正半轴上一点,C为AB的中点,连接CP,设△ACP的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,直线y=kx﹣12k交x轴、y轴于点D、E,交直线AB于点F,,G为y轴负半轴上一点,连接CG交x轴于点H,,过点P作PI⊥x轴交DE于点I,L为PI上一点,连接EL,J为EL上一点,连接JG,∠DIP+∠EJG=180°,且∠FAD﹣∠FDA=2∠OED﹣∠BFE,EJ:I=5;,M为x轴负半轴上一点,连接EM、LM、LN,若N为EM的中点,∠LEN+∠MLN=∠AFD,求直线LM的解析式.
30.(2025 雁塔区校级模拟)【问题提出】
如图①,在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,点P,Q分别是BC,AC上的动点,则EP+PQ的最小值是 ;
【问题解决】
如图②,某大型工厂生产区域内,有一个矩形场地ABCD,其中点D为原材料入口,修建在DC段的点G为成品出口.在生产区域内,有两处重要的生产加工点E和F,分别位于场地的DA,DB段,并且DE=DF.为了实现从生产加工点到成品出口的高效运输(即成品从生产加工点经质检区域输送到出口的过程更为高效),工厂规划修建一个调度中心P与一处位于BC段的半圆形自动化质检区域(圆心为O).该调度中心需同时满足以下两个条件:①使P到生产加工点E,F的距离相等,即PE=PF;②使运输线路PM+NG的长度最短(其中M,N为半圆质检区域O上的任意两点).已知AD=300米,AB=400米,CG=100米,质检区域半径r=20米.请问是否存在符合要求的调度中心点P,若存在,求出PM+NG的最小值和此时OC的距离;若不存在,请说明理由.
【抢分秘籍】各地区中考数学真题分类突破:解答题
参考答案与试题解析
一.解答题(共30小题)
1.(2025 鼓楼区校级模拟)有三个购房者在售楼部进行抽签选房,在一个不透明的盒子中,共有标号为1至3的3个小球,除颜色外其他完全相同.买房者按照到达的先后顺序进行抽签,不放回地从盒中抽球,将球的编号作为最终选房的顺序(如抽到2号球的人第2个选房)
(1)第一个抽签的人第1个选房的概率为 .
(2)有买房者质疑这种选房规则,认为先抽签的人第一个选房的概率更大.请判断这种说法是正确?用概率知识并结合树状图说明理由.
【解答】解:(1)第一个抽签的人可能抽到1或2或3,共3种等可能的情况,
∴第一个抽签的人第1个选房的概率为,
故答案为:;
(2)这种说法不正确,理由如下:
根据题意画出树状图如下:
一共有6种等可能的情况,其中第一个人第一个选房的有2种,第二个人第一个选房的有2种,第三个人第一个选房的有2种,
∴三个抽签的人第一个选房的概率都是.
2.(2025 思明区二模)如图,点B,C,D,E在一条直线上,∠B=∠FCE,AB=FC,BC=DE.求证:AD∥FE.
【解答】证明:∵BC=DE,
∴BC+CD=DE+CD,
∴BD=CE,
在△ABC和△FCE中,
,
∴△ABC≌△FCE(SAS),
∴∠ADB=∠E,
∴AD∥FE.
3.(2025 梁溪区校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
∴∠ABC﹣∠EBC=∠ECB﹣∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得
180﹣2x=360﹣60﹣2(90﹣x),
x=15,
180﹣2×15=150,
∴∠AED为150度.
4.(2025 锦江区校级模拟)随着人民生活水平的日益提高,许多农村的房屋普遍进行了改造,小明家改造时在门前安装了一个遮阳棚,如图,在侧面示意图中,遮阳篷AB长为4米,与墙面AD的夹角∠BAD=75.5°,靠墙端A离地高AD为3米,当太阳光线BC与地面DE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据:sin75.5°≈0.97,cos75.5°≈0.25,tan75.5°≈3.87)
【解答】解:如图,过B作BT⊥AD于点T,BK⊥DE于点K,
在Rt△ABT中,
sin∠BAT,cos∠BAT,
∴BT=AB sin∠BAT=4×sin75.5°≈3.9(米),AT=AB cos∠BAT=4×cos75.5°≈1.0(米),
∵∠BTD=∠D=∠CKB=90°,
∴四边形BTDK是矩形,
∴DK=BT=3.9米,BK=DT=AD﹣AT=3﹣1=2(米),
在Rt△BKC中,∠BCK=45°,
∴CK=BK=2米,
∴CD=DK﹣CK=3.9﹣2=1.9(米),
答:阴影CD的长约为1.9米.
5.(2025 海珠区校级二模)某文具店准备购进甲、乙两种圆规,若购进甲种圆规15个,乙种圆规20个,需要310元;若购进甲种圆规20个,乙种圆规30个,需要440元.
(1)求购进甲、乙两种圆规的单价各是多少元;
(2)文具店购进甲、乙两种圆规共100个,每个甲种圆规的售价为15元,每个乙种圆规的售价为12元,销售这两种圆规的总利润不低于480元,且购进两种圆规所用费用不超过964元,那么这个文具店购进甲种圆规的方案有几种?
【解答】解:(1)设甲种圆规的单价是x元,乙种圆规的单价是y元,
根据题意得:,
解得:.
答:甲种圆规的单价是10元,乙种圆规的单价是8元;
(2)设购进m个甲种圆规,则购进(100﹣m)个乙种圆规,
根据题意得:,
解得:80≤m≤82,
∵m为正整数,
∴m可以为80,81,82,
∴这个文具店购进甲种圆规的方案有3种.
答:这个文具店购进甲种圆规的方案有3种.
6.(2025 上栗县二模)如图,在矩形ABCD中,P,M分别是AD,CD的中点.请仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△APB的BP边上的中线;
(2)在图2中,以PM为边作一个菱形.
【解答】解:(1)如图1,AE即为所作;
(2)如图2,四边形PEFM即为所作.
7.(2025 惠州二模)某中学举行了迎国庆中华传统文化节活动.本次文化节共有五项活动:A.书法比赛;B.国画竞技;C.诗歌朗诵;D.汉字大赛;E.古典乐器演奏.活动结束后,某数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据调查结果绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)此次随机抽取共 100 名学生,m= 10 ,并补全条形统计图;
(2)若该校共有3000名学生,请估计最喜欢D活动的学生人数;
(3)该校准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用画树状图法或列表法求选出的两名选手正好是一男一女的概率.
【解答】解:(1)调查的总人数为25÷25%=100(人),
所以m%10%,即m=10,
B选项的人数为100﹣25﹣30﹣20﹣10=15(人),
补全条形统计图为:
故答案为:100,10;
(2)3000600(人),
答:估计最喜欢D活动的学生人数为600人;
(3)画树状图为:
共有20种等可能的结果数,其中选出的两名选手正好是一男一女的结果数为12,
所以选出的两名选手正好是一男一女的概率为.
8.(2025 开封二模)某校兴趣小组在广场进行无人机飞行表演,一架无人机的飞行线路是一条抛物线,其飞行高度y(m)与水平距离x(m)满足二次函数关系.
(1)用配方法求出抛物线的顶点坐标,并说明其顶点坐标的实际意义.
(2)若距飞行起始点正前方10m处有一个16m高的大型广告牌,请通过计算判断该无人机在飞行过程中,是否存在与广告牌发生碰撞的风险.
【解答】解:(1)将解析式配方可得:
;
顶点坐标为(8,18),表示当飞行的水平距离为8m时,飞行达到最大高度为18m.
(2)当x=10m时,,
答:不存在碰撞的风险.
9.(2025 开封二模)如图①是2025年春晚一群活泼又喜感的人形机器人扭秧歌,该节目吸引了无数观众的目光,不仅展示了人工智能技术的进步,还体现了科技为传统文化注入新的活力.如图②是一个人形机器人跳舞时的侧面示意图.已知其上半身AB=100cm,大、小腿的长BC=DC=40cm,胳膊EF=34cm,AE=EF,当∠AEF=120°,∠BCD=74°,AB⊥MN且A、B、D共线时,点F到水平地面MN的距离是多少.(参考数据:,,)
【解答】解:连接BD,过点F分别作FP⊥AB,FG⊥MN,垂足分别为点P、G,过点C作CQ⊥BD于点Q.
则四边形DGFP为矩形,
∵∠AEF=120°,
∴∠FEP=60°,∠EFP=30°,
∴EF=34cm,
∴EP17(cm),
∵AB=100cm,AE=34cm,
∴PB=AB﹣AE﹣EP=100﹣34﹣17=49(cm),
∵BC=DC=40cm,CQ⊥BD,∠BCD=74°,
∴∠BCQ=∠DCQ=37°,BD=2BQ,
∵,
∴BQ=24cm,BD=2BQ=48cm,
∴FG=PD,
∴FG=PD=PB+BD=49+48=97(cm),
答:点F到水平地面的距离FG为97cm.
10.(2025 兴庆区三模)如图,在平行四边形ABCD中,AB<BC.
(1)请用无刻度的直尺和圆规按要求作图,保留作图痕迹,不写作法.
①在线段BC上找一点E,使点E到AB,AD的距离相等;
②在线段AD上截取DF,使DF=CE;
(2)在(1)所作的图形中,连接EF,求证:四边形ABEF是菱形.
【解答】(1)解:图形如图所示:
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵DF=CE,
∴BE=AF,
∴四边形ABEF是平行四边形,
∵点E到AB,AD的距离相等,
∴AE平分∠BAD,
∴∠BAE=∠EAD,
∵AD∥BC,
∴∠BEA=∠EAD,
∴∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是菱形.
11.(2025 太康县一模)为迎接2026年米兰一科尔蒂纳丹佩佐冬奥会,某市扩建了一座国际标准室内滑雪训练场,该滑雪场采用最新造雪技术,整个赛道长180米,可模拟高山滑雪环境,国家队运动员小明为备战冬奥会,在此进行技术训练.如图,他从赛道顶端A处开始下滑,滑行3秒后,教练操控一台无人机从A处沿赛道方向保持安全高度跟拍训练过程(安全高度可忽略不计).训练中心记录了小明离A处的滑行距离y(单位:m)以及无人机离A处的距离s(单位:m)随滑行时间x(单位:s)的变化数据如下:
滑行时间x/s 0 1 2 3 4 5 6
滑行距离y/m 0 4 10 18 28 40 54
无人机离A处的距离s/m 0 0 0 0 12 24 36
经探究发现,y与x之间成二次函数关系,s与x(x≥3)之间成一次函数关系.
(1)直接写出y关于x的函数解析式和x关于x(x≥3)的函数解析式;(不要求写出自变量的取值范围)
(2)小明滑完整个训练赛道需要耗时多久?
(3)分析在小明到达终点前,无人机能否追上小明,若能,求出相遇时间;若不能,求出无人机与小明的最小距离.
【解答】解:(1)设y=ax2+bx+c,由题意可得:
,
解得,
∴y=x2+3x;
设s=kx+n,由题意可得:
,
解得,
∴s=12x﹣36(x≥3),
∴y关于x的函数解析式为y=x2+3x,s关于x的函数解析式为s=12x﹣36(x≥3);
(2)在y=x2+3x中,令y=180得:
180=x2+3x,
解得x=12或x=﹣15(舍去),
∴小明滑完整个赛道需要耗时12s;
(3)联立得x2+3x=12x﹣36,
整理得x2﹣9x+36=0,
∵Δ=b2﹣4ac=(﹣9)2﹣4×36=﹣63<0,
∴无人机不能追上小明,
由题意得x2+3x﹣(12x﹣36)=(x﹣4.5)2+15.75,
∵(x﹣4.5)2≥0,
∴无人机与小明的最小距离为15.75m.
12.(2025 上栗县二模)某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整
收集数据:七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70.
整理数据:七年级20名学生测试成绩频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的成绩范围为50≤x<60):
八年级20名学生测试成绩频数分布表:
成绩 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数 0 4 5 7 4
分析数据:两组样本数据的平均数、中位数、众数方差如表所示:
年级 平均数 中位数 众数 方差
七年级 76.9 a b 119.89
八年级 79.2 81 74 100.4
(1)补全七年级20名学生测试成绩频数分布直方图.
(2)请直接写出a,b的值.
(3)请根据抽样调查数据,估计全校七年级垃圾分类知识测试成绩在80分及以上的大约有多少人.
(4)通过以上分析,你认为哪个年级学生对垃圾分类知识掌握得更好?请说明推断的理由(两条即可).
【解答】解:(1)20﹣2﹣3﹣5﹣3=7(人),
补全频数分布直方图如下:
(2)七年级20名学生的测试成绩从小到大排列处在中间位置的两个数的平均数为77.5,因此中位数是77.5,即a=77.5,
七年级20名学生的测试成绩出现次数最多的是86分,共出现4次,因此众数是86,即b=86,
答:a=77.5,b=86;
(3)500200(人),
答:全校七年级垃圾分类知识测试成绩在80分及以上的大约有200人;
(4)八年级成绩较好,理由为:八年级学生测试成绩的平均数、中位数均比七年级的高,而八年级的方差较小.
13.(2025 天府新区模拟)如图,在△ABC中,∠BAC=90°,D为AB上一点,以AD为直径作⊙O,交BC于E,F两点,点E为BC中点,连接AE,DE.
(1)求证:AE AC=AB DE;
(2)若,,求⊙O的直径和EF的长.
【解答】(1)证明:∵∠BAC=90°,点E为BC中点,
∴AE=BE=CE,
∴∠B=∠BAE,
∵AD是直径,
∴∠AED=90°,
∴tan∠DAE,tanB,
∴,
∴AE AC=AB DE;
(2)解:∵AE=BE=CE,
∴BC=2,
∵tanC,
∴ABAC,
∵BC2=AC2+AB2,
∴120=6AC2,
∴AC=2,
∴ABAC=10,
∵AE AC=AB DE,
∴210DE,
∴DE,
∴AD6,
∴BD=4,⊙O的直径为6,
如图,连接AF,
∵四边形ADEF是圆内接四边形,
∴∠AFE+∠ADE=180°,
∵∠ADE+∠BDE=180°,
∴∠AFE=∠BDE,
又∵∠B=∠B,
∴△BDE∽△BFA,
∴,
∴4×10BF,
∴BF,
∴EF=BF﹣EF.
14.(2025 上栗县二模)如图,在平面直角坐标系中,点B坐标为(0,1),点A(m,3)在函数y(k>0,x>0)的图象上,将线段AB向右下方平移,得到线段CD,此时点C落在函数y的图象上,点D落在x轴正半轴上,且点D坐标为(1,0).
(1)求k的值;
(2)求直线AC所对应的函数表达式.
【解答】解:(1)由条件可知C(m+1,2).
∵点A和点C在函数的图象上,
∴3m=2(m+1),
∴m=2,
∴k=2×3=6.
(2)设直线AC所对应的函数表达式为y=ax+b.
将A(2,3),C(3,2)代入得:,
解得:,
∴直线AC所对应的函数表达式为y=﹣x+5.
15.(2025 铁岭模拟)某工厂加工某种型号芯片,成本价为20元/个.根据市场调查发现,销售量y(个)是关于销售单价提高x(元)的一次函数(x≥0,且x为整数),其关系如下表:
提高x元 单价(元/个) 销售量(个)
0 25 500
1 26 480
2 27 460
… … …
x 25+x
(1)求销售量y与x之间的函数关系式;
(2)由于工厂生产规模受限,每日加工该种芯片不能少于340个且不能超过620个,每日加工的芯片全部售出,该芯片销售单价定为多少元时,才能获得最大销售利润?最大销售利润是多少?
【解答】解:(1)∵销售量y(件)是关于销价单价提高x(元)的一次函数,
∴可设 y=kx+b.
∴.
∴.
∴y=500﹣20x.
(2)由题意,∵每日加工量限制为340≤y≤620,且y=﹣20x+500,
∴0≤x≤8且x为整数.
又∵销售单价为(25+x)元,
∴单个利润为(25+x﹣20)=(x+5)元.
∴总利润P=(x+5)(﹣20x+500)=﹣20x2+400x+2500=﹣20(x﹣10)2+4500.
∵0≤x≤8且x为整数,
∴当x=8时:销售单价为25+8=33元,此时销售量为y=﹣20×8+500=340,总利润为P=(8+5)×340=4420元.
答:销售单价定为33元时,利润最大,最大利润为4420元.
16.(2025 开封二模)如图,△ABC的顶点为网格线的交点,反比例函数的图象过格点A,B.将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′.
(1)求过点C′的反比例函数解析式,并画出其图象(x<0).
(2)在过点C′的反比例函数图象上任取一点D,过点D向y轴作垂线,交的图象于点E,连接DO,EO,△ODE的面积会发生变化吗?若不变化,求出△ODE的面积;若变化,请说明理由.
【解答】解:(1)如图1,C(4,4),
∵将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′,
∴C′(﹣1,3),
设点C′的反比例函数解析式为,
∴,
∴k=﹣3,
∴过点C′的反比例函数解析式为,其图象(x<0);
(2)△ODE的面积不会发生变化;理由如下:
如图2,设DE交y轴于点F,
∵DE⊥y轴,过点C′的反比例函数解析式为,反比例函数的图象过格点A,B,
∴S△ODF,S△OEF,
∴S△ODE=S△ODF+S△OEF3,
∴△ODE的面积不会发生变化,△ODE的面积为3.
17.(2025 扬州一模)如图①,在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)如图②,连接CE,若∠FCB=90°,CE=5,求AB的长.
【解答】(1)证明:∵E为AD中点,
∴AE=DE,
∵AF∥BC,
∴∠DBE=∠AFE
∵∠DEB=∠AEF
∴△DEB≌△AEF,
∴AF=DB,
∵AD是直角三角形CAB斜边CB上的中线,
∴AD=BD=DC,
∴AF=DC,
∵AF∥DC,
∴四边形ADCF是平行四边形,
∵AD=DC,
∴四边形ADCF是菱形.
(2)解:∵∠FCB=90° 且四边形ADCF是菱形,
∴四边形ADCF是正方形,
∴∠ADC=90°,
∵DC=DB,AD⊥BC,
∴AC=AB,
∴AD=CD=DB,设 AE=DE=x,则 CD=BD=AD=2x,
∵EC2=CD2+DE2,
∴5x2=25,
∴ (负根已经舍弃),
∴,
∴.
18.(2025 鼓楼区二模)如图①所示,沪宁高速公路可近似看作一条直线.一辆货车以80km/h的速度从南京出发匀速驶往上海;同时,一列轿车以120km/h的速度从苏州出发匀速驶往上海,停留0.5h后,按照原速度继续开往南京,最终两车同时到达目的地.设货车行驶的时间为t h,货车与南京的距离y1km,轿车与南京的距离y2km.
(1)在图2中,分别画出和补全y1、y2关于t的函数图象;
(2)分别求苏州到上海的距离,南京到上海的距离;
(3)若镇江距离南京90km,直接写出货车和轿车经过镇江的时间间隔.
【解答】解:(1)画出和补全y1、y2关于t的函数图象如图所示:
(2)苏州到上海的距离为12080(km),
设南京到上海的距离为x km,
根据题意,得,
解得x=280.
∴南京到上海的距离280km.
(3)货车经过镇江时的时间为90÷80(h),
轿车经过镇江时的时间为(280﹣90)÷120(h),
(h).
答:货车和轿车经过镇江的时间间隔为h.
19.(2025 上栗县二模)秋水广场音乐喷泉是江西省南昌市红谷滩新区赣江边上的一道亮丽风景线,它不仅是城市景观的重要组成部分,也成为了市民休闲娱乐的好去处.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)用含a,b的代数式表示抛物线y=ax2+bx的顶点坐标为(, );
(2)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a,b的值;
(3)若k=3,,则喷出的抛物线水线能否达到岸边?
【解答】解:(1)在y=ax2+bx中,
当时,,
故答案为:;
(2)∵y=ax2+bx的顶点坐标为,抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴,,
解得,,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是,2;
(3)当k=3,时,
∵y=ax2+bx的顶点坐标为,抛物线的顶点在直线y=3x上,
∴,
解得:b=6或b=0(舍去),
∴抛物线解析式为.
当y=0时,,
解得:x1=27,x2=0,
∵27>18,
∴喷出的抛物线水线能达到岸边.
20.(2025 深圳校级二模)新课标中,数学课程要培养的学生核心素养是“用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界”,这集中体现了数学课程的育人价值,也说明数学和实际生活密不可分.数学老师给小明小组布置了一项数学与实际的作业,让他们到菜市场进行调研,并利用所学的数学知识对销售提出合理化建议.小明小组经调研发现,某店铺蔬菜的售卖情况大致遵循以下规律.
规律一 当每千克蔬菜的售价为8元时,每天能销售80千克.
规律二 当每千克蔬菜的售价每降低0.5元,每天的销售量就会增加10千克.
经小组讨论,发现里面可能存在函数关系,考虑用已学的函数知识帮助店家解决问题.
【建立模型】
(1)设每天销售这种蔬菜的销售额为y元,每千克蔬菜降价x元,求y与x的函数关系式;
【设计方案】
(2)当每千克蔬菜降价多少元时,该店铺每天销售这种蔬菜的销售额最多?最多为多少元?
【实际需求】
(3)若该店铺老板希望每天销售这种蔬菜的销售额不低于540元,求这个蔬菜应参考的售价范围.
【解答】解:(1)由题意,∵每千克蔬菜的售价为8元时,销量为80千克,每降价0.5元,销量增加10千克,
∴设降价为x元,则销量增加量为(千克).
∴总销量为(80+20x)千克.
又∵此时售价变为(8﹣x)元/千克,
∴销售额y与x的函数关系式为:y=(8﹣x)(80+20x)=﹣20x2+80x+640.
(2)由题意,结合(1)y=﹣20x2+80x+640=﹣20(x﹣2)2+720.
∴当x=2时,y取最大值,最大销售额为720元.
答:当每千克蔬菜降价2元时,该店铺每天销售这种蔬菜的销售额最多,最多为720元.
(3)由题意,令y=﹣20x2+80x+640=540,
∴x=﹣1或x=5.
又∵二次函数y=﹣20x2+80x+100≥0的图象开口向下,
∴该店铺老板希望每天销售这种蔬菜的销售额不低于540元,则0≤x≤5.
∴对应售价为:8﹣5=3元至8﹣0=8元,即这个蔬菜应参考的售价范围是3元至8元.
21.(2025 琼山区校级一模)在平面直角坐标系中,已知抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C.
(1)如图,若抛物线经过A(1,6),B(﹣2,3)两点,
①求抛物线的解析式;
②设抛物线顶点为D,求△ACD的面积;
③点P是抛物线对称轴上的动点,则PA+PC的最小值为 3 ;
(2)若抛物线经过E(2a,3),F(x1,y1),G(x2,y2)三点,对于x1=3a,3≤x2≤4,都有y1<y2,求a的取值范围.
【解答】解:(1)①∵抛物线y=ax2+bx+3经过A(1,6),B(﹣2,3)两点,
∴,解得,
∴抛物线的解析式为y=x2+2x+3;
②∵抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C,
∴C(0,3),
∵y=x2+2x+3=(x+1)2+2,
∴抛物线顶点D(﹣1,2),
设直线AD的解析式为y=mx+n,与y轴的交点为M,
∴解得,
∴直线AD的解析式为y=2x+4,
∴M(0,4),
∴CM=4﹣3=1,
∴S△ACD=S△ACM+S△BCM;
③连接AB交抛物线的对称轴于P,此时,PA+PC的值最小,最小值为AB,
∴A(1,6),B(﹣2,3),
∴AB3
即PA+PC的最小值为3,
故答案为:3;
(3)由条件可知:抛物线的对称轴是直线xa,
①当a>0时,此时抛物线开口向上,
当x>a时,y随着x的增大而增大,
∵对于x1=3a,3≤x2≤4,都有y1<y2,
∴3a<3,
∴a<1,
又∵a>0,
∴0<a<1;
②当a<0时,抛物线开口向下,对称轴为直线x=a,
此时a﹣3a>4﹣a,
解得a<﹣4,
又∵a<0,
∴a<﹣4;
综上,当0<a<1或a<﹣4时,都有y1<y2.
22.(2025 张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
【解答】解:(1)点D在半圆O所在的圆上.
理由如下:如图,连接OD.
∵DC=AC,∠OCD=∠OCA,OC=OC,
∴△OCD≌△OCA(SAS),
∴OD=OA,
∴点D在半圆O所在的圆上;
(2)①∵点D在半圆O所在的圆上,
∴∠CDE=∠CAB.
由条件可知∠CDE=∠OCD,
∴OC∥DE,
由条件可知∠OCE=90°,
∴∠E=90°;
②由题意,得∠CAB=∠CDB=∠OCA=∠OCD=30°,
∴∠BOC=60°,
∴BC的长度为,
由条件可知∠ACB=90°,
∴,∠BCD=∠ACB﹣∠OCA﹣∠OCD=30°,
∴∠BCD=∠CDB,
∴BC=BD=5.
∵,
∴.
23.(2025 镇江模拟)如图,在平面直角坐标系中,直线yx+b经过点A(﹣6,0),与y轴交于点B,与反比例函数y(x>0)交于点C,连接OC,且S△AOB=2S△BOC.
(1)求b,k的值;
(2)若点D为反比例函数y(x>0)图象上一点,连接CD,使得CD⊥OC,求点D的坐标.
【解答】解:(1)作CE⊥x轴于点E,
∵直线yx+b经过点A(﹣6,0),与y轴交于点B
∴0b,
∴b=4,
∴B(0,4),
∴OA=6,OB=4,
∵S△AOB=2S△BOC,
∴AB=2BC,
∴,
∵CE∥OB,
∴△AOB∽△AEC,
∴,
∴CE=6,AE=9,
∴OE=9﹣6=3,
∴C(3,6),
∵反比例函数y(x>0)过点C,
∴k=3×6=18;
(2)作DF⊥CE于点F,
由(1)可知反比例函数为y,C(3,6),
设D(m,),则CF=6,DF=m﹣3,
∵CD⊥OC,
∴∠OCE+∠DCF=90°,
∵∠OCE+∠COE=90°,
∴∠DCF=∠COE,
∵∠CEO=∠DFC=90°,
∴△CEO∽△DFC,
∴,即,
整理得m2﹣15m+36=0,
解得m=12或m=3(舍去),
∴D(12,).
24.(2025 厦门模拟)如图1,AB为半圆O的直径,AB=4,C为半圆上的动点,连接OC,点A关于OC的对称点为点D,连接BD.(0°<∠AOC<45°)
(1)若∠AOC=40°,连接AC,AD,求∠CAD的度数;
(2)如图2,若点E在半圆O上,BE的长度为π,连接DE,F为DE中点,连接OF交BD于点M,Q为OE上一点,OQ=1.2.
①当∠AOC=30°时,判断点Q与直线BD的位置关系,并说明理由;
②如图3,连接QM,在点C运动过程中,当BQ=QM时,记α=45°﹣∠AOC,求tanα的值.
【解答】解:(1)连接OD,
∵AB为半圆O的直径,点A关于OC对称点为点D,
∴OA=OD,OC⊥AD,
∴点D在半圆O上,
∴∠COD=∠AOC=40°,
∴;
(2)①点Q在直线BD外,理由如下:
连接OD,
∵AB为⊙O直径,点A关于OC对称点为点D,
∴OA=OD,OC⊥AD,
∴点D在半圆O上,
∴,
∵,
∴∠B=∠AOC,
∵的长度为π,半圆O的直径AB=4,
∴,
∴∠BOE=90°,
∴∠AOE=180°﹣∠BOE=90°,
∵∠AOC=30°,
∴∠B=∠AOC=30°,
设OE与BD交于点P,直角三角形BOP中,,
∴,
又∵Q在OE上,OQ=1.2,OP≠OQ,
∴点Q在直线BD外;
②连接OD,EM,BE,如图所示,
则,
∵OD=OE,F为DE中点,
∴EF=DF,OF⊥ED,,
∴ME=MD,
∴∠DEM=∠EDM=45°,
∴∠EMD=90°,
∴∠EMB=180°﹣∠EMD=90°,
设OE交BD于点N,
∵∠QEM=90°﹣∠ENM,∠DBO=90°﹣∠BNO,∠ENM=∠BNO,
∴∠QEM=∠DBO,
∵EQ=QM,BO=DO,
∴∠QME=∠QEM=∠DBO=∠BDO,
∴△QME∽△ODB,
∴,
∵OQ=1.2,OE=2,
∴QE=OE﹣OQ=0.8,
∴,
设EM=2x,BD=5x,
∴ME=MD=2x,BM=BD﹣DM=3x,
∴,
在直角三角形EBM中,∠EMB=90°,
∴,
∵,
∴∠EBM=∠DOF,
∵,,
∴,
∴∠DOF=45°﹣∠AOC,
∴∠EBM=∠DOF=α,
∴.
25.(2025 湖州一模)纵观古今,解码测量背后的数学智慧.
(1)【古】《周髀算经》中记载了“偃矩以望高”的方法.意思是把“矩(曲尺)”仰立放,可测物体的高度.如图,点B,D,E在同一水平线上,∠ABE=∠CDE=90°,AE与CD交于点F.测得DF=0.35米,DE=0.55米,BE=22米,求树AB的高度.
(2)【今】某综合实践活动小组,尝试通过利用无人机(无人机限高120米)测算某山体的海拔高度,设计了如下两种方案.请选择其中一种可行的测算方案,计算该山体的海拔高度(AB的长).(精确到1米)
测量示意图 方案说明
方案一
无人机位于海拔高度为60米的C处,测得与山顶A处的仰角α为45°,与山脚D处的俯角β为65°.(参考数据:sin65°≈0.90,cos65°≈0.42,tan65°≈2.14)
方案二
当无人机位于海拔高度为60米的C处时,测得与山顶A处的仰角γ为45°;当无人机垂直上升到海拔高度为113米的G处时,测得与山顶处A的仰角θ为25°.(参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47)
【解答】解:(1)∵∠ABE=∠CDE=90°,∠AEB=∠FED,
∴△ABE∽△FDE,
∴,
∵DF=0.35米,DE=0.55米,BE=22米,
∴,
∴AB=14,
答:树AB的高度为14米;
(2)选择方案二进行问题解决:
∵∠ACE=γ=45°,∠AEC=90°,
∴AE=CE,
∵∠AGH=θ=25°,∠AHG=90°,
∴,
可得,
∴(米),
∴AB=AE+EB=CE+CF=160(米),
∴山体高度约为160米.
26.(2025 上蔡县三模)如图,正方形ABCD的两个顶点A(2,m),C(4,n)都在反比例函数y(x>0)的图象上.
(1)求这个反比例函数的表达式.
(2)反比例函数y(x>0)的图象经过点B,直线x=t(t>0)分别与反比例函数y(x>0),y(x>0)的图象交于点M,N.若1<t<6,求MN的长的取值范围.
【解答】解:(1)由条件可知k1=2m=4n,
∵点A(2,m),C(4,n)是正方形ABCD的两个顶点,
∴AB=BC=4﹣2=2,
∴m﹣n=2,
联立,
解得:,
∴A(2,4),C(4,2),
∴k1=2×4=8,
∴这个反比例函数的表达式为;
(2)由条件可知B(2,2),
∵反比例函数的图象经过点B(2,2),
∴k2=2×2=4,
即,
∴,,
∴,
∵1<t<6,
∴,
∴,
∴MN的长的取值范围是.
27.(2025 雁塔区校级模拟)如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴分别相交于A,B两点,与y轴交于点C,直线y=﹣x+3经过B、C两点.
(1)求抛物线的表达式;
(2)抛物线的顶点为M,点N是y轴上一点,点Q是平面内一点,是否存在以B、M、N、Q为顶点的四边形是以BM为边的矩形?若存在,请求出点N、Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵B、C分别是直线y=﹣x+3与x轴,y轴的交点,
∴点B的坐标为(3,0),点C的坐标为(0,3),
∵B、C在抛物线y=﹣x2+bx+c上,
∴,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4),
设N(0,n),Q(p,q),
①如图:当∠BMN=90°时,
则,
解得:,
∴,;
②如图:当∠NBM=90°时,
则,
解得:,
∴,;
综上所述:,或,.
28.(2025 思明区校级二模)研究发现人的身体每天消耗的热量主要由碳水化合物和脂肪(不考虑蛋白质及其他有机物)提供,碳水化合物和脂肪分解时所消耗的氧气、生成的二氧化碳、释放的热量三个方面的相关数据如表:
分解的营养物质 氧气消耗量/克 二氧化碳生成量/克 释放热量/千焦
1克碳水化合物 1 1.5 15
1克脂肪 3 3 45
请解答下列问题:
(1)研究人员测出小祺在某次运动中平均每分钟消耗氧气2.5克,产生二氧化碳3克,求小祺的身体平均每分钟分解碳水化合物与脂肪各多少克.
(2)已知小祺骑脚踏车每分钟消耗热量20千焦,快走每分钟消耗热量27千焦,小祺某天骑脚踏车和快走共1小时,若要消耗完40克碳水化合物与20克脂肪分解后释放的热量,小祺至少需要分配多少分钟进行快走?(精确到1分钟)
【解答】解:(1)设小祺的身体平均每分钟分解碳水化合物x克,脂肪y克.
根据题意,得.
解得,
即小祺的身体平均每分钟分解碳水化合物1克,脂肪0.5克,
答:小祺的身体平均每分钟分解碳水化合物1克,脂肪0.5克;
(2)设小祺分配m分钟进行快走,则分配(60﹣m)分钟骑脚踏车,
根据题意,得27m+20(60﹣m)≥40×15+20×45.
解得:,
∵结果精确到1分钟,
∴m的最小值为43.
答:小祺至少需要分配43分钟进行快走.
29.(2025 香坊区校级三模)在平面直角坐标系中,O为坐标原点,直线AB交x轴负半轴于点A,交y轴正半轴于点B,,AB=20.
(1)如图1,求直线AB的解析式;
(2)如图2,P为x轴正半轴上一点,C为AB的中点,连接CP,设△ACP的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,直线y=kx﹣12k交x轴、y轴于点D、E,交直线AB于点F,,G为y轴负半轴上一点,连接CG交x轴于点H,,过点P作PI⊥x轴交DE于点I,L为PI上一点,连接EL,J为EL上一点,连接JG,∠DIP+∠EJG=180°,且∠FAD﹣∠FDA=2∠OED﹣∠BFE,EJ:I=5;,M为x轴负半轴上一点,连接EM、LM、LN,若N为EM的中点,∠LEN+∠MLN=∠AFD,求直线LM的解析式.
【解答】解:(1)∵∠AOB=90°,,AB=20,
∴,,
∴A(﹣12,0),B(0,16),
设直线AB的解析式为y=ax+b,
则,
解得,,
∴;
(2)如图,作CQ⊥x轴于点H,则,
∵点P在x轴正半轴上,且横坐标为t,
∴OP=t,
∴;
(3)∵直线y=kx﹣12k交x轴于点D,
∴D(12,0),
∴OP+DP=OD=12,
∵,OA=12,
∴OP=8,
∵,OH+AH=OA=12,
∴,
∴,
∵∠FAD﹣∠FDA=2∠OED﹣∠BFE,
∴∠FAD﹣∠FDA=2(90°﹣∠FDA)﹣(∠FAD+∠FDA)=180°﹣3∠FDA﹣∠FAD,
∴∠FAD+∠FDA=90°,
∴∠AFD=90°,
∵C(﹣6,8),,
∴直线CH的解析式为,
∴G(0,﹣1),
∵OD=12,,
∴E(0,9),
∴EG=10,
∵PI⊥x轴,EG⊥x轴,
∴PI∥EG,
∴∠ELI=∠GEJ,
∵∠DIP+∠EJG=180°,
∴∠EJG=180°﹣∠DIP=∠LIE,
∴△EJG∽△LIE,
∴,
∴,
如图,作MS⊥EL于点S,交NL于点T,连接NS,则∠LEN+∠EMS=90°,
∵点N为EM的中点,
∴,
∴∠NSM=∠NMS,
∵∠LEN+∠MLN=∠AFD,∠AFD=90°,
∴∠NLM=∠EMS=∠NSM,
又∵∠NTS=∠LTM,
∴△NST∽△MTL,
∴,
又∵∠NTM=∠STL,
∴△NTM∽△STL,
∴∠MNT=∠LST=90°,
又∵点N为EM的中点,
∴,
如图,作LK⊥EG于点K,则KL=OP=8,
∴,
∴LP=KO=1,
∴L(8,1),,
∴,
设直线ML的解析式为y=mx+n,
则,
解得:,
∴.
30.(2025 雁塔区校级模拟)【问题提出】
如图①,在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,点P,Q分别是BC,AC上的动点,则EP+PQ的最小值是 ;
【问题解决】
如图②,某大型工厂生产区域内,有一个矩形场地ABCD,其中点D为原材料入口,修建在DC段的点G为成品出口.在生产区域内,有两处重要的生产加工点E和F,分别位于场地的DA,DB段,并且DE=DF.为了实现从生产加工点到成品出口的高效运输(即成品从生产加工点经质检区域输送到出口的过程更为高效),工厂规划修建一个调度中心P与一处位于BC段的半圆形自动化质检区域(圆心为O).该调度中心需同时满足以下两个条件:①使P到生产加工点E,F的距离相等,即PE=PF;②使运输线路PM+NG的长度最短(其中M,N为半圆质检区域O上的任意两点).已知AD=300米,AB=400米,CG=100米,质检区域半径r=20米.请问是否存在符合要求的调度中心点P,若存在,求出PM+NG的最小值和此时OC的距离;若不存在,请说明理由.
【解答】解:(1)如图所示,作点E关于BC的对称点H,连接PH,
∵在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,
∴AE=BEAB=2,∠A=∠C=45°,
由轴对称的性质可得EP=HP,EB=BH=2,
∴PE+PQ=PH+PQ,
∴当H、P、Q三点共线,且HQ⊥AC时,PH+PQ有最小值,即此时PE+PQ有最小值,最小值为HQ的长,
在Rt△AHQ中,,
∴PE+PQ的最小值为,
故答案为:;
(2)∵PE=PF,
∴点P在线段EF的垂直平分线上,
∵DE=DF,
∴点D在线段EF的垂直平分线上,
∴DP垂直平分EF,
∴点P在∠ADB的角平分线上,
如图所示,作∠ADB的角平分线交AB于H,作点G关于BC的对称点G',作G'P⊥DH交BC于O',此时PM+NG有最小值,理由如下:
∵PM+GN=PO+OG﹣2r=PO+OG﹣40,
∴当PO+OG最小时,PM+GN最小,
由轴对称的性质可得G'O=OG,
则PO+OG=PO+OG',故当P、O、G'三点共线且G'P⊥DH时,PO+OG'有最小值,即此时PO+OG有最小值,最小值为线段PG'的长;
在Rt△ABD中,由勾股定理得长;
如图所示,连接HG',过点H作HA'⊥BD于A',
∴AH=A'H,
∵S△ABD=S△ADH+S△BDH,
∴,
∴AH=A'H=150米,
∴,
∵,
∴,
∴米;
在Rt△G'PD中,由勾股定理得;
∵,
∴,
∴O'C=50米;
综上所述,PM+NG的最小值为米,此时OC的距离为50米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【抢分秘籍】各地区中考数学真题分类突破:解答题
1.(2025 鼓楼区校级模拟)有三个购房者在售楼部进行抽签选房,在一个不透明的盒子中,共有标号为1至3的3个小球,除颜色外其他完全相同.买房者按照到达的先后顺序进行抽签,不放回地从盒中抽球,将球的编号作为最终选房的顺序(如抽到2号球的人第2个选房)
(1)第一个抽签的人第1个选房的概率为 .
(2)有买房者质疑这种选房规则,认为先抽签的人第一个选房的概率更大.请判断这种说法是正确?用概率知识并结合树状图说明理由.
2.(2025 思明区二模)如图,点B,C,D,E在一条直线上,∠B=∠FCE,AB=FC,BC=DE.求证:AD∥FE.
3.(2025 梁溪区校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
4.(2025 锦江区校级模拟)随着人民生活水平的日益提高,许多农村的房屋普遍进行了改造,小明家改造时在门前安装了一个遮阳棚,如图,在侧面示意图中,遮阳篷AB长为4米,与墙面AD的夹角∠BAD=75.5°,靠墙端A离地高AD为3米,当太阳光线BC与地面DE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据:sin75.5°≈0.97,cos75.5°≈0.25,tan75.5°≈3.87)
5.(2025 海珠区校级二模)某文具店准备购进甲、乙两种圆规,若购进甲种圆规15个,乙种圆规20个,需要310元;若购进甲种圆规20个,乙种圆规30个,需要440元.
(1)求购进甲、乙两种圆规的单价各是多少元;
(2)文具店购进甲、乙两种圆规共100个,每个甲种圆规的售价为15元,每个乙种圆规的售价为12元,销售这两种圆规的总利润不低于480元,且购进两种圆规所用费用不超过964元,那么这个文具店购进甲种圆规的方案有几种?
6.(2025 上栗县二模)如图,在矩形ABCD中,P,M分别是AD,CD的中点.请仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△APB的BP边上的中线;
(2)在图2中,以PM为边作一个菱形.
7.(2025 惠州二模)某中学举行了迎国庆中华传统文化节活动.本次文化节共有五项活动:A.书法比赛;B.国画竞技;C.诗歌朗诵;D.汉字大赛;E.古典乐器演奏.活动结束后,某数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据调查结果绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)此次随机抽取共 名学生,m= ,并补全条形统计图;
(2)若该校共有3000名学生,请估计最喜欢D活动的学生人数;
(3)该校准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用画树状图法或列表法求选出的两名选手正好是一男一女的概率.
8.(2025 开封二模)某校兴趣小组在广场进行无人机飞行表演,一架无人机的飞行线路是一条抛物线,其飞行高度y(m)与水平距离x(m)满足二次函数关系.
(1)用配方法求出抛物线的顶点坐标,并说明其顶点坐标的实际意义.
(2)若距飞行起始点正前方10m处有一个16m高的大型广告牌,请通过计算判断该无人机在飞行过程中,是否存在与广告牌发生碰撞的风险.
9.(2025 开封二模)如图①是2025年春晚一群活泼又喜感的人形机器人扭秧歌,该节目吸引了无数观众的目光,不仅展示了人工智能技术的进步,还体现了科技为传统文化注入新的活力.如图②是一个人形机器人跳舞时的侧面示意图.已知其上半身AB=100cm,大、小腿的长BC=DC=40cm,胳膊EF=34cm,AE=EF,当∠AEF=120°,∠BCD=74°,AB⊥MN且A、B、D共线时,点F到水平地面MN的距离是多少.(参考数据:,,)
10.(2025 兴庆区三模)如图,在平行四边形ABCD中,AB<BC.
(1)请用无刻度的直尺和圆规按要求作图,保留作图痕迹,不写作法.
①在线段BC上找一点E,使点E到AB,AD的距离相等;
②在线段AD上截取DF,使DF=CE;
(2)在(1)所作的图形中,连接EF,求证:四边形ABEF是菱形.
11.(2025 太康县一模)为迎接2026年米兰一科尔蒂纳丹佩佐冬奥会,某市扩建了一座国际标准室内滑雪训练场,该滑雪场采用最新造雪技术,整个赛道长180米,可模拟高山滑雪环境,国家队运动员小明为备战冬奥会,在此进行技术训练.如图,他从赛道顶端A处开始下滑,滑行3秒后,教练操控一台无人机从A处沿赛道方向保持安全高度跟拍训练过程(安全高度可忽略不计).训练中心记录了小明离A处的滑行距离y(单位:m)以及无人机离A处的距离s(单位:m)随滑行时间x(单位:s)的变化数据如下:
滑行时间x/s 0 1 2 3 4 5 6
滑行距离y/m 0 4 10 18 28 40 54
无人机离A处的距离s/m 0 0 0 0 12 24 36
经探究发现,y与x之间成二次函数关系,s与x(x≥3)之间成一次函数关系.
(1)直接写出y关于x的函数解析式和x关于x(x≥3)的函数解析式;(不要求写出自变量的取值范围)
(2)小明滑完整个训练赛道需要耗时多久?
(3)分析在小明到达终点前,无人机能否追上小明,若能,求出相遇时间;若不能,求出无人机与小明的最小距离.
12.(2025 上栗县二模)某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整
收集数据:七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70.
整理数据:七年级20名学生测试成绩频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的成绩范围为50≤x<60):
八年级20名学生测试成绩频数分布表:
成绩 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数 0 4 5 7 4
分析数据:两组样本数据的平均数、中位数、众数方差如表所示:
年级 平均数 中位数 众数 方差
七年级 76.9 a b 119.89
八年级 79.2 81 74 100.4
(1)补全七年级20名学生测试成绩频数分布直方图.
(2)请直接写出a,b的值.
(3)请根据抽样调查数据,估计全校七年级垃圾分类知识测试成绩在80分及以上的大约有多少人.
(4)通过以上分析,你认为哪个年级学生对垃圾分类知识掌握得更好?请说明推断的理由(两条即可).
13.(2025 天府新区模拟)如图,在△ABC中,∠BAC=90°,D为AB上一点,以AD为直径作⊙O,交BC于E,F两点,点E为BC中点,连接AE,DE.
(1)求证:AE AC=AB DE;
(2)若,,求⊙O的直径和EF的长.
14.(2025 上栗县二模)如图,在平面直角坐标系中,点B坐标为(0,1),点A(m,3)在函数y(k>0,x>0)的图象上,将线段AB向右下方平移,得到线段CD,此时点C落在函数y的图象上,点D落在x轴正半轴上,且点D坐标为(1,0).
(1)求k的值;
(2)求直线AC所对应的函数表达式.
15.(2025 铁岭模拟)某工厂加工某种型号芯片,成本价为20元/个.根据市场调查发现,销售量y(个)是关于销售单价提高x(元)的一次函数(x≥0,且x为整数),其关系如下表:
提高x元 单价(元/个) 销售量(个)
0 25 500
1 26 480
2 27 460
… … …
x 25+x
(1)求销售量y与x之间的函数关系式;
(2)由于工厂生产规模受限,每日加工该种芯片不能少于340个且不能超过620个,每日加工的芯片全部售出,该芯片销售单价定为多少元时,才能获得最大销售利润?最大销售利润是多少?
16.(2025 开封二模)如图,△ABC的顶点为网格线的交点,反比例函数的图象过格点A,B.将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′.
(1)求过点C′的反比例函数解析式,并画出其图象(x<0).
(2)在过点C′的反比例函数图象上任取一点D,过点D向y轴作垂线,交的图象于点E,连接DO,EO,△ODE的面积会发生变化吗?若不变化,求出△ODE的面积;若变化,请说明理由.
17.(2025 扬州一模)如图①,在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)如图②,连接CE,若∠FCB=90°,CE=5,求AB的长.
18.(2025 鼓楼区二模)如图①所示,沪宁高速公路可近似看作一条直线.一辆货车以80km/h的速度从南京出发匀速驶往上海;同时,一列轿车以120km/h的速度从苏州出发匀速驶往上海,停留0.5h后,按照原速度继续开往南京,最终两车同时到达目的地.设货车行驶的时间为t h,货车与南京的距离y1km,轿车与南京的距离y2km.
(1)在图2中,分别画出和补全y1、y2关于t的函数图象;
(2)分别求苏州到上海的距离,南京到上海的距离;
(3)若镇江距离南京90km,直接写出货车和轿车经过镇江的时间间隔.
19.(2025 上栗县二模)秋水广场音乐喷泉是江西省南昌市红谷滩新区赣江边上的一道亮丽风景线,它不仅是城市景观的重要组成部分,也成为了市民休闲娱乐的好去处.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)用含a,b的代数式表示抛物线y=ax2+bx的顶点坐标为(, );
(2)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a,b的值;
(3)若k=3,,则喷出的抛物线水线能否达到岸边?
20.(2025 深圳校级二模)新课标中,数学课程要培养的学生核心素养是“用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界”,这集中体现了数学课程的育人价值,也说明数学和实际生活密不可分.数学老师给小明小组布置了一项数学与实际的作业,让他们到菜市场进行调研,并利用所学的数学知识对销售提出合理化建议.小明小组经调研发现,某店铺蔬菜的售卖情况大致遵循以下规律.
规律一 当每千克蔬菜的售价为8元时,每天能销售80千克.
规律二 当每千克蔬菜的售价每降低0.5元,每天的销售量就会增加10千克.
经小组讨论,发现里面可能存在函数关系,考虑用已学的函数知识帮助店家解决问题.
【建立模型】
(1)设每天销售这种蔬菜的销售额为y元,每千克蔬菜降价x元,求y与x的函数关系式;
【设计方案】
(2)当每千克蔬菜降价多少元时,该店铺每天销售这种蔬菜的销售额最多?最多为多少元?
【实际需求】
(3)若该店铺老板希望每天销售这种蔬菜的销售额不低于540元,求这个蔬菜应参考的售价范围.
21.(2025 琼山区校级一模)在平面直角坐标系中,已知抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C.
(1)如图,若抛物线经过A(1,6),B(﹣2,3)两点,
①求抛物线的解析式;
②设抛物线顶点为D,求△ACD的面积;
③点P是抛物线对称轴上的动点,则PA+PC的最小值为 ;
(2)若抛物线经过E(2a,3),F(x1,y1),G(x2,y2)三点,对于x1=3a,3≤x2≤4,都有y1<y2,求a的取值范围.
22.(2025 张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
23.(2025 镇江模拟)如图,在平面直角坐标系中,直线yx+b经过点A(﹣6,0),与y轴交于点B,与反比例函数y(x>0)交于点C,连接OC,且S△AOB=2S△BOC.
(1)求b,k的值;
(2)若点D为反比例函数y(x>0)图象上一点,连接CD,使得CD⊥OC,求点D的坐标.
24.(2025 厦门模拟)如图1,AB为半圆O的直径,AB=4,C为半圆上的动点,连接OC,点A关于OC的对称点为点D,连接BD.(0°<∠AOC<45°)
(1)若∠AOC=40°,连接AC,AD,求∠CAD的度数;
(2)如图2,若点E在半圆O上,BE的长度为π,连接DE,F为DE中点,连接OF交BD于点M,Q为OE上一点,OQ=1.2.
①当∠AOC=30°时,判断点Q与直线BD的位置关系,并说明理由;
②如图3,连接QM,在点C运动过程中,当BQ=QM时,记α=45°﹣∠AOC,求tanα的值.
25.(2025 湖州一模)纵观古今,解码测量背后的数学智慧.
(1)【古】《周髀算经》中记载了“偃矩以望高”的方法.意思是把“矩(曲尺)”仰立放,可测物体的高度.如图,点B,D,E在同一水平线上,∠ABE=∠CDE=90°,AE与CD交于点F.测得DF=0.35米,DE=0.55米,BE=22米,求树AB的高度.
(2)【今】某综合实践活动小组,尝试通过利用无人机(无人机限高120米)测算某山体的海拔高度,设计了如下两种方案.请选择其中一种可行的测算方案,计算该山体的海拔高度(AB的长).(精确到1米)
测量示意图 方案说明
方案一
无人机位于海拔高度为60米的C处,测得与山顶A处的仰角α为45°,与山脚D处的俯角β为65°.(参考数据:sin65°≈0.90,cos65°≈0.42,tan65°≈2.14)
方案二
当无人机位于海拔高度为60米的C处时,测得与山顶A处的仰角γ为45°;当无人机垂直上升到海拔高度为113米的G处时,测得与山顶处A的仰角θ为25°.(参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47)
26.(2025 上蔡县三模)如图,正方形ABCD的两个顶点A(2,m),C(4,n)都在反比例函数y(x>0)的图象上.
(1)求这个反比例函数的表达式.
(2)反比例函数y(x>0)的图象经过点B,直线x=t(t>0)分别与反比例函数y(x>0),y(x>0)的图象交于点M,N.若1<t<6,求MN的长的取值范围.
27.(2025 雁塔区校级模拟)如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴分别相交于A,B两点,与y轴交于点C,直线y=﹣x+3经过B、C两点.
(1)求抛物线的表达式;
(2)抛物线的顶点为M,点N是y轴上一点,点Q是平面内一点,是否存在以B、M、N、Q为顶点的四边形是以BM为边的矩形?若存在,请求出点N、Q的坐标;若不存在,请说明理由.
28.(2025 思明区校级二模)研究发现人的身体每天消耗的热量主要由碳水化合物和脂肪(不考虑蛋白质及其他有机物)提供,碳水化合物和脂肪分解时所消耗的氧气、生成的二氧化碳、释放的热量三个方面的相关数据如表:
分解的营养物质 氧气消耗量/克 二氧化碳生成量/克 释放热量/千焦
1克碳水化合物 1 1.5 15
1克脂肪 3 3 45
请解答下列问题:
(1)研究人员测出小祺在某次运动中平均每分钟消耗氧气2.5克,产生二氧化碳3克,求小祺的身体平均每分钟分解碳水化合物与脂肪各多少克.
(2)已知小祺骑脚踏车每分钟消耗热量20千焦,快走每分钟消耗热量27千焦,小祺某天骑脚踏车和快走共1小时,若要消耗完40克碳水化合物与20克脂肪分解后释放的热量,小祺至少需要分配多少分钟进行快走?(精确到1分钟)
29.(2025 香坊区校级三模)在平面直角坐标系中,O为坐标原点,直线AB交x轴负半轴于点A,交y轴正半轴于点B,,AB=20.
(1)如图1,求直线AB的解析式;
(2)如图2,P为x轴正半轴上一点,C为AB的中点,连接CP,设△ACP的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,直线y=kx﹣12k交x轴、y轴于点D、E,交直线AB于点F,,G为y轴负半轴上一点,连接CG交x轴于点H,,过点P作PI⊥x轴交DE于点I,L为PI上一点,连接EL,J为EL上一点,连接JG,∠DIP+∠EJG=180°,且∠FAD﹣∠FDA=2∠OED﹣∠BFE,EJ:I=5;,M为x轴负半轴上一点,连接EM、LM、LN,若N为EM的中点,∠LEN+∠MLN=∠AFD,求直线LM的解析式.
30.(2025 雁塔区校级模拟)【问题提出】
如图①,在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,点P,Q分别是BC,AC上的动点,则EP+PQ的最小值是 ;
【问题解决】
如图②,某大型工厂生产区域内,有一个矩形场地ABCD,其中点D为原材料入口,修建在DC段的点G为成品出口.在生产区域内,有两处重要的生产加工点E和F,分别位于场地的DA,DB段,并且DE=DF.为了实现从生产加工点到成品出口的高效运输(即成品从生产加工点经质检区域输送到出口的过程更为高效),工厂规划修建一个调度中心P与一处位于BC段的半圆形自动化质检区域(圆心为O).该调度中心需同时满足以下两个条件:①使P到生产加工点E,F的距离相等,即PE=PF;②使运输线路PM+NG的长度最短(其中M,N为半圆质检区域O上的任意两点).已知AD=300米,AB=400米,CG=100米,质检区域半径r=20米.请问是否存在符合要求的调度中心点P,若存在,求出PM+NG的最小值和此时OC的距离;若不存在,请说明理由.
【抢分秘籍】各地区中考数学真题分类突破:解答题
参考答案与试题解析
一.解答题(共30小题)
1.(2025 鼓楼区校级模拟)有三个购房者在售楼部进行抽签选房,在一个不透明的盒子中,共有标号为1至3的3个小球,除颜色外其他完全相同.买房者按照到达的先后顺序进行抽签,不放回地从盒中抽球,将球的编号作为最终选房的顺序(如抽到2号球的人第2个选房)
(1)第一个抽签的人第1个选房的概率为 .
(2)有买房者质疑这种选房规则,认为先抽签的人第一个选房的概率更大.请判断这种说法是正确?用概率知识并结合树状图说明理由.
【解答】解:(1)第一个抽签的人可能抽到1或2或3,共3种等可能的情况,
∴第一个抽签的人第1个选房的概率为,
故答案为:;
(2)这种说法不正确,理由如下:
根据题意画出树状图如下:
一共有6种等可能的情况,其中第一个人第一个选房的有2种,第二个人第一个选房的有2种,第三个人第一个选房的有2种,
∴三个抽签的人第一个选房的概率都是.
2.(2025 思明区二模)如图,点B,C,D,E在一条直线上,∠B=∠FCE,AB=FC,BC=DE.求证:AD∥FE.
【解答】证明:∵BC=DE,
∴BC+CD=DE+CD,
∴BD=CE,
在△ABC和△FCE中,
,
∴△ABC≌△FCE(SAS),
∴∠ADB=∠E,
∴AD∥FE.
3.(2025 梁溪区校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
∴∠ABC﹣∠EBC=∠ECB﹣∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得
180﹣2x=360﹣60﹣2(90﹣x),
x=15,
180﹣2×15=150,
∴∠AED为150度.
4.(2025 锦江区校级模拟)随着人民生活水平的日益提高,许多农村的房屋普遍进行了改造,小明家改造时在门前安装了一个遮阳棚,如图,在侧面示意图中,遮阳篷AB长为4米,与墙面AD的夹角∠BAD=75.5°,靠墙端A离地高AD为3米,当太阳光线BC与地面DE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据:sin75.5°≈0.97,cos75.5°≈0.25,tan75.5°≈3.87)
【解答】解:如图,过B作BT⊥AD于点T,BK⊥DE于点K,
在Rt△ABT中,
sin∠BAT,cos∠BAT,
∴BT=AB sin∠BAT=4×sin75.5°≈3.9(米),AT=AB cos∠BAT=4×cos75.5°≈1.0(米),
∵∠BTD=∠D=∠CKB=90°,
∴四边形BTDK是矩形,
∴DK=BT=3.9米,BK=DT=AD﹣AT=3﹣1=2(米),
在Rt△BKC中,∠BCK=45°,
∴CK=BK=2米,
∴CD=DK﹣CK=3.9﹣2=1.9(米),
答:阴影CD的长约为1.9米.
5.(2025 海珠区校级二模)某文具店准备购进甲、乙两种圆规,若购进甲种圆规15个,乙种圆规20个,需要310元;若购进甲种圆规20个,乙种圆规30个,需要440元.
(1)求购进甲、乙两种圆规的单价各是多少元;
(2)文具店购进甲、乙两种圆规共100个,每个甲种圆规的售价为15元,每个乙种圆规的售价为12元,销售这两种圆规的总利润不低于480元,且购进两种圆规所用费用不超过964元,那么这个文具店购进甲种圆规的方案有几种?
【解答】解:(1)设甲种圆规的单价是x元,乙种圆规的单价是y元,
根据题意得:,
解得:.
答:甲种圆规的单价是10元,乙种圆规的单价是8元;
(2)设购进m个甲种圆规,则购进(100﹣m)个乙种圆规,
根据题意得:,
解得:80≤m≤82,
∵m为正整数,
∴m可以为80,81,82,
∴这个文具店购进甲种圆规的方案有3种.
答:这个文具店购进甲种圆规的方案有3种.
6.(2025 上栗县二模)如图,在矩形ABCD中,P,M分别是AD,CD的中点.请仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△APB的BP边上的中线;
(2)在图2中,以PM为边作一个菱形.
【解答】解:(1)如图1,AE即为所作;
(2)如图2,四边形PEFM即为所作.
7.(2025 惠州二模)某中学举行了迎国庆中华传统文化节活动.本次文化节共有五项活动:A.书法比赛;B.国画竞技;C.诗歌朗诵;D.汉字大赛;E.古典乐器演奏.活动结束后,某数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据调查结果绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)此次随机抽取共 100 名学生,m= 10 ,并补全条形统计图;
(2)若该校共有3000名学生,请估计最喜欢D活动的学生人数;
(3)该校准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用画树状图法或列表法求选出的两名选手正好是一男一女的概率.
【解答】解:(1)调查的总人数为25÷25%=100(人),
所以m%10%,即m=10,
B选项的人数为100﹣25﹣30﹣20﹣10=15(人),
补全条形统计图为:
故答案为:100,10;
(2)3000600(人),
答:估计最喜欢D活动的学生人数为600人;
(3)画树状图为:
共有20种等可能的结果数,其中选出的两名选手正好是一男一女的结果数为12,
所以选出的两名选手正好是一男一女的概率为.
8.(2025 开封二模)某校兴趣小组在广场进行无人机飞行表演,一架无人机的飞行线路是一条抛物线,其飞行高度y(m)与水平距离x(m)满足二次函数关系.
(1)用配方法求出抛物线的顶点坐标,并说明其顶点坐标的实际意义.
(2)若距飞行起始点正前方10m处有一个16m高的大型广告牌,请通过计算判断该无人机在飞行过程中,是否存在与广告牌发生碰撞的风险.
【解答】解:(1)将解析式配方可得:
;
顶点坐标为(8,18),表示当飞行的水平距离为8m时,飞行达到最大高度为18m.
(2)当x=10m时,,
答:不存在碰撞的风险.
9.(2025 开封二模)如图①是2025年春晚一群活泼又喜感的人形机器人扭秧歌,该节目吸引了无数观众的目光,不仅展示了人工智能技术的进步,还体现了科技为传统文化注入新的活力.如图②是一个人形机器人跳舞时的侧面示意图.已知其上半身AB=100cm,大、小腿的长BC=DC=40cm,胳膊EF=34cm,AE=EF,当∠AEF=120°,∠BCD=74°,AB⊥MN且A、B、D共线时,点F到水平地面MN的距离是多少.(参考数据:,,)
【解答】解:连接BD,过点F分别作FP⊥AB,FG⊥MN,垂足分别为点P、G,过点C作CQ⊥BD于点Q.
则四边形DGFP为矩形,
∵∠AEF=120°,
∴∠FEP=60°,∠EFP=30°,
∴EF=34cm,
∴EP17(cm),
∵AB=100cm,AE=34cm,
∴PB=AB﹣AE﹣EP=100﹣34﹣17=49(cm),
∵BC=DC=40cm,CQ⊥BD,∠BCD=74°,
∴∠BCQ=∠DCQ=37°,BD=2BQ,
∵,
∴BQ=24cm,BD=2BQ=48cm,
∴FG=PD,
∴FG=PD=PB+BD=49+48=97(cm),
答:点F到水平地面的距离FG为97cm.
10.(2025 兴庆区三模)如图,在平行四边形ABCD中,AB<BC.
(1)请用无刻度的直尺和圆规按要求作图,保留作图痕迹,不写作法.
①在线段BC上找一点E,使点E到AB,AD的距离相等;
②在线段AD上截取DF,使DF=CE;
(2)在(1)所作的图形中,连接EF,求证:四边形ABEF是菱形.
【解答】(1)解:图形如图所示:
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵DF=CE,
∴BE=AF,
∴四边形ABEF是平行四边形,
∵点E到AB,AD的距离相等,
∴AE平分∠BAD,
∴∠BAE=∠EAD,
∵AD∥BC,
∴∠BEA=∠EAD,
∴∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是菱形.
11.(2025 太康县一模)为迎接2026年米兰一科尔蒂纳丹佩佐冬奥会,某市扩建了一座国际标准室内滑雪训练场,该滑雪场采用最新造雪技术,整个赛道长180米,可模拟高山滑雪环境,国家队运动员小明为备战冬奥会,在此进行技术训练.如图,他从赛道顶端A处开始下滑,滑行3秒后,教练操控一台无人机从A处沿赛道方向保持安全高度跟拍训练过程(安全高度可忽略不计).训练中心记录了小明离A处的滑行距离y(单位:m)以及无人机离A处的距离s(单位:m)随滑行时间x(单位:s)的变化数据如下:
滑行时间x/s 0 1 2 3 4 5 6
滑行距离y/m 0 4 10 18 28 40 54
无人机离A处的距离s/m 0 0 0 0 12 24 36
经探究发现,y与x之间成二次函数关系,s与x(x≥3)之间成一次函数关系.
(1)直接写出y关于x的函数解析式和x关于x(x≥3)的函数解析式;(不要求写出自变量的取值范围)
(2)小明滑完整个训练赛道需要耗时多久?
(3)分析在小明到达终点前,无人机能否追上小明,若能,求出相遇时间;若不能,求出无人机与小明的最小距离.
【解答】解:(1)设y=ax2+bx+c,由题意可得:
,
解得,
∴y=x2+3x;
设s=kx+n,由题意可得:
,
解得,
∴s=12x﹣36(x≥3),
∴y关于x的函数解析式为y=x2+3x,s关于x的函数解析式为s=12x﹣36(x≥3);
(2)在y=x2+3x中,令y=180得:
180=x2+3x,
解得x=12或x=﹣15(舍去),
∴小明滑完整个赛道需要耗时12s;
(3)联立得x2+3x=12x﹣36,
整理得x2﹣9x+36=0,
∵Δ=b2﹣4ac=(﹣9)2﹣4×36=﹣63<0,
∴无人机不能追上小明,
由题意得x2+3x﹣(12x﹣36)=(x﹣4.5)2+15.75,
∵(x﹣4.5)2≥0,
∴无人机与小明的最小距离为15.75m.
12.(2025 上栗县二模)某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整
收集数据:七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70.
整理数据:七年级20名学生测试成绩频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的成绩范围为50≤x<60):
八年级20名学生测试成绩频数分布表:
成绩 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数 0 4 5 7 4
分析数据:两组样本数据的平均数、中位数、众数方差如表所示:
年级 平均数 中位数 众数 方差
七年级 76.9 a b 119.89
八年级 79.2 81 74 100.4
(1)补全七年级20名学生测试成绩频数分布直方图.
(2)请直接写出a,b的值.
(3)请根据抽样调查数据,估计全校七年级垃圾分类知识测试成绩在80分及以上的大约有多少人.
(4)通过以上分析,你认为哪个年级学生对垃圾分类知识掌握得更好?请说明推断的理由(两条即可).
【解答】解:(1)20﹣2﹣3﹣5﹣3=7(人),
补全频数分布直方图如下:
(2)七年级20名学生的测试成绩从小到大排列处在中间位置的两个数的平均数为77.5,因此中位数是77.5,即a=77.5,
七年级20名学生的测试成绩出现次数最多的是86分,共出现4次,因此众数是86,即b=86,
答:a=77.5,b=86;
(3)500200(人),
答:全校七年级垃圾分类知识测试成绩在80分及以上的大约有200人;
(4)八年级成绩较好,理由为:八年级学生测试成绩的平均数、中位数均比七年级的高,而八年级的方差较小.
13.(2025 天府新区模拟)如图,在△ABC中,∠BAC=90°,D为AB上一点,以AD为直径作⊙O,交BC于E,F两点,点E为BC中点,连接AE,DE.
(1)求证:AE AC=AB DE;
(2)若,,求⊙O的直径和EF的长.
【解答】(1)证明:∵∠BAC=90°,点E为BC中点,
∴AE=BE=CE,
∴∠B=∠BAE,
∵AD是直径,
∴∠AED=90°,
∴tan∠DAE,tanB,
∴,
∴AE AC=AB DE;
(2)解:∵AE=BE=CE,
∴BC=2,
∵tanC,
∴ABAC,
∵BC2=AC2+AB2,
∴120=6AC2,
∴AC=2,
∴ABAC=10,
∵AE AC=AB DE,
∴210DE,
∴DE,
∴AD6,
∴BD=4,⊙O的直径为6,
如图,连接AF,
∵四边形ADEF是圆内接四边形,
∴∠AFE+∠ADE=180°,
∵∠ADE+∠BDE=180°,
∴∠AFE=∠BDE,
又∵∠B=∠B,
∴△BDE∽△BFA,
∴,
∴4×10BF,
∴BF,
∴EF=BF﹣EF.
14.(2025 上栗县二模)如图,在平面直角坐标系中,点B坐标为(0,1),点A(m,3)在函数y(k>0,x>0)的图象上,将线段AB向右下方平移,得到线段CD,此时点C落在函数y的图象上,点D落在x轴正半轴上,且点D坐标为(1,0).
(1)求k的值;
(2)求直线AC所对应的函数表达式.
【解答】解:(1)由条件可知C(m+1,2).
∵点A和点C在函数的图象上,
∴3m=2(m+1),
∴m=2,
∴k=2×3=6.
(2)设直线AC所对应的函数表达式为y=ax+b.
将A(2,3),C(3,2)代入得:,
解得:,
∴直线AC所对应的函数表达式为y=﹣x+5.
15.(2025 铁岭模拟)某工厂加工某种型号芯片,成本价为20元/个.根据市场调查发现,销售量y(个)是关于销售单价提高x(元)的一次函数(x≥0,且x为整数),其关系如下表:
提高x元 单价(元/个) 销售量(个)
0 25 500
1 26 480
2 27 460
… … …
x 25+x
(1)求销售量y与x之间的函数关系式;
(2)由于工厂生产规模受限,每日加工该种芯片不能少于340个且不能超过620个,每日加工的芯片全部售出,该芯片销售单价定为多少元时,才能获得最大销售利润?最大销售利润是多少?
【解答】解:(1)∵销售量y(件)是关于销价单价提高x(元)的一次函数,
∴可设 y=kx+b.
∴.
∴.
∴y=500﹣20x.
(2)由题意,∵每日加工量限制为340≤y≤620,且y=﹣20x+500,
∴0≤x≤8且x为整数.
又∵销售单价为(25+x)元,
∴单个利润为(25+x﹣20)=(x+5)元.
∴总利润P=(x+5)(﹣20x+500)=﹣20x2+400x+2500=﹣20(x﹣10)2+4500.
∵0≤x≤8且x为整数,
∴当x=8时:销售单价为25+8=33元,此时销售量为y=﹣20×8+500=340,总利润为P=(8+5)×340=4420元.
答:销售单价定为33元时,利润最大,最大利润为4420元.
16.(2025 开封二模)如图,△ABC的顶点为网格线的交点,反比例函数的图象过格点A,B.将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′.
(1)求过点C′的反比例函数解析式,并画出其图象(x<0).
(2)在过点C′的反比例函数图象上任取一点D,过点D向y轴作垂线,交的图象于点E,连接DO,EO,△ODE的面积会发生变化吗?若不变化,求出△ODE的面积;若变化,请说明理由.
【解答】解:(1)如图1,C(4,4),
∵将△ABC先向左平移5个单位长度,再向下平移1个单位长度,得到点C的对应点C′,
∴C′(﹣1,3),
设点C′的反比例函数解析式为,
∴,
∴k=﹣3,
∴过点C′的反比例函数解析式为,其图象(x<0);
(2)△ODE的面积不会发生变化;理由如下:
如图2,设DE交y轴于点F,
∵DE⊥y轴,过点C′的反比例函数解析式为,反比例函数的图象过格点A,B,
∴S△ODF,S△OEF,
∴S△ODE=S△ODF+S△OEF3,
∴△ODE的面积不会发生变化,△ODE的面积为3.
17.(2025 扬州一模)如图①,在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)如图②,连接CE,若∠FCB=90°,CE=5,求AB的长.
【解答】(1)证明:∵E为AD中点,
∴AE=DE,
∵AF∥BC,
∴∠DBE=∠AFE
∵∠DEB=∠AEF
∴△DEB≌△AEF,
∴AF=DB,
∵AD是直角三角形CAB斜边CB上的中线,
∴AD=BD=DC,
∴AF=DC,
∵AF∥DC,
∴四边形ADCF是平行四边形,
∵AD=DC,
∴四边形ADCF是菱形.
(2)解:∵∠FCB=90° 且四边形ADCF是菱形,
∴四边形ADCF是正方形,
∴∠ADC=90°,
∵DC=DB,AD⊥BC,
∴AC=AB,
∴AD=CD=DB,设 AE=DE=x,则 CD=BD=AD=2x,
∵EC2=CD2+DE2,
∴5x2=25,
∴ (负根已经舍弃),
∴,
∴.
18.(2025 鼓楼区二模)如图①所示,沪宁高速公路可近似看作一条直线.一辆货车以80km/h的速度从南京出发匀速驶往上海;同时,一列轿车以120km/h的速度从苏州出发匀速驶往上海,停留0.5h后,按照原速度继续开往南京,最终两车同时到达目的地.设货车行驶的时间为t h,货车与南京的距离y1km,轿车与南京的距离y2km.
(1)在图2中,分别画出和补全y1、y2关于t的函数图象;
(2)分别求苏州到上海的距离,南京到上海的距离;
(3)若镇江距离南京90km,直接写出货车和轿车经过镇江的时间间隔.
【解答】解:(1)画出和补全y1、y2关于t的函数图象如图所示:
(2)苏州到上海的距离为12080(km),
设南京到上海的距离为x km,
根据题意,得,
解得x=280.
∴南京到上海的距离280km.
(3)货车经过镇江时的时间为90÷80(h),
轿车经过镇江时的时间为(280﹣90)÷120(h),
(h).
答:货车和轿车经过镇江的时间间隔为h.
19.(2025 上栗县二模)秋水广场音乐喷泉是江西省南昌市红谷滩新区赣江边上的一道亮丽风景线,它不仅是城市景观的重要组成部分,也成为了市民休闲娱乐的好去处.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)用含a,b的代数式表示抛物线y=ax2+bx的顶点坐标为(, );
(2)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a,b的值;
(3)若k=3,,则喷出的抛物线水线能否达到岸边?
【解答】解:(1)在y=ax2+bx中,
当时,,
故答案为:;
(2)∵y=ax2+bx的顶点坐标为,抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴,,
解得,,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是,2;
(3)当k=3,时,
∵y=ax2+bx的顶点坐标为,抛物线的顶点在直线y=3x上,
∴,
解得:b=6或b=0(舍去),
∴抛物线解析式为.
当y=0时,,
解得:x1=27,x2=0,
∵27>18,
∴喷出的抛物线水线能达到岸边.
20.(2025 深圳校级二模)新课标中,数学课程要培养的学生核心素养是“用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界”,这集中体现了数学课程的育人价值,也说明数学和实际生活密不可分.数学老师给小明小组布置了一项数学与实际的作业,让他们到菜市场进行调研,并利用所学的数学知识对销售提出合理化建议.小明小组经调研发现,某店铺蔬菜的售卖情况大致遵循以下规律.
规律一 当每千克蔬菜的售价为8元时,每天能销售80千克.
规律二 当每千克蔬菜的售价每降低0.5元,每天的销售量就会增加10千克.
经小组讨论,发现里面可能存在函数关系,考虑用已学的函数知识帮助店家解决问题.
【建立模型】
(1)设每天销售这种蔬菜的销售额为y元,每千克蔬菜降价x元,求y与x的函数关系式;
【设计方案】
(2)当每千克蔬菜降价多少元时,该店铺每天销售这种蔬菜的销售额最多?最多为多少元?
【实际需求】
(3)若该店铺老板希望每天销售这种蔬菜的销售额不低于540元,求这个蔬菜应参考的售价范围.
【解答】解:(1)由题意,∵每千克蔬菜的售价为8元时,销量为80千克,每降价0.5元,销量增加10千克,
∴设降价为x元,则销量增加量为(千克).
∴总销量为(80+20x)千克.
又∵此时售价变为(8﹣x)元/千克,
∴销售额y与x的函数关系式为:y=(8﹣x)(80+20x)=﹣20x2+80x+640.
(2)由题意,结合(1)y=﹣20x2+80x+640=﹣20(x﹣2)2+720.
∴当x=2时,y取最大值,最大销售额为720元.
答:当每千克蔬菜降价2元时,该店铺每天销售这种蔬菜的销售额最多,最多为720元.
(3)由题意,令y=﹣20x2+80x+640=540,
∴x=﹣1或x=5.
又∵二次函数y=﹣20x2+80x+100≥0的图象开口向下,
∴该店铺老板希望每天销售这种蔬菜的销售额不低于540元,则0≤x≤5.
∴对应售价为:8﹣5=3元至8﹣0=8元,即这个蔬菜应参考的售价范围是3元至8元.
21.(2025 琼山区校级一模)在平面直角坐标系中,已知抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C.
(1)如图,若抛物线经过A(1,6),B(﹣2,3)两点,
①求抛物线的解析式;
②设抛物线顶点为D,求△ACD的面积;
③点P是抛物线对称轴上的动点,则PA+PC的最小值为 3 ;
(2)若抛物线经过E(2a,3),F(x1,y1),G(x2,y2)三点,对于x1=3a,3≤x2≤4,都有y1<y2,求a的取值范围.
【解答】解:(1)①∵抛物线y=ax2+bx+3经过A(1,6),B(﹣2,3)两点,
∴,解得,
∴抛物线的解析式为y=x2+2x+3;
②∵抛物线y=ax2+bx+3(a,b是常数,a≠0)与y轴交于点C,
∴C(0,3),
∵y=x2+2x+3=(x+1)2+2,
∴抛物线顶点D(﹣1,2),
设直线AD的解析式为y=mx+n,与y轴的交点为M,
∴解得,
∴直线AD的解析式为y=2x+4,
∴M(0,4),
∴CM=4﹣3=1,
∴S△ACD=S△ACM+S△BCM;
③连接AB交抛物线的对称轴于P,此时,PA+PC的值最小,最小值为AB,
∴A(1,6),B(﹣2,3),
∴AB3
即PA+PC的最小值为3,
故答案为:3;
(3)由条件可知:抛物线的对称轴是直线xa,
①当a>0时,此时抛物线开口向上,
当x>a时,y随着x的增大而增大,
∵对于x1=3a,3≤x2≤4,都有y1<y2,
∴3a<3,
∴a<1,
又∵a>0,
∴0<a<1;
②当a<0时,抛物线开口向下,对称轴为直线x=a,
此时a﹣3a>4﹣a,
解得a<﹣4,
又∵a<0,
∴a<﹣4;
综上,当0<a<1或a<﹣4时,都有y1<y2.
22.(2025 张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
【解答】解:(1)点D在半圆O所在的圆上.
理由如下:如图,连接OD.
∵DC=AC,∠OCD=∠OCA,OC=OC,
∴△OCD≌△OCA(SAS),
∴OD=OA,
∴点D在半圆O所在的圆上;
(2)①∵点D在半圆O所在的圆上,
∴∠CDE=∠CAB.
由条件可知∠CDE=∠OCD,
∴OC∥DE,
由条件可知∠OCE=90°,
∴∠E=90°;
②由题意,得∠CAB=∠CDB=∠OCA=∠OCD=30°,
∴∠BOC=60°,
∴BC的长度为,
由条件可知∠ACB=90°,
∴,∠BCD=∠ACB﹣∠OCA﹣∠OCD=30°,
∴∠BCD=∠CDB,
∴BC=BD=5.
∵,
∴.
23.(2025 镇江模拟)如图,在平面直角坐标系中,直线yx+b经过点A(﹣6,0),与y轴交于点B,与反比例函数y(x>0)交于点C,连接OC,且S△AOB=2S△BOC.
(1)求b,k的值;
(2)若点D为反比例函数y(x>0)图象上一点,连接CD,使得CD⊥OC,求点D的坐标.
【解答】解:(1)作CE⊥x轴于点E,
∵直线yx+b经过点A(﹣6,0),与y轴交于点B
∴0b,
∴b=4,
∴B(0,4),
∴OA=6,OB=4,
∵S△AOB=2S△BOC,
∴AB=2BC,
∴,
∵CE∥OB,
∴△AOB∽△AEC,
∴,
∴CE=6,AE=9,
∴OE=9﹣6=3,
∴C(3,6),
∵反比例函数y(x>0)过点C,
∴k=3×6=18;
(2)作DF⊥CE于点F,
由(1)可知反比例函数为y,C(3,6),
设D(m,),则CF=6,DF=m﹣3,
∵CD⊥OC,
∴∠OCE+∠DCF=90°,
∵∠OCE+∠COE=90°,
∴∠DCF=∠COE,
∵∠CEO=∠DFC=90°,
∴△CEO∽△DFC,
∴,即,
整理得m2﹣15m+36=0,
解得m=12或m=3(舍去),
∴D(12,).
24.(2025 厦门模拟)如图1,AB为半圆O的直径,AB=4,C为半圆上的动点,连接OC,点A关于OC的对称点为点D,连接BD.(0°<∠AOC<45°)
(1)若∠AOC=40°,连接AC,AD,求∠CAD的度数;
(2)如图2,若点E在半圆O上,BE的长度为π,连接DE,F为DE中点,连接OF交BD于点M,Q为OE上一点,OQ=1.2.
①当∠AOC=30°时,判断点Q与直线BD的位置关系,并说明理由;
②如图3,连接QM,在点C运动过程中,当BQ=QM时,记α=45°﹣∠AOC,求tanα的值.
【解答】解:(1)连接OD,
∵AB为半圆O的直径,点A关于OC对称点为点D,
∴OA=OD,OC⊥AD,
∴点D在半圆O上,
∴∠COD=∠AOC=40°,
∴;
(2)①点Q在直线BD外,理由如下:
连接OD,
∵AB为⊙O直径,点A关于OC对称点为点D,
∴OA=OD,OC⊥AD,
∴点D在半圆O上,
∴,
∵,
∴∠B=∠AOC,
∵的长度为π,半圆O的直径AB=4,
∴,
∴∠BOE=90°,
∴∠AOE=180°﹣∠BOE=90°,
∵∠AOC=30°,
∴∠B=∠AOC=30°,
设OE与BD交于点P,直角三角形BOP中,,
∴,
又∵Q在OE上,OQ=1.2,OP≠OQ,
∴点Q在直线BD外;
②连接OD,EM,BE,如图所示,
则,
∵OD=OE,F为DE中点,
∴EF=DF,OF⊥ED,,
∴ME=MD,
∴∠DEM=∠EDM=45°,
∴∠EMD=90°,
∴∠EMB=180°﹣∠EMD=90°,
设OE交BD于点N,
∵∠QEM=90°﹣∠ENM,∠DBO=90°﹣∠BNO,∠ENM=∠BNO,
∴∠QEM=∠DBO,
∵EQ=QM,BO=DO,
∴∠QME=∠QEM=∠DBO=∠BDO,
∴△QME∽△ODB,
∴,
∵OQ=1.2,OE=2,
∴QE=OE﹣OQ=0.8,
∴,
设EM=2x,BD=5x,
∴ME=MD=2x,BM=BD﹣DM=3x,
∴,
在直角三角形EBM中,∠EMB=90°,
∴,
∵,
∴∠EBM=∠DOF,
∵,,
∴,
∴∠DOF=45°﹣∠AOC,
∴∠EBM=∠DOF=α,
∴.
25.(2025 湖州一模)纵观古今,解码测量背后的数学智慧.
(1)【古】《周髀算经》中记载了“偃矩以望高”的方法.意思是把“矩(曲尺)”仰立放,可测物体的高度.如图,点B,D,E在同一水平线上,∠ABE=∠CDE=90°,AE与CD交于点F.测得DF=0.35米,DE=0.55米,BE=22米,求树AB的高度.
(2)【今】某综合实践活动小组,尝试通过利用无人机(无人机限高120米)测算某山体的海拔高度,设计了如下两种方案.请选择其中一种可行的测算方案,计算该山体的海拔高度(AB的长).(精确到1米)
测量示意图 方案说明
方案一
无人机位于海拔高度为60米的C处,测得与山顶A处的仰角α为45°,与山脚D处的俯角β为65°.(参考数据:sin65°≈0.90,cos65°≈0.42,tan65°≈2.14)
方案二
当无人机位于海拔高度为60米的C处时,测得与山顶A处的仰角γ为45°;当无人机垂直上升到海拔高度为113米的G处时,测得与山顶处A的仰角θ为25°.(参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47)
【解答】解:(1)∵∠ABE=∠CDE=90°,∠AEB=∠FED,
∴△ABE∽△FDE,
∴,
∵DF=0.35米,DE=0.55米,BE=22米,
∴,
∴AB=14,
答:树AB的高度为14米;
(2)选择方案二进行问题解决:
∵∠ACE=γ=45°,∠AEC=90°,
∴AE=CE,
∵∠AGH=θ=25°,∠AHG=90°,
∴,
可得,
∴(米),
∴AB=AE+EB=CE+CF=160(米),
∴山体高度约为160米.
26.(2025 上蔡县三模)如图,正方形ABCD的两个顶点A(2,m),C(4,n)都在反比例函数y(x>0)的图象上.
(1)求这个反比例函数的表达式.
(2)反比例函数y(x>0)的图象经过点B,直线x=t(t>0)分别与反比例函数y(x>0),y(x>0)的图象交于点M,N.若1<t<6,求MN的长的取值范围.
【解答】解:(1)由条件可知k1=2m=4n,
∵点A(2,m),C(4,n)是正方形ABCD的两个顶点,
∴AB=BC=4﹣2=2,
∴m﹣n=2,
联立,
解得:,
∴A(2,4),C(4,2),
∴k1=2×4=8,
∴这个反比例函数的表达式为;
(2)由条件可知B(2,2),
∵反比例函数的图象经过点B(2,2),
∴k2=2×2=4,
即,
∴,,
∴,
∵1<t<6,
∴,
∴,
∴MN的长的取值范围是.
27.(2025 雁塔区校级模拟)如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴分别相交于A,B两点,与y轴交于点C,直线y=﹣x+3经过B、C两点.
(1)求抛物线的表达式;
(2)抛物线的顶点为M,点N是y轴上一点,点Q是平面内一点,是否存在以B、M、N、Q为顶点的四边形是以BM为边的矩形?若存在,请求出点N、Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵B、C分别是直线y=﹣x+3与x轴,y轴的交点,
∴点B的坐标为(3,0),点C的坐标为(0,3),
∵B、C在抛物线y=﹣x2+bx+c上,
∴,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4),
设N(0,n),Q(p,q),
①如图:当∠BMN=90°时,
则,
解得:,
∴,;
②如图:当∠NBM=90°时,
则,
解得:,
∴,;
综上所述:,或,.
28.(2025 思明区校级二模)研究发现人的身体每天消耗的热量主要由碳水化合物和脂肪(不考虑蛋白质及其他有机物)提供,碳水化合物和脂肪分解时所消耗的氧气、生成的二氧化碳、释放的热量三个方面的相关数据如表:
分解的营养物质 氧气消耗量/克 二氧化碳生成量/克 释放热量/千焦
1克碳水化合物 1 1.5 15
1克脂肪 3 3 45
请解答下列问题:
(1)研究人员测出小祺在某次运动中平均每分钟消耗氧气2.5克,产生二氧化碳3克,求小祺的身体平均每分钟分解碳水化合物与脂肪各多少克.
(2)已知小祺骑脚踏车每分钟消耗热量20千焦,快走每分钟消耗热量27千焦,小祺某天骑脚踏车和快走共1小时,若要消耗完40克碳水化合物与20克脂肪分解后释放的热量,小祺至少需要分配多少分钟进行快走?(精确到1分钟)
【解答】解:(1)设小祺的身体平均每分钟分解碳水化合物x克,脂肪y克.
根据题意,得.
解得,
即小祺的身体平均每分钟分解碳水化合物1克,脂肪0.5克,
答:小祺的身体平均每分钟分解碳水化合物1克,脂肪0.5克;
(2)设小祺分配m分钟进行快走,则分配(60﹣m)分钟骑脚踏车,
根据题意,得27m+20(60﹣m)≥40×15+20×45.
解得:,
∵结果精确到1分钟,
∴m的最小值为43.
答:小祺至少需要分配43分钟进行快走.
29.(2025 香坊区校级三模)在平面直角坐标系中,O为坐标原点,直线AB交x轴负半轴于点A,交y轴正半轴于点B,,AB=20.
(1)如图1,求直线AB的解析式;
(2)如图2,P为x轴正半轴上一点,C为AB的中点,连接CP,设△ACP的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,直线y=kx﹣12k交x轴、y轴于点D、E,交直线AB于点F,,G为y轴负半轴上一点,连接CG交x轴于点H,,过点P作PI⊥x轴交DE于点I,L为PI上一点,连接EL,J为EL上一点,连接JG,∠DIP+∠EJG=180°,且∠FAD﹣∠FDA=2∠OED﹣∠BFE,EJ:I=5;,M为x轴负半轴上一点,连接EM、LM、LN,若N为EM的中点,∠LEN+∠MLN=∠AFD,求直线LM的解析式.
【解答】解:(1)∵∠AOB=90°,,AB=20,
∴,,
∴A(﹣12,0),B(0,16),
设直线AB的解析式为y=ax+b,
则,
解得,,
∴;
(2)如图,作CQ⊥x轴于点H,则,
∵点P在x轴正半轴上,且横坐标为t,
∴OP=t,
∴;
(3)∵直线y=kx﹣12k交x轴于点D,
∴D(12,0),
∴OP+DP=OD=12,
∵,OA=12,
∴OP=8,
∵,OH+AH=OA=12,
∴,
∴,
∵∠FAD﹣∠FDA=2∠OED﹣∠BFE,
∴∠FAD﹣∠FDA=2(90°﹣∠FDA)﹣(∠FAD+∠FDA)=180°﹣3∠FDA﹣∠FAD,
∴∠FAD+∠FDA=90°,
∴∠AFD=90°,
∵C(﹣6,8),,
∴直线CH的解析式为,
∴G(0,﹣1),
∵OD=12,,
∴E(0,9),
∴EG=10,
∵PI⊥x轴,EG⊥x轴,
∴PI∥EG,
∴∠ELI=∠GEJ,
∵∠DIP+∠EJG=180°,
∴∠EJG=180°﹣∠DIP=∠LIE,
∴△EJG∽△LIE,
∴,
∴,
如图,作MS⊥EL于点S,交NL于点T,连接NS,则∠LEN+∠EMS=90°,
∵点N为EM的中点,
∴,
∴∠NSM=∠NMS,
∵∠LEN+∠MLN=∠AFD,∠AFD=90°,
∴∠NLM=∠EMS=∠NSM,
又∵∠NTS=∠LTM,
∴△NST∽△MTL,
∴,
又∵∠NTM=∠STL,
∴△NTM∽△STL,
∴∠MNT=∠LST=90°,
又∵点N为EM的中点,
∴,
如图,作LK⊥EG于点K,则KL=OP=8,
∴,
∴LP=KO=1,
∴L(8,1),,
∴,
设直线ML的解析式为y=mx+n,
则,
解得:,
∴.
30.(2025 雁塔区校级模拟)【问题提出】
如图①,在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,点P,Q分别是BC,AC上的动点,则EP+PQ的最小值是 ;
【问题解决】
如图②,某大型工厂生产区域内,有一个矩形场地ABCD,其中点D为原材料入口,修建在DC段的点G为成品出口.在生产区域内,有两处重要的生产加工点E和F,分别位于场地的DA,DB段,并且DE=DF.为了实现从生产加工点到成品出口的高效运输(即成品从生产加工点经质检区域输送到出口的过程更为高效),工厂规划修建一个调度中心P与一处位于BC段的半圆形自动化质检区域(圆心为O).该调度中心需同时满足以下两个条件:①使P到生产加工点E,F的距离相等,即PE=PF;②使运输线路PM+NG的长度最短(其中M,N为半圆质检区域O上的任意两点).已知AD=300米,AB=400米,CG=100米,质检区域半径r=20米.请问是否存在符合要求的调度中心点P,若存在,求出PM+NG的最小值和此时OC的距离;若不存在,请说明理由.
【解答】解:(1)如图所示,作点E关于BC的对称点H,连接PH,
∵在Rt△ABC中,∠B=90°,AB=BC=4,E是AB边上的中点,
∴AE=BEAB=2,∠A=∠C=45°,
由轴对称的性质可得EP=HP,EB=BH=2,
∴PE+PQ=PH+PQ,
∴当H、P、Q三点共线,且HQ⊥AC时,PH+PQ有最小值,即此时PE+PQ有最小值,最小值为HQ的长,
在Rt△AHQ中,,
∴PE+PQ的最小值为,
故答案为:;
(2)∵PE=PF,
∴点P在线段EF的垂直平分线上,
∵DE=DF,
∴点D在线段EF的垂直平分线上,
∴DP垂直平分EF,
∴点P在∠ADB的角平分线上,
如图所示,作∠ADB的角平分线交AB于H,作点G关于BC的对称点G',作G'P⊥DH交BC于O',此时PM+NG有最小值,理由如下:
∵PM+GN=PO+OG﹣2r=PO+OG﹣40,
∴当PO+OG最小时,PM+GN最小,
由轴对称的性质可得G'O=OG,
则PO+OG=PO+OG',故当P、O、G'三点共线且G'P⊥DH时,PO+OG'有最小值,即此时PO+OG有最小值,最小值为线段PG'的长;
在Rt△ABD中,由勾股定理得长;
如图所示,连接HG',过点H作HA'⊥BD于A',
∴AH=A'H,
∵S△ABD=S△ADH+S△BDH,
∴,
∴AH=A'H=150米,
∴,
∵,
∴,
∴米;
在Rt△G'PD中,由勾股定理得;
∵,
∴,
∴O'C=50米;
综上所述,PM+NG的最小值为米,此时OC的距离为50米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
