期末综合模拟试题 2024-2025学年下期初中数学人教版八年级下册
文档属性
| 名称 | 期末综合模拟试题 2024-2025学年下期初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末综合模拟试题 2024-2025学年
下期初中数学人教版八年级下册
一、单选题
1.下列各数中,能使有意义的是( )
A.6 B.0 C.3 D.
2.下列各组数据中,不是勾股数的是( )
A.3,4,5 B.5,7,9 C.8,15,17 D.7,24,25
3.下列命题是假命题的是( )
A.平行四边形的对边相等 B.四条边都相等的四边形是菱形
C.矩形的两条对角线互相垂直 D.正方形的对角线垂直平分且相等
4.下列等式成立的是( )
A. B. C. D.
5.菲尔兹奖是数学领域的一项国际大奖,被视为数学界的诺贝尔奖,其规定获奖数学家年龄不得超过40岁.截至目前,菲尔兹奖得主中最年轻的8位数学家获奖时年龄分别为:29,27,31,31,31,29,29,31,则该组由年龄组成的数据的众数和中位数是( )
A.29,31 B.29,29 C.31,30 D.31,31
6.如图,在平坦的地面上,为测量位于水塘旁的两点A,B间的距离,先确定一点O,分别取的中点C,D,量得m,则A,B之间的距离是( )
A.20m B.40m C.60m D.80m
7.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
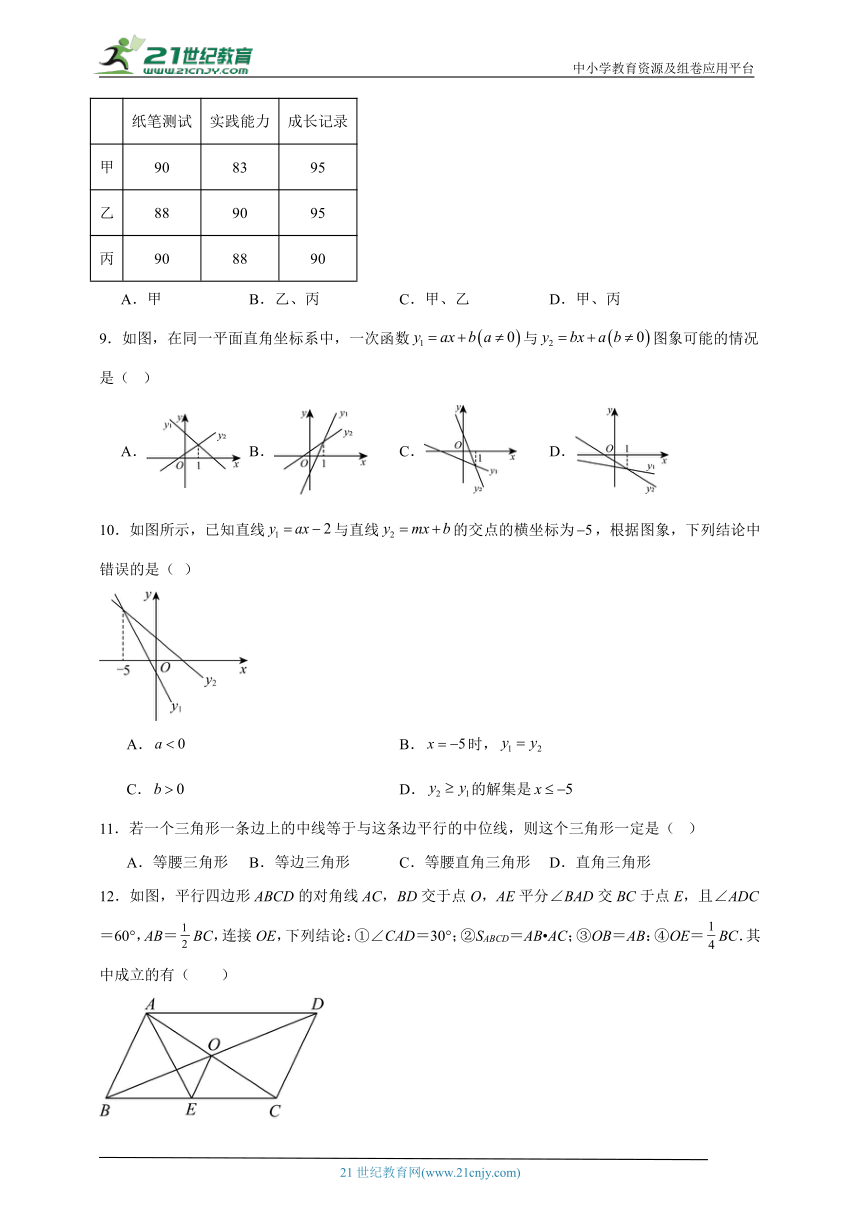
8.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
9.如图,在同一平面直角坐标系中,一次函数与图象可能的情况是( )
A. B. C. D.
10.如图所示,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.时,
C. D.的解集是
11.若一个三角形一条边上的中线等于与这条边平行的中位线,则这个三角形一定是( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
12.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②SABCD=AB AC;③OB=AB:④OE=BC.其中成立的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
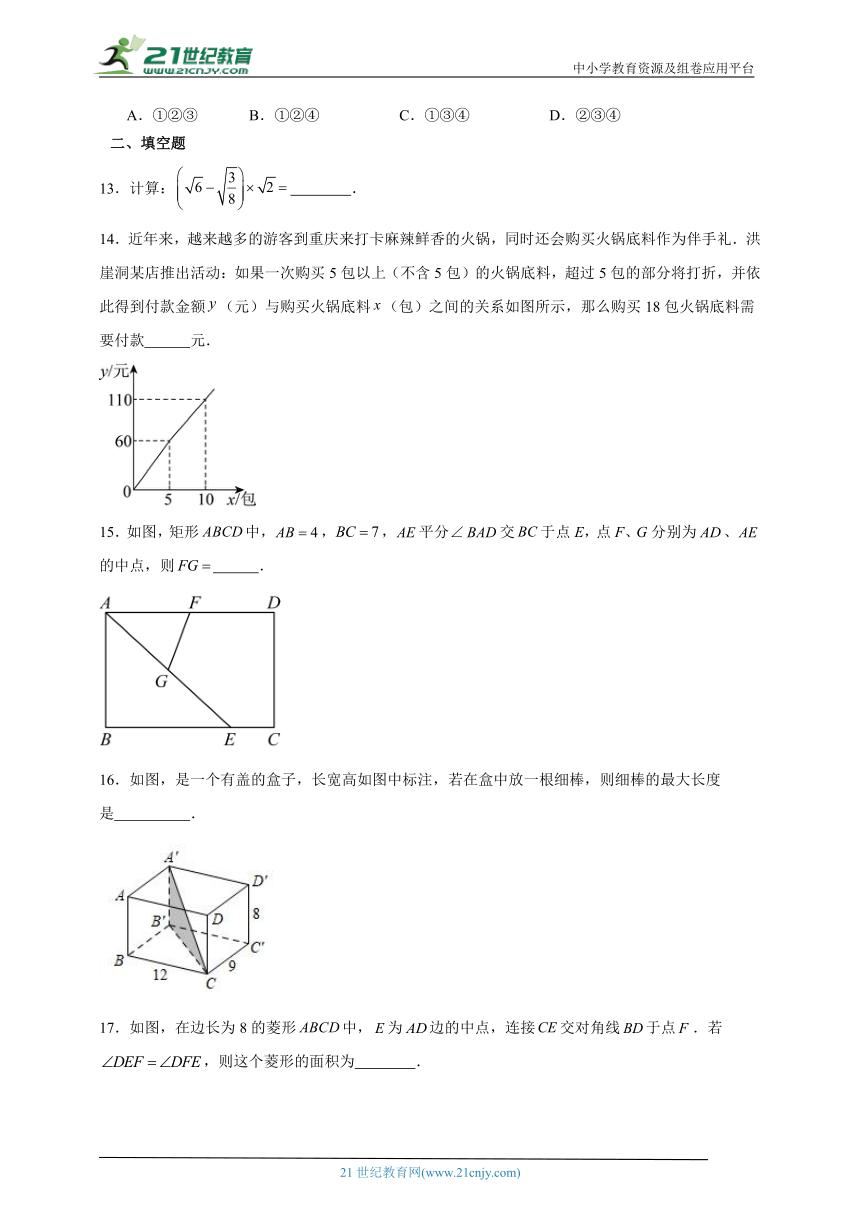
13.计算: .
14.近年来,越来越多的游客到重庆来打卡麻辣鲜香的火锅,同时还会购买火锅底料作为伴手礼.洪崖洞某店推出活动:如果一次购买5包以上(不含5包)的火锅底料,超过5包的部分将打折,并依此得到付款金额(元)与购买火锅底料(包)之间的关系如图所示,那么购买18包火锅底料需要付款 元.
15.如图,矩形中,,,平分∠交于点E,点F、G分别为、的中点,则 .
16.如图,是一个有盖的盒子,长宽高如图中标注,若在盒中放一根细棒,则细棒的最大长度是 .
17.如图,在边长为8的菱形中,为边的中点,连接交对角线于点.若,则这个菱形的面积为 .
18.已知,直线与轴相交于点,以为边作等边三角形,点在第一象限内,过点作轴的平行线与直线交于点,与轴交于点,以为边作等边三角形(点在点的上方),以同样的方式依次作等边三角形,等边三角形,则点的横坐标为 .
三、解答题
19.已知:,,求的值.
20.先化简,再求值:,其中.
21.如图,在中,点F是中点,连接并延长交的延长线于点E.求证:.
22.如图,在四边形中,,点E在的延长线上,,连接交边于点F,且,连接,且.
(1)求证:四边形为菱形;
(2)若,,求菱形的面积.
23.一次函数的图象经过,两点.
(1)此一次函数的解析式;
(2)求的面积.
24.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目段和段均由不锈钢管材打造,总长度为26米,矩形和矩形均为木质平台的横截面,点G在上,点C在上,点D在上,经过现场测量得知米,米.
(1)求立柱的长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索,经测量米,请你求出要焊接的钢索的长.
25.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共儒投入34万元.
(1)种植A、B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
26.如图1,在矩形中,点,分别在轴、轴正半轴上,点在第一象限,,.
(1)请直接写出点的坐标;
(2)如图2,平分交于点,求的面积;
(3)如图3,动点在第一象限,且点在直线上,点在线段上,是否存在以点为直角顶点的等腰直角三角形,若存在,请求出直线的解析式;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D C C D D
题号 11 12
答案 D B
1.A
【分析】本题考查了二次根式有意义的条件,根据题意可得,解不等式即可求解.
【详解】解:∵有意义
∴,
∴,只有A选项正确,
故选:A.
2.B
【分析】判断是否为勾股数,首先这三个数都要是正整数,同时还需验证两较小数的平方和是否等于最大数的平方.
【详解】、,能构成直角三角形,都是正整数,故选项错误;
、,不能构成直角三角形,故选项正确;
、,能构成直角三角形,都是正整数,故选项错误;
、,能构成直角三角形,都是正整数,故选项错误.
故选:.
【点睛】此题主要考查了勾股数的定义,熟记勾股数的定义是解题的关键.
3.C
【分析】.
【详解】解:A、平行四边形的对边相等,是真命题,选项说法正确,不符合题意;
B、四条边都相等的四边形是菱形,是真命题,选项说法正确,不符合题意;
C、矩形的对角线不垂直,是假命题,选项说法错误,符合题意;
D、正方形的对角线垂直平分且相等,是真命题,选项说法正确,不符合题意;
故选:C.
4.D
【分析】根据二次根式的运算法则即可逐一判断.
【详解】解:A、3和不能合并,故A错误;
B、,故B错误;
C、,故C错误;
D、,正确;
故选:D.
【点睛】本题考查了二次根式的运算,解题的关键是掌握基本的运算法则.
5.C
【分析】由数据可知,31出现4次,次数最多,所以众数为31;将数据按从小到大的顺序排列,可求出中位数.
【详解】解:由数据可知,31出现4次,次数最多,所以众数为31;
将数据从小到大排列为:27,29,29,29,31,31,31,31
所以中位数为:;
故答案为:C.
【点睛】本题考查众数和中位数,属于基础题,解题的关键在于理解众数和中位数的定义,并将数据按大小顺序排列.
6.D
【分析】根据三角形的中位线定理进行求解即可.
【详解】解:∵C,D为的中点,
∴是的中位线,
∴;
故选D.
【点睛】本题考查三角形的中位线定理.熟练掌握三角形的中位线定理,是解题的关键.
7.C
【分析】本题可根据两个非负数相加和为0,则这两个非负数的值均为0解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.
【详解】依题意得:,
∴,
斜边长,
所以正方形的面积.
故选C.
考点:本题综合考查了勾股定理与非负数的性质
点评:解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.
8.C
【分析】利用平均数的定义分别进行计算成绩,然后判断谁优秀.
【详解】由题意知,甲的总评成绩=90×50%+83×20%+95×30%=90.1,
乙的总评成绩=88×50%+90×20%+95×30%=90.5,
丙的总评成绩=90×50%+88×20%+90×30%=89.6,
∴甲乙的学期总评成绩是优秀.
故选:C.
【点睛】本题考查了加权平均数的计算方法.
9.D
【分析】对于每个选项,先确定一个解析式所对应的图象,根据一次函数图象与系数的关系确定、的符号,然后根据此符号看另一个函数图象的位置是否正确.
本题考查了一次函数图象:一次函数、为常数,是一条直线,当,图象经过第一、三象限,随的增大而增大;当,图象经过第二、四象限,随的增大而减小;图象与轴的交点坐标为.
【详解】解:根据题意,得,解得,故交点坐标为;
A、对于,,;对于,则,,a的符号不一致,
∴A选项不正确,不符合题意;
B、对于,,;对于,则,,b的符号不一致,
∴B选项错误,不符合题意;
C、对于,,;对于,则,,a的符号不一致,
∴C选项错误,不符合题意;
D、对于,,;对于,则,,
∴D选项正确,符合题意.
故选:D.
10.D
【分析】本题主要考查了一次函数与一元一次不等式、一次函数与一元一次方程的应用,依据题意,根据所给函数图象的分布及两直线的交点的横坐标为-5进而逐个判断可以得解.
【详解】解:由题意,∵直线的图象经过第二、三、四象限,
∴,故A正确,不合题意.
∵直线与直线的交点的横坐标为,
∴方程的解是,故B正确,不合题意.
∵直线的图象与y轴交于正半轴,
∴,故C正确,不合题意.
结合图象可得,当时,直线上的点都不在直线的下方,
∴不等式的解集为,即不等式的解集是,故D错误,符合题意.
故选:D.
11.D
【分析】本题考查三角形的中位线定理,等腰三角形的判定和性质,根据题意,画出图形,证明三角形为直角三角形即可得.
【详解】解:如图,为的中位线,为的中线,且,
∴
∴,,
∵,
即,
∴,即.
∴是直角三角形.
故选D.
12.B
【分析】由 ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②S ABCD=AB AC;可得OE是三角形的中位线,证得④OE=BC.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
,故④正确.
故选B.
【点睛】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形,OE是△ABC的中位线是关键.
13./
【分析】本题考查了二次根式的混合运算,二次根式的性质化简,掌握相关运算法则是解题关键.先根据乘法分配律展开,再计算乘法,然后化为最简二次根式计算即可.
【详解】解:
,
故答案为:.
14.
【分析】本题考查了一次函数的应用,待定系数法求得时的解析式,进而将代入,即可求解.
【详解】解:设时,与的函数关系式为,
将代入得,
解得:
∴
当时,
故答案为:.
15.
【分析】连接.由矩形的性质可间接证明,结合角平分线的定义得出,即得出,从而可求出,再由勾股定理可求出,最后根据三角形中位线定理求解即可.
【详解】解:如图,连接.
∵四边形为矩形,
∴,,,,
∴.
∵平分交于点E,
∴,
∴,
∴,
∴,
∴.
∵点F、G分别为、的中点,
∴.
故答案为:.
【点睛】本题考查矩形的性质,平行线的性质,角平分线的定义,等腰三角形的判定和性质,勾股定理,三角形中位线定理.正确连接辅助线是解题关键.
16.17
【分析】在,根据勾股定理求得,中,根据勾股定理即可得到结论.
【详解】解:依题意,在中,,
在中,,
故答案为:17.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
17.
【分析】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形面积,连接交于O,如图,根据菱形的性质得到,,再利用得到,证明得,则,所以,接着利用勾股定理计算出,从而得到,然后根据菱形的面积公式计算它的面积.
【详解】解:连接交于O,如图,
∵四边形为菱形,
∴,,
∵E为边的中点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴,
∴菱形的面积.
故答案为:.
18.
【分析】直线直线可知,点坐标为,可得,由于是等边三角形,可得点,把代入直线解析式即可求得的横坐标,可得,由于是等边三角形,可得点;同理,,发现规律即可得解,准确发现坐标与字母的序号之间的规律是解题的关键.
【详解】解:∵直线l:与x轴负半轴交于点,
∴点坐标为,
∴,
过,,作轴交x轴于点M,轴交于点D,交x轴于点N,
∵为等边三角形,
∴
∴,
∴
∴,
当时,,解得:,
∴,,
∴,
∴,
∴,
∴当时,,解得:,
∴;
而,
同理可得:的横坐标为,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了一次函数图象上点的坐标的特征,勾股定理的应用,等边三角形的性质,特殊图形点的坐标的规律,掌握探究的方法是解本题的关键.
19.
【分析】本题考查了二次根式的化简求值,分母有理化,解题的关键是正确对所求的式子分解因式.
先对所求的式子分解因式然后代入数值计算求解.
【详解】解:∵,,
∴
.
20.,
【分析】本题主要考查了分式的化简求值,分母有理化,先把除法变成乘法后约分化简,再通分化简,最后代值计算即可得到答案.
【详解】解:
,
当时,.
21.见解析
【分析】本题主要考查了平行四边形的性质,全等三角形的性质与判定,由平行四边形的性质得到,则,再由线段中点的定义得到,据此证明,得到,则可证明.
【详解】证明:∵四边形是平行四边形,
∴,
∴,
∵点F是中点,
∴,
在和中,
,
∴,
∴,
∴.
22.(1)见解析
(2)
【分析】本题考查菱形的判定和性质,直角三角形斜边中线的性质,含度角的直角三角形的性质,全等三角形的判定和性质,勾股定理等,熟练掌握以上知识点是解题的关键.
(1)根据可证,,再证,推出,等量代换可得,根据,证明四边形为平行四边形,再根据直角三角形斜边中线的性质推出,即可证明四边形为菱形;
(2)先求出菱形的边长,作于点,根据含度角的直角三角形的性质求出,再利用勾股定理求出,即可求出菱形的面积.
【详解】(1)证明:,点E在的延长线上,
,
,,
在和中,
,
,
,
,
;
,
四边形为平行四边形,
,,
是斜边的中线,
,
四边形为菱形;
(2)解:如图,作于点,
,,
,
四边形为菱形,
,
,,
,
,
,
菱形的面积.
23.(1)
(2)8
【分析】本题考查了一次函数的解析式求解、一次函数与坐标轴的交点问题,掌握待定系数法求出解析式是解题关键.
(1)将,两点代入即可求解;
(2)求出一次函数与坐标轴的交点,根据即可求解.
【详解】(1)解:将,两点代入得:
,
解得:
∴
(2)解:如图所示:
令,则;
∴,
∴
.
24.(1)立柱的长度为9米
(2)米
【分析】(1)根据题意得米,米,设米,则米,则由勾股定理可得出关于x的等式,解出x,即得出BG的长,从而即可求出AB的长.
(2)由题意得米,从而可求出米.进而可由勾股定理求出BF的长.
【详解】(1)(1)由题意得米,米,
设米,则米,
在中,由勾股定理得,
即,解得.
∴米.
∴米.
∴立柱的长度为9米.
(2)由题意得米,
∴米.
在中,由勾股定理得米.
【点睛】本题考查矩形的性质,勾股定理.掌握利用勾股定理解直角三角形的方法是解题关键.
25.(1)种植A,B两种蔬菜,每亩各需投入0.6万元、0.8万元
(2)w=-0.1m+150
(3)当种植A种蔬菜100亩,B种蔬菜50亩时,总获利最大,最大总获利为140万元.
【分析】(1)设种植A,B两种蔬菜,每亩各需投入x万元、y万元,然后根据“若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共儒投入34万元”列方程组求解即可;
(2)设种植A种蔬菜m亩,则 种植B种蔬菜,然后根据“利润=单件利润×数量”列式解答即可;
(3)先根据“若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍”列求出m的取值范围,再结合(2)的解析式求最值即可.
【详解】(1)解:设种植A,B两种蔬菜,每亩各需投入x万元、y万元.
根据题意,得,解得
答:种植A,B两种蔬菜,每亩各需投入0.6万元、0.8万元.
(2)解:设种植A种蔬菜m亩,
由题意,得w=0.8m+1.2×-0.1m+150.
(3)解:由题意,得,解得m≥100.
∵w=-0.1m+150,-0.1<0,
∴w随m的增大而减小.
∴当m=100时,w最大=140,此时=50(亩).
∴当种植A种蔬菜100亩,B种蔬菜50亩时,总获利最大,最大总获利为140万元.
【点睛】本题主要考查了二元一次方程组的应用、一元一次不等式的应用、运用一次函数的性质求最值等知识点,灵活应用所学知识成为解答本题的关键.
26.(1)
(2)
(3)存在,
【分析】本题考查矩形的性质,勾股定理,一次函数与几何图形综合,待定系数法求解析式,等腰三角形的性质,数形结合是解题的关键;
(1)根据矩形的性质写出点的坐标,即可求解.
(2)根据勾股定理求得证明,得出,,,进而勾股定理建立方程求得,再根据三角形的面积公式,即可求解;
(3)设点.分类讨论:①当点在下方时,过点作,交轴于点,交于点,证明,得出此时点不合题意舍去; ②当点在的上方时,过点作,交轴于点,交的延长线于点同理,可证,得出的长,根据点,,待定系数法求解析即可求解.
【详解】(1)解:∵在矩形中,,.
∴,,,,
∴;
(2)过点作交于,如图:
,,
,
平分,
,
在和中,
,
,
,,,
,
,
,
解得,
;
(3)存在,理由如下:
设点.
①当点在下方时,过点作,交轴于点,交于点,如图:
是等腰直角三角形,
,,
,
,
,
,,
,
解得,此时点不合题意舍去;
②当点在的上方时,过点作,交轴于点,交的延长线于点,如图:
同理,可证,
,
,
解得,
,
点,,
设解析式为,将,代入得:
,解得,
直线的解析式为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合模拟试题 2024-2025学年
下期初中数学人教版八年级下册
一、单选题
1.下列各数中,能使有意义的是( )
A.6 B.0 C.3 D.
2.下列各组数据中,不是勾股数的是( )
A.3,4,5 B.5,7,9 C.8,15,17 D.7,24,25
3.下列命题是假命题的是( )
A.平行四边形的对边相等 B.四条边都相等的四边形是菱形
C.矩形的两条对角线互相垂直 D.正方形的对角线垂直平分且相等
4.下列等式成立的是( )
A. B. C. D.
5.菲尔兹奖是数学领域的一项国际大奖,被视为数学界的诺贝尔奖,其规定获奖数学家年龄不得超过40岁.截至目前,菲尔兹奖得主中最年轻的8位数学家获奖时年龄分别为:29,27,31,31,31,29,29,31,则该组由年龄组成的数据的众数和中位数是( )
A.29,31 B.29,29 C.31,30 D.31,31
6.如图,在平坦的地面上,为测量位于水塘旁的两点A,B间的距离,先确定一点O,分别取的中点C,D,量得m,则A,B之间的距离是( )
A.20m B.40m C.60m D.80m
7.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
8.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
9.如图,在同一平面直角坐标系中,一次函数与图象可能的情况是( )
A. B. C. D.
10.如图所示,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.时,
C. D.的解集是
11.若一个三角形一条边上的中线等于与这条边平行的中位线,则这个三角形一定是( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
12.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②SABCD=AB AC;③OB=AB:④OE=BC.其中成立的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13.计算: .
14.近年来,越来越多的游客到重庆来打卡麻辣鲜香的火锅,同时还会购买火锅底料作为伴手礼.洪崖洞某店推出活动:如果一次购买5包以上(不含5包)的火锅底料,超过5包的部分将打折,并依此得到付款金额(元)与购买火锅底料(包)之间的关系如图所示,那么购买18包火锅底料需要付款 元.
15.如图,矩形中,,,平分∠交于点E,点F、G分别为、的中点,则 .
16.如图,是一个有盖的盒子,长宽高如图中标注,若在盒中放一根细棒,则细棒的最大长度是 .
17.如图,在边长为8的菱形中,为边的中点,连接交对角线于点.若,则这个菱形的面积为 .
18.已知,直线与轴相交于点,以为边作等边三角形,点在第一象限内,过点作轴的平行线与直线交于点,与轴交于点,以为边作等边三角形(点在点的上方),以同样的方式依次作等边三角形,等边三角形,则点的横坐标为 .
三、解答题
19.已知:,,求的值.
20.先化简,再求值:,其中.
21.如图,在中,点F是中点,连接并延长交的延长线于点E.求证:.
22.如图,在四边形中,,点E在的延长线上,,连接交边于点F,且,连接,且.
(1)求证:四边形为菱形;
(2)若,,求菱形的面积.
23.一次函数的图象经过,两点.
(1)此一次函数的解析式;
(2)求的面积.
24.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目段和段均由不锈钢管材打造,总长度为26米,矩形和矩形均为木质平台的横截面,点G在上,点C在上,点D在上,经过现场测量得知米,米.
(1)求立柱的长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索,经测量米,请你求出要焊接的钢索的长.
25.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共儒投入34万元.
(1)种植A、B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
26.如图1,在矩形中,点,分别在轴、轴正半轴上,点在第一象限,,.
(1)请直接写出点的坐标;
(2)如图2,平分交于点,求的面积;
(3)如图3,动点在第一象限,且点在直线上,点在线段上,是否存在以点为直角顶点的等腰直角三角形,若存在,请求出直线的解析式;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D C C D D
题号 11 12
答案 D B
1.A
【分析】本题考查了二次根式有意义的条件,根据题意可得,解不等式即可求解.
【详解】解:∵有意义
∴,
∴,只有A选项正确,
故选:A.
2.B
【分析】判断是否为勾股数,首先这三个数都要是正整数,同时还需验证两较小数的平方和是否等于最大数的平方.
【详解】、,能构成直角三角形,都是正整数,故选项错误;
、,不能构成直角三角形,故选项正确;
、,能构成直角三角形,都是正整数,故选项错误;
、,能构成直角三角形,都是正整数,故选项错误.
故选:.
【点睛】此题主要考查了勾股数的定义,熟记勾股数的定义是解题的关键.
3.C
【分析】.
【详解】解:A、平行四边形的对边相等,是真命题,选项说法正确,不符合题意;
B、四条边都相等的四边形是菱形,是真命题,选项说法正确,不符合题意;
C、矩形的对角线不垂直,是假命题,选项说法错误,符合题意;
D、正方形的对角线垂直平分且相等,是真命题,选项说法正确,不符合题意;
故选:C.
4.D
【分析】根据二次根式的运算法则即可逐一判断.
【详解】解:A、3和不能合并,故A错误;
B、,故B错误;
C、,故C错误;
D、,正确;
故选:D.
【点睛】本题考查了二次根式的运算,解题的关键是掌握基本的运算法则.
5.C
【分析】由数据可知,31出现4次,次数最多,所以众数为31;将数据按从小到大的顺序排列,可求出中位数.
【详解】解:由数据可知,31出现4次,次数最多,所以众数为31;
将数据从小到大排列为:27,29,29,29,31,31,31,31
所以中位数为:;
故答案为:C.
【点睛】本题考查众数和中位数,属于基础题,解题的关键在于理解众数和中位数的定义,并将数据按大小顺序排列.
6.D
【分析】根据三角形的中位线定理进行求解即可.
【详解】解:∵C,D为的中点,
∴是的中位线,
∴;
故选D.
【点睛】本题考查三角形的中位线定理.熟练掌握三角形的中位线定理,是解题的关键.
7.C
【分析】本题可根据两个非负数相加和为0,则这两个非负数的值均为0解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.
【详解】依题意得:,
∴,
斜边长,
所以正方形的面积.
故选C.
考点:本题综合考查了勾股定理与非负数的性质
点评:解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.
8.C
【分析】利用平均数的定义分别进行计算成绩,然后判断谁优秀.
【详解】由题意知,甲的总评成绩=90×50%+83×20%+95×30%=90.1,
乙的总评成绩=88×50%+90×20%+95×30%=90.5,
丙的总评成绩=90×50%+88×20%+90×30%=89.6,
∴甲乙的学期总评成绩是优秀.
故选:C.
【点睛】本题考查了加权平均数的计算方法.
9.D
【分析】对于每个选项,先确定一个解析式所对应的图象,根据一次函数图象与系数的关系确定、的符号,然后根据此符号看另一个函数图象的位置是否正确.
本题考查了一次函数图象:一次函数、为常数,是一条直线,当,图象经过第一、三象限,随的增大而增大;当,图象经过第二、四象限,随的增大而减小;图象与轴的交点坐标为.
【详解】解:根据题意,得,解得,故交点坐标为;
A、对于,,;对于,则,,a的符号不一致,
∴A选项不正确,不符合题意;
B、对于,,;对于,则,,b的符号不一致,
∴B选项错误,不符合题意;
C、对于,,;对于,则,,a的符号不一致,
∴C选项错误,不符合题意;
D、对于,,;对于,则,,
∴D选项正确,符合题意.
故选:D.
10.D
【分析】本题主要考查了一次函数与一元一次不等式、一次函数与一元一次方程的应用,依据题意,根据所给函数图象的分布及两直线的交点的横坐标为-5进而逐个判断可以得解.
【详解】解:由题意,∵直线的图象经过第二、三、四象限,
∴,故A正确,不合题意.
∵直线与直线的交点的横坐标为,
∴方程的解是,故B正确,不合题意.
∵直线的图象与y轴交于正半轴,
∴,故C正确,不合题意.
结合图象可得,当时,直线上的点都不在直线的下方,
∴不等式的解集为,即不等式的解集是,故D错误,符合题意.
故选:D.
11.D
【分析】本题考查三角形的中位线定理,等腰三角形的判定和性质,根据题意,画出图形,证明三角形为直角三角形即可得.
【详解】解:如图,为的中位线,为的中线,且,
∴
∴,,
∵,
即,
∴,即.
∴是直角三角形.
故选D.
12.B
【分析】由 ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②S ABCD=AB AC;可得OE是三角形的中位线,证得④OE=BC.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
,故④正确.
故选B.
【点睛】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形,OE是△ABC的中位线是关键.
13./
【分析】本题考查了二次根式的混合运算,二次根式的性质化简,掌握相关运算法则是解题关键.先根据乘法分配律展开,再计算乘法,然后化为最简二次根式计算即可.
【详解】解:
,
故答案为:.
14.
【分析】本题考查了一次函数的应用,待定系数法求得时的解析式,进而将代入,即可求解.
【详解】解:设时,与的函数关系式为,
将代入得,
解得:
∴
当时,
故答案为:.
15.
【分析】连接.由矩形的性质可间接证明,结合角平分线的定义得出,即得出,从而可求出,再由勾股定理可求出,最后根据三角形中位线定理求解即可.
【详解】解:如图,连接.
∵四边形为矩形,
∴,,,,
∴.
∵平分交于点E,
∴,
∴,
∴,
∴,
∴.
∵点F、G分别为、的中点,
∴.
故答案为:.
【点睛】本题考查矩形的性质,平行线的性质,角平分线的定义,等腰三角形的判定和性质,勾股定理,三角形中位线定理.正确连接辅助线是解题关键.
16.17
【分析】在,根据勾股定理求得,中,根据勾股定理即可得到结论.
【详解】解:依题意,在中,,
在中,,
故答案为:17.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
17.
【分析】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形面积,连接交于O,如图,根据菱形的性质得到,,再利用得到,证明得,则,所以,接着利用勾股定理计算出,从而得到,然后根据菱形的面积公式计算它的面积.
【详解】解:连接交于O,如图,
∵四边形为菱形,
∴,,
∵E为边的中点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴,
∴菱形的面积.
故答案为:.
18.
【分析】直线直线可知,点坐标为,可得,由于是等边三角形,可得点,把代入直线解析式即可求得的横坐标,可得,由于是等边三角形,可得点;同理,,发现规律即可得解,准确发现坐标与字母的序号之间的规律是解题的关键.
【详解】解:∵直线l:与x轴负半轴交于点,
∴点坐标为,
∴,
过,,作轴交x轴于点M,轴交于点D,交x轴于点N,
∵为等边三角形,
∴
∴,
∴
∴,
当时,,解得:,
∴,,
∴,
∴,
∴,
∴当时,,解得:,
∴;
而,
同理可得:的横坐标为,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了一次函数图象上点的坐标的特征,勾股定理的应用,等边三角形的性质,特殊图形点的坐标的规律,掌握探究的方法是解本题的关键.
19.
【分析】本题考查了二次根式的化简求值,分母有理化,解题的关键是正确对所求的式子分解因式.
先对所求的式子分解因式然后代入数值计算求解.
【详解】解:∵,,
∴
.
20.,
【分析】本题主要考查了分式的化简求值,分母有理化,先把除法变成乘法后约分化简,再通分化简,最后代值计算即可得到答案.
【详解】解:
,
当时,.
21.见解析
【分析】本题主要考查了平行四边形的性质,全等三角形的性质与判定,由平行四边形的性质得到,则,再由线段中点的定义得到,据此证明,得到,则可证明.
【详解】证明:∵四边形是平行四边形,
∴,
∴,
∵点F是中点,
∴,
在和中,
,
∴,
∴,
∴.
22.(1)见解析
(2)
【分析】本题考查菱形的判定和性质,直角三角形斜边中线的性质,含度角的直角三角形的性质,全等三角形的判定和性质,勾股定理等,熟练掌握以上知识点是解题的关键.
(1)根据可证,,再证,推出,等量代换可得,根据,证明四边形为平行四边形,再根据直角三角形斜边中线的性质推出,即可证明四边形为菱形;
(2)先求出菱形的边长,作于点,根据含度角的直角三角形的性质求出,再利用勾股定理求出,即可求出菱形的面积.
【详解】(1)证明:,点E在的延长线上,
,
,,
在和中,
,
,
,
,
;
,
四边形为平行四边形,
,,
是斜边的中线,
,
四边形为菱形;
(2)解:如图,作于点,
,,
,
四边形为菱形,
,
,,
,
,
,
菱形的面积.
23.(1)
(2)8
【分析】本题考查了一次函数的解析式求解、一次函数与坐标轴的交点问题,掌握待定系数法求出解析式是解题关键.
(1)将,两点代入即可求解;
(2)求出一次函数与坐标轴的交点,根据即可求解.
【详解】(1)解:将,两点代入得:
,
解得:
∴
(2)解:如图所示:
令,则;
∴,
∴
.
24.(1)立柱的长度为9米
(2)米
【分析】(1)根据题意得米,米,设米,则米,则由勾股定理可得出关于x的等式,解出x,即得出BG的长,从而即可求出AB的长.
(2)由题意得米,从而可求出米.进而可由勾股定理求出BF的长.
【详解】(1)(1)由题意得米,米,
设米,则米,
在中,由勾股定理得,
即,解得.
∴米.
∴米.
∴立柱的长度为9米.
(2)由题意得米,
∴米.
在中,由勾股定理得米.
【点睛】本题考查矩形的性质,勾股定理.掌握利用勾股定理解直角三角形的方法是解题关键.
25.(1)种植A,B两种蔬菜,每亩各需投入0.6万元、0.8万元
(2)w=-0.1m+150
(3)当种植A种蔬菜100亩,B种蔬菜50亩时,总获利最大,最大总获利为140万元.
【分析】(1)设种植A,B两种蔬菜,每亩各需投入x万元、y万元,然后根据“若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共儒投入34万元”列方程组求解即可;
(2)设种植A种蔬菜m亩,则 种植B种蔬菜,然后根据“利润=单件利润×数量”列式解答即可;
(3)先根据“若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍”列求出m的取值范围,再结合(2)的解析式求最值即可.
【详解】(1)解:设种植A,B两种蔬菜,每亩各需投入x万元、y万元.
根据题意,得,解得
答:种植A,B两种蔬菜,每亩各需投入0.6万元、0.8万元.
(2)解:设种植A种蔬菜m亩,
由题意,得w=0.8m+1.2×-0.1m+150.
(3)解:由题意,得,解得m≥100.
∵w=-0.1m+150,-0.1<0,
∴w随m的增大而减小.
∴当m=100时,w最大=140,此时=50(亩).
∴当种植A种蔬菜100亩,B种蔬菜50亩时,总获利最大,最大总获利为140万元.
【点睛】本题主要考查了二元一次方程组的应用、一元一次不等式的应用、运用一次函数的性质求最值等知识点,灵活应用所学知识成为解答本题的关键.
26.(1)
(2)
(3)存在,
【分析】本题考查矩形的性质,勾股定理,一次函数与几何图形综合,待定系数法求解析式,等腰三角形的性质,数形结合是解题的关键;
(1)根据矩形的性质写出点的坐标,即可求解.
(2)根据勾股定理求得证明,得出,,,进而勾股定理建立方程求得,再根据三角形的面积公式,即可求解;
(3)设点.分类讨论:①当点在下方时,过点作,交轴于点,交于点,证明,得出此时点不合题意舍去; ②当点在的上方时,过点作,交轴于点,交的延长线于点同理,可证,得出的长,根据点,,待定系数法求解析即可求解.
【详解】(1)解:∵在矩形中,,.
∴,,,,
∴;
(2)过点作交于,如图:
,,
,
平分,
,
在和中,
,
,
,,,
,
,
,
解得,
;
(3)存在,理由如下:
设点.
①当点在下方时,过点作,交轴于点,交于点,如图:
是等腰直角三角形,
,,
,
,
,
,,
,
解得,此时点不合题意舍去;
②当点在的上方时,过点作,交轴于点,交的延长线于点,如图:
同理,可证,
,
,
解得,
,
点,,
设解析式为,将,代入得:
,解得,
直线的解析式为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
