7.2相交线巩固强化练习（含解析）

中小学教育资源及组卷应用平台
7.2相交线
学校:___________姓名：___________班级：___________考号：___________
一、单选题
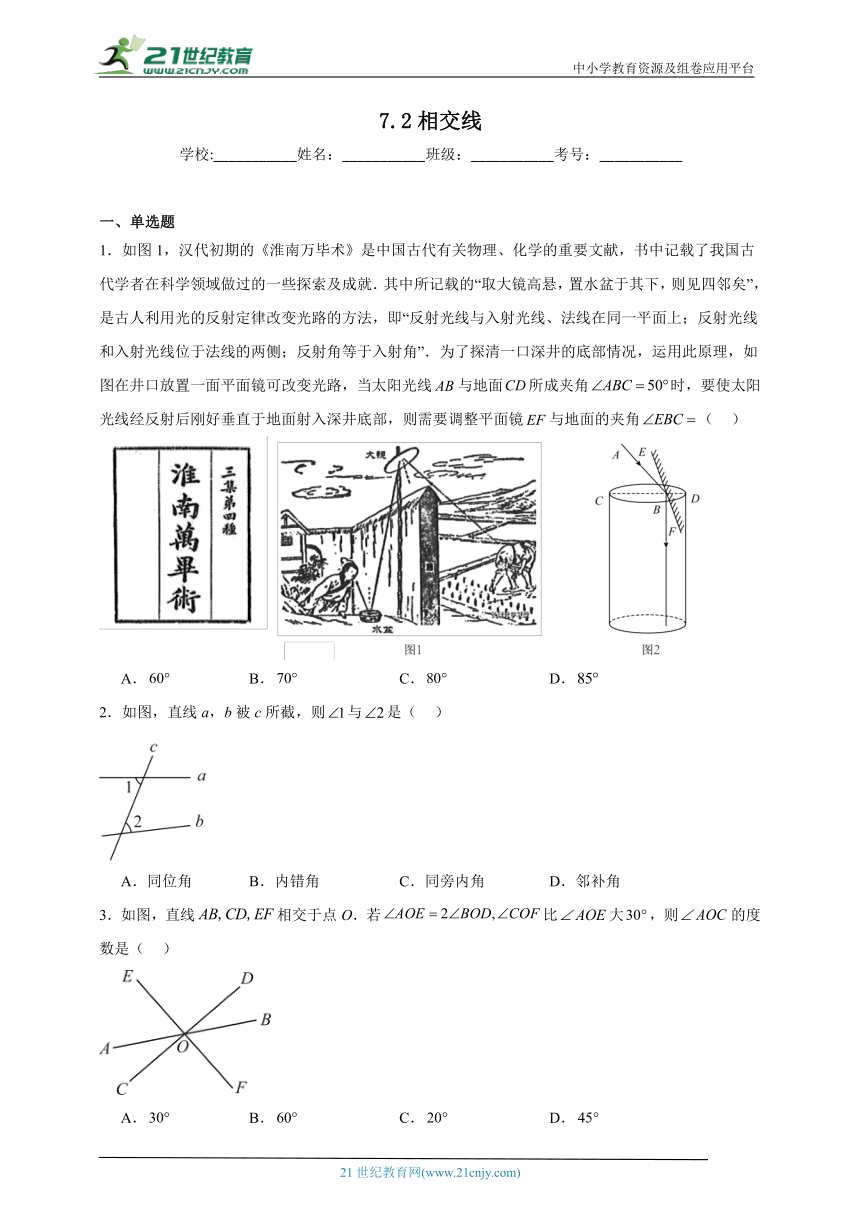
1．如图1，汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献，书中记载了我国古代学者在科学领域做过的一些探索及成就．其中所记载的“取大镜高悬，置水盆于其下，则见四邻矣”，是古人利用光的反射定律改变光路的方法，即“反射光线与入射光线、法线在同一平面上；反射光线和入射光线位于法线的两侧；反射角等于入射角”．为了探清一口深井的底部情况，运用此原理，如图在井口放置一面平面镜可改变光路，当太阳光线与地面所成夹角时，要使太阳光线经反射后刚好垂直于地面射入深井底部，则需要调整平面镜与地面的夹角（ ）

A． B． C． D．
2．如图，直线a，b被c所截，则与是（ ）

A．同位角 B．内错角 C．同旁内角 D．邻补角
3．如图，直线相交于点O．若比大，则的度数是（ ）
A． B． C． D．
4．风筝是中国古代劳动人民发明于春秋时期的产物，其材质在不断改进之后，坊间开始用纸做风筝，同位角、内错角、同旁内角称为“纸鸢”．如图所示的纸骨架中，与构成同旁内角的是（ ）

A． B． C． D．
5．下列图形中，与互为对顶角的是（ ）
A． B． C． D．
6．如图，直线，相交于点O，射线平分，若，则等于（ ）
A． B． C． D．
7．下列命题：①能被3整除的数也能被6整除；②等式两边除以同一个数，结果仍是等式：③一元一次方程的根是；④对顶角相等．其中可以作为定理的有（　　）
A．1个 B．2个 C．3个 D．4个
8．如图，在所标识的角中，下列说法不正确的是（ ）
A．与是内错角 B．与是对顶角
C．与是同位角 D．与是同旁内角
9．下列各图中，与是对顶角的是（ ）
A． B． C． D．
10．如图，过直线上一点作，直线经过点，若，则的度数是（　　）
A． B． C． D．
11．如图，直线与相交于点，，，射线平分，则（　　）
A． B． C． D．
12．如图，属于同位角是（ ）

A．和 B．和 C．和 D．和
二、填空题
13．如图，于点C，若，则∠BCE的度数为 ．
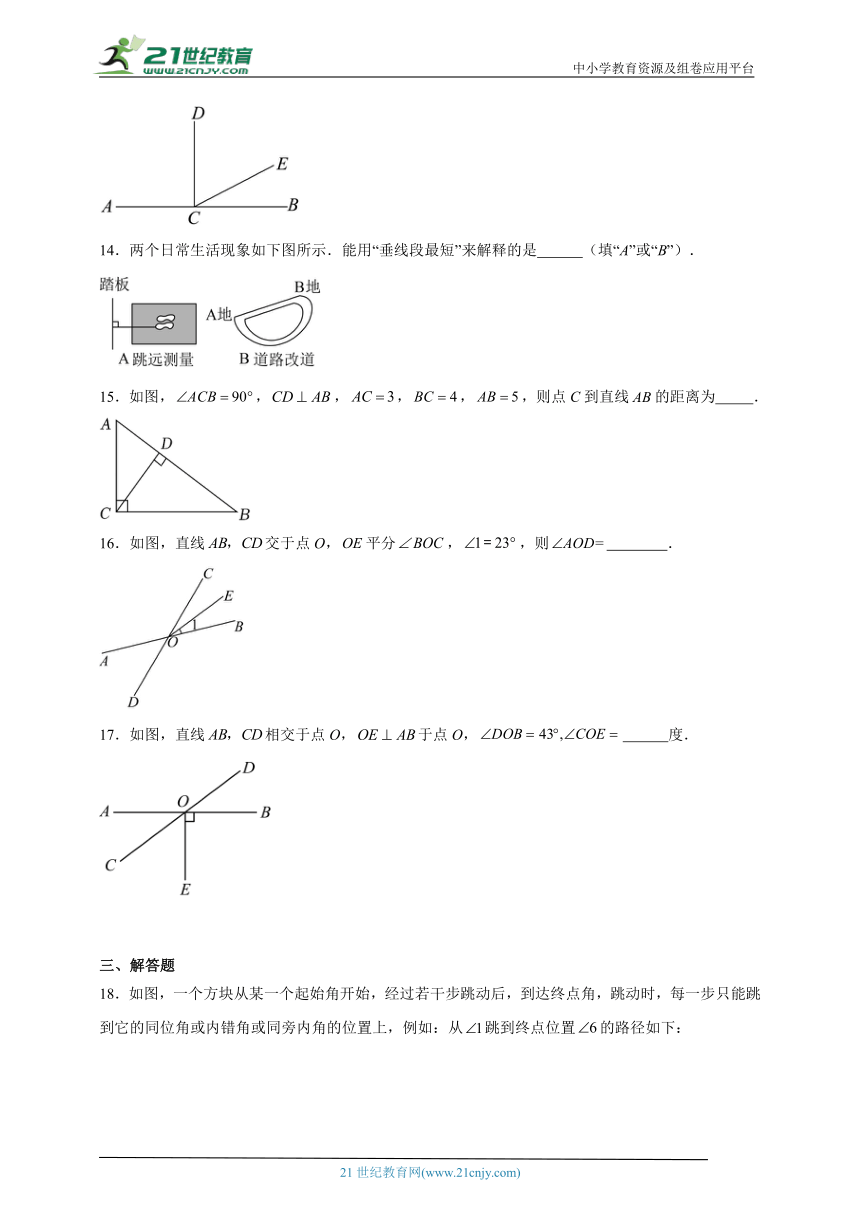
14．两个日常生活现象如下图所示．能用“垂线段最短”来解释的是 （填“A”或“B”）．
15．如图，，，，，，则点C到直线的距离为 ．
16．如图，直线交于点O，平分，，则 ．
17．如图，直线相交于点O，于点O， 度．
三、解答题
18．如图，一个方块从某一个起始角开始，经过若干步跳动后，到达终点角，跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上，例如：从跳到终点位置的路径如下：
路径1：→内错角→同旁内角；
路径2：→同旁内角→内错角→同位角→同旁内角→同旁内角．
…
(1)写出任意一条从起始位置→终点位置的路径；
(2)从起始位置依次按内错角、同位角、同旁内角的顺序能否到达终点位置？并写出路径．
19．如图，相交于点O．
(1)如果，那么__________，__________；
(2)如果，，，求x，y的值．
20．请根据图形回答下列问题：
(1)图中的对顶角有________对；
(2)与，与各是什么位置关系的角？是哪两条直线被哪一条直线所截得到的？
(3)的内错角有哪些？
21．如图①，点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
(1)将图①中的三角板OMN摆放成如图②所示的位置，使一边OM在∠BOC的内部，当OM平分∠BOC时，求∠BON的度数；
(2)在（1）的条件下，作线段NO的延长线OP（如图③所示），试说明射线OP是∠AOC的平分线；
(3)将图①中的三角板OMN摆放成如图④所示的位置，请探究∠NOC与∠AOM之间的数量关系，并说明理由．
22．如图，直线相交于点，已知，射线将分成两个角，且，
(1)求的度数；
(2)若平分，试说明平分．
23．如图，直线AB，CD相交于点O，于点O，连接CE．
(1)若OC＝2，OE＝1.5，CE＝2.5，则点E到直线CD的距离是______；
(2)若∠BOD＝25°，则∠AOE＝______．
24．如图，两直线，相交于点，平分，．
(1)求的度数；
(2)若射线，请在图中画出，并求的度数．
《7.2相交线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A A C A A C A B
题号 11 12
答案 D C
1．B
【分析】如图，过作平面镜，可得，，而，再建立方程，可得，从而可得答案．
【详解】解：如图，过作平面镜，

∴，，
而，
∴，
∴，
∴，
故选B．
【点睛】本题考查的是垂直的定义，角的和差运算，角平分线的含义，属于跨学科题，熟记基础概念是解本题的关键．
2．B
【分析】由内错角的定义（两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角）进行解答．
【详解】解：如图所示，

两条直线a、b被直线c所截形成的角中，与都在a、b直线的之间，并且在直线c的两旁，所以与是内错角．
故选：B．
【点睛】本题考查了同位角，内错角以及同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
3．A
【分析】本题主要考查了几何图形中角度的计算，对顶角相等，根据已知条件得出，根据对顶角相等得出，根据得出，求出结果即可．
【详解】解：∵ 比大，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
故选：A．
4．A
【分析】本题考查的是同旁内角的定义，关键是知道哪两条直线被第三条直线所截．
根据同旁内角的定义解答即可，即两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角．
【详解】解：与构成同旁内角．
故选：A．
5．C
【分析】根据对顶角的定义判断解答即可．
本题考查了对顶角的定义，熟练掌握定义是解题的关键．
【详解】解：根据题意，得是对顶角的是：
故选：C．
6．A
【分析】由角平分线定义得到，由对顶角相等得出，代入即可求解．
【详解】解：∵射线平分，
∴，
∵，
∴．
故选：A．
【点睛】本题考查了对顶角相等，与角平分线有关的角的计算；解题的关键是熟练掌握以上知识．
7．A
【分析】本题考查了定理的含义，演绎推理的过程称为证明，经过证明的真命题称为定理．
根据定理的含义求解即可．
【详解】①能被3整除的数，不一定能被6整除，故①是假命题；
②等式两边除以同一个不为零的数，结果仍是等式，故②是假命题；
③是一个运算过程，不能作为定理；
④对顶角相等是定理．
故选A．
8．C
【分析】根据内错角，对顶角，同位角，同旁内角的定义解答即可．
【详解】解：A. 与是内错角，本选项正确，不符合题意，
B. 与是对顶角，本选项正确，不符合题意，
C. 与不是同位角，本选项错误，符合题意，
D. 与是同旁内角，本选项正确，不符合题意，
故选：C．
【点睛】本题考查了内错角，对顶角，同位角，同旁内角的定义，正确理解定义是解题的关键．
9．A
【分析】本题重点考查了对顶角相等，根据对顶角的定义即有公共顶点边互为反向延长线判断即可．
【详解】解：A、与是对顶角，故符合题意；
B、与边不是为反向延长，不是对顶角，故不符合题意；
C、与边不是为反向延长，不是对顶角，故不符合题意；
D、与没有公共顶点，不是对顶角，故不符合题意；
故选：A．
10．B
【分析】本题考查垂直的定义，对顶角性质，几何角度计算，熟练掌握对顶角的性质是解题的关键；根据，可得，进而求得的度数，进而求解；
【详解】解：，
，
，
，
，
；
故选：B．
11．D
【分析】此题考查了角的和差，对顶角相等，首先设，，然后表示出和，再根据平角定义列出方程，解方程求出，进而可求出，解题的关键是理清图中角之间的关系，利用方程思想解决问题．
【详解】解：设，，
∵，
∴，
∵射线平分，
∴，
∵，
∴，
解得，
∴，
∴，
故选：．
12．C
【分析】根据同位角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．进行判断即可．
【详解】解：由图可知，和是同位角；
故选：C．
【点睛】本题考查的是同位角的定义，掌握两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角是同位角是解题的关键．
13．/32度
【分析】根据垂线的定义即可求解．
【详解】解：∵，
∴∠BCD=90°，
∴∠BCE=∠BCD-∠DCE=90°-58°=32°，
故答案为：32°．
【点睛】本题考查了垂直的定义，熟练掌握两直线垂直，构成的角为90°是解题的关键．
14．A
【分析】根据垂线最短的含义进行分析即可得到答案：直线外一点与直线上各点连接的所有线段中，垂线段最短，简称垂线段最短．
【详解】解：A：跳远测量需要测量出脚印到起跳线的最短距离，故符合题意；
B：道路改到是应用的两点直线，线段最短，故不符合题意；
故选：A．
【点睛】本题考查垂线段最短的定义，简体的关键是熟知垂线段最短的含义．
15．
【分析】运用直角三角形面积的两种求法求的长即可．
【详解】解：题意可知，的面积为，
，
，
，
．
故答案为．
【点睛】本题考查点到直线的距离，能够灵活运用三角形的面积公式是解答本题的关键．
16．46°/46度
【分析】本题考查角平分线的定义及对顶角相等，熟练找到角度之间的关系是解题的关键．
根据角平分线求出，再根据对顶角相等求出即可．
【详解】解：∵平分，，，
∴，
∴，
故答案为：46°．
17．
【分析】此题主要考查了垂线的性质．根据垂直定义可得的度数，然后再根据可得．
【详解】解：，
，
，
．
故答案为：．
18．(1)→同旁内角→同位角（答案不唯一）；
(2)能，→内错角→同位角→同旁内角（答案不唯一）；
【分析】本题考查内错角，同位角，同旁内角的判断：
（1）根据内错角，同位角，同旁内角直接逐个判断即可得到答案；
（2）根据内错角、同位角、同旁内角反向推导即可得到答案；
【详解】（1）解：由题意可得，
→同旁内角→同位角（答案不唯一）；
（2）解：能，理由如下，
由题意可得，
→内错角→同位角→同旁内角（答案不唯一）．
19．(1)，
(2)，
【分析】本题考查了对顶角相等，邻补角互补．应用方程思想是解题关键．
（1）结合已知条件，利用邻补角互补计算；
（2）根据对顶角相等和邻补角互补的性质来列方程计算．
【详解】（1）解：∵，且，
∴，
故答案为：，
（2）由，，
得，
解得．
∵，
∴，
∴．
20．(1)6
(2)与是同旁内角，与是同位角，都是直线和直线被直线所截得到的
(3)和
【分析】本题主要考查了同位角、同旁内角、内错角定义，对顶角定义，解题的关键是熟练掌握相关的定义．
（1）根据对顶角定义进行判断即可；
（2）根据同旁内角，同位角定义进行判断即可；
（3）根据内错角定义寻找即可．
【详解】（1）解：图中以C为顶点的对顶角有2对，以D为顶点的对顶角有2对，以E为顶点的对顶角有2对，
∴图中的对顶角有（对）；
（2）解：与是同旁内角，与是同位角，都是直线和直线被直线所截得到的；
（3）解：的内错角有和．
21．(1)60°
(2)见解析
(3)，理由见解析
【分析】（1）由求出的度数，取出的值，根据计算求解即可；
（2）对顶角相等可知，由求的值，进而结论得证；
（3）由题意知，，则，整理可得的关系．
【详解】（1）解：∵，
∴，
又∵OM平分∠BOC，
∴，
又∵，
∴，
∴∠BON的值为60°．
（2）解：∵，
∴，
∴，
∴射线OP是∠AOC的平分线．
（3）解：．
理由如下：∵，
∴，
∵，
∴，
∴，
∴．
【点睛】本题考查了角平分线，与三角板有关的计算，对顶角等知识．解题的关键在于找出角度的数量关系．
22．(1)
(2)见解析
【分析】本题考查角度的计算，对顶角相等，角平分线的定义；
（1）根据对顶角相等求出，再由求解即可；
（2）先求出的度数，再根据平分得到，即可证明平分．
【详解】（1）∵，
∴，
∵，
∴，
∵，
∴，
解得；
（2）∵，
∴，
∵平分，
∴，
∴，
∴平分．
23． 1.5/ 115°/度
【分析】（1）根据点到线的距离解答即可；
（2）根据垂直的定义求出∠COE=90°，根据对顶角相等得到∠AOC=∠BOD＝25°，即可求出∠AOE．
【详解】解：（1）∵于点O，
∴点E到直线CD的距离是OE＝1.5，
故答案为：1.5；
（2）∵于点O，
∴∠COE=90°，
∵∠AOC=∠BOD＝25°，
∴∠AOE=∠AOC+∠COE=25°+90°=115°，
故答案为：115°．
【点睛】此题考查了点到直线的距离定义，垂直的性质，对顶角相等，熟练掌握各知识点并综合应用是解题的关键．
24．(1)
(2)见解析，或
【分析】（1）根据已知得出，，根据对顶角相等得出，根据角平分线的定义得出，根据邻补角相等即可求解；
（2）分在内和内两种情况分别画出图形，即可求解．
【详解】（1）解：∵，，
∴，，
∴.
又∵平分，
∴，
∴.
（2）分两种情况：
如图①，∵，∴，
∴.
如图②，.
综上，的度数为或.
【点睛】本题考查了垂直的定义，角平分线的定义，对顶角相等，几何图形中角度的计算，数形结合是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)