第十七章方差与频数分布巩固强化练习(含解析)
文档属性
| 名称 | 第十七章方差与频数分布巩固强化练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 904.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:44:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十七章方差与频数分布
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小杰调查了本班同学体重情况,画出了频数分布直方图,那么下列结论不正确的是( )
A.全班总人数为45人
B.体重在50千克千克的人数最多
C.学生体重的众数是14
D.体重在60千克千克的人数占全班总人数的
2.为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制了扇形图和条形图.下列结论错误的是( )
A.被抽测学生中参加其他体育项目活动人数占
B.被抽测学生中参加羽毛球项目人数为人
C.估计全区九年级参加篮球项目的学生比参加足球项目的学生多
D.全区九年级大约有名学生参加乒乓球项目
3.把一组数据分成若干组后,每个小组的两个端点之间的距离(组内数据的取值范围)称为( )
A.组数 B.组距 C.频数 D.样本容量
4.某商店在一段时间内销售了某种女鞋30双,各种尺码的销售量如表:
尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 12 6 3 1
如果鞋店要购进100双这种女鞋,那么购进24厘米、24.5厘米和25厘米三种女鞋数量之和最合适的是( )
A.20双 B.33双 C.50双 D.80双
5.某班抽取名同学参加体能测试,成绩如下:,,,,,下列表述错误的是( )
A.平均数是 B.极差是 C.中位数是 D.标准差是
6.为了考察甲、乙两班期中考试数学成绩的波动大小,从这两班各抽10人的数学成绩进行比 较,算出甲班10人的成绩方差比乙班10人的成绩方差大,由此可估计出( )
A.甲班比乙班整齐 B.乙班比甲班整齐 C.甲、乙两班成绩一样整齐 D.无法确定
7.甲、乙两学生在一年里,学科平均分相等,但它们的方差不相等,正确评价他们的学习情况是( )
A.因为他们平均分相等,所以学习近平一样
B.成绩虽然一样,方差较大的,说明潜力大,学习态度踏实
C.表面上看这两个学生平均成绩一样,但方差小的学习成绩较稳定
D.平均分相等,方差不等,说明学习近平不一样,方差较小的同学学习较稳定
8.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约( )
A.2000只 B.14000只 C.21000只 D.98000只
9.有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )
A.10 B. C. D.2
10.数据1,6,3,9,8的极差是( )
A.1 B.5 C.6 D.8
11.如图是两名同学最近10次射击训练成绩的折线统计图,如果其他班级参赛选手的射击成绩都环左右,本班应该选择___参赛,理由是( )
A.甲,甲的平均成绩高于7,且方差小,发挥较稳定
B.甲,甲的平均成绩高于7,且方差大,发挥较稳定
C.乙,乙的平均成绩高于7,且方差小,发挥较稳定
D.乙,乙的平均成绩高于7,且方差大,发挥较稳定
12.甲、乙两学生在军训打靶训练中,打靶的总次数相同,且所中环数的平均数也相同,但甲的成绩比乙的成绩稳定,那么两者的方差的大小关系是( )
A. B. C. D.不能确定
二、填空题
13.小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如下图所示,则小明5次成绩的方差与小兵5次成绩的方差之间的大小关系为 .(填“>”、“<”、“=”)
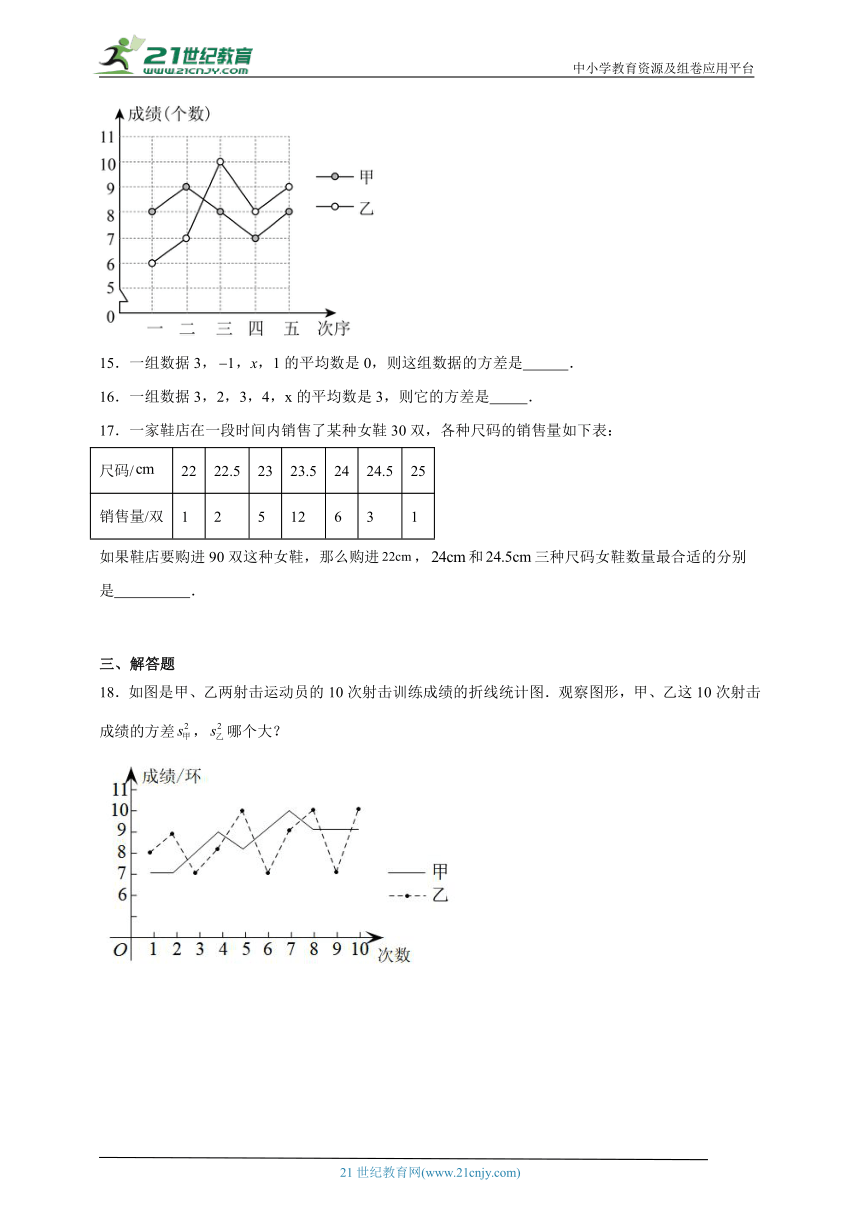
14.甲、乙两名同学本学期第五次引体向上的测试成绩(个数)如图所示,若甲,乙五次成绩的方差分别为,,则 (填“>,<,=”).
15.一组数据3,,x,1的平均数是0,则这组数据的方差是 .
16.一组数据3,2,3,4,x的平均数是3,则它的方差是 .
17.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
尺码/ 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 12 6 3 1
如果鞋店要购进90双这种女鞋,那么购进,和三种尺码女鞋数量最合适的分别是 .
三、解答题
18.如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图.观察图形,甲、乙这10次射击成绩的方差,哪个大?
19.为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级名学生中抽取名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”“良”“中”“差”的人数比例情况;其次,老师发给每人一张调查问卷,其中有一个调查问题是“你的英语作业完成情况如何?”,给出五个选项:.独立完成;.辅导完成;.有时抄袭完成;.经常抄袭完成;.经常不完成;供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占,明显高于他平时观察到的比例,请回答下列问题:
(1)班主任和英语教师所用的调查方式是______;
(2)指出问题中的总体,个体,样本,样本容量;
(3)如果其中英语作业得“差”的同学有名,那么估计全年级的英语作业中可能有多少同学得“差”.
20.某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x 甲=8和方差S2甲=3.2.
(1)求乙进球的平均数x 乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
21.为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
22.国家规定,中小学生每天在校体育活动时间不低于1小时.为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间(小时)进行分组(A组:,B组:,C组:,D组:),绘制成如下两幅统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为________人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是__________;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有__________人.
23.学史明理,学史增信,学史崇德,学史力行,在建党100周年之际,某校对全校学生进行了一次党史知识测试,成绩评定共分为A,B,C,D四个等级,随机抽取了部分学生的成绩进行调查,将获得的数据整理绘制成如下两幅不完整的统计图.
根据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了__________名学生;
(2)请根据以上信息直接在答题卡上补全条形统计图;
(3)扇形统计图中,D等级对应的圆心角度数是__________度;
(4)根据抽样调查的结果,请你估计该校2000学生中有多少名学生的成绩评定为C等级.
24.某厂用罐头分装机分装某种鱼罐头(每只罐头的标准质量为207g).为了监控分装质量,该厂决定定期对罐头的质量进行抽样检查,并规定抽检产品的平均质量与标准质量相差大于5g或罐头质量的标准差大于8g时,就认为该分装机运行不正常,将对它进行检修,现抽取了20只罐头,它们的质量(单位:g)如下:200,205,208,212,223,199,193,208,204,200,208,201,215,190,193,206,215,198,206,216,该分装机运行是否正常?
《第十七章方差与频数分布》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B D B C B D D
题号 11 12
答案 C A
1.C
【详解】试题解析:由频数直方图可以看出:全班总人数为8+10+14+8+5=45人;A正确;
体重在50千克到55千克的人数最多为14人;故众数在50千克到55千克之间.B正确,但C错误;
在体重在60千克到65千克的人数为5人,则占全班总人数的5÷45=;D正确.
故选C.
2.C
【分析】结合参加足球的人数与其所占的百分比, 计算可得本次调查共抽取的学生数, 进而求出被抽测学生中参加羽毛球项目人数为, 再计算出区九年级参加篮球项目的学生和参加足球项目的学生所占的百分比即可知道答案C是否正确, 估计九年级大约名学生参加乒乓球项目的人数和1500比较大小即可.
【详解】解:参加足球的人数是 40 人, 所占的百分比为,
本次抽取的总人数为(人),
被抽测学生中参加其他体育项目活动人数占,故A正确,不合题意;
被抽测学生中参加羽毛球项目人数为人, 故B正确,不合题意;
全区九年级参加篮球项目的学生比所占百分比为,
参加足球项目的学生所占百分比为,
估计全区九年级参加篮球项目的学生比参加足球项目的学生多,故C错误,符合题意;
从该年级学生中随机抽取了的学生,
九年级大约有名学生参加乒乓球项目, 故D正确,不合题意.
故选:C.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
3.B
【分析】根据组距的定义即可选出答案.
【详解】把一组数据分成若干组后,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距,故答案选B.
【点睛】本题主要考查了组距的定义,解本题的要点在于熟知组距等相关知识点.
4.B
【分析】求得销售这三种鞋数量之和为10双,是30的三分之一,故要购进的这三种鞋应是100的三分之一.
【详解】解:根据题意可得:销售的某种女鞋30双,24厘米、24.5厘米和25厘米三种女鞋数量之和为10;所占比例为,
则要购进100双这种女鞋,购进这三种女鞋数量之和应是;
故选:B.
【点睛】本题考查了由样本数据估算总体,解题的关键是理解题意.
5.D
【分析】根据平均数,中位数,方差,极差的概念逐项分析.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;利用方差公式计算方差,利用平均数和极差的定义可分别求出.
【详解】A. 由平均数公式求得:,故此选项正确,不符合题意;
B. 极差是,故此选项正确,不符合题意;
C. 把数据按大小排列,中间两个数为,,所以中位数是,故此选项正确,不符合题意;
D. ,故标准差为:,故此选项错误,符合题意.
故选:D.
【点睛】本题考查了统计学中的平均数,方差,中位数与极差的定义,解答这类题学生常常对中位数的计算方法掌握不好而错选.
6.B
【分析】根据方差的意义,反映了一组数据的波动大小,方差越大,波动性越大,反之也成立即可解答.
【详解】根据题意可得,甲班10人的成绩方差比乙班10人的成绩方差大,
∴乙班的成绩比甲班的成绩整齐.
故选B.
【点睛】本题考查了方差的意义,熟知方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定是解题的关键.
7.C
【分析】判断两组数据的关系时,在平均分相同或相近的情况下比较方差,方差越大,成绩越不稳定;方差越小,成绩越稳定,根据这种原理得到结果.
【详解】在平均分相同或相近的情况下比较方差,
方差越大,成绩越不稳定,
方差越小,成绩越稳定.
因此A. B. D均不正确,C正确.
故选C.
【点睛】本题考查了方差,解题的关键是掌握方差的概念.
8.B
【详解】(6+5+7+8+7+5+8+10+5+9)×2000=14000只.
故选B.
9.D
【详解】解:∵3、a、4、6、7,它们的平均数是5
∴(3+a+4+6+7)=5
解得,a=5
S2=[(3-5)2+(5-5)2+(4-5)2+(6-5)2+(7-5)2]
=2
故选D.
10.D
【分析】极差就是这组数中最大值与最小值的差.
【详解】数据1,6,3,9,8的极差是8.故选D.
【点睛】本题考查了极差,解题的关键是掌握极差的概念.
11.C
【分析】此题考查了平均数和方差,掌握方差以及平均数的定义是解题的关键.方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.根据平均数以及方差的意义分别对每一项进行分析,即可得出答案.
【详解】解:①(环,
(环,
则甲、乙的射击成绩的平均数都是8环;
从统计图中可以看出,甲成绩的方差比乙成绩的方差大;
所以乙成绩比甲成绩稳定,
故选:C
12.A
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:根据方差的意义知,成绩越稳定,则方差越小,
∵甲、乙学生所中环数的平均数相同,且甲的成绩比乙的成绩稳定,
∴.
故选A.
【点睛】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
13.<
【分析】先从图片中读出小明和小兵的测试数据,分别求出方差后比较大小.也可从图看出来小明的都在8到10之间相对小兵的波动更小.
【详解】解:小明数据的平均数,
方差s12=[(9-9)2+(8-9)2+(10-9)2+(9-9)2+(9-9)2]=0.4,
小兵数据的平均数,
方差s22=[(7-9)2+(10-9)2+(10-9)2+(8-9)2+(10-9)2]=2.6,
∴S12<S22.
故答案为:<.
14.
【分析】直接根据图表数据的波动大小进行判断即可.
【详解】解:图表数据可知,
乙数据偏离平均数数据较大,甲数据偏离平均数数据较小,
即乙的波动性较大,即方差大,即,
故答案为:<.
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
15.5
【分析】先根据平均数的定义确定x的值,再根据方差的计算公式出这组数据的方差.
【详解】解:由平均数公式得:,
解得,
则,
故答案为:5.
【点睛】本题主要考查平均数和方差,解题的关键是熟练掌握平均数和方差的计算公式.
16.0.4
【分析】根据数据2、3、3、4、x的平均数是3,先利用平均数的计算公式可求出x,然后利用方差的计算公式进行求解即可.
【详解】∵数据2、3、3、4、x的平均数是3,
∴,
∴,
∴,
故答案为.
【点睛】本题主要考查了平均数和方差的计算,解题的关键是熟练掌握平均数和方差的计算公式.
17.3,18,9
【分析】分别求得这三种鞋销售数量的占比,然后×90即可算出.
【详解】解:根据题意可得:销售的某种女鞋30双,24厘米、24.5厘米和25厘米三种女鞋数量各为1、6、3;则要购进90双这种女鞋,购进这三种女鞋数量各应是:
(双)、(双)、(双),
故填:3,18,9.
【点睛】考查了综合运用统计知识解决问题的能力,属于基础题型.
18.大.
【分析】利用方差公式,分别计算甲乙的方差,再比较大小即可.
【详解】解:
,
= 0.85,
=1.45,
所以,
故答案为.
【点睛】本题考查了折线统计图的读图和方差公式,掌握这些是本题解题关键.
19.(1)抽样调查;
(2)总体是全年级名学生英语作业的完成情况,个体是每一名同学英语作业的完成情况,样本是抽取的名学生的英语作业完成情况,样本容量为;
(3)人.
【分析】本题考查了用样本估计总体、全面调查与抽样调查、总体、个体、样本及样本容量的知识,掌握知识点的应用是解题的关键.
()根据从名学生中抽取名学生可以得到该抽查方式为抽样调查;
()总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量;
()用样本的差的情况估计总体的差的人数即可.
【详解】(1)解:根据题意可得:班主任和英语教师所用的调查方式是抽样调查,
故答案为:抽样调查;
(2)解:总体是全年级名学生英语作业的完成情况,
个体是每一名同学英语作业的完成情况,
样本是抽取的名学生的英语作业完成情况,样本容量为;
(3)解:∵名学生中得“差”的同学有名,
∴名学生中得“差”的为(人).
20.(1)x 乙=8,S2乙=0.8;(2)乙成绩稳,选乙合适,见解析.
【分析】(1)根据平均数、方差的计算公式计算即可;
(2)根据方差越大,波动越大,成绩越不稳定;方差越小,波动越小,成绩越稳定进行解答.
【详解】(1)x 乙=(7+9+8+9+7)÷5=8,
S2乙=[(7-8)2+(9-8)2+…+(9-8)2]÷5=0.8.
(2)∵S甲2=3.2,S乙2=0.8,
∴S甲2>S乙2,
∴乙的波动小,
∴应选乙去参加3分球投篮大赛.
【点睛】本题考查了方差、平均数,掌握它们的计算方法以及它们的性质是解题的关键.
21.(1)120,45%;(2)补图见解析;(3)1980人
【分析】(1)利用12÷10%=120,即可得到m的值;用120×40%即可得到n的值.
(2)根据n的值即可补全条形统计图;
(3)根据用样本估计总体,用3600××100%,即可得到答案.
【详解】(1)本次调查的总人数为12÷10%=120(人),
∴m==45%.
故答案为:120,45%;
(2)n=48,画出条形图:
(3)3600××100%=1980(人),
答:估计该景区服务工作平均每天得到1980人游客的肯定.
【点睛】本题考查了条形统计图、扇形统计图等知识,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
22.(1)300;(2)答案见解析;(3)40%;(4)720.
【分析】(1)用D组人数÷20%求得总人数;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
【详解】解:(1)60÷20%=300(人)
答:此次抽查的学生数为300人,
故答案为:300;
(2)C组的人数=300×40%=120人,A组的人数=300﹣100﹣120﹣60=20人,补全条形统计图如图所示;
(3)该生当天在校体育活动时间低于1小时的概率是=40%;
故答案为:40%;
(4)当天达到国家规定体育活动时间的学生有1200×=720人.
故答案为:720.
【点睛】本题考查概率公式、条形统计图、扇形统计图,用样本估计总体,解题的关键是明确题意,找出所求问需要的条件.
23.(1)80;(2)见解析;(3)36;(4)600名
【分析】(1)根据等级的人数以及所占的百分比即可求出本次调查中共抽取的学生数;
(2)根据(1)中的结果和扇形统计图中的数据,可以计算出等级的人数,然后即可将条形统计图补充完整;
(3)根据等级的人数以及抽取的学生数计算出等级所对应的扇形圆心角的度数;
(4)求出等级所占整体的百分比即可求出相应的人数.
【详解】解:(1)(名,
故答案为:80;
(2)等级的学生为:(名,
补全条形图如下,
(3)等级所对应的扇形圆心角的度数为:;
(4)(名,
答:估计该校2000学生中有600名学生的成绩评定为等级.
【点睛】本题考查扇形统计图、条形统计图,用样本估计总体,理解两个统计图中数量关系是解决问题的关键.
24.该分装机运行不正常,理由见解析
【分析】先根据平均数公式求得抽取的20只罐头质量的平均数,再根据方差公式求得它们的方差,进而可求得标准差,再用所求得的标准差与8g比较大小即可求得答案.
【详解】解:抽取的20只罐头质量的平均数=(200+205+208+212+223+199+193+208+204+200+208+201+215+190+193+206+215+198+206+216)÷20
=4100÷20
=205(g),
∴抽取的20只罐头质量的方差=[(200-205)2+(205-205)2+(208-205)2+(212-205)2+(223-205)2+(199-205)2+(193-205)2+(208-205)2+(204-205)2+(200-205)2+(208-205)2+(201-205)2+(215-205)2+(190-205)2+(193-205)2+(206-205)2+(215-205)2+(198-205)2+(206-205)2+(216-205)2]÷20
=1388÷20
=69.4,
∴标准差为,
∵>8,
∴该分装机运行不正常.
【点睛】本题考查了平均数和方差、标准差的计算和应用,熟练掌握平均数、方差以及标准差的计算公式是解决本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十七章方差与频数分布
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小杰调查了本班同学体重情况,画出了频数分布直方图,那么下列结论不正确的是( )
A.全班总人数为45人
B.体重在50千克千克的人数最多
C.学生体重的众数是14
D.体重在60千克千克的人数占全班总人数的
2.为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制了扇形图和条形图.下列结论错误的是( )
A.被抽测学生中参加其他体育项目活动人数占
B.被抽测学生中参加羽毛球项目人数为人
C.估计全区九年级参加篮球项目的学生比参加足球项目的学生多
D.全区九年级大约有名学生参加乒乓球项目
3.把一组数据分成若干组后,每个小组的两个端点之间的距离(组内数据的取值范围)称为( )
A.组数 B.组距 C.频数 D.样本容量
4.某商店在一段时间内销售了某种女鞋30双,各种尺码的销售量如表:
尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 12 6 3 1
如果鞋店要购进100双这种女鞋,那么购进24厘米、24.5厘米和25厘米三种女鞋数量之和最合适的是( )
A.20双 B.33双 C.50双 D.80双
5.某班抽取名同学参加体能测试,成绩如下:,,,,,下列表述错误的是( )
A.平均数是 B.极差是 C.中位数是 D.标准差是
6.为了考察甲、乙两班期中考试数学成绩的波动大小,从这两班各抽10人的数学成绩进行比 较,算出甲班10人的成绩方差比乙班10人的成绩方差大,由此可估计出( )
A.甲班比乙班整齐 B.乙班比甲班整齐 C.甲、乙两班成绩一样整齐 D.无法确定
7.甲、乙两学生在一年里,学科平均分相等,但它们的方差不相等,正确评价他们的学习情况是( )
A.因为他们平均分相等,所以学习近平一样
B.成绩虽然一样,方差较大的,说明潜力大,学习态度踏实
C.表面上看这两个学生平均成绩一样,但方差小的学习成绩较稳定
D.平均分相等,方差不等,说明学习近平不一样,方差较小的同学学习较稳定
8.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约( )
A.2000只 B.14000只 C.21000只 D.98000只
9.有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )
A.10 B. C. D.2
10.数据1,6,3,9,8的极差是( )
A.1 B.5 C.6 D.8
11.如图是两名同学最近10次射击训练成绩的折线统计图,如果其他班级参赛选手的射击成绩都环左右,本班应该选择___参赛,理由是( )
A.甲,甲的平均成绩高于7,且方差小,发挥较稳定
B.甲,甲的平均成绩高于7,且方差大,发挥较稳定
C.乙,乙的平均成绩高于7,且方差小,发挥较稳定
D.乙,乙的平均成绩高于7,且方差大,发挥较稳定
12.甲、乙两学生在军训打靶训练中,打靶的总次数相同,且所中环数的平均数也相同,但甲的成绩比乙的成绩稳定,那么两者的方差的大小关系是( )
A. B. C. D.不能确定
二、填空题
13.小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如下图所示,则小明5次成绩的方差与小兵5次成绩的方差之间的大小关系为 .(填“>”、“<”、“=”)
14.甲、乙两名同学本学期第五次引体向上的测试成绩(个数)如图所示,若甲,乙五次成绩的方差分别为,,则 (填“>,<,=”).
15.一组数据3,,x,1的平均数是0,则这组数据的方差是 .
16.一组数据3,2,3,4,x的平均数是3,则它的方差是 .
17.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
尺码/ 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 12 6 3 1
如果鞋店要购进90双这种女鞋,那么购进,和三种尺码女鞋数量最合适的分别是 .
三、解答题
18.如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图.观察图形,甲、乙这10次射击成绩的方差,哪个大?
19.为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级名学生中抽取名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”“良”“中”“差”的人数比例情况;其次,老师发给每人一张调查问卷,其中有一个调查问题是“你的英语作业完成情况如何?”,给出五个选项:.独立完成;.辅导完成;.有时抄袭完成;.经常抄袭完成;.经常不完成;供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占,明显高于他平时观察到的比例,请回答下列问题:
(1)班主任和英语教师所用的调查方式是______;
(2)指出问题中的总体,个体,样本,样本容量;
(3)如果其中英语作业得“差”的同学有名,那么估计全年级的英语作业中可能有多少同学得“差”.
20.某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x 甲=8和方差S2甲=3.2.
(1)求乙进球的平均数x 乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
21.为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
22.国家规定,中小学生每天在校体育活动时间不低于1小时.为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间(小时)进行分组(A组:,B组:,C组:,D组:),绘制成如下两幅统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为________人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是__________;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有__________人.
23.学史明理,学史增信,学史崇德,学史力行,在建党100周年之际,某校对全校学生进行了一次党史知识测试,成绩评定共分为A,B,C,D四个等级,随机抽取了部分学生的成绩进行调查,将获得的数据整理绘制成如下两幅不完整的统计图.
根据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了__________名学生;
(2)请根据以上信息直接在答题卡上补全条形统计图;
(3)扇形统计图中,D等级对应的圆心角度数是__________度;
(4)根据抽样调查的结果,请你估计该校2000学生中有多少名学生的成绩评定为C等级.
24.某厂用罐头分装机分装某种鱼罐头(每只罐头的标准质量为207g).为了监控分装质量,该厂决定定期对罐头的质量进行抽样检查,并规定抽检产品的平均质量与标准质量相差大于5g或罐头质量的标准差大于8g时,就认为该分装机运行不正常,将对它进行检修,现抽取了20只罐头,它们的质量(单位:g)如下:200,205,208,212,223,199,193,208,204,200,208,201,215,190,193,206,215,198,206,216,该分装机运行是否正常?
《第十七章方差与频数分布》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B D B C B D D
题号 11 12
答案 C A
1.C
【详解】试题解析:由频数直方图可以看出:全班总人数为8+10+14+8+5=45人;A正确;
体重在50千克到55千克的人数最多为14人;故众数在50千克到55千克之间.B正确,但C错误;
在体重在60千克到65千克的人数为5人,则占全班总人数的5÷45=;D正确.
故选C.
2.C
【分析】结合参加足球的人数与其所占的百分比, 计算可得本次调查共抽取的学生数, 进而求出被抽测学生中参加羽毛球项目人数为, 再计算出区九年级参加篮球项目的学生和参加足球项目的学生所占的百分比即可知道答案C是否正确, 估计九年级大约名学生参加乒乓球项目的人数和1500比较大小即可.
【详解】解:参加足球的人数是 40 人, 所占的百分比为,
本次抽取的总人数为(人),
被抽测学生中参加其他体育项目活动人数占,故A正确,不合题意;
被抽测学生中参加羽毛球项目人数为人, 故B正确,不合题意;
全区九年级参加篮球项目的学生比所占百分比为,
参加足球项目的学生所占百分比为,
估计全区九年级参加篮球项目的学生比参加足球项目的学生多,故C错误,符合题意;
从该年级学生中随机抽取了的学生,
九年级大约有名学生参加乒乓球项目, 故D正确,不合题意.
故选:C.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
3.B
【分析】根据组距的定义即可选出答案.
【详解】把一组数据分成若干组后,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距,故答案选B.
【点睛】本题主要考查了组距的定义,解本题的要点在于熟知组距等相关知识点.
4.B
【分析】求得销售这三种鞋数量之和为10双,是30的三分之一,故要购进的这三种鞋应是100的三分之一.
【详解】解:根据题意可得:销售的某种女鞋30双,24厘米、24.5厘米和25厘米三种女鞋数量之和为10;所占比例为,
则要购进100双这种女鞋,购进这三种女鞋数量之和应是;
故选:B.
【点睛】本题考查了由样本数据估算总体,解题的关键是理解题意.
5.D
【分析】根据平均数,中位数,方差,极差的概念逐项分析.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;利用方差公式计算方差,利用平均数和极差的定义可分别求出.
【详解】A. 由平均数公式求得:,故此选项正确,不符合题意;
B. 极差是,故此选项正确,不符合题意;
C. 把数据按大小排列,中间两个数为,,所以中位数是,故此选项正确,不符合题意;
D. ,故标准差为:,故此选项错误,符合题意.
故选:D.
【点睛】本题考查了统计学中的平均数,方差,中位数与极差的定义,解答这类题学生常常对中位数的计算方法掌握不好而错选.
6.B
【分析】根据方差的意义,反映了一组数据的波动大小,方差越大,波动性越大,反之也成立即可解答.
【详解】根据题意可得,甲班10人的成绩方差比乙班10人的成绩方差大,
∴乙班的成绩比甲班的成绩整齐.
故选B.
【点睛】本题考查了方差的意义,熟知方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定是解题的关键.
7.C
【分析】判断两组数据的关系时,在平均分相同或相近的情况下比较方差,方差越大,成绩越不稳定;方差越小,成绩越稳定,根据这种原理得到结果.
【详解】在平均分相同或相近的情况下比较方差,
方差越大,成绩越不稳定,
方差越小,成绩越稳定.
因此A. B. D均不正确,C正确.
故选C.
【点睛】本题考查了方差,解题的关键是掌握方差的概念.
8.B
【详解】(6+5+7+8+7+5+8+10+5+9)×2000=14000只.
故选B.
9.D
【详解】解:∵3、a、4、6、7,它们的平均数是5
∴(3+a+4+6+7)=5
解得,a=5
S2=[(3-5)2+(5-5)2+(4-5)2+(6-5)2+(7-5)2]
=2
故选D.
10.D
【分析】极差就是这组数中最大值与最小值的差.
【详解】数据1,6,3,9,8的极差是8.故选D.
【点睛】本题考查了极差,解题的关键是掌握极差的概念.
11.C
【分析】此题考查了平均数和方差,掌握方差以及平均数的定义是解题的关键.方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.根据平均数以及方差的意义分别对每一项进行分析,即可得出答案.
【详解】解:①(环,
(环,
则甲、乙的射击成绩的平均数都是8环;
从统计图中可以看出,甲成绩的方差比乙成绩的方差大;
所以乙成绩比甲成绩稳定,
故选:C
12.A
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:根据方差的意义知,成绩越稳定,则方差越小,
∵甲、乙学生所中环数的平均数相同,且甲的成绩比乙的成绩稳定,
∴.
故选A.
【点睛】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
13.<
【分析】先从图片中读出小明和小兵的测试数据,分别求出方差后比较大小.也可从图看出来小明的都在8到10之间相对小兵的波动更小.
【详解】解:小明数据的平均数,
方差s12=[(9-9)2+(8-9)2+(10-9)2+(9-9)2+(9-9)2]=0.4,
小兵数据的平均数,
方差s22=[(7-9)2+(10-9)2+(10-9)2+(8-9)2+(10-9)2]=2.6,
∴S12<S22.
故答案为:<.
14.
【分析】直接根据图表数据的波动大小进行判断即可.
【详解】解:图表数据可知,
乙数据偏离平均数数据较大,甲数据偏离平均数数据较小,
即乙的波动性较大,即方差大,即,
故答案为:<.
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
15.5
【分析】先根据平均数的定义确定x的值,再根据方差的计算公式出这组数据的方差.
【详解】解:由平均数公式得:,
解得,
则,
故答案为:5.
【点睛】本题主要考查平均数和方差,解题的关键是熟练掌握平均数和方差的计算公式.
16.0.4
【分析】根据数据2、3、3、4、x的平均数是3,先利用平均数的计算公式可求出x,然后利用方差的计算公式进行求解即可.
【详解】∵数据2、3、3、4、x的平均数是3,
∴,
∴,
∴,
故答案为.
【点睛】本题主要考查了平均数和方差的计算,解题的关键是熟练掌握平均数和方差的计算公式.
17.3,18,9
【分析】分别求得这三种鞋销售数量的占比,然后×90即可算出.
【详解】解:根据题意可得:销售的某种女鞋30双,24厘米、24.5厘米和25厘米三种女鞋数量各为1、6、3;则要购进90双这种女鞋,购进这三种女鞋数量各应是:
(双)、(双)、(双),
故填:3,18,9.
【点睛】考查了综合运用统计知识解决问题的能力,属于基础题型.
18.大.
【分析】利用方差公式,分别计算甲乙的方差,再比较大小即可.
【详解】解:
,
= 0.85,
=1.45,
所以,
故答案为.
【点睛】本题考查了折线统计图的读图和方差公式,掌握这些是本题解题关键.
19.(1)抽样调查;
(2)总体是全年级名学生英语作业的完成情况,个体是每一名同学英语作业的完成情况,样本是抽取的名学生的英语作业完成情况,样本容量为;
(3)人.
【分析】本题考查了用样本估计总体、全面调查与抽样调查、总体、个体、样本及样本容量的知识,掌握知识点的应用是解题的关键.
()根据从名学生中抽取名学生可以得到该抽查方式为抽样调查;
()总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量;
()用样本的差的情况估计总体的差的人数即可.
【详解】(1)解:根据题意可得:班主任和英语教师所用的调查方式是抽样调查,
故答案为:抽样调查;
(2)解:总体是全年级名学生英语作业的完成情况,
个体是每一名同学英语作业的完成情况,
样本是抽取的名学生的英语作业完成情况,样本容量为;
(3)解:∵名学生中得“差”的同学有名,
∴名学生中得“差”的为(人).
20.(1)x 乙=8,S2乙=0.8;(2)乙成绩稳,选乙合适,见解析.
【分析】(1)根据平均数、方差的计算公式计算即可;
(2)根据方差越大,波动越大,成绩越不稳定;方差越小,波动越小,成绩越稳定进行解答.
【详解】(1)x 乙=(7+9+8+9+7)÷5=8,
S2乙=[(7-8)2+(9-8)2+…+(9-8)2]÷5=0.8.
(2)∵S甲2=3.2,S乙2=0.8,
∴S甲2>S乙2,
∴乙的波动小,
∴应选乙去参加3分球投篮大赛.
【点睛】本题考查了方差、平均数,掌握它们的计算方法以及它们的性质是解题的关键.
21.(1)120,45%;(2)补图见解析;(3)1980人
【分析】(1)利用12÷10%=120,即可得到m的值;用120×40%即可得到n的值.
(2)根据n的值即可补全条形统计图;
(3)根据用样本估计总体,用3600××100%,即可得到答案.
【详解】(1)本次调查的总人数为12÷10%=120(人),
∴m==45%.
故答案为:120,45%;
(2)n=48,画出条形图:
(3)3600××100%=1980(人),
答:估计该景区服务工作平均每天得到1980人游客的肯定.
【点睛】本题考查了条形统计图、扇形统计图等知识,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
22.(1)300;(2)答案见解析;(3)40%;(4)720.
【分析】(1)用D组人数÷20%求得总人数;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
【详解】解:(1)60÷20%=300(人)
答:此次抽查的学生数为300人,
故答案为:300;
(2)C组的人数=300×40%=120人,A组的人数=300﹣100﹣120﹣60=20人,补全条形统计图如图所示;
(3)该生当天在校体育活动时间低于1小时的概率是=40%;
故答案为:40%;
(4)当天达到国家规定体育活动时间的学生有1200×=720人.
故答案为:720.
【点睛】本题考查概率公式、条形统计图、扇形统计图,用样本估计总体,解题的关键是明确题意,找出所求问需要的条件.
23.(1)80;(2)见解析;(3)36;(4)600名
【分析】(1)根据等级的人数以及所占的百分比即可求出本次调查中共抽取的学生数;
(2)根据(1)中的结果和扇形统计图中的数据,可以计算出等级的人数,然后即可将条形统计图补充完整;
(3)根据等级的人数以及抽取的学生数计算出等级所对应的扇形圆心角的度数;
(4)求出等级所占整体的百分比即可求出相应的人数.
【详解】解:(1)(名,
故答案为:80;
(2)等级的学生为:(名,
补全条形图如下,
(3)等级所对应的扇形圆心角的度数为:;
(4)(名,
答:估计该校2000学生中有600名学生的成绩评定为等级.
【点睛】本题考查扇形统计图、条形统计图,用样本估计总体,理解两个统计图中数量关系是解决问题的关键.
24.该分装机运行不正常,理由见解析
【分析】先根据平均数公式求得抽取的20只罐头质量的平均数,再根据方差公式求得它们的方差,进而可求得标准差,再用所求得的标准差与8g比较大小即可求得答案.
【详解】解:抽取的20只罐头质量的平均数=(200+205+208+212+223+199+193+208+204+200+208+201+215+190+193+206+215+198+206+216)÷20
=4100÷20
=205(g),
∴抽取的20只罐头质量的方差=[(200-205)2+(205-205)2+(208-205)2+(212-205)2+(223-205)2+(199-205)2+(193-205)2+(208-205)2+(204-205)2+(200-205)2+(208-205)2+(201-205)2+(215-205)2+(190-205)2+(193-205)2+(206-205)2+(215-205)2+(198-205)2+(206-205)2+(216-205)2]÷20
=1388÷20
=69.4,
∴标准差为,
∵>8,
∴该分装机运行不正常.
【点睛】本题考查了平均数和方差、标准差的计算和应用,熟练掌握平均数、方差以及标准差的计算公式是解决本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
