(期末培优卷)期末核心素养培优卷-2024-2025学年五年级下学期数学北师大版(含解析)
文档属性
| 名称 | (期末培优卷)期末核心素养培优卷-2024-2025学年五年级下学期数学北师大版(含解析) | 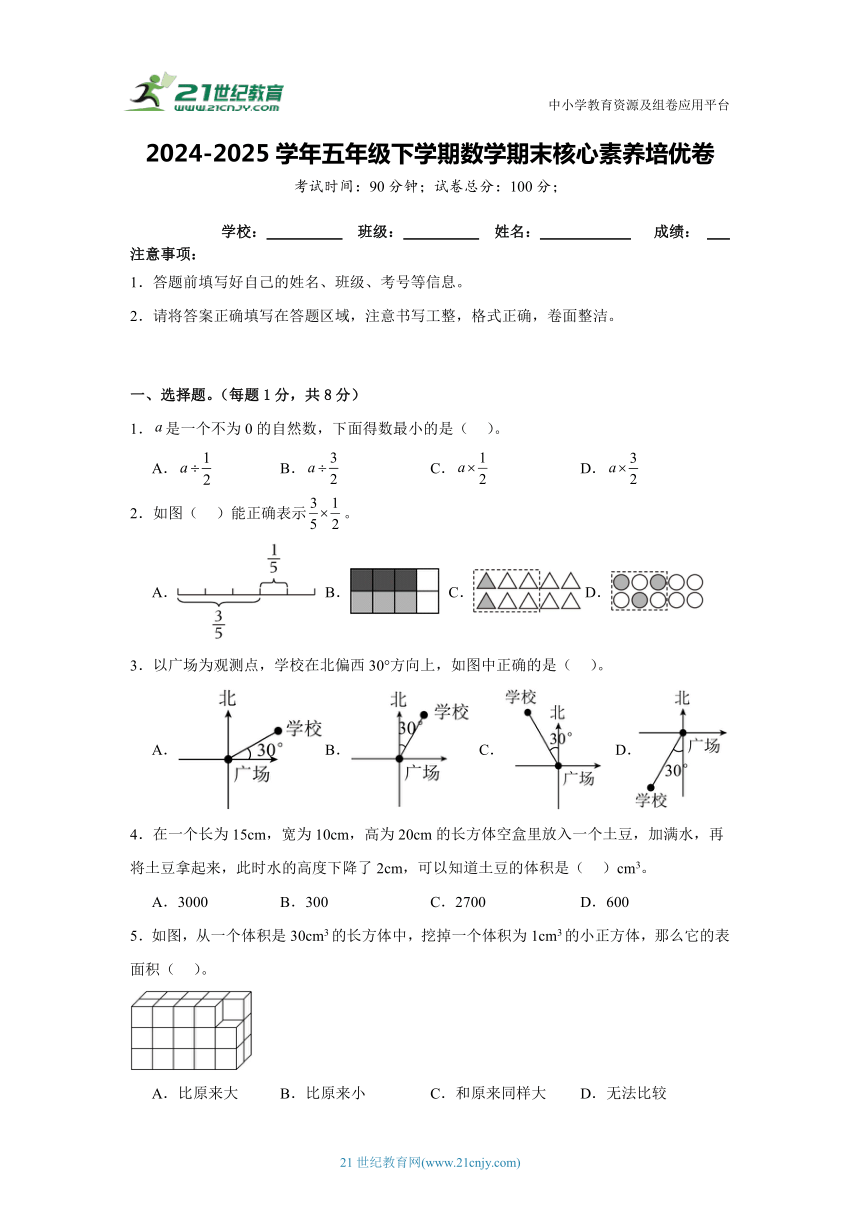 | |
| 格式 | docx | ||
| 文件大小 | 621.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 19:03:41 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.是一个不为0的自然数,下面得数最小的是( )。
A. B. C. D.
2.如图( )能正确表示。
A. B. C. D.
3.以广场为观测点,学校在北偏西30°方向上,如图中正确的是( )。
A.B. C. D.
4.在一个长为15cm,宽为10cm,高为20cm的长方体空盒里放入一个土豆,加满水,再将土豆拿起来,此时水的高度下降了2cm,可以知道土豆的体积是( )cm3。
A.3000 B.300 C.2700 D.600
5.如图,从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,那么它的表面积( )。
A.比原来大 B.比原来小 C.和原来同样大 D.无法比较
6.下图的正方体有两个圆形孔,一个三角形孔,它的展开图是( )。
A. B. C. D.
7.已知 a÷=b÷=c÷(a、b、c均大于0),( )最大。
A.a B.b C.c D.无法确定
8.把一个长方体切成两个长方体,下面( )种切法增加的表面积最少。
A. B. C. D.
二、填空题。(每空1分,共18分)
9.运动会时,卓玛、小红和次仁参加了一项跑步比赛,她们各跑了2圈,一圈长400米,卓玛跑了( )千米。比赛结束后,3人各喝了一瓶350毫升的水,他们一共喝了( )升的水。
10.如果(甲、Z、丙、丁都不为0),那么把甲、乙、丙、丁数从小到大依次排列后第三个是( )。
11.如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
12.笑笑家有一个长1米,宽5分米,高8分米的长方体玻璃鱼缸,鱼缸里面盛了40厘米高的水,水有( )升,笑笑在鱼缸里放了一个体积为75000立方厘米的珊瑚,这时水面的高度为( )分米。
13.美术课上,萱萱用硬纸板制作了一个正方体盒子,并在每个面上分别写上一个字。如图是这个正方体盒子的平面展开图,那么“核”字对面的字是( )。
14.六年级同学进行毕业体检,小明、小强、小方、小力和小军的体重情况记录如下。如果我们把他们五人的平均体重记作0kg,超过平均体重的部分记为正,那么小方的体重应记作( )。
小明 小强 小方 小力 小军
43kg 42kg 39kg 41kg 45kg
15.光明小学少先队辅导员王老师和章老师带领94名少先队员代表参观纪念馆,需乘车出行。了解到租车公司有以下两种车:大车限乘36人,小车限乘24人。租车后,辅导员和少先队员正好坐满位置(租了两种类型的车)。他们租了( )辆大车,( )辆小车。
16.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是( )cm3。
17.哥哥的邮票张数是妹妹的2倍,如果哥哥给妹妹6张,两人的邮票张数就一样多,妹妹原有( )张邮票。
18.把一个棱长是4厘米的正方体表面上涂上红漆,然后锯成棱长1厘米的正方体小木块,这些正方体小木块中3个面涂色的有( )块,2个面涂色的有( )块。
19.用( )个棱长1厘米的小正方体可以拼成一个棱长1分米的大正方体。把一个棱长1米的正方体大石头切割成棱长1分米的正方体小石头后紧挨着排成一排放在路边,这排小石头的长度是( )米。
20.李老师在一个袋子中装入红、黄两种颜色的球共10个,这些球除颜色外其他完全相同,如果想从袋子中任意摸出一个红球的可能性是,应该在袋子中放入( )个红球。
三、判断题。(每题1分,共5分)
21.一段木料,若锯成4段需用8分钟,则锯成7段需用16分钟。( )
22.妙想看奇思在南偏西的方向上,奇思看妙想在北偏东的方向上。( )
23.笑笑买课外书用了自己零花钱的,淘气买课外书也用了自己零花钱的,他们花的钱一样多。( )
24.用钢笔吸一次墨水,大约能吸2至3毫升。( )
25.分数加减法就是把分子相加减,分母相加减。( )
四、计算题。(共24分)
26.直接写出得数。(共8分)
27.计算下面各题,能简算的要简算。(共6分)
28.解方程。(共6分)
-x= x+= ×+x=
29.计算下面立体图形的表面积和体积。(单位:厘米,共4分)
五、操作题。(共9分)
30.某地大力发展农村定制客运,实行农村公交延伸和客运公交化改造。为方便出行,该地为A、B村建造了便民公交站。
(1)根据下面的描述,在图上标出A村和B村的位置。
①A村在公交站的西偏南30°方向1km处;
②B村在公交站的北偏西45°方向1.5km处。
(2)医院在公交站东偏北20°方向2.5km处,在图中标出医院的位置。
(3)王大爷住在B村,他要去医院,可以先骑车向( )( )°方向行( )km,再乘公交车向( )( )°方向行( )km。
六、解答题。(每题6分,共36分)
31.A、B两个码头相距880千米,一艘邮轮和一艘货轮分别从A、B两个码头相对开出,10小时后相遇。货轮的速度是邮轮速度的1.2倍,邮轮和货轮的速度分别是多少千米/时?
32.机床厂今年一月份生产机床1300台,二月份生产1200台,三月份生产1400台。前3个月平均每个月生产机床多少台?照这样计算,全年可以生产机床多少台?
33.甲乙两地之间的公路长700千米,一辆小汽车和一辆货车同时从两地出发,相向而行。小汽车每小时行驶80千米,货车每小时行驶60千米,行驶几小时后两车相遇?
34.如图,聪聪家和明明家正好分别处在一段路的两端,在他们两家之间有学校和文化馆。聪聪从家到学校,正好要走这段路的;明明从家到文化馆,正好要走这段路的。
(1)两人同时出发,同时到达各自的目的地,谁走得快?
(2)学校和文化馆之间的距离是这段路的几分之几?
35.政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
36.林叔叔要从成都到北京出差,在铁路购票网站上购买了一张6月21日中午11:00发车的复兴号高铁票,花费980元。他在6月19日上午9:00接到取消出差的通知,按照规定,火车票退票需要扣除手续费,相关规定如下表。
距离开车时间 8天以上 (含8天) 48时以上, 8天以内 24小时以上, 48小时以内 24小时以内
退票手续费 免费 票面价的 票面价的 票面价的
如果林叔叔收到取消出差通知后立即申请退票,那么应扣除手续费多少元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.C
【分析】先把选项中的分数除法转化为分数乘法,观察可知,四个乘法算式都有一个相同的因数,比较另一个因数的大小关系,另一个因数大的积就大,另一个因数小的积就小,据此解答。
【解答】=,=,,,因为<<<2,所以<<<,即得数最小的是。
故答案为:C
2.D
【分析】算式可以看作先将单位“1”平均分成5份,取其中的3份;再将这3份平均分成2份,取其中的1份;据此逐项分析出各个选项中图示表示的意义,看哪个选项中的图示能表示即可。
【解答】A.将一条线段的全长看作单位“1”,平均分成5份,其中的3份用分数表示,1份用分数表示,不能用算式表示;
B.将整个长方形看作单位“1”,先平均分成4份,浅色阴影部分占3份,用分数表示;再把浅色阴影部分看作单位“1”,平均分成2份,深色阴影部分占1份,用分数表示;那么深色阴影部分占整个长方形的的,列式为;
C.将所有的小三角形看作单位“1”,先平均分成5份,其中的3份用分数表示;再将这3份看作单位“1”,平均分成3份,涂色部分占1份,用分数表示;那么涂色部分占所有小三角形的的,列式为;
D.将所有的圆看作单位“1”,先平均分成5份,其中的3份用分数表示;再将这3份看作单位“1”,平均分成2份,涂色部分占1份,用分数表示;那么涂色部分占所有圆的的,列式为。
故答案为:D
3.C
【分析】以广场为观测点,以图上的“上北下南,左西右东”为准,结合方向、角度和距离确定各选项中学校与广场的位置关系,找出符合题意的即可。
【解答】A.图中表示:以广场为观测点,学校在东偏北30°方向上,不符合题意;
B.图中表示:以广场为观测点,学校在北偏东30°方向上,不符合题意;
C.图中表示:以广场为观测点,学校在北偏西30°方向上,符合题意;
D.图中表示:以广场为观测点,学校在南偏西30°方向上,不符合题意。
故答案为:C
4.B
【分析】从装有水的长方体盒子中取出一个土豆,水的高度下降了2cm,那么水下降部分的体积等于土豆的体积;根据长方体的体积=长×宽×高,代入数据计算,求出土豆的体积。
【解答】15×10×2
=150×2
=300(cm3)
土豆的体积是300cm3。
故答案为:B
5.C
【分析】从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,表面积减少了3个面,又增加了3个相同的面,相当于没变,所以它的表面积与原来这个长方体的表面积大小相等。
【解答】由分析可知:
从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,那么它的表面积和原来同样大。
故答案为:C
6.B
【分析】根据正方体展开图的特征,两个圆形孔是相对的,把各个选项的展开图还原成正方体,即可解答。
【解答】
A.,折叠成正方体,两个圆形孔是相邻,不是相对,不符合题意。
B.,折叠成正方体,两个圆形孔相对,符合题意。
C.,折叠成正方体,两个圆形孔相对,多一个圆形孔,不符合题意。
D.,折叠成正方体,两个圆形孔相对,多一个圆形孔,不符合题意。
正方体有两个圆形孔,一个三角形孔,它的展开图是。
故答案为:B
7.C
【分析】观察发现三个乘法算式的积相等,可以设它们的积都等于1;然后根据“因数=积÷另一个因数”,分别求出a、b、c的值,再比较大小,得出结论。
【解答】设a÷=b÷=c÷=1;
a=1×=
b=1×=
c=1×=
=,=,=
>>,即>>;
c>b>a,所以c最大。
故答案为:C
8.B
【分析】根据长方体切割的特征,明确将一个长方体切成两个长方体,如果平行于上、下底面切割,表面积增加2个(长×宽)的面积;如果平行于前、后面切割,表面积增加2个(长×高)的面积,如果平行于左、右面切割,表面积增加2个(宽×高)的面积,分别计算出增加的表面积,再进行比较,即可解答。
【解答】A.表面积增加了:6×5×2=60;
B.表面积增加了:5×4×2=40;
C.表面积增加了:6×4×2=48;
D.表面积增加了:6×5×2=60。
60=60>48>40,这种切法表面积增加最少。
把一个长方体切成两个长方体,种切法增加的表面积最少。
故答案为:B
9.0.8/ 1.05/
【分析】用一圈的长度×2,求出一个人跑的长度,即卓玛跑的长度,1千米=1000米,再换算成千米即可。
用1瓶水的容积×3,求出3瓶水的容积,也就是他们一共喝水的容积,1升=1000毫升,再换算成升即可。
【解答】400×2=800(米)
800米=0.8千米
350×3=1050(毫升)
1050毫升=1.05升
运动会时,卓玛、小红和次仁参加了一项跑步比赛,她们各跑了2圈,一圈长400米,卓玛跑了0.8千米。比赛结束后,3人各喝了一瓶350毫升的水,他们一共喝了1.05升的水。
10.丁
【分析】设1.6×甲=乙÷=丙×=丁÷=1,分别求出甲、乙、丙、丁的值,再进行比较,即可解答。
【解答】设1.6×甲=乙÷=丙×=丁÷=1
1.6×甲=1
甲=1÷1.6
甲=
乙÷=1
乙=1×
乙=
丙×=1
丙=1÷
丙=1×
丙=
丁÷=1
丁=1×
丁=
甲=;乙==;丙==;丁==。
<<<,即甲<乙<丁<丙。
如果1.6×甲=乙÷=丙×=丁÷,那么把甲、乙、丙、丁数从小到大依次排列后第三个是丁。
11.(2a+1) 15
【分析】探究摆a个三角形所需小棒数量规律:
从简单情形入手:摆1个三角形,直接可知需要3根小棒。
分析数量递增关系:摆2个三角形时,第二个三角形与第一个三角形共用1条边,所以相比摆1个三角形,只多了2根小棒,总共用3+2=5根小棒;摆3个三角形时,第三个三角形与前面图形共用1条边,相比摆2个三角形又多了2根小棒,即5+2=7根小棒。依此类推,每增加1个三角形,就增加2根小棒。
推导通用表达式:摆a个三角形,第一个三角形用3根小棒,后面(a-1)个三角形每个都增加2根小棒,所以总共需要小棒数为3+2×(a-1)根。对其化简:
已知摆a个三角形需要2a+1根小棒,现有31根小棒,可据此列出式子2a+1=31,求出三角形的个数。
【解答】摆a个△所需小棒数:
3+2×(a-1)
=3+2a-2
=(2a+1)个
求31根小棒能摆△的个数设31根小棒能摆a个△,则2a+1=31。
2a+1=31
解:2a+1-1=31-1
2a=30a
a=30÷2
a=15
综上,摆a个△需要2a+1根小棒,31根小棒可以摆15个△。
12.200 5.5
【分析】根据长方体体积=长×宽×高计算鱼缸中水的体积,注意水的高度是4分米;用珊瑚的体积除以鱼缸的底面积得出水的高度,再加放入珊瑚前水的高度就是这时水的高度。根据1米=10分米,1分米=10厘米,1立方分米=1升,1立方分米=1000立方厘米,将单位换算统一再进行计算。
【解答】1米=10分米
40厘米=4分米
10×5×4
=50×4
=200(立方分米)
200立方分米=200升
75000立方厘米=75立方分米
75÷(10×5)+4
=75÷50+4
=1.5+4
=5.5(分米)
鱼缸里面盛了40厘米高的水,水有200升;放了一个体积为75000平方厘米的珊瑚,这时水面的高度为5.5分米。
13.学
【分析】2-2-2型正方体展开图,如果“核”字在下面,则“心”字在右面,“数”字在后面,“学”字在上面,上下面相对,据此分析。
【解答】根据分析,“核”字对面的字是学。
14.﹣3
【分析】根据平均体重=5人体重之和÷5,先代入数据计算,求出平均体重。再求出小方的体重与平均体重的差,根据题意平均体重记作0kg记作0kg,超过平均体重的部分记为正,低于平均体重的部分记为负。据此表示小方的体重即可。
【解答】
=
=
小方的体重应记作﹣3kg。
15.2 1
【分析】分析题目,先用老师的人数加上少先队员的人数求出总人数,再设租了x辆大车,租了y辆小车,根据等量关系式:大车的数量×36+小车的数量×24=总人数列出方程,并进一步求出x和y的关系式,最后依次代入可能的x值求出对应的y值,再根据x、y都大于0且为整数解答即可。
【解答】94+2=96(人)
解:设租了x辆大车,租了y辆小车。
36x+24y=96
36x÷12+24y÷12=96÷12
3x+2y=8
当x=1时,
3×1+2y=8
3+2y=8
2y=8-3
2y=5
2y÷2=5÷2
y=2.5
因为x和y都必须是整数,所以不符合条件,舍去;
当x=2时,
3×2+2y=8
6+2y=8
2y=8-6
2y=2
2y÷2=2÷2
y=1
因为x和y都是整数,所以符合条件,即租了2辆大车,1辆小车。
光明小学少先队辅导员王老师和章老师带领94名少先队员代表参观纪念馆,需乘车出行。了解到租车公司有以下两种车:大车限乘36人,小车限乘24人。租车后,辅导员和少先队员正好坐满位置(租了两种类型的车)。他们租了2辆大车,1辆小车。
16.80
【分析】根据题意可知,把这个长方体横截成3段,表面积比原来增加4个截面的面积,据此可以求出一个截面的面积,然后根据长方体的体积公式:V=Sh,计算原来长方体的体积。
【解答】32÷4×10
=8×10
=80(cm3)
故原来长方体的体积是80cm3。
17.12
【分析】根据题意, 设妹妹原有x张邮票,因为哥哥的邮票张数是妹妹的2倍,则哥哥原有2x张邮票。哥哥给妹妹6张后,哥哥剩下 (2x 6) 张,妹妹有 (x+6) 张,此时两人邮票张数一样多,可列方程: 2x 6=x+6 ;据此解答。
【解答】解:设妹妹原有x张邮票,那么哥哥原有2x张邮票。
2x 6=x+6
2x 6 x=x+6 x
x 6=6
x 6+6=6+6
x=12
所以妹妹原有 12 张邮票。
18.8 24
【分析】把一个棱长4厘米的正方体木块的表面涂上红漆,再切成棱长1厘米的小正方体,那么把一条棱按照1厘米的长度切割时,能切出4块,两端的两块正好是大正方体的顶点位置且3面被涂色,所以每条棱上2面涂色的有2块,正方体共有12条棱,据此解答。
【解答】2面涂色:2×12=24(块)
3面涂色的小正方体是在大正方体顶点处的8块。
故这些正方体小木块中3个面涂色的有8块,2个面涂色的有24块。
19.1000 100
【分析】根据题意可知,1分米=10厘米,所以棱长1分米的大正方体,每条棱长都需要10个棱长为1厘米的小正方体,根据正方体的体积=棱长×棱长×棱长,用10×10×10即可求出小正方体的个数;同理,1米=10分米,棱长为1米的大正方体可以切割成(10×10×10)个的棱长为1分米的正方体,将它们排成1排,每个的长度是1分米,据此求出总长度,再把单位换算成米。
【解答】1分米=10厘米
10×10×10=1000(个)
1米=10分米
10×10×10=1000(个)
1000×1=1000(分米)
1000分米=100米
用1000个棱长1厘米的小正方体可以拼成一个棱长1分米的大正方体。把一个棱长1米的正方体大石头切割成棱长1分米的正方体小石头后紧挨着排成一排放在路边,这排小石头的长度是100米。
20.4
【分析】根据摸出红球的可能性求出红球占总球数的几分之几,再用总球数乘这个分率即可。
【解答】10×=4(个)
应该在袋子中放入4个红球。
21.√
【分析】次数=段数-1,用锯4段的时间除以锯4段的次数即是锯1次的时间,用锯1次的时间乘锯7段的次数即可判断。
【解答】8÷(4-1)×(7-1)
=8÷3×6
=16(分钟)
即一段木料,若锯成4段需用8分钟,则锯成7段需用16分钟,原说法正确。
故答案为:√
22.√
【分析】根据方向和位置的相对性,方向相反,角度相同,据此解答即可。
【解答】由分析可知:
妙想看奇思在南偏西的方向上,奇思看妙想在北偏东的方向上。原说法正确。
故答案为:√
23.×
【分析】第一个是把笑笑的零花钱看作单位“1”,第二个是把淘气的零花钱看作单位“1”,假设笑笑的零花钱是30元,而淘气的零花钱是60元,根据求一个数的几分之几是多少,用乘法计算,分别算出他们零花钱的是多少,再判断。
【解答】假设笑笑的零花钱是30元,而淘气的零花钱是60元。
(元)
(元)
笑笑买课外书用了自己零花钱的,淘气买课外书也用了自己零花线的,他们花的钱不一定一样多。原题说法错误。
故答案为:×
24.√
【分析】根据生活经验以及对容积单位和数据大小的认识,可知:1颗花生豆的体积大约是1立方厘米,1立方厘米=1毫升,所以用钢笔吸一次墨水量,用“毫升”为单位。据此解答。
【解答】用钢笔吸一次墨水,大约能吸2至3毫升,原题说法正确。
故答案为:√。
25.×
【分析】同分母分数相减,分子相加减,分母不变,即其分数单位不变,所以同分母相加减的是分数单位的个数。所以同分母分数相加减,就是把分数单位的个数相加减;异分母的分数相加减,先化成同分母的分数再计算。
【解答】由分析可知:同分母分数加减法是分母不变,分子相加减,异分母分数加减法是先通分,再按照同分母分数加减法的计算方法计算,原题说法错误。
故答案为:×
26.2;;;
;18;;
【解答】略
27.;;2
【分析】分数与分数的乘法:分子乘分子的积作为积的分子,分母乘分母的积作为积的分母,能约分的先进行约分;
运用加法交换律进行简便计算即可;
运用加法交换律和加法结合律进行简便计算即可。
【解答】
28.x=;x=;x=
【分析】-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可。
x+=,根据等式的性质1,方程两边同时减去即可。
×+x=,先计算出×的积,再根据等式的性质1,方程两边同时减去×的积即可。
【解答】-x=
解:-x+x-=-+x
x=-
x=-
x=
x+=
解:x+-=-
x=-
x=
×+x=
解:+x=
+x-=-
x=-
x=
29.表面积:216平方厘米;体积:208立方厘米
【分析】观察该立体图形可知,这个图形的表面积少了3个边长为2厘米的正方形的面积,又多了3个边长为2厘米的正方形的面积,所以该立体图形的表面积不变,根据正方体的表面积公式:S=6a2,据此进行计算即可;该立体图形的体积等于棱长为6厘米的正方体的体积减去棱长为2厘米的正方体的体积,根据正方体的体积公式:V=a3,据此进行计算即可。
【解答】表面积:6×6×6
=36×6
=216(平方厘米)
体积:6×6×6-2×2×2
=216-8
=208(立方厘米)
表面积是216平方厘米,体积是208立方厘米。
30.(1)(2)见详解;
(3)南偏东;45;1.5;东偏北;20;2.5
【分析】图上的1cm表示实际的500m,1km=1000m据此把实际距离换算成以米为单位再除以500即可得到图上的距离,再根据“上北下南,左西右东”的方位辨别方法确定方向,并结合给出的角度确定对应的角度,最后画出对应的图上距离,据此完成(1)(2);根据画出的图确定王大爷从B村到医院的具体路线,据此完成(3)。
【解答】(1)1km=1000m
1000÷500=2(cm)
1.5km=1500m
1500÷500=3(cm)
(2)2.5km=2500m
2500÷500=5(cm)
(1)(2)作图如下:
(3)王大爷住在B村,他要去医院,可以先骑车向南偏东45°方向行1.5km,再乘公交车向东偏北20°方向行2.5km。
31.邮轮40千米/时;货轮48千米/时
【分析】根据“货轮的速度是邮轮速度的1.2倍”,可以设邮轮的速度是千米/时,则货轮的速度1.2千米/时;
根据“速度和×相遇时间=路程”可得出等量关系:(邮轮的速度+货轮的速度)×相遇时间=A、B两个码头的距离,据此列出方程,并求解。
【解答】解:设邮轮的速度是千米/时,则货轮的速度1.2千米/时。
(+1.2)×10=880
2.2×10=880
22=880
=880÷22
=40
货轮的速度:40×1.2=48(千米/时)
答:邮轮的速度是40千米/时,货轮的速度是48千米/时。
32.1300台;15600台
【分析】运用加法求出前3个月生产的台数,再除以3,即为平均每个月生产机床多少台;用平均每个月生产的台数乘12,即为全年可以生产机床多少台。
【解答】(1300+1200+1400)÷3
=3900÷3
=1300(台)
1300×12=15600(台)
答:前3个月平均每个月生产机床1300台,全年可以生产机床15600台。
33.5小时
【分析】由题意知:两车同时相向而行,根据等量关系:速度和×时间=总路程,设行驶x小时后两车相遇,列方程求解即可。
【解答】解:设行驶x小时后两车相遇。
(80+60)x=700
140x=700
140x÷140=700÷140
x=5
答:行驶5小时后两车相遇。
34.(1)聪聪走得快
(2)
【分析】(1)比较他们用相同时间走完各自的路程,即比较和大小,路程越长,时间相同,那么速度越快,即可解答。
(2)把这条路的全长看作单位“1”,用1减去聪聪从家到学校,正好要走这段路的分率,减去明明从家到文化馆,正好要走这段路的分率,即可解答。
【解答】(1)=;=。
>,即>,聪聪走得快些。
答:聪聪走得快些。
(2)1--
=-
=-
=
答:学校和文化馆之间的距离是这段路的。
35.甲工程队15米;乙工程队10米
【分析】设乙工程队平均每天掘进米,则甲工程队平均每天掘进米,根据,,由题意可知等量关系式:甲工程队的工作效率×20+(甲工程队的工作效率+乙工程队的工作效率)×5=425,据此列方程并求解即可得乙工程队的工作效率,用乙工程队的工作效率+5,可得甲工程队的工作效率。
【解答】解:设乙工程队平均每天掘进米,则甲工程队平均每天掘进米。
10+5=15(米)
答:甲工程队平均每天分别掘进15米,乙工程队平均每天分别掘进10米。
36.49元
【分析】一天24小时,从6月19日上午9:00到6月21日上午9:00,这是整整两天,即这部分时长是48时;从6月21日上午9:00到中午11:00,又过了2时,因此林叔叔申请退票时距离开车的时长是50小时,属于距离开车时间是在48时以上,8天以内,所以应该按照票面价的,扣除手续费。将票价看作为单位“1”,根据求一个数的几分之几是多少,用乘法计算,即可求出扣除手续费多少元,据此解答。
【解答】21-19=2(日)=48(时)
11:00-9:00=2(时)
48+2=50(时)
距离开车时间50时,在48时以上,8天以内,退票手续费是票面价的。
980×=49(元)
答:应扣除手续费49元。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.是一个不为0的自然数,下面得数最小的是( )。
A. B. C. D.
2.如图( )能正确表示。
A. B. C. D.
3.以广场为观测点,学校在北偏西30°方向上,如图中正确的是( )。
A.B. C. D.
4.在一个长为15cm,宽为10cm,高为20cm的长方体空盒里放入一个土豆,加满水,再将土豆拿起来,此时水的高度下降了2cm,可以知道土豆的体积是( )cm3。
A.3000 B.300 C.2700 D.600
5.如图,从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,那么它的表面积( )。
A.比原来大 B.比原来小 C.和原来同样大 D.无法比较
6.下图的正方体有两个圆形孔,一个三角形孔,它的展开图是( )。
A. B. C. D.
7.已知 a÷=b÷=c÷(a、b、c均大于0),( )最大。
A.a B.b C.c D.无法确定
8.把一个长方体切成两个长方体,下面( )种切法增加的表面积最少。
A. B. C. D.
二、填空题。(每空1分,共18分)
9.运动会时,卓玛、小红和次仁参加了一项跑步比赛,她们各跑了2圈,一圈长400米,卓玛跑了( )千米。比赛结束后,3人各喝了一瓶350毫升的水,他们一共喝了( )升的水。
10.如果(甲、Z、丙、丁都不为0),那么把甲、乙、丙、丁数从小到大依次排列后第三个是( )。
11.如图,摆一个△需要用3根小棒,摆2个△需要用5根小棒,摆3个△需要用7根小棒,……,照这样,摆a个△需要用 ( )根小棒,用31根小棒可以摆( )个△。
12.笑笑家有一个长1米,宽5分米,高8分米的长方体玻璃鱼缸,鱼缸里面盛了40厘米高的水,水有( )升,笑笑在鱼缸里放了一个体积为75000立方厘米的珊瑚,这时水面的高度为( )分米。
13.美术课上,萱萱用硬纸板制作了一个正方体盒子,并在每个面上分别写上一个字。如图是这个正方体盒子的平面展开图,那么“核”字对面的字是( )。
14.六年级同学进行毕业体检,小明、小强、小方、小力和小军的体重情况记录如下。如果我们把他们五人的平均体重记作0kg,超过平均体重的部分记为正,那么小方的体重应记作( )。
小明 小强 小方 小力 小军
43kg 42kg 39kg 41kg 45kg
15.光明小学少先队辅导员王老师和章老师带领94名少先队员代表参观纪念馆,需乘车出行。了解到租车公司有以下两种车:大车限乘36人,小车限乘24人。租车后,辅导员和少先队员正好坐满位置(租了两种类型的车)。他们租了( )辆大车,( )辆小车。
16.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是( )cm3。
17.哥哥的邮票张数是妹妹的2倍,如果哥哥给妹妹6张,两人的邮票张数就一样多,妹妹原有( )张邮票。
18.把一个棱长是4厘米的正方体表面上涂上红漆,然后锯成棱长1厘米的正方体小木块,这些正方体小木块中3个面涂色的有( )块,2个面涂色的有( )块。
19.用( )个棱长1厘米的小正方体可以拼成一个棱长1分米的大正方体。把一个棱长1米的正方体大石头切割成棱长1分米的正方体小石头后紧挨着排成一排放在路边,这排小石头的长度是( )米。
20.李老师在一个袋子中装入红、黄两种颜色的球共10个,这些球除颜色外其他完全相同,如果想从袋子中任意摸出一个红球的可能性是,应该在袋子中放入( )个红球。
三、判断题。(每题1分,共5分)
21.一段木料,若锯成4段需用8分钟,则锯成7段需用16分钟。( )
22.妙想看奇思在南偏西的方向上,奇思看妙想在北偏东的方向上。( )
23.笑笑买课外书用了自己零花钱的,淘气买课外书也用了自己零花钱的,他们花的钱一样多。( )
24.用钢笔吸一次墨水,大约能吸2至3毫升。( )
25.分数加减法就是把分子相加减,分母相加减。( )
四、计算题。(共24分)
26.直接写出得数。(共8分)
27.计算下面各题,能简算的要简算。(共6分)
28.解方程。(共6分)
-x= x+= ×+x=
29.计算下面立体图形的表面积和体积。(单位:厘米,共4分)
五、操作题。(共9分)
30.某地大力发展农村定制客运,实行农村公交延伸和客运公交化改造。为方便出行,该地为A、B村建造了便民公交站。
(1)根据下面的描述,在图上标出A村和B村的位置。
①A村在公交站的西偏南30°方向1km处;
②B村在公交站的北偏西45°方向1.5km处。
(2)医院在公交站东偏北20°方向2.5km处,在图中标出医院的位置。
(3)王大爷住在B村,他要去医院,可以先骑车向( )( )°方向行( )km,再乘公交车向( )( )°方向行( )km。
六、解答题。(每题6分,共36分)
31.A、B两个码头相距880千米,一艘邮轮和一艘货轮分别从A、B两个码头相对开出,10小时后相遇。货轮的速度是邮轮速度的1.2倍,邮轮和货轮的速度分别是多少千米/时?
32.机床厂今年一月份生产机床1300台,二月份生产1200台,三月份生产1400台。前3个月平均每个月生产机床多少台?照这样计算,全年可以生产机床多少台?
33.甲乙两地之间的公路长700千米,一辆小汽车和一辆货车同时从两地出发,相向而行。小汽车每小时行驶80千米,货车每小时行驶60千米,行驶几小时后两车相遇?
34.如图,聪聪家和明明家正好分别处在一段路的两端,在他们两家之间有学校和文化馆。聪聪从家到学校,正好要走这段路的;明明从家到文化馆,正好要走这段路的。
(1)两人同时出发,同时到达各自的目的地,谁走得快?
(2)学校和文化馆之间的距离是这段路的几分之几?
35.政府决定修建一条海洋隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米。已知甲工程队平均每天比乙工程队多掘进5米。求甲、乙两个工程队平均每天分别掘进多少米?
36.林叔叔要从成都到北京出差,在铁路购票网站上购买了一张6月21日中午11:00发车的复兴号高铁票,花费980元。他在6月19日上午9:00接到取消出差的通知,按照规定,火车票退票需要扣除手续费,相关规定如下表。
距离开车时间 8天以上 (含8天) 48时以上, 8天以内 24小时以上, 48小时以内 24小时以内
退票手续费 免费 票面价的 票面价的 票面价的
如果林叔叔收到取消出差通知后立即申请退票,那么应扣除手续费多少元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.C
【分析】先把选项中的分数除法转化为分数乘法,观察可知,四个乘法算式都有一个相同的因数,比较另一个因数的大小关系,另一个因数大的积就大,另一个因数小的积就小,据此解答。
【解答】=,=,,,因为<<<2,所以<<<,即得数最小的是。
故答案为:C
2.D
【分析】算式可以看作先将单位“1”平均分成5份,取其中的3份;再将这3份平均分成2份,取其中的1份;据此逐项分析出各个选项中图示表示的意义,看哪个选项中的图示能表示即可。
【解答】A.将一条线段的全长看作单位“1”,平均分成5份,其中的3份用分数表示,1份用分数表示,不能用算式表示;
B.将整个长方形看作单位“1”,先平均分成4份,浅色阴影部分占3份,用分数表示;再把浅色阴影部分看作单位“1”,平均分成2份,深色阴影部分占1份,用分数表示;那么深色阴影部分占整个长方形的的,列式为;
C.将所有的小三角形看作单位“1”,先平均分成5份,其中的3份用分数表示;再将这3份看作单位“1”,平均分成3份,涂色部分占1份,用分数表示;那么涂色部分占所有小三角形的的,列式为;
D.将所有的圆看作单位“1”,先平均分成5份,其中的3份用分数表示;再将这3份看作单位“1”,平均分成2份,涂色部分占1份,用分数表示;那么涂色部分占所有圆的的,列式为。
故答案为:D
3.C
【分析】以广场为观测点,以图上的“上北下南,左西右东”为准,结合方向、角度和距离确定各选项中学校与广场的位置关系,找出符合题意的即可。
【解答】A.图中表示:以广场为观测点,学校在东偏北30°方向上,不符合题意;
B.图中表示:以广场为观测点,学校在北偏东30°方向上,不符合题意;
C.图中表示:以广场为观测点,学校在北偏西30°方向上,符合题意;
D.图中表示:以广场为观测点,学校在南偏西30°方向上,不符合题意。
故答案为:C
4.B
【分析】从装有水的长方体盒子中取出一个土豆,水的高度下降了2cm,那么水下降部分的体积等于土豆的体积;根据长方体的体积=长×宽×高,代入数据计算,求出土豆的体积。
【解答】15×10×2
=150×2
=300(cm3)
土豆的体积是300cm3。
故答案为:B
5.C
【分析】从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,表面积减少了3个面,又增加了3个相同的面,相当于没变,所以它的表面积与原来这个长方体的表面积大小相等。
【解答】由分析可知:
从一个体积是30cm3的长方体中,挖掉一个体积为1cm3的小正方体,那么它的表面积和原来同样大。
故答案为:C
6.B
【分析】根据正方体展开图的特征,两个圆形孔是相对的,把各个选项的展开图还原成正方体,即可解答。
【解答】
A.,折叠成正方体,两个圆形孔是相邻,不是相对,不符合题意。
B.,折叠成正方体,两个圆形孔相对,符合题意。
C.,折叠成正方体,两个圆形孔相对,多一个圆形孔,不符合题意。
D.,折叠成正方体,两个圆形孔相对,多一个圆形孔,不符合题意。
正方体有两个圆形孔,一个三角形孔,它的展开图是。
故答案为:B
7.C
【分析】观察发现三个乘法算式的积相等,可以设它们的积都等于1;然后根据“因数=积÷另一个因数”,分别求出a、b、c的值,再比较大小,得出结论。
【解答】设a÷=b÷=c÷=1;
a=1×=
b=1×=
c=1×=
=,=,=
>>,即>>;
c>b>a,所以c最大。
故答案为:C
8.B
【分析】根据长方体切割的特征,明确将一个长方体切成两个长方体,如果平行于上、下底面切割,表面积增加2个(长×宽)的面积;如果平行于前、后面切割,表面积增加2个(长×高)的面积,如果平行于左、右面切割,表面积增加2个(宽×高)的面积,分别计算出增加的表面积,再进行比较,即可解答。
【解答】A.表面积增加了:6×5×2=60;
B.表面积增加了:5×4×2=40;
C.表面积增加了:6×4×2=48;
D.表面积增加了:6×5×2=60。
60=60>48>40,这种切法表面积增加最少。
把一个长方体切成两个长方体,种切法增加的表面积最少。
故答案为:B
9.0.8/ 1.05/
【分析】用一圈的长度×2,求出一个人跑的长度,即卓玛跑的长度,1千米=1000米,再换算成千米即可。
用1瓶水的容积×3,求出3瓶水的容积,也就是他们一共喝水的容积,1升=1000毫升,再换算成升即可。
【解答】400×2=800(米)
800米=0.8千米
350×3=1050(毫升)
1050毫升=1.05升
运动会时,卓玛、小红和次仁参加了一项跑步比赛,她们各跑了2圈,一圈长400米,卓玛跑了0.8千米。比赛结束后,3人各喝了一瓶350毫升的水,他们一共喝了1.05升的水。
10.丁
【分析】设1.6×甲=乙÷=丙×=丁÷=1,分别求出甲、乙、丙、丁的值,再进行比较,即可解答。
【解答】设1.6×甲=乙÷=丙×=丁÷=1
1.6×甲=1
甲=1÷1.6
甲=
乙÷=1
乙=1×
乙=
丙×=1
丙=1÷
丙=1×
丙=
丁÷=1
丁=1×
丁=
甲=;乙==;丙==;丁==。
<<<,即甲<乙<丁<丙。
如果1.6×甲=乙÷=丙×=丁÷,那么把甲、乙、丙、丁数从小到大依次排列后第三个是丁。
11.(2a+1) 15
【分析】探究摆a个三角形所需小棒数量规律:
从简单情形入手:摆1个三角形,直接可知需要3根小棒。
分析数量递增关系:摆2个三角形时,第二个三角形与第一个三角形共用1条边,所以相比摆1个三角形,只多了2根小棒,总共用3+2=5根小棒;摆3个三角形时,第三个三角形与前面图形共用1条边,相比摆2个三角形又多了2根小棒,即5+2=7根小棒。依此类推,每增加1个三角形,就增加2根小棒。
推导通用表达式:摆a个三角形,第一个三角形用3根小棒,后面(a-1)个三角形每个都增加2根小棒,所以总共需要小棒数为3+2×(a-1)根。对其化简:
已知摆a个三角形需要2a+1根小棒,现有31根小棒,可据此列出式子2a+1=31,求出三角形的个数。
【解答】摆a个△所需小棒数:
3+2×(a-1)
=3+2a-2
=(2a+1)个
求31根小棒能摆△的个数设31根小棒能摆a个△,则2a+1=31。
2a+1=31
解:2a+1-1=31-1
2a=30a
a=30÷2
a=15
综上,摆a个△需要2a+1根小棒,31根小棒可以摆15个△。
12.200 5.5
【分析】根据长方体体积=长×宽×高计算鱼缸中水的体积,注意水的高度是4分米;用珊瑚的体积除以鱼缸的底面积得出水的高度,再加放入珊瑚前水的高度就是这时水的高度。根据1米=10分米,1分米=10厘米,1立方分米=1升,1立方分米=1000立方厘米,将单位换算统一再进行计算。
【解答】1米=10分米
40厘米=4分米
10×5×4
=50×4
=200(立方分米)
200立方分米=200升
75000立方厘米=75立方分米
75÷(10×5)+4
=75÷50+4
=1.5+4
=5.5(分米)
鱼缸里面盛了40厘米高的水,水有200升;放了一个体积为75000平方厘米的珊瑚,这时水面的高度为5.5分米。
13.学
【分析】2-2-2型正方体展开图,如果“核”字在下面,则“心”字在右面,“数”字在后面,“学”字在上面,上下面相对,据此分析。
【解答】根据分析,“核”字对面的字是学。
14.﹣3
【分析】根据平均体重=5人体重之和÷5,先代入数据计算,求出平均体重。再求出小方的体重与平均体重的差,根据题意平均体重记作0kg记作0kg,超过平均体重的部分记为正,低于平均体重的部分记为负。据此表示小方的体重即可。
【解答】
=
=
小方的体重应记作﹣3kg。
15.2 1
【分析】分析题目,先用老师的人数加上少先队员的人数求出总人数,再设租了x辆大车,租了y辆小车,根据等量关系式:大车的数量×36+小车的数量×24=总人数列出方程,并进一步求出x和y的关系式,最后依次代入可能的x值求出对应的y值,再根据x、y都大于0且为整数解答即可。
【解答】94+2=96(人)
解:设租了x辆大车,租了y辆小车。
36x+24y=96
36x÷12+24y÷12=96÷12
3x+2y=8
当x=1时,
3×1+2y=8
3+2y=8
2y=8-3
2y=5
2y÷2=5÷2
y=2.5
因为x和y都必须是整数,所以不符合条件,舍去;
当x=2时,
3×2+2y=8
6+2y=8
2y=8-6
2y=2
2y÷2=2÷2
y=1
因为x和y都是整数,所以符合条件,即租了2辆大车,1辆小车。
光明小学少先队辅导员王老师和章老师带领94名少先队员代表参观纪念馆,需乘车出行。了解到租车公司有以下两种车:大车限乘36人,小车限乘24人。租车后,辅导员和少先队员正好坐满位置(租了两种类型的车)。他们租了2辆大车,1辆小车。
16.80
【分析】根据题意可知,把这个长方体横截成3段,表面积比原来增加4个截面的面积,据此可以求出一个截面的面积,然后根据长方体的体积公式:V=Sh,计算原来长方体的体积。
【解答】32÷4×10
=8×10
=80(cm3)
故原来长方体的体积是80cm3。
17.12
【分析】根据题意, 设妹妹原有x张邮票,因为哥哥的邮票张数是妹妹的2倍,则哥哥原有2x张邮票。哥哥给妹妹6张后,哥哥剩下 (2x 6) 张,妹妹有 (x+6) 张,此时两人邮票张数一样多,可列方程: 2x 6=x+6 ;据此解答。
【解答】解:设妹妹原有x张邮票,那么哥哥原有2x张邮票。
2x 6=x+6
2x 6 x=x+6 x
x 6=6
x 6+6=6+6
x=12
所以妹妹原有 12 张邮票。
18.8 24
【分析】把一个棱长4厘米的正方体木块的表面涂上红漆,再切成棱长1厘米的小正方体,那么把一条棱按照1厘米的长度切割时,能切出4块,两端的两块正好是大正方体的顶点位置且3面被涂色,所以每条棱上2面涂色的有2块,正方体共有12条棱,据此解答。
【解答】2面涂色:2×12=24(块)
3面涂色的小正方体是在大正方体顶点处的8块。
故这些正方体小木块中3个面涂色的有8块,2个面涂色的有24块。
19.1000 100
【分析】根据题意可知,1分米=10厘米,所以棱长1分米的大正方体,每条棱长都需要10个棱长为1厘米的小正方体,根据正方体的体积=棱长×棱长×棱长,用10×10×10即可求出小正方体的个数;同理,1米=10分米,棱长为1米的大正方体可以切割成(10×10×10)个的棱长为1分米的正方体,将它们排成1排,每个的长度是1分米,据此求出总长度,再把单位换算成米。
【解答】1分米=10厘米
10×10×10=1000(个)
1米=10分米
10×10×10=1000(个)
1000×1=1000(分米)
1000分米=100米
用1000个棱长1厘米的小正方体可以拼成一个棱长1分米的大正方体。把一个棱长1米的正方体大石头切割成棱长1分米的正方体小石头后紧挨着排成一排放在路边,这排小石头的长度是100米。
20.4
【分析】根据摸出红球的可能性求出红球占总球数的几分之几,再用总球数乘这个分率即可。
【解答】10×=4(个)
应该在袋子中放入4个红球。
21.√
【分析】次数=段数-1,用锯4段的时间除以锯4段的次数即是锯1次的时间,用锯1次的时间乘锯7段的次数即可判断。
【解答】8÷(4-1)×(7-1)
=8÷3×6
=16(分钟)
即一段木料,若锯成4段需用8分钟,则锯成7段需用16分钟,原说法正确。
故答案为:√
22.√
【分析】根据方向和位置的相对性,方向相反,角度相同,据此解答即可。
【解答】由分析可知:
妙想看奇思在南偏西的方向上,奇思看妙想在北偏东的方向上。原说法正确。
故答案为:√
23.×
【分析】第一个是把笑笑的零花钱看作单位“1”,第二个是把淘气的零花钱看作单位“1”,假设笑笑的零花钱是30元,而淘气的零花钱是60元,根据求一个数的几分之几是多少,用乘法计算,分别算出他们零花钱的是多少,再判断。
【解答】假设笑笑的零花钱是30元,而淘气的零花钱是60元。
(元)
(元)
笑笑买课外书用了自己零花钱的,淘气买课外书也用了自己零花线的,他们花的钱不一定一样多。原题说法错误。
故答案为:×
24.√
【分析】根据生活经验以及对容积单位和数据大小的认识,可知:1颗花生豆的体积大约是1立方厘米,1立方厘米=1毫升,所以用钢笔吸一次墨水量,用“毫升”为单位。据此解答。
【解答】用钢笔吸一次墨水,大约能吸2至3毫升,原题说法正确。
故答案为:√。
25.×
【分析】同分母分数相减,分子相加减,分母不变,即其分数单位不变,所以同分母相加减的是分数单位的个数。所以同分母分数相加减,就是把分数单位的个数相加减;异分母的分数相加减,先化成同分母的分数再计算。
【解答】由分析可知:同分母分数加减法是分母不变,分子相加减,异分母分数加减法是先通分,再按照同分母分数加减法的计算方法计算,原题说法错误。
故答案为:×
26.2;;;
;18;;
【解答】略
27.;;2
【分析】分数与分数的乘法:分子乘分子的积作为积的分子,分母乘分母的积作为积的分母,能约分的先进行约分;
运用加法交换律进行简便计算即可;
运用加法交换律和加法结合律进行简便计算即可。
【解答】
28.x=;x=;x=
【分析】-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可。
x+=,根据等式的性质1,方程两边同时减去即可。
×+x=,先计算出×的积,再根据等式的性质1,方程两边同时减去×的积即可。
【解答】-x=
解:-x+x-=-+x
x=-
x=-
x=
x+=
解:x+-=-
x=-
x=
×+x=
解:+x=
+x-=-
x=-
x=
29.表面积:216平方厘米;体积:208立方厘米
【分析】观察该立体图形可知,这个图形的表面积少了3个边长为2厘米的正方形的面积,又多了3个边长为2厘米的正方形的面积,所以该立体图形的表面积不变,根据正方体的表面积公式:S=6a2,据此进行计算即可;该立体图形的体积等于棱长为6厘米的正方体的体积减去棱长为2厘米的正方体的体积,根据正方体的体积公式:V=a3,据此进行计算即可。
【解答】表面积:6×6×6
=36×6
=216(平方厘米)
体积:6×6×6-2×2×2
=216-8
=208(立方厘米)
表面积是216平方厘米,体积是208立方厘米。
30.(1)(2)见详解;
(3)南偏东;45;1.5;东偏北;20;2.5
【分析】图上的1cm表示实际的500m,1km=1000m据此把实际距离换算成以米为单位再除以500即可得到图上的距离,再根据“上北下南,左西右东”的方位辨别方法确定方向,并结合给出的角度确定对应的角度,最后画出对应的图上距离,据此完成(1)(2);根据画出的图确定王大爷从B村到医院的具体路线,据此完成(3)。
【解答】(1)1km=1000m
1000÷500=2(cm)
1.5km=1500m
1500÷500=3(cm)
(2)2.5km=2500m
2500÷500=5(cm)
(1)(2)作图如下:
(3)王大爷住在B村,他要去医院,可以先骑车向南偏东45°方向行1.5km,再乘公交车向东偏北20°方向行2.5km。
31.邮轮40千米/时;货轮48千米/时
【分析】根据“货轮的速度是邮轮速度的1.2倍”,可以设邮轮的速度是千米/时,则货轮的速度1.2千米/时;
根据“速度和×相遇时间=路程”可得出等量关系:(邮轮的速度+货轮的速度)×相遇时间=A、B两个码头的距离,据此列出方程,并求解。
【解答】解:设邮轮的速度是千米/时,则货轮的速度1.2千米/时。
(+1.2)×10=880
2.2×10=880
22=880
=880÷22
=40
货轮的速度:40×1.2=48(千米/时)
答:邮轮的速度是40千米/时,货轮的速度是48千米/时。
32.1300台;15600台
【分析】运用加法求出前3个月生产的台数,再除以3,即为平均每个月生产机床多少台;用平均每个月生产的台数乘12,即为全年可以生产机床多少台。
【解答】(1300+1200+1400)÷3
=3900÷3
=1300(台)
1300×12=15600(台)
答:前3个月平均每个月生产机床1300台,全年可以生产机床15600台。
33.5小时
【分析】由题意知:两车同时相向而行,根据等量关系:速度和×时间=总路程,设行驶x小时后两车相遇,列方程求解即可。
【解答】解:设行驶x小时后两车相遇。
(80+60)x=700
140x=700
140x÷140=700÷140
x=5
答:行驶5小时后两车相遇。
34.(1)聪聪走得快
(2)
【分析】(1)比较他们用相同时间走完各自的路程,即比较和大小,路程越长,时间相同,那么速度越快,即可解答。
(2)把这条路的全长看作单位“1”,用1减去聪聪从家到学校,正好要走这段路的分率,减去明明从家到文化馆,正好要走这段路的分率,即可解答。
【解答】(1)=;=。
>,即>,聪聪走得快些。
答:聪聪走得快些。
(2)1--
=-
=-
=
答:学校和文化馆之间的距离是这段路的。
35.甲工程队15米;乙工程队10米
【分析】设乙工程队平均每天掘进米,则甲工程队平均每天掘进米,根据,,由题意可知等量关系式:甲工程队的工作效率×20+(甲工程队的工作效率+乙工程队的工作效率)×5=425,据此列方程并求解即可得乙工程队的工作效率,用乙工程队的工作效率+5,可得甲工程队的工作效率。
【解答】解:设乙工程队平均每天掘进米,则甲工程队平均每天掘进米。
10+5=15(米)
答:甲工程队平均每天分别掘进15米,乙工程队平均每天分别掘进10米。
36.49元
【分析】一天24小时,从6月19日上午9:00到6月21日上午9:00,这是整整两天,即这部分时长是48时;从6月21日上午9:00到中午11:00,又过了2时,因此林叔叔申请退票时距离开车的时长是50小时,属于距离开车时间是在48时以上,8天以内,所以应该按照票面价的,扣除手续费。将票价看作为单位“1”,根据求一个数的几分之几是多少,用乘法计算,即可求出扣除手续费多少元,据此解答。
【解答】21-19=2(日)=48(时)
11:00-9:00=2(时)
48+2=50(时)
距离开车时间50时,在48时以上,8天以内,退票手续费是票面价的。
980×=49(元)
答:应扣除手续费49元。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
