苏教版六年级下册数学期末专题训练:应用题(含解析)
文档属性
| 名称 | 苏教版六年级下册数学期末专题训练:应用题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 684.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 19:10:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
苏教版六年级下册数学期末专题训练:应用题
1.一名工人搬运1000只花瓶,规定每搬运一只花瓶得劳务费0.4元,如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元。这名工人运完后共得劳务费360元,他打碎了多少只花瓶?
2.下面是小明和爸爸乘出租车从家去展览馆参观的路线图。已知乘车里程在3千米以内(含3千米)车费按起步价8元计算,以后每增加1千米(不足1千米按1千米算)车费就增加1.4元。请按图中提供的信息算一算,小明和爸爸到达展览馆应付车费多少元?
3.同学们在美术课上学习制作中国结,制作一个小中国结需要7分米红绳,制作一个大中国结需要11分米红绳,一共做了20个中国结,共用去184分米红绳。请问同学们制作了多少个大中国结?
4.太湖大桥被誉为中国内湖第一长桥,它由三座大桥组合而成,全长约4300米,画在一幅图上只有4.3厘米长。你知道这幅图的比例尺是多少吗?
5.如图,要给100个圆柱形易拉罐的侧面贴一圈商标纸(侧面贴满),至少需要多少平方分米商标纸?如果要做一个长方体纸盒,将这100个易拉罐放进去,这个长方体纸盒的长、宽、高至少是多少厘米?
6.一根圆柱形木料,用去一段后,剩余部分如下图。剩余部分的体积是多少立方分米?
7.如图,一个生日蛋糕有上、下两层,每层高度都是8厘米,底面直径分别是20厘米、30厘米。如果蛋糕的表面要浇上奶油,浇奶油部分的面积是多少平方厘米?
8.如图,一筒卫生卷纸的高度是10厘米,中间硬纸轴的直径是3.5厘米。制作10筒这样的卫生卷纸,中间的硬纸轴共需要硬纸板多少平方厘米?
9.一个圆锥形稻谷堆的底面周长是6.28米,高是1.5米。把这堆稻谷运到一个圆柱形粮囤,已知粮囤的底面直径是1米,则稻谷在粮囤里的高度是多少米?
10.一辆大客车限坐45人,一天租金800元;一辆小客车限坐25人,一天租金500元。师生364人旅游一天,怎样租车最省钱?最少要花多少钱?
11.在比例尺是1∶4000000的地图上,量得甲、乙两地相距2.5厘米。一辆汽车以50千米/时的速度从甲地开往乙地,多少小时可以到达?
12.一个圆柱形油桶,量得它的底面内直径是8分米,高10分米。这个油桶的容积是多少升?已知每升油重0.82千克,这个油桶里装了桶油,这些油重多少千克?(第二问得数保留整数)
13.学校准备用方砖铺设走廊。如果用面积是9平方分米的方砖铺,需要480块。如果改用面积是16平方分米的方砖铺,需要多少块?(列方程解答)
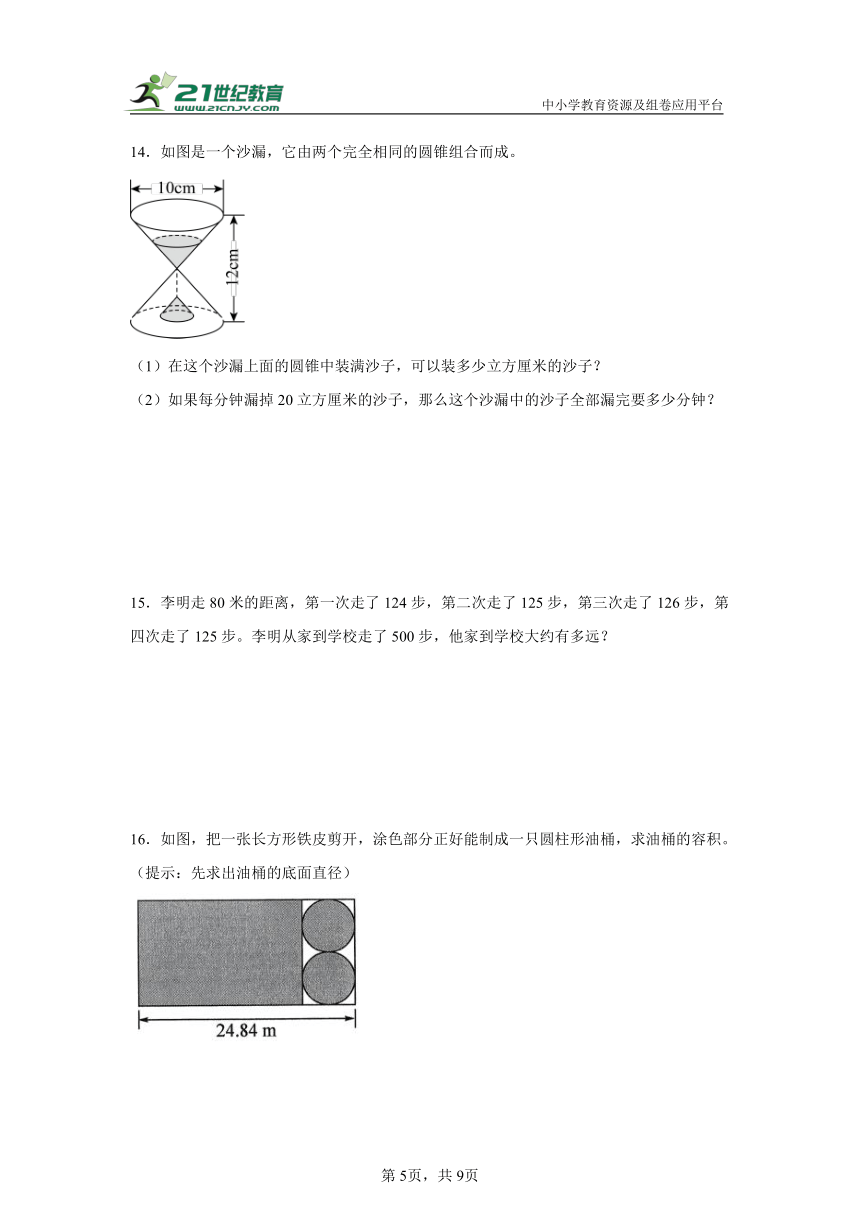
14.如图是一个沙漏,它由两个完全相同的圆锥组合而成。
(1)在这个沙漏上面的圆锥中装满沙子,可以装多少立方厘米的沙子?
(2)如果每分钟漏掉20立方厘米的沙子,那么这个沙漏中的沙子全部漏完要多少分钟?
15.李明走80米的距离,第一次走了124步,第二次走了125步,第三次走了126步,第四次走了125步。李明从家到学校走了500步,他家到学校大约有多远?
16.如图,把一张长方形铁皮剪开,涂色部分正好能制成一只圆柱形油桶,求油桶的容积。(提示:先求出油桶的底面直径)
17.把一个圆锥沿着底面直径和高分成两部分,表面积比原来增加120平方厘米。已知圆锥的高是10厘米,圆锥的体积是多少立方厘米?
18.在比例尺是1∶30000000的地图上,甲、乙两地之间的航空线长4.5厘米。在比例尺是1∶25000000的地图上,甲、乙两地之间的航空线长多少厘米?
19.参加某次数学竞赛的男生和女生人数的比是3∶1,这次数学竞赛的平均成绩是82分,男生的平均成绩是80分,女生的平均成绩是多少分?
20.如图,一个圆柱形玻璃缸的底面积是3平方分米,这个玻璃缸可以装多少升水?如果这个玻璃缸里有2升水,水面高度是多少分米?在图中标出水面位置。
21.在一幅地图上相距5厘米的两地实际距离是200千米,如果在这幅地图上量得A、B两地相距12厘米,A、B两地的实际距离是多少千米?
22.张帅是校篮球队的得分高手,在一次跟兄弟学校的篮球联谊赛上张帅一个人就赢得了28分,队友帮他数了,他一共投进12个球,有2分球,也有3分球,你能算出张帅投进几个2分球,几个3分球吗?
23.五一小长假,小宇一家人去灵丘花塔村野营。晚上他们准备搭个近似于圆锥体的帐篷。这个帐篷的底面半径大约3米,高约2米,帐篷里面的空间约有多大?
24.早在2000多年前,我国古代劳动人民就会用自己的方法计算各种物体的体积。《九章算术》中记载的圆柱体积的计算方法是“周自相乘,以高乘之,十二而一”,也就是说,用底面周长的平方乘高,再除以12,可以求出圆柱的体积。
(1)如果一个圆柱的底面周长是20厘米,高是10厘米,你能用上面的方法算出这个圆柱的体积吗?(得数保留整立方厘米)
(2)如果用现在的方法计算这个圆柱的体积,计算结果是多少立方厘米?(提示:计算时可以先保留进行约分和计算,最后再用3.14代入,得数保留整立方厘米。)
25.如图,玩具店出售一种陀螺,它的上面是圆柱,下面是圆锥。圆柱与圆锥等底等高,圆柱的直径是8厘米,高是6厘米。这种陀螺的体积是多少立方厘米?如果给这样的一个陀螺制作一个长方体的包装盒,至少需要多少平方分米的包装纸?
26.上午10时,聪聪和明明做了如下测量活动:
(1)找一根竹竿和一把卷尺,量得竹竿长2米;
(2)把竹竿直立在旗杆旁,量得竹竿的影长为1.2米,同时量得旗杆的影长为7.2米。根据他们的测量数据,你能求出学校旗杆有多高吗?
27.欢欢和迎迎进行100米轮滑比赛,迎迎让欢欢先滑15秒。两人滑行的路程与时间的关系如下图。
(1)在整个滑行过程中,谁滑行的路程与时间成正比例关系?为什么?
(2)滑完全程,欢欢比迎迎多用了几秒?
(3)欢欢前15秒平均每秒滑行多少米?后50秒平均每秒滑行多少米?
28.订阅《少年科普世界》的数量与总价的情况如下表。
数量/份 1 2 3 5 7 9
总价/元 12 24
(1)把上面的表格填写完整。
(2)根据表中数据,先在图中描出数量和总价所对应的点,再把这些点依次连起来。
(3)订阅《少年科普世界》的总价和数量成正比例吗?为什么?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第8页,共9页
第9页,共9页
《苏教版六年级下册数学期末专题训练:应用题》参考答案
1.20只
【分析】根据题意,设他打碎了只花瓶,那么没打碎的花瓶有(1000-)只,每只可得劳务费0.4元;如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元,那么打碎只花瓶,要赔1.6元;
等量关系:搬运一只花瓶的劳务费×完好的花瓶数量-打碎一只花瓶要赔的钱数×打碎花瓶的数量=最终得到的劳务费,据此列出方程,并求解。
【详解】解:设他打碎了只花瓶。
0.4×(1000-)-1.6=360
400-0.4-1.6=360
400-(0.4+1.6)=360
400-2=360
400-2+2=360+2
360+2=400
360+2-360=400-360
2=40
2÷2=40÷2
=20
答:他打碎了20只花瓶。
2.45.8元
【分析】由图可知:小明家到展览馆的图上距离为4+8=12(厘米),再根据实际距离=图上距离÷比例尺,求出小明家到展览馆的实际距离。再按照出租车在3千米以内(含3千米)按起步价8元计算,以后每增加1千米车费就增加1.4元分段计费。
【详解】4+8=12(厘米)
12÷=12×250000=3000000(厘米)
3000000厘米=30千米
8+(30-3)×1.4
=8+27×1.4
=8+37.8
=45.8(元)
答:小明到达展览馆要花45.8元出租车费。
3.11个
【分析】分析题目,设同学们制作了x个大中国结,则制作了(20-x)个小中国结,根据等量关系式:制作一个大中国结需要的红绳长度×制作的大中国结的个数+制作一个小中国结需要的红绳长度×制作的小中国结的个数=184列出方程11x+7(20-x)=184,进一步解出方程即可。
【详解】解:设同学们制作了x个大中国结,则制作了(20-x)个小中国结。
11x+7(20-x)=184
11x+140-7x=184
4x=184-140
4x=44
4x÷4=44÷4
x=11
答:同学们制作了11个大中国结。
4.1∶100000
【分析】已知太湖大桥的实际长度和图上长度,根据“比例尺=图上距离∶实际距离”以及进率“1米=100厘米”,求出这幅图的比例尺。
【详解】4.3厘米∶4300米
=4.3厘米∶(4300×100)厘米
=4.3∶430000
=(4.3÷4.3)∶(430000÷4.3)
=1∶100000
答:这幅图的比例尺是1∶100000。
5.188.4平方分米;60厘米;60厘米;10厘米
【分析】一圈商标纸的面积就是圆柱形易拉罐的侧面积,根据圆柱的侧面积=底面周长×高=πdh,代入数据计算可以求出一圈商标纸的面积,再乘100即可求出100个商标纸的面积;
将这100个易拉罐放进长方体纸盒,因为100=10×10,则可以每排放10个,放10排,那么这个纸盒的长和宽至少是6×10=60(厘米),高至少等于易拉罐的高10厘米。
【详解】6×3.14×10×100
=188.4×100
=18840(平方厘米)
18840平方厘米=188.4平方分米
长:6×10=60(厘米)
宽:6×10=60(厘米)
高是10厘米。
答:至少需要188.4平方分米商标纸。这个长方体纸盒的长是60厘米,宽是60厘米,高是10厘米。
6.282.6立方分米
【分析】如图:
本题可通过补全法,将两个剩余部分拼成完整圆柱来求解。先根据图中数据求出圆柱底面半径和拼接后圆柱的高,再利用圆柱体积公式V=πr2h算出完整圆柱体积;由于两个剩余部分可拼成完整圆柱,所以剩余部分体积是完整圆柱体积的一半,用完整圆柱体积除以2即可。
【详解】8+12=20(分米)
6÷2=3(分米)
3.14×32×20÷2
=3.14×9×20÷2
=28.26×20÷2
=565.2÷2
=282.6(立方分米)
答:剩余部分的体积是282.6立方分米。
7.1962.5平方厘米
【分析】观察图形可知,浇奶油部分面积由大圆柱一个底面积、大圆柱侧面积和小圆柱侧面积构成。 根据圆面积公式S=πr2,已知大圆柱底面直径,先求出半径,再代入公式算出底面积;依据圆柱侧面积公式S=πdh,已知大圆柱底面直径和高,代入数据求出大圆柱侧面积;同样根据圆柱侧面积公式S=πdh,已知小圆柱底面直径和高,算出小圆柱侧面积;最后把大圆柱底面积、大圆柱侧面积和小圆柱侧面积相加,得到浇奶油部分的总面积。
【详解】30÷2=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
3.14×30×8
=94.2×8
=753.6(平方厘米)
3.14×20×8
=62.8×8
=502.4(平方厘米)
706.5 +753.6+502.4
=1460.1+502.4
=1962.5(平方厘米)
答:浇奶油部分的面积是1962.5平方厘米。
8.1099平方厘米
【分析】硬纸轴是圆柱形,求制作它所需硬纸板面积就是求侧面积,根据圆柱侧面积公式S=πdh,已知硬纸轴的直径和高度,代入数据就能算出一个硬纸轴的侧面积;要制作10筒卫生卷纸,用一个硬纸轴的侧面积乘10,即可得到制作10个硬纸轴共需硬纸板的面积。
【详解】3.14×3.5×10×10
=10.99×10×10
=109.9×10
=1099(平方厘米)
答:中间的硬纸轴共需要硬纸板1099平方厘米。
9.2米
【分析】根据底面周长6.28米,可以求出底面的半径,再根据圆锥的体积公式,即可求出圆锥形稻谷的体积,由于稻谷的体积不变,所以再根据圆柱的体积公式的逆运算,即可求出稻谷堆的高度.
【详解】(米)
(米)
答:稻谷在粮囤里的高度是2米。
10.租7辆大客车、2辆小客车最省钱;6600元
【分析】先根据“单价=总价÷数量”分别计算出租大客车和小客车时每人需要的钱,要使租车最省钱,则应尽量租最便宜的一种车型,并且使每辆车都坐满,没有空位;因此用总人数除以最便宜的一种车型可坐的人数,再根据计算出的结果进行解答即可。
一共需要的租金=租小客车的辆数×每辆小客车的租金+租大客车的辆数×每辆大客车的租金,依此计算并解答。
【详解】800÷45=(元)
500÷25=20(元)
20元>元,因此尽量多租大客车。
364÷45=7(辆)……49(人)
方案1:租8辆大客车,1辆小客车,共需要:
8×800+500
=6400+500
=6900(元)
方案2:租7辆大客车和2辆小客车,共需要:
800×7+500×2
=5600+1000
=6600(元)
6600<6900
答:租8辆大客车和2辆小客车最省钱,最少要花6600元。
11.2小时
【分析】先根据实际距离=图上距离÷比例尺,据此求出实际距离是多少厘米,再把厘米化为千米,然后根据路程÷速度=时间,据此解答即可。
【详解】2.5÷
=2.5×4000000
=10000000(厘米)
10000000厘米=100千米
100÷50=2(小时)
答:2小时可以到达。
12.502.4升;247千克
【分析】油桶的内直径是8分米,则半径是8÷2=4分米,高是10分米,根据圆柱的体积=×半径的平方×高,代入数据求出这个油桶的容积是多少立方分米,再把立方分米化为升;把这个油桶的容积看作单位“1”,求一个数的几分之几是多少,用乘法解答,据此用乘法求出桶油是多少升,再乘每升油重即可解答。
【详解】8÷2=4(分米)
3.14××10
=3.14×16×10
=50.24×10
=502.4(立方分米)
502.4立方分米=502.4升
502.4××0.82
=301.44×0.82
=247.1808
≈247(千克)
答:这个油桶的容积是502.4升,这些油重247千克。
13.270块
【分析】根据题意,每块方砖的面积×块数=学校走廊的面积,学校走廊的面积是一定的,则方砖的面积与方砖的块数成反比例。设如果改用面积是16平方分米的方砖铺,需要x块,可列出方程:16x=9×480,解出方程即可。
【详解】解:设需要x块。
16x=9×480
16x=4320
16x÷16=4320÷16
x=270
答:需要270块。
14.(1)157立方厘米
(2)7.85分钟
【分析】(1)根据题意可知,每个圆锥的底面半径是10÷2=5(厘米),高是12÷2=6(厘米),根据圆锥的体积=底面积×高×=πr2h,代入数据计算即可求出沙子的体积。
(2)根据除法的意义,用(1)求得的沙子的体积除以20,即可求出所需时间。
【详解】(1)10÷2=5(厘米)
12÷2=6(厘米)
3.14×52×6×
=3.14×25×6×
=3.14×50
=157(立方厘米)
答:可以装157立方厘米的沙子。
(2)157÷20=7.85(分钟)
答:这个沙漏中的沙子全部漏完要7.85分钟。
15.320米
【分析】通过多次测量,求平均数,减小误差,先算出李明走80米,4次平均走的步数为125步。再看李明从家到学校走了500步里面有多少个125步,即有多少个80米,即可作答。
【详解】(124+125+125+126)÷4
=(249+125+126)÷4
=(374+126)÷4
=500÷4
=125(步)
500÷125×80
=4×80
=320(米)
答:他家到学校大约有320米远。
16.339.12立方米
【分析】根据题意可知,图中的2个圆是圆柱形油桶的上下底面,阴影长方形是圆柱形油桶的侧面;根据圆柱侧面展开图的特征可知,阴影长方形的长等于圆柱的底面周长,宽等于圆柱的高;
从图中可以看出,圆柱的底面周长+底面直径=24.84米,根据圆的周长公式C=πd,据此列出方程,并求出油桶的底面直径;
底面半径=底面直径÷2,圆柱的高=底面直径×2,根据圆柱的体积(容积)公式V=πr2h,代入数据计算,求出油桶的容积。
【详解】解:设油桶的底面直径是d米。
3.14d+d=24.84
4.14d=24.84
d=24.84÷4.14
d=6
3.14×(6÷2)2×(6×2)
=3.14×32×12
=3.14×9×12
=339.12(立方米)
答:油桶的容积是339.12立方米。
17.376.8立方厘米
【分析】一个圆锥沿底面直径和高被平均分成体积相等、形状相同的两部分,表面积比原来增加了两个截面,共120平方厘米,每个截面都是高为10厘米、底为圆锥的底面直径的三角形,三角形的底边a=S×2÷h,由此计算出三角形的底(圆锥的底面直径),再根据圆锥的体积公式V=πr2h÷3列式解答即可。
【详解】120÷2×2÷10
=60×2÷10
=12(厘米)
3.14×(12÷2)2×10÷3
=3.14×36×10÷3
=1130.4÷3
=376.8(立方厘米)
答:圆锥的体积是376.8立方厘米。
18.5.4厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据可求出甲、乙两地之间的实际距离,再根据图上距离=实际距离×比例尺,代入第二幅地图的比例尺即可得解。
【详解】(厘米)
(厘米)
答:甲、乙两地之间的航空线长5.4厘米。
19.88分
【分析】已知男生和女生人数的比是3∶1,可以设男生有3人,女生有1人。
根据平均分×人数=总分,可得出等量关系:男生的平均成绩×男生人数+女生的平均成绩×女生人数=总平均成绩×总人数,据此列出方程,并求解。
【详解】设男生有3人,女生有1人。
解:设女生的平均成绩是分。
80×3+=82×(3+1)
240+=82×4
240+=328
=328-240
=88
答:女生的平均成绩是88分。
20.6升;分米;图见详解
【分析】已知圆柱形玻璃缸的底面积是3平方分米,高是2分米,根据圆柱的体积(容积)公式V=Sh,求出这个玻璃缸可以装水的体积;
如果这个玻璃缸里有2升水,根据圆柱的高h=V÷S,求出水面的高度。
用水面的高度除以玻璃缸的高度,求出水面的高度是玻璃缸高度的几分之几,再根据分数的意义,画出水面的高度。
注意单位的换算:1立方分米=1升。
【详解】3×2=6(立方分米)
6立方分米=6升
2升=2立方分米
2÷3=(分米)
水面高度是玻璃缸高度的:
÷2
=×
=
如图:
答:这个玻璃缸可以装6升水。如果这个玻璃缸里有2升水,水面高度是分米。
21.480千米
【分析】根据题意,这幅地图上5厘米表示实际距离200千米,则图上1厘米表示实际距离200÷5=40(千米)。如果在这幅地图上量得A、B两地相距12厘米,根据乘法的意义,用40乘12即可求出A、B两地的实际距离。
【详解】200÷5=40(千米)
40×12=480(千米)
答:A、B两地的实际距离是480千米。
22.8个2分球,4个3分球。
【分析】假设张帅投进的12个球全是2分球,则共计24分,而实际得分是28分,少算了4分,这时因为张帅投进的12个球中,有些是3分球,而我们算成了2分球,投进1个3分球,就少算了1分,现在总共少算了4分,即可算出3分球的个数。
【详解】12×2=24(分)
28-24=4(分)
3-2=1(分)
4÷1=4(个)
12-4=8(个)
答:张帅投进8个2分球,4个3分球。
【点睛】本题主要考查鸡兔同笼问题,我们可以用假设法解答,解答中假设的全是2分,也可以假设全是3分。或者本题也可以用方程作答。
23.18.84立方米
【分析】求帐篷的空间大小就是求圆锥的体积,根据圆锥的体积,代入数据计算得出空间的大小。
【详解】3.14×32×2÷3
=3.14×9×2÷3
=3.14×3×2
=3.14×6
=18.84(立方米)
答:帐篷里面的空间是18.84立方米。
24.(1)333立方厘米;
(2)318立方厘米
【分析】(1)由题意可知,圆柱的体积=底面周长×底面周长×高÷12,把题目中的数据代入公式求出结果;
(2)先根据圆柱的底面周长求出圆柱的底面半径,再利用“”求出这个圆柱的体积,据此解答。
【详解】(1)20×20×10÷12
=400×10÷12
=4000÷12
≈333(立方厘米)
答:这个圆柱的体积是333立方厘米。
(2)20÷÷2
=20÷2÷
=10÷
=(厘米)
××10
=××10
=×10
=
≈318(立方厘米)
答:这个圆柱的体积是318立方厘米。
25.401.92立方厘米;5.12平方分米
【分析】根据圆柱与圆锥等底等高,则可以先根据圆柱的体积,代入数据计算,再根据等底等高的圆柱是圆锥的3倍,得出圆锥的体积,最后用圆柱的体积+圆锥的体积得出陀螺的体积;
这个长方体的包装盒的长是8厘米,宽是8厘米,高是12厘米,再根据,代入数据计算即可。最后注意根据1平方分米=100平方厘米以及低级单位转化为高级单位用除法换算单位。
【详解】π(8÷2)2×6+π(8÷2)2×6
=π×42×6+π×42×6
=π×16×6+π×16×6
=96π+32π
=128π
=401.92(立方厘米)
[8×8+8×(6×2)+8×(6×2)]×2
=[8×8+8×12+8×12]×2
=(64+96+96)×2
=256×2
=512(平方厘米)
512平方厘米=5.12平方分米
答:这种陀螺的体积是401.92立方厘米,至少需要5.12平方分米的包装纸。
26.12米
【分析】因相同的时间,阳光下物体的长度和影子长度的比相等,既竹竿的长度:竹竿的影长=旗杆的长度:旗杆的影长。据此可列比例解答.
【详解】解:设学校旗杆有x米。
2:1.2=x∶7.2
1.2x=7.2×2
1.2x=14.4
x=14.4÷1.2
x=12
答:学校旗杆有12米。
27.(1)迎迎;速度一定
(2)20秒
(3)2米;1.4米
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;从图上可见,迎迎的图线是一条过原点的直线,即始终保持匀速滑行,路程与时间成正比例;而欢欢的图线分成两段,速度并不恒定,不能视作正比例。
(2)由图可知,滑完全程,欢欢用了65秒,因为迎迎让欢欢先滑15秒,所以迎迎用了(60-15)秒,用欢欢所用时间减去迎迎所用时间即可求得欢欢比迎迎多用了多少秒。
(3)由图可知,欢欢前15秒滑行了30米,后50秒滑行了(100-30)米,根据速度=路程÷时间,分别求得欢欢前15秒平均每秒滑行多少米和后50秒平均每秒滑行多少米。
【详解】(1)由分析可知:
在整个滑行过程中,迎迎滑行的路程与时间成正比例关系,因为路程与时间的比值一定,即速度一定。
(2)65-(60-15)
=65-45
=20(秒)
答:欢欢比迎迎多用了20秒。
(3)30÷15=2(米)
(100-30)÷50
=70÷50
=1.4(米)
答:欢欢前15秒平均每秒滑行2米,后50秒平均每秒滑行1.4米。
28.(1)见详解
(2)见详解
(3)成正比例;因为总价和数量的比值一定。
【分析】(1)《少年科普世界》的单价是12元,用单价×份数=总价,据此填表格;
(2)在横轴上找到份数,再在纵轴上找到对应的总价,依次描点连线并标注数据;
(3)判断两个相关联的量呈正比例时,要看两个变量的比值是否为定值,据此解答。
【详解】(1)12×3=36(元)
12×5=60(元)
12×7=84(元)
12×9=108(元)
数量/份 1 2 3 5 7 9
总价/元 12 24 36 60 84 108
(2)
(3)因为总价÷数量=单价(一定),所以订阅《少年科普世界》的总价和数量成正比例。
答案第14页,共15页
答案第3页,共15页
中小学教育资源及组卷应用平台
苏教版六年级下册数学期末专题训练:应用题
1.一名工人搬运1000只花瓶,规定每搬运一只花瓶得劳务费0.4元,如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元。这名工人运完后共得劳务费360元,他打碎了多少只花瓶?
2.下面是小明和爸爸乘出租车从家去展览馆参观的路线图。已知乘车里程在3千米以内(含3千米)车费按起步价8元计算,以后每增加1千米(不足1千米按1千米算)车费就增加1.4元。请按图中提供的信息算一算,小明和爸爸到达展览馆应付车费多少元?
3.同学们在美术课上学习制作中国结,制作一个小中国结需要7分米红绳,制作一个大中国结需要11分米红绳,一共做了20个中国结,共用去184分米红绳。请问同学们制作了多少个大中国结?
4.太湖大桥被誉为中国内湖第一长桥,它由三座大桥组合而成,全长约4300米,画在一幅图上只有4.3厘米长。你知道这幅图的比例尺是多少吗?
5.如图,要给100个圆柱形易拉罐的侧面贴一圈商标纸(侧面贴满),至少需要多少平方分米商标纸?如果要做一个长方体纸盒,将这100个易拉罐放进去,这个长方体纸盒的长、宽、高至少是多少厘米?
6.一根圆柱形木料,用去一段后,剩余部分如下图。剩余部分的体积是多少立方分米?
7.如图,一个生日蛋糕有上、下两层,每层高度都是8厘米,底面直径分别是20厘米、30厘米。如果蛋糕的表面要浇上奶油,浇奶油部分的面积是多少平方厘米?
8.如图,一筒卫生卷纸的高度是10厘米,中间硬纸轴的直径是3.5厘米。制作10筒这样的卫生卷纸,中间的硬纸轴共需要硬纸板多少平方厘米?
9.一个圆锥形稻谷堆的底面周长是6.28米,高是1.5米。把这堆稻谷运到一个圆柱形粮囤,已知粮囤的底面直径是1米,则稻谷在粮囤里的高度是多少米?
10.一辆大客车限坐45人,一天租金800元;一辆小客车限坐25人,一天租金500元。师生364人旅游一天,怎样租车最省钱?最少要花多少钱?
11.在比例尺是1∶4000000的地图上,量得甲、乙两地相距2.5厘米。一辆汽车以50千米/时的速度从甲地开往乙地,多少小时可以到达?
12.一个圆柱形油桶,量得它的底面内直径是8分米,高10分米。这个油桶的容积是多少升?已知每升油重0.82千克,这个油桶里装了桶油,这些油重多少千克?(第二问得数保留整数)
13.学校准备用方砖铺设走廊。如果用面积是9平方分米的方砖铺,需要480块。如果改用面积是16平方分米的方砖铺,需要多少块?(列方程解答)
14.如图是一个沙漏,它由两个完全相同的圆锥组合而成。
(1)在这个沙漏上面的圆锥中装满沙子,可以装多少立方厘米的沙子?
(2)如果每分钟漏掉20立方厘米的沙子,那么这个沙漏中的沙子全部漏完要多少分钟?
15.李明走80米的距离,第一次走了124步,第二次走了125步,第三次走了126步,第四次走了125步。李明从家到学校走了500步,他家到学校大约有多远?
16.如图,把一张长方形铁皮剪开,涂色部分正好能制成一只圆柱形油桶,求油桶的容积。(提示:先求出油桶的底面直径)
17.把一个圆锥沿着底面直径和高分成两部分,表面积比原来增加120平方厘米。已知圆锥的高是10厘米,圆锥的体积是多少立方厘米?
18.在比例尺是1∶30000000的地图上,甲、乙两地之间的航空线长4.5厘米。在比例尺是1∶25000000的地图上,甲、乙两地之间的航空线长多少厘米?
19.参加某次数学竞赛的男生和女生人数的比是3∶1,这次数学竞赛的平均成绩是82分,男生的平均成绩是80分,女生的平均成绩是多少分?
20.如图,一个圆柱形玻璃缸的底面积是3平方分米,这个玻璃缸可以装多少升水?如果这个玻璃缸里有2升水,水面高度是多少分米?在图中标出水面位置。
21.在一幅地图上相距5厘米的两地实际距离是200千米,如果在这幅地图上量得A、B两地相距12厘米,A、B两地的实际距离是多少千米?
22.张帅是校篮球队的得分高手,在一次跟兄弟学校的篮球联谊赛上张帅一个人就赢得了28分,队友帮他数了,他一共投进12个球,有2分球,也有3分球,你能算出张帅投进几个2分球,几个3分球吗?
23.五一小长假,小宇一家人去灵丘花塔村野营。晚上他们准备搭个近似于圆锥体的帐篷。这个帐篷的底面半径大约3米,高约2米,帐篷里面的空间约有多大?
24.早在2000多年前,我国古代劳动人民就会用自己的方法计算各种物体的体积。《九章算术》中记载的圆柱体积的计算方法是“周自相乘,以高乘之,十二而一”,也就是说,用底面周长的平方乘高,再除以12,可以求出圆柱的体积。
(1)如果一个圆柱的底面周长是20厘米,高是10厘米,你能用上面的方法算出这个圆柱的体积吗?(得数保留整立方厘米)
(2)如果用现在的方法计算这个圆柱的体积,计算结果是多少立方厘米?(提示:计算时可以先保留进行约分和计算,最后再用3.14代入,得数保留整立方厘米。)
25.如图,玩具店出售一种陀螺,它的上面是圆柱,下面是圆锥。圆柱与圆锥等底等高,圆柱的直径是8厘米,高是6厘米。这种陀螺的体积是多少立方厘米?如果给这样的一个陀螺制作一个长方体的包装盒,至少需要多少平方分米的包装纸?
26.上午10时,聪聪和明明做了如下测量活动:
(1)找一根竹竿和一把卷尺,量得竹竿长2米;
(2)把竹竿直立在旗杆旁,量得竹竿的影长为1.2米,同时量得旗杆的影长为7.2米。根据他们的测量数据,你能求出学校旗杆有多高吗?
27.欢欢和迎迎进行100米轮滑比赛,迎迎让欢欢先滑15秒。两人滑行的路程与时间的关系如下图。
(1)在整个滑行过程中,谁滑行的路程与时间成正比例关系?为什么?
(2)滑完全程,欢欢比迎迎多用了几秒?
(3)欢欢前15秒平均每秒滑行多少米?后50秒平均每秒滑行多少米?
28.订阅《少年科普世界》的数量与总价的情况如下表。
数量/份 1 2 3 5 7 9
总价/元 12 24
(1)把上面的表格填写完整。
(2)根据表中数据,先在图中描出数量和总价所对应的点,再把这些点依次连起来。
(3)订阅《少年科普世界》的总价和数量成正比例吗?为什么?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第8页,共9页
第9页,共9页
《苏教版六年级下册数学期末专题训练:应用题》参考答案
1.20只
【分析】根据题意,设他打碎了只花瓶,那么没打碎的花瓶有(1000-)只,每只可得劳务费0.4元;如果打碎,不但得不到这只花瓶的劳务费,还要赔1.6元,那么打碎只花瓶,要赔1.6元;
等量关系:搬运一只花瓶的劳务费×完好的花瓶数量-打碎一只花瓶要赔的钱数×打碎花瓶的数量=最终得到的劳务费,据此列出方程,并求解。
【详解】解:设他打碎了只花瓶。
0.4×(1000-)-1.6=360
400-0.4-1.6=360
400-(0.4+1.6)=360
400-2=360
400-2+2=360+2
360+2=400
360+2-360=400-360
2=40
2÷2=40÷2
=20
答:他打碎了20只花瓶。
2.45.8元
【分析】由图可知:小明家到展览馆的图上距离为4+8=12(厘米),再根据实际距离=图上距离÷比例尺,求出小明家到展览馆的实际距离。再按照出租车在3千米以内(含3千米)按起步价8元计算,以后每增加1千米车费就增加1.4元分段计费。
【详解】4+8=12(厘米)
12÷=12×250000=3000000(厘米)
3000000厘米=30千米
8+(30-3)×1.4
=8+27×1.4
=8+37.8
=45.8(元)
答:小明到达展览馆要花45.8元出租车费。
3.11个
【分析】分析题目,设同学们制作了x个大中国结,则制作了(20-x)个小中国结,根据等量关系式:制作一个大中国结需要的红绳长度×制作的大中国结的个数+制作一个小中国结需要的红绳长度×制作的小中国结的个数=184列出方程11x+7(20-x)=184,进一步解出方程即可。
【详解】解:设同学们制作了x个大中国结,则制作了(20-x)个小中国结。
11x+7(20-x)=184
11x+140-7x=184
4x=184-140
4x=44
4x÷4=44÷4
x=11
答:同学们制作了11个大中国结。
4.1∶100000
【分析】已知太湖大桥的实际长度和图上长度,根据“比例尺=图上距离∶实际距离”以及进率“1米=100厘米”,求出这幅图的比例尺。
【详解】4.3厘米∶4300米
=4.3厘米∶(4300×100)厘米
=4.3∶430000
=(4.3÷4.3)∶(430000÷4.3)
=1∶100000
答:这幅图的比例尺是1∶100000。
5.188.4平方分米;60厘米;60厘米;10厘米
【分析】一圈商标纸的面积就是圆柱形易拉罐的侧面积,根据圆柱的侧面积=底面周长×高=πdh,代入数据计算可以求出一圈商标纸的面积,再乘100即可求出100个商标纸的面积;
将这100个易拉罐放进长方体纸盒,因为100=10×10,则可以每排放10个,放10排,那么这个纸盒的长和宽至少是6×10=60(厘米),高至少等于易拉罐的高10厘米。
【详解】6×3.14×10×100
=188.4×100
=18840(平方厘米)
18840平方厘米=188.4平方分米
长:6×10=60(厘米)
宽:6×10=60(厘米)
高是10厘米。
答:至少需要188.4平方分米商标纸。这个长方体纸盒的长是60厘米,宽是60厘米,高是10厘米。
6.282.6立方分米
【分析】如图:
本题可通过补全法,将两个剩余部分拼成完整圆柱来求解。先根据图中数据求出圆柱底面半径和拼接后圆柱的高,再利用圆柱体积公式V=πr2h算出完整圆柱体积;由于两个剩余部分可拼成完整圆柱,所以剩余部分体积是完整圆柱体积的一半,用完整圆柱体积除以2即可。
【详解】8+12=20(分米)
6÷2=3(分米)
3.14×32×20÷2
=3.14×9×20÷2
=28.26×20÷2
=565.2÷2
=282.6(立方分米)
答:剩余部分的体积是282.6立方分米。
7.1962.5平方厘米
【分析】观察图形可知,浇奶油部分面积由大圆柱一个底面积、大圆柱侧面积和小圆柱侧面积构成。 根据圆面积公式S=πr2,已知大圆柱底面直径,先求出半径,再代入公式算出底面积;依据圆柱侧面积公式S=πdh,已知大圆柱底面直径和高,代入数据求出大圆柱侧面积;同样根据圆柱侧面积公式S=πdh,已知小圆柱底面直径和高,算出小圆柱侧面积;最后把大圆柱底面积、大圆柱侧面积和小圆柱侧面积相加,得到浇奶油部分的总面积。
【详解】30÷2=15(厘米)
3.14×152
=3.14×225
=706.5(平方厘米)
3.14×30×8
=94.2×8
=753.6(平方厘米)
3.14×20×8
=62.8×8
=502.4(平方厘米)
706.5 +753.6+502.4
=1460.1+502.4
=1962.5(平方厘米)
答:浇奶油部分的面积是1962.5平方厘米。
8.1099平方厘米
【分析】硬纸轴是圆柱形,求制作它所需硬纸板面积就是求侧面积,根据圆柱侧面积公式S=πdh,已知硬纸轴的直径和高度,代入数据就能算出一个硬纸轴的侧面积;要制作10筒卫生卷纸,用一个硬纸轴的侧面积乘10,即可得到制作10个硬纸轴共需硬纸板的面积。
【详解】3.14×3.5×10×10
=10.99×10×10
=109.9×10
=1099(平方厘米)
答:中间的硬纸轴共需要硬纸板1099平方厘米。
9.2米
【分析】根据底面周长6.28米,可以求出底面的半径,再根据圆锥的体积公式,即可求出圆锥形稻谷的体积,由于稻谷的体积不变,所以再根据圆柱的体积公式的逆运算,即可求出稻谷堆的高度.
【详解】(米)
(米)
答:稻谷在粮囤里的高度是2米。
10.租7辆大客车、2辆小客车最省钱;6600元
【分析】先根据“单价=总价÷数量”分别计算出租大客车和小客车时每人需要的钱,要使租车最省钱,则应尽量租最便宜的一种车型,并且使每辆车都坐满,没有空位;因此用总人数除以最便宜的一种车型可坐的人数,再根据计算出的结果进行解答即可。
一共需要的租金=租小客车的辆数×每辆小客车的租金+租大客车的辆数×每辆大客车的租金,依此计算并解答。
【详解】800÷45=(元)
500÷25=20(元)
20元>元,因此尽量多租大客车。
364÷45=7(辆)……49(人)
方案1:租8辆大客车,1辆小客车,共需要:
8×800+500
=6400+500
=6900(元)
方案2:租7辆大客车和2辆小客车,共需要:
800×7+500×2
=5600+1000
=6600(元)
6600<6900
答:租8辆大客车和2辆小客车最省钱,最少要花6600元。
11.2小时
【分析】先根据实际距离=图上距离÷比例尺,据此求出实际距离是多少厘米,再把厘米化为千米,然后根据路程÷速度=时间,据此解答即可。
【详解】2.5÷
=2.5×4000000
=10000000(厘米)
10000000厘米=100千米
100÷50=2(小时)
答:2小时可以到达。
12.502.4升;247千克
【分析】油桶的内直径是8分米,则半径是8÷2=4分米,高是10分米,根据圆柱的体积=×半径的平方×高,代入数据求出这个油桶的容积是多少立方分米,再把立方分米化为升;把这个油桶的容积看作单位“1”,求一个数的几分之几是多少,用乘法解答,据此用乘法求出桶油是多少升,再乘每升油重即可解答。
【详解】8÷2=4(分米)
3.14××10
=3.14×16×10
=50.24×10
=502.4(立方分米)
502.4立方分米=502.4升
502.4××0.82
=301.44×0.82
=247.1808
≈247(千克)
答:这个油桶的容积是502.4升,这些油重247千克。
13.270块
【分析】根据题意,每块方砖的面积×块数=学校走廊的面积,学校走廊的面积是一定的,则方砖的面积与方砖的块数成反比例。设如果改用面积是16平方分米的方砖铺,需要x块,可列出方程:16x=9×480,解出方程即可。
【详解】解:设需要x块。
16x=9×480
16x=4320
16x÷16=4320÷16
x=270
答:需要270块。
14.(1)157立方厘米
(2)7.85分钟
【分析】(1)根据题意可知,每个圆锥的底面半径是10÷2=5(厘米),高是12÷2=6(厘米),根据圆锥的体积=底面积×高×=πr2h,代入数据计算即可求出沙子的体积。
(2)根据除法的意义,用(1)求得的沙子的体积除以20,即可求出所需时间。
【详解】(1)10÷2=5(厘米)
12÷2=6(厘米)
3.14×52×6×
=3.14×25×6×
=3.14×50
=157(立方厘米)
答:可以装157立方厘米的沙子。
(2)157÷20=7.85(分钟)
答:这个沙漏中的沙子全部漏完要7.85分钟。
15.320米
【分析】通过多次测量,求平均数,减小误差,先算出李明走80米,4次平均走的步数为125步。再看李明从家到学校走了500步里面有多少个125步,即有多少个80米,即可作答。
【详解】(124+125+125+126)÷4
=(249+125+126)÷4
=(374+126)÷4
=500÷4
=125(步)
500÷125×80
=4×80
=320(米)
答:他家到学校大约有320米远。
16.339.12立方米
【分析】根据题意可知,图中的2个圆是圆柱形油桶的上下底面,阴影长方形是圆柱形油桶的侧面;根据圆柱侧面展开图的特征可知,阴影长方形的长等于圆柱的底面周长,宽等于圆柱的高;
从图中可以看出,圆柱的底面周长+底面直径=24.84米,根据圆的周长公式C=πd,据此列出方程,并求出油桶的底面直径;
底面半径=底面直径÷2,圆柱的高=底面直径×2,根据圆柱的体积(容积)公式V=πr2h,代入数据计算,求出油桶的容积。
【详解】解:设油桶的底面直径是d米。
3.14d+d=24.84
4.14d=24.84
d=24.84÷4.14
d=6
3.14×(6÷2)2×(6×2)
=3.14×32×12
=3.14×9×12
=339.12(立方米)
答:油桶的容积是339.12立方米。
17.376.8立方厘米
【分析】一个圆锥沿底面直径和高被平均分成体积相等、形状相同的两部分,表面积比原来增加了两个截面,共120平方厘米,每个截面都是高为10厘米、底为圆锥的底面直径的三角形,三角形的底边a=S×2÷h,由此计算出三角形的底(圆锥的底面直径),再根据圆锥的体积公式V=πr2h÷3列式解答即可。
【详解】120÷2×2÷10
=60×2÷10
=12(厘米)
3.14×(12÷2)2×10÷3
=3.14×36×10÷3
=1130.4÷3
=376.8(立方厘米)
答:圆锥的体积是376.8立方厘米。
18.5.4厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据可求出甲、乙两地之间的实际距离,再根据图上距离=实际距离×比例尺,代入第二幅地图的比例尺即可得解。
【详解】(厘米)
(厘米)
答:甲、乙两地之间的航空线长5.4厘米。
19.88分
【分析】已知男生和女生人数的比是3∶1,可以设男生有3人,女生有1人。
根据平均分×人数=总分,可得出等量关系:男生的平均成绩×男生人数+女生的平均成绩×女生人数=总平均成绩×总人数,据此列出方程,并求解。
【详解】设男生有3人,女生有1人。
解:设女生的平均成绩是分。
80×3+=82×(3+1)
240+=82×4
240+=328
=328-240
=88
答:女生的平均成绩是88分。
20.6升;分米;图见详解
【分析】已知圆柱形玻璃缸的底面积是3平方分米,高是2分米,根据圆柱的体积(容积)公式V=Sh,求出这个玻璃缸可以装水的体积;
如果这个玻璃缸里有2升水,根据圆柱的高h=V÷S,求出水面的高度。
用水面的高度除以玻璃缸的高度,求出水面的高度是玻璃缸高度的几分之几,再根据分数的意义,画出水面的高度。
注意单位的换算:1立方分米=1升。
【详解】3×2=6(立方分米)
6立方分米=6升
2升=2立方分米
2÷3=(分米)
水面高度是玻璃缸高度的:
÷2
=×
=
如图:
答:这个玻璃缸可以装6升水。如果这个玻璃缸里有2升水,水面高度是分米。
21.480千米
【分析】根据题意,这幅地图上5厘米表示实际距离200千米,则图上1厘米表示实际距离200÷5=40(千米)。如果在这幅地图上量得A、B两地相距12厘米,根据乘法的意义,用40乘12即可求出A、B两地的实际距离。
【详解】200÷5=40(千米)
40×12=480(千米)
答:A、B两地的实际距离是480千米。
22.8个2分球,4个3分球。
【分析】假设张帅投进的12个球全是2分球,则共计24分,而实际得分是28分,少算了4分,这时因为张帅投进的12个球中,有些是3分球,而我们算成了2分球,投进1个3分球,就少算了1分,现在总共少算了4分,即可算出3分球的个数。
【详解】12×2=24(分)
28-24=4(分)
3-2=1(分)
4÷1=4(个)
12-4=8(个)
答:张帅投进8个2分球,4个3分球。
【点睛】本题主要考查鸡兔同笼问题,我们可以用假设法解答,解答中假设的全是2分,也可以假设全是3分。或者本题也可以用方程作答。
23.18.84立方米
【分析】求帐篷的空间大小就是求圆锥的体积,根据圆锥的体积,代入数据计算得出空间的大小。
【详解】3.14×32×2÷3
=3.14×9×2÷3
=3.14×3×2
=3.14×6
=18.84(立方米)
答:帐篷里面的空间是18.84立方米。
24.(1)333立方厘米;
(2)318立方厘米
【分析】(1)由题意可知,圆柱的体积=底面周长×底面周长×高÷12,把题目中的数据代入公式求出结果;
(2)先根据圆柱的底面周长求出圆柱的底面半径,再利用“”求出这个圆柱的体积,据此解答。
【详解】(1)20×20×10÷12
=400×10÷12
=4000÷12
≈333(立方厘米)
答:这个圆柱的体积是333立方厘米。
(2)20÷÷2
=20÷2÷
=10÷
=(厘米)
××10
=××10
=×10
=
≈318(立方厘米)
答:这个圆柱的体积是318立方厘米。
25.401.92立方厘米;5.12平方分米
【分析】根据圆柱与圆锥等底等高,则可以先根据圆柱的体积,代入数据计算,再根据等底等高的圆柱是圆锥的3倍,得出圆锥的体积,最后用圆柱的体积+圆锥的体积得出陀螺的体积;
这个长方体的包装盒的长是8厘米,宽是8厘米,高是12厘米,再根据,代入数据计算即可。最后注意根据1平方分米=100平方厘米以及低级单位转化为高级单位用除法换算单位。
【详解】π(8÷2)2×6+π(8÷2)2×6
=π×42×6+π×42×6
=π×16×6+π×16×6
=96π+32π
=128π
=401.92(立方厘米)
[8×8+8×(6×2)+8×(6×2)]×2
=[8×8+8×12+8×12]×2
=(64+96+96)×2
=256×2
=512(平方厘米)
512平方厘米=5.12平方分米
答:这种陀螺的体积是401.92立方厘米,至少需要5.12平方分米的包装纸。
26.12米
【分析】因相同的时间,阳光下物体的长度和影子长度的比相等,既竹竿的长度:竹竿的影长=旗杆的长度:旗杆的影长。据此可列比例解答.
【详解】解:设学校旗杆有x米。
2:1.2=x∶7.2
1.2x=7.2×2
1.2x=14.4
x=14.4÷1.2
x=12
答:学校旗杆有12米。
27.(1)迎迎;速度一定
(2)20秒
(3)2米;1.4米
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;从图上可见,迎迎的图线是一条过原点的直线,即始终保持匀速滑行,路程与时间成正比例;而欢欢的图线分成两段,速度并不恒定,不能视作正比例。
(2)由图可知,滑完全程,欢欢用了65秒,因为迎迎让欢欢先滑15秒,所以迎迎用了(60-15)秒,用欢欢所用时间减去迎迎所用时间即可求得欢欢比迎迎多用了多少秒。
(3)由图可知,欢欢前15秒滑行了30米,后50秒滑行了(100-30)米,根据速度=路程÷时间,分别求得欢欢前15秒平均每秒滑行多少米和后50秒平均每秒滑行多少米。
【详解】(1)由分析可知:
在整个滑行过程中,迎迎滑行的路程与时间成正比例关系,因为路程与时间的比值一定,即速度一定。
(2)65-(60-15)
=65-45
=20(秒)
答:欢欢比迎迎多用了20秒。
(3)30÷15=2(米)
(100-30)÷50
=70÷50
=1.4(米)
答:欢欢前15秒平均每秒滑行2米,后50秒平均每秒滑行1.4米。
28.(1)见详解
(2)见详解
(3)成正比例;因为总价和数量的比值一定。
【分析】(1)《少年科普世界》的单价是12元,用单价×份数=总价,据此填表格;
(2)在横轴上找到份数,再在纵轴上找到对应的总价,依次描点连线并标注数据;
(3)判断两个相关联的量呈正比例时,要看两个变量的比值是否为定值,据此解答。
【详解】(1)12×3=36(元)
12×5=60(元)
12×7=84(元)
12×9=108(元)
数量/份 1 2 3 5 7 9
总价/元 12 24 36 60 84 108
(2)
(3)因为总价÷数量=单价(一定),所以订阅《少年科普世界》的总价和数量成正比例。
答案第14页,共15页
答案第3页,共15页
同课章节目录
