华师大版数学八年级下册第十七章第二节17. 2. 2函数的图象课时练习
文档属性
| 名称 | 华师大版数学八年级下册第十七章第二节17. 2. 2函数的图象课时练习 | 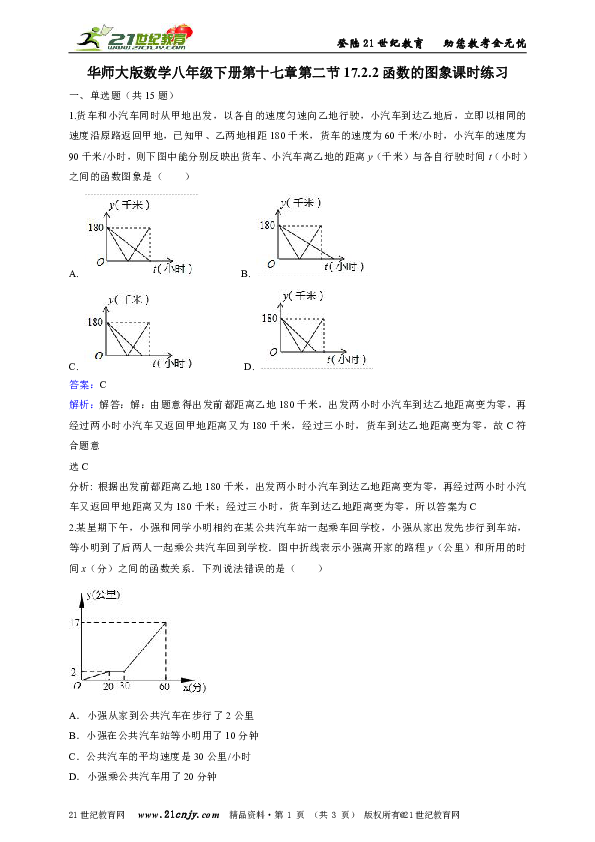 | |
| 格式 | doc | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 13:21:55 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学八年级下册第十七章第二节17.2.2函数的图象课时练习
一、单选题(共15题)
1.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲、乙两地相距180千米,货车的速度为60千米/小时,小汽车的速度为90千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
A. B.
C. D.
答案:C
解析:解答:解:由题意得出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米,经过三小时,货车到达乙地距离变为零,故C符合题意
选C
分析: 根据出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米;经过三小时,货车到达乙地距离变为零,所以答案为C
2.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
答案:D
解析:解答:A.依题意得小强从家到公共汽车步行了2公里,故选项正确;
B.依题意得小强在公共汽车站等小明用了10分钟,故选项正确;
C.公交车的速度为15÷=30公里/小时,故选项正确.
D.小强和小明一起乘公共汽车,时间为30分钟,故选项错误.
选:D.
分析:根据图象可以确定小强离公共汽车站2公里,步行用了多长时间,等公交车时间是多少,两人乘公交车运行的时间和对应的路程,然后确定各自的速度
3.一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:
①l1描述的是无月租费的收费方式;
②l2描述的是有月租费的收费方式;
③当每月的通话时间为500分钟时,选择有月租费的收费方式省钱.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
答案:D
解析:解答: ①l1描述的是无月租费的收费方式,说法正确;
②l2描述的是有月租费的收费方式,说法正确;
③当每月的通话时间为500分钟时,选择有月租费的收费方式省钱,说法正确
选D.
分析: 根据l1是从原点出发可得不打电话缴费为0元,因此是无月租费的收费方式;l2是从(0,20)出发可得不打电话缴费为20元,因此是有月租费的收费方式;两函数图象交点为(400,40),说明打电话400分钟时,两种收费相同,超过500分钟后,当x取定一个值时,l1所对应的函数值总比l2所对应的函数值大,因此当每月的通话时间为500分钟时,选择有月租费的收费方式省钱
4.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
答案:C
解析:解答: A.∵由图象可知,在凌晨4点函数图象在最低点-3,∴凌晨4时气温最低为-3℃,故本选项正确;
B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误;
D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确
选C.
分析: 根据函数的图象对各选项进行逐一分析点在第三象限内,那么横坐标小于0,纵坐标小于0,可得到一个关于a的不等式组,求解即可
5.下面说法中正确的是( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
答案:C
解析:解答: A.两个变量间的关系只能用关系式表示,还能用列表法和图象法表示,故错误;
B.图象能直观的表示两个变量间的数量关系,故错误;
C.借助表格可以表示出因变量随自变量的变化情况,正确;
D.以上说法都不对,错误
选C.
分析: 表示函数的方法有三种:解析法、列表法和图象法
6.在函数关系式y=|x-1|中,当x=-1时,函数值y是( )
A.0 B.2 C.-2 D.±2
答案:B
解析:解答: 当x=-1时,y=|x-1|=|-1-1|=2选B.
分析: 把x=-1直接代入函数y=|x-1|即可求出函数值.
7.当x=2时,函数y=2x-1的值是( )
A.0 B.-3 C.3 D.4
答案:C
解析:解答: x=2时,y=2×2-1=4-1=3
选:C.
分析:把x=2代入函数解析式计算即可得解.
8.当x=2时,函数y=2x-1的值是( )
A.0 B.-3 C.3 D.4
答案:C
解析:解答: x=2时,y=2×2-1=4-1=3
选C.
分析:把x=2代入函数解析式计算即可得解
9.已知函数y=3x-1,当x=3时,y的值是( )
A.6 B.7 C.8 D.9
答案:C
解析:解答: x=3时,y=3×3-1=8选:C.
分析: 把x=3代入函数关系式进行计算
10.函数y=中,自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≤-2 D.x≥2或x≤-2
答案:B
解析:解答: 根据题意得:x-2≥0,
解得:x≥2.选:B.
分析: 根据二次根式的性质,被开方数大于等于0,就可以求解.
11.在函数y=中,自变量x的取值范围是( )
A.x≠-2 B.x>2 C.x<2 D.x≠2
答案:D
解析:解答: 根据题意,有x-2≠0,解可得x≠2
选:D.
分析:根据分式有意义的条件是分母不为0;分析原函数式可得关系式x-2≠0,解可得自变量x的取值范围.
12.地铁1号线是重庆轨道交通线网东西方向的主干线,也是贯穿中区和沙坪坝区的重要交通通道,它的开通极大地方便了市民的出行,现某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,等了一会,然后搭乘一号线地铁直达两路口(忽略途中停靠站的时间).在此过程中,他离南开中学的距离y与时间x的函数关系的大致图象是( )
A. B.
C. D.
答案:C
解析:解答:某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,他离南开中学的距离y随时间x的增大而增大,等了一会,他离南开中学的距离y随时间x的增大不变,然后搭乘一号线地铁直达两路口(忽略途中停靠站的时间),他离南开中学的距离y与时间x的增大而增大,并且增加的速度更快了,符合以上的图象是C.选:C.
分析:根据某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,他离南开中学的距离y随时间x的增大而增大,等了一会,他离南开中学的距离y随时间x的增大不变,然后搭乘一号线地铁直达两路口,他离南开中学的距离y与时间x的增大而增大,并且增加的速度更快了,即可得出函数的大致图象
13.小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与x的函数关系的大致图象是( )
A. B.
C. D.
答案:D
解析:解答: A.随着时间的变化,离家的距离越来越远,故A错误;
B.随着时间的、变化,离家的距离越来越远,故B错误;
C.随着时间的变化,步行离家的距离变化快,搭轻轨的距离变化慢,不符合题意,故C错误;
D.随着时间的变化,步行离家的距离变化慢,搭轻轨的距离变化快,符合题意,故D正确;选:D.
分析:根据从学校回家,可得与家的距离是越来越近,根据步行的速度慢,可得离家的距离变化小,根据搭轻轨的速度快,可得离家的距离变化大.
14.一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是y和x,则y关于x的函数图象大致是图中的( )
A. B.
C. D.
答案:A
解析:解答:A.根据题意小三角形的面积减小,梯形的面积增大,而且x与y满足一次函数关系.选:A.
分析:通过求函数解析式的方法求解则可
15.小亮家与学校相距1500m,一天放学后他步行回家,最初以某一速度匀速前进,途中遇到熟人小强,说话耽误了几分钟,与小强告别后他就改为匀速慢跑,最后回答了家,设小亮从学校出发后所用的时间为t(min),与家的距离为s(m),下列图象中,能表示上述过程的是( )
A. B.
C. D.
答案:C
解析:解答:由题意得,最初与家的距离s随时间t的增大而减小,与小强说话时,时间增大而s不变,慢跑时,与家的距离s随时间t的增大而减小选:C.
分析:分三段分析,最初步行、与小强说话、匀速慢跑,分析函数的性质,进行判断
二、填空题(共5题)
16.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为________平方米
答案:100
解析:解答: 由纵坐标看出:休息前绿化面积是60平方米,休息后绿化面积是160-60=100平方米.
分析:根据函数图象的纵坐标,可得答案
17.如图所示的是春季某地一天气温随时间变化的图象,根据图象判断,在这天中,最高温度与最低温度的差是__________℃.
答案: 10
解析:解答:观察图象,由纵坐标看出最高气温是12℃,最低气温是2℃,
所以温差是12-2=10℃
分析:根据观察函数图象的纵坐标,可得最低气温,最高气温,根据有理数的减法,可得温差
18.函数y=的自变量x的取值范围是_________
答案: x≥7
解析:解答: 根据题意得:x-7≥0,
解得x≥7,
分析: 函数关系中主要有二次根式.根据二次根式的意义,被开方数是非负数.
19.当x=3时,函数y=-x+2的值为_____.
答案:-1
解析:解答:当x=3时,y=-x+2=-3+2=-1
分析:根据函数值的求解方法,把x=3代入y=-x+2,求出函数y=-x+2的值
20.小强想给爷爷买双鞋,爷爷说他自己的脚长25.5cm,若用x(cm)表示脚长,用y(码)表示鞋码,则有2x-y=10,根据上述关系式,小强应给爷爷买________码的鞋
答案:41
解析:解答: ∵用x表示脚长,用y表示鞋码,
则有2x-y=10,而x=25.5,
则51-y=10,
解得:y=41
分析:由于已知用x表示脚长,用y表示鞋码,则有2x-y=10,而爷爷只告诉他自己的脚长25.5cm,代入公式即可求出小强该买多少码的鞋
三、解答题(共5题)
21.已知x无论取何正值,y1=-3x+7都比y2=kx+5大,求k的取值范围
答案: 解答: 由题意得,-3x+7>kx+5,
所以(k+3)x<2,
∵x无论取何正值,y1=-3x+7都比y2=kx+5大,
∴k+3≤0,
解得x≤-3
分析:根据函数值列出不等式,再根据对任意正数x不等式都成立列出关于k的不等式,然后求解
22.地壳的厚度约为8到40km,在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.
(1)在这个变化过程中,自变量和因变量分别是什么?
答案: 解:自变量是地表以下的深度x,
因变量是所达深度的温度y;
(2)如果地表温度为2℃,计算当x为5km时地壳的温度.
答案: 解:当t=2,x=5时,
y=3.5×5+2=19.5;
所以此时地壳的温度是19.5℃
分析:(1)因为温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度,所以自变量是x,因变量是y.(2)令t=2,x=5,代入函数解析式,即可求解
23.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
答案:解答:根据图象知道:
点A到点B是匀速运动、点E到点F是匀加速运动、点G到点H匀减速运动;
(2)汽车在点A的速度是多少?在点C呢?
答案:解答:根据图象知道:
汽车在点A的速度是30千米每小时,在点C的速度为0千米每小时;
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图
答案:解答:如图所示:
分析: (1)根据图象可以确定从点A到点B、点E到点F、点G到点H分别表明汽车的运动状态;(2)根据图象可以直接得到汽车在点A和点C的速度;(3)结合已知条件利用图象可以画出从28分钟以后汽车速度与行驶时间的关系图
24.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
答案:解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)10时和13时,他分别离家多远?
答案:解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)他到达离家最远的地方是什么时间?离家多远?
答案:解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)11时到12时他行驶了多少千米?
答案:解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
(5)他可能在哪段时间内休息,并吃午餐?
答案:解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)他由离家最远的地方返回时的平均速度是多少?
答案:解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
分析:(1)根据函数图象,可得自变量、因变量;(2)根据函数图象的纵坐标,可得答案;(3)根据函数图象的横坐标、纵坐标,可得答案;(4)根据函数图象的横坐标,可得函数值,根据函数值相减,可得答案;(5)根据函数图象的纵坐标,可得答案;(6)根据函数图象的纵坐标,可得距离,根据函数图象的横坐标,可得时间,根据路程除以时间,可得答案
25.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
答案:解答:观察图象可知:玲玲到离家最远的地方需要3小时,此时离家30千米;(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
答案:解答:玲玲郊游过程中,各时间段的速度分别为:
9~10时,速度为10÷(10-9)=10千米/时;
10~10.5时,速度约为(17.5-10)÷(10.5-10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30-17.5)÷(12-11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15-13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15-13)=15千米/小时;
(4)玲玲全程骑车的平均速度是多少?
答案:解答:玲玲全程骑车的平均速度为:(30+30)÷(15-9)=10千米/小时
分析: (1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;(2)休息是路程不在随时间的增加而增加;(3)往返全程中回来时候速度最快,用距离除以所用时间即可;(4)用玲玲全称所行的路程除以所用的时间即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
华师大版数学八年级下册第十七章第二节17.2.2函数的图象课时练习
一、单选题(共15题)
1.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲、乙两地相距180千米,货车的速度为60千米/小时,小汽车的速度为90千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
A. B.
C. D.
答案:C
解析:解答:解:由题意得出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米,经过三小时,货车到达乙地距离变为零,故C符合题意
选C
分析: 根据出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米;经过三小时,货车到达乙地距离变为零,所以答案为C
2.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
答案:D
解析:解答:A.依题意得小强从家到公共汽车步行了2公里,故选项正确;
B.依题意得小强在公共汽车站等小明用了10分钟,故选项正确;
C.公交车的速度为15÷=30公里/小时,故选项正确.
D.小强和小明一起乘公共汽车,时间为30分钟,故选项错误.
选:D.
分析:根据图象可以确定小强离公共汽车站2公里,步行用了多长时间,等公交车时间是多少,两人乘公交车运行的时间和对应的路程,然后确定各自的速度
3.一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:
①l1描述的是无月租费的收费方式;
②l2描述的是有月租费的收费方式;
③当每月的通话时间为500分钟时,选择有月租费的收费方式省钱.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
答案:D
解析:解答: ①l1描述的是无月租费的收费方式,说法正确;
②l2描述的是有月租费的收费方式,说法正确;
③当每月的通话时间为500分钟时,选择有月租费的收费方式省钱,说法正确
选D.
分析: 根据l1是从原点出发可得不打电话缴费为0元,因此是无月租费的收费方式;l2是从(0,20)出发可得不打电话缴费为20元,因此是有月租费的收费方式;两函数图象交点为(400,40),说明打电话400分钟时,两种收费相同,超过500分钟后,当x取定一个值时,l1所对应的函数值总比l2所对应的函数值大,因此当每月的通话时间为500分钟时,选择有月租费的收费方式省钱
4.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
答案:C
解析:解答: A.∵由图象可知,在凌晨4点函数图象在最低点-3,∴凌晨4时气温最低为-3℃,故本选项正确;
B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误;
D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确
选C.
分析: 根据函数的图象对各选项进行逐一分析点在第三象限内,那么横坐标小于0,纵坐标小于0,可得到一个关于a的不等式组,求解即可
5.下面说法中正确的是( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
答案:C
解析:解答: A.两个变量间的关系只能用关系式表示,还能用列表法和图象法表示,故错误;
B.图象能直观的表示两个变量间的数量关系,故错误;
C.借助表格可以表示出因变量随自变量的变化情况,正确;
D.以上说法都不对,错误
选C.
分析: 表示函数的方法有三种:解析法、列表法和图象法
6.在函数关系式y=|x-1|中,当x=-1时,函数值y是( )
A.0 B.2 C.-2 D.±2
答案:B
解析:解答: 当x=-1时,y=|x-1|=|-1-1|=2选B.
分析: 把x=-1直接代入函数y=|x-1|即可求出函数值.
7.当x=2时,函数y=2x-1的值是( )
A.0 B.-3 C.3 D.4
答案:C
解析:解答: x=2时,y=2×2-1=4-1=3
选:C.
分析:把x=2代入函数解析式计算即可得解.
8.当x=2时,函数y=2x-1的值是( )
A.0 B.-3 C.3 D.4
答案:C
解析:解答: x=2时,y=2×2-1=4-1=3
选C.
分析:把x=2代入函数解析式计算即可得解
9.已知函数y=3x-1,当x=3时,y的值是( )
A.6 B.7 C.8 D.9
答案:C
解析:解答: x=3时,y=3×3-1=8选:C.
分析: 把x=3代入函数关系式进行计算
10.函数y=中,自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≤-2 D.x≥2或x≤-2
答案:B
解析:解答: 根据题意得:x-2≥0,
解得:x≥2.选:B.
分析: 根据二次根式的性质,被开方数大于等于0,就可以求解.
11.在函数y=中,自变量x的取值范围是( )
A.x≠-2 B.x>2 C.x<2 D.x≠2
答案:D
解析:解答: 根据题意,有x-2≠0,解可得x≠2
选:D.
分析:根据分式有意义的条件是分母不为0;分析原函数式可得关系式x-2≠0,解可得自变量x的取值范围.
12.地铁1号线是重庆轨道交通线网东西方向的主干线,也是贯穿中区和沙坪坝区的重要交通通道,它的开通极大地方便了市民的出行,现某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,等了一会,然后搭乘一号线地铁直达两路口(忽略途中停靠站的时间).在此过程中,他离南开中学的距离y与时间x的函数关系的大致图象是( )
A. B.
C. D.
答案:C
解析:解答:某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,他离南开中学的距离y随时间x的增大而增大,等了一会,他离南开中学的距离y随时间x的增大不变,然后搭乘一号线地铁直达两路口(忽略途中停靠站的时间),他离南开中学的距离y与时间x的增大而增大,并且增加的速度更快了,符合以上的图象是C.选:C.
分析:根据某同学要从沙坪坝南开中学到两路口,他先匀速步行至沙坪坝地铁站,他离南开中学的距离y随时间x的增大而增大,等了一会,他离南开中学的距离y随时间x的增大不变,然后搭乘一号线地铁直达两路口,他离南开中学的距离y与时间x的增大而增大,并且增加的速度更快了,即可得出函数的大致图象
13.小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与x的函数关系的大致图象是( )
A. B.
C. D.
答案:D
解析:解答: A.随着时间的变化,离家的距离越来越远,故A错误;
B.随着时间的、变化,离家的距离越来越远,故B错误;
C.随着时间的变化,步行离家的距离变化快,搭轻轨的距离变化慢,不符合题意,故C错误;
D.随着时间的变化,步行离家的距离变化慢,搭轻轨的距离变化快,符合题意,故D正确;选:D.
分析:根据从学校回家,可得与家的距离是越来越近,根据步行的速度慢,可得离家的距离变化小,根据搭轻轨的速度快,可得离家的距离变化大.
14.一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是y和x,则y关于x的函数图象大致是图中的( )
A. B.
C. D.
答案:A
解析:解答:A.根据题意小三角形的面积减小,梯形的面积增大,而且x与y满足一次函数关系.选:A.
分析:通过求函数解析式的方法求解则可
15.小亮家与学校相距1500m,一天放学后他步行回家,最初以某一速度匀速前进,途中遇到熟人小强,说话耽误了几分钟,与小强告别后他就改为匀速慢跑,最后回答了家,设小亮从学校出发后所用的时间为t(min),与家的距离为s(m),下列图象中,能表示上述过程的是( )
A. B.
C. D.
答案:C
解析:解答:由题意得,最初与家的距离s随时间t的增大而减小,与小强说话时,时间增大而s不变,慢跑时,与家的距离s随时间t的增大而减小选:C.
分析:分三段分析,最初步行、与小强说话、匀速慢跑,分析函数的性质,进行判断
二、填空题(共5题)
16.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为________平方米
答案:100
解析:解答: 由纵坐标看出:休息前绿化面积是60平方米,休息后绿化面积是160-60=100平方米.
分析:根据函数图象的纵坐标,可得答案
17.如图所示的是春季某地一天气温随时间变化的图象,根据图象判断,在这天中,最高温度与最低温度的差是__________℃.
答案: 10
解析:解答:观察图象,由纵坐标看出最高气温是12℃,最低气温是2℃,
所以温差是12-2=10℃
分析:根据观察函数图象的纵坐标,可得最低气温,最高气温,根据有理数的减法,可得温差
18.函数y=的自变量x的取值范围是_________
答案: x≥7
解析:解答: 根据题意得:x-7≥0,
解得x≥7,
分析: 函数关系中主要有二次根式.根据二次根式的意义,被开方数是非负数.
19.当x=3时,函数y=-x+2的值为_____.
答案:-1
解析:解答:当x=3时,y=-x+2=-3+2=-1
分析:根据函数值的求解方法,把x=3代入y=-x+2,求出函数y=-x+2的值
20.小强想给爷爷买双鞋,爷爷说他自己的脚长25.5cm,若用x(cm)表示脚长,用y(码)表示鞋码,则有2x-y=10,根据上述关系式,小强应给爷爷买________码的鞋
答案:41
解析:解答: ∵用x表示脚长,用y表示鞋码,
则有2x-y=10,而x=25.5,
则51-y=10,
解得:y=41
分析:由于已知用x表示脚长,用y表示鞋码,则有2x-y=10,而爷爷只告诉他自己的脚长25.5cm,代入公式即可求出小强该买多少码的鞋
三、解答题(共5题)
21.已知x无论取何正值,y1=-3x+7都比y2=kx+5大,求k的取值范围
答案: 解答: 由题意得,-3x+7>kx+5,
所以(k+3)x<2,
∵x无论取何正值,y1=-3x+7都比y2=kx+5大,
∴k+3≤0,
解得x≤-3
分析:根据函数值列出不等式,再根据对任意正数x不等式都成立列出关于k的不等式,然后求解
22.地壳的厚度约为8到40km,在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.
(1)在这个变化过程中,自变量和因变量分别是什么?
答案: 解:自变量是地表以下的深度x,
因变量是所达深度的温度y;
(2)如果地表温度为2℃,计算当x为5km时地壳的温度.
答案: 解:当t=2,x=5时,
y=3.5×5+2=19.5;
所以此时地壳的温度是19.5℃
分析:(1)因为温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度,所以自变量是x,因变量是y.(2)令t=2,x=5,代入函数解析式,即可求解
23.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
答案:解答:根据图象知道:
点A到点B是匀速运动、点E到点F是匀加速运动、点G到点H匀减速运动;
(2)汽车在点A的速度是多少?在点C呢?
答案:解答:根据图象知道:
汽车在点A的速度是30千米每小时,在点C的速度为0千米每小时;
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图
答案:解答:如图所示:
分析: (1)根据图象可以确定从点A到点B、点E到点F、点G到点H分别表明汽车的运动状态;(2)根据图象可以直接得到汽车在点A和点C的速度;(3)结合已知条件利用图象可以画出从28分钟以后汽车速度与行驶时间的关系图
24.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
答案:解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)10时和13时,他分别离家多远?
答案:解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)他到达离家最远的地方是什么时间?离家多远?
答案:解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)11时到12时他行驶了多少千米?
答案:解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
(5)他可能在哪段时间内休息,并吃午餐?
答案:解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)他由离家最远的地方返回时的平均速度是多少?
答案:解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
分析:(1)根据函数图象,可得自变量、因变量;(2)根据函数图象的纵坐标,可得答案;(3)根据函数图象的横坐标、纵坐标,可得答案;(4)根据函数图象的横坐标,可得函数值,根据函数值相减,可得答案;(5)根据函数图象的纵坐标,可得答案;(6)根据函数图象的纵坐标,可得距离,根据函数图象的横坐标,可得时间,根据路程除以时间,可得答案
25.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
答案:解答:观察图象可知:玲玲到离家最远的地方需要3小时,此时离家30千米;(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
答案:解答:玲玲郊游过程中,各时间段的速度分别为:
9~10时,速度为10÷(10-9)=10千米/时;
10~10.5时,速度约为(17.5-10)÷(10.5-10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30-17.5)÷(12-11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15-13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15-13)=15千米/小时;
(4)玲玲全程骑车的平均速度是多少?
答案:解答:玲玲全程骑车的平均速度为:(30+30)÷(15-9)=10千米/小时
分析: (1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;(2)休息是路程不在随时间的增加而增加;(3)往返全程中回来时候速度最快,用距离除以所用时间即可;(4)用玲玲全称所行的路程除以所用的时间即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
