【期末押题预测】题型专项培优 应用题(含解析)-广东省2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 【期末押题预测】题型专项培优 应用题(含解析)-广东省2024-2025学年六年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 314.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:49:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
题型专项培优 应用题
一、解答题
1.号码分别为2005,2006,2007,2008的4名运动员进行乒乓球比赛,规定每两人比赛的场数是他们号码的和被4除所得的余数。那么,2008号运动员赛了多少场?
2.甲、乙两车分别从A、B两地同时相对开出,甲车每小时行75千米,乙车每小时行55千米,经过两小时后两车还相距20千米,A、B两地相距多少千米 (先画图表示出信息和问题,再列式解答)
画图:
列式:
3.用绿、蓝、橙三色去涂下面的圆,每种颜色涂一次,每个圆涂一种颜色。共有多少种不同的涂法?
4.甲数是4.5,乙数是45,在它们的末尾都添上两个0,这时乙数是甲数的多少倍?
5.在一个边长为6米的正方形花坛四周铺上宽为1米的碎石路(如下图),碎石路的面积是多少平方米?
6.乐乐做一道加法题,把加数9.8十分位上的8看成了3,把个位上的9看成了6,结果得到的答案是11.5,正确的结果是多少?
7.甲、乙、丙共同制作了一批零件,甲制作了总数的30%,乙、丙制作的件数之比是3: 4。已知丙制作了20件,则甲制作了多少件?
8.把1~4这四个数填在下面的方格里,使每行、每列都有这四个数。
9.(模型意识)甲、乙两人分别沿铁轨反向而行,此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15 秒,然后在乙身旁开过,用了17 秒。已知两人的步行速度都是3.6千米/小时,则这列火车有多长?
10.如图,常用的热量单位有千卡、千焦、卡路里等,营养学界用这些单位来计算食物和运动能量。
1千卡=4.184千焦 1千焦=0.239千卡 1千卡=1000卡路里
(1)10克油条的热量为39.2千卡,照这样计算,1千克油条的热量是多少千卡?
(2)慢跑半小时大约能消耗300000卡路里的能量,照这样计算,慢跑1小时能消耗多少千卡的能量?
11.在下表中划去一些数(每行中至少剩下一个数),使剩下的数符合以下要求:第一行剩下的各数之和乘以第二行剩下的各数之和的积小于第三行剩下的各数之和。(直接在表中划)
4.5 0.8 12.5 5.6
3.4 8.8 0.6 4.5
12.5 10.2 5.6 15.8
12.(几何直观)如下图,在一个棱长为20 cm的正方体密闭容器底部固定了一个实心圆柱体,容器内盛有一些水,水面恰好经过圆柱体的上底面。如果将容器倒置,那么圆柱体有8 cm露出水面。已知圆柱体的底面积是正方体底面积的,求实心圆柱体的体积。
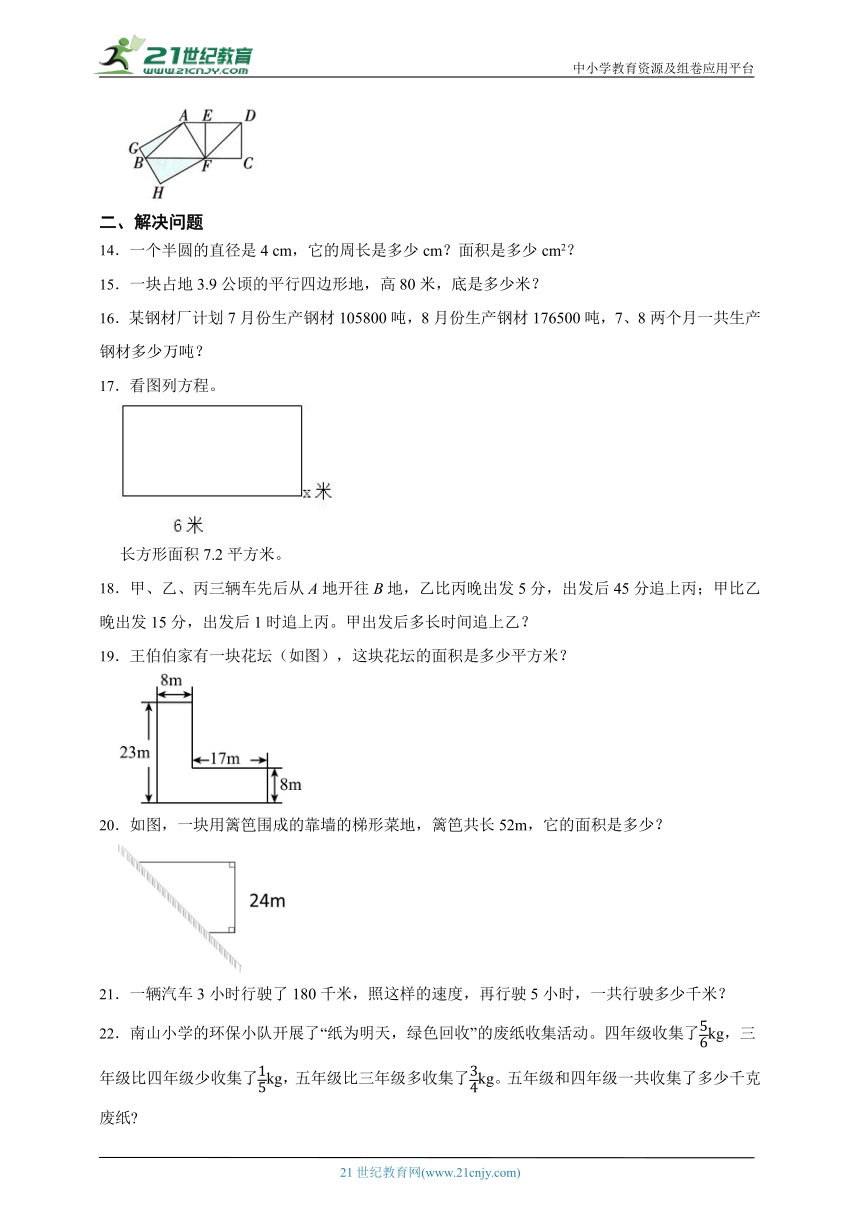
13.如图,四边形ABFD是平行四边形,四边形CDEF是正方形,四边形AGHF是长方形。已知AD=14 cm,BC=22cm,阴影部分的面积是多少平方厘米?
二、解决问题
14.一个半圆的直径是4 cm,它的周长是多少cm?面积是多少cm2?
15.一块占地3.9公顷的平行四边形地,高80米,底是多少米?
16.某钢材厂计划7月份生产钢材105800吨,8月份生产钢材176500吨,7、8两个月一共生产钢材多少万吨?
17.看图列方程。
长方形面积7.2平方米。
18.甲、乙、丙三辆车先后从A地开往B地,乙比丙晚出发5分,出发后45分追上丙;甲比乙晚出发15分,出发后1时追上丙。甲出发后多长时间追上乙?
19.王伯伯家有一块花坛(如图),这块花坛的面积是多少平方米?
20.如图,一块用篱笆围成的靠墙的梯形菜地,篱笆共长52m,它的面积是多少?
21.一辆汽车3小时行驶了180千米,照这样的速度,再行驶5小时,一共行驶多少千米?
22.南山小学的环保小队开展了“纸为明天,绿色回收”的废纸收集活动。四年级收集了kg,三年级比四年级少收集了kg,五年级比三年级多收集了kg。五年级和四年级一共收集了多少千克废纸
23.南昌西站到北京西站之间的高速铁路大约长1404km。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
24.一件棉衣按七五折出售的价格是300元,这件棉衣的原价是多少元?
25.一个圆柱形茶叶罐的底面半径是3厘米,高是8厘米,茶叶罐的侧面和上面都贴上了商标纸,贴商标纸的面积是多少平方厘米?
26. 一辆汽车每小时行驶95千米,上午8:40从甲地出发去乙地,下午2:40到达乙地。甲、乙两地相距多少千米
27.粮食加工厂有一个长方体仓库,仓库里面长8m,宽6m,里面存放的小麦高度是1.5m,1m3小麦重0.7t,这个仓库存放的小麦最多有多少吨?
28.清晨,两名行人行走在广场的石板路上。根据图中的信息,你能求出左侧行人的影子长度是多少米吗?
29.笑笑的爸爸去某城参加教研活动,在上午11时之前需要到某酒店签到,他乘坐的大巴车上午10时50分才在离酒店最近的高速出口下高速。在比例尺是1:50000的地图上量得这个高速出口到该酒店的图上距离是25cm,在城市道路行驶时,大巴车的最高时速是60千米/时,他能准时签到吗?
30.张奶奶沿着一面墙围一个长30米、宽12米的长方形菜地,最少需要准备多少米长的篱笆?
31.求组合图形的面积。
32.李师傅和刘师傅同时加工一种服装,李师傅加工了150套,刘师傅加工的比李师傅多,刘师傅加工了多少套?
33.小明、小东、小华、小刚、小聪参加短跑比赛.小明说:“我跑在最前面.”小华说:“我的后面没有人.”小东说:“我的前面有两个人.”小聪说:“我在小东的前面.”根据他们五个人此时的描述,写出前后顺序.
34.花园里有太阳花350棵,(
),月季花有多少棵
(1)根据下面的线段图,将题中的信息补充完整。
(2)根据补充的信息解答。
35.甲、乙、丙三个村合修一条水渠,修完后,甲、乙、丙村可灌溉的面积比是8:7:5.原来三个村计划按可灌溉的面积比派出劳力,后来因为丙村抽不出劳力,经协商,丙村应抽出的劳力由甲、乙两村分担,丙村付给甲、乙两村工钱1350元,结果,甲村共派出60人,乙村共派出40人,甲、乙两村各应分得工钱多少元?多少元?
36.一幢大楼高59米,除一楼高度是4.6米外,其余每层的高度都是3.2米。这幢楼房一共有多少层?
37.人民商场平均每月洗衣粉的销量是320箱,上半年平均每月洗衣粉的销量是240箱,下半年平均每月洗衣粉的销量是多少箱?
38. (商品经济)某服装店第一次用8000元购进A,B两种服装120件,这两种服装的进价、标价如下表所示。
种服装 种服装
进价 (元/件) 60 100
标价 (元/件) 100 160
(1)求这两种服装各购进的件数;
(2)第一次购买的服装按标价全部售完后,该服装店再次以相同的进价购进同样数量的A,B两种服装,但将A种服装在标价的基础上涨价20% ,B种服装在标价的基础上打折销售,结果销售第二批服装比第一批服装所获总利润多了1360元,求B种服装在标价的基础上打了几折销售?
39.海纳酒店在录制现场的正西方向1300米处,百川酒店在录制现场的正东方向1100米处。住在海纳酒店的李叔叔和住在百川酒店的王叔叔两人约好晚上8时到录制现场,两人在晚上7:35分别从两个酒店出发走向录制现场,约定相遇后才一起去录制现场。从出发到两人相遇用了20分钟,王叔叔每分钟步行65米,李叔叔每分钟步行多少米?要想准时到录制现场观看,他们相遇后一起步行的速度至少是多少?
答案解析
1.【答案】解:由于能被整除,,,除以的余数分别为,,,
所以号运动员与号运动员赛了场,与号运动员赛了场,与号运动员赛了场,
总共赛了:(场)。
答:2008号运动员赛了6场
【解析】【分析】本题的关键是根据每两人比赛场数等于号码和对4取余的规则,计算2008号运动员与其他三名运动员的每一场数,然后求总和。
2.【答案】解:画图:
列式:
(75+55)×2+20
=130×2+20
=260+20
=280(千米)
答:A、B两地相距280千米。
【解析】【分析】甲、乙两车的速度和×行驶的时间=甲、乙两车行驶的路程,甲、乙两车行驶的路程+两车还相距的路程=A、B两地的距离。
3.【答案】解:对于第一个圆,可以从三种颜色中任选一种进行涂色,因此有3种涂法。
对于第二个圆,由于第一种颜色已被使用,只能从剩下的两种颜色中选择一种进行涂色,因此有2种涂法。
对于第三个圆,由于前两种颜色都已被使用,只能使用剩下的那一种颜色进行涂色,因此只有1种涂法。
根据乘法原理,三个圆的涂法总数为:3×2×1=6(种)
答:共有6种不同的涂法
【解析】【分析】本题要求计算用三种不同颜色涂三个圆的所有不同涂法。由于每种颜色只能使用一次,且每个圆只能涂一种颜色,因此这实际上是一个排列组合问题。我们需要应用排列组合的基本原理,即乘法原理,来计算总的不同涂法数。
4.【答案】解:4500÷4.500=1000
答:这时乙数是甲数的1000倍。
【解析】【分析】甲数末尾添上两个0是4.500,乙数末尾添上两个0是4500,将添0后的甲数的小数点向右移动三位正好是添0后的乙数,因此这时乙数是甲数的1000倍。
5.【答案】解:6+1×2=8(米)
8×8=64(平方米)
6×6=36(平方米)
64-36= 28(平方米)
答:碎石路的面积是28平方米。
【解析】【分析】碎石路的面积=(花坛的边长+小路的宽×2)×(花坛的边长+小路的宽×2)-花坛的边长×花坛的边长。
6.【答案】解:11.5-6.3=5.2
9.8+5.2=15
答:正确的结果是15。
【解析】【分析】也就是把9.8看作6.3来计算了,用11.5减去6.3求出第一个加数,然后用第一个加数加上9.8即可求出正确的结果。
7.【答案】解:(20+20×) ÷(1-30%)=50(件)
50×30%=15(件)
答:甲制作了15件零件。
【解析】【分析】乙、丙制作的件数之比是3:4,且丙制作了20件,则乙、丙制作的总件数是(20+20×÷)件,甲制作了总件数的30%,则乙、丙制作了总件数的70% ,相除可得总件数是50件,再求甲制作的件数。
8.【答案】解:
【解析】【分析】依据题意可以在第一行填上1、2、3、4,第二行可以把4放在最前面,即4、1、2、3,第三行可以把3放在最前面,即3、4、1、2,第四行可以把2放在最前面,即2、3、4、1,据此写数。
9.【答案】解:3.6千米/时=1米/秒;
设这列火车的速度为x米/秒,则火车的长度可以表示为(15x+15×1)米,即(15x + 15)米,也可以表示为(17x- 17×1)米,即(17x- 17)米。
15x+15=17x-17
解得x=16
15×16+15= 255(米)
答:这列火车长255米。
【解析】【分析】火车与甲是相遇,火车长=火车行驶的路程+甲行驶的路程; 火车与乙是追及,火车长=火车行驶的路程-乙行驶的路程。设出火车行驶的速度,根据路程=时间×速度,将火车的长度用含x的代数式表示出来,解方程得到火车行驶的速度;再根据“火车长=火车行驶的路程+甲行驶的路程”求出火车的长。
10.【答案】解:(1)1千克=1000克
1000÷10×39.2
=100×39.2
=3920(千卡)
答:1千克油条的热量是3920千卡。
(2)300000×2=600000(卡)
600000卡=600千卡
答:慢跑1小时能消耗600千卡的能量。
【解析】【分析】先单位换算1千克=1000克,1千克油条的热量=1000克是10克的倍数×10克油条的热量;
(2)慢跑1小时能消耗的能量=1小时是半小时的倍数×半小时消耗的能量。
11.【答案】解:(4.5+0.8)×(0.6+4.5)
=5.3×5.1
=27.03
12.5+15.8=28.3
27.03<28.3
【解析】【分析】第一行划去后面两个数,第二行划去前面两个数,第三行划去中间两个数,然后计算第一行剩下两数的和×第二行剩下两数的和,再与第三行剩下两数的和比较大小。
12.【答案】解:圆柱的底面积:20×20×=50(平方厘米)
容器倒置后内部无水部分的体积:
20× 20× 8-50× 8= 2800(立方厘米)
容器正放时内部无水部分的高:
2800÷ (20× 20)=7(厘米)
圆柱的体积:50× (20-7)= 650(立方厘米)
答: 实心圆柱体的体为650立方厘米。
【解析】【分析】依据题意“圆柱体的底面积是正方体底面积的”,可知圆柱的底面积为20×20×=50平方厘米;因为容器倒置后,无水部分体积为无水的长方体体积-高为8厘米的柱体,即:20×20×8-50×8=2800立方厘米,又因为容器正放和倒置时无水部分的体积不变,所以用倒置后无水部分的体积除以正方体容器的底面积,可得容器正放时内部无水部分的高,即2800÷(20×20)=7厘米,再依据圆柱体积公式V=Sh,得出圆柱的体积为50×(20-7)=650立方厘米。
13.【答案】解:14×(22-14)÷2=56(cm2)
答:阴影部分的面积是56cm2。
【解析】【分析】观察题图可知,长方形AGHF中,阴影部分的面积与空白部分的面积相等,而空白部分的面积等于平行四边形 ABFD 面积的一半,由题意得平行四边形ABFD的底是14cm,高是正方形CDEF的边长,正方形CDEF的边长为(22-14)cm,根据平行四边形的面积=底x高,代人数据求出平行四边形的面积后,再除以2就是阴影部分的面积。
14.【答案】解:3.14×4=12.56(cm)
12.56÷2+4=10.28(cm)
3.14×(4÷2) =12.56(cm )
12.56÷2=6.28(cm )
答:它的周长是10.28cm,面积是6.28cm 。
【解析】【分析】根据圆周长公式为C=πd、圆面积公式为S=πr ,先求出圆的周长和面积,再根据半圆的周长=圆周长+直径以及半圆的面积=面积解答即可.
15.【答案】解:3.9公顷=39000平方米,39000÷80=487.5(米)
答:底是487.5米。
【解析】【分析】题目中告诉了这块平行四边形地的占地面积和高,由于单位不统一,先利用面积单位间的进率换算单位,即1公顷=10000平方米,然后再利用平行四边形的面积公式算出底,即平行四边形的底=平行四边形的面积÷平行四边形的高。
16.【答案】解:105800+176500=282300(吨)=28.23(万吨)
答:7、8两个月一共生产钢材28.23万吨.
【解析】【分析】根据题意可知,用7月份生产的钢材吨数+8月份生产的钢材吨数=7、8两个月一共生产的钢材吨数,然后将吨化成万吨,小数点向左移动4位,据此解答.
17.【答案】解:6x=7.2
【解析】【分析】长方形的面积=长×宽,代入对应的数字和字母列出方程即可。
18.【答案】解:乙与丙的时间比:
45:(45+5)
=45:50
=9:10
乙与丙的速度比:10:9
甲与丙的时间比:
60:(60+5+15)
=60:80
=3:4
甲与丙的速度比:4:3=12:9
甲、乙、丙的速度比:12:10:9
甲与乙的时间比:10:12=5:6
15÷(6-5)×5
=15÷1×5
=75(分钟)
答:甲出发75分钟后追上乙。
【解析】【分析】由题意可知,当乙行45分钟时,丙行(45+5)分钟,据此可得乙与丙的时间比,再根据“路程一定,时间与速度成反比例”可得,乙与丙的速度比;当甲行60分钟时,丙行(60+5+15)分钟,据此可得乙与丙的时间比,同理,可得甲与丙的速度比,进而可求出甲、乙、丙的速度比;由甲与乙的速度比,又可得到甲与乙的时间比,然后用甲乙的时间差除以份数差,再乘以甲所占的份数,即可得解。
19.【答案】320平方米
20.【答案】336平方米
21.【答案】解:180÷3×(3+5)
=60×8
=480(千米)
答:一共行驶了480千米。
【解析】【分析】3小时行驶的路程÷3=1小时行驶的路程,1小时行驶的路程×一共行驶的时间=一共行驶的路程。
22.【答案】解:
=
=(千克)
答: 五年级和四年级一共收集了千克废纸。
【解析】【分析】用四年级的收集量减去 ,即可求出三年级的收集量,再用三年级的收集量加 ,即可求出五年级的收集量,最后用五年级的收集量加上四年级的收集量即可。
23.【答案】解:10时50分-7时20分=3时30分
3时30分=3.5时
13时20分-7时20分=6时
设南昌西站到郑州东站的高速铁路大约有xkm。
1404:6=x:3.5
6x=4914
x=819
答:南昌西站到郑州东站的高速铁路大约有819km。
【解析】【分析】设南昌西站到郑州东站的高速铁路大约有xkm。依据南昌西站到北京西站之间的高速铁路大约的长度:时间=南昌西站到郑州东站的高速铁路大约的时间:3.5,列比例,解比例。
24.【答案】400元
25.【答案】178.98平方厘米
26.【答案】解:下午2:40是14:40,
14时40分-8时40分=6小时
95×6=570(千米)
答:甲、乙两地相距570千米。
【解析】【分析】先计算出上午8:40到下午2:40经过的时数,然后用每小时行驶的路程乘行驶的时间求出两地的距离。
27.【答案】解:8×6×1.5=72(m3)
72×0.7=50.4(t)
答:这个仓库存放的小麦最多有50.4t。
【解析】【分析】先根据长×宽×高求出小麦的体积, 由于1m3 小麦重0.7t, 用体积×0.7得到小麦的重量。
28.【答案】2.55米
29.【答案】解:11时-10时50分=10分
1250000cm=12.5km
12.5÷60= (时)=12.5分
12.5分>10分
答:他不能准时签到。
【解析】【分析】已知笑笑的爸爸要在上午11时之前需要到某酒店签到,他乘坐的大巴车上午10时50分才在离酒店最近的高速出口下高速,所以他从高速出口到酒店的时间只有小于11时-10时50分=10分,才能准时签到。已知高速出口到酒店的图上距离和比例尺,根据实际距离=图上距离比例尺,计算得到高速出口到酒店的距离是,也就是12.5km(1km=100000cm),进而根据时间=路程速度,代入数据求出需要时间是12.5÷60= (时),即12.5分(1时=60分),12.5分大于10分,所以他不能准时签到。
30.【答案】解:30+12×2
=30+24
=54(米)
答:最少需要准备54米长的篱笆。
【解析】【分析】最少需要准备篱笆的长度=长方形菜地的长+宽×2。
31.【答案】解:(60+100)×48÷2
=160×48÷2
=7680÷2
=3840(平方米)
60×(78-48)÷2
=60×30÷2
=1800÷2
=900(平方米)
3840+900=4740(平方米)
【解析】【分析】组合图形的面积=三角形的面积+梯形的面积;其中,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2。
32.【答案】解:150×(1+)
=150×
=180(套)
答:刘师傅加工了180套。
【解析】【分析】求比一个数多几分之几的数是多少,方法是:这个数×(1+多的几分之几)。
33.【答案】解:从前往后排依次是:小明、小聪、小东、小刚、小华。
34.【答案】(1)解:太阳花比月季花少。
(2)解:320÷(1-)
=320÷
=400(棵)
答:月季花有400棵。
【解析】【分析】(1)太阳花比月季花少;
(2)月季花的棵数=太阳花的棵数÷(1-)。
35.【答案】解:设甲、乙、丙三个村可灌溉的面积比为8:7:5,则它们应派出的劳力人数比也为8:7:5。设甲、乙、丙三个村应派出的劳力人数分别为8份、7份、5份。
计算每份的人数:甲、乙两村共派出的劳力人数为60+40=100人
每份的人数为100-(8+7+5)=5人
计算甲、乙村多派出的劳力:
甲村实际派出的劳力人数为60人,应派出的劳力人数为5x8=40人,因此甲村多派出了60-40=20人。
乙村实际派出的劳力人数为40人,应派出的劳力人数为5x7=35人,因此乙村多派出了40-35=5人。
计算甲、乙村应分得的工钱:
丙村支付的工钱为1350元,应按照甲、乙两村实际多派出的劳力人数进行分配
甲村应分得的工钱为1350x(20÷(20+5))=1080元,乙村应分得的工钱为1350-1080=270元。
1080-270=810
答:甲村应分得工钱1080元,乙村应分得工钱270元.多810元。
【解析】【分析】首先,根据甲、乙、丙三个村可灌溉的面积比,设定未知数并计算出每个村应派出的劳力人数比。接着,根据甲、乙两村实际派出的人数和丙村应派出的人数,计算出甲、乙两村实际多派出的劳力人数。然后,根据甲乙两村实际多派出的劳力人数和丙村支付的工钱,计算出甲、乙两村应分得的工钱。最后,将计算结果作为答案输出。
36.【答案】解:(59-4.6)÷3.2+1
=54.4÷3.2+1
=17+1
=18(层)
答:这幢楼房一共有18层。
【解析】【分析】根据题意可知,(这幢大楼的总高度-一楼的高度)÷每层的高度+1=这幢楼房的层数,据此列式解答。
37.【答案】解:(320×12-240×6)÷6
=(3840-1440)÷6
=2400÷6
=400(箱)
答:下半年平均每月洗衣粉的销量是400箱。
【解析】【分析】下半年平均每月洗衣粉的销量=(人民商场平均每月洗衣粉的销量×12-上半年平均每月洗衣粉的销量×6)÷6。
38.【答案】(1)解:设 种服装购进 件, 种服装购进 件。
解得
则 种服装购进 (件)
答: 种服装购进 100 件, 种服装购进 20 件。
(2)解:设 种服装在标价的基础上打 折销售。
解得
答: 种服装打八折销售。
【解析】【分析】(1)设 种服装购进 件, 种服装购进 件,A的进价×A的件数+B的进价×B的件数=总金额,再解出A的件数,由此也可知B的件数。
(2)设 种服装在标价的基础上打 折销售,明确利润、进价和售价的关系,利润 = (售价 - 进价) / 进价 。确定A种服装涨价后的售价,再结合题目给定的总利润增加量,计算出B种服装的打折比例。
39.【答案】解:(1300+1100)÷20﹣65
=2400÷20﹣65
=120﹣65
=55(米/分)
8时﹣7时35分=25分
(1300﹣55×20)÷(25﹣20)
=(1300﹣1100)÷5
=200÷5
=40(米/分)
答:李叔叔每分钟步行55米,要想准时到录制现场观看,他们相遇后一起步行的速度至少是每分钟40米。
【解析】【分析】用两人之间的路程除以相遇时间求出速度和,用速度和减去王叔叔的速度即可求出李叔叔每分钟步行的长度。先计算出7:35到8时需要经过的分钟数;用王叔叔速度快,因此相遇点应该在录制现场左边,用1300米减去相遇时李叔叔走的长度求出距离录制现场的长度,用这个长度除以还剩下的时间(25-20)即可求出相遇后一起步行的速度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
题型专项培优 应用题
一、解答题
1.号码分别为2005,2006,2007,2008的4名运动员进行乒乓球比赛,规定每两人比赛的场数是他们号码的和被4除所得的余数。那么,2008号运动员赛了多少场?
2.甲、乙两车分别从A、B两地同时相对开出,甲车每小时行75千米,乙车每小时行55千米,经过两小时后两车还相距20千米,A、B两地相距多少千米 (先画图表示出信息和问题,再列式解答)
画图:
列式:
3.用绿、蓝、橙三色去涂下面的圆,每种颜色涂一次,每个圆涂一种颜色。共有多少种不同的涂法?
4.甲数是4.5,乙数是45,在它们的末尾都添上两个0,这时乙数是甲数的多少倍?
5.在一个边长为6米的正方形花坛四周铺上宽为1米的碎石路(如下图),碎石路的面积是多少平方米?
6.乐乐做一道加法题,把加数9.8十分位上的8看成了3,把个位上的9看成了6,结果得到的答案是11.5,正确的结果是多少?
7.甲、乙、丙共同制作了一批零件,甲制作了总数的30%,乙、丙制作的件数之比是3: 4。已知丙制作了20件,则甲制作了多少件?
8.把1~4这四个数填在下面的方格里,使每行、每列都有这四个数。
9.(模型意识)甲、乙两人分别沿铁轨反向而行,此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15 秒,然后在乙身旁开过,用了17 秒。已知两人的步行速度都是3.6千米/小时,则这列火车有多长?
10.如图,常用的热量单位有千卡、千焦、卡路里等,营养学界用这些单位来计算食物和运动能量。
1千卡=4.184千焦 1千焦=0.239千卡 1千卡=1000卡路里
(1)10克油条的热量为39.2千卡,照这样计算,1千克油条的热量是多少千卡?
(2)慢跑半小时大约能消耗300000卡路里的能量,照这样计算,慢跑1小时能消耗多少千卡的能量?
11.在下表中划去一些数(每行中至少剩下一个数),使剩下的数符合以下要求:第一行剩下的各数之和乘以第二行剩下的各数之和的积小于第三行剩下的各数之和。(直接在表中划)
4.5 0.8 12.5 5.6
3.4 8.8 0.6 4.5
12.5 10.2 5.6 15.8
12.(几何直观)如下图,在一个棱长为20 cm的正方体密闭容器底部固定了一个实心圆柱体,容器内盛有一些水,水面恰好经过圆柱体的上底面。如果将容器倒置,那么圆柱体有8 cm露出水面。已知圆柱体的底面积是正方体底面积的,求实心圆柱体的体积。
13.如图,四边形ABFD是平行四边形,四边形CDEF是正方形,四边形AGHF是长方形。已知AD=14 cm,BC=22cm,阴影部分的面积是多少平方厘米?
二、解决问题
14.一个半圆的直径是4 cm,它的周长是多少cm?面积是多少cm2?
15.一块占地3.9公顷的平行四边形地,高80米,底是多少米?
16.某钢材厂计划7月份生产钢材105800吨,8月份生产钢材176500吨,7、8两个月一共生产钢材多少万吨?
17.看图列方程。
长方形面积7.2平方米。
18.甲、乙、丙三辆车先后从A地开往B地,乙比丙晚出发5分,出发后45分追上丙;甲比乙晚出发15分,出发后1时追上丙。甲出发后多长时间追上乙?
19.王伯伯家有一块花坛(如图),这块花坛的面积是多少平方米?
20.如图,一块用篱笆围成的靠墙的梯形菜地,篱笆共长52m,它的面积是多少?
21.一辆汽车3小时行驶了180千米,照这样的速度,再行驶5小时,一共行驶多少千米?
22.南山小学的环保小队开展了“纸为明天,绿色回收”的废纸收集活动。四年级收集了kg,三年级比四年级少收集了kg,五年级比三年级多收集了kg。五年级和四年级一共收集了多少千克废纸
23.南昌西站到北京西站之间的高速铁路大约长1404km。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
24.一件棉衣按七五折出售的价格是300元,这件棉衣的原价是多少元?
25.一个圆柱形茶叶罐的底面半径是3厘米,高是8厘米,茶叶罐的侧面和上面都贴上了商标纸,贴商标纸的面积是多少平方厘米?
26. 一辆汽车每小时行驶95千米,上午8:40从甲地出发去乙地,下午2:40到达乙地。甲、乙两地相距多少千米
27.粮食加工厂有一个长方体仓库,仓库里面长8m,宽6m,里面存放的小麦高度是1.5m,1m3小麦重0.7t,这个仓库存放的小麦最多有多少吨?
28.清晨,两名行人行走在广场的石板路上。根据图中的信息,你能求出左侧行人的影子长度是多少米吗?
29.笑笑的爸爸去某城参加教研活动,在上午11时之前需要到某酒店签到,他乘坐的大巴车上午10时50分才在离酒店最近的高速出口下高速。在比例尺是1:50000的地图上量得这个高速出口到该酒店的图上距离是25cm,在城市道路行驶时,大巴车的最高时速是60千米/时,他能准时签到吗?
30.张奶奶沿着一面墙围一个长30米、宽12米的长方形菜地,最少需要准备多少米长的篱笆?
31.求组合图形的面积。
32.李师傅和刘师傅同时加工一种服装,李师傅加工了150套,刘师傅加工的比李师傅多,刘师傅加工了多少套?
33.小明、小东、小华、小刚、小聪参加短跑比赛.小明说:“我跑在最前面.”小华说:“我的后面没有人.”小东说:“我的前面有两个人.”小聪说:“我在小东的前面.”根据他们五个人此时的描述,写出前后顺序.
34.花园里有太阳花350棵,(
),月季花有多少棵
(1)根据下面的线段图,将题中的信息补充完整。
(2)根据补充的信息解答。
35.甲、乙、丙三个村合修一条水渠,修完后,甲、乙、丙村可灌溉的面积比是8:7:5.原来三个村计划按可灌溉的面积比派出劳力,后来因为丙村抽不出劳力,经协商,丙村应抽出的劳力由甲、乙两村分担,丙村付给甲、乙两村工钱1350元,结果,甲村共派出60人,乙村共派出40人,甲、乙两村各应分得工钱多少元?多少元?
36.一幢大楼高59米,除一楼高度是4.6米外,其余每层的高度都是3.2米。这幢楼房一共有多少层?
37.人民商场平均每月洗衣粉的销量是320箱,上半年平均每月洗衣粉的销量是240箱,下半年平均每月洗衣粉的销量是多少箱?
38. (商品经济)某服装店第一次用8000元购进A,B两种服装120件,这两种服装的进价、标价如下表所示。
种服装 种服装
进价 (元/件) 60 100
标价 (元/件) 100 160
(1)求这两种服装各购进的件数;
(2)第一次购买的服装按标价全部售完后,该服装店再次以相同的进价购进同样数量的A,B两种服装,但将A种服装在标价的基础上涨价20% ,B种服装在标价的基础上打折销售,结果销售第二批服装比第一批服装所获总利润多了1360元,求B种服装在标价的基础上打了几折销售?
39.海纳酒店在录制现场的正西方向1300米处,百川酒店在录制现场的正东方向1100米处。住在海纳酒店的李叔叔和住在百川酒店的王叔叔两人约好晚上8时到录制现场,两人在晚上7:35分别从两个酒店出发走向录制现场,约定相遇后才一起去录制现场。从出发到两人相遇用了20分钟,王叔叔每分钟步行65米,李叔叔每分钟步行多少米?要想准时到录制现场观看,他们相遇后一起步行的速度至少是多少?
答案解析
1.【答案】解:由于能被整除,,,除以的余数分别为,,,
所以号运动员与号运动员赛了场,与号运动员赛了场,与号运动员赛了场,
总共赛了:(场)。
答:2008号运动员赛了6场
【解析】【分析】本题的关键是根据每两人比赛场数等于号码和对4取余的规则,计算2008号运动员与其他三名运动员的每一场数,然后求总和。
2.【答案】解:画图:
列式:
(75+55)×2+20
=130×2+20
=260+20
=280(千米)
答:A、B两地相距280千米。
【解析】【分析】甲、乙两车的速度和×行驶的时间=甲、乙两车行驶的路程,甲、乙两车行驶的路程+两车还相距的路程=A、B两地的距离。
3.【答案】解:对于第一个圆,可以从三种颜色中任选一种进行涂色,因此有3种涂法。
对于第二个圆,由于第一种颜色已被使用,只能从剩下的两种颜色中选择一种进行涂色,因此有2种涂法。
对于第三个圆,由于前两种颜色都已被使用,只能使用剩下的那一种颜色进行涂色,因此只有1种涂法。
根据乘法原理,三个圆的涂法总数为:3×2×1=6(种)
答:共有6种不同的涂法
【解析】【分析】本题要求计算用三种不同颜色涂三个圆的所有不同涂法。由于每种颜色只能使用一次,且每个圆只能涂一种颜色,因此这实际上是一个排列组合问题。我们需要应用排列组合的基本原理,即乘法原理,来计算总的不同涂法数。
4.【答案】解:4500÷4.500=1000
答:这时乙数是甲数的1000倍。
【解析】【分析】甲数末尾添上两个0是4.500,乙数末尾添上两个0是4500,将添0后的甲数的小数点向右移动三位正好是添0后的乙数,因此这时乙数是甲数的1000倍。
5.【答案】解:6+1×2=8(米)
8×8=64(平方米)
6×6=36(平方米)
64-36= 28(平方米)
答:碎石路的面积是28平方米。
【解析】【分析】碎石路的面积=(花坛的边长+小路的宽×2)×(花坛的边长+小路的宽×2)-花坛的边长×花坛的边长。
6.【答案】解:11.5-6.3=5.2
9.8+5.2=15
答:正确的结果是15。
【解析】【分析】也就是把9.8看作6.3来计算了,用11.5减去6.3求出第一个加数,然后用第一个加数加上9.8即可求出正确的结果。
7.【答案】解:(20+20×) ÷(1-30%)=50(件)
50×30%=15(件)
答:甲制作了15件零件。
【解析】【分析】乙、丙制作的件数之比是3:4,且丙制作了20件,则乙、丙制作的总件数是(20+20×÷)件,甲制作了总件数的30%,则乙、丙制作了总件数的70% ,相除可得总件数是50件,再求甲制作的件数。
8.【答案】解:
【解析】【分析】依据题意可以在第一行填上1、2、3、4,第二行可以把4放在最前面,即4、1、2、3,第三行可以把3放在最前面,即3、4、1、2,第四行可以把2放在最前面,即2、3、4、1,据此写数。
9.【答案】解:3.6千米/时=1米/秒;
设这列火车的速度为x米/秒,则火车的长度可以表示为(15x+15×1)米,即(15x + 15)米,也可以表示为(17x- 17×1)米,即(17x- 17)米。
15x+15=17x-17
解得x=16
15×16+15= 255(米)
答:这列火车长255米。
【解析】【分析】火车与甲是相遇,火车长=火车行驶的路程+甲行驶的路程; 火车与乙是追及,火车长=火车行驶的路程-乙行驶的路程。设出火车行驶的速度,根据路程=时间×速度,将火车的长度用含x的代数式表示出来,解方程得到火车行驶的速度;再根据“火车长=火车行驶的路程+甲行驶的路程”求出火车的长。
10.【答案】解:(1)1千克=1000克
1000÷10×39.2
=100×39.2
=3920(千卡)
答:1千克油条的热量是3920千卡。
(2)300000×2=600000(卡)
600000卡=600千卡
答:慢跑1小时能消耗600千卡的能量。
【解析】【分析】先单位换算1千克=1000克,1千克油条的热量=1000克是10克的倍数×10克油条的热量;
(2)慢跑1小时能消耗的能量=1小时是半小时的倍数×半小时消耗的能量。
11.【答案】解:(4.5+0.8)×(0.6+4.5)
=5.3×5.1
=27.03
12.5+15.8=28.3
27.03<28.3
【解析】【分析】第一行划去后面两个数,第二行划去前面两个数,第三行划去中间两个数,然后计算第一行剩下两数的和×第二行剩下两数的和,再与第三行剩下两数的和比较大小。
12.【答案】解:圆柱的底面积:20×20×=50(平方厘米)
容器倒置后内部无水部分的体积:
20× 20× 8-50× 8= 2800(立方厘米)
容器正放时内部无水部分的高:
2800÷ (20× 20)=7(厘米)
圆柱的体积:50× (20-7)= 650(立方厘米)
答: 实心圆柱体的体为650立方厘米。
【解析】【分析】依据题意“圆柱体的底面积是正方体底面积的”,可知圆柱的底面积为20×20×=50平方厘米;因为容器倒置后,无水部分体积为无水的长方体体积-高为8厘米的柱体,即:20×20×8-50×8=2800立方厘米,又因为容器正放和倒置时无水部分的体积不变,所以用倒置后无水部分的体积除以正方体容器的底面积,可得容器正放时内部无水部分的高,即2800÷(20×20)=7厘米,再依据圆柱体积公式V=Sh,得出圆柱的体积为50×(20-7)=650立方厘米。
13.【答案】解:14×(22-14)÷2=56(cm2)
答:阴影部分的面积是56cm2。
【解析】【分析】观察题图可知,长方形AGHF中,阴影部分的面积与空白部分的面积相等,而空白部分的面积等于平行四边形 ABFD 面积的一半,由题意得平行四边形ABFD的底是14cm,高是正方形CDEF的边长,正方形CDEF的边长为(22-14)cm,根据平行四边形的面积=底x高,代人数据求出平行四边形的面积后,再除以2就是阴影部分的面积。
14.【答案】解:3.14×4=12.56(cm)
12.56÷2+4=10.28(cm)
3.14×(4÷2) =12.56(cm )
12.56÷2=6.28(cm )
答:它的周长是10.28cm,面积是6.28cm 。
【解析】【分析】根据圆周长公式为C=πd、圆面积公式为S=πr ,先求出圆的周长和面积,再根据半圆的周长=圆周长+直径以及半圆的面积=面积解答即可.
15.【答案】解:3.9公顷=39000平方米,39000÷80=487.5(米)
答:底是487.5米。
【解析】【分析】题目中告诉了这块平行四边形地的占地面积和高,由于单位不统一,先利用面积单位间的进率换算单位,即1公顷=10000平方米,然后再利用平行四边形的面积公式算出底,即平行四边形的底=平行四边形的面积÷平行四边形的高。
16.【答案】解:105800+176500=282300(吨)=28.23(万吨)
答:7、8两个月一共生产钢材28.23万吨.
【解析】【分析】根据题意可知,用7月份生产的钢材吨数+8月份生产的钢材吨数=7、8两个月一共生产的钢材吨数,然后将吨化成万吨,小数点向左移动4位,据此解答.
17.【答案】解:6x=7.2
【解析】【分析】长方形的面积=长×宽,代入对应的数字和字母列出方程即可。
18.【答案】解:乙与丙的时间比:
45:(45+5)
=45:50
=9:10
乙与丙的速度比:10:9
甲与丙的时间比:
60:(60+5+15)
=60:80
=3:4
甲与丙的速度比:4:3=12:9
甲、乙、丙的速度比:12:10:9
甲与乙的时间比:10:12=5:6
15÷(6-5)×5
=15÷1×5
=75(分钟)
答:甲出发75分钟后追上乙。
【解析】【分析】由题意可知,当乙行45分钟时,丙行(45+5)分钟,据此可得乙与丙的时间比,再根据“路程一定,时间与速度成反比例”可得,乙与丙的速度比;当甲行60分钟时,丙行(60+5+15)分钟,据此可得乙与丙的时间比,同理,可得甲与丙的速度比,进而可求出甲、乙、丙的速度比;由甲与乙的速度比,又可得到甲与乙的时间比,然后用甲乙的时间差除以份数差,再乘以甲所占的份数,即可得解。
19.【答案】320平方米
20.【答案】336平方米
21.【答案】解:180÷3×(3+5)
=60×8
=480(千米)
答:一共行驶了480千米。
【解析】【分析】3小时行驶的路程÷3=1小时行驶的路程,1小时行驶的路程×一共行驶的时间=一共行驶的路程。
22.【答案】解:
=
=(千克)
答: 五年级和四年级一共收集了千克废纸。
【解析】【分析】用四年级的收集量减去 ,即可求出三年级的收集量,再用三年级的收集量加 ,即可求出五年级的收集量,最后用五年级的收集量加上四年级的收集量即可。
23.【答案】解:10时50分-7时20分=3时30分
3时30分=3.5时
13时20分-7时20分=6时
设南昌西站到郑州东站的高速铁路大约有xkm。
1404:6=x:3.5
6x=4914
x=819
答:南昌西站到郑州东站的高速铁路大约有819km。
【解析】【分析】设南昌西站到郑州东站的高速铁路大约有xkm。依据南昌西站到北京西站之间的高速铁路大约的长度:时间=南昌西站到郑州东站的高速铁路大约的时间:3.5,列比例,解比例。
24.【答案】400元
25.【答案】178.98平方厘米
26.【答案】解:下午2:40是14:40,
14时40分-8时40分=6小时
95×6=570(千米)
答:甲、乙两地相距570千米。
【解析】【分析】先计算出上午8:40到下午2:40经过的时数,然后用每小时行驶的路程乘行驶的时间求出两地的距离。
27.【答案】解:8×6×1.5=72(m3)
72×0.7=50.4(t)
答:这个仓库存放的小麦最多有50.4t。
【解析】【分析】先根据长×宽×高求出小麦的体积, 由于1m3 小麦重0.7t, 用体积×0.7得到小麦的重量。
28.【答案】2.55米
29.【答案】解:11时-10时50分=10分
1250000cm=12.5km
12.5÷60= (时)=12.5分
12.5分>10分
答:他不能准时签到。
【解析】【分析】已知笑笑的爸爸要在上午11时之前需要到某酒店签到,他乘坐的大巴车上午10时50分才在离酒店最近的高速出口下高速,所以他从高速出口到酒店的时间只有小于11时-10时50分=10分,才能准时签到。已知高速出口到酒店的图上距离和比例尺,根据实际距离=图上距离比例尺,计算得到高速出口到酒店的距离是,也就是12.5km(1km=100000cm),进而根据时间=路程速度,代入数据求出需要时间是12.5÷60= (时),即12.5分(1时=60分),12.5分大于10分,所以他不能准时签到。
30.【答案】解:30+12×2
=30+24
=54(米)
答:最少需要准备54米长的篱笆。
【解析】【分析】最少需要准备篱笆的长度=长方形菜地的长+宽×2。
31.【答案】解:(60+100)×48÷2
=160×48÷2
=7680÷2
=3840(平方米)
60×(78-48)÷2
=60×30÷2
=1800÷2
=900(平方米)
3840+900=4740(平方米)
【解析】【分析】组合图形的面积=三角形的面积+梯形的面积;其中,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2。
32.【答案】解:150×(1+)
=150×
=180(套)
答:刘师傅加工了180套。
【解析】【分析】求比一个数多几分之几的数是多少,方法是:这个数×(1+多的几分之几)。
33.【答案】解:从前往后排依次是:小明、小聪、小东、小刚、小华。
34.【答案】(1)解:太阳花比月季花少。
(2)解:320÷(1-)
=320÷
=400(棵)
答:月季花有400棵。
【解析】【分析】(1)太阳花比月季花少;
(2)月季花的棵数=太阳花的棵数÷(1-)。
35.【答案】解:设甲、乙、丙三个村可灌溉的面积比为8:7:5,则它们应派出的劳力人数比也为8:7:5。设甲、乙、丙三个村应派出的劳力人数分别为8份、7份、5份。
计算每份的人数:甲、乙两村共派出的劳力人数为60+40=100人
每份的人数为100-(8+7+5)=5人
计算甲、乙村多派出的劳力:
甲村实际派出的劳力人数为60人,应派出的劳力人数为5x8=40人,因此甲村多派出了60-40=20人。
乙村实际派出的劳力人数为40人,应派出的劳力人数为5x7=35人,因此乙村多派出了40-35=5人。
计算甲、乙村应分得的工钱:
丙村支付的工钱为1350元,应按照甲、乙两村实际多派出的劳力人数进行分配
甲村应分得的工钱为1350x(20÷(20+5))=1080元,乙村应分得的工钱为1350-1080=270元。
1080-270=810
答:甲村应分得工钱1080元,乙村应分得工钱270元.多810元。
【解析】【分析】首先,根据甲、乙、丙三个村可灌溉的面积比,设定未知数并计算出每个村应派出的劳力人数比。接着,根据甲、乙两村实际派出的人数和丙村应派出的人数,计算出甲、乙两村实际多派出的劳力人数。然后,根据甲乙两村实际多派出的劳力人数和丙村支付的工钱,计算出甲、乙两村应分得的工钱。最后,将计算结果作为答案输出。
36.【答案】解:(59-4.6)÷3.2+1
=54.4÷3.2+1
=17+1
=18(层)
答:这幢楼房一共有18层。
【解析】【分析】根据题意可知,(这幢大楼的总高度-一楼的高度)÷每层的高度+1=这幢楼房的层数,据此列式解答。
37.【答案】解:(320×12-240×6)÷6
=(3840-1440)÷6
=2400÷6
=400(箱)
答:下半年平均每月洗衣粉的销量是400箱。
【解析】【分析】下半年平均每月洗衣粉的销量=(人民商场平均每月洗衣粉的销量×12-上半年平均每月洗衣粉的销量×6)÷6。
38.【答案】(1)解:设 种服装购进 件, 种服装购进 件。
解得
则 种服装购进 (件)
答: 种服装购进 100 件, 种服装购进 20 件。
(2)解:设 种服装在标价的基础上打 折销售。
解得
答: 种服装打八折销售。
【解析】【分析】(1)设 种服装购进 件, 种服装购进 件,A的进价×A的件数+B的进价×B的件数=总金额,再解出A的件数,由此也可知B的件数。
(2)设 种服装在标价的基础上打 折销售,明确利润、进价和售价的关系,利润 = (售价 - 进价) / 进价 。确定A种服装涨价后的售价,再结合题目给定的总利润增加量,计算出B种服装的打折比例。
39.【答案】解:(1300+1100)÷20﹣65
=2400÷20﹣65
=120﹣65
=55(米/分)
8时﹣7时35分=25分
(1300﹣55×20)÷(25﹣20)
=(1300﹣1100)÷5
=200÷5
=40(米/分)
答:李叔叔每分钟步行55米,要想准时到录制现场观看,他们相遇后一起步行的速度至少是每分钟40米。
【解析】【分析】用两人之间的路程除以相遇时间求出速度和,用速度和减去王叔叔的速度即可求出李叔叔每分钟步行的长度。先计算出7:35到8时需要经过的分钟数;用王叔叔速度快,因此相遇点应该在录制现场左边,用1300米减去相遇时李叔叔走的长度求出距离录制现场的长度,用这个长度除以还剩下的时间(25-20)即可求出相遇后一起步行的速度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
