【押题预测卷】江苏省各地区真题重组训练(一)(含答案)-2025年中考数学
文档属性
| 名称 | 【押题预测卷】江苏省各地区真题重组训练(一)(含答案)-2025年中考数学 |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 05:12:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【押题预测卷】江苏省各地区真题重组训练(一)-2025年中考数学
一.选择题(共10小题)
1.(2025 泗阳县三模)下列对称图形中,既是中心对称又是轴对称图形的是( )
A. B.
C. D.
2.(2025 盐城一模)在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
3.(2025 武进区校级模拟)斗拱是中国古典建筑上的重要部件,如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
4.(2025 沭阳县校级模拟)下列说法正确的是( )
A.甲、乙两人10次测试成绩的方差分别是,,则乙的成绩更稳定
B.某奖券的中奖率为,买1000张奖券,一定会中奖1次
C.要了解小明一家三口的身体健康状况,适合采用抽样调查
D.x=3是不等式2(x﹣1)>3的解,这是一个必然事件
5.(2025 武进区校级模拟)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … ﹣4 ﹣2 0 3 5 …
y … ﹣24 ﹣8 0 ﹣3 ﹣15 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当x>0时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线x=1
6.(2025 盐城一模)随着人们对环境的日益重视,骑行单车这种“低碳“出行方式已融入人们的日常生活,如图是某单车车架的示意图,线段AB,CE,DE分别为前叉、下管和立管,EF为后下叉.已知AB∥DE,AD∥EF,∠BCE=70°,∠CEF=130°,则∠A的度数为( )
A.100° B.110° C.120° D.130°
7.(2025 盐城一模)点P(a,b)在函数y=3x﹣2的图象上,则代数式6a﹣2b+1的值等于( )
A.﹣1 B.﹣3 C.3 D.5
8.(2025 盐城一模)如图,A,B分别是棱长为1的正方体两个相邻的面的中心.将这个正方体的表面展开成平面图形后,点A,B之间的最大距离是( )
A. B. C. D.2
9.(2025 姑苏区一模)我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.(2025 南通模拟)如图,在平面直角坐标系中,点A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点C是y轴负半轴上一点,连接AC交x轴于点D,若OD是△ABC的中位线,△OCD的面积为3,则k的值是( )
A.﹣12 B.﹣6 C.6 D.12
二.填空题(共6小题)
11.(2025 沭阳县校级模拟)根据宿迁市文化广电和旅游局统计显示,2024年五一假期,全市纳入统计的29家重点旅游景区接待国内外游客177.95万人次,同比增长62.19%,177.95万用科学记数法表示为 .
12.(2020 鼓楼区校级模拟)不等式组的最小整数解是 .
13.(2025 沭阳县校级模拟)如图,四边形ABCD是矩形,AB=3,AD=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,求2BG+BE的最小值 .
14.(2025 盐城一模)在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 .
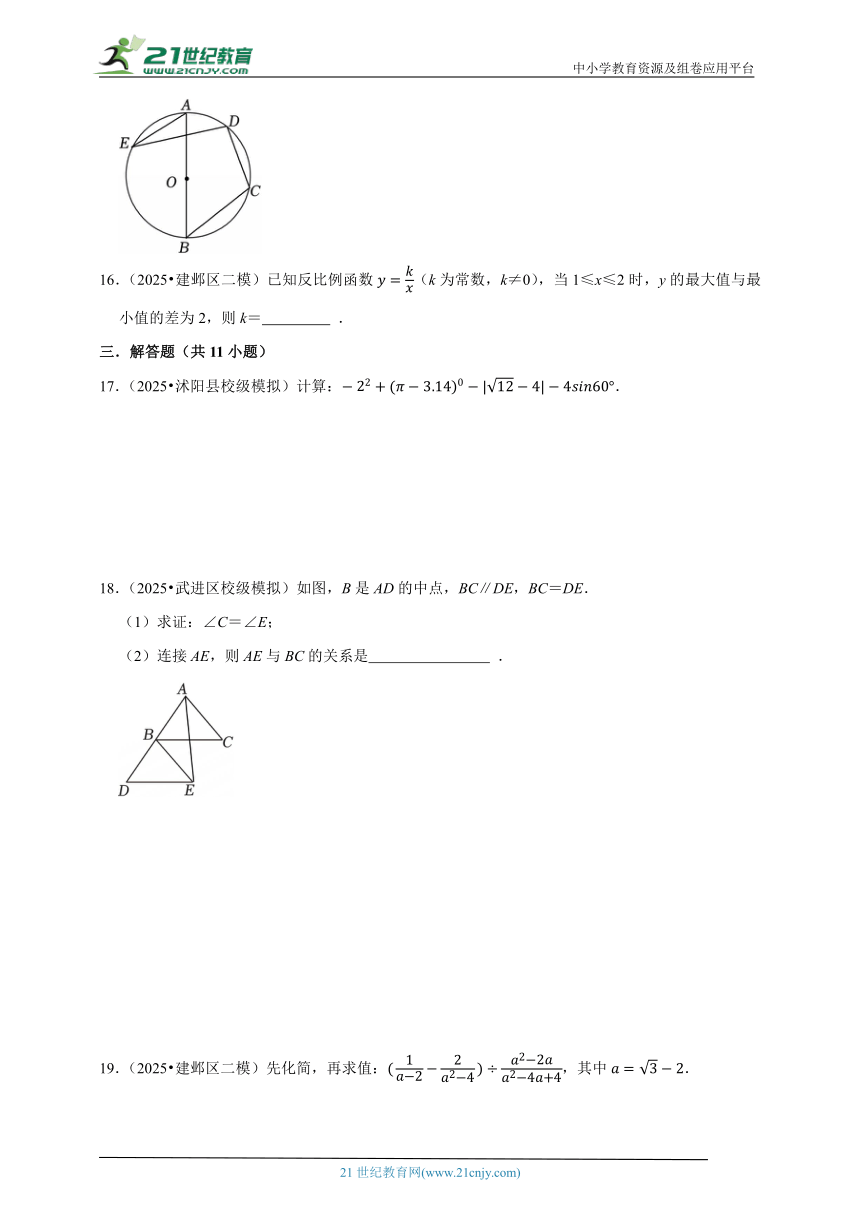
15.(2025 武进区校级模拟)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 .
16.(2025 建邺区二模)已知反比例函数(k为常数,k≠0),当1≤x≤2时,y的最大值与最小值的差为2,则k= .
三.解答题(共11小题)
17.(2025 沭阳县校级模拟)计算:.
18.(2025 武进区校级模拟)如图,B是AD的中点,BC∥DE,BC=DE.
(1)求证:∠C=∠E;
(2)连接AE,则AE与BC的关系是 .
19.(2025 建邺区二模)先化简,再求值:,其中.
20.(2025 武进区校级模拟)解不等式组:.
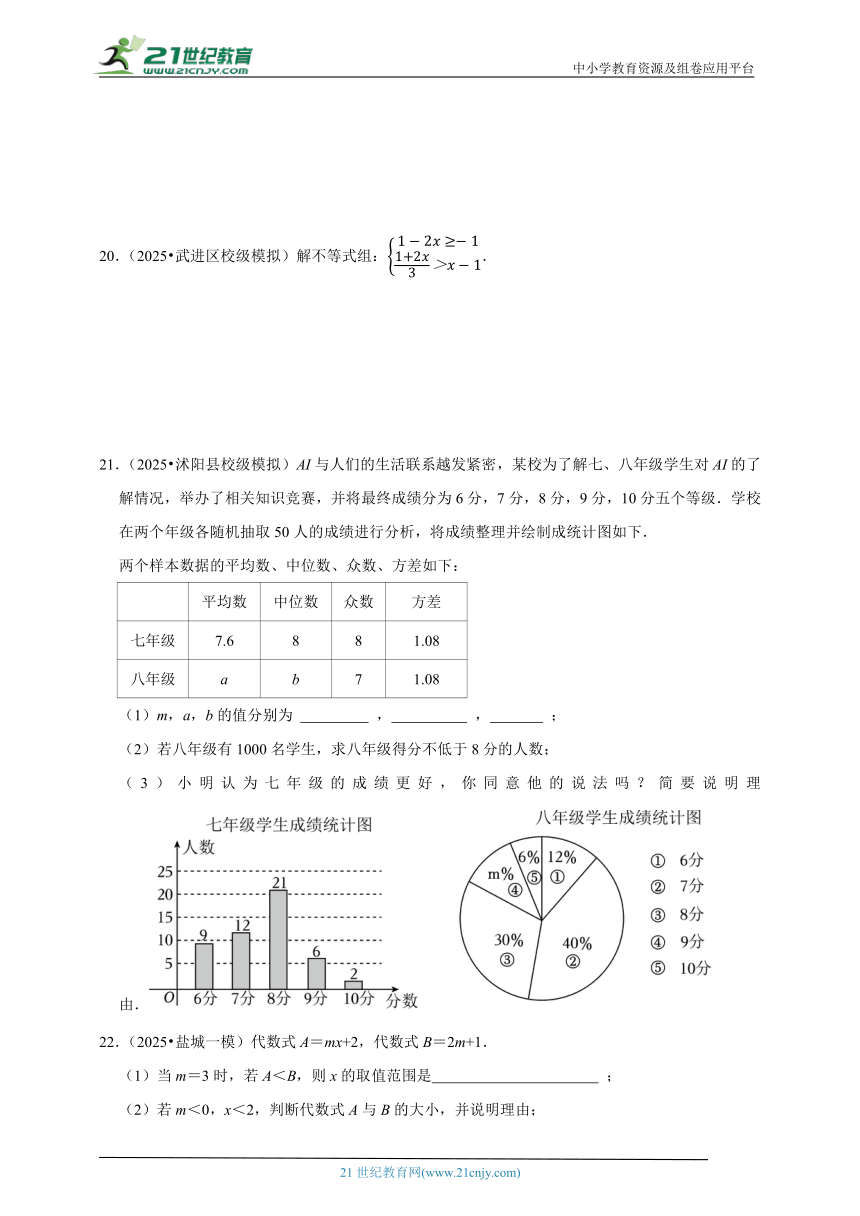
21.(2025 沭阳县校级模拟)AI与人们的生活联系越发紧密,某校为了解七、八年级学生对AI的了解情况,举办了相关知识竞赛,并将最终成绩分为6分,7分,8分,9分,10分五个等级.学校在两个年级各随机抽取50人的成绩进行分析,将成绩整理并绘制成统计图如下.
两个样本数据的平均数、中位数、众数、方差如下:
平均数 中位数 众数 方差
七年级 7.6 8 8 1.08
八年级 a b 7 1.08
(1)m,a,b的值分别为 , , ;
(2)若八年级有1000名学生,求八年级得分不低于8分的人数;
(3)小明认为七年级的成绩更好,你同意他的说法吗?简要说明理由.
22.(2025 盐城一模)代数式A=mx+2,代数式B=2m+1.
(1)当m=3时,若A<B,则x的取值范围是 ;
(2)若m<0,x<2,判断代数式A与B的大小,并说明理由;
(3)将“A与B的差”记为C,即C=A﹣B.当﹣2≤x≤3时,要使C的值满足﹣3≤C≤2,直接写出m的取值范围.
23.(2025 梁溪区校级二模)实验是培养学生的创新能力的重要途径之一.如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,AB=30cm,BEAB,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF(点C,D,N,F在一条直线上),经测得:DE=21.7cm,MN=8cm,∠ABM=145°,求线段DN的长度.
(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
24.(2025 姜堰区一模)如图,A、B为⊙O上的两点,且∠AOB=60°,延长OA至点C,使AC=OA,连接BC.
(1)判断BC与⊙O的位置关系,并说明理由;
(2)用无刻度的直尺和圆规在BC上求作一点D,使BD=CD.(两种工具分别只限使用一次,并保留作图痕迹)
25.(2025 盐城一模)如图1,一个小球以v0=10cm/s的初速度,在一条足够长且平直的轨道上运动.轨道初段AC绝对光滑;除AC段外,剩下轨道粗糙.小球在绝对光滑轨道上不存在阻力;在粗糙轨道上,存在恒定的摩擦力,速度会逐渐减小,直至停止.小球运动过程中,其速度v(cm/s)与时间t(s)之间的关系如图2所示,其路程s(cm)与时间t(s)之间的关系如图3所示(PQ段是抛物线的一部分).
(1)轨道初段AC的总长为 cm;小球在粗糙轨道(图中射线CB上)运动时,v(cm/s)与t(s)之间的函数关系式为 ;
(2)若测得小球从开始出发到最终停止,行进的总路程为140cm,如果直线OP与抛物线有且只有一个交点,则称线段OP与抛物线光滑连接.请你通过计算和推理判断线段OP与抛物线是否光滑连接?
(3)在(2)的条件下,在射线CB上,是否存在一节长为8.75cm的轨道段,使得小球在通过该段过程中,所用时间恰好为1s.若存在,请求出这节轨道的起点与点A之间的距离;若不存在,请说明理由.
26.(2025 沭阳县校级模拟)已知二次函数y=ax2+bx+c(a>0).
(1)若该二次函数的图象过点(2,0)、、(0,﹣1),求二次函数解析式;
(2)如图所示,在平面直角坐标系Oxy中,该二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<0<x2,点D在⊙O上且在第二象限内,点E在x轴正半轴上,连接DE,且线段DE交y轴正半轴于点F,∠DOF=∠DEO,OFDF.
①求证:;
②当点E在线段OB上,且BE=1.⊙O的半径长为线段OA的长度的2倍,若4ac=﹣a2﹣b2,求2a+b的值.
27.(2025 江苏二模)综合探究
【阅读材料】
学习小组遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.
小文是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小文同学的思考问题的方法,解决下列问题:
(1)如图2,请直接写出△BDE的面积为 .
(2)如图3,△ABC的三条中线分别为AD,BE,CF,若△ABC的面积为2,求出以AD,BE,CF的长度为三边长的三角形的面积.
【深入探究】
(3)已知点P是 ABCD内的一点,连接PA,PB,PC,PD,∠BAP=∠BCP,证明:∠ABP=∠ADP.
【实践操作】
(4)如图,已知三条线段a、b、c,请利用无刻度直尺和圆规作一个三角形,使得三角形的三条中线长分别为线段a、b、c的长.(保留作图痕迹,不写作法)
【押题预测卷】江苏省各地区真题重组训练(一)-2025年中考数学
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C D D C D C A A
一.选择题(共10小题)
1.(2025 泗阳县三模)下列对称图形中,既是中心对称又是轴对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.是中心对称图形,不是轴对称图形,故本选项不符合题意;
D.是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:B.
2.(2025 盐城一模)在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
【解答】解:点M(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
3.(2025 武进区校级模拟)斗拱是中国古典建筑上的重要部件,如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
【解答】解:左视图是从物体左面看所得到的图形.
从左面看,上面部分是矩形,下面部分是梯形,矩形部分有一条看不见的线,应该画虚线,
故选:C.
4.(2025 沭阳县校级模拟)下列说法正确的是( )
A.甲、乙两人10次测试成绩的方差分别是,,则乙的成绩更稳定
B.某奖券的中奖率为,买1000张奖券,一定会中奖1次
C.要了解小明一家三口的身体健康状况,适合采用抽样调查
D.x=3是不等式2(x﹣1)>3的解,这是一个必然事件
【解答】解:A、甲、乙两人10次测试成绩的方差分别是,,则甲的成绩更稳定,故该选项不符合题意;
B、某奖券的中奖率为,买1000张奖券,不一定会中奖,故该选项不符合题意;
C、要了解小明一家三口的身体健康状况,适合采用全面调查,故该选项不符合题意;
D、x=3是不等式2(x﹣1)>3的解,这是一个必然事件,故该选项符合题意;
故选:D.
5.(2025 武进区校级模拟)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … ﹣4 ﹣2 0 3 5 …
y … ﹣24 ﹣8 0 ﹣3 ﹣15 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当x>0时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线x=1
【解答】解:由题意得,
解得,
∴二次函数的解析式为y=﹣x2+2x=﹣(x﹣1)2+1,
∵a=﹣1<0,
∴图象的开口向下,故选项A不符合题意;
图象的对称轴是直线x=1,故选项D符合题意;
当0<x<1时,y的值随x的值增大而增大,当x>1时,y的值随x的值增大而减小,故选项B不符合题意;
∵顶点坐标为(1,1)且经过原点,图象的开口向下,
∴图象经过第一、三、四象限,故选项C不符合题意;
故选:D.
6.(2025 盐城一模)随着人们对环境的日益重视,骑行单车这种“低碳“出行方式已融入人们的日常生活,如图是某单车车架的示意图,线段AB,CE,DE分别为前叉、下管和立管,EF为后下叉.已知AB∥DE,AD∥EF,∠BCE=70°,∠CEF=130°,则∠A的度数为( )
A.100° B.110° C.120° D.130°
【解答】解:∵AB∥DE,∠BCE=70°,
∴∠CED=∠BCE=70°,
∵∠CEF=130°,
∴∠DEF=130°﹣70°=60°,
∵AD∥EF,
∴∠D=∠DEF=60°,
∵AB∥DE,
∴∠A=180°﹣∠D=180°﹣60°=120°,
故选:C.
7.(2025 盐城一模)点P(a,b)在函数y=3x﹣2的图象上,则代数式6a﹣2b+1的值等于( )
A.﹣1 B.﹣3 C.3 D.5
【解答】解:∵点P(a,b)在函数y=3x﹣2的图象上,
∴b=3a﹣2,
∴6a﹣2b+1=6a﹣2(3a﹣2)+1=5.
故选:D.
8.(2025 盐城一模)如图,A,B分别是棱长为1的正方体两个相邻的面的中心.将这个正方体的表面展开成平面图形后,点A,B之间的最大距离是( )
A. B. C. D.2
【解答】解:根据点A,B的位置关系和正方体的表面展开图可得:当点A,B的位置在如图所示位置时,点A,B之间的最大距离,
∴点A,B之间的最大距离.
故选:C.
9.(2025 姑苏区一模)我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
【解答】解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
10.(2025 南通模拟)如图,在平面直角坐标系中,点A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点C是y轴负半轴上一点,连接AC交x轴于点D,若OD是△ABC的中位线,△OCD的面积为3,则k的值是( )
A.﹣12 B.﹣6 C.6 D.12
【解答】解:设点A的坐标为A(a,b),则AB=﹣a,OB=b,k=ab,
∵OD是△ABC的中位线,
∴OC=OB=b,
∵△OCD的面积为3,∠COD=90°,
∴,即ab=﹣12,
∴k=ab=﹣12,
故选:A.
二.填空题(共6小题)
11.(2025 沭阳县校级模拟)根据宿迁市文化广电和旅游局统计显示,2024年五一假期,全市纳入统计的29家重点旅游景区接待国内外游客177.95万人次,同比增长62.19%,177.95万用科学记数法表示为 1.7795×106 .
【解答】解:177.95万=1779500=1.7795×106.
故答案为:1.7795×106.
12.(2020 鼓楼区校级模拟)不等式组的最小整数解是 0 .
【解答】解:不等式组整理得:,
∴不等式组的解集为﹣1<x≤2,
则最小的整数解为0,
故答案为:0
13.(2025 沭阳县校级模拟)如图,四边形ABCD是矩形,AB=3,AD=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,求2BG+BE的最小值 .
【解答】解:∵四边形ABCD是矩形,四边形CEFG是矩形,
∴∠BCD=∠ECG=90°,AB=CD=3,
∴∠BCE=∠DCG,
又∵,
∴△BEC∽△DGC,
∴,
即,
作EN⊥BC交BC于点N,GM⊥BC交BC的延长线于点M,作点D关于直线MG的对称点D',连接DD',与MG交于点H,连接D'G,如图:
则DG=D'G,DD'=2DH,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠ADC=∠ACD=90°,
又∵EN⊥BC,GM⊥BC,
∴四边形ABNE是矩形,四边形DCMH是矩形,
∴AB=EN=3,CM=DH,
∵四边形CEFG是矩形,
∴∠ECG=90°,
∵∠ECN+∠CEN=90°,∠ECN+∠GCM=90°,
∴∠CEN=∠GCM,
又∵∠ENC=∠GMC=90°,
∴△ECN∽△CGM,
∴,
即CM,
∴DH,DD′=2DH=3,
∴BG+=BE=BG+DG=BG+D'G≥BD',
故当点B、G、D'三点共线时,BGBE的值最小,最小值为BD',
在Rt△ABD'中,BD',
故BGBE的最小值为,
∴2BG+BE的最小值,
故答案为:.
14.(2025 盐城一模)在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 .
【解答】解:过A作AH⊥y轴于H,连接OA,如图:
∵A(3,3),
∴AH=OH=3,
∴△AOH是等腰直角三角形,
∴∠HOA=∠HAO=45°,
∴∠OQA+∠OAQ=∠HOA=45°,
∵以点A为旋转心把直线AP逆时针旋转45°得直线AP,
∴∠PAQ=45°,即∠CAO+∠OAQ=45°,
∴∠OQA=∠CAO,
∵∠ACO=∠QCA,
∴△ACO∽△QCA,
∴,
∵AC=OQ,
∴,
解得OCOQ或OCOQ(舍去),
∴,
故答案为:.
15.(2025 武进区校级模拟)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 10° .
【解答】解:如图,连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BCD=100°,
∴∠ACD=∠BCD﹣∠ACB=10°,
∴∠E=∠ACD=10°,
故答案为:10°.
16.(2025 建邺区二模)已知反比例函数(k为常数,k≠0),当1≤x≤2时,y的最大值与最小值的差为2,则k= ±4 .
【解答】解:当k>0时,在其每一象限内,反比例函数y随x的增大而减小.
∴2,
解得k=4,
当k<0时,在其每一象限内,反比例函数y随x的增大而增大.
∴2,
解得k=﹣4,
综上所述,k=±4.
故答案为:±4.
三.解答题(共11小题)
17.(2025 沭阳县校级模拟)计算:.
【解答】解:原式=﹣4+1﹣(4)﹣4
=﹣4+1﹣4+22
=﹣7.
18.(2025 武进区校级模拟)如图,B是AD的中点,BC∥DE,BC=DE.
(1)求证:∠C=∠E;
(2)连接AE,则AE与BC的关系是 AE与BC互相平分 .
【解答】(1)证明:∵B是AD的中点,
∴AB=DB,
∵BC∥DE,
∴∠ABC=∠D,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(SAS),
∴∠C=∠E;
(2)解:如图,连接CE,
由(1)知,△ABC≌△BDE,
∴∠BAC=∠DBE,AC=BE,
∴AC∥BE,
∴四边形ABEC是平行四边形,
∴AE与BC互相平分,
故答案为:AE与BC互相平分.
19.(2025 建邺区二模)先化简,再求值:,其中.
【解答】解:
,
当时,原式.
20.(2025 武进区校级模拟)解不等式组:.
【解答】解:,
解不等式①,得:x≤1,
解不等式②,得:x<4,
∴该不等式组的解集为x≤1.
21.(2025 沭阳县校级模拟)AI与人们的生活联系越发紧密,某校为了解七、八年级学生对AI的了解情况,举办了相关知识竞赛,并将最终成绩分为6分,7分,8分,9分,10分五个等级.学校在两个年级各随机抽取50人的成绩进行分析,将成绩整理并绘制成统计图如下.
两个样本数据的平均数、中位数、众数、方差如下:
平均数 中位数 众数 方差
七年级 7.6 8 8 1.08
八年级 a b 7 1.08
(1)m,a,b的值分别为 12 , 7.6 , 7 ;
(2)若八年级有1000名学生,求八年级得分不低于8分的人数;
(3)小明认为七年级的成绩更好,你同意他的说法吗?简要说明理由.
【解答】解:(1)m%=1﹣(12%+40%+30%+6%)=12%,即m=12,
a=6×12%+7×40%+8×30%+9×12%+10×6%=7.6(分),
6分人数为50×12%=6(人),7分人数为50×40%=20(人),
所以其中位数b7(分),
故答案为:12、7.6、7;
(2)1000×(1﹣12%﹣40%)=480(人),
答:八年级得分不低于8分的人数约为480人;
(3)同意,
因为七年级成绩的中位数大于八年级,
所以七年级成绩的高分人数多于八年级.
22.(2025 盐城一模)代数式A=mx+2,代数式B=2m+1.
(1)当m=3时,若A<B,则x的取值范围是 ;
(2)若m<0,x<2,判断代数式A与B的大小,并说明理由;
(3)将“A与B的差”记为C,即C=A﹣B.当﹣2≤x≤3时,要使C的值满足﹣3≤C≤2,直接写出m的取值范围.
【解答】解:(1)∵A=mx+2,B=2m+1,
∴当m=3时,A=3x+2,B=7,
∵A<B,
∴3x+2<7,解得:x.
故答案为:x;
(2)∵A= mx+2,B=2m+1,
∴A﹣B=mx+2﹣(2m+l)=m(x﹣2)+1,
∵m<0,x<2,
∴x﹣2<0,
∴m(x﹣2)>0,
∴m(x﹣2)+1>0,
∴A﹣B>0,即A>B;
(3)∵A= mx+2,B=2m+1,
∴C=A﹣B=m(x﹣2)+1,
﹣2<x≤3,﹣3≤C<3,
①当m>0时,C随着x的增大而增大,
则当x=3时,C的最大值是m+1,
当x=一2时,C的最小值是﹣4m+1,
可得:,解得:0<m≤1;
②当m=0时,C=1,满足﹣3≤C≤2,
∴m=0满足题意;
③当m<0时,C随着x的增大而减小,
则当x=﹣2时,C的最大值是﹣4m+1,
当x=3时,C的最小值是m+1,
可得:,解得:﹣4≤m<0;
综上所述,m的取值范围为m≤1.
23.(2025 梁溪区校级二模)实验是培养学生的创新能力的重要途径之一.如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,AB=30cm,BEAB,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF(点C,D,N,F在一条直线上),经测得:DE=21.7cm,MN=8cm,∠ABM=145°,求线段DN的长度.
(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
【解答】解:(1)过点E作EG⊥AC于点G,
∵AB=30cm,BEAB,
∴BE=10cm,AE=20cm,
∵∠AEG=α=10°,
∴GE=AE cosα=20×cos10°≈19.6(cm),
∴CD=GE=19.6cm,
答:酒精灯与铁架台的水平距离CD的长度为19.6cm;
(2)过点B作BH⊥CF于点H,BP⊥DE于点P,过点M作MQ⊥BH于点Q,
则BP=BE cosα=10×cos10°≈9.8(cm),
EP=BE sinα=10×sin10°≈1.7(cm),
∵DE=21.7cm,
∴PD=DE﹣EP=21.7﹣1.7=20(cm),
∴BH=20cm,
∵MN=8cm,
∴QH=8cm,
∴BQ=BH﹣QH=20﹣8=12(cm),
∵∠ABM=145°,
∴∠QBM=∠ABM﹣α﹣90°=145°﹣10°﹣90°=45°,
∴QM=BQ=12cm,
∴DN=DH+HN=BP+QM=9.8+12=21.8(cm),
答:线段DN的长度为21.8cm.
24.(2025 姜堰区一模)如图,A、B为⊙O上的两点,且∠AOB=60°,延长OA至点C,使AC=OA,连接BC.
(1)判断BC与⊙O的位置关系,并说明理由;
(2)用无刻度的直尺和圆规在BC上求作一点D,使BD=CD.(两种工具分别只限使用一次,并保留作图痕迹)
【解答】解:(1)结论:直线BC是⊙O的切线.
理由:连接AB.
∵OB=OA,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,
∵AC=OA,
∴AB=AO=AC,
∴∠OBC=90°,
∴BC⊥OB,
∴直线BC是⊙O的切线;
(2)如图,点D即为所求.
25.(2025 盐城一模)如图1,一个小球以v0=10cm/s的初速度,在一条足够长且平直的轨道上运动.轨道初段AC绝对光滑;除AC段外,剩下轨道粗糙.小球在绝对光滑轨道上不存在阻力;在粗糙轨道上,存在恒定的摩擦力,速度会逐渐减小,直至停止.小球运动过程中,其速度v(cm/s)与时间t(s)之间的关系如图2所示,其路程s(cm)与时间t(s)之间的关系如图3所示(PQ段是抛物线的一部分).
(1)轨道初段AC的总长为 40 cm;小球在粗糙轨道(图中射线CB上)运动时,v(cm/s)与t(s)之间的函数关系式为 vt+12 ;
(2)若测得小球从开始出发到最终停止,行进的总路程为140cm,如果直线OP与抛物线有且只有一个交点,则称线段OP与抛物线光滑连接.请你通过计算和推理判断线段OP与抛物线是否光滑连接?
(3)在(2)的条件下,在射线CB上,是否存在一节长为8.75cm的轨道段,使得小球在通过该段过程中,所用时间恰好为1s.若存在,请求出这节轨道的起点与点A之间的距离;若不存在,请说明理由.
【解答】解:(1)由图3可知,轨道初段AC的总长为10×4=40(cm);
设v=kt+b,
则,
解得,
∴vt+12,
故答案为:40;vt+12;
(2)由题意,Q为顶点,设Q(h,140),
则s(t﹣h)2+140,
把P(4,40)代入解析式得:40(4﹣h)2+140,
解得h=24(舍去 h=﹣16),
∴s(t﹣24)2+140t2+12t﹣4;
设直线OP表达式:s=k1t,代入P(4,40),有k1=10,
即s=10t,
联立,
得t2+2t﹣4=0,
∵Δ=22﹣4×()×(﹣4)=0,
∴直线OP与抛物线有且只有一个交点P,且直线OP不与抛物线对称轴平行,故线段OP与抛物线光滑连接;
(3)假设存在这节轨道,且小球第m秒行驶至轨道起点,则第 (m+1)秒行驶至轨道终点,
由题意得:(m+1)2+12(m+1)﹣4﹣(m2+12m﹣4)=8.75,
解得:m=6
当m=6时,m2+12m﹣436+12×6﹣4=59,
∴轨道起点与点A之间的距离为59米.
26.(2025 沭阳县校级模拟)已知二次函数y=ax2+bx+c(a>0).
(1)若该二次函数的图象过点(2,0)、、(0,﹣1),求二次函数解析式;
(2)如图所示,在平面直角坐标系Oxy中,该二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<0<x2,点D在⊙O上且在第二象限内,点E在x轴正半轴上,连接DE,且线段DE交y轴正半轴于点F,∠DOF=∠DEO,OFDF.
①求证:;
②当点E在线段OB上,且BE=1.⊙O的半径长为线段OA的长度的2倍,若4ac=﹣a2﹣b2,求2a+b的值.
【解答】解:(1)根据二次函数图象与x轴交于两点(2,0)、,设y=a(x﹣2)(x),
把(0,﹣1)代入得:﹣1=a (0﹣2) (0),则a=1.
∴y=(x﹣2)(x)=x2x﹣1.
(2)①证明:在△DOF和△DEO中,∠DOF=∠DEO,∠ODF=∠EDO,
∴△DOF∽△DEO.
∴,即.
∵OFDF,
∴.
②根据题意x1<0<x2,设OA=m,OD=2m.
由①可知EO=3m,则点A横坐标x1=﹣m,点B横坐标x2=3m+1.
∴对于ax2+bx+c=0,由根与系数的关系可得:x1+x2,x1 x2.
由4ac=﹣a2﹣b2得出,即:﹣4m(3m+1)=﹣1﹣(﹣m+3m+1)2,解得m.
∴x1+x2=2m+1=2,
故2a+b=0.
27.(2025 江苏二模)综合探究
【阅读材料】
学习小组遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.
小文是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小文同学的思考问题的方法,解决下列问题:
(1)如图2,请直接写出△BDE的面积为 1 .
(2)如图3,△ABC的三条中线分别为AD,BE,CF,若△ABC的面积为2,求出以AD,BE,CF的长度为三边长的三角形的面积.
【深入探究】
(3)已知点P是 ABCD内的一点,连接PA,PB,PC,PD,∠BAP=∠BCP,证明:∠ABP=∠ADP.
【实践操作】
(4)如图,已知三条线段a、b、c,请利用无刻度直尺和圆规作一个三角形,使得三角形的三条中线长分别为线段a、b、c的长.(保留作图痕迹,不写作法)
【解答】(1)解:∵AD∥BC,AC∥DE,
∴四边形ACED是平行四边形,
∴△ADC的面积=△ECD的面积=△ABD的面积,
∴△BDE的面积=梯形ABCD的面积=1,
故答案为:1;
(2)解:平移AF到PE,可得AF∥PE,AF=PE,延长FE交PC于点N,
∴四边形AFEP为平行四边形,
∴AE与PF互相平分,即M为PF的中点,
又∵AP∥FN∥BC,F为AB的中点,
∴N为PC的中点,
∴E为△PFC各边中线的交点,
∴△PEC的面积为△PFC面积的,
连接DE,可知DE与PE在一条直线上,
∴△EDC的面积是△ABC面积的,
所以△PFC的面积是23,
∴以AD、BE、CF的长度为三边长的三角形的面积等于;
(3)证明:如图,过点P作PE∥AD交AB于E,GH∥AB交BC、AD于G、H.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
∴AD∥BC∥PE,AB∥CD∥GH.
∴∠PEA=∠ABC=∠PGC,∠PEB=∠BAD=∠PHD.
∵∠BAP=∠BCP,∠PEA=∠PGC,
∴△PAE∽△PCG,
∴,
∵四边形AEPH、BGPE、CDHG都是平行四边形,
∴AE=PH,BE=PG,DH=CG,
∴,
又∵∠PEB=∠PHD,
∴△PBE∽△PDH;
∴∠ABP=∠ADP;
(4)解:如图所示,△ABC即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【押题预测卷】江苏省各地区真题重组训练(一)-2025年中考数学
一.选择题(共10小题)
1.(2025 泗阳县三模)下列对称图形中,既是中心对称又是轴对称图形的是( )
A. B.
C. D.
2.(2025 盐城一模)在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
3.(2025 武进区校级模拟)斗拱是中国古典建筑上的重要部件,如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
4.(2025 沭阳县校级模拟)下列说法正确的是( )
A.甲、乙两人10次测试成绩的方差分别是,,则乙的成绩更稳定
B.某奖券的中奖率为,买1000张奖券,一定会中奖1次
C.要了解小明一家三口的身体健康状况,适合采用抽样调查
D.x=3是不等式2(x﹣1)>3的解,这是一个必然事件
5.(2025 武进区校级模拟)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … ﹣4 ﹣2 0 3 5 …
y … ﹣24 ﹣8 0 ﹣3 ﹣15 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当x>0时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线x=1
6.(2025 盐城一模)随着人们对环境的日益重视,骑行单车这种“低碳“出行方式已融入人们的日常生活,如图是某单车车架的示意图,线段AB,CE,DE分别为前叉、下管和立管,EF为后下叉.已知AB∥DE,AD∥EF,∠BCE=70°,∠CEF=130°,则∠A的度数为( )
A.100° B.110° C.120° D.130°
7.(2025 盐城一模)点P(a,b)在函数y=3x﹣2的图象上,则代数式6a﹣2b+1的值等于( )
A.﹣1 B.﹣3 C.3 D.5
8.(2025 盐城一模)如图,A,B分别是棱长为1的正方体两个相邻的面的中心.将这个正方体的表面展开成平面图形后,点A,B之间的最大距离是( )
A. B. C. D.2
9.(2025 姑苏区一模)我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.(2025 南通模拟)如图,在平面直角坐标系中,点A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点C是y轴负半轴上一点,连接AC交x轴于点D,若OD是△ABC的中位线,△OCD的面积为3,则k的值是( )
A.﹣12 B.﹣6 C.6 D.12
二.填空题(共6小题)
11.(2025 沭阳县校级模拟)根据宿迁市文化广电和旅游局统计显示,2024年五一假期,全市纳入统计的29家重点旅游景区接待国内外游客177.95万人次,同比增长62.19%,177.95万用科学记数法表示为 .
12.(2020 鼓楼区校级模拟)不等式组的最小整数解是 .
13.(2025 沭阳县校级模拟)如图,四边形ABCD是矩形,AB=3,AD=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,求2BG+BE的最小值 .
14.(2025 盐城一模)在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 .
15.(2025 武进区校级模拟)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 .
16.(2025 建邺区二模)已知反比例函数(k为常数,k≠0),当1≤x≤2时,y的最大值与最小值的差为2,则k= .
三.解答题(共11小题)
17.(2025 沭阳县校级模拟)计算:.
18.(2025 武进区校级模拟)如图,B是AD的中点,BC∥DE,BC=DE.
(1)求证:∠C=∠E;
(2)连接AE,则AE与BC的关系是 .
19.(2025 建邺区二模)先化简,再求值:,其中.
20.(2025 武进区校级模拟)解不等式组:.
21.(2025 沭阳县校级模拟)AI与人们的生活联系越发紧密,某校为了解七、八年级学生对AI的了解情况,举办了相关知识竞赛,并将最终成绩分为6分,7分,8分,9分,10分五个等级.学校在两个年级各随机抽取50人的成绩进行分析,将成绩整理并绘制成统计图如下.
两个样本数据的平均数、中位数、众数、方差如下:
平均数 中位数 众数 方差
七年级 7.6 8 8 1.08
八年级 a b 7 1.08
(1)m,a,b的值分别为 , , ;
(2)若八年级有1000名学生,求八年级得分不低于8分的人数;
(3)小明认为七年级的成绩更好,你同意他的说法吗?简要说明理由.
22.(2025 盐城一模)代数式A=mx+2,代数式B=2m+1.
(1)当m=3时,若A<B,则x的取值范围是 ;
(2)若m<0,x<2,判断代数式A与B的大小,并说明理由;
(3)将“A与B的差”记为C,即C=A﹣B.当﹣2≤x≤3时,要使C的值满足﹣3≤C≤2,直接写出m的取值范围.
23.(2025 梁溪区校级二模)实验是培养学生的创新能力的重要途径之一.如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,AB=30cm,BEAB,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF(点C,D,N,F在一条直线上),经测得:DE=21.7cm,MN=8cm,∠ABM=145°,求线段DN的长度.
(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
24.(2025 姜堰区一模)如图,A、B为⊙O上的两点,且∠AOB=60°,延长OA至点C,使AC=OA,连接BC.
(1)判断BC与⊙O的位置关系,并说明理由;
(2)用无刻度的直尺和圆规在BC上求作一点D,使BD=CD.(两种工具分别只限使用一次,并保留作图痕迹)
25.(2025 盐城一模)如图1,一个小球以v0=10cm/s的初速度,在一条足够长且平直的轨道上运动.轨道初段AC绝对光滑;除AC段外,剩下轨道粗糙.小球在绝对光滑轨道上不存在阻力;在粗糙轨道上,存在恒定的摩擦力,速度会逐渐减小,直至停止.小球运动过程中,其速度v(cm/s)与时间t(s)之间的关系如图2所示,其路程s(cm)与时间t(s)之间的关系如图3所示(PQ段是抛物线的一部分).
(1)轨道初段AC的总长为 cm;小球在粗糙轨道(图中射线CB上)运动时,v(cm/s)与t(s)之间的函数关系式为 ;
(2)若测得小球从开始出发到最终停止,行进的总路程为140cm,如果直线OP与抛物线有且只有一个交点,则称线段OP与抛物线光滑连接.请你通过计算和推理判断线段OP与抛物线是否光滑连接?
(3)在(2)的条件下,在射线CB上,是否存在一节长为8.75cm的轨道段,使得小球在通过该段过程中,所用时间恰好为1s.若存在,请求出这节轨道的起点与点A之间的距离;若不存在,请说明理由.
26.(2025 沭阳县校级模拟)已知二次函数y=ax2+bx+c(a>0).
(1)若该二次函数的图象过点(2,0)、、(0,﹣1),求二次函数解析式;
(2)如图所示,在平面直角坐标系Oxy中,该二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<0<x2,点D在⊙O上且在第二象限内,点E在x轴正半轴上,连接DE,且线段DE交y轴正半轴于点F,∠DOF=∠DEO,OFDF.
①求证:;
②当点E在线段OB上,且BE=1.⊙O的半径长为线段OA的长度的2倍,若4ac=﹣a2﹣b2,求2a+b的值.
27.(2025 江苏二模)综合探究
【阅读材料】
学习小组遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.
小文是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小文同学的思考问题的方法,解决下列问题:
(1)如图2,请直接写出△BDE的面积为 .
(2)如图3,△ABC的三条中线分别为AD,BE,CF,若△ABC的面积为2,求出以AD,BE,CF的长度为三边长的三角形的面积.
【深入探究】
(3)已知点P是 ABCD内的一点,连接PA,PB,PC,PD,∠BAP=∠BCP,证明:∠ABP=∠ADP.
【实践操作】
(4)如图,已知三条线段a、b、c,请利用无刻度直尺和圆规作一个三角形,使得三角形的三条中线长分别为线段a、b、c的长.(保留作图痕迹,不写作法)
【押题预测卷】江苏省各地区真题重组训练(一)-2025年中考数学
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C D D C D C A A
一.选择题(共10小题)
1.(2025 泗阳县三模)下列对称图形中,既是中心对称又是轴对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.是中心对称图形,不是轴对称图形,故本选项不符合题意;
D.是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:B.
2.(2025 盐城一模)在平面直角坐标系xOy中,点M(﹣3,2)关于x轴对称的点的坐标是( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
【解答】解:点M(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
3.(2025 武进区校级模拟)斗拱是中国古典建筑上的重要部件,如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
【解答】解:左视图是从物体左面看所得到的图形.
从左面看,上面部分是矩形,下面部分是梯形,矩形部分有一条看不见的线,应该画虚线,
故选:C.
4.(2025 沭阳县校级模拟)下列说法正确的是( )
A.甲、乙两人10次测试成绩的方差分别是,,则乙的成绩更稳定
B.某奖券的中奖率为,买1000张奖券,一定会中奖1次
C.要了解小明一家三口的身体健康状况,适合采用抽样调查
D.x=3是不等式2(x﹣1)>3的解,这是一个必然事件
【解答】解:A、甲、乙两人10次测试成绩的方差分别是,,则甲的成绩更稳定,故该选项不符合题意;
B、某奖券的中奖率为,买1000张奖券,不一定会中奖,故该选项不符合题意;
C、要了解小明一家三口的身体健康状况,适合采用全面调查,故该选项不符合题意;
D、x=3是不等式2(x﹣1)>3的解,这是一个必然事件,故该选项符合题意;
故选:D.
5.(2025 武进区校级模拟)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … ﹣4 ﹣2 0 3 5 …
y … ﹣24 ﹣8 0 ﹣3 ﹣15 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当x>0时,y的值随x的值增大而增大
C.图象经过第二、三、四象限
D.图象的对称轴是直线x=1
【解答】解:由题意得,
解得,
∴二次函数的解析式为y=﹣x2+2x=﹣(x﹣1)2+1,
∵a=﹣1<0,
∴图象的开口向下,故选项A不符合题意;
图象的对称轴是直线x=1,故选项D符合题意;
当0<x<1时,y的值随x的值增大而增大,当x>1时,y的值随x的值增大而减小,故选项B不符合题意;
∵顶点坐标为(1,1)且经过原点,图象的开口向下,
∴图象经过第一、三、四象限,故选项C不符合题意;
故选:D.
6.(2025 盐城一模)随着人们对环境的日益重视,骑行单车这种“低碳“出行方式已融入人们的日常生活,如图是某单车车架的示意图,线段AB,CE,DE分别为前叉、下管和立管,EF为后下叉.已知AB∥DE,AD∥EF,∠BCE=70°,∠CEF=130°,则∠A的度数为( )
A.100° B.110° C.120° D.130°
【解答】解:∵AB∥DE,∠BCE=70°,
∴∠CED=∠BCE=70°,
∵∠CEF=130°,
∴∠DEF=130°﹣70°=60°,
∵AD∥EF,
∴∠D=∠DEF=60°,
∵AB∥DE,
∴∠A=180°﹣∠D=180°﹣60°=120°,
故选:C.
7.(2025 盐城一模)点P(a,b)在函数y=3x﹣2的图象上,则代数式6a﹣2b+1的值等于( )
A.﹣1 B.﹣3 C.3 D.5
【解答】解:∵点P(a,b)在函数y=3x﹣2的图象上,
∴b=3a﹣2,
∴6a﹣2b+1=6a﹣2(3a﹣2)+1=5.
故选:D.
8.(2025 盐城一模)如图,A,B分别是棱长为1的正方体两个相邻的面的中心.将这个正方体的表面展开成平面图形后,点A,B之间的最大距离是( )
A. B. C. D.2
【解答】解:根据点A,B的位置关系和正方体的表面展开图可得:当点A,B的位置在如图所示位置时,点A,B之间的最大距离,
∴点A,B之间的最大距离.
故选:C.
9.(2025 姑苏区一模)我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
【解答】解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
10.(2025 南通模拟)如图,在平面直角坐标系中,点A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点C是y轴负半轴上一点,连接AC交x轴于点D,若OD是△ABC的中位线,△OCD的面积为3,则k的值是( )
A.﹣12 B.﹣6 C.6 D.12
【解答】解:设点A的坐标为A(a,b),则AB=﹣a,OB=b,k=ab,
∵OD是△ABC的中位线,
∴OC=OB=b,
∵△OCD的面积为3,∠COD=90°,
∴,即ab=﹣12,
∴k=ab=﹣12,
故选:A.
二.填空题(共6小题)
11.(2025 沭阳县校级模拟)根据宿迁市文化广电和旅游局统计显示,2024年五一假期,全市纳入统计的29家重点旅游景区接待国内外游客177.95万人次,同比增长62.19%,177.95万用科学记数法表示为 1.7795×106 .
【解答】解:177.95万=1779500=1.7795×106.
故答案为:1.7795×106.
12.(2020 鼓楼区校级模拟)不等式组的最小整数解是 0 .
【解答】解:不等式组整理得:,
∴不等式组的解集为﹣1<x≤2,
则最小的整数解为0,
故答案为:0
13.(2025 沭阳县校级模拟)如图,四边形ABCD是矩形,AB=3,AD=6,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,求2BG+BE的最小值 .
【解答】解:∵四边形ABCD是矩形,四边形CEFG是矩形,
∴∠BCD=∠ECG=90°,AB=CD=3,
∴∠BCE=∠DCG,
又∵,
∴△BEC∽△DGC,
∴,
即,
作EN⊥BC交BC于点N,GM⊥BC交BC的延长线于点M,作点D关于直线MG的对称点D',连接DD',与MG交于点H,连接D'G,如图:
则DG=D'G,DD'=2DH,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠ADC=∠ACD=90°,
又∵EN⊥BC,GM⊥BC,
∴四边形ABNE是矩形,四边形DCMH是矩形,
∴AB=EN=3,CM=DH,
∵四边形CEFG是矩形,
∴∠ECG=90°,
∵∠ECN+∠CEN=90°,∠ECN+∠GCM=90°,
∴∠CEN=∠GCM,
又∵∠ENC=∠GMC=90°,
∴△ECN∽△CGM,
∴,
即CM,
∴DH,DD′=2DH=3,
∴BG+=BE=BG+DG=BG+D'G≥BD',
故当点B、G、D'三点共线时,BGBE的值最小,最小值为BD',
在Rt△ABD'中,BD',
故BGBE的最小值为,
∴2BG+BE的最小值,
故答案为:.
14.(2025 盐城一模)在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 .
【解答】解:过A作AH⊥y轴于H,连接OA,如图:
∵A(3,3),
∴AH=OH=3,
∴△AOH是等腰直角三角形,
∴∠HOA=∠HAO=45°,
∴∠OQA+∠OAQ=∠HOA=45°,
∵以点A为旋转心把直线AP逆时针旋转45°得直线AP,
∴∠PAQ=45°,即∠CAO+∠OAQ=45°,
∴∠OQA=∠CAO,
∵∠ACO=∠QCA,
∴△ACO∽△QCA,
∴,
∵AC=OQ,
∴,
解得OCOQ或OCOQ(舍去),
∴,
故答案为:.
15.(2025 武进区校级模拟)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 10° .
【解答】解:如图,连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BCD=100°,
∴∠ACD=∠BCD﹣∠ACB=10°,
∴∠E=∠ACD=10°,
故答案为:10°.
16.(2025 建邺区二模)已知反比例函数(k为常数,k≠0),当1≤x≤2时,y的最大值与最小值的差为2,则k= ±4 .
【解答】解:当k>0时,在其每一象限内,反比例函数y随x的增大而减小.
∴2,
解得k=4,
当k<0时,在其每一象限内,反比例函数y随x的增大而增大.
∴2,
解得k=﹣4,
综上所述,k=±4.
故答案为:±4.
三.解答题(共11小题)
17.(2025 沭阳县校级模拟)计算:.
【解答】解:原式=﹣4+1﹣(4)﹣4
=﹣4+1﹣4+22
=﹣7.
18.(2025 武进区校级模拟)如图,B是AD的中点,BC∥DE,BC=DE.
(1)求证:∠C=∠E;
(2)连接AE,则AE与BC的关系是 AE与BC互相平分 .
【解答】(1)证明:∵B是AD的中点,
∴AB=DB,
∵BC∥DE,
∴∠ABC=∠D,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(SAS),
∴∠C=∠E;
(2)解:如图,连接CE,
由(1)知,△ABC≌△BDE,
∴∠BAC=∠DBE,AC=BE,
∴AC∥BE,
∴四边形ABEC是平行四边形,
∴AE与BC互相平分,
故答案为:AE与BC互相平分.
19.(2025 建邺区二模)先化简,再求值:,其中.
【解答】解:
,
当时,原式.
20.(2025 武进区校级模拟)解不等式组:.
【解答】解:,
解不等式①,得:x≤1,
解不等式②,得:x<4,
∴该不等式组的解集为x≤1.
21.(2025 沭阳县校级模拟)AI与人们的生活联系越发紧密,某校为了解七、八年级学生对AI的了解情况,举办了相关知识竞赛,并将最终成绩分为6分,7分,8分,9分,10分五个等级.学校在两个年级各随机抽取50人的成绩进行分析,将成绩整理并绘制成统计图如下.
两个样本数据的平均数、中位数、众数、方差如下:
平均数 中位数 众数 方差
七年级 7.6 8 8 1.08
八年级 a b 7 1.08
(1)m,a,b的值分别为 12 , 7.6 , 7 ;
(2)若八年级有1000名学生,求八年级得分不低于8分的人数;
(3)小明认为七年级的成绩更好,你同意他的说法吗?简要说明理由.
【解答】解:(1)m%=1﹣(12%+40%+30%+6%)=12%,即m=12,
a=6×12%+7×40%+8×30%+9×12%+10×6%=7.6(分),
6分人数为50×12%=6(人),7分人数为50×40%=20(人),
所以其中位数b7(分),
故答案为:12、7.6、7;
(2)1000×(1﹣12%﹣40%)=480(人),
答:八年级得分不低于8分的人数约为480人;
(3)同意,
因为七年级成绩的中位数大于八年级,
所以七年级成绩的高分人数多于八年级.
22.(2025 盐城一模)代数式A=mx+2,代数式B=2m+1.
(1)当m=3时,若A<B,则x的取值范围是 ;
(2)若m<0,x<2,判断代数式A与B的大小,并说明理由;
(3)将“A与B的差”记为C,即C=A﹣B.当﹣2≤x≤3时,要使C的值满足﹣3≤C≤2,直接写出m的取值范围.
【解答】解:(1)∵A=mx+2,B=2m+1,
∴当m=3时,A=3x+2,B=7,
∵A<B,
∴3x+2<7,解得:x.
故答案为:x;
(2)∵A= mx+2,B=2m+1,
∴A﹣B=mx+2﹣(2m+l)=m(x﹣2)+1,
∵m<0,x<2,
∴x﹣2<0,
∴m(x﹣2)>0,
∴m(x﹣2)+1>0,
∴A﹣B>0,即A>B;
(3)∵A= mx+2,B=2m+1,
∴C=A﹣B=m(x﹣2)+1,
﹣2<x≤3,﹣3≤C<3,
①当m>0时,C随着x的增大而增大,
则当x=3时,C的最大值是m+1,
当x=一2时,C的最小值是﹣4m+1,
可得:,解得:0<m≤1;
②当m=0时,C=1,满足﹣3≤C≤2,
∴m=0满足题意;
③当m<0时,C随着x的增大而减小,
则当x=﹣2时,C的最大值是﹣4m+1,
当x=3时,C的最小值是m+1,
可得:,解得:﹣4≤m<0;
综上所述,m的取值范围为m≤1.
23.(2025 梁溪区校级二模)实验是培养学生的创新能力的重要途径之一.如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,AB=30cm,BEAB,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF(点C,D,N,F在一条直线上),经测得:DE=21.7cm,MN=8cm,∠ABM=145°,求线段DN的长度.
(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
【解答】解:(1)过点E作EG⊥AC于点G,
∵AB=30cm,BEAB,
∴BE=10cm,AE=20cm,
∵∠AEG=α=10°,
∴GE=AE cosα=20×cos10°≈19.6(cm),
∴CD=GE=19.6cm,
答:酒精灯与铁架台的水平距离CD的长度为19.6cm;
(2)过点B作BH⊥CF于点H,BP⊥DE于点P,过点M作MQ⊥BH于点Q,
则BP=BE cosα=10×cos10°≈9.8(cm),
EP=BE sinα=10×sin10°≈1.7(cm),
∵DE=21.7cm,
∴PD=DE﹣EP=21.7﹣1.7=20(cm),
∴BH=20cm,
∵MN=8cm,
∴QH=8cm,
∴BQ=BH﹣QH=20﹣8=12(cm),
∵∠ABM=145°,
∴∠QBM=∠ABM﹣α﹣90°=145°﹣10°﹣90°=45°,
∴QM=BQ=12cm,
∴DN=DH+HN=BP+QM=9.8+12=21.8(cm),
答:线段DN的长度为21.8cm.
24.(2025 姜堰区一模)如图,A、B为⊙O上的两点,且∠AOB=60°,延长OA至点C,使AC=OA,连接BC.
(1)判断BC与⊙O的位置关系,并说明理由;
(2)用无刻度的直尺和圆规在BC上求作一点D,使BD=CD.(两种工具分别只限使用一次,并保留作图痕迹)
【解答】解:(1)结论:直线BC是⊙O的切线.
理由:连接AB.
∵OB=OA,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,
∵AC=OA,
∴AB=AO=AC,
∴∠OBC=90°,
∴BC⊥OB,
∴直线BC是⊙O的切线;
(2)如图,点D即为所求.
25.(2025 盐城一模)如图1,一个小球以v0=10cm/s的初速度,在一条足够长且平直的轨道上运动.轨道初段AC绝对光滑;除AC段外,剩下轨道粗糙.小球在绝对光滑轨道上不存在阻力;在粗糙轨道上,存在恒定的摩擦力,速度会逐渐减小,直至停止.小球运动过程中,其速度v(cm/s)与时间t(s)之间的关系如图2所示,其路程s(cm)与时间t(s)之间的关系如图3所示(PQ段是抛物线的一部分).
(1)轨道初段AC的总长为 40 cm;小球在粗糙轨道(图中射线CB上)运动时,v(cm/s)与t(s)之间的函数关系式为 vt+12 ;
(2)若测得小球从开始出发到最终停止,行进的总路程为140cm,如果直线OP与抛物线有且只有一个交点,则称线段OP与抛物线光滑连接.请你通过计算和推理判断线段OP与抛物线是否光滑连接?
(3)在(2)的条件下,在射线CB上,是否存在一节长为8.75cm的轨道段,使得小球在通过该段过程中,所用时间恰好为1s.若存在,请求出这节轨道的起点与点A之间的距离;若不存在,请说明理由.
【解答】解:(1)由图3可知,轨道初段AC的总长为10×4=40(cm);
设v=kt+b,
则,
解得,
∴vt+12,
故答案为:40;vt+12;
(2)由题意,Q为顶点,设Q(h,140),
则s(t﹣h)2+140,
把P(4,40)代入解析式得:40(4﹣h)2+140,
解得h=24(舍去 h=﹣16),
∴s(t﹣24)2+140t2+12t﹣4;
设直线OP表达式:s=k1t,代入P(4,40),有k1=10,
即s=10t,
联立,
得t2+2t﹣4=0,
∵Δ=22﹣4×()×(﹣4)=0,
∴直线OP与抛物线有且只有一个交点P,且直线OP不与抛物线对称轴平行,故线段OP与抛物线光滑连接;
(3)假设存在这节轨道,且小球第m秒行驶至轨道起点,则第 (m+1)秒行驶至轨道终点,
由题意得:(m+1)2+12(m+1)﹣4﹣(m2+12m﹣4)=8.75,
解得:m=6
当m=6时,m2+12m﹣436+12×6﹣4=59,
∴轨道起点与点A之间的距离为59米.
26.(2025 沭阳县校级模拟)已知二次函数y=ax2+bx+c(a>0).
(1)若该二次函数的图象过点(2,0)、、(0,﹣1),求二次函数解析式;
(2)如图所示,在平面直角坐标系Oxy中,该二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<0<x2,点D在⊙O上且在第二象限内,点E在x轴正半轴上,连接DE,且线段DE交y轴正半轴于点F,∠DOF=∠DEO,OFDF.
①求证:;
②当点E在线段OB上,且BE=1.⊙O的半径长为线段OA的长度的2倍,若4ac=﹣a2﹣b2,求2a+b的值.
【解答】解:(1)根据二次函数图象与x轴交于两点(2,0)、,设y=a(x﹣2)(x),
把(0,﹣1)代入得:﹣1=a (0﹣2) (0),则a=1.
∴y=(x﹣2)(x)=x2x﹣1.
(2)①证明:在△DOF和△DEO中,∠DOF=∠DEO,∠ODF=∠EDO,
∴△DOF∽△DEO.
∴,即.
∵OFDF,
∴.
②根据题意x1<0<x2,设OA=m,OD=2m.
由①可知EO=3m,则点A横坐标x1=﹣m,点B横坐标x2=3m+1.
∴对于ax2+bx+c=0,由根与系数的关系可得:x1+x2,x1 x2.
由4ac=﹣a2﹣b2得出,即:﹣4m(3m+1)=﹣1﹣(﹣m+3m+1)2,解得m.
∴x1+x2=2m+1=2,
故2a+b=0.
27.(2025 江苏二模)综合探究
【阅读材料】
学习小组遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.
小文是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小文同学的思考问题的方法,解决下列问题:
(1)如图2,请直接写出△BDE的面积为 1 .
(2)如图3,△ABC的三条中线分别为AD,BE,CF,若△ABC的面积为2,求出以AD,BE,CF的长度为三边长的三角形的面积.
【深入探究】
(3)已知点P是 ABCD内的一点,连接PA,PB,PC,PD,∠BAP=∠BCP,证明:∠ABP=∠ADP.
【实践操作】
(4)如图,已知三条线段a、b、c,请利用无刻度直尺和圆规作一个三角形,使得三角形的三条中线长分别为线段a、b、c的长.(保留作图痕迹,不写作法)
【解答】(1)解:∵AD∥BC,AC∥DE,
∴四边形ACED是平行四边形,
∴△ADC的面积=△ECD的面积=△ABD的面积,
∴△BDE的面积=梯形ABCD的面积=1,
故答案为:1;
(2)解:平移AF到PE,可得AF∥PE,AF=PE,延长FE交PC于点N,
∴四边形AFEP为平行四边形,
∴AE与PF互相平分,即M为PF的中点,
又∵AP∥FN∥BC,F为AB的中点,
∴N为PC的中点,
∴E为△PFC各边中线的交点,
∴△PEC的面积为△PFC面积的,
连接DE,可知DE与PE在一条直线上,
∴△EDC的面积是△ABC面积的,
所以△PFC的面积是23,
∴以AD、BE、CF的长度为三边长的三角形的面积等于;
(3)证明:如图,过点P作PE∥AD交AB于E,GH∥AB交BC、AD于G、H.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
∴AD∥BC∥PE,AB∥CD∥GH.
∴∠PEA=∠ABC=∠PGC,∠PEB=∠BAD=∠PHD.
∵∠BAP=∠BCP,∠PEA=∠PGC,
∴△PAE∽△PCG,
∴,
∵四边形AEPH、BGPE、CDHG都是平行四边形,
∴AE=PH,BE=PG,DH=CG,
∴,
又∵∠PEB=∠PHD,
∴△PBE∽△PDH;
∴∠ABP=∠ADP;
(4)解:如图所示,△ABC即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
