浙教版2024—2025学年八年级下学期数学期末调研检测卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末调研检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 582.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:48:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A.3 B.
C.()2=9 D.
2.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
3.若反比例函数的图象经过点(2,﹣3),则一次函数y=kx﹣k(k≠0)的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知一次函数y=kx+b(k≠0)与反比例函数的图象交于A(1,m)、B(﹣3,n)两点,则不等式的解集为( )
A.﹣3<x<1 B.﹣3<x<0或x>1
C.x<﹣3或0<x<1 D.x<﹣1或0<x<3
5.一个多边形的内角和与它的外角和的和为1800°,则这个多边形的边数为( )
A.11 B.10 C.9 D.8
6.一家鞋店在一段时间内销售了某种运动鞋30双,各种尺码鞋的销售量如表所示:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26
销售量(双) 1 2 5 11 7 3 1
若每双鞋的销售利润相同,下列统计量中店主最关注的是( )
A.中位数 B.方差 C.平均数 D.众数
7.一元二次方程2x2+3x+1=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
8.若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
9.化简得( )
A.2 B.﹣4x+4 C.﹣2 D.4x﹣4
10.已知点A(x1,y1),B(x2,y2)在反比例函数(k为常数,k<0)的图象上,x1<x2,则以下说法正确的是( )
A.若x1+x2>0,则y1+y2>0
B.若x1+x2>0,则y1+y2<0
C.若x1 x2>0,则y1>y2
D.若x1 x2<0,则y1>y2
二、填空题(6小题,每题3分,共18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.已知关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,则关于x的一元二次方程m(x﹣h+3)2=k的解是 .
15.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长为 .
16.已知A,B是直线y1=x上两点,分别过点A和点B作AC∥BD∥x轴,AC和BD分别交双曲线y2(x>0)于点C和点D,连接OC,OD.
(1)直线y1和双曲线y2的交点坐标为 ;
(2)若BDAC,则2OC2﹣OD2的值为 .
浙教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、_____、_____
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);
(2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.某校为了解初中学生每天的睡眠情况,随机调查了该校部分初中学生平均每天睡眠时间(单位:h).根据调查结果
请根据相关信息,解答下列问题:
(1)直接写出本次接受调查的学生人数和图1中m的值;
(2)求被调查的学生平均每天睡眠时间数据的平均数和中位数;
(3)全校共有1200名学生,请估算全校学生平均每天睡眠时间不低于8h的人数.
20.已知△ABC的周长为,其中,.
(1)求BC的长度;
(2)判断△ABC的形状,并说明理由.
21.已知:,.
(1)求a2+b2﹣ab的值;
(2)若m为a整数部分,n为b小数部分,求的值.
22.如图,一次函数y=k1x+2与x轴相交于点B(2,0),与反比例函数相交于点C、点D.
(1)求一次函数的表达式及∠ABO的度数;
(2)若点E为线段OB上一点,且∠OCE=45°,CO=CE,求点C的坐标及反比例函数的表达式.
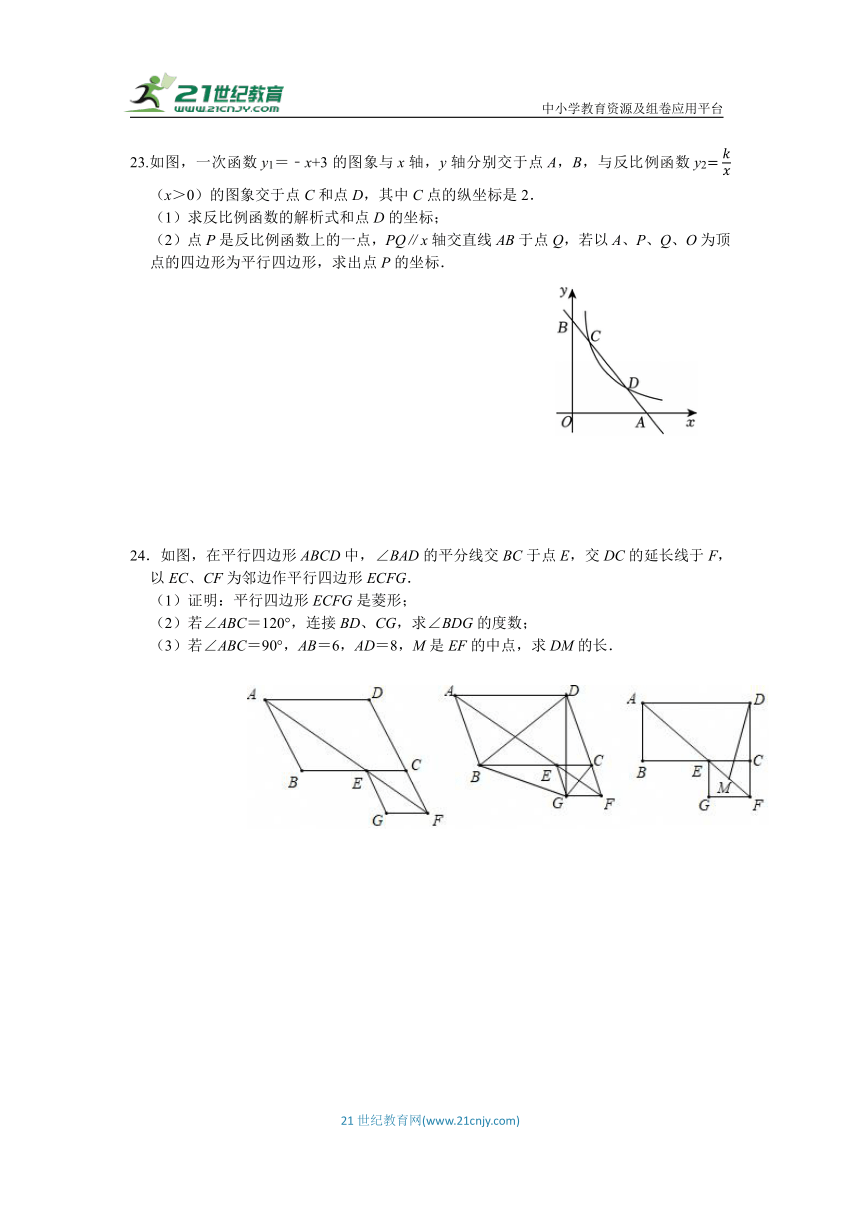
23.如图,一次函数y1=﹣x+3的图象与x轴,y轴分别交于点A,B,与反比例函数y2(x>0)的图象交于点C和点D,其中C点的纵坐标是2.
(1)求反比例函数的解析式和点D的坐标;
(2)点P是反比例函数上的一点,PQ∥x轴交直线AB于点Q,若以A、P、Q、O为顶点的四边形为平行四边形,求出点P的坐标.
24.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.
(1)证明:平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
25.如图1,在平行四边形ABCD中,∠ABC为钝角,BE,BF分别为边AD,CD上的高,交边AD,CD于点E,F,连结EF,BF=EF.
(1)求证:∠EBF=∠C;
(2)求证:CF=DF;
(3)如图2,若∠DBC=45°,以点B为原点建立平面直角坐标系,点C坐标为,点P为直线CE上一动点,当S△BCP=S△BDE时,求出此时点P的坐标.
参考答案
一、选择题
1—10:DBCBB DACAD
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:∵关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,即的解为x1=2,x2=5;
令x+3=y,
∴关于x的一元二次方程m(x﹣h+3)2=k化为m(y﹣h)2=k,
∵的解为x1=2,x2=5,
∴的解为y1=2,y2=5,即x+3=2或x+3=5,
∴x3=﹣1,x4=2,
∴关于x的一元二次方程m(x﹣h+3)2=k的解是x3=﹣1,x4=2,
故答案为:x3=﹣1,x4=2.
15.【解答】解:取AB的中点F,连接NF,MF,
∵∠CAB+∠CBA=90°,
∵点M是AD的中点,
∴MF是△ABD的中位线,
∴,MF∥BD,
∴∠AFM=∠CBA,
∵NF是△ABE的中位线,
∴,NF∥AE,
∴∠BFN=∠BAC,
∴∠BFN+∠AFM=∠BAC+∠CBA=90°,
∴∠MFN=90°,
∴MN2=MF2+NF2,
∴MN2=32+22=13,
∴.
故答案为:.
16.【解答】解:(1)根据题意,得,
解得x=2或x=﹣2(舍去),
则y=x=2,
∴直线y1和双曲线y2的交点坐标为(2,2).
(2)如图,延长AC和DB分别交y轴于点E和点F.
则OF=BF,OE=AE,即△AOE和△BOF都是等腰直角三角形.
设AE=OE=m,则,
∴.
同理设BF=OF=n,则,
∴.
又∵,
∴,两边同时平方得.
在Rt△COE中,,
同理,
∴,
故答案为:(1)(2,2);(2)8.
三、解答题
17.【解答】解:(1)原式=(53)
=2
;
(2)原式=1﹣2
=1.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)50,40
5÷10%=50(人),
20÷50=40%,即m=40,
∴本次接受调查的学生人数为50人;图1中m的值为40;
(2)这组学生平均每天睡眠时间数据的平均数为:7×20%+8×40%+7×30%+7×10%=7.7;
将这50个数据从小到大排列后,处在中间位置的两个数都是6;
答:这组数据的平均数是7.7,中位数是2;
(3)1200×(40%+20%)=720(人),
答:全校学生平均每天睡眠时间不低于8h的人数约为720人
20.【解答】解:(1)由条件可知
,
∴BC的长度为;
(2)直角三角形,理由如下:
∵,
,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
21.【解答】解:(1)∵a,b2,
∴a+b22=2,ab=(2)(2)=1,
∴a2+b2﹣ab
=(a+b)2﹣3ab
=(2)2﹣3×1
=20﹣3
=17;
(2)∵,
∴23,
∴42<5,
∴02<1,
∴m=4,n2,
∴48.
22.【解答】解:(1)将点B(2,0)代入y=k1x+2得k1=﹣1,
所以y=﹣x+2,
∴点A的坐标为(0,2),
∴OA=OB,
∴∠ABO=45°;
(2)连接OC、OE,过点C作 CF⊥x轴,如答图所示;
∵∠OCE=45°,CO=CE,
∴∠COE=67.5°,
∵∠ABO=45°,
∴∠BCO=180°﹣∠COB﹣∠CBO=180°﹣67.5°﹣45°=67.5°,
∴BC=BO=2,
∴∠FCB=∠OCB∠OCE=45°=∠ABO,
∴在等腰Rt△CFB 中,,
∴OF=OB﹣BF=2,
∴C(2,),
将C(2,)代入得,
∴反比例函数表达式为.
23.【解答】解:(1)设C点的坐标是(m,2),
∵一次函数y1=﹣x+3的图象与反比例函数y2(x>0)的图象交于点C和点D,
∴﹣m+3=2,
解得:m=1,
∴C(1,2),
∴2,
解得:k=2,
∴y2(x>0),
令x+3,
解得:x1=1,x2=2,
经检验:x1=1,x2=2是此方程的根,
∴y=﹣2+3=1,
∴D(2,1);
故反比例函数的解析式为y2(x>0)、点D的坐标为(2,1);
(2)当y=0时,一次函数y1=﹣x+3=0,
∴x=3,
∴OA=3,
∵PQ∥x轴交直线AB于点Q,以A、P、Q、O为顶点的四边形为平行四边形,
∴PQ=OA=3,
∵点P是反比例函数上的一点,
∴设P(m,),
∵PQ∥x轴,
∴yQ,
∴﹣x+3,
解得:xQ=3,
∵PQ=3,
∴|xP﹣xQ|=3,
∴|m﹣(3)|=3,
∴m﹣(3)=3或m﹣(3)=﹣3,
当m﹣(3)=3时,
解得m1=3,m2=3,
经检验:m1=3,m2=3是此方程的根;
当m﹣(3)=﹣3时,
∴m2+2=0,
∴m不存在;
当m=3时,
yP3;
当m=3时,
yP3;
∴P的坐标为(3,3)或(3,3).
24.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
25.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BE,BF分别为边AD,CD上的高,
∴AD⊥BE,∠BFC=90°,
∴BE⊥BC,
∴∠EBC=90°=∠BFC,
∴∠EBF+∠CBF=90°=∠C+∠CBF,
∴∠EBF=∠C;
(2)证明:如图2,延长EF,BC交于点H,
∵BF=EF,
∴∠FEB=∠FBE,
∵∠EBC=90°,
∴∠FBH=∠FHB,
∴BF=FH,
∴EF=FH,
∵AD∥BC,
∴∠ADC=∠DCH,
在△EDF和△HCF中,
,
∴△EDF≌△HCF(AAS),
∴DF=CF;
(3)解:分两种情况:
①如图3,点P在x轴的上方,过点P作PG⊥x轴于G,
∵点C坐标为,
∴BC,
∵BF⊥CD,DF=CF,
∴BD=BC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴△BED是等腰直角三角形,
∴BE=DE=1,
∴S△BED1×1,
∵S△BCP=S△BDE,
∴ PG,
∴PG,
∵E(0,1),C(,0),
设直线CE的解析式为:y=kx+b,
∴,
解得:,
∴直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
如图4,P在x轴的下方,过点P作PG⊥x轴于G,
由①可知:PG,直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
综上,点P的坐标为(1,)或(1,).
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A.3 B.
C.()2=9 D.
2.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
3.若反比例函数的图象经过点(2,﹣3),则一次函数y=kx﹣k(k≠0)的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知一次函数y=kx+b(k≠0)与反比例函数的图象交于A(1,m)、B(﹣3,n)两点,则不等式的解集为( )
A.﹣3<x<1 B.﹣3<x<0或x>1
C.x<﹣3或0<x<1 D.x<﹣1或0<x<3
5.一个多边形的内角和与它的外角和的和为1800°,则这个多边形的边数为( )
A.11 B.10 C.9 D.8
6.一家鞋店在一段时间内销售了某种运动鞋30双,各种尺码鞋的销售量如表所示:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26
销售量(双) 1 2 5 11 7 3 1
若每双鞋的销售利润相同,下列统计量中店主最关注的是( )
A.中位数 B.方差 C.平均数 D.众数
7.一元二次方程2x2+3x+1=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
8.若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
9.化简得( )
A.2 B.﹣4x+4 C.﹣2 D.4x﹣4
10.已知点A(x1,y1),B(x2,y2)在反比例函数(k为常数,k<0)的图象上,x1<x2,则以下说法正确的是( )
A.若x1+x2>0,则y1+y2>0
B.若x1+x2>0,则y1+y2<0
C.若x1 x2>0,则y1>y2
D.若x1 x2<0,则y1>y2
二、填空题(6小题,每题3分,共18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.已知关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,则关于x的一元二次方程m(x﹣h+3)2=k的解是 .
15.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长为 .
16.已知A,B是直线y1=x上两点,分别过点A和点B作AC∥BD∥x轴,AC和BD分别交双曲线y2(x>0)于点C和点D,连接OC,OD.
(1)直线y1和双曲线y2的交点坐标为 ;
(2)若BDAC,则2OC2﹣OD2的值为 .
浙教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、_____、_____
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);
(2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.某校为了解初中学生每天的睡眠情况,随机调查了该校部分初中学生平均每天睡眠时间(单位:h).根据调查结果
请根据相关信息,解答下列问题:
(1)直接写出本次接受调查的学生人数和图1中m的值;
(2)求被调查的学生平均每天睡眠时间数据的平均数和中位数;
(3)全校共有1200名学生,请估算全校学生平均每天睡眠时间不低于8h的人数.
20.已知△ABC的周长为,其中,.
(1)求BC的长度;
(2)判断△ABC的形状,并说明理由.
21.已知:,.
(1)求a2+b2﹣ab的值;
(2)若m为a整数部分,n为b小数部分,求的值.
22.如图,一次函数y=k1x+2与x轴相交于点B(2,0),与反比例函数相交于点C、点D.
(1)求一次函数的表达式及∠ABO的度数;
(2)若点E为线段OB上一点,且∠OCE=45°,CO=CE,求点C的坐标及反比例函数的表达式.
23.如图,一次函数y1=﹣x+3的图象与x轴,y轴分别交于点A,B,与反比例函数y2(x>0)的图象交于点C和点D,其中C点的纵坐标是2.
(1)求反比例函数的解析式和点D的坐标;
(2)点P是反比例函数上的一点,PQ∥x轴交直线AB于点Q,若以A、P、Q、O为顶点的四边形为平行四边形,求出点P的坐标.
24.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.
(1)证明:平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
25.如图1,在平行四边形ABCD中,∠ABC为钝角,BE,BF分别为边AD,CD上的高,交边AD,CD于点E,F,连结EF,BF=EF.
(1)求证:∠EBF=∠C;
(2)求证:CF=DF;
(3)如图2,若∠DBC=45°,以点B为原点建立平面直角坐标系,点C坐标为,点P为直线CE上一动点,当S△BCP=S△BDE时,求出此时点P的坐标.
参考答案
一、选择题
1—10:DBCBB DACAD
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:∵关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,即的解为x1=2,x2=5;
令x+3=y,
∴关于x的一元二次方程m(x﹣h+3)2=k化为m(y﹣h)2=k,
∵的解为x1=2,x2=5,
∴的解为y1=2,y2=5,即x+3=2或x+3=5,
∴x3=﹣1,x4=2,
∴关于x的一元二次方程m(x﹣h+3)2=k的解是x3=﹣1,x4=2,
故答案为:x3=﹣1,x4=2.
15.【解答】解:取AB的中点F,连接NF,MF,
∵∠CAB+∠CBA=90°,
∵点M是AD的中点,
∴MF是△ABD的中位线,
∴,MF∥BD,
∴∠AFM=∠CBA,
∵NF是△ABE的中位线,
∴,NF∥AE,
∴∠BFN=∠BAC,
∴∠BFN+∠AFM=∠BAC+∠CBA=90°,
∴∠MFN=90°,
∴MN2=MF2+NF2,
∴MN2=32+22=13,
∴.
故答案为:.
16.【解答】解:(1)根据题意,得,
解得x=2或x=﹣2(舍去),
则y=x=2,
∴直线y1和双曲线y2的交点坐标为(2,2).
(2)如图,延长AC和DB分别交y轴于点E和点F.
则OF=BF,OE=AE,即△AOE和△BOF都是等腰直角三角形.
设AE=OE=m,则,
∴.
同理设BF=OF=n,则,
∴.
又∵,
∴,两边同时平方得.
在Rt△COE中,,
同理,
∴,
故答案为:(1)(2,2);(2)8.
三、解答题
17.【解答】解:(1)原式=(53)
=2
;
(2)原式=1﹣2
=1.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)50,40
5÷10%=50(人),
20÷50=40%,即m=40,
∴本次接受调查的学生人数为50人;图1中m的值为40;
(2)这组学生平均每天睡眠时间数据的平均数为:7×20%+8×40%+7×30%+7×10%=7.7;
将这50个数据从小到大排列后,处在中间位置的两个数都是6;
答:这组数据的平均数是7.7,中位数是2;
(3)1200×(40%+20%)=720(人),
答:全校学生平均每天睡眠时间不低于8h的人数约为720人
20.【解答】解:(1)由条件可知
,
∴BC的长度为;
(2)直角三角形,理由如下:
∵,
,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
21.【解答】解:(1)∵a,b2,
∴a+b22=2,ab=(2)(2)=1,
∴a2+b2﹣ab
=(a+b)2﹣3ab
=(2)2﹣3×1
=20﹣3
=17;
(2)∵,
∴23,
∴42<5,
∴02<1,
∴m=4,n2,
∴48.
22.【解答】解:(1)将点B(2,0)代入y=k1x+2得k1=﹣1,
所以y=﹣x+2,
∴点A的坐标为(0,2),
∴OA=OB,
∴∠ABO=45°;
(2)连接OC、OE,过点C作 CF⊥x轴,如答图所示;
∵∠OCE=45°,CO=CE,
∴∠COE=67.5°,
∵∠ABO=45°,
∴∠BCO=180°﹣∠COB﹣∠CBO=180°﹣67.5°﹣45°=67.5°,
∴BC=BO=2,
∴∠FCB=∠OCB∠OCE=45°=∠ABO,
∴在等腰Rt△CFB 中,,
∴OF=OB﹣BF=2,
∴C(2,),
将C(2,)代入得,
∴反比例函数表达式为.
23.【解答】解:(1)设C点的坐标是(m,2),
∵一次函数y1=﹣x+3的图象与反比例函数y2(x>0)的图象交于点C和点D,
∴﹣m+3=2,
解得:m=1,
∴C(1,2),
∴2,
解得:k=2,
∴y2(x>0),
令x+3,
解得:x1=1,x2=2,
经检验:x1=1,x2=2是此方程的根,
∴y=﹣2+3=1,
∴D(2,1);
故反比例函数的解析式为y2(x>0)、点D的坐标为(2,1);
(2)当y=0时,一次函数y1=﹣x+3=0,
∴x=3,
∴OA=3,
∵PQ∥x轴交直线AB于点Q,以A、P、Q、O为顶点的四边形为平行四边形,
∴PQ=OA=3,
∵点P是反比例函数上的一点,
∴设P(m,),
∵PQ∥x轴,
∴yQ,
∴﹣x+3,
解得:xQ=3,
∵PQ=3,
∴|xP﹣xQ|=3,
∴|m﹣(3)|=3,
∴m﹣(3)=3或m﹣(3)=﹣3,
当m﹣(3)=3时,
解得m1=3,m2=3,
经检验:m1=3,m2=3是此方程的根;
当m﹣(3)=﹣3时,
∴m2+2=0,
∴m不存在;
当m=3时,
yP3;
当m=3时,
yP3;
∴P的坐标为(3,3)或(3,3).
24.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
25.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BE,BF分别为边AD,CD上的高,
∴AD⊥BE,∠BFC=90°,
∴BE⊥BC,
∴∠EBC=90°=∠BFC,
∴∠EBF+∠CBF=90°=∠C+∠CBF,
∴∠EBF=∠C;
(2)证明:如图2,延长EF,BC交于点H,
∵BF=EF,
∴∠FEB=∠FBE,
∵∠EBC=90°,
∴∠FBH=∠FHB,
∴BF=FH,
∴EF=FH,
∵AD∥BC,
∴∠ADC=∠DCH,
在△EDF和△HCF中,
,
∴△EDF≌△HCF(AAS),
∴DF=CF;
(3)解:分两种情况:
①如图3,点P在x轴的上方,过点P作PG⊥x轴于G,
∵点C坐标为,
∴BC,
∵BF⊥CD,DF=CF,
∴BD=BC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴△BED是等腰直角三角形,
∴BE=DE=1,
∴S△BED1×1,
∵S△BCP=S△BDE,
∴ PG,
∴PG,
∵E(0,1),C(,0),
设直线CE的解析式为:y=kx+b,
∴,
解得:,
∴直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
如图4,P在x轴的下方,过点P作PG⊥x轴于G,
由①可知:PG,直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
综上,点P的坐标为(1,)或(1,).
21世纪教育网(www.21cnjy.com)
同课章节目录
