浙教版2024—2025学年八年级下学期数学期末总复习综合训练(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末总复习综合训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 745.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 21:00:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末总复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
2.下列图标中,是中心对称图形的是( )
A. B. C. D.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
5.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
6.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
7.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
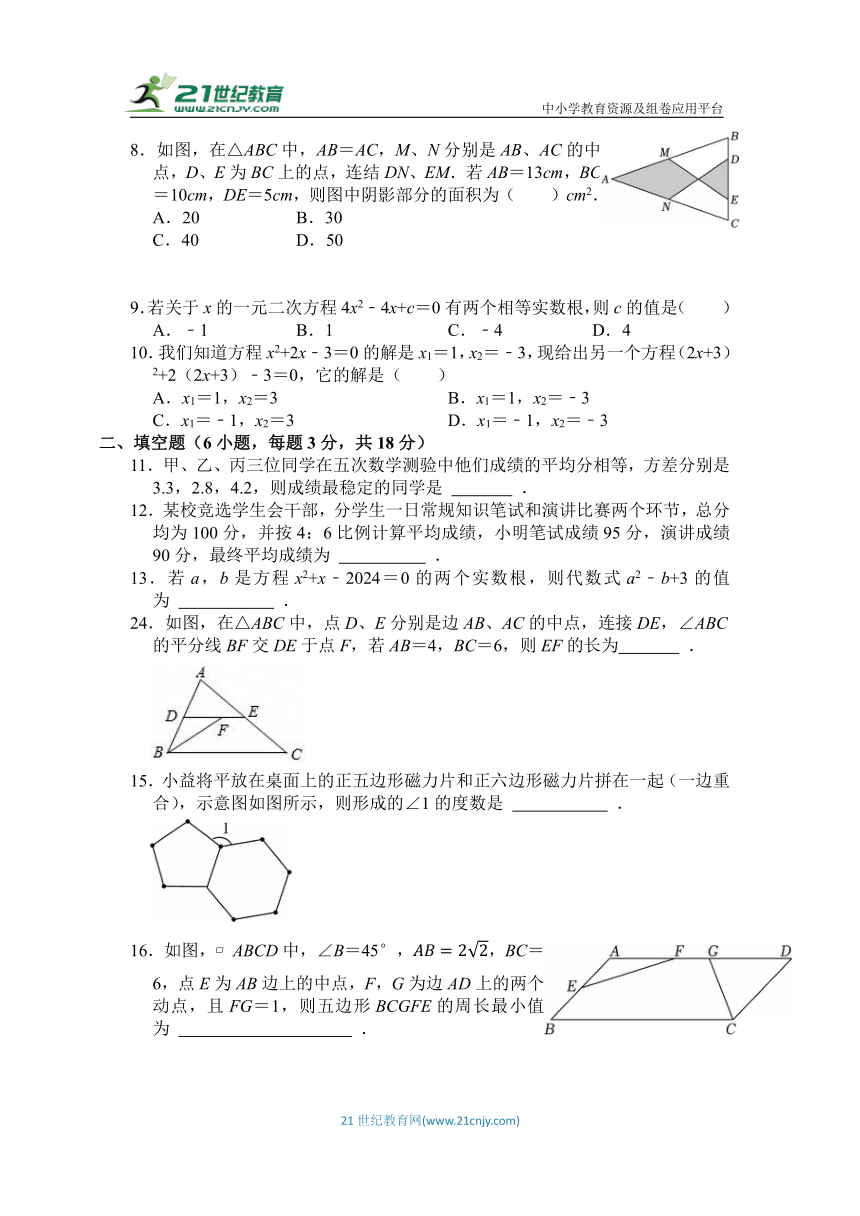
8.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30
C.40 D.50
9.若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1 B.1 C.﹣4 D.4
10.我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )
A.x1=1,x2=3 B.x1=1,x2=﹣3
C.x1=﹣1,x2=3 D.x1=﹣1,x2=﹣3
二、填空题(6小题,每题3分,共18分)
11.甲、乙、丙三位同学在五次数学测验中他们成绩的平均分相等,方差分别是3.3,2.8,4.2,则成绩最稳定的同学是 .
12.某校竞选学生会干部,分学生一日常规知识笔试和演讲比赛两个环节,总分均为100分,并按4:6比例计算平均成绩,小明笔试成绩95分,演讲成绩90分,最终平均成绩为 .
13.若a,b是方程x2+x﹣2024=0的两个实数根,则代数式a2﹣b+3的值为 .
24.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为 .
15.小益将平放在桌面上的正五边形磁力片和正六边形磁力片拼在一起(一边重合),示意图如图所示,则形成的∠1的度数是 .
16.如图, ABCD中,∠B=45°,,BC=6,点E为AB边上的中点,F,G为边AD上的两个动点,且FG=1,则五边形BCGFE的周长最小值为 .
第II卷
浙教版2024—2025学年八年级下学期数学期末总复习综合训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
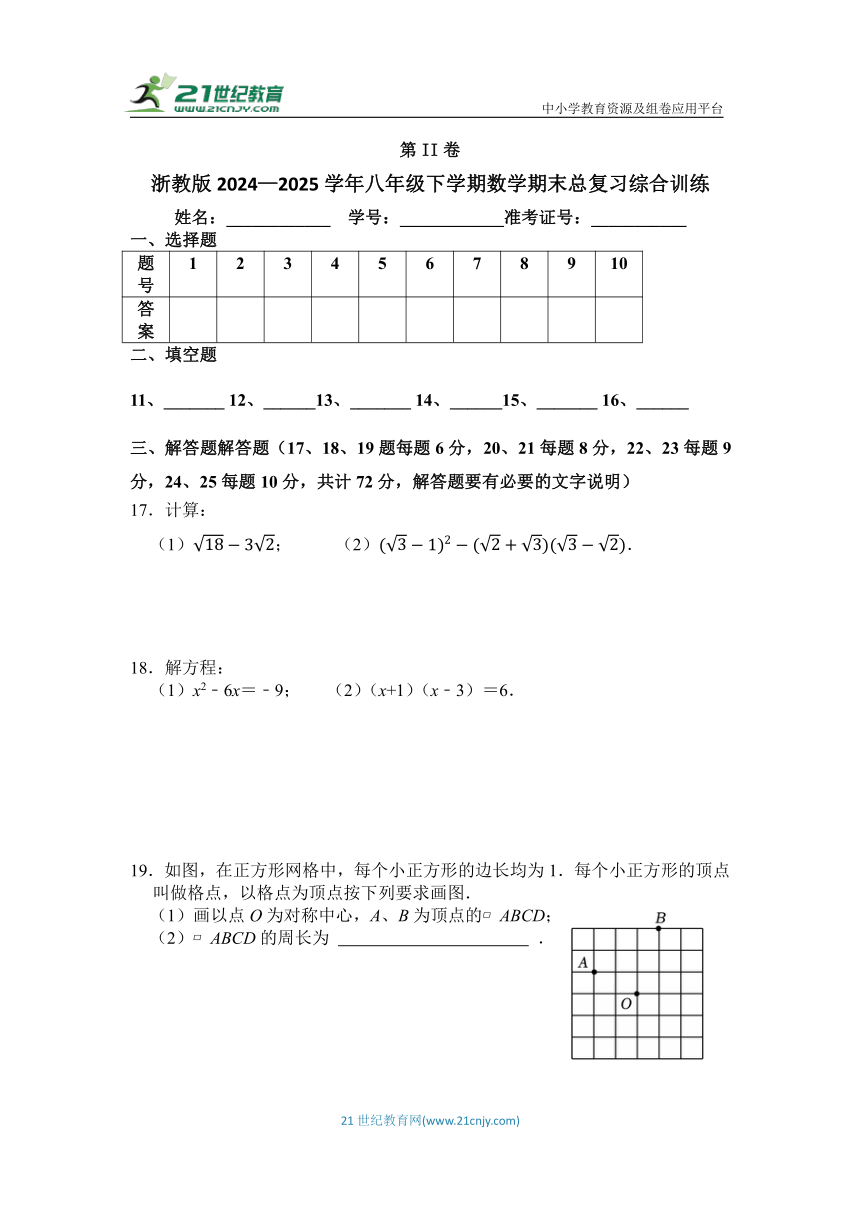
19.如图,在正方形网格中,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,以格点为顶点按下列要求画图.
(1)画以点O为对称中心,A、B为顶点的 ABCD;
(2) ABCD的周长为 .
20.设函数,函数y2=k2x+b(k1,k2,b是常数,k1≠0,k2≠0).若函数y1和函数y2的图象交于点A(2,m),B(3,2)
(1)求m的值.
(2)求函数y1,y2的表达式.
(3)请直接写出当y1>y2时,x的取值范围.
21.已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+3=0.
(1)若该方程有一个根是﹣2,求k的值.
(2)若该方程有两个实数根,求k的取值范围.
(3)若该方程的两个实数根x1,x2满足(x1﹣1)(x2﹣1)=14,求k的值.
22.东新社区为了解决社区停车难的问题,利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示.已知AD=50m,AB=30m,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x米的道路.已知铺花砖的面积(即阴影面积)为800m2.
(1)求道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10120元,同时尽可能让利于居民?
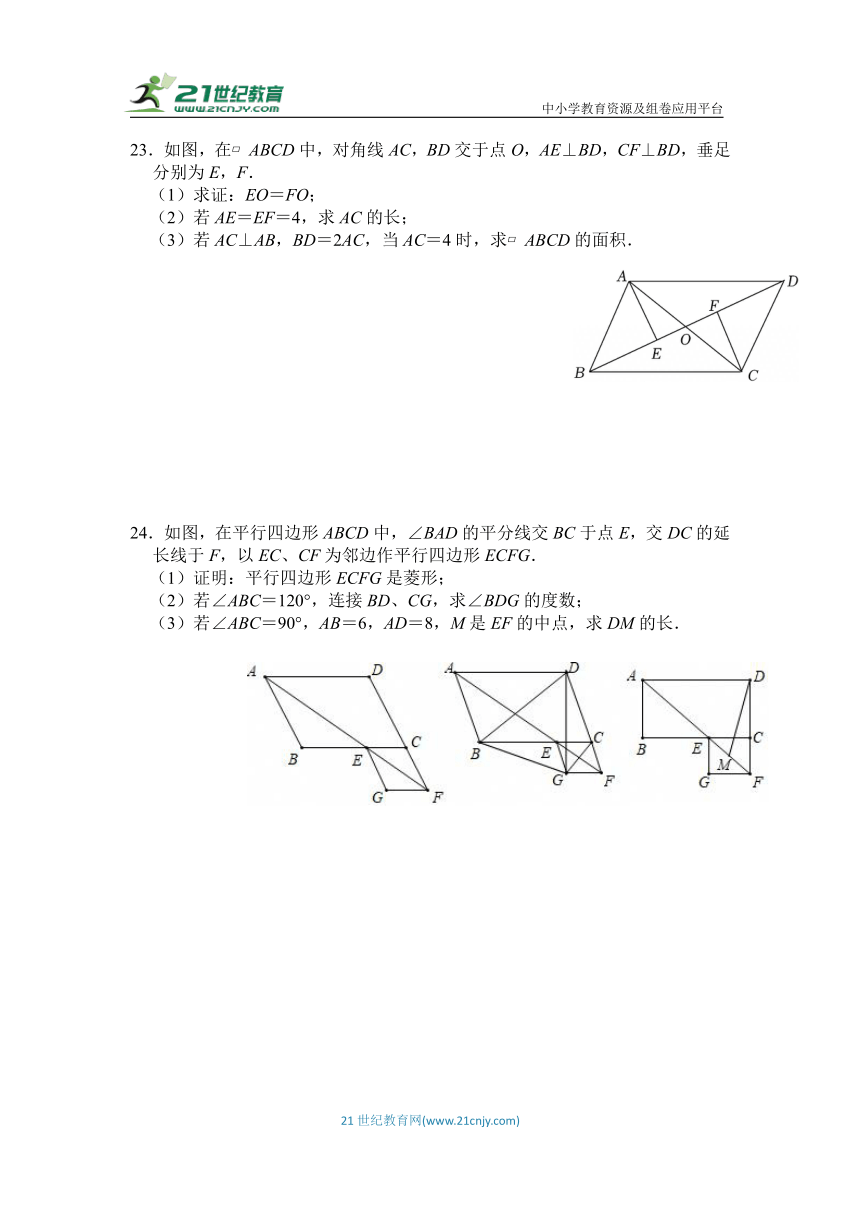
23.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
24.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.
(1)证明:平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
25.如图,已知直线y=2x分别与双曲线y,y(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
参考答案
选择题
1—10:CBCBC CCBBD
二、填空题
11.【解答】解:∵S甲2=3.3,S乙2=2.8,S丙2=4.2,
∴S丙2>S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
12.【解答】解:(95×4+90×6)÷(4+6)=92(分),
即最终平均成绩为92分.
故答案为:92分.
13.【解答】解:∵a,b是方程x2+x﹣2024=0的两个实数根,
∴a2+a﹣2024=0,a+b=﹣1,
∴a2=2024﹣a,
∴a2﹣b+3
=2024﹣a﹣b+3
=2024﹣(a+b)+3
=2024+1+3
=2028.
故答案为:2028.
14.【解答】解:∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DEBC=3,
∴∠DFB=∠HBF,
∵BF平分∠ABC,
∴∠DBF=∠CBF,
∴∠DFB=∠DBF,
∴DB=DFAB=2,
∴EF=DE﹣DF=1,
故答案为:1.
15.【解答】解:如图所示:
∵正五边形的内角度数为:(5﹣2)×180°=108°,
∴∠2=108°,
∵正六边形的内角度数为:(6﹣2)×180°=120°,
∴∠3=120°,
∵∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣108﹣120=132°.
故答案为:132°.
16.【解答】解:∵AB,点E为AB边上的中点,
∴AE=BE,
∵BC=6,FG=1,
∴五边形BCGFE的周长=BC+CG+FG+EF+BE=6+CG+1+EF7CG+EF,
在BC上截取CC'=FG=1,连接FC',作点E关于直线AD的对称点E',连接E'F,E'C',
则四边形FGCC'是平行四边形,EF=E'F,
∴C'F=CG,
∴五边形BCGFE的周长=7CG+EF=7C'F+E'F≥7C'E',
因此只要求出C'E'即可求出五边形BCGFE的周长最小值,
令E'E的延长线交BC于点H,
则∠E'HC=90°,
∵BE,∠B=45°,
∴EH=BH=1,
∴E'H=3,HC'=BC﹣BH﹣CC'=4,
在Rt△E'C'H中.
由勾股定理,得C'E'5,
∴五边形BCGFE的周长最小值为:75=12,
故答案为:12.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】(1)如图, ABCD即为所求.
(2)由勾股定理得,AB=CD,BC=AD,
∴ ABCD的周长为AB+CD+BC+AD.
故答案为:.
20.【解答】解:(1)由题意,∵B(3,2)在函数y1上,
∴k1=3×2=6.
∴y1.
又A(2,m)在函数y1上,
∴2m=6.
∴m=3.
(2)由题意,根据(1)得,y1,A(2,3),
又B(3,2),
∴.
∴.
∴y2=﹣x+5.
(3)由题意,在同一坐标系中画出y1和y2=﹣x+5的图象如下,
∵当y1>y2时,x的取值范围即为反比例函数的图象在一次函数图象上方时对应的自变量的取值范围,
又A(2,3),B(3,2),
∴当y1>y2时,0<x<2或x>3.
21.【解答】解:(1)x=﹣2时,4﹣2(k﹣1)×(﹣2)+k2+3=0,
整理得k2+4k+3=0,
解得:k=﹣1或﹣3.
(2)根据题意得Δ=(2k﹣2)2﹣4(k2+3)≥0,
解得k≤﹣1;
(3)根据题意得x1+x2=2k﹣2,x1x2=k2+3,
∵(x1﹣1)(x2﹣1)=14,
∴x1x2﹣(x1+x2)+1=14,
即k2+3﹣(2k﹣2)+1=14,
整理得k2﹣2k﹣8=0,解得k1=﹣2,k2=4,
∵k≤﹣1,
∴k=﹣2.
22.【解答】解:(1)道路的宽为x米,
由题意得:(50﹣2x)(30﹣2x)=800,
整理得:x2﹣40x+175=0,
解得:x1=35(不合题意,舍去),x2=5,
答:道路的宽是5米;
(2)设每个车位的月租金上涨y元时,停车场的月租金收入为10120元,
由题意得:(200+y)(50)=10120,
整理得:y2﹣50y+600=0,
解得:y1=20,y2=30,
∵尽可能让利于居民,
∴y=20,
答:每个车位的月租金上涨20元时,停车场的月租金收入为10120元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB﹣BE=OD﹣DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB2,
∴ ABCD的面积=AB AC=24=8.
24.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
25.【解答】解:(1)过点Q作QE⊥x轴,垂足为E,过点P作PF⊥x轴,垂足为F,如图1,
联立,
解得:或.
∵x>0,
∴点P的坐标为(2,4).
∴OF=2,PF=4.
∵QE⊥x轴,PF⊥x轴,
∴QE∥PF.
∵OP=2OQ,
∴OF=2OE=2,PF=2EQ=4.
∴OE=1,EQ=2.
∴点Q的坐标为(1,2).
∵点Q(1,2)在双曲线y上,
∴k=1×2=2.
∴k的值为2;
(2)如图2,
设点A的坐标为(a,b),
∵点A(a,b)在双曲线y上,
∴b.
∵.AB∥x轴,AC∥y轴,
∴xC=xA=a,yB=yA=b.
∵点B、C在双曲线y上,
∴xB,yC.
∴点B的坐标为(,),点C的坐标为(a,).
∴AB=aa,AC.
∴S△ABCAB AC
.
∴在点A运动过程中,△ABC的面积不变,始终等于.
(3)①AC为平行四边形的一边,
Ⅰ.当点B在点Q的右边时,如图3,
∵四边形ACBD是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴.
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b.
∴点A的坐标为(2,).
Ⅱ.当点B在点Q的左边且点C在点Q的右边时,如图4,
∵四边形ACDB是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴,
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b4.
∴点A的坐标为(2,4);
②AC为平行四边形的对角线,
此时点B、点C都在点Q的左边,如图5,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴yD=yC.
∴xD.
∴CDa.
∵AB=a,
∴a.
解得:a=±.
经检验:a=±是该方程的解.
∵a>0,
∴a.
∴b4.
∴点A的坐标为(,4).
综上所述:当点A、B、C、D为顶点的四边形为平行四边形时,此时点A的坐标为(2,)或(2,4)或(,4).
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末总复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
2.下列图标中,是中心对称图形的是( )
A. B. C. D.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
5.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
6.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
7.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
8.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30
C.40 D.50
9.若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1 B.1 C.﹣4 D.4
10.我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )
A.x1=1,x2=3 B.x1=1,x2=﹣3
C.x1=﹣1,x2=3 D.x1=﹣1,x2=﹣3
二、填空题(6小题,每题3分,共18分)
11.甲、乙、丙三位同学在五次数学测验中他们成绩的平均分相等,方差分别是3.3,2.8,4.2,则成绩最稳定的同学是 .
12.某校竞选学生会干部,分学生一日常规知识笔试和演讲比赛两个环节,总分均为100分,并按4:6比例计算平均成绩,小明笔试成绩95分,演讲成绩90分,最终平均成绩为 .
13.若a,b是方程x2+x﹣2024=0的两个实数根,则代数式a2﹣b+3的值为 .
24.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为 .
15.小益将平放在桌面上的正五边形磁力片和正六边形磁力片拼在一起(一边重合),示意图如图所示,则形成的∠1的度数是 .
16.如图, ABCD中,∠B=45°,,BC=6,点E为AB边上的中点,F,G为边AD上的两个动点,且FG=1,则五边形BCGFE的周长最小值为 .
第II卷
浙教版2024—2025学年八年级下学期数学期末总复习综合训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.如图,在正方形网格中,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,以格点为顶点按下列要求画图.
(1)画以点O为对称中心,A、B为顶点的 ABCD;
(2) ABCD的周长为 .
20.设函数,函数y2=k2x+b(k1,k2,b是常数,k1≠0,k2≠0).若函数y1和函数y2的图象交于点A(2,m),B(3,2)
(1)求m的值.
(2)求函数y1,y2的表达式.
(3)请直接写出当y1>y2时,x的取值范围.
21.已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+3=0.
(1)若该方程有一个根是﹣2,求k的值.
(2)若该方程有两个实数根,求k的取值范围.
(3)若该方程的两个实数根x1,x2满足(x1﹣1)(x2﹣1)=14,求k的值.
22.东新社区为了解决社区停车难的问题,利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示.已知AD=50m,AB=30m,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x米的道路.已知铺花砖的面积(即阴影面积)为800m2.
(1)求道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10120元,同时尽可能让利于居民?
23.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
24.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.
(1)证明:平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
25.如图,已知直线y=2x分别与双曲线y,y(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
参考答案
选择题
1—10:CBCBC CCBBD
二、填空题
11.【解答】解:∵S甲2=3.3,S乙2=2.8,S丙2=4.2,
∴S丙2>S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
12.【解答】解:(95×4+90×6)÷(4+6)=92(分),
即最终平均成绩为92分.
故答案为:92分.
13.【解答】解:∵a,b是方程x2+x﹣2024=0的两个实数根,
∴a2+a﹣2024=0,a+b=﹣1,
∴a2=2024﹣a,
∴a2﹣b+3
=2024﹣a﹣b+3
=2024﹣(a+b)+3
=2024+1+3
=2028.
故答案为:2028.
14.【解答】解:∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DEBC=3,
∴∠DFB=∠HBF,
∵BF平分∠ABC,
∴∠DBF=∠CBF,
∴∠DFB=∠DBF,
∴DB=DFAB=2,
∴EF=DE﹣DF=1,
故答案为:1.
15.【解答】解:如图所示:
∵正五边形的内角度数为:(5﹣2)×180°=108°,
∴∠2=108°,
∵正六边形的内角度数为:(6﹣2)×180°=120°,
∴∠3=120°,
∵∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣108﹣120=132°.
故答案为:132°.
16.【解答】解:∵AB,点E为AB边上的中点,
∴AE=BE,
∵BC=6,FG=1,
∴五边形BCGFE的周长=BC+CG+FG+EF+BE=6+CG+1+EF7CG+EF,
在BC上截取CC'=FG=1,连接FC',作点E关于直线AD的对称点E',连接E'F,E'C',
则四边形FGCC'是平行四边形,EF=E'F,
∴C'F=CG,
∴五边形BCGFE的周长=7CG+EF=7C'F+E'F≥7C'E',
因此只要求出C'E'即可求出五边形BCGFE的周长最小值,
令E'E的延长线交BC于点H,
则∠E'HC=90°,
∵BE,∠B=45°,
∴EH=BH=1,
∴E'H=3,HC'=BC﹣BH﹣CC'=4,
在Rt△E'C'H中.
由勾股定理,得C'E'5,
∴五边形BCGFE的周长最小值为:75=12,
故答案为:12.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】(1)如图, ABCD即为所求.
(2)由勾股定理得,AB=CD,BC=AD,
∴ ABCD的周长为AB+CD+BC+AD.
故答案为:.
20.【解答】解:(1)由题意,∵B(3,2)在函数y1上,
∴k1=3×2=6.
∴y1.
又A(2,m)在函数y1上,
∴2m=6.
∴m=3.
(2)由题意,根据(1)得,y1,A(2,3),
又B(3,2),
∴.
∴.
∴y2=﹣x+5.
(3)由题意,在同一坐标系中画出y1和y2=﹣x+5的图象如下,
∵当y1>y2时,x的取值范围即为反比例函数的图象在一次函数图象上方时对应的自变量的取值范围,
又A(2,3),B(3,2),
∴当y1>y2时,0<x<2或x>3.
21.【解答】解:(1)x=﹣2时,4﹣2(k﹣1)×(﹣2)+k2+3=0,
整理得k2+4k+3=0,
解得:k=﹣1或﹣3.
(2)根据题意得Δ=(2k﹣2)2﹣4(k2+3)≥0,
解得k≤﹣1;
(3)根据题意得x1+x2=2k﹣2,x1x2=k2+3,
∵(x1﹣1)(x2﹣1)=14,
∴x1x2﹣(x1+x2)+1=14,
即k2+3﹣(2k﹣2)+1=14,
整理得k2﹣2k﹣8=0,解得k1=﹣2,k2=4,
∵k≤﹣1,
∴k=﹣2.
22.【解答】解:(1)道路的宽为x米,
由题意得:(50﹣2x)(30﹣2x)=800,
整理得:x2﹣40x+175=0,
解得:x1=35(不合题意,舍去),x2=5,
答:道路的宽是5米;
(2)设每个车位的月租金上涨y元时,停车场的月租金收入为10120元,
由题意得:(200+y)(50)=10120,
整理得:y2﹣50y+600=0,
解得:y1=20,y2=30,
∵尽可能让利于居民,
∴y=20,
答:每个车位的月租金上涨20元时,停车场的月租金收入为10120元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB﹣BE=OD﹣DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB2,
∴ ABCD的面积=AB AC=24=8.
24.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
25.【解答】解:(1)过点Q作QE⊥x轴,垂足为E,过点P作PF⊥x轴,垂足为F,如图1,
联立,
解得:或.
∵x>0,
∴点P的坐标为(2,4).
∴OF=2,PF=4.
∵QE⊥x轴,PF⊥x轴,
∴QE∥PF.
∵OP=2OQ,
∴OF=2OE=2,PF=2EQ=4.
∴OE=1,EQ=2.
∴点Q的坐标为(1,2).
∵点Q(1,2)在双曲线y上,
∴k=1×2=2.
∴k的值为2;
(2)如图2,
设点A的坐标为(a,b),
∵点A(a,b)在双曲线y上,
∴b.
∵.AB∥x轴,AC∥y轴,
∴xC=xA=a,yB=yA=b.
∵点B、C在双曲线y上,
∴xB,yC.
∴点B的坐标为(,),点C的坐标为(a,).
∴AB=aa,AC.
∴S△ABCAB AC
.
∴在点A运动过程中,△ABC的面积不变,始终等于.
(3)①AC为平行四边形的一边,
Ⅰ.当点B在点Q的右边时,如图3,
∵四边形ACBD是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴.
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b.
∴点A的坐标为(2,).
Ⅱ.当点B在点Q的左边且点C在点Q的右边时,如图4,
∵四边形ACDB是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴,
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b4.
∴点A的坐标为(2,4);
②AC为平行四边形的对角线,
此时点B、点C都在点Q的左边,如图5,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴yD=yC.
∴xD.
∴CDa.
∵AB=a,
∴a.
解得:a=±.
经检验:a=±是该方程的解.
∵a>0,
∴a.
∴b4.
∴点A的坐标为(,4).
综上所述:当点A、B、C、D为顶点的四边形为平行四边形时,此时点A的坐标为(2,)或(2,4)或(,4).
21世纪教育网(www.21cnjy.com)
同课章节目录
