浙教版2024—2025学年八年级下册数学期末复习强化训练(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下册数学期末复习强化训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 819.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:53:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下册数学期末复习强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.“二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )
A. B. C. D.
2.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
3.用反证法证明“三角形中至少有一个内角大于或等于60°时,应假设( )
A.三角形的二个内角小于60° B.三角形的三个内角都小于60°
C.三角形的二个内角大于60° D.三角形的三个内角都大于60°
4.一元二次方程x2﹣4x=5配方后变形为( )
A.(x﹣4)2=5 B.(x﹣2)2=5
C.(x﹣4)2=9 D.(x﹣2)2=9
5.已知,则的值为( )
A. B. C.2025 D.4050
6.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
7.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2) B.图象位于第二、四象限
C.x<0,则y>0 D.y随x的增大而增大
8.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
9.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
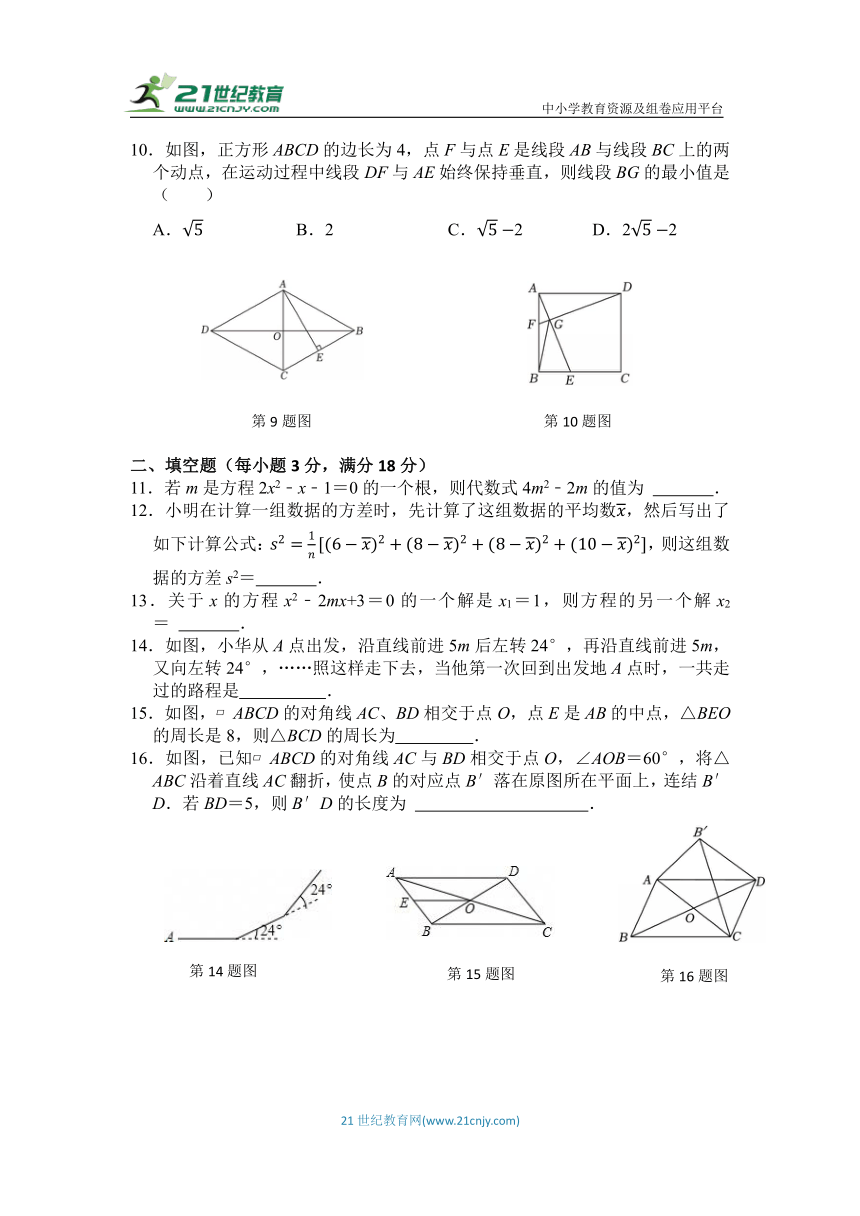
10.如图,正方形ABCD的边长为4,点F与点E是线段AB与线段BC上的两个动点,在运动过程中线段DF与AE始终保持垂直,则线段BG的最小值是( )
A. B.2 C.2 D.22
二、填空题(每小题3分,满分18分)
11.若m是方程2x2﹣x﹣1=0的一个根,则代数式4m2﹣2m的值为 .
12.小明在计算一组数据的方差时,先计算了这组数据的平均数,然后写出了如下计算公式:,则这组数据的方差s2= .
13.关于x的方程x2﹣2mx+3=0的一个解是x1=1,则方程的另一个解x2= .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
第II卷
浙教版2024—2025学年八年级下册数学期末复习强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
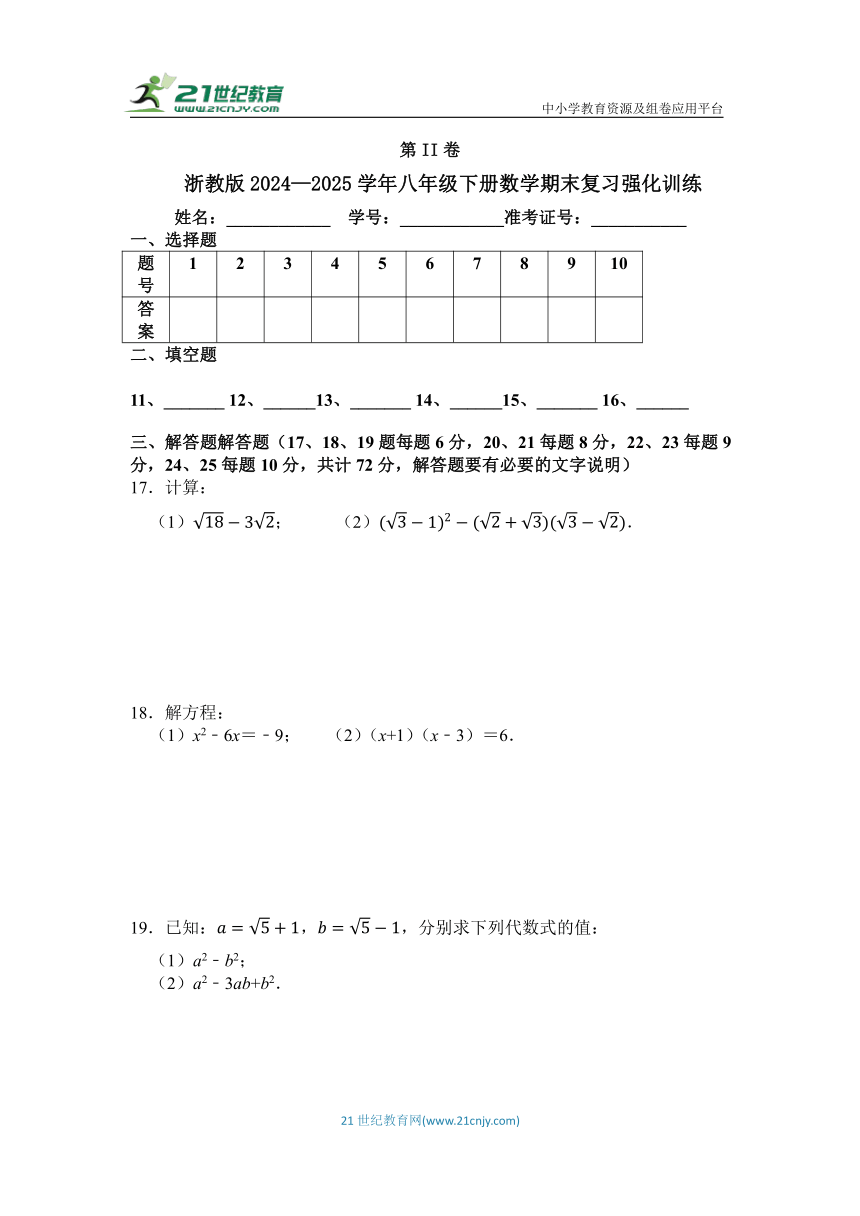
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.已知:,,分别求下列代数式的值:
(1)a2﹣b2;
(2)a2﹣3ab+b2.
20.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
21.已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程一定有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
22.诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利1200元.
(3)要想平均每天盈利2000元,可能吗?请说明理由.
23.如图1,在 ABCD中,点E为AD中点,BA,CE的延长线交于点F.
(1)求证:BA=AF.
(2)若∠BCF=∠DCF时,记AB与CD之间的距离为h1,AD与BC之间的距离为h2,求h1:h2的值.
(3)如图2,连结AC,BD,在(2)的条件下,求证:AC2+BD2=10AB2.
24.阅读理解:
材料1:若代数式ax2+bx+c=0(a≠0)在实数范围内可因式分解为ax2+bx+c=a(x﹣x1)(x﹣x2).
令a(x﹣x1)(x﹣x2)=0我们可以得到该方程的两个解为x1,x2,则我们也可以得到关于x的方程ax2+bx+c=0(a≠0)的两个解也为x1,x2,那么我们称这两个解为“共生根”,由ax2+bx+c=a(x﹣x1)(x﹣x2)得到两个“共生根”与各项系数之间的关系为:,.
材料2:已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,根据材料1求的值.
解:由题知m,n是方程足m2﹣m﹣1=0的两个不相等的“共生根”,
根据材料1得:m+n=1,mn=﹣1,
∴.
解决以下问题:
(1)方程x2﹣4x﹣3=0的两个“共生根”为x1,x2,则x1+x2= ,x1x2= ;
(2)已知实数m,n满足m2﹣3m+1=0,n2﹣3n+1=0,且m≠n,求的值;
(3)已知实数p,q满足p2=3p+2,2q2=1﹣3q,且p q≠1,求.
25.如图,在平面直角坐标系中,点A是直线l:,点B在x轴正半轴上.以OA,OB(OA<OB),点P关于直线AB的对称点为Q,连接AQ,线段AQ与x轴的交点为C.
(1)求证:AC=BC;
(2)当AC⊥OB时,求;
(3)若B点坐标为(4,0),求出当△BCQ是等腰三角形时P点的坐标.
参考答案
一、选择题
1—10:DBBDBADDAD
二、填空题
11.【解答】解:把x=m代入方程2x2﹣x﹣1=0,可得:2m2﹣m=1,
4m2﹣2m=2(2m2﹣m)=2×1=2.
故答案为:2.
12.【解答】解:∵计算公式:,
∴这组数据为6、8、8、10,
∴这组数据的平均数为:(6+8+8+10)=8.
∴S2[(6﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=2.
故答案为:2.
13.【解答】解:根据根与系数的关系得x1x2=3,
而x1=1,
所以x2=3.
故答案为:3.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)∵,,
∴,,
∴;
(2)∵,,
∴,,
∴a2﹣3ab+b2
=(a2+2ab+b2)﹣5ab
=(a+b)2﹣5ab
=0.
20.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
21.【解答】(1)证明:
∵方程x2﹣(m+2)x+(2m﹣1)=0,
∴Δ=(m+2)2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+4+4=(m﹣2)2+4>0,
∴方程一定有两个不相等的实数根;
(2)解:把x=1代入方程可得1﹣(m+2)+2m﹣1=0,解得m=2,
∴方程为x2﹣4x+3=0,解得x=1或x=3,
∴方程的另一根为x=3,
当边长为1和3的线段为直角三角形的直角边时,则斜边,此时直角三角形的周长=4,
当边长为3的直角三角形斜边时,则另一直角边2,此时直角三角形的周长=4+2,
综上可知直角三角形的周长为4或4+2.
22.【解答】解:(1)设每件童装降价x元时,每天可销售(20+2x)件,每件盈利(40﹣x)元,
故答案为:(20+2x),(40﹣x);
(2)根据题意,得:(20+2x)(40﹣x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价20元,平均每天盈利1200元;
(3)不能,理由如下:
(20+2x)(40﹣x)=2000,
整理,得:x2﹣30x+600=0,
∵Δ=(﹣30)2﹣4×600=﹣1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利2000元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠F=∠ECD,∠FAE=∠D,
∵E为AD的中点,
∴AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AB=AF;
(2)解:由(1)知AB∥CD,
∴∠F=∠DCE,
∵∠BCF=∠DCF,
∴∠F=∠BCF,
∴BF=BC,
∵AB=AF,
∴BC=2AB,
∵,
∴h1:h2=BC:AB=2;
(3)证明:过点A作AM⊥BC于点M,DN⊥BC,交BC的延长线于点N,
∵AB∥CD,
∴∠B=∠DCN,
∵AB=CD,∠AMB=∠DNC,
∴△ABM≌△DCN(AAS),
∴BM=CN,AM=DN=h2,
在Rt△DBN中,DB2=DN2+BN2=DN2+(BC+CN)2,
在Rt△ACM中,AC2=AM2+(BC﹣BM)2=DN2+(BC﹣CN)2,
∴AC2+BD2=2DN2+(BC+CN)2+(BC﹣CN)2
=2DN2+2BC2+2CN2
=2DC2+2BC2,
由(2)知,BC=2AB,
∴AC2+BD2=2AB2+8AB2=10AB2.
24.【解答】解:(1)根据题意得:x1+x2=4,x1x2=﹣3,
故答案为:4,﹣3;
(2)∵m2﹣3m+1=0,n2﹣3n+1=0,且m≠n,
∴m,n可看作方程x2﹣3x+1=0的两个不相等的“共生根”,
∴m+n=3,mn=1,
∴,
∴;
(3)∵2q2=1﹣3q,
∴1﹣3q﹣2q2=0,
∴,
∵p2=3p+2,即p2﹣3p﹣2=0,且p q≠1,
∴p,可看作方程x2﹣3x﹣2=0的两个不相等的“共生根”,
∴,,
∴.
25.【解答】(1)证明:∵四边形AOBP是平行四边形,
∴AP∥OB,
∴∠BAP=∠ABO,
∵点P关于直线AB的对称点为Q,
∴∠BAP=∠QAB,
∴∠QAB=∠ABO,
∴AC=BC.
(2)解:过点P作PM⊥x轴于点M,
在平行四边形OAPB中,OA=BP,
∴∠AOC=∠PBM,
在△AOC和△PBM中,
,
∴△AOC≌△PBM(AAS),
∵四边形AOBP是平行四边形,AC⊥OB,
∴OB=AP,AC⊥AP,
设A点坐标(3a,4a),
∴OC=7a,AC=4a,
∵AC=BC,
∴BC=AC=4a,AP=AQ=8a,PM=4a,
∴,
,
∴..
(3)解:过点A作AN垂直x轴于点N,
设AN=4m,ON=8m,
当点A在第一象限时:
①当BC=BQ时,
BC=5m,OC=4﹣4m,
∵AC=BC,
∴AC=5m,
∴在Rt△ACN中,AN2+CN5=AC2,
∴(4m)3+(4﹣8m)4=(5m)2,
解得,(舍去),
∴;
②当BC=CQ时,
∵OB=AQ,AC=BC,
∴OB﹣BC=AQ﹣AC,即CQ=OC,
∴OC=BC=BC=AC=2,
∴CN=8﹣3m,
∴在Rt△ACN中,AN2+CN8=AC2,
即(4m)8+(2﹣3m)8=22,
解得,
∴;
③当CQ=BQ时,
OC=CQ=BQ=5m,
∴CN=2m,AC=BC=4﹣2m,
∴在Rt△ACN中,AN2+CN2=AC3,
即(2m)2+(5m)2=(4﹣6m)2,
解得(舍去),,
∴;
综上,P点坐标(或或.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下册数学期末复习强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.“二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )
A. B. C. D.
2.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
3.用反证法证明“三角形中至少有一个内角大于或等于60°时,应假设( )
A.三角形的二个内角小于60° B.三角形的三个内角都小于60°
C.三角形的二个内角大于60° D.三角形的三个内角都大于60°
4.一元二次方程x2﹣4x=5配方后变形为( )
A.(x﹣4)2=5 B.(x﹣2)2=5
C.(x﹣4)2=9 D.(x﹣2)2=9
5.已知,则的值为( )
A. B. C.2025 D.4050
6.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
7.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2) B.图象位于第二、四象限
C.x<0,则y>0 D.y随x的增大而增大
8.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
9.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
10.如图,正方形ABCD的边长为4,点F与点E是线段AB与线段BC上的两个动点,在运动过程中线段DF与AE始终保持垂直,则线段BG的最小值是( )
A. B.2 C.2 D.22
二、填空题(每小题3分,满分18分)
11.若m是方程2x2﹣x﹣1=0的一个根,则代数式4m2﹣2m的值为 .
12.小明在计算一组数据的方差时,先计算了这组数据的平均数,然后写出了如下计算公式:,则这组数据的方差s2= .
13.关于x的方程x2﹣2mx+3=0的一个解是x1=1,则方程的另一个解x2= .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
第II卷
浙教版2024—2025学年八年级下册数学期末复习强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.已知:,,分别求下列代数式的值:
(1)a2﹣b2;
(2)a2﹣3ab+b2.
20.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
21.已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程一定有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
22.诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利1200元.
(3)要想平均每天盈利2000元,可能吗?请说明理由.
23.如图1,在 ABCD中,点E为AD中点,BA,CE的延长线交于点F.
(1)求证:BA=AF.
(2)若∠BCF=∠DCF时,记AB与CD之间的距离为h1,AD与BC之间的距离为h2,求h1:h2的值.
(3)如图2,连结AC,BD,在(2)的条件下,求证:AC2+BD2=10AB2.
24.阅读理解:
材料1:若代数式ax2+bx+c=0(a≠0)在实数范围内可因式分解为ax2+bx+c=a(x﹣x1)(x﹣x2).
令a(x﹣x1)(x﹣x2)=0我们可以得到该方程的两个解为x1,x2,则我们也可以得到关于x的方程ax2+bx+c=0(a≠0)的两个解也为x1,x2,那么我们称这两个解为“共生根”,由ax2+bx+c=a(x﹣x1)(x﹣x2)得到两个“共生根”与各项系数之间的关系为:,.
材料2:已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,根据材料1求的值.
解:由题知m,n是方程足m2﹣m﹣1=0的两个不相等的“共生根”,
根据材料1得:m+n=1,mn=﹣1,
∴.
解决以下问题:
(1)方程x2﹣4x﹣3=0的两个“共生根”为x1,x2,则x1+x2= ,x1x2= ;
(2)已知实数m,n满足m2﹣3m+1=0,n2﹣3n+1=0,且m≠n,求的值;
(3)已知实数p,q满足p2=3p+2,2q2=1﹣3q,且p q≠1,求.
25.如图,在平面直角坐标系中,点A是直线l:,点B在x轴正半轴上.以OA,OB(OA<OB),点P关于直线AB的对称点为Q,连接AQ,线段AQ与x轴的交点为C.
(1)求证:AC=BC;
(2)当AC⊥OB时,求;
(3)若B点坐标为(4,0),求出当△BCQ是等腰三角形时P点的坐标.
参考答案
一、选择题
1—10:DBBDBADDAD
二、填空题
11.【解答】解:把x=m代入方程2x2﹣x﹣1=0,可得:2m2﹣m=1,
4m2﹣2m=2(2m2﹣m)=2×1=2.
故答案为:2.
12.【解答】解:∵计算公式:,
∴这组数据为6、8、8、10,
∴这组数据的平均数为:(6+8+8+10)=8.
∴S2[(6﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=2.
故答案为:2.
13.【解答】解:根据根与系数的关系得x1x2=3,
而x1=1,
所以x2=3.
故答案为:3.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)∵,,
∴,,
∴;
(2)∵,,
∴,,
∴a2﹣3ab+b2
=(a2+2ab+b2)﹣5ab
=(a+b)2﹣5ab
=0.
20.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
21.【解答】(1)证明:
∵方程x2﹣(m+2)x+(2m﹣1)=0,
∴Δ=(m+2)2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+4+4=(m﹣2)2+4>0,
∴方程一定有两个不相等的实数根;
(2)解:把x=1代入方程可得1﹣(m+2)+2m﹣1=0,解得m=2,
∴方程为x2﹣4x+3=0,解得x=1或x=3,
∴方程的另一根为x=3,
当边长为1和3的线段为直角三角形的直角边时,则斜边,此时直角三角形的周长=4,
当边长为3的直角三角形斜边时,则另一直角边2,此时直角三角形的周长=4+2,
综上可知直角三角形的周长为4或4+2.
22.【解答】解:(1)设每件童装降价x元时,每天可销售(20+2x)件,每件盈利(40﹣x)元,
故答案为:(20+2x),(40﹣x);
(2)根据题意,得:(20+2x)(40﹣x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价20元,平均每天盈利1200元;
(3)不能,理由如下:
(20+2x)(40﹣x)=2000,
整理,得:x2﹣30x+600=0,
∵Δ=(﹣30)2﹣4×600=﹣1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利2000元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠F=∠ECD,∠FAE=∠D,
∵E为AD的中点,
∴AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AB=AF;
(2)解:由(1)知AB∥CD,
∴∠F=∠DCE,
∵∠BCF=∠DCF,
∴∠F=∠BCF,
∴BF=BC,
∵AB=AF,
∴BC=2AB,
∵,
∴h1:h2=BC:AB=2;
(3)证明:过点A作AM⊥BC于点M,DN⊥BC,交BC的延长线于点N,
∵AB∥CD,
∴∠B=∠DCN,
∵AB=CD,∠AMB=∠DNC,
∴△ABM≌△DCN(AAS),
∴BM=CN,AM=DN=h2,
在Rt△DBN中,DB2=DN2+BN2=DN2+(BC+CN)2,
在Rt△ACM中,AC2=AM2+(BC﹣BM)2=DN2+(BC﹣CN)2,
∴AC2+BD2=2DN2+(BC+CN)2+(BC﹣CN)2
=2DN2+2BC2+2CN2
=2DC2+2BC2,
由(2)知,BC=2AB,
∴AC2+BD2=2AB2+8AB2=10AB2.
24.【解答】解:(1)根据题意得:x1+x2=4,x1x2=﹣3,
故答案为:4,﹣3;
(2)∵m2﹣3m+1=0,n2﹣3n+1=0,且m≠n,
∴m,n可看作方程x2﹣3x+1=0的两个不相等的“共生根”,
∴m+n=3,mn=1,
∴,
∴;
(3)∵2q2=1﹣3q,
∴1﹣3q﹣2q2=0,
∴,
∵p2=3p+2,即p2﹣3p﹣2=0,且p q≠1,
∴p,可看作方程x2﹣3x﹣2=0的两个不相等的“共生根”,
∴,,
∴.
25.【解答】(1)证明:∵四边形AOBP是平行四边形,
∴AP∥OB,
∴∠BAP=∠ABO,
∵点P关于直线AB的对称点为Q,
∴∠BAP=∠QAB,
∴∠QAB=∠ABO,
∴AC=BC.
(2)解:过点P作PM⊥x轴于点M,
在平行四边形OAPB中,OA=BP,
∴∠AOC=∠PBM,
在△AOC和△PBM中,
,
∴△AOC≌△PBM(AAS),
∵四边形AOBP是平行四边形,AC⊥OB,
∴OB=AP,AC⊥AP,
设A点坐标(3a,4a),
∴OC=7a,AC=4a,
∵AC=BC,
∴BC=AC=4a,AP=AQ=8a,PM=4a,
∴,
,
∴..
(3)解:过点A作AN垂直x轴于点N,
设AN=4m,ON=8m,
当点A在第一象限时:
①当BC=BQ时,
BC=5m,OC=4﹣4m,
∵AC=BC,
∴AC=5m,
∴在Rt△ACN中,AN2+CN5=AC2,
∴(4m)3+(4﹣8m)4=(5m)2,
解得,(舍去),
∴;
②当BC=CQ时,
∵OB=AQ,AC=BC,
∴OB﹣BC=AQ﹣AC,即CQ=OC,
∴OC=BC=BC=AC=2,
∴CN=8﹣3m,
∴在Rt△ACN中,AN2+CN8=AC2,
即(4m)8+(2﹣3m)8=22,
解得,
∴;
③当CQ=BQ时,
OC=CQ=BQ=5m,
∴CN=2m,AC=BC=4﹣2m,
∴在Rt△ACN中,AN2+CN2=AC3,
即(2m)2+(5m)2=(4﹣6m)2,
解得(舍去),,
∴;
综上,P点坐标(或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
