苏教版高一下册数学必修第二册 13.2.3 第2课时 直线与平面垂直 同步练习(含答案)
文档属性
| 名称 | 苏教版高一下册数学必修第二册 13.2.3 第2课时 直线与平面垂直 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 11:27:45 | ||
图片预览




文档简介
苏教版高一下册数学必修第二册-13.2.3 第2课时 直线与平面垂直-同步练习
[A 基础达标]
1.在空间中,下列命题正确的是( )
①平行于同一条直线的两条直线平行;
②垂直于同一条直线的两条直线平行;
③平行于同一个平面的两条直线平行;
④垂直于同一个平面的两条直线平行.
A.①③④ B.①④
C.① D.①②③④
2.过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC,若PA=PB=PC,则点O是△ABC的( )
A.垂心 B.外心
C.内心 D.重心
3.在三棱柱ABC A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是( )
A.30° B.45°
C.60° D.90°
4.在正方体ABCD A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.B1D1
C.A1D D.A1A
5.如图,下列4个正方体中,点A,B,M,N,Q分别为正方体的顶点或所在棱的中点,则在这4个正方体中,满足直线AB⊥平面MNQ的个数为( )
A.1 B.2
C.3 D.4
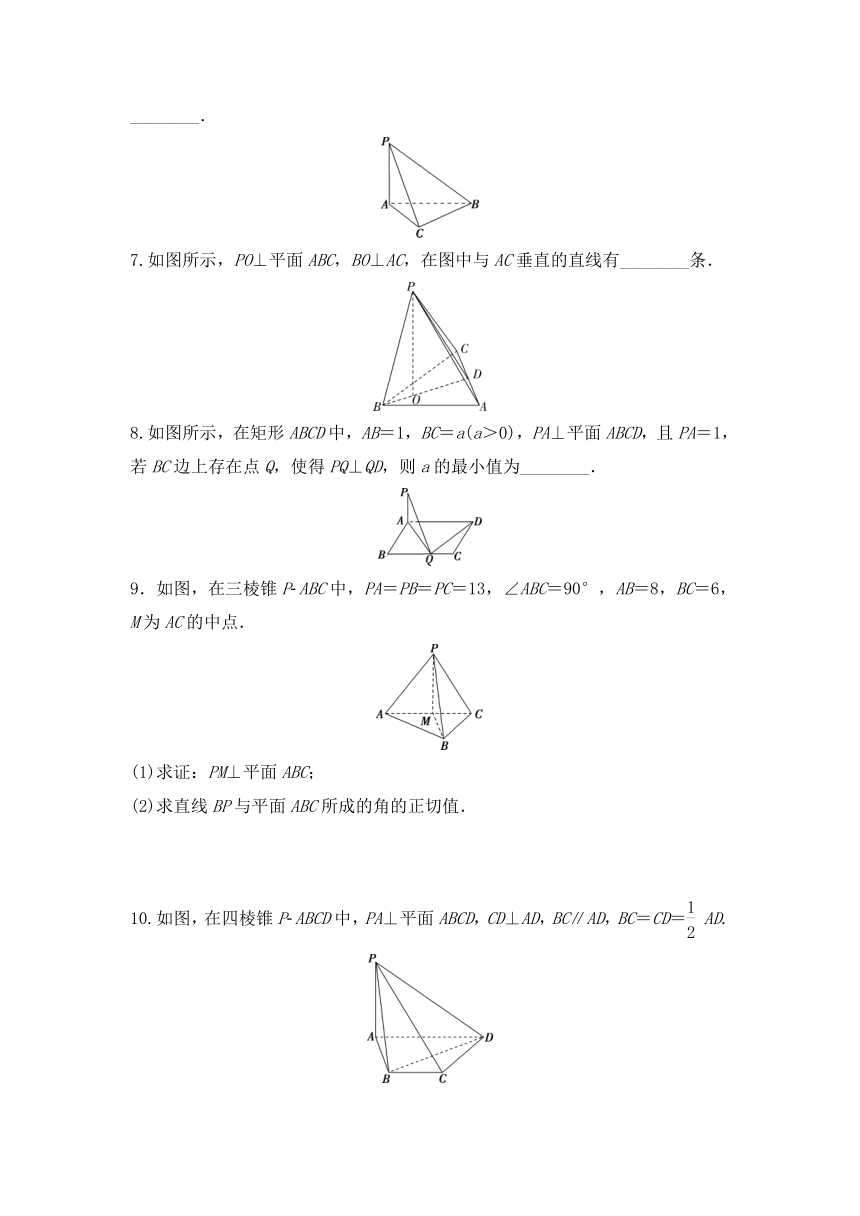
6.如图所示,PA⊥平面ABC,△ABC中BC⊥AC,则图中直角三角形的个数为________.
7.如图所示,PO⊥平面ABC,BO⊥AC,在图中与AC垂直的直线有________条.
8.如图所示,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1,若BC边上存在点Q,使得PQ⊥QD,则a的最小值为________.
9.如图,在三棱锥P ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
(1)求证:PM⊥平面ABC;
(2)求直线BP与平面ABC所成的角的正切值.
10.如图,在四棱锥P ABCD中,PA⊥平面ABCD,CD⊥AD,BC∥AD,BC=CD=AD.
(1)求证:CD⊥PD;
(2)求证:BD⊥平面PAB;
(3)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置;若不存在,请说明理由.
[B 能力提升]
11.(多选)已知α是一个平面,m,n是两条直线,有下列四个结论,正确的是( )
A.如果m∥α,m∥n,那么n∥α
B.如果m⊥α,n∥α,那么m⊥n
C.若直线m垂直于平面α内的无数条直线,则m⊥α
D.如果m⊥α,m∥n,那么n⊥α
12.(多选)如图所示,PA垂直于以AB为直径的圆所在的平面,点C为圆上异于点A,B的任意一点,则下列关系中正确的是( )
A.PA⊥BC B.AC⊥PB
C.BC⊥平面PAC D.PC⊥PB
13.(多选)如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现在沿着SE,SF,EF把这个正方形折成一个四面体,使G1,G2,G3重合,重合后的点记为G.给出下列关系,其中成立的为( )
A.SG⊥平面EFG B.SE⊥平面EFG
C.GF⊥SE D.EF⊥平面SEG
[C 拓展探究]
14.刘徽注《九章算术 商功》“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”如图一解释了由一个长方体得到“堑堵”“阳马”“鳖臑”的过程.堑堵是底面为直角三角形的直棱柱;阳马是一条侧棱垂直于底面且底面为矩形的四棱锥;鳖臑是四个面都为直角三角形的四面体.
在如图二所示由正方体得到的堑堵ABC A1B1C1中,当点P在下列三个位置:A1A中点、A1B中点、A1C中点时,分别形成的四面体P ABC中,鳖臑有( )
A.0个 B.1个
C.2个 D.3个
15.如图,在三棱锥P ABC中,棱PA垂直于平面ABC,∠ACB=90°.
(1)求证:BC⊥PC;
(2)若PA=AB=2,直线PC与平面ABC所成的角的正切值为,求直线AB与平面PBC所成的角的正弦值.
参考答案
[A 基础达标]
1.答案:B
2.解析:选B.因为PO⊥α,PA=PB=PC,可由射影定理得OA=OB=OC.
即点O是△ABC 的外心.
3.解析:选C.如图,取BC的中点E,连接AE,ED,AD,则AE⊥平面BB1C1C,故∠ADE为直线AD与平面BB1C1C所成的角.设各棱长为a,则AE=a,DE=a.所以tan ∠ADE=,所以∠ADE=60°.
4.解析:选B.如图,直线CE垂直于直线B1D1.
因为AC1为正方体,所以A1B1C1D1为正方形,连接B1D1,又因为E为A1C1的中点,所以E∈B1D1.所以B1D1⊥C1E,CC1⊥平面A1B1C1D1,所以CC1⊥B1D1,又CC1∩C1E=C1,
所以B1D1⊥平面CC1E,而CE 平面CC1E,所以直线CE垂直于直线B1D1;故选B.
5.解析:选B.对于题图1,如图,连接BC.因为BC⊥MN,AC⊥MN,BC,AC 平面ABC,BC∩AC=C,所以MN⊥平面ABC,从而MN⊥AB.同理可得NQ⊥AB.因为MN,NQ 平面MNQ,MN∩NQ=N,所以AB⊥平面MNQ.
对于题图2,因为NQ⊥AB,MN⊥AB,MN,NQ 平面MNQ,MN∩NQ=N,所以AB⊥平面MNQ.
对于题图3,因为AB与MQ不垂直,所以AB与平面MNQ不垂直.
对于题图4,因为AB与NQ不垂直,所以AB与平面MNQ不垂直.故满足直线AB⊥平面MNQ的个数为2.故选B.
6.解析:
BC⊥平面PAC BC⊥PC,
所以直角三角形有△PAB、△PAC、△ABC、△PBC.
答案:4
7.解析:因为PO⊥平面ABC,AC 平面ABC,所以PO⊥AC.又AC⊥BO,PO∩BO=O,所以AC⊥平面PBD,所以PBD内的4条直线PB,PD,PO,BD都与AC垂直,所以图中共有4条直线与AC垂直.
答案:4
8.解析:因为PA⊥平面ABCD,所以PA⊥QD.
若BC边上存在一点Q,使得QD⊥PQ,PA∩PQ=P,
则有QD⊥平面PAQ,从而QD⊥AQ.
在矩形ABCD中,当AD=a<2时,直线BC与以AD为直径的圆相离,故不存在点Q,使PQ⊥DQ.
所以当a≥2时,才存在点Q,使得PQ⊥QD.所以a的最小值为2.
答案:2
9.解:(1)证明:因为PA=PC,M为AC的中点,
所以PM⊥AC,①
又∠ABC=90°,AB=8,BC=6,
所以AM=MC=MB=AC=5.
在△PMB中,PB=13,MB=5.
PM===12.
所以PB2=MB2+PM2,所以PM⊥MB.②
由①②可知PM⊥平面ABC.
(2)因为PM⊥平面ABC,
所以MB为BP在平面ABC内的射影,
所以∠PBM为BP与底面ABC所成的角.
在Rt△PMB中,tan ∠PBM==.
10.解:(1)证明:因为PA⊥平面ABCD,CD 平面ABCD,
所以CD⊥PA.
因为CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD.
因为PD 平面PAD,
所以CD⊥PD.
(2)证明:因为PA⊥平面ABCD,BD 平面ABCD,
所以BD⊥PA.
在直角梯形ABCD中,BC=CD=AD,
由题意可得AB=BD=BC,
所以AD2=AB2+BD2,
所以BD⊥AB.
因为PA∩AB=A,
所以BD⊥平面PAB.
(3)在棱PD上存在点M,使CM∥平面PAB,且M是PD的中点.
证明如下:取PA的中点N,连接MN,BN,
因为M是PD的中点,所以MNAD.因为BCAD,所以MNBC.
所以MNBC是平行四边形,所以CM∥BN.因为CM 平面PAB, BN 平面PAB.
所以CM∥平面PAB.
[B 能力提升]
11.解析:选BD.对于A中,如果m∥α,m∥n,那么n∥α或n α,所以不正确;
对于B中,根据线面垂直的性质,可得若m⊥α,n∥α,那么m⊥n,所以是正确的;
对于C中,根据线面垂直的定义,直线m垂直于平面α内的任意直线,则m⊥α,而直线m垂直于平面α内的无数条直线,则m与α不一定垂直,所以不正确;
对于D中,平行线中的一条垂直一个平面,另一条也垂直于这个平面,可得若m⊥α,m∥n,那么n⊥α,所以是正确的.故选BD.
12.解析:选AC.由题意知,PA⊥平面ABC,因为BC 平面ABC,
所以PA⊥BC,故A对;而AC⊥BC,且PA∩AC=A,PA,AC 平面PAC,
所以BC⊥平面PAC,故C对;若AC⊥PB,因为AC⊥BC,可得AC⊥平面PBC,则AC⊥PC,与题目矛盾,故B错;由BC⊥平面PAC可得,BC⊥PC,则△PBC为直角三角形,若PC⊥PB,则BC,PB重合,与已知矛盾,故D错;故选AC.
13.解析:选AC.对于A,SG⊥GE,SG⊥GF,GE 平面GEF,GF 平面GEF,GE∩GF=G,SG⊥平面GEF,故A正确.
对于B,若SE⊥平面EFG,结合选项A,则SE∥SG,显然矛盾,故B错误.
对于C,FG⊥GE,SG⊥GF,GE 平面GES,GS 平面GES,GE∩GS=G,所以FG⊥平面GES,又SE 平面GES,所以GF⊥SE, 故C正确.
对于D,若EF⊥平面SEG,因为FG⊥平面GES(C项已经证明),则FE∥FG,显然矛盾,故D错误.故选AC.
[C 拓展探究]
14.解析:选C.设正方体的棱长为a,则由题意知, A1C1=AC=a,A1B=a,A1C=a,
当P为A1A的中点时,因为PA⊥平面ABC,则∠PAC=∠PAB=90°,∠ABC=90°,
则PB===a,PC===a,又BC=a,则BC2+PB2=PC2,则△PBC是直角三角形,即此时P ABC是鳖臑;
当P为A1B的中点时,因为BC⊥平面ABB1A1,所以BC⊥PB,BC⊥AB,
所以△PBC,△ABC为直角三角形,因为ABB1A1是正方形,所以AP⊥BP,
则△PAB是直角三角形,则PA=a,PC===a,
又BC=a,由勾股定理可知,△PAC是直角三角形,则此时P ABC是鳖臑;
当P为A1C的中点时,此时PA=PC=A1C=,又AC=a,由勾股定理可知,
△PAC不是直角三角形,则此时P ABC不是鳖臑;故选C.
15.解:(1)证明:因为∠ACB=90°,所以BC⊥AC,
因为PA⊥平面ABC,BC 平面ABC,
所以BC⊥PA,
又因为PA∩AC=A,PA,AC 平面PAC,
所以BC⊥平面PAC,
所以BC⊥PC.
(2)如图所示,
过A作AH⊥PC于H,
因为BC⊥平面PAC,AH 平面PAC,
所以BC⊥AH,
又PC∩BC=C,PC,BC 平面PBC,
所以AH⊥平面PBC,
所以∠ABH是直线AB与平面PBC所成的角.
因为PA⊥平面ABC,
所以∠PCA是PC与平面ABC所成的角,
因为tan ∠PCA==,
又PA=2,所以AC=,
所以在Rt△PAC中,AH==.
又AB=2,所以在Rt△ABH中,sin ∠ABH===.
即直线AB与平面PBC所成角的正弦值为.
[A 基础达标]
1.在空间中,下列命题正确的是( )
①平行于同一条直线的两条直线平行;
②垂直于同一条直线的两条直线平行;
③平行于同一个平面的两条直线平行;
④垂直于同一个平面的两条直线平行.
A.①③④ B.①④
C.① D.①②③④
2.过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC,若PA=PB=PC,则点O是△ABC的( )
A.垂心 B.外心
C.内心 D.重心
3.在三棱柱ABC A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是( )
A.30° B.45°
C.60° D.90°
4.在正方体ABCD A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.B1D1
C.A1D D.A1A
5.如图,下列4个正方体中,点A,B,M,N,Q分别为正方体的顶点或所在棱的中点,则在这4个正方体中,满足直线AB⊥平面MNQ的个数为( )
A.1 B.2
C.3 D.4
6.如图所示,PA⊥平面ABC,△ABC中BC⊥AC,则图中直角三角形的个数为________.
7.如图所示,PO⊥平面ABC,BO⊥AC,在图中与AC垂直的直线有________条.
8.如图所示,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1,若BC边上存在点Q,使得PQ⊥QD,则a的最小值为________.
9.如图,在三棱锥P ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
(1)求证:PM⊥平面ABC;
(2)求直线BP与平面ABC所成的角的正切值.
10.如图,在四棱锥P ABCD中,PA⊥平面ABCD,CD⊥AD,BC∥AD,BC=CD=AD.
(1)求证:CD⊥PD;
(2)求证:BD⊥平面PAB;
(3)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置;若不存在,请说明理由.
[B 能力提升]
11.(多选)已知α是一个平面,m,n是两条直线,有下列四个结论,正确的是( )
A.如果m∥α,m∥n,那么n∥α
B.如果m⊥α,n∥α,那么m⊥n
C.若直线m垂直于平面α内的无数条直线,则m⊥α
D.如果m⊥α,m∥n,那么n⊥α
12.(多选)如图所示,PA垂直于以AB为直径的圆所在的平面,点C为圆上异于点A,B的任意一点,则下列关系中正确的是( )
A.PA⊥BC B.AC⊥PB
C.BC⊥平面PAC D.PC⊥PB
13.(多选)如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现在沿着SE,SF,EF把这个正方形折成一个四面体,使G1,G2,G3重合,重合后的点记为G.给出下列关系,其中成立的为( )
A.SG⊥平面EFG B.SE⊥平面EFG
C.GF⊥SE D.EF⊥平面SEG
[C 拓展探究]
14.刘徽注《九章算术 商功》“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”如图一解释了由一个长方体得到“堑堵”“阳马”“鳖臑”的过程.堑堵是底面为直角三角形的直棱柱;阳马是一条侧棱垂直于底面且底面为矩形的四棱锥;鳖臑是四个面都为直角三角形的四面体.
在如图二所示由正方体得到的堑堵ABC A1B1C1中,当点P在下列三个位置:A1A中点、A1B中点、A1C中点时,分别形成的四面体P ABC中,鳖臑有( )
A.0个 B.1个
C.2个 D.3个
15.如图,在三棱锥P ABC中,棱PA垂直于平面ABC,∠ACB=90°.
(1)求证:BC⊥PC;
(2)若PA=AB=2,直线PC与平面ABC所成的角的正切值为,求直线AB与平面PBC所成的角的正弦值.
参考答案
[A 基础达标]
1.答案:B
2.解析:选B.因为PO⊥α,PA=PB=PC,可由射影定理得OA=OB=OC.
即点O是△ABC 的外心.
3.解析:选C.如图,取BC的中点E,连接AE,ED,AD,则AE⊥平面BB1C1C,故∠ADE为直线AD与平面BB1C1C所成的角.设各棱长为a,则AE=a,DE=a.所以tan ∠ADE=,所以∠ADE=60°.
4.解析:选B.如图,直线CE垂直于直线B1D1.
因为AC1为正方体,所以A1B1C1D1为正方形,连接B1D1,又因为E为A1C1的中点,所以E∈B1D1.所以B1D1⊥C1E,CC1⊥平面A1B1C1D1,所以CC1⊥B1D1,又CC1∩C1E=C1,
所以B1D1⊥平面CC1E,而CE 平面CC1E,所以直线CE垂直于直线B1D1;故选B.
5.解析:选B.对于题图1,如图,连接BC.因为BC⊥MN,AC⊥MN,BC,AC 平面ABC,BC∩AC=C,所以MN⊥平面ABC,从而MN⊥AB.同理可得NQ⊥AB.因为MN,NQ 平面MNQ,MN∩NQ=N,所以AB⊥平面MNQ.
对于题图2,因为NQ⊥AB,MN⊥AB,MN,NQ 平面MNQ,MN∩NQ=N,所以AB⊥平面MNQ.
对于题图3,因为AB与MQ不垂直,所以AB与平面MNQ不垂直.
对于题图4,因为AB与NQ不垂直,所以AB与平面MNQ不垂直.故满足直线AB⊥平面MNQ的个数为2.故选B.
6.解析:
BC⊥平面PAC BC⊥PC,
所以直角三角形有△PAB、△PAC、△ABC、△PBC.
答案:4
7.解析:因为PO⊥平面ABC,AC 平面ABC,所以PO⊥AC.又AC⊥BO,PO∩BO=O,所以AC⊥平面PBD,所以PBD内的4条直线PB,PD,PO,BD都与AC垂直,所以图中共有4条直线与AC垂直.
答案:4
8.解析:因为PA⊥平面ABCD,所以PA⊥QD.
若BC边上存在一点Q,使得QD⊥PQ,PA∩PQ=P,
则有QD⊥平面PAQ,从而QD⊥AQ.
在矩形ABCD中,当AD=a<2时,直线BC与以AD为直径的圆相离,故不存在点Q,使PQ⊥DQ.
所以当a≥2时,才存在点Q,使得PQ⊥QD.所以a的最小值为2.
答案:2
9.解:(1)证明:因为PA=PC,M为AC的中点,
所以PM⊥AC,①
又∠ABC=90°,AB=8,BC=6,
所以AM=MC=MB=AC=5.
在△PMB中,PB=13,MB=5.
PM===12.
所以PB2=MB2+PM2,所以PM⊥MB.②
由①②可知PM⊥平面ABC.
(2)因为PM⊥平面ABC,
所以MB为BP在平面ABC内的射影,
所以∠PBM为BP与底面ABC所成的角.
在Rt△PMB中,tan ∠PBM==.
10.解:(1)证明:因为PA⊥平面ABCD,CD 平面ABCD,
所以CD⊥PA.
因为CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD.
因为PD 平面PAD,
所以CD⊥PD.
(2)证明:因为PA⊥平面ABCD,BD 平面ABCD,
所以BD⊥PA.
在直角梯形ABCD中,BC=CD=AD,
由题意可得AB=BD=BC,
所以AD2=AB2+BD2,
所以BD⊥AB.
因为PA∩AB=A,
所以BD⊥平面PAB.
(3)在棱PD上存在点M,使CM∥平面PAB,且M是PD的中点.
证明如下:取PA的中点N,连接MN,BN,
因为M是PD的中点,所以MNAD.因为BCAD,所以MNBC.
所以MNBC是平行四边形,所以CM∥BN.因为CM 平面PAB, BN 平面PAB.
所以CM∥平面PAB.
[B 能力提升]
11.解析:选BD.对于A中,如果m∥α,m∥n,那么n∥α或n α,所以不正确;
对于B中,根据线面垂直的性质,可得若m⊥α,n∥α,那么m⊥n,所以是正确的;
对于C中,根据线面垂直的定义,直线m垂直于平面α内的任意直线,则m⊥α,而直线m垂直于平面α内的无数条直线,则m与α不一定垂直,所以不正确;
对于D中,平行线中的一条垂直一个平面,另一条也垂直于这个平面,可得若m⊥α,m∥n,那么n⊥α,所以是正确的.故选BD.
12.解析:选AC.由题意知,PA⊥平面ABC,因为BC 平面ABC,
所以PA⊥BC,故A对;而AC⊥BC,且PA∩AC=A,PA,AC 平面PAC,
所以BC⊥平面PAC,故C对;若AC⊥PB,因为AC⊥BC,可得AC⊥平面PBC,则AC⊥PC,与题目矛盾,故B错;由BC⊥平面PAC可得,BC⊥PC,则△PBC为直角三角形,若PC⊥PB,则BC,PB重合,与已知矛盾,故D错;故选AC.
13.解析:选AC.对于A,SG⊥GE,SG⊥GF,GE 平面GEF,GF 平面GEF,GE∩GF=G,SG⊥平面GEF,故A正确.
对于B,若SE⊥平面EFG,结合选项A,则SE∥SG,显然矛盾,故B错误.
对于C,FG⊥GE,SG⊥GF,GE 平面GES,GS 平面GES,GE∩GS=G,所以FG⊥平面GES,又SE 平面GES,所以GF⊥SE, 故C正确.
对于D,若EF⊥平面SEG,因为FG⊥平面GES(C项已经证明),则FE∥FG,显然矛盾,故D错误.故选AC.
[C 拓展探究]
14.解析:选C.设正方体的棱长为a,则由题意知, A1C1=AC=a,A1B=a,A1C=a,
当P为A1A的中点时,因为PA⊥平面ABC,则∠PAC=∠PAB=90°,∠ABC=90°,
则PB===a,PC===a,又BC=a,则BC2+PB2=PC2,则△PBC是直角三角形,即此时P ABC是鳖臑;
当P为A1B的中点时,因为BC⊥平面ABB1A1,所以BC⊥PB,BC⊥AB,
所以△PBC,△ABC为直角三角形,因为ABB1A1是正方形,所以AP⊥BP,
则△PAB是直角三角形,则PA=a,PC===a,
又BC=a,由勾股定理可知,△PAC是直角三角形,则此时P ABC是鳖臑;
当P为A1C的中点时,此时PA=PC=A1C=,又AC=a,由勾股定理可知,
△PAC不是直角三角形,则此时P ABC不是鳖臑;故选C.
15.解:(1)证明:因为∠ACB=90°,所以BC⊥AC,
因为PA⊥平面ABC,BC 平面ABC,
所以BC⊥PA,
又因为PA∩AC=A,PA,AC 平面PAC,
所以BC⊥平面PAC,
所以BC⊥PC.
(2)如图所示,
过A作AH⊥PC于H,
因为BC⊥平面PAC,AH 平面PAC,
所以BC⊥AH,
又PC∩BC=C,PC,BC 平面PBC,
所以AH⊥平面PBC,
所以∠ABH是直线AB与平面PBC所成的角.
因为PA⊥平面ABC,
所以∠PCA是PC与平面ABC所成的角,
因为tan ∠PCA==,
又PA=2,所以AC=,
所以在Rt△PAC中,AH==.
又AB=2,所以在Rt△ABH中,sin ∠ABH===.
即直线AB与平面PBC所成角的正弦值为.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
