【期末押题卷】广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷二(人教A版)(含解析)
文档属性
| 名称 | 【期末押题卷】广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷二(人教A版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 594.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 23:30:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2022 杭州模拟)已知集合A={0,2a+1,a2+3a+1},若﹣1∈A,则实数a=( )
A.﹣1 B.﹣2 C.﹣3 D.﹣1或﹣2
2.(5分)(2022 满洲里市三模)复数z满足(1+2i)z=3﹣i,则z的虚部为( )
A. B.i C.i D.
3.(5分)(2021春 舒城县校级月考)函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=1 B.a+b=0 C.a=b D.a2+b2=0
4.(5分)(2024 朝阳区校级模拟)一组数据按从小到大的顺序排列为2,4,m,12,16,17,若该组数据的中位数是极差的,则该组数据的第40百分位数是( )
A.4 B.5 C.6 D.9
5.(5分)(2022秋 湘潭期末)已知圆C:x2+y2+4x﹣8y+12=0,过点P(﹣4,﹣2)作圆C的切线PA,PB,切点为A,B,则△ABC的面积为( )
A. B. C. D.
6.(5分)(2023 武侯区校级模拟)如图,在△ABC中,AF=BF=6,EF=5,则( )
A.﹣11 B.﹣13 C.﹣15 D.15
7.(5分)(2022 齐齐哈尔三模)某单位为了解夏季用电量与月份的关系,对本单位2021年5月份到8月份的日平均用电量y(单位:千度)进行了统计分析,得出下表数据:
月份(x) 5 6 7 8
日平均用电量(y) 1.9 3.4 t 7.1
若y与x线性相关,且求得其线性回归方程,则表中t的值为( )
A.5.8 B.5.6 C.5.4 D.5.2
8.(5分)(2022秋 东莞市校级期中)椭圆上一点A关于原点的对称点为B,F为其左焦点,若AF⊥BF,设∠ABF=α,且α∈,则该椭圆离心率的取值范围为( )
A.[,1] B.[,] C.[,1) D.[,]
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)(2023 梅州二模)已知函数f(x)=cos2x+|sinx|,则( )
A.f(x)是一个最小正周期为T=2π的周期函数
B.f(x)是一个偶函数
C.f(x)在区间上单调递增
D.f(x)的最小值为0,最大值为
(多选)10.(6分)(2024秋 贾汪区校级月考)设函数f(x)=2x3﹣3ax2+1,则( )
A.当a>1时,f(x)有三个零点
B.当a<0时,x=0是f(x)的极小值点
C.存在a,b,使得x=b为曲线y=f(x)的对称轴
D.存在a,使得点(1,f(1))为曲线y=f(x)的对称中心
(多选)11.(6分)(2023秋 蚌山区校级期中)如图,棱长为2的正方体ABCD﹣A1B1C1D1中,P为线段B1D1上动点(包括端点).则下列结论正确的是( )
A.当点P在线段B1D1上运动时,三棱锥P﹣A1BD的体积为定值
B.记过点P平行于平面A1BD的平面为α,α截正方体ABCD﹣A1B1C1D1截得多边形的周长为
C.当点P为B1D1中点时,异面直线A1P与BD所成角为
D.当点P为B1D1中点时,三棱锥P﹣A1BD的外接球表面积为11π
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)(2024 碑林区校级模拟)已知,则二项式展开式中的常数项为 .
13.(5分)随机变量X服从正态分布N(μ,σ2),且P(X>4)=P(X<﹣2),则μ= .
14.(5分)(2022春 宾阳县校级月考)△ABC的内角A,B,C的对边分别为a,b,c,已知,,且a>b,则2a+c的最大值为 .
四.解答题(共5小题,满分77分)
15.(13分)(2024春 淮安区期中)某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角△ABC和以BC为直径的半圆拼接而成,点P为半圆上一点(异于B,C),点H在线段AB上,且满足CH⊥AB.已知∠ACB=90°,AB=1dm,设∠ABC=θ.
(1)为了使工艺礼品达到最佳观赏效果,需满足∠ABC=∠PCB,且CA+CP达到最大.当θ为何值时,工艺礼品达到最佳观赏效果?
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足∠PBA=60°,且CH+CP达到最大.当θ为何值时,工艺礼品达到最佳稳定性?并求此时CH+CP的值.
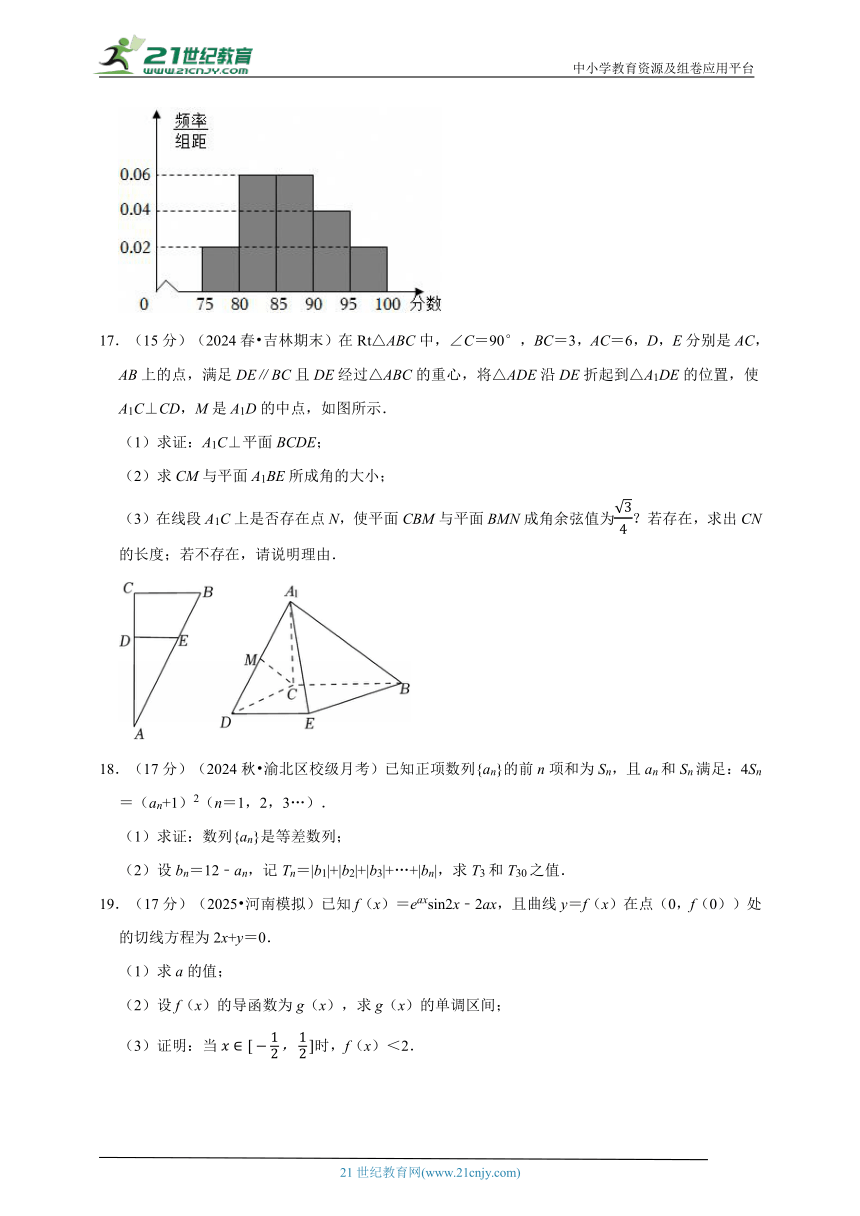
16.(15分)某公司对400名求职员工进行业务水平测试,根据测试成绩评定是否预录用.公司对400名求值员工的测试得分(测试得分都在[75,100]内)进行了统计分析,得分不低于90分为“优”,得分低于90分为“良”,得到如下的频率分布直方图和2×2列联表.
男 女 合计
优(得分不低于90分) 80
良(得分低于90分) 120
合计 400
(1)完成上面的2×2列联表、并依据α=0.05的独立性检验,能否认为求职员工的业务水平优良与否与性别有关联;
(2)该公司拟在业务测试成绩为优秀的求职人员中抽取部分人员进行个人发展的问卷调查,以获取采职者的心理需求,进而制定正式录用的方案.按照表中得分为优秀的男女比例分层抽取9个人的样本,并在9人中再随机抽取5人进行调查,记5人中男性的人数为X,求X的分布列以及数学期望.
17.(15分)(2024春 吉林期末)在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,满足DE∥BC且DE经过△ABC的重心,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,M是A1D的中点,如图所示.
(1)求证:A1C⊥平面BCDE;
(2)求CM与平面A1BE所成角的大小;
(3)在线段A1C上是否存在点N,使平面CBM与平面BMN成角余弦值为?若存在,求出CN的长度;若不存在,请说明理由.
18.(17分)(2024秋 渝北区校级月考)已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…).
(1)求证:数列{an}是等差数列;
(2)设bn=12﹣an,记Tn=|b1|+|b2|+|b3|+…+|bn|,求T3和T30之值.
19.(17分)(2025 河南模拟)已知f(x)=eaxsin2x﹣2ax,且曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0.
(1)求a的值;
(2)设f(x)的导函数为g(x),求g(x)的单调区间;
(3)证明:当时,f(x)<2.
广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2022 杭州模拟)已知集合A={0,2a+1,a2+3a+1},若﹣1∈A,则实数a=( )
A.﹣1 B.﹣2 C.﹣3 D.﹣1或﹣2
【考点】元素与集合关系的判断.
【专题】分类讨论;综合法;分类法;集合;运算求解.
【答案】B
【分析】由已知可得2a+1=﹣1或a2+3a+1=﹣1,求出a,然后根据集合元素的性质,确定a的值.
【解答】解:因为集合A={0,2a+1,a2+3a+1},
若﹣1∈A,则2a+1=﹣1或a2+3a+1=﹣1,解得a=﹣1或﹣2,
当a=﹣1时,集合A={0,﹣1,﹣1}与集合元素的互异性矛盾,故a≠﹣1,
当a=﹣2时,集合A={0,﹣3,﹣1}成立,
故a=﹣2,
故选:B.
【点评】本题考查了元素与集合的关系,考查了分类讨论思想,属于基础题.
2.(5分)(2022 满洲里市三模)复数z满足(1+2i)z=3﹣i,则z的虚部为( )
A. B.i C.i D.
【考点】复数的运算.
【专题】转化思想;转化法;数系的扩充和复数;运算求解.
【答案】A
【分析】结合虚部的定义,以及复数的运算法则,即可求解.
【解答】解:∵(1+2i)z=3﹣i,
∴,
∴z的虚部为.
故选:A.
【点评】本题主要考查虚部的定义,以及复数的运算法则,属于基础题.
3.(5分)(2021春 舒城县校级月考)函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=1 B.a+b=0 C.a=b D.a2+b2=0
【考点】充分条件必要条件的判断;奇函数偶函数的性质.
【专题】计算题;函数思想;综合法;函数的性质及应用;运算求解.
【答案】D
【分析】由奇函数的性质可得:f(0)=b=0,于是f(x)=x|x+a|,由f(﹣x)+f(x)=0,x≠0时,|x﹣a|=|x+a|恒成立,解得a=0.
【解答】解:由奇函数的性质可得:f(0)=b=0,
∴f(x)=x|x+a|,
则f(﹣x)=﹣f(x),∴﹣x|﹣x+a|=﹣x|x+a|,
∴x≠0时,|x﹣a|=|x+a|恒成立,则a=0.
∴函数f(x)=x|x+a|+b是奇函数的充要条件是a=b=0,即a2+b2=0.
故选:D.
【点评】本题考查了函数的奇偶性,考查了推理能力与计算能力,属于中档题.
4.(5分)(2024 朝阳区校级模拟)一组数据按从小到大的顺序排列为2,4,m,12,16,17,若该组数据的中位数是极差的,则该组数据的第40百分位数是( )
A.4 B.5 C.6 D.9
【考点】中位数;极差;百分位数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】C
【分析】根据已知条件,结合中位数、极差、百分位数的定义,即可求解.
【解答】解:根据题意,数据按从小到大的顺序排列为2,4,m,12,16,17,
则极差为17﹣2=15,故该组数据的中位数是,
数据共6个,故中位数为,解得m=6,
6×40%=2.4,故该组数据的40百分位数为从小到大第3个数,
故该组数据的40百分位数是m=6.
故选:C.
【点评】本题考查百分位数的计算,涉及数据中位数、极差的计算,属于基础题.
5.(5分)(2022秋 湘潭期末)已知圆C:x2+y2+4x﹣8y+12=0,过点P(﹣4,﹣2)作圆C的切线PA,PB,切点为A,B,则△ABC的面积为( )
A. B. C. D.
【考点】圆的切线方程.
【专题】转化思想;转化法;直线与圆;运算求解.
【答案】C
【分析】设AB与PC交于点D,根据切线的性质及勾股定理求得|PA|,再根据等面积法求出|AD|,再利用勾股定理求出|CD|,从而可得出答案.
【解答】解:设AB与PC交于点D,
则AB⊥PC且D为AB的中点,
圆C:x2+y2+4x﹣8y+12=0,化为(x+2)2+(y﹣4)2=8,
则圆心C(﹣2,4),半径,,
则,
∵,
∴,
∴,
∴.
故选:C.
【点评】本题主要考查圆的切线方程,考查转化能力,属于中档题.
6.(5分)(2023 武侯区校级模拟)如图,在△ABC中,AF=BF=6,EF=5,则( )
A.﹣11 B.﹣13 C.﹣15 D.15
【考点】平面向量数量积的性质及其运算.
【专题】转化思想;综合法;平面向量及应用;运算求解.
【答案】A
【分析】利用、表示和即可.
【解答】解:() ()=() ()23﹣36=﹣11.
故选:A.
【点评】本题考查了平面向量的数量积运算,属于中档题.
7.(5分)(2022 齐齐哈尔三模)某单位为了解夏季用电量与月份的关系,对本单位2021年5月份到8月份的日平均用电量y(单位:千度)进行了统计分析,得出下表数据:
月份(x) 5 6 7 8
日平均用电量(y) 1.9 3.4 t 7.1
若y与x线性相关,且求得其线性回归方程,则表中t的值为( )
A.5.8 B.5.6 C.5.4 D.5.2
【考点】经验回归方程与经验回归直线.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】B
【分析】根据已知条件,求出x,y的平均值,再结合线性回归方程过样本中心,即可求解.
【解答】解:由表格中的数据可得,,,
将点(,)代入回归直线方程可得,,解得t=5.6.
故选:B.
【点评】本题主要考查了线性回归方程的性质,以及平均值的求解,属于基础题.
8.(5分)(2022秋 东莞市校级期中)椭圆上一点A关于原点的对称点为B,F为其左焦点,若AF⊥BF,设∠ABF=α,且α∈,则该椭圆离心率的取值范围为( )
A.[,1] B.[,] C.[,1) D.[,]
【考点】椭圆的几何特征.
【专题】计算题;转化思想;综合法;三角函数的求值;三角函数的图象与性质;圆锥曲线的定义、性质与方程;逻辑思维;运算求解.
【答案】B
【分析】首先利用椭圆的定义整理得a=ccosα+csinα,利用椭圆的离心率关系式的变换,利用三角函数的定义域求出函数的值域,即椭圆的离心率.
【解答】解:如图所示:
已知椭圆的焦点在x轴上,点A关于原点的对称点为B,F为其左焦点,F1为右焦点,
连接AF,BF,BF1,AF1为长方形,
根据椭圆的定义:|AF|+|AF1|=2a,
设∠ABF=α,所以∠AF1F=α,
所以2a=2ccosα+2csinα,
故a=ccosα+csinα,
椭圆的离心率,
由于α∈,
所以,故.
整理得.即椭圆离心率的取值范围为.
故选:B.
【点评】本题考查的知识要点:椭圆的定义,椭圆的离心率,三角函数的关系式的变换,正弦型函数的性质的应用,主要考查学生的运算能力和数学思维能力,属于中档题.
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)(2023 梅州二模)已知函数f(x)=cos2x+|sinx|,则( )
A.f(x)是一个最小正周期为T=2π的周期函数
B.f(x)是一个偶函数
C.f(x)在区间上单调递增
D.f(x)的最小值为0,最大值为
【考点】三角函数的周期性;三角函数的最值;函数的奇偶性.
【专题】计算题;整体思想;综合法;三角函数的图象与性质;运算求解.
【答案】BC
【分析】利用函数周期性的定义可判断A选项;利用函数奇偶性的定义可判断B选项;利用复合函数的单调性可判断C选项;求得,利用二次函数的基本性质可求得函数f(x)的最大值和最小值,可判断D选项.
【解答】解:对于A选项,f(x+π)=cos[2(x+π)]+|sin(x+π)|=cos(2x+2π)+|﹣sinx|
=cos2x+|sinx|=f(x),
所以,函数f(x)为周期函数,且该函数的最小正周期不是2π,A错;
对于B选项,对任意的x∈R,f(﹣x)=cos(﹣2x)+|sin(﹣x)|=cos2x+|sinx|=f(x),
所以,函数f(x)为偶函数,B对;
对于C选项,当时,,
,
令t=sinx,则,因为函数在上单调递减,
函数t=sinx在上单调递减,
由复合函数的单调性可知,函数f(x)在区间上单调递增,C对;
对于D选项,,
因为0≤|sinx|≤1,令,
则二次函数g(u)在上单调递增,在上单调递减,所以,,
又因为g(0)=1,g(1)=0,所以,g(u)min=0,
因此,f(x)的最小值为0,最大值为,D错.
故选:BC.
【点评】本题考查了三角函数的性质,属于中档题.
(多选)10.(6分)(2024秋 贾汪区校级月考)设函数f(x)=2x3﹣3ax2+1,则( )
A.当a>1时,f(x)有三个零点
B.当a<0时,x=0是f(x)的极小值点
C.存在a,b,使得x=b为曲线y=f(x)的对称轴
D.存在a,使得点(1,f(1))为曲线y=f(x)的对称中心
【考点】函数的零点与方程根的关系;利用导数求解函数的极值.
【专题】函数思想;综合法;导数的综合应用;逻辑思维;运算求解.
【答案】ABD
【分析】对于A,先分析出函数的极值点为x=0,x=a,根据零点存在定理和极值的符号判断出f(x)在(﹣1,0),(0,a),(a,2a)上各有一个零点;对于B,根据极值和导函数符号的关系进行分析;对于C,假设存在这样的a,b,使得x=b为f(x)的对称轴,则f(x)=f(2b﹣x)为恒等式,据此计算判断;对于D,若存在这样的a,使得(1,3﹣3a)为f(x)的对称中心,则f(x)+f(2﹣x)=6﹣6a,据此进行计算判断,亦可利用拐点结论直接求解.
【解答】解:对于选项A,由题意可知:f(x)的定义域为R,且f′(x)=6x2﹣6ax=6x(x﹣a),
因为a>1,当x∈(﹣∞,0)∪(a,+∞)时,f′(x)>0;x∈(0,a)时,f′(x)<0;
可知f(x)在(﹣∞,0),(a,+∞)上单调递增,在(0,a)上单调递减,
则f(x)在x=0处取到极大值,在x=a处取到极小值,
且f(0)=1>0,f(a)=1﹣a3<0,f(﹣1)=﹣1﹣3a<0,f(2a)=4a3+1>0,
则f(x)在(﹣∞,0),(0,a),(a,+∞)上各有一个零点,
所以当a>1时,f(x)有三个零点,故A正确;
对于选项B,因为f′(x)=6x(x﹣a),
若a<0,当x∈(a,0)时,f′(x)<0,当x∈(0,+∞)时,f′(x)>0,
可知f(x)在(a,0)内单调递减,在(0,+∞)内单调递增,
所有f(x)在x=0处取到极小值,故B正确;
对于选项C:假设存在这样的a,b,使得x=b为f(x)的对称轴,
即存在这样的a,b使得f(x)=f(2b﹣x),
即2x3﹣3ax2+1=2(2b﹣x)3﹣3a(2b﹣x)2+1,
因为等式右边2(2b﹣x)3展开式含有x3的项为,
可知等式左右两边x3的系数不相等,原等式不可能恒成立,
于是不存在这样的a,b,使得x=b为f(x)的对称轴,C选项错误;
对于选项D:因为f(1)=3﹣3a,
若存在a,使得(1,3﹣3a)为f(x)的对称中心,则f(x)+f(2﹣x)=6﹣6a,
且f(x)+f(2﹣x)=2x3﹣3ax2+1+2(2﹣x)3﹣3a(2﹣x)2+1=(12﹣6a)x2+(12a﹣24)x+18﹣12a,
可得6﹣6a=(12﹣6a)x2+(12a﹣24)x+18﹣12a,则,
解得a=2,所以存在a=2使得(1,f(1))是f(x)的对称中心,故D正确.
故选:ABD.
【点评】本题考查了函数性质的应用及导数的综合应用,考查了函数思想及转化思想,属于中档题.
(多选)11.(6分)(2023秋 蚌山区校级期中)如图,棱长为2的正方体ABCD﹣A1B1C1D1中,P为线段B1D1上动点(包括端点).则下列结论正确的是( )
A.当点P在线段B1D1上运动时,三棱锥P﹣A1BD的体积为定值
B.记过点P平行于平面A1BD的平面为α,α截正方体ABCD﹣A1B1C1D1截得多边形的周长为
C.当点P为B1D1中点时,异面直线A1P与BD所成角为
D.当点P为B1D1中点时,三棱锥P﹣A1BD的外接球表面积为11π
【考点】球的体积和表面积;异面直线及其所成的角;命题的真假判断与应用;棱柱、棱锥、棱台的体积.
【专题】转化思想;综合法;立体几何;逻辑思维;运算求解.
【答案】ACD
【分析】对A,显然B1D1∥平面A1BD,所以P在任何位置时到平面A1BD的距离相等,即可得解;
对B,由P在B1D1上且B1D1∥BD,故截面为△B1CD1,算出周长即可;
对C,当点P为B1D1中点时,由于A1B1C1D1为正方形,所以A1P⊥B1D1,即可得到垂直;
对D,是线面垂直型的外接球问题,当点P为B1D1中点时,A1P⊥B1D1,设△BPD外接圆直径2r,所以三棱锥P﹣A1BD的外接球的直径,即可得解.
【解答】解:对A,由于B1D1∥BD,显然B1D1∥平面A1BD,
又P∈B1D1,所以P在任何位置时到平面A1BD的距离相等,
所以三棱锥P﹣A1BD的体积为定值,故A正确;
对B,由P在B1D1上且B1D1∥BD,故截面为△B1CD1,
所以截面周长为,故B错误;
对C,当点P为B1D1中点时,由于A1B1C1D1为正方形,
所以A1P⊥B1D1,又BD∥B1D1,所以A1P⊥BD,故C正确;
对D,当点P为B1D1中点时,A1P⊥B1D1,
所以在正方体中A1P⊥平面BDP,
由,,
所以,,
所以△BPD外接圆直径,
所以三棱锥P﹣A1BD的外接球的直径,
所以三棱锥P﹣A1BD的外接球表面积为,故D正确;
故选:ACD.
【点评】本题考查三棱锥的体积问题,线面平行的判断,异面直线所成角的求解,三棱锥的外接球问题,属中档题.
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)(2024 碑林区校级模拟)已知,则二项式展开式中的常数项为 15 .
【考点】二项展开式的通项与项的系数.
【专题】计算题;转化思想;综合法;二项式定理;逻辑思维;运算求解.
【答案】15.
【分析】直接利用定积分以及组合数和二项式的展开式求出结果.
【解答】解:由,得二项式为,
其常数项为.
故答案为:15.
【点评】本题考查的知识点:二项式的展开式,组合数,主要考查学生的运算能力,属于中档题.
13.(5分)随机变量X服从正态分布N(μ,σ2),且P(X>4)=P(X<﹣2),则μ= 1 .
【考点】正态分布.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】1.
【分析】利用正态分布曲线的对称性求解.
【解答】解:∵X~N(μ,σ2),且P(X>4)=P(X<﹣2),
∴μ1.
故答案为:1.
【点评】本题主要考查了正态分布曲线的对称性,属于基础题.
14.(5分)(2022春 宾阳县校级月考)△ABC的内角A,B,C的对边分别为a,b,c,已知,,且a>b,则2a+c的最大值为 2 .
【考点】正弦定理.
【专题】计算题;转化思想;综合法;解三角形;运算求解.
【答案】2.
【分析】由正弦定理整理条件可求得B,再由正弦定理可将2a+c转化为2sin(A+φ),其中tanφ,由正弦函数的性质即可求得2a+c的取值范围.
【解答】解:因为asinBcosC+csinBcosA,,
可得sinAsinBcosC+sinCsinBcosAsinB,
所以sinAcosC+sinCcosA,即sin(A+C)=sinB,
所以B或,
因为a>b,所以B,
由正弦定理2,可得:a=2sinA,c=2sinC=2sin(A),
则2a+c=4sinA+2sin(A)=5sinAcosA=2sin(A+φ)≤2,其中tanφ,
则2a+c的最大值为2.
故答案为:2.
【点评】此题考查了两角和与差的正弦函数公式,以及特殊角的三角函数值,正弦定理应用,熟练掌握公式是解本题的关键,属于中档题.
四.解答题(共5小题,满分77分)
15.(13分)(2024春 淮安区期中)某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角△ABC和以BC为直径的半圆拼接而成,点P为半圆上一点(异于B,C),点H在线段AB上,且满足CH⊥AB.已知∠ACB=90°,AB=1dm,设∠ABC=θ.
(1)为了使工艺礼品达到最佳观赏效果,需满足∠ABC=∠PCB,且CA+CP达到最大.当θ为何值时,工艺礼品达到最佳观赏效果?
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足∠PBA=60°,且CH+CP达到最大.当θ为何值时,工艺礼品达到最佳稳定性?并求此时CH+CP的值.
【考点】解三角形.
【专题】应用题;转化思想;综合法;解三角形;运算求解.
【答案】(1)30°,θ;
(2)15°,.
【分析】(1)利用直角三角形的边角关系,求出CA+CP的解析式,从而可得CA+CP取得最大值时θ的值;
(2)由等积法求出CH的值,再计算CH+CP的最大值以及对应的θ值.
【解答】解:(1)由题意可得∠ABC=∠PCB=θ,
因为AB=1dm,
在直角△ABC中,可得AC=sinθ,BC=cosθ,
在直角△PBC中,可得PC=BC cosθ=cosθ cosθ=cos2θ,PB=BC sinθ=sinθ cosθ=sinθcosθ,
可得AC+CP=sinθ+cos2θ
=sinθ+1﹣sin2θ
=﹣sin2θ+sinθ+1
,
所以当,即θ=30°时,AC+CP的最大值为,
即θ=30°时,工艺礼品达到最佳观赏效果;
(2)在直角△ABC中,由,
因为AB=1dm,AC=sinθ,BC=cosθ,
可得CH,
因为∠PBA=60°,
所以在直角△PBC中,PC=BC sin(60°﹣θ)=cosθ (sin60°cosθ﹣cos60°sinθ),
所以,0<θ<60°,
所以CH+CP
sin2θ()sin2θ
,
可得当θ=15°时,工艺礼品达到最佳稳定性,此时CH+CP取得最大值,且最大值为.
【点评】本题考查了解三角形以及三角函数的应用问题,也考查了运算求解能力,是中档题.
16.(15分)某公司对400名求职员工进行业务水平测试,根据测试成绩评定是否预录用.公司对400名求值员工的测试得分(测试得分都在[75,100]内)进行了统计分析,得分不低于90分为“优”,得分低于90分为“良”,得到如下的频率分布直方图和2×2列联表.
男 女 合计
优(得分不低于90分) 80
良(得分低于90分) 120
合计 400
(1)完成上面的2×2列联表、并依据α=0.05的独立性检验,能否认为求职员工的业务水平优良与否与性别有关联;
(2)该公司拟在业务测试成绩为优秀的求职人员中抽取部分人员进行个人发展的问卷调查,以获取采职者的心理需求,进而制定正式录用的方案.按照表中得分为优秀的男女比例分层抽取9个人的样本,并在9人中再随机抽取5人进行调查,记5人中男性的人数为X,求X的分布列以及数学期望.
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;对应思想;定义法;概率与统计;运算求解;数据分析.
【答案】(1)依据小概率值α=0.05的独立性检验,不能认为求职员工的业务水平优良与否与性别有关联;
(2)X的分布列为:
X
2 3 4 5
p
E(X).
【分析】(1)由已知数据完善列联表,计算K2后与临界值比较可得;
(2)求出9人中男性和女性的人数,然后由求出X的各概率得分布列,由期望公式计算期望.
【解答】解:得分不低于90分的人数为:400×(0.04+0.02)×5=120,所以填表如下:
男 女 合计
优(得分不低于90分) 80 40 120
良(得分低于90分) 160 120 280
合计 240 160 400
根据列联表中的数据,经计算得到:
K23.175<3.841=x0.05,
所以依据小概率值α=0.05的独立性检验,不能认为求职员工的业务水平优良与否与性别有关联.
(2)得分为优秀的男女比例为80:40=2:1,所以9人中男性有6人,女性有3人.
因此
X
的可能值为2,3,4,5,
P(X=2);
P(X=3);
P(X=4);
P(X=5).
所以
X
的分布列为:
X
2 3 4 5
p
X
的数学期望为:
E(X)=2345.
【点评】本题考查独立性检验以及离散型随机变量的概率分布列与期望,是中档题.
17.(15分)(2024春 吉林期末)在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,满足DE∥BC且DE经过△ABC的重心,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,M是A1D的中点,如图所示.
(1)求证:A1C⊥平面BCDE;
(2)求CM与平面A1BE所成角的大小;
(3)在线段A1C上是否存在点N,使平面CBM与平面BMN成角余弦值为?若存在,求出CN的长度;若不存在,请说明理由.
【考点】几何法求解直线与平面所成的角;几何法求解二面角及两平面的夹角;直线与平面垂直.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】(1)证明见解析;(2);(3)存在,或.
【分析】(1)应用线面垂直的判定定理证明线面垂直关系,再由性质定理得到线线垂直关系,进而再利用判定定理证明所求证的线面垂直关系;
(2)建立空间直角坐标系.用向量法求CM与平面A1BE所成角的大小;
(3)假设存在点N,使平面CBM与平面BMN成角余弦值为,设,分别求解两平面的法向量,用λ表示余弦值解方程可得.
【解答】解:(1)证明:因为在Rt△ABC中,∠C=90°,DE∥BC,且BC⊥CD,
所以DE⊥CD,DE⊥AD,则折叠后,DE⊥A1D,
又A1D∩CD=D,A1D,CD 平面A1CD,
所以DE⊥平面A1CD,A1C 平面A1CD,
所以DE⊥A1C,
又已知A1C⊥CD,CD∩DE=D,且都在面BCDE内,
所以A1C⊥平面BCDE;
(2)由(1),分别以CD,CB,CA1所在直线为x轴,y轴,z轴,建立空间直角坐标系C﹣xyz,
因为AD=2CD,故,
由几何关系可知,CD=2,A1D=4,,
故C(0,0,0),D(2,0,0),E(2,2,0),B(0,3,0),,,
,,,
设平面A1BE的法向量为,
则,
不妨令y=2,则,x=1,
所以,
设CM与平面A1BE所成角的大小为θ,
则有,
故,
即CM与平面A1BE所成角的大小为;
(3)假设在线段AC上存在点N,使平面CBM与平面BMN成角余弦值为,
在空间直角坐标系中,,,,
设,则,,
设平面BMN的先向量为,
则,
不妨令,则y2=2λ,x2=6λ﹣3,
所以,
设平面CBM的法向量为,
则,
不妨令,则x3=﹣3,y3=0,
所以,
若平面CBM与平面BMN成角余弦值为,
则满足,
化简得2λ2﹣3λ+1=0,
解得λ=1或,
即或,
故在线段A1C上存在这样的点N,使平面CBM与平面BMN成角余弦值为,此时CN的长度为或.
【点评】本题考查线面垂直的判定以及空间向量的应用,属于中档题.
18.(17分)(2024秋 渝北区校级月考)已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…).
(1)求证:数列{an}是等差数列;
(2)设bn=12﹣an,记Tn=|b1|+|b2|+|b3|+…+|bn|,求T3和T30之值.
【考点】数列递推式;等差数列的概念与判定;等比数列的概念与判定;数列的求和.
【专题】转化思想;综合法;等差数列与等比数列;运算求解.
【答案】(1)证明见解答;(2)T3=27,T30=612.
【分析】(1)由数列的通项与求和的关系,结合等差数列的定义可得证明;
(2)由等差数列的通项公式求得bn,讨论bn的符号,再由等差数列的求和公式,可得所求和.
【解答】解:(1)证明:正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…),
可得4a1=4S1=(a1+1)2,解得a1=1;
当n≥2时,由4Sn=(an+1)2,可得4Sn﹣1=(an﹣1+1)2,
相减可得4an=(an+1)2﹣(an﹣1+1)2,即为(an﹣1)2=(an﹣1+1)2,
化为(an+an﹣1)(an﹣an﹣1﹣2)=0,
由an>0,可得an﹣an﹣1=2,则数列{an}是首项为1,公差为2的等差数列;
(2)bn=12﹣an=12﹣(2n﹣1)=13﹣2n,
当1≤n≤6时,bn>0,Tnn(11+13﹣2n)=12n﹣n2;
当n≥7时,bn<0,Tn=b1+b2+...+b6﹣b7﹣b8﹣...﹣bn=12×6﹣36(n﹣6)(﹣1+13﹣2n)
=36+(n﹣6)2,
则T3=36﹣9=27,
T30=36+242=612.
【点评】本题考查数列的通项与求和的关系,以及等差数列的通项公式与求和公式,考查转化思想和运算能力,属于中档题.
19.(17分)(2025 河南模拟)已知f(x)=eaxsin2x﹣2ax,且曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0.
(1)求a的值;
(2)设f(x)的导函数为g(x),求g(x)的单调区间;
(3)证明:当时,f(x)<2.
【考点】利用导数求解函数的单调性和单调区间;利用导数求解函数的最值;利用导数求解曲线在某点上的切线方程.
【专题】转化思想;转化法;导数的综合应用;运算求解.
【答案】(1)2;(2)单调递增区间为,单调递减区间为;(3)证明见解析.
【分析】(1)求出函数的导函数,根据f′(0)=﹣2计算可得;
(2)求出g(x)的解析式,从而求出其导函数,再解关于导函数的不等式,即可求出函数的单调区间;
(3)由(2)可得g(x)的单调性,结合零点存在性定理得到,使得g(x0)=0,即可得到f(x)的单调性,从而求出f(x)max,即可得证.
【解答】解:(1)因为f(x)=eaxsin2x﹣2ax,
所以f′(x)=aeaxsin2x+2eaxcos2x﹣2a,
因为曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0,
所以f′(0)=2﹣2a=﹣2,
解得a=2;
(2)由(1)可得f(x)=e2xsin2x﹣4x,
所以f′(x)=2e2xsin2x+2e2xcos2x﹣4,
则g(x)=f′(x)=2e2x(sin2x+cos2x)﹣4,定义域为R,
所以g′(x)=2[2e2x(sin2x+cos2x)+e2x(2cos2x﹣2sin2x)]=8e2xcos2x,
因为e2x>0,
令g′(x)<0,即cos2x<0,
解得,
所以g(x)的单调递减区间为,
令g′(x)>0,即cos2x>0,
解得;
所以g(x)的单调递增区间为;
(3)证明:由(2)可知g(x)在上单调递增,
又g(0)=﹣2<0,,
又,
所以e(sin1+cos1)﹣2>e2>0,即,
所以,使得g(x0)=0,
当时g(x)>0,即f′(x)>0,所以f(x)在上单调递增;
当时g(x)<0,即f′(x)<0,所以f(x)在上单调递减;
又,,
所以,
所以当时,f(x)<2.
【点评】本题考查利用导数证明或判定不等式问题,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2022 杭州模拟)已知集合A={0,2a+1,a2+3a+1},若﹣1∈A,则实数a=( )
A.﹣1 B.﹣2 C.﹣3 D.﹣1或﹣2
2.(5分)(2022 满洲里市三模)复数z满足(1+2i)z=3﹣i,则z的虚部为( )
A. B.i C.i D.
3.(5分)(2021春 舒城县校级月考)函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=1 B.a+b=0 C.a=b D.a2+b2=0
4.(5分)(2024 朝阳区校级模拟)一组数据按从小到大的顺序排列为2,4,m,12,16,17,若该组数据的中位数是极差的,则该组数据的第40百分位数是( )
A.4 B.5 C.6 D.9
5.(5分)(2022秋 湘潭期末)已知圆C:x2+y2+4x﹣8y+12=0,过点P(﹣4,﹣2)作圆C的切线PA,PB,切点为A,B,则△ABC的面积为( )
A. B. C. D.
6.(5分)(2023 武侯区校级模拟)如图,在△ABC中,AF=BF=6,EF=5,则( )
A.﹣11 B.﹣13 C.﹣15 D.15
7.(5分)(2022 齐齐哈尔三模)某单位为了解夏季用电量与月份的关系,对本单位2021年5月份到8月份的日平均用电量y(单位:千度)进行了统计分析,得出下表数据:
月份(x) 5 6 7 8
日平均用电量(y) 1.9 3.4 t 7.1
若y与x线性相关,且求得其线性回归方程,则表中t的值为( )
A.5.8 B.5.6 C.5.4 D.5.2
8.(5分)(2022秋 东莞市校级期中)椭圆上一点A关于原点的对称点为B,F为其左焦点,若AF⊥BF,设∠ABF=α,且α∈,则该椭圆离心率的取值范围为( )
A.[,1] B.[,] C.[,1) D.[,]
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)(2023 梅州二模)已知函数f(x)=cos2x+|sinx|,则( )
A.f(x)是一个最小正周期为T=2π的周期函数
B.f(x)是一个偶函数
C.f(x)在区间上单调递增
D.f(x)的最小值为0,最大值为
(多选)10.(6分)(2024秋 贾汪区校级月考)设函数f(x)=2x3﹣3ax2+1,则( )
A.当a>1时,f(x)有三个零点
B.当a<0时,x=0是f(x)的极小值点
C.存在a,b,使得x=b为曲线y=f(x)的对称轴
D.存在a,使得点(1,f(1))为曲线y=f(x)的对称中心
(多选)11.(6分)(2023秋 蚌山区校级期中)如图,棱长为2的正方体ABCD﹣A1B1C1D1中,P为线段B1D1上动点(包括端点).则下列结论正确的是( )
A.当点P在线段B1D1上运动时,三棱锥P﹣A1BD的体积为定值
B.记过点P平行于平面A1BD的平面为α,α截正方体ABCD﹣A1B1C1D1截得多边形的周长为
C.当点P为B1D1中点时,异面直线A1P与BD所成角为
D.当点P为B1D1中点时,三棱锥P﹣A1BD的外接球表面积为11π
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)(2024 碑林区校级模拟)已知,则二项式展开式中的常数项为 .
13.(5分)随机变量X服从正态分布N(μ,σ2),且P(X>4)=P(X<﹣2),则μ= .
14.(5分)(2022春 宾阳县校级月考)△ABC的内角A,B,C的对边分别为a,b,c,已知,,且a>b,则2a+c的最大值为 .
四.解答题(共5小题,满分77分)
15.(13分)(2024春 淮安区期中)某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角△ABC和以BC为直径的半圆拼接而成,点P为半圆上一点(异于B,C),点H在线段AB上,且满足CH⊥AB.已知∠ACB=90°,AB=1dm,设∠ABC=θ.
(1)为了使工艺礼品达到最佳观赏效果,需满足∠ABC=∠PCB,且CA+CP达到最大.当θ为何值时,工艺礼品达到最佳观赏效果?
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足∠PBA=60°,且CH+CP达到最大.当θ为何值时,工艺礼品达到最佳稳定性?并求此时CH+CP的值.
16.(15分)某公司对400名求职员工进行业务水平测试,根据测试成绩评定是否预录用.公司对400名求值员工的测试得分(测试得分都在[75,100]内)进行了统计分析,得分不低于90分为“优”,得分低于90分为“良”,得到如下的频率分布直方图和2×2列联表.
男 女 合计
优(得分不低于90分) 80
良(得分低于90分) 120
合计 400
(1)完成上面的2×2列联表、并依据α=0.05的独立性检验,能否认为求职员工的业务水平优良与否与性别有关联;
(2)该公司拟在业务测试成绩为优秀的求职人员中抽取部分人员进行个人发展的问卷调查,以获取采职者的心理需求,进而制定正式录用的方案.按照表中得分为优秀的男女比例分层抽取9个人的样本,并在9人中再随机抽取5人进行调查,记5人中男性的人数为X,求X的分布列以及数学期望.
17.(15分)(2024春 吉林期末)在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,满足DE∥BC且DE经过△ABC的重心,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,M是A1D的中点,如图所示.
(1)求证:A1C⊥平面BCDE;
(2)求CM与平面A1BE所成角的大小;
(3)在线段A1C上是否存在点N,使平面CBM与平面BMN成角余弦值为?若存在,求出CN的长度;若不存在,请说明理由.
18.(17分)(2024秋 渝北区校级月考)已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…).
(1)求证:数列{an}是等差数列;
(2)设bn=12﹣an,记Tn=|b1|+|b2|+|b3|+…+|bn|,求T3和T30之值.
19.(17分)(2025 河南模拟)已知f(x)=eaxsin2x﹣2ax,且曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0.
(1)求a的值;
(2)设f(x)的导函数为g(x),求g(x)的单调区间;
(3)证明:当时,f(x)<2.
广东省广州市2024-2025学年高二下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2022 杭州模拟)已知集合A={0,2a+1,a2+3a+1},若﹣1∈A,则实数a=( )
A.﹣1 B.﹣2 C.﹣3 D.﹣1或﹣2
【考点】元素与集合关系的判断.
【专题】分类讨论;综合法;分类法;集合;运算求解.
【答案】B
【分析】由已知可得2a+1=﹣1或a2+3a+1=﹣1,求出a,然后根据集合元素的性质,确定a的值.
【解答】解:因为集合A={0,2a+1,a2+3a+1},
若﹣1∈A,则2a+1=﹣1或a2+3a+1=﹣1,解得a=﹣1或﹣2,
当a=﹣1时,集合A={0,﹣1,﹣1}与集合元素的互异性矛盾,故a≠﹣1,
当a=﹣2时,集合A={0,﹣3,﹣1}成立,
故a=﹣2,
故选:B.
【点评】本题考查了元素与集合的关系,考查了分类讨论思想,属于基础题.
2.(5分)(2022 满洲里市三模)复数z满足(1+2i)z=3﹣i,则z的虚部为( )
A. B.i C.i D.
【考点】复数的运算.
【专题】转化思想;转化法;数系的扩充和复数;运算求解.
【答案】A
【分析】结合虚部的定义,以及复数的运算法则,即可求解.
【解答】解:∵(1+2i)z=3﹣i,
∴,
∴z的虚部为.
故选:A.
【点评】本题主要考查虚部的定义,以及复数的运算法则,属于基础题.
3.(5分)(2021春 舒城县校级月考)函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=1 B.a+b=0 C.a=b D.a2+b2=0
【考点】充分条件必要条件的判断;奇函数偶函数的性质.
【专题】计算题;函数思想;综合法;函数的性质及应用;运算求解.
【答案】D
【分析】由奇函数的性质可得:f(0)=b=0,于是f(x)=x|x+a|,由f(﹣x)+f(x)=0,x≠0时,|x﹣a|=|x+a|恒成立,解得a=0.
【解答】解:由奇函数的性质可得:f(0)=b=0,
∴f(x)=x|x+a|,
则f(﹣x)=﹣f(x),∴﹣x|﹣x+a|=﹣x|x+a|,
∴x≠0时,|x﹣a|=|x+a|恒成立,则a=0.
∴函数f(x)=x|x+a|+b是奇函数的充要条件是a=b=0,即a2+b2=0.
故选:D.
【点评】本题考查了函数的奇偶性,考查了推理能力与计算能力,属于中档题.
4.(5分)(2024 朝阳区校级模拟)一组数据按从小到大的顺序排列为2,4,m,12,16,17,若该组数据的中位数是极差的,则该组数据的第40百分位数是( )
A.4 B.5 C.6 D.9
【考点】中位数;极差;百分位数.
【专题】计算题;方程思想;转化思想;综合法;概率与统计;运算求解.
【答案】C
【分析】根据已知条件,结合中位数、极差、百分位数的定义,即可求解.
【解答】解:根据题意,数据按从小到大的顺序排列为2,4,m,12,16,17,
则极差为17﹣2=15,故该组数据的中位数是,
数据共6个,故中位数为,解得m=6,
6×40%=2.4,故该组数据的40百分位数为从小到大第3个数,
故该组数据的40百分位数是m=6.
故选:C.
【点评】本题考查百分位数的计算,涉及数据中位数、极差的计算,属于基础题.
5.(5分)(2022秋 湘潭期末)已知圆C:x2+y2+4x﹣8y+12=0,过点P(﹣4,﹣2)作圆C的切线PA,PB,切点为A,B,则△ABC的面积为( )
A. B. C. D.
【考点】圆的切线方程.
【专题】转化思想;转化法;直线与圆;运算求解.
【答案】C
【分析】设AB与PC交于点D,根据切线的性质及勾股定理求得|PA|,再根据等面积法求出|AD|,再利用勾股定理求出|CD|,从而可得出答案.
【解答】解:设AB与PC交于点D,
则AB⊥PC且D为AB的中点,
圆C:x2+y2+4x﹣8y+12=0,化为(x+2)2+(y﹣4)2=8,
则圆心C(﹣2,4),半径,,
则,
∵,
∴,
∴,
∴.
故选:C.
【点评】本题主要考查圆的切线方程,考查转化能力,属于中档题.
6.(5分)(2023 武侯区校级模拟)如图,在△ABC中,AF=BF=6,EF=5,则( )
A.﹣11 B.﹣13 C.﹣15 D.15
【考点】平面向量数量积的性质及其运算.
【专题】转化思想;综合法;平面向量及应用;运算求解.
【答案】A
【分析】利用、表示和即可.
【解答】解:() ()=() ()23﹣36=﹣11.
故选:A.
【点评】本题考查了平面向量的数量积运算,属于中档题.
7.(5分)(2022 齐齐哈尔三模)某单位为了解夏季用电量与月份的关系,对本单位2021年5月份到8月份的日平均用电量y(单位:千度)进行了统计分析,得出下表数据:
月份(x) 5 6 7 8
日平均用电量(y) 1.9 3.4 t 7.1
若y与x线性相关,且求得其线性回归方程,则表中t的值为( )
A.5.8 B.5.6 C.5.4 D.5.2
【考点】经验回归方程与经验回归直线.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】B
【分析】根据已知条件,求出x,y的平均值,再结合线性回归方程过样本中心,即可求解.
【解答】解:由表格中的数据可得,,,
将点(,)代入回归直线方程可得,,解得t=5.6.
故选:B.
【点评】本题主要考查了线性回归方程的性质,以及平均值的求解,属于基础题.
8.(5分)(2022秋 东莞市校级期中)椭圆上一点A关于原点的对称点为B,F为其左焦点,若AF⊥BF,设∠ABF=α,且α∈,则该椭圆离心率的取值范围为( )
A.[,1] B.[,] C.[,1) D.[,]
【考点】椭圆的几何特征.
【专题】计算题;转化思想;综合法;三角函数的求值;三角函数的图象与性质;圆锥曲线的定义、性质与方程;逻辑思维;运算求解.
【答案】B
【分析】首先利用椭圆的定义整理得a=ccosα+csinα,利用椭圆的离心率关系式的变换,利用三角函数的定义域求出函数的值域,即椭圆的离心率.
【解答】解:如图所示:
已知椭圆的焦点在x轴上,点A关于原点的对称点为B,F为其左焦点,F1为右焦点,
连接AF,BF,BF1,AF1为长方形,
根据椭圆的定义:|AF|+|AF1|=2a,
设∠ABF=α,所以∠AF1F=α,
所以2a=2ccosα+2csinα,
故a=ccosα+csinα,
椭圆的离心率,
由于α∈,
所以,故.
整理得.即椭圆离心率的取值范围为.
故选:B.
【点评】本题考查的知识要点:椭圆的定义,椭圆的离心率,三角函数的关系式的变换,正弦型函数的性质的应用,主要考查学生的运算能力和数学思维能力,属于中档题.
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)(2023 梅州二模)已知函数f(x)=cos2x+|sinx|,则( )
A.f(x)是一个最小正周期为T=2π的周期函数
B.f(x)是一个偶函数
C.f(x)在区间上单调递增
D.f(x)的最小值为0,最大值为
【考点】三角函数的周期性;三角函数的最值;函数的奇偶性.
【专题】计算题;整体思想;综合法;三角函数的图象与性质;运算求解.
【答案】BC
【分析】利用函数周期性的定义可判断A选项;利用函数奇偶性的定义可判断B选项;利用复合函数的单调性可判断C选项;求得,利用二次函数的基本性质可求得函数f(x)的最大值和最小值,可判断D选项.
【解答】解:对于A选项,f(x+π)=cos[2(x+π)]+|sin(x+π)|=cos(2x+2π)+|﹣sinx|
=cos2x+|sinx|=f(x),
所以,函数f(x)为周期函数,且该函数的最小正周期不是2π,A错;
对于B选项,对任意的x∈R,f(﹣x)=cos(﹣2x)+|sin(﹣x)|=cos2x+|sinx|=f(x),
所以,函数f(x)为偶函数,B对;
对于C选项,当时,,
,
令t=sinx,则,因为函数在上单调递减,
函数t=sinx在上单调递减,
由复合函数的单调性可知,函数f(x)在区间上单调递增,C对;
对于D选项,,
因为0≤|sinx|≤1,令,
则二次函数g(u)在上单调递增,在上单调递减,所以,,
又因为g(0)=1,g(1)=0,所以,g(u)min=0,
因此,f(x)的最小值为0,最大值为,D错.
故选:BC.
【点评】本题考查了三角函数的性质,属于中档题.
(多选)10.(6分)(2024秋 贾汪区校级月考)设函数f(x)=2x3﹣3ax2+1,则( )
A.当a>1时,f(x)有三个零点
B.当a<0时,x=0是f(x)的极小值点
C.存在a,b,使得x=b为曲线y=f(x)的对称轴
D.存在a,使得点(1,f(1))为曲线y=f(x)的对称中心
【考点】函数的零点与方程根的关系;利用导数求解函数的极值.
【专题】函数思想;综合法;导数的综合应用;逻辑思维;运算求解.
【答案】ABD
【分析】对于A,先分析出函数的极值点为x=0,x=a,根据零点存在定理和极值的符号判断出f(x)在(﹣1,0),(0,a),(a,2a)上各有一个零点;对于B,根据极值和导函数符号的关系进行分析;对于C,假设存在这样的a,b,使得x=b为f(x)的对称轴,则f(x)=f(2b﹣x)为恒等式,据此计算判断;对于D,若存在这样的a,使得(1,3﹣3a)为f(x)的对称中心,则f(x)+f(2﹣x)=6﹣6a,据此进行计算判断,亦可利用拐点结论直接求解.
【解答】解:对于选项A,由题意可知:f(x)的定义域为R,且f′(x)=6x2﹣6ax=6x(x﹣a),
因为a>1,当x∈(﹣∞,0)∪(a,+∞)时,f′(x)>0;x∈(0,a)时,f′(x)<0;
可知f(x)在(﹣∞,0),(a,+∞)上单调递增,在(0,a)上单调递减,
则f(x)在x=0处取到极大值,在x=a处取到极小值,
且f(0)=1>0,f(a)=1﹣a3<0,f(﹣1)=﹣1﹣3a<0,f(2a)=4a3+1>0,
则f(x)在(﹣∞,0),(0,a),(a,+∞)上各有一个零点,
所以当a>1时,f(x)有三个零点,故A正确;
对于选项B,因为f′(x)=6x(x﹣a),
若a<0,当x∈(a,0)时,f′(x)<0,当x∈(0,+∞)时,f′(x)>0,
可知f(x)在(a,0)内单调递减,在(0,+∞)内单调递增,
所有f(x)在x=0处取到极小值,故B正确;
对于选项C:假设存在这样的a,b,使得x=b为f(x)的对称轴,
即存在这样的a,b使得f(x)=f(2b﹣x),
即2x3﹣3ax2+1=2(2b﹣x)3﹣3a(2b﹣x)2+1,
因为等式右边2(2b﹣x)3展开式含有x3的项为,
可知等式左右两边x3的系数不相等,原等式不可能恒成立,
于是不存在这样的a,b,使得x=b为f(x)的对称轴,C选项错误;
对于选项D:因为f(1)=3﹣3a,
若存在a,使得(1,3﹣3a)为f(x)的对称中心,则f(x)+f(2﹣x)=6﹣6a,
且f(x)+f(2﹣x)=2x3﹣3ax2+1+2(2﹣x)3﹣3a(2﹣x)2+1=(12﹣6a)x2+(12a﹣24)x+18﹣12a,
可得6﹣6a=(12﹣6a)x2+(12a﹣24)x+18﹣12a,则,
解得a=2,所以存在a=2使得(1,f(1))是f(x)的对称中心,故D正确.
故选:ABD.
【点评】本题考查了函数性质的应用及导数的综合应用,考查了函数思想及转化思想,属于中档题.
(多选)11.(6分)(2023秋 蚌山区校级期中)如图,棱长为2的正方体ABCD﹣A1B1C1D1中,P为线段B1D1上动点(包括端点).则下列结论正确的是( )
A.当点P在线段B1D1上运动时,三棱锥P﹣A1BD的体积为定值
B.记过点P平行于平面A1BD的平面为α,α截正方体ABCD﹣A1B1C1D1截得多边形的周长为
C.当点P为B1D1中点时,异面直线A1P与BD所成角为
D.当点P为B1D1中点时,三棱锥P﹣A1BD的外接球表面积为11π
【考点】球的体积和表面积;异面直线及其所成的角;命题的真假判断与应用;棱柱、棱锥、棱台的体积.
【专题】转化思想;综合法;立体几何;逻辑思维;运算求解.
【答案】ACD
【分析】对A,显然B1D1∥平面A1BD,所以P在任何位置时到平面A1BD的距离相等,即可得解;
对B,由P在B1D1上且B1D1∥BD,故截面为△B1CD1,算出周长即可;
对C,当点P为B1D1中点时,由于A1B1C1D1为正方形,所以A1P⊥B1D1,即可得到垂直;
对D,是线面垂直型的外接球问题,当点P为B1D1中点时,A1P⊥B1D1,设△BPD外接圆直径2r,所以三棱锥P﹣A1BD的外接球的直径,即可得解.
【解答】解:对A,由于B1D1∥BD,显然B1D1∥平面A1BD,
又P∈B1D1,所以P在任何位置时到平面A1BD的距离相等,
所以三棱锥P﹣A1BD的体积为定值,故A正确;
对B,由P在B1D1上且B1D1∥BD,故截面为△B1CD1,
所以截面周长为,故B错误;
对C,当点P为B1D1中点时,由于A1B1C1D1为正方形,
所以A1P⊥B1D1,又BD∥B1D1,所以A1P⊥BD,故C正确;
对D,当点P为B1D1中点时,A1P⊥B1D1,
所以在正方体中A1P⊥平面BDP,
由,,
所以,,
所以△BPD外接圆直径,
所以三棱锥P﹣A1BD的外接球的直径,
所以三棱锥P﹣A1BD的外接球表面积为,故D正确;
故选:ACD.
【点评】本题考查三棱锥的体积问题,线面平行的判断,异面直线所成角的求解,三棱锥的外接球问题,属中档题.
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)(2024 碑林区校级模拟)已知,则二项式展开式中的常数项为 15 .
【考点】二项展开式的通项与项的系数.
【专题】计算题;转化思想;综合法;二项式定理;逻辑思维;运算求解.
【答案】15.
【分析】直接利用定积分以及组合数和二项式的展开式求出结果.
【解答】解:由,得二项式为,
其常数项为.
故答案为:15.
【点评】本题考查的知识点:二项式的展开式,组合数,主要考查学生的运算能力,属于中档题.
13.(5分)随机变量X服从正态分布N(μ,σ2),且P(X>4)=P(X<﹣2),则μ= 1 .
【考点】正态分布.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】1.
【分析】利用正态分布曲线的对称性求解.
【解答】解:∵X~N(μ,σ2),且P(X>4)=P(X<﹣2),
∴μ1.
故答案为:1.
【点评】本题主要考查了正态分布曲线的对称性,属于基础题.
14.(5分)(2022春 宾阳县校级月考)△ABC的内角A,B,C的对边分别为a,b,c,已知,,且a>b,则2a+c的最大值为 2 .
【考点】正弦定理.
【专题】计算题;转化思想;综合法;解三角形;运算求解.
【答案】2.
【分析】由正弦定理整理条件可求得B,再由正弦定理可将2a+c转化为2sin(A+φ),其中tanφ,由正弦函数的性质即可求得2a+c的取值范围.
【解答】解:因为asinBcosC+csinBcosA,,
可得sinAsinBcosC+sinCsinBcosAsinB,
所以sinAcosC+sinCcosA,即sin(A+C)=sinB,
所以B或,
因为a>b,所以B,
由正弦定理2,可得:a=2sinA,c=2sinC=2sin(A),
则2a+c=4sinA+2sin(A)=5sinAcosA=2sin(A+φ)≤2,其中tanφ,
则2a+c的最大值为2.
故答案为:2.
【点评】此题考查了两角和与差的正弦函数公式,以及特殊角的三角函数值,正弦定理应用,熟练掌握公式是解本题的关键,属于中档题.
四.解答题(共5小题,满分77分)
15.(13分)(2024春 淮安区期中)某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角△ABC和以BC为直径的半圆拼接而成,点P为半圆上一点(异于B,C),点H在线段AB上,且满足CH⊥AB.已知∠ACB=90°,AB=1dm,设∠ABC=θ.
(1)为了使工艺礼品达到最佳观赏效果,需满足∠ABC=∠PCB,且CA+CP达到最大.当θ为何值时,工艺礼品达到最佳观赏效果?
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足∠PBA=60°,且CH+CP达到最大.当θ为何值时,工艺礼品达到最佳稳定性?并求此时CH+CP的值.
【考点】解三角形.
【专题】应用题;转化思想;综合法;解三角形;运算求解.
【答案】(1)30°,θ;
(2)15°,.
【分析】(1)利用直角三角形的边角关系,求出CA+CP的解析式,从而可得CA+CP取得最大值时θ的值;
(2)由等积法求出CH的值,再计算CH+CP的最大值以及对应的θ值.
【解答】解:(1)由题意可得∠ABC=∠PCB=θ,
因为AB=1dm,
在直角△ABC中,可得AC=sinθ,BC=cosθ,
在直角△PBC中,可得PC=BC cosθ=cosθ cosθ=cos2θ,PB=BC sinθ=sinθ cosθ=sinθcosθ,
可得AC+CP=sinθ+cos2θ
=sinθ+1﹣sin2θ
=﹣sin2θ+sinθ+1
,
所以当,即θ=30°时,AC+CP的最大值为,
即θ=30°时,工艺礼品达到最佳观赏效果;
(2)在直角△ABC中,由,
因为AB=1dm,AC=sinθ,BC=cosθ,
可得CH,
因为∠PBA=60°,
所以在直角△PBC中,PC=BC sin(60°﹣θ)=cosθ (sin60°cosθ﹣cos60°sinθ),
所以,0<θ<60°,
所以CH+CP
sin2θ()sin2θ
,
可得当θ=15°时,工艺礼品达到最佳稳定性,此时CH+CP取得最大值,且最大值为.
【点评】本题考查了解三角形以及三角函数的应用问题,也考查了运算求解能力,是中档题.
16.(15分)某公司对400名求职员工进行业务水平测试,根据测试成绩评定是否预录用.公司对400名求值员工的测试得分(测试得分都在[75,100]内)进行了统计分析,得分不低于90分为“优”,得分低于90分为“良”,得到如下的频率分布直方图和2×2列联表.
男 女 合计
优(得分不低于90分) 80
良(得分低于90分) 120
合计 400
(1)完成上面的2×2列联表、并依据α=0.05的独立性检验,能否认为求职员工的业务水平优良与否与性别有关联;
(2)该公司拟在业务测试成绩为优秀的求职人员中抽取部分人员进行个人发展的问卷调查,以获取采职者的心理需求,进而制定正式录用的方案.按照表中得分为优秀的男女比例分层抽取9个人的样本,并在9人中再随机抽取5人进行调查,记5人中男性的人数为X,求X的分布列以及数学期望.
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;对应思想;定义法;概率与统计;运算求解;数据分析.
【答案】(1)依据小概率值α=0.05的独立性检验,不能认为求职员工的业务水平优良与否与性别有关联;
(2)X的分布列为:
X
2 3 4 5
p
E(X).
【分析】(1)由已知数据完善列联表,计算K2后与临界值比较可得;
(2)求出9人中男性和女性的人数,然后由求出X的各概率得分布列,由期望公式计算期望.
【解答】解:得分不低于90分的人数为:400×(0.04+0.02)×5=120,所以填表如下:
男 女 合计
优(得分不低于90分) 80 40 120
良(得分低于90分) 160 120 280
合计 240 160 400
根据列联表中的数据,经计算得到:
K23.175<3.841=x0.05,
所以依据小概率值α=0.05的独立性检验,不能认为求职员工的业务水平优良与否与性别有关联.
(2)得分为优秀的男女比例为80:40=2:1,所以9人中男性有6人,女性有3人.
因此
X
的可能值为2,3,4,5,
P(X=2);
P(X=3);
P(X=4);
P(X=5).
所以
X
的分布列为:
X
2 3 4 5
p
X
的数学期望为:
E(X)=2345.
【点评】本题考查独立性检验以及离散型随机变量的概率分布列与期望,是中档题.
17.(15分)(2024春 吉林期末)在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,满足DE∥BC且DE经过△ABC的重心,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,M是A1D的中点,如图所示.
(1)求证:A1C⊥平面BCDE;
(2)求CM与平面A1BE所成角的大小;
(3)在线段A1C上是否存在点N,使平面CBM与平面BMN成角余弦值为?若存在,求出CN的长度;若不存在,请说明理由.
【考点】几何法求解直线与平面所成的角;几何法求解二面角及两平面的夹角;直线与平面垂直.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】(1)证明见解析;(2);(3)存在,或.
【分析】(1)应用线面垂直的判定定理证明线面垂直关系,再由性质定理得到线线垂直关系,进而再利用判定定理证明所求证的线面垂直关系;
(2)建立空间直角坐标系.用向量法求CM与平面A1BE所成角的大小;
(3)假设存在点N,使平面CBM与平面BMN成角余弦值为,设,分别求解两平面的法向量,用λ表示余弦值解方程可得.
【解答】解:(1)证明:因为在Rt△ABC中,∠C=90°,DE∥BC,且BC⊥CD,
所以DE⊥CD,DE⊥AD,则折叠后,DE⊥A1D,
又A1D∩CD=D,A1D,CD 平面A1CD,
所以DE⊥平面A1CD,A1C 平面A1CD,
所以DE⊥A1C,
又已知A1C⊥CD,CD∩DE=D,且都在面BCDE内,
所以A1C⊥平面BCDE;
(2)由(1),分别以CD,CB,CA1所在直线为x轴,y轴,z轴,建立空间直角坐标系C﹣xyz,
因为AD=2CD,故,
由几何关系可知,CD=2,A1D=4,,
故C(0,0,0),D(2,0,0),E(2,2,0),B(0,3,0),,,
,,,
设平面A1BE的法向量为,
则,
不妨令y=2,则,x=1,
所以,
设CM与平面A1BE所成角的大小为θ,
则有,
故,
即CM与平面A1BE所成角的大小为;
(3)假设在线段AC上存在点N,使平面CBM与平面BMN成角余弦值为,
在空间直角坐标系中,,,,
设,则,,
设平面BMN的先向量为,
则,
不妨令,则y2=2λ,x2=6λ﹣3,
所以,
设平面CBM的法向量为,
则,
不妨令,则x3=﹣3,y3=0,
所以,
若平面CBM与平面BMN成角余弦值为,
则满足,
化简得2λ2﹣3λ+1=0,
解得λ=1或,
即或,
故在线段A1C上存在这样的点N,使平面CBM与平面BMN成角余弦值为,此时CN的长度为或.
【点评】本题考查线面垂直的判定以及空间向量的应用,属于中档题.
18.(17分)(2024秋 渝北区校级月考)已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…).
(1)求证:数列{an}是等差数列;
(2)设bn=12﹣an,记Tn=|b1|+|b2|+|b3|+…+|bn|,求T3和T30之值.
【考点】数列递推式;等差数列的概念与判定;等比数列的概念与判定;数列的求和.
【专题】转化思想;综合法;等差数列与等比数列;运算求解.
【答案】(1)证明见解答;(2)T3=27,T30=612.
【分析】(1)由数列的通项与求和的关系,结合等差数列的定义可得证明;
(2)由等差数列的通项公式求得bn,讨论bn的符号,再由等差数列的求和公式,可得所求和.
【解答】解:(1)证明:正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3…),
可得4a1=4S1=(a1+1)2,解得a1=1;
当n≥2时,由4Sn=(an+1)2,可得4Sn﹣1=(an﹣1+1)2,
相减可得4an=(an+1)2﹣(an﹣1+1)2,即为(an﹣1)2=(an﹣1+1)2,
化为(an+an﹣1)(an﹣an﹣1﹣2)=0,
由an>0,可得an﹣an﹣1=2,则数列{an}是首项为1,公差为2的等差数列;
(2)bn=12﹣an=12﹣(2n﹣1)=13﹣2n,
当1≤n≤6时,bn>0,Tnn(11+13﹣2n)=12n﹣n2;
当n≥7时,bn<0,Tn=b1+b2+...+b6﹣b7﹣b8﹣...﹣bn=12×6﹣36(n﹣6)(﹣1+13﹣2n)
=36+(n﹣6)2,
则T3=36﹣9=27,
T30=36+242=612.
【点评】本题考查数列的通项与求和的关系,以及等差数列的通项公式与求和公式,考查转化思想和运算能力,属于中档题.
19.(17分)(2025 河南模拟)已知f(x)=eaxsin2x﹣2ax,且曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0.
(1)求a的值;
(2)设f(x)的导函数为g(x),求g(x)的单调区间;
(3)证明:当时,f(x)<2.
【考点】利用导数求解函数的单调性和单调区间;利用导数求解函数的最值;利用导数求解曲线在某点上的切线方程.
【专题】转化思想;转化法;导数的综合应用;运算求解.
【答案】(1)2;(2)单调递增区间为,单调递减区间为;(3)证明见解析.
【分析】(1)求出函数的导函数,根据f′(0)=﹣2计算可得;
(2)求出g(x)的解析式,从而求出其导函数,再解关于导函数的不等式,即可求出函数的单调区间;
(3)由(2)可得g(x)的单调性,结合零点存在性定理得到,使得g(x0)=0,即可得到f(x)的单调性,从而求出f(x)max,即可得证.
【解答】解:(1)因为f(x)=eaxsin2x﹣2ax,
所以f′(x)=aeaxsin2x+2eaxcos2x﹣2a,
因为曲线y=f(x)在点(0,f(0))处的切线方程为2x+y=0,
所以f′(0)=2﹣2a=﹣2,
解得a=2;
(2)由(1)可得f(x)=e2xsin2x﹣4x,
所以f′(x)=2e2xsin2x+2e2xcos2x﹣4,
则g(x)=f′(x)=2e2x(sin2x+cos2x)﹣4,定义域为R,
所以g′(x)=2[2e2x(sin2x+cos2x)+e2x(2cos2x﹣2sin2x)]=8e2xcos2x,
因为e2x>0,
令g′(x)<0,即cos2x<0,
解得,
所以g(x)的单调递减区间为,
令g′(x)>0,即cos2x>0,
解得;
所以g(x)的单调递增区间为;
(3)证明:由(2)可知g(x)在上单调递增,
又g(0)=﹣2<0,,
又,
所以e(sin1+cos1)﹣2>e2>0,即,
所以,使得g(x0)=0,
当时g(x)>0,即f′(x)>0,所以f(x)在上单调递增;
当时g(x)<0,即f′(x)<0,所以f(x)在上单调递减;
又,,
所以,
所以当时,f(x)<2.
【点评】本题考查利用导数证明或判定不等式问题,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
