【期末押题预测】期末核心考点 随机抽样(含解析)2024-2025学年高一下学期数学人教A版(2019)
文档属性
| 名称 | 【期末押题预测】期末核心考点 随机抽样(含解析)2024-2025学年高一下学期数学人教A版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 368.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 10:48:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 随机抽样
一.选择题(共7小题)
1.(2025春 辽宁月考)某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,用分层随机抽样的方法从中抽取130件产品进行质量检测,则A类与B类产品共抽取的件数为( )
A.110 B.90 C.60 D.50
2.(2025 西安校级学业考试)某厂质检员利用随机数表对生产的600个产品进行抽样调查,先将这600个产品进行编号:001,002,003,…,600.从中抽取120个样本,下图是随机数表的第2行到第3行,若从随机数表的第2行第5列开始从左向右读取数据,则得到的第5个编号是( )
32 12 67 12 31 02 37 02 14 72 31 09 81 47 80 25 13 25 46 08
71 20 34 51 19 72 01 38 47 18 04 92 51 28 02 31 27 46 51 30
A.098 B.147 C.513 D.310
3.(2025 青岛模拟)某市开展“全民阅读”实施效果的调查研究,按区域划分为核心区、开发区、远郊区,各区的人口比例为2:3:4.现采用分层抽样的方法从各区中抽取人员进行调研,已知从开发区抽取的人数为300,则从核心区抽取的人数为( )
A.90 B.120 C.180 D.200
4.(2025春 浦东新区校级期中)在以下调查中,适合用普查的是( )
A.调查某批次汽车的抗撞击能力
B.调查一批LED灯的寿命
C.调查某城市居民的食品消费结构
D.调查一个班级学生的身高情况
5.(2025 南开区二模)某中学三个不同选课组合的学生在一次高三质量监测的数学平均分分别为a,b,c,若按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,则估计这三个不同选课组合学生的数学平均分为( )
A. B.
C. D.
6.(2025春 清远期中)教育局为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从市一中的美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20、30、50名学生,则不同的抽样结果共有( )
A. B.
C. D.
7.(2025 通辽三模)某中学有高中生1000人,初中生3000人.为了解学生的身心发展情况,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,则抽中的高中生人数为( )
A.5 B.10 C.20 D.30
二.多选题(共3小题)
(多选)8.(2025 乐陵市校级模拟)某校高二年级有男生600人,女生400人,张华按男生、女生进行分层,通过分层抽样的方法,得到一个总样本量为100的样本,计算得到男生、女生的平均身高分别为170cm和160cm,方差分别为15和30,则下列说法正确的有( )
A.若张华采用样本量比例分配的方式进行抽样,则男生、女生分别应抽取60人和40人
B.若张华采用样本量比例分配的方式进行抽样,则样本的方差为37.8
C.若张华采用样本量比例分配的方式进行抽样,则样本的平均数为166,此时可用样本平均数估计总体的平均数
D.若张华采用等额抽取,即男生、女生分别抽取50人,则某男生甲被抽到的概率为.
(多选)9.(2025 昆明一模)某校有男生m人,女生n人,且男生身高的均值为,方差为,女生身高的均值为,方差为,全体学生身高均值和方差分别为,S2,则下列说法一定正确的是( )
A.若,则
B.若m=n,则
C.若,则
D.若m=n,则
(多选)10.(2024秋 平凉校级期末)珠江源位于云南东部曲靖市以北47公里处,整个景区由马雄山珠江源、花山湖和城区部分景点组成,总面积50平方公里.珠江源风景区是森林公园、省级风景名胜区、国际水利风景名胜区.景区森林茂密,溪流淙淙,有“一水滴三江,一脉隔双盘”的奇异景观.其美景吸引着大批的游客前往参观,某旅行社分年龄段统计了前往珠江源的老、中、青旅客的人数比为5:2:3,现使用分层随机抽样的方法从这些旅客中随机抽取n名,若青年旅客抽到90人,则下列说法正确的是( )
A.被抽到的老年旅客和中年旅客人数之和超过200
B.n=300
C.中年旅客抽到40人
D.老年旅客抽到150人
三.填空题(共3小题)
11.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 .
12.(2025 浦东新区模拟)浦东某学校有学生2000人,为了加强学生的锻炼意识,学校举行了跑步和登山比赛,每人都参加且只能参加其中一项比赛,各年级参加比赛的人数情况如表所示:
高一年级 高二年级 高三年级
跑步人数(单位:人) a b c
登山人数(单位:人) x y z
其中a:b:c=2:5:3,参加登山的人数占总人数的,为了解学生对本次比赛的满意程度,按分层抽样的方式从中抽取一个200人的样本进行调查,则高三年级参加跑步的学生中应抽取 人.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
四.解答题(共2小题)
14.(2025春 武威月考)某志愿者组织有男成员48人,其中35岁以上的有12人;有女成员36人,其中35岁以上的有18人.
(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,那么男、女成员各应抽取多少人?
(2)如果按照年龄进行分层抽样,要抽取一个容量为28的样本,那么35岁以上的成员应抽取多少人?
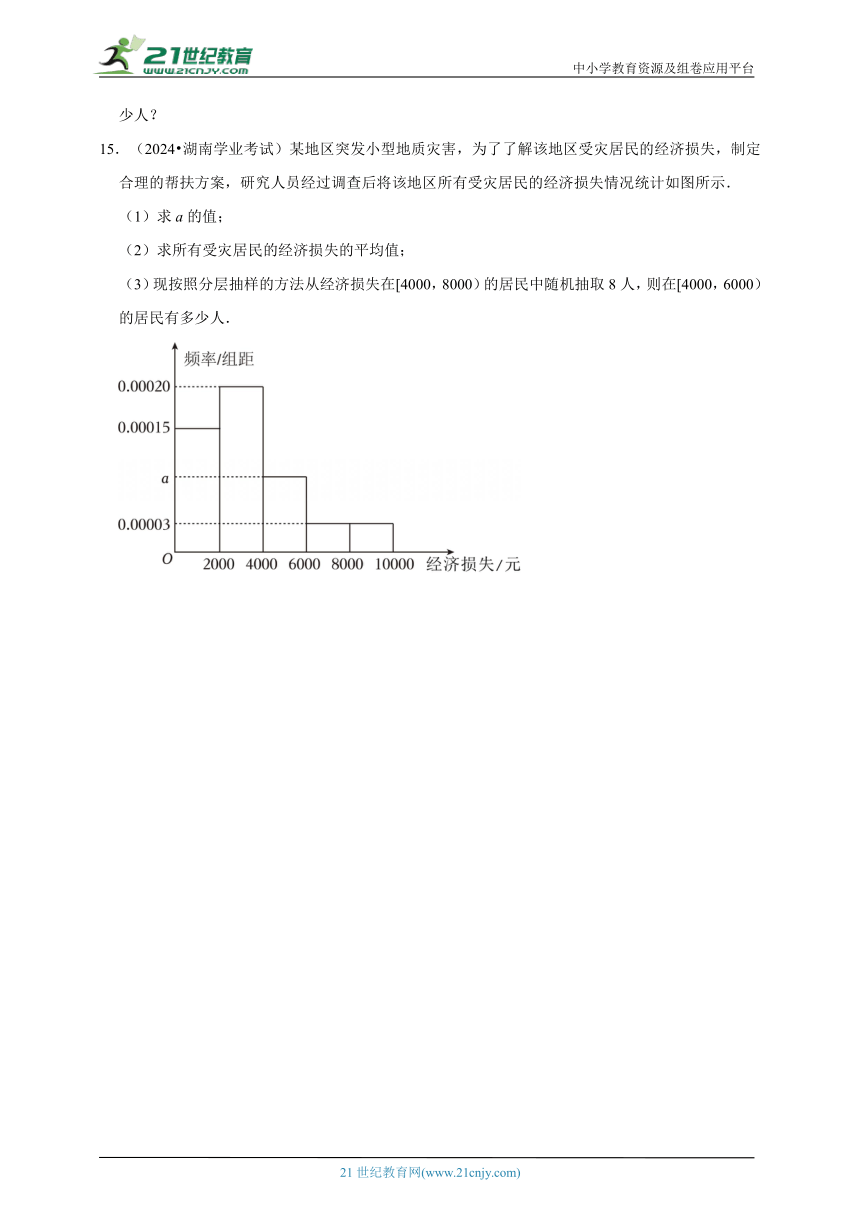
15.(2024 湖南学业考试)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
期末核心考点 随机抽样
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 辽宁月考)某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,用分层随机抽样的方法从中抽取130件产品进行质量检测,则A类与B类产品共抽取的件数为( )
A.110 B.90 C.60 D.50
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】对应思想;定义法;概率与统计;运算求解.
【答案】A
【分析】由分层抽样抽样比即可求解.
【解答】解:某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,
用分层随机抽样的方法从中抽取130件产品进行质量检测,
设A类与B类产品共抽取的件数为t,
由题意,可得,
解得t=110.
故选:A.
【点评】本题考查分层抽样相关知识,属于基础题.
2.(2025 西安校级学业考试)某厂质检员利用随机数表对生产的600个产品进行抽样调查,先将这600个产品进行编号:001,002,003,…,600.从中抽取120个样本,下图是随机数表的第2行到第3行,若从随机数表的第2行第5列开始从左向右读取数据,则得到的第5个编号是( )
32 12 67 12 31 02 37 02 14 72 31 09 81 47 80 25 13 25 46 08
71 20 34 51 19 72 01 38 47 18 04 92 51 28 02 31 27 46 51 30
A.098 B.147 C.513 D.310
【考点】求随机数法抽样的样本.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】C
【分析】根据随机数表的读法读出前5个符合的编号即可得解.
【解答】解:由题意可知,从随机数表的第2行第5列开始从左向右读取数据,
得到的编号依次为231,023,147,098,513,…,
则得到的第5个编号是513.
故选:C.
【点评】本题主要考查了随机数法的应用,属于基础题.
3.(2025 青岛模拟)某市开展“全民阅读”实施效果的调查研究,按区域划分为核心区、开发区、远郊区,各区的人口比例为2:3:4.现采用分层抽样的方法从各区中抽取人员进行调研,已知从开发区抽取的人数为300,则从核心区抽取的人数为( )
A.90 B.120 C.180 D.200
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】D
【分析】结合分层抽样的定义,即可求解.
【解答】解:设从核心区抽取的人数为x,
由题意可知,,解得x=200.
故选:D.
【点评】本题主要考查分层抽样的应用,属于基础题.
4.(2025春 浦东新区校级期中)在以下调查中,适合用普查的是( )
A.调查某批次汽车的抗撞击能力
B.调查一批LED灯的寿命
C.调查某城市居民的食品消费结构
D.调查一个班级学生的身高情况
【考点】普查与抽样.
【专题】对应思想;定义法;概率与统计;逻辑思维.
【答案】D
【分析】根据普查的概念判断即可.
【解答】解:A选项,每个批次生产的汽车的数量非常多,且调查汽车抗重击能力具有破坏性,不适合使用普查,应使用抽样调查,选项A错误;
B选项,调查一批LED灯的寿命具有破坏性,不宜使用普查,应使用抽样调查,选项B错误;
C选项,某城市居民数量非常多,不适合使用全面普查,应使用抽样调查,选项C错误;
D选项,一个班级学生的身高情况,人数较少,适合用普查,选项D正确.
故选:D.
【点评】本题考查普查和抽样调查的概念与区别,属于基础题.
5.(2025 南开区二模)某中学三个不同选课组合的学生在一次高三质量监测的数学平均分分别为a,b,c,若按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,则估计这三个不同选课组合学生的数学平均分为( )
A. B.
C. D.
【考点】由分层随机抽样的样本平均数估计总体平均数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】C
【分析】结合分层抽样的定义,以及平均数公式,即可求解.
【解答】解:按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,
则占比为,
高三质量监测的数学平均分分别为a,b,c,
则估计这三个不同选课组合学生的数学平均分为.
故选:C.
【点评】本题主要考查分层抽样的定义,属于基础题.
6.(2025春 清远期中)教育局为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从市一中的美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20、30、50名学生,则不同的抽样结果共有( )
A. B.
C. D.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】整体思想;综合法;排列组合;运算求解.
【答案】C
【分析】根据分层抽样的定义,分别求出每个兴趣小组要抽取的学生人数,结合分步乘法计数原理计算即可.
【解答】解:由题意,美术组要抽取的学生数为,音乐组要抽取的学生数为,
舞蹈组要抽取的学生数为,
所以不同的抽样结果.
故选:C.
【点评】本题主要考查了分层抽样的定义,考查了组合数的定义,以及计数原理的应用,属于基础题.
7.(2025 通辽三模)某中学有高中生1000人,初中生3000人.为了解学生的身心发展情况,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,则抽中的高中生人数为( )
A.5 B.10 C.20 D.30
【考点】分层随机抽样.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】C
【分析】计算分层抽样的抽取比例乘以样本容量可得答案.
【解答】解:由题意中学有高中生1000人,初中生3000人,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,
则抽中的高中生人数为8020.
故选:C.
【点评】本题考查了分层抽样,是基础题.
二.多选题(共3小题)
(多选)8.(2025 乐陵市校级模拟)某校高二年级有男生600人,女生400人,张华按男生、女生进行分层,通过分层抽样的方法,得到一个总样本量为100的样本,计算得到男生、女生的平均身高分别为170cm和160cm,方差分别为15和30,则下列说法正确的有( )
A.若张华采用样本量比例分配的方式进行抽样,则男生、女生分别应抽取60人和40人
B.若张华采用样本量比例分配的方式进行抽样,则样本的方差为37.8
C.若张华采用样本量比例分配的方式进行抽样,则样本的平均数为166,此时可用样本平均数估计总体的平均数
D.若张华采用等额抽取,即男生、女生分别抽取50人,则某男生甲被抽到的概率为.
【考点】分层随机抽样;用样本估计总体的集中趋势参数;用样本估计总体的离散程度参数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】AC
【分析】根据分层抽样、方差、平均数、古典概型等知识对选项进行分析,从而确定正确答案.
【解答】解:A选项,男生抽取,女生抽取10﹣60=40人,A选项正确;
C选项,样本平均数为,可以用样本平均数估计总体的平均数,C选项正确;
B选项,样本方差为,所以B选项错误;
D选项,男生甲被抽到的概率为,D选项错误.
故选:AC.
【点评】本题主要考查分层抽样方法,属于基础题.
(多选)9.(2025 昆明一模)某校有男生m人,女生n人,且男生身高的均值为,方差为,女生身高的均值为,方差为,全体学生身高均值和方差分别为,S2,则下列说法一定正确的是( )
A.若,则
B.若m=n,则
C.若,则
D.若m=n,则
【考点】由分层随机抽样的样本平均数估计总体平均数;平均数;方差.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】ABD
【分析】根据题意,利用分层抽样中数据的平均数与方差的计算公式,分别求得和S2的表达式,结合选项,逐项求解,即可得到答案.
【解答】解:对于A,若,
则,
所以,故A正确;
对于B,若m=n,则,故B正确;
对于C,若,可得,
则,
又由,
此时无法判定的符号,故C错误;
对于D,若m=n,
则,故D正确.
故选:ABD.
【点评】本题主要考查了分层随机抽样的平均数公式和方差公式,属于基础题.
(多选)10.(2024秋 平凉校级期末)珠江源位于云南东部曲靖市以北47公里处,整个景区由马雄山珠江源、花山湖和城区部分景点组成,总面积50平方公里.珠江源风景区是森林公园、省级风景名胜区、国际水利风景名胜区.景区森林茂密,溪流淙淙,有“一水滴三江,一脉隔双盘”的奇异景观.其美景吸引着大批的游客前往参观,某旅行社分年龄段统计了前往珠江源的老、中、青旅客的人数比为5:2:3,现使用分层随机抽样的方法从这些旅客中随机抽取n名,若青年旅客抽到90人,则下列说法正确的是( )
A.被抽到的老年旅客和中年旅客人数之和超过200
B.n=300
C.中年旅客抽到40人
D.老年旅客抽到150人
【考点】分层随机抽样.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】ABD
【分析】利用分层抽样的方法求出n,然后分别求出各段抽取的人数逐项分析即可.
【解答】解:由题意从这些旅客中随机抽取n名,青年旅客抽到90人,
老、中、青旅客的人数比为5:2:3,
则,
所以n=300,故B正确;
则中年旅客抽到人,故C错误;
老年旅客抽到人,故D正确;
被抽到的老年旅客和中年旅客人数之和为60+150=210人超过200人,
故A正确.
故选:ABD.
【点评】本题主要考查分层抽样的应用,考查计算能力,属于基础题.
三.填空题(共3小题)
11.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 120,110,90 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】对应思想;定义法;概率与统计;运算求解.
【答案】120,110,90.
【分析】先求出各层比例,根据分层抽样的定义建立式子计算即可得到结论..
【解答】解:某地区有小学生12000人,初中生11000人,高中生9000人
所占的人数的比例分别为12000:11000:9000=12:11:9,
故抽取的小学生,初中生,高中生的人数分别.
故答案为:120,110,90.
【点评】本题考查分层抽样的应用,属于基础题.
12.(2025 浦东新区模拟)浦东某学校有学生2000人,为了加强学生的锻炼意识,学校举行了跑步和登山比赛,每人都参加且只能参加其中一项比赛,各年级参加比赛的人数情况如表所示:
高一年级 高二年级 高三年级
跑步人数(单位:人) a b c
登山人数(单位:人) x y z
其中a:b:c=2:5:3,参加登山的人数占总人数的,为了解学生对本次比赛的满意程度,按分层抽样的方式从中抽取一个200人的样本进行调查,则高三年级参加跑步的学生中应抽取 45 人.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】45.
【分析】先求得参与跑步的总人数,再乘以抽样比例,得出样本中参与跑步的人数.
【解答】解:全校参与跑步有20001500人,高三年级参与跑步的学生=150045人.
故答案为:45.
【点评】本题主要考查了分成抽样,分层抽样又称按比例抽样,是高考中常见的题型,同时考查了分析问题、解决问题的能力,属于基础题.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】15.
【分析】确定抽样比,即可求解;
【解答】解:某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,
该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,
采取分层抽样,且按年级来分层,
由题意可知抽样比为:,
∴高一年级应抽取的人数是.
故答案为:15.
【点评】本题考查分层抽样等基础知识,考查运算求解能力,是基础题.
四.解答题(共2小题)
14.(2025春 武威月考)某志愿者组织有男成员48人,其中35岁以上的有12人;有女成员36人,其中35岁以上的有18人.
(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,那么男、女成员各应抽取多少人?
(2)如果按照年龄进行分层抽样,要抽取一个容量为28的样本,那么35岁以上的成员应抽取多少人?
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】(1)应该抽取男成员12人,女成员9人;
(2)35岁以上的成员应抽取10人.
【分析】由分层抽样的原理求解即可.
【解答】解:(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,
则男成员应该抽取人,
女成员应该抽取人.
(2)由题意可知35岁以上的成员应抽取人.
【点评】本题主要考查分层抽样的原理,属于基础题.
15.(2024 湖南学业考试)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
【考点】分层随机抽样;频率分布直方图.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】(1)a=0.00009;
(2)3360元;
(3)6.
【分析】(1)根据直方图中频率和为1列方程求参数;
(2)根据直方图计算平均值;
(3)根据分层抽样的等比例性质求在[4000,6000)的居民数量.
【解答】解:(1)依题意,(0.00003×2+a+0.00015+0.0002)×2000=1,解得a=0.00009.
(2)所有受灾居民经济损失的平均值为1000×0.3+3000×0.4+5000×0.18+7000×0.06+9000×0.06=3360元.
(3)由(1)得经济损失在[4000,6000)和在[6000,8000)的人数比例为3:1,
由分层抽样知,经济损失在[4000,6000)的居民有人.
【点评】本题主要考查频率分布直方图的应用,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 随机抽样
一.选择题(共7小题)
1.(2025春 辽宁月考)某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,用分层随机抽样的方法从中抽取130件产品进行质量检测,则A类与B类产品共抽取的件数为( )
A.110 B.90 C.60 D.50
2.(2025 西安校级学业考试)某厂质检员利用随机数表对生产的600个产品进行抽样调查,先将这600个产品进行编号:001,002,003,…,600.从中抽取120个样本,下图是随机数表的第2行到第3行,若从随机数表的第2行第5列开始从左向右读取数据,则得到的第5个编号是( )
32 12 67 12 31 02 37 02 14 72 31 09 81 47 80 25 13 25 46 08
71 20 34 51 19 72 01 38 47 18 04 92 51 28 02 31 27 46 51 30
A.098 B.147 C.513 D.310
3.(2025 青岛模拟)某市开展“全民阅读”实施效果的调查研究,按区域划分为核心区、开发区、远郊区,各区的人口比例为2:3:4.现采用分层抽样的方法从各区中抽取人员进行调研,已知从开发区抽取的人数为300,则从核心区抽取的人数为( )
A.90 B.120 C.180 D.200
4.(2025春 浦东新区校级期中)在以下调查中,适合用普查的是( )
A.调查某批次汽车的抗撞击能力
B.调查一批LED灯的寿命
C.调查某城市居民的食品消费结构
D.调查一个班级学生的身高情况
5.(2025 南开区二模)某中学三个不同选课组合的学生在一次高三质量监测的数学平均分分别为a,b,c,若按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,则估计这三个不同选课组合学生的数学平均分为( )
A. B.
C. D.
6.(2025春 清远期中)教育局为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从市一中的美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20、30、50名学生,则不同的抽样结果共有( )
A. B.
C. D.
7.(2025 通辽三模)某中学有高中生1000人,初中生3000人.为了解学生的身心发展情况,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,则抽中的高中生人数为( )
A.5 B.10 C.20 D.30
二.多选题(共3小题)
(多选)8.(2025 乐陵市校级模拟)某校高二年级有男生600人,女生400人,张华按男生、女生进行分层,通过分层抽样的方法,得到一个总样本量为100的样本,计算得到男生、女生的平均身高分别为170cm和160cm,方差分别为15和30,则下列说法正确的有( )
A.若张华采用样本量比例分配的方式进行抽样,则男生、女生分别应抽取60人和40人
B.若张华采用样本量比例分配的方式进行抽样,则样本的方差为37.8
C.若张华采用样本量比例分配的方式进行抽样,则样本的平均数为166,此时可用样本平均数估计总体的平均数
D.若张华采用等额抽取,即男生、女生分别抽取50人,则某男生甲被抽到的概率为.
(多选)9.(2025 昆明一模)某校有男生m人,女生n人,且男生身高的均值为,方差为,女生身高的均值为,方差为,全体学生身高均值和方差分别为,S2,则下列说法一定正确的是( )
A.若,则
B.若m=n,则
C.若,则
D.若m=n,则
(多选)10.(2024秋 平凉校级期末)珠江源位于云南东部曲靖市以北47公里处,整个景区由马雄山珠江源、花山湖和城区部分景点组成,总面积50平方公里.珠江源风景区是森林公园、省级风景名胜区、国际水利风景名胜区.景区森林茂密,溪流淙淙,有“一水滴三江,一脉隔双盘”的奇异景观.其美景吸引着大批的游客前往参观,某旅行社分年龄段统计了前往珠江源的老、中、青旅客的人数比为5:2:3,现使用分层随机抽样的方法从这些旅客中随机抽取n名,若青年旅客抽到90人,则下列说法正确的是( )
A.被抽到的老年旅客和中年旅客人数之和超过200
B.n=300
C.中年旅客抽到40人
D.老年旅客抽到150人
三.填空题(共3小题)
11.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 .
12.(2025 浦东新区模拟)浦东某学校有学生2000人,为了加强学生的锻炼意识,学校举行了跑步和登山比赛,每人都参加且只能参加其中一项比赛,各年级参加比赛的人数情况如表所示:
高一年级 高二年级 高三年级
跑步人数(单位:人) a b c
登山人数(单位:人) x y z
其中a:b:c=2:5:3,参加登山的人数占总人数的,为了解学生对本次比赛的满意程度,按分层抽样的方式从中抽取一个200人的样本进行调查,则高三年级参加跑步的学生中应抽取 人.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
四.解答题(共2小题)
14.(2025春 武威月考)某志愿者组织有男成员48人,其中35岁以上的有12人;有女成员36人,其中35岁以上的有18人.
(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,那么男、女成员各应抽取多少人?
(2)如果按照年龄进行分层抽样,要抽取一个容量为28的样本,那么35岁以上的成员应抽取多少人?
15.(2024 湖南学业考试)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
期末核心考点 随机抽样
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 辽宁月考)某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,用分层随机抽样的方法从中抽取130件产品进行质量检测,则A类与B类产品共抽取的件数为( )
A.110 B.90 C.60 D.50
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】对应思想;定义法;概率与统计;运算求解.
【答案】A
【分析】由分层抽样抽样比即可求解.
【解答】解:某工厂生产了A类、B类、C类三种产品各1080件、900件、360件,
用分层随机抽样的方法从中抽取130件产品进行质量检测,
设A类与B类产品共抽取的件数为t,
由题意,可得,
解得t=110.
故选:A.
【点评】本题考查分层抽样相关知识,属于基础题.
2.(2025 西安校级学业考试)某厂质检员利用随机数表对生产的600个产品进行抽样调查,先将这600个产品进行编号:001,002,003,…,600.从中抽取120个样本,下图是随机数表的第2行到第3行,若从随机数表的第2行第5列开始从左向右读取数据,则得到的第5个编号是( )
32 12 67 12 31 02 37 02 14 72 31 09 81 47 80 25 13 25 46 08
71 20 34 51 19 72 01 38 47 18 04 92 51 28 02 31 27 46 51 30
A.098 B.147 C.513 D.310
【考点】求随机数法抽样的样本.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】C
【分析】根据随机数表的读法读出前5个符合的编号即可得解.
【解答】解:由题意可知,从随机数表的第2行第5列开始从左向右读取数据,
得到的编号依次为231,023,147,098,513,…,
则得到的第5个编号是513.
故选:C.
【点评】本题主要考查了随机数法的应用,属于基础题.
3.(2025 青岛模拟)某市开展“全民阅读”实施效果的调查研究,按区域划分为核心区、开发区、远郊区,各区的人口比例为2:3:4.现采用分层抽样的方法从各区中抽取人员进行调研,已知从开发区抽取的人数为300,则从核心区抽取的人数为( )
A.90 B.120 C.180 D.200
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】D
【分析】结合分层抽样的定义,即可求解.
【解答】解:设从核心区抽取的人数为x,
由题意可知,,解得x=200.
故选:D.
【点评】本题主要考查分层抽样的应用,属于基础题.
4.(2025春 浦东新区校级期中)在以下调查中,适合用普查的是( )
A.调查某批次汽车的抗撞击能力
B.调查一批LED灯的寿命
C.调查某城市居民的食品消费结构
D.调查一个班级学生的身高情况
【考点】普查与抽样.
【专题】对应思想;定义法;概率与统计;逻辑思维.
【答案】D
【分析】根据普查的概念判断即可.
【解答】解:A选项,每个批次生产的汽车的数量非常多,且调查汽车抗重击能力具有破坏性,不适合使用普查,应使用抽样调查,选项A错误;
B选项,调查一批LED灯的寿命具有破坏性,不宜使用普查,应使用抽样调查,选项B错误;
C选项,某城市居民数量非常多,不适合使用全面普查,应使用抽样调查,选项C错误;
D选项,一个班级学生的身高情况,人数较少,适合用普查,选项D正确.
故选:D.
【点评】本题考查普查和抽样调查的概念与区别,属于基础题.
5.(2025 南开区二模)某中学三个不同选课组合的学生在一次高三质量监测的数学平均分分别为a,b,c,若按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,则估计这三个不同选课组合学生的数学平均分为( )
A. B.
C. D.
【考点】由分层随机抽样的样本平均数估计总体平均数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】C
【分析】结合分层抽样的定义,以及平均数公式,即可求解.
【解答】解:按不同选课组合采用分层抽样的方法抽取了一个120人的样本,抽到三个不同选课组合的学生人数分别为20,40,60,
则占比为,
高三质量监测的数学平均分分别为a,b,c,
则估计这三个不同选课组合学生的数学平均分为.
故选:C.
【点评】本题主要考查分层抽样的定义,属于基础题.
6.(2025春 清远期中)教育局为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从市一中的美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20、30、50名学生,则不同的抽样结果共有( )
A. B.
C. D.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】整体思想;综合法;排列组合;运算求解.
【答案】C
【分析】根据分层抽样的定义,分别求出每个兴趣小组要抽取的学生人数,结合分步乘法计数原理计算即可.
【解答】解:由题意,美术组要抽取的学生数为,音乐组要抽取的学生数为,
舞蹈组要抽取的学生数为,
所以不同的抽样结果.
故选:C.
【点评】本题主要考查了分层抽样的定义,考查了组合数的定义,以及计数原理的应用,属于基础题.
7.(2025 通辽三模)某中学有高中生1000人,初中生3000人.为了解学生的身心发展情况,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,则抽中的高中生人数为( )
A.5 B.10 C.20 D.30
【考点】分层随机抽样.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】C
【分析】计算分层抽样的抽取比例乘以样本容量可得答案.
【解答】解:由题意中学有高中生1000人,初中生3000人,按比例采用分层随机抽样的方法从该校学生中抽取一个容量为80的样本,
则抽中的高中生人数为8020.
故选:C.
【点评】本题考查了分层抽样,是基础题.
二.多选题(共3小题)
(多选)8.(2025 乐陵市校级模拟)某校高二年级有男生600人,女生400人,张华按男生、女生进行分层,通过分层抽样的方法,得到一个总样本量为100的样本,计算得到男生、女生的平均身高分别为170cm和160cm,方差分别为15和30,则下列说法正确的有( )
A.若张华采用样本量比例分配的方式进行抽样,则男生、女生分别应抽取60人和40人
B.若张华采用样本量比例分配的方式进行抽样,则样本的方差为37.8
C.若张华采用样本量比例分配的方式进行抽样,则样本的平均数为166,此时可用样本平均数估计总体的平均数
D.若张华采用等额抽取,即男生、女生分别抽取50人,则某男生甲被抽到的概率为.
【考点】分层随机抽样;用样本估计总体的集中趋势参数;用样本估计总体的离散程度参数.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】AC
【分析】根据分层抽样、方差、平均数、古典概型等知识对选项进行分析,从而确定正确答案.
【解答】解:A选项,男生抽取,女生抽取10﹣60=40人,A选项正确;
C选项,样本平均数为,可以用样本平均数估计总体的平均数,C选项正确;
B选项,样本方差为,所以B选项错误;
D选项,男生甲被抽到的概率为,D选项错误.
故选:AC.
【点评】本题主要考查分层抽样方法,属于基础题.
(多选)9.(2025 昆明一模)某校有男生m人,女生n人,且男生身高的均值为,方差为,女生身高的均值为,方差为,全体学生身高均值和方差分别为,S2,则下列说法一定正确的是( )
A.若,则
B.若m=n,则
C.若,则
D.若m=n,则
【考点】由分层随机抽样的样本平均数估计总体平均数;平均数;方差.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】ABD
【分析】根据题意,利用分层抽样中数据的平均数与方差的计算公式,分别求得和S2的表达式,结合选项,逐项求解,即可得到答案.
【解答】解:对于A,若,
则,
所以,故A正确;
对于B,若m=n,则,故B正确;
对于C,若,可得,
则,
又由,
此时无法判定的符号,故C错误;
对于D,若m=n,
则,故D正确.
故选:ABD.
【点评】本题主要考查了分层随机抽样的平均数公式和方差公式,属于基础题.
(多选)10.(2024秋 平凉校级期末)珠江源位于云南东部曲靖市以北47公里处,整个景区由马雄山珠江源、花山湖和城区部分景点组成,总面积50平方公里.珠江源风景区是森林公园、省级风景名胜区、国际水利风景名胜区.景区森林茂密,溪流淙淙,有“一水滴三江,一脉隔双盘”的奇异景观.其美景吸引着大批的游客前往参观,某旅行社分年龄段统计了前往珠江源的老、中、青旅客的人数比为5:2:3,现使用分层随机抽样的方法从这些旅客中随机抽取n名,若青年旅客抽到90人,则下列说法正确的是( )
A.被抽到的老年旅客和中年旅客人数之和超过200
B.n=300
C.中年旅客抽到40人
D.老年旅客抽到150人
【考点】分层随机抽样.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】ABD
【分析】利用分层抽样的方法求出n,然后分别求出各段抽取的人数逐项分析即可.
【解答】解:由题意从这些旅客中随机抽取n名,青年旅客抽到90人,
老、中、青旅客的人数比为5:2:3,
则,
所以n=300,故B正确;
则中年旅客抽到人,故C错误;
老年旅客抽到人,故D正确;
被抽到的老年旅客和中年旅客人数之和为60+150=210人超过200人,
故A正确.
故选:ABD.
【点评】本题主要考查分层抽样的应用,考查计算能力,属于基础题.
三.填空题(共3小题)
11.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 120,110,90 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】对应思想;定义法;概率与统计;运算求解.
【答案】120,110,90.
【分析】先求出各层比例,根据分层抽样的定义建立式子计算即可得到结论..
【解答】解:某地区有小学生12000人,初中生11000人,高中生9000人
所占的人数的比例分别为12000:11000:9000=12:11:9,
故抽取的小学生,初中生,高中生的人数分别.
故答案为:120,110,90.
【点评】本题考查分层抽样的应用,属于基础题.
12.(2025 浦东新区模拟)浦东某学校有学生2000人,为了加强学生的锻炼意识,学校举行了跑步和登山比赛,每人都参加且只能参加其中一项比赛,各年级参加比赛的人数情况如表所示:
高一年级 高二年级 高三年级
跑步人数(单位:人) a b c
登山人数(单位:人) x y z
其中a:b:c=2:5:3,参加登山的人数占总人数的,为了解学生对本次比赛的满意程度,按分层抽样的方式从中抽取一个200人的样本进行调查,则高三年级参加跑步的学生中应抽取 45 人.
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】45.
【分析】先求得参与跑步的总人数,再乘以抽样比例,得出样本中参与跑步的人数.
【解答】解:全校参与跑步有20001500人,高三年级参与跑步的学生=150045人.
故答案为:45.
【点评】本题主要考查了分成抽样,分层抽样又称按比例抽样,是高考中常见的题型,同时考查了分析问题、解决问题的能力,属于基础题.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】15.
【分析】确定抽样比,即可求解;
【解答】解:某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,
该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,
采取分层抽样,且按年级来分层,
由题意可知抽样比为:,
∴高一年级应抽取的人数是.
故答案为:15.
【点评】本题考查分层抽样等基础知识,考查运算求解能力,是基础题.
四.解答题(共2小题)
14.(2025春 武威月考)某志愿者组织有男成员48人,其中35岁以上的有12人;有女成员36人,其中35岁以上的有18人.
(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,那么男、女成员各应抽取多少人?
(2)如果按照年龄进行分层抽样,要抽取一个容量为28的样本,那么35岁以上的成员应抽取多少人?
【考点】分层随机抽样的比例分配与各层个体数及抽取样本量.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】(1)应该抽取男成员12人,女成员9人;
(2)35岁以上的成员应抽取10人.
【分析】由分层抽样的原理求解即可.
【解答】解:(1)如果按照性别进行分层抽样,要抽取一个容量为21的样本,
则男成员应该抽取人,
女成员应该抽取人.
(2)由题意可知35岁以上的成员应抽取人.
【点评】本题主要考查分层抽样的原理,属于基础题.
15.(2024 湖南学业考试)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
【考点】分层随机抽样;频率分布直方图.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】(1)a=0.00009;
(2)3360元;
(3)6.
【分析】(1)根据直方图中频率和为1列方程求参数;
(2)根据直方图计算平均值;
(3)根据分层抽样的等比例性质求在[4000,6000)的居民数量.
【解答】解:(1)依题意,(0.00003×2+a+0.00015+0.0002)×2000=1,解得a=0.00009.
(2)所有受灾居民经济损失的平均值为1000×0.3+3000×0.4+5000×0.18+7000×0.06+9000×0.06=3360元.
(3)由(1)得经济损失在[4000,6000)和在[6000,8000)的人数比例为3:1,
由分层抽样知,经济损失在[4000,6000)的居民有人.
【点评】本题主要考查频率分布直方图的应用,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
