【期末押题预测】期末核心考点 离散型随机变量的数字特征(含解析)2024-2025学年高二下学期数学人教A版(2019)
文档属性
| 名称 | 【期末押题预测】期末核心考点 离散型随机变量的数字特征(含解析)2024-2025学年高二下学期数学人教A版(2019) |

|
|
| 格式 | docx | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 10:50:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 离散型随机变量的数字特征
一.选择题(共7小题)
1.(2025 四川模拟)若随机变量X的分布列如表,表中数列{pn}是公比为2的等比数列,则E(X)=( )
X 1 2 3
P p1 p2 p3
A. B. C. D.
2.(2025春 九龙坡区校级期中)高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小球从通道口落下,第一次与第2层中间的小木块碰撞,以的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉入编号(从左至右)为1,2,3,4,5,6,7,8,9,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分an,否则不得分.若,为使所得积分的数学期望最大,每次试验前选定的球槽编号为( )
A.5 B.6 C.7 D.8
3.(2025 江苏校级三模)设正数a,b,随机变量X的分布列,若随机变量X的期望为1,则最小值为( )
X 0 a b
P c
A.1 B. C.4 D.2
4.(2025春 沙坪坝区校级期中)随机变量X的分布列如表,则方差D(X)=( )
X 0 1 2
P a 3a
A. B. C. D.
5.(2025 西安校级模拟)盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,随机无放回的摸两次球,记Y为摸到黑球的个数,则( )
A.E(X)<E(Y),DX>DY
B.E(X)=E(Y),D(X)>D(Y)
C.E(X)<E(Y),DX<DY
D.E(X)=E(Y),D(X)<D(Y)
6.(2025春 周口期中)2025年2月深圳福田区推出基于DeepSeek开发的AI数智员工,并上线福田区政务大模型2.0版,该模型能进一步驱动政务效能全面跃升.某地也准备推出20名AI数智员工(假定这20名AI数智员工没有区别),分别从事A,B,C三个服务项目,若每个项目至少需要5名AI数智员工,则不同的分配方法种数为( )
A.21 B.18 C.15 D.12
7.(2025春 周口期中)若随机变量X的分布列为,则a=( )
A.12 B.10 C.9 D.8
二.多选题(共3小题)
(多选)8.(2025春 如皋市期中)某高校强基计划分面试和笔试两部分,500名参加的考生面试成绩Y近似服从正态分布N(15,σ2),.笔试一共两道题,第1题答对得4分,第2题答对得6分,每道题答错得0分,考生每道题答对与否互不影响.某考生笔试第1题答对的概率为,第2题答对的概率为,则( )
A.
B.500名考生中面试成绩不低于20分约有125人
C.该考生笔试成绩未达6分的概率为
D.该考生笔试成绩的期望为
(多选)9.(2025 凉山州模拟)下列说法正确的有( )
A.69,63,65,55,71,73,77,78,83,82这组数据的第80百分位数是80
B.若一组数据x1,x2, ,xn的方差为,则2x1,2x2, ,2xn的方差为1
C.若变量X~B(4,),则E(X)=2
D.若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,则P(ξ<87)=0.2
(多选)10.(2025 吉林模拟)已知集合M={1,2,3, ,19},现随机选取集合M中3个元素组成子集(简称3元子集),记该子集中的最小数为k.( )
A.k的最小取值为1,最大取值为19
B.集合M中以k为最小数的3元子集共有个
C.取到“集合M中以k为最小数的3元子集”的概率为
D.E(k)=5
三.填空题(共3小题)
11.(2025春 浙江期中)老师从10篇课文中随机抽3篇让学生背诵,背诵篇数没达到2篇的为不合格,不合格者积分扣1分;能背诵篇数2篇的为合格,不扣分也不加分;3篇都能背诵的为优秀,优秀者积分加2分,某位同学只能背诵其中的6篇课文,记该同学的得分为X,则E(X)= .
12.(2025 重庆模拟)甲同学有3本故事书和1本科普书,乙同学有1本故事书和3本科普书,若甲、乙两位同学各取出i(i=1,2,3)本书进行交换,记交换后甲同学有故事书的本数为X,X的均值为Ei(X),则E1(X)+E3(X)= .
13.(2025 河西区校级模拟)对某实验项目进行测试,测试方法:①共进行3轮测试;②每轮测试2次,若至少合格1次,则本轮通过,否则不通过.已知测试1次合格的概率为,如果各次测试合格与否互不影响,则在一轮测试中,通过的概率为 ;在3轮测试中,通过的次数X的期望是 .
四.解答题(共2小题)
14.(2025 滨州二模)某学校组织“一带一路”有奖知识竞赛,有A,B两个问题,已知甲同学答对问题A的概率为0.6,回答正确得奖金10元,回答错误得奖金0元;答对问题B的概率为0.5,回答正确得奖金x元,回答错误得奖金0元,甲同学回答A,B两个问题正确与否相互独立,
(1)若甲同学对两个问题都作答,求他仅答对其中一个问题的概率;
(2)若规定只有在答对第一个问题的情况下,才能回答下一个问题,若甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,求x的值.
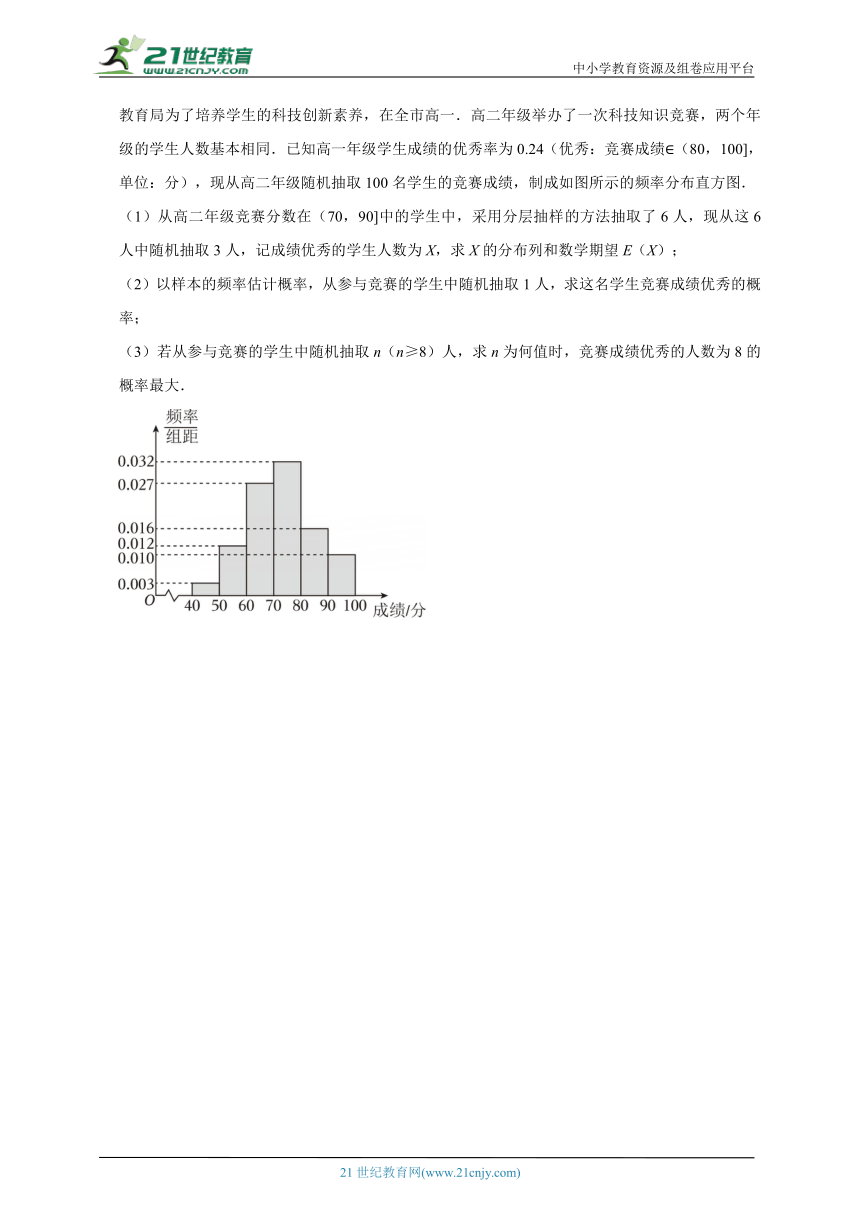
15.(2025 东昌府区校级模拟)2024年2月27日,电动垂直起降航空器eVTOL“盛世龙”成功飞越深圳至珠海的航线,实现了“飞行汽车”的首飞,打开了未来城际通勤的巨大想象空间,某市教育局为了培养学生的科技创新素养,在全市高一.高二年级举办了一次科技知识竞赛,两个年级的学生人数基本相同.已知高一年级学生成绩的优秀率为0.24(优秀:竞赛成绩∈(80,100],单位:分),现从高二年级随机抽取100名学生的竞赛成绩,制成如图所示的频率分布直方图.
(1)从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,现从这6人中随机抽取3人,记成绩优秀的学生人数为X,求X的分布列和数学期望E(X);
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,求这名学生竞赛成绩优秀的概率;
(3)若从参与竞赛的学生中随机抽取n(n≥8)人,求n为何值时,竞赛成绩优秀的人数为8的概率最大.
期末核心考点 离散型随机变量的数字特征
参考答案与试题解析
一.选择题(共7小题)
1.(2025 四川模拟)若随机变量X的分布列如表,表中数列{pn}是公比为2的等比数列,则E(X)=( )
X 1 2 3
P p1 p2 p3
A. B. C. D.
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;综合法;概率与统计;运算求解.
【答案】D
【分析】因为数列{pn}是公比为2的等比数列,又p1+p2+p3=1,所以p1+2p1+4p1=1,即,p3=4,即可得出E(X).
【解答】解:由已知可得,,又p1+p2+p3=1,
∴p1+2p1+4p1=1,即,p3=4,
∴.
故选:D.
【点评】本题考查离散型随机变量的均值(数学期望),属于中档题.
2.(2025春 九龙坡区校级期中)高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小球从通道口落下,第一次与第2层中间的小木块碰撞,以的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉入编号(从左至右)为1,2,3,4,5,6,7,8,9,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分an,否则不得分.若,为使所得积分的数学期望最大,每次试验前选定的球槽编号为( )
A.5 B.6 C.7 D.8
【考点】离散型随机变量的均值(数学期望).
【专题】对应思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】D
【分析】根据给定条件,求出小球落入第k号格子的概率,进而求出其数学期望,再求出取得最大值的编号.
【解答】解:设选定的格子编号为k(1≤k≤10,k∈N),
此时小球碰撞过程中有k﹣1次向右边滚落,
落到该格子的概率为,
则数学期望为,
令,
此时,
当k>7.5时,;当k<7.5时,,
所以当k=8时,bk取得最大,
则每次试验前选定的球槽编号为8,故选项D正确.
故选:D.
【点评】本题考查离散型随机变量的期望,考查了逻辑推理和运算能力,属于基础题.
3.(2025 江苏校级三模)设正数a,b,随机变量X的分布列,若随机变量X的期望为1,则最小值为( )
X 0 a b
P c
A.1 B. C.4 D.2
【考点】离散型随机变量的均值(数学期望);运用基本不等式求最值;离散型随机变量及其分布列.
【专题】计算题;整体思想;综合法;概率与统计;运算求解.
【答案】D
【分析】根据离散型随机变量分布列的性质求出c的值,再利用期望公式得到a与b的关系,然后换元,将所求式子进行变形,结合m与n的关系,运用基本不等式求出其最小值.
【解答】解:设正数a,b,随机变量X的分布列,若随机变量X的期望为1,
根据离散型随机变量分布列的性质:所有概率之和为1,即,解得,
已知随机变量X的期望为1,根据随机变量的期望公式可得,
化简可得:,进一步变形为2a+b=4,
设a+1=m,b+2=n,则2m+n=8,
将进行变形,
根据“1”的代换得到,
展开式子:,
根据基本不等式,有,
所以,当且仅当,即m=2,n=4时等号成立,
则最小值为2.
故选:D.
【点评】本题考查了分布列的性质、随机变量的期望公式和基本不等式的应用,属于中档题.
4.(2025春 沙坪坝区校级期中)随机变量X的分布列如表,则方差D(X)=( )
X 0 1 2
P a 3a
A. B. C. D.
【考点】离散型随机变量的方差与标准差.
【专题】对应思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】C
【分析】由题意,根据分布列的性质求出a的值,利用期望和方差公式求解即可.
【解答】解:因为a3a=1,
所以a,
此时E(X)=012,
则D(X)=(0)2(1)2(2)2.
故选:C.
【点评】本题考查离散型随机变量的期望和方差,考查了逻辑推理和运算能力,属于基础题.
5.(2025 西安校级模拟)盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,随机无放回的摸两次球,记Y为摸到黑球的个数,则( )
A.E(X)<E(Y),DX>DY
B.E(X)=E(Y),D(X)>D(Y)
C.E(X)<E(Y),DX<DY
D.E(X)=E(Y),D(X)<D(Y)
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据二项分布求E(X),D(X),根据超几何分布求E(Y),D(Y),即可得结果.
【解答】解:盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,
则,
所以,
随机无放回的摸两次球,记Y为摸到黑球的个数,则Y的所有可能取值为0,1,2,
则,
所以,
,
所以E(X)=E(Y),D(X)>D(Y).
故选:B.
【点评】本题主要考查离散型随机变量的期望和方差,考查运算求解能力,属于中档题.
6.(2025春 周口期中)2025年2月深圳福田区推出基于DeepSeek开发的AI数智员工,并上线福田区政务大模型2.0版,该模型能进一步驱动政务效能全面跃升.某地也准备推出20名AI数智员工(假定这20名AI数智员工没有区别),分别从事A,B,C三个服务项目,若每个项目至少需要5名AI数智员工,则不同的分配方法种数为( )
A.21 B.18 C.15 D.12
【考点】离散型随机变量的均值(数学期望);排列组合的综合应用.
【专题】计算题;对应思想;综合法;排列组合;运算求解.
【答案】A
【分析】先每组分5名员工,然后剩余5名分成三组,采用隔板法即可.
【解答】解:先每组分5名员工,然后剩余5名分成三组,
采用隔板法,五名员工和两个板,共有七个位置,
∴不同的分配方法种数为21种.
故选:A.
【点评】本题主要考查组合的应用,考查运算求解能力,属于基础题.
7.(2025春 周口期中)若随机变量X的分布列为,则a=( )
A.12 B.10 C.9 D.8
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;方程思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据分布列中概率之和为1,列方程求得a的值.
【解答】解:由题意可得:,
即,解得a=10.
故选:B.
【点评】本题主要考查离散型随机变量分布列的性质,考查运算求解能力,属于基础题.
二.多选题(共3小题)
(多选)8.(2025春 如皋市期中)某高校强基计划分面试和笔试两部分,500名参加的考生面试成绩Y近似服从正态分布N(15,σ2),.笔试一共两道题,第1题答对得4分,第2题答对得6分,每道题答错得0分,考生每道题答对与否互不影响.某考生笔试第1题答对的概率为,第2题答对的概率为,则( )
A.
B.500名考生中面试成绩不低于20分约有125人
C.该考生笔试成绩未达6分的概率为
D.该考生笔试成绩的期望为
【考点】离散型随机变量的均值(数学期望);正态分布曲线的特点及曲线所表示的意义.
【专题】分类讨论;分类法;概率与统计;运算求解.
【答案】ABD
【分析】利用正态分布的对称性判断A,B选项;考生两道题都未答对,或只答对第1题时,笔试成绩未达6分,计算概率判断C选项;由题意X的可能取值为0,4,6,10,分别计算各概率,再求期望判断D选项.
【解答】解:对于A,因为考生面试成绩Y近似服从正态分布N(15,σ2),,
所以P(Y<10),故A正确;
对于B,P(Y≥20),
所以500名考生中面试成绩不低于20分约有500125人,故B正确;
对于C,考生两道题都未答对,或只答对第1题时,笔试成绩未达6分,
所以其概率为,故C错误;
对于D,由题意,X的可能取值为0,4,6,10,
且P(X=0),P(X=4),
P(X=6),P(X=10),
所以该考生笔试成绩的期望为04610,故D正确.
故选:ABD.
【点评】本题考查正态分布的对称性、离散型随机变量的数学期望,综合性较强,属于中档题.
(多选)9.(2025 凉山州模拟)下列说法正确的有( )
A.69,63,65,55,71,73,77,78,83,82这组数据的第80百分位数是80
B.若一组数据x1,x2, ,xn的方差为,则2x1,2x2, ,2xn的方差为1
C.若变量X~B(4,),则E(X)=2
D.若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,则P(ξ<87)=0.2
【考点】离散型随机变量的均值(数学期望);正态分布曲线的特点及曲线所表示的意义;方差;百分位数.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】利用百分位数的定义计算判断A;由方差的性质判断B;由二项分布期望公式判断C;由正态分布曲线的对称性判断D.
【解答】解:对于A,将数据从小到大排序为55,63,65,69,71,73,77,78,82,83,
因为10×80%=8,所以这组数据的第80百分位数是80,A正确;
对于B,若一组数据x1,x2, ,xn的方差为,
则2x1,2x2, ,2xn的方差为222,故B错误;
对于C,若变量X~B(4,),则E(X)=42,故C正确;
对于D,若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,
则由对称性可知,P(87≤ξ<100)=0.3,所以P(ξ<87)=0.5﹣0.3=0.2,故D正确.
故选:ACD.
【点评】本题考查百分位数的定义、方差的性质、二项分布的期望公式、正态分布等知识点,属于基础题.
(多选)10.(2025 吉林模拟)已知集合M={1,2,3, ,19},现随机选取集合M中3个元素组成子集(简称3元子集),记该子集中的最小数为k.( )
A.k的最小取值为1,最大取值为19
B.集合M中以k为最小数的3元子集共有个
C.取到“集合M中以k为最小数的3元子集”的概率为
D.E(k)=5
【考点】离散型随机变量的均值(数学期望);子集的个数;古典概型及其概率计算公式.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】BCD
【分析】A最小为17;B问题转化为在k+1,k+2, ,19中选出2个数即可;C利用古典概型的概率公式可求;D以模型“随机选取集合N={1,2, ,20}中4个元素组成子集的种类数”证明即可求得.
【解答】解:对于A,由题意可知,k的最小取值为1,最大取值为17,故A错误;
对于B,以k为最小元的子集只需在k+1,k+2, ,19中选出2个数与k共同组成一个集合,
所以有个,故B正确;
对于C,集合M共有个3元子集,由B选项可知集合M中以k为最小数的3元子集共有个,
所以取到“集合M中以k为最小数的3元子集”的概率为,故C正确;
对于D,随机选取集合N={1,2, ,20}中4个元素组成子集共有种,
由于N={1, ,k}∪{k+1}∪{k+2, ,20},k=1, ,17,
其中k为集合{1, ,k}中的最大数,k+2是集合{k+2, ,20}中的最小数,
则从{1, ,k}中任取1个元素有种,从{k+2, ,20}中任取2个元素有种,
再取k+1,则从集合N中任取4个元素共有种,
则,
则,故D正确.
故选:BCD.
【点评】本题主要考查了古典概型的概率公式,考查了离散型随机变量的期望,属于中档题.
三.填空题(共3小题)
11.(2025春 浙江期中)老师从10篇课文中随机抽3篇让学生背诵,背诵篇数没达到2篇的为不合格,不合格者积分扣1分;能背诵篇数2篇的为合格,不扣分也不加分;3篇都能背诵的为优秀,优秀者积分加2分,某位同学只能背诵其中的6篇课文,记该同学的得分为X,则E(X)= 0 .
【考点】离散型随机变量的均值(数学期望).
【专题】分类讨论;分类法;概率与统计;逻辑思维.
【答案】0
【分析】由题意,X的可能取值为﹣1,0,1,分别求出每种取值对应的概率,可得X的分布列,进而计算E(X).
【解答】解:由题意,X的可能取值为﹣1,0,2,
所以,
,,
则X的分布列为:
X ﹣1 0 2
P
所以.
故答案为:0.
【点评】本题考查离散型随机变量的分布列与数学期望,结合超几何分布等相关知识,属于基础题.
12.(2025 重庆模拟)甲同学有3本故事书和1本科普书,乙同学有1本故事书和3本科普书,若甲、乙两位同学各取出i(i=1,2,3)本书进行交换,记交换后甲同学有故事书的本数为X,X的均值为Ei(X),则E1(X)+E3(X)= 4 .
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;综合法;概率与统计;运算求解.
【答案】4.
【分析】分别计算交换1本书和3本书时甲同学故事书数量的期望值E1(X)和E3(X),再求和.解题分为两步:先分析交换1本书的情况,再分析交换3本书的情况.
【解答】解:当i=1时,X的取值可能是2,3,4,
且,
,
,
则,
当i=3时,X的取值可能是0,1,2,
且,
,
,
则.
故E1(X)+E3(X)=4.
故答案为:4.
【点评】本题考查离散型随机变量的均值(数学期望),属于中档题.
13.(2025 河西区校级模拟)对某实验项目进行测试,测试方法:①共进行3轮测试;②每轮测试2次,若至少合格1次,则本轮通过,否则不通过.已知测试1次合格的概率为,如果各次测试合格与否互不影响,则在一轮测试中,通过的概率为 ;在3轮测试中,通过的次数X的期望是 .
【考点】离散型随机变量的均值(数学期望).
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】;.
【分析】根据已知条件,结合相互独立事件的概率乘法公式,以及二项分布的期望公式,即可求解.
【解答】解:由题意可得,一轮测试2次都不合格的概率,
故在一轮测试中,通过的概率为1,
在3轮测试中,通过的次数X的所有可能取值为0,1,2,3,
各次测试合格与否互不影响,通过的次数X服从二项分布,即X~B(3,).
E(X)=3.
故答案为:;.
【点评】本题主要考查相互独立事件的概率乘法公式,以及二项分布的期望公式,属于基础题.
四.解答题(共2小题)
14.(2025 滨州二模)某学校组织“一带一路”有奖知识竞赛,有A,B两个问题,已知甲同学答对问题A的概率为0.6,回答正确得奖金10元,回答错误得奖金0元;答对问题B的概率为0.5,回答正确得奖金x元,回答错误得奖金0元,甲同学回答A,B两个问题正确与否相互独立,
(1)若甲同学对两个问题都作答,求他仅答对其中一个问题的概率;
(2)若规定只有在答对第一个问题的情况下,才能回答下一个问题,若甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,求x的值.
【考点】离散型随机变量的均值(数学期望);相互独立事件的概率乘法公式.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】(1)0.5;
(2)15.
【分析】(1)根据独立事件的乘法公式计算可得结果;
(2)求出甲先回答A问题和先回答B问题所获得的奖金总额的分布列,再由期望值相等解方程求得x=15.
【解答】解:(1)设甲同学答对问题A的概率为P(A),答对问题B的概率为P(B);
易知P(A)=0.6,P(B)=0.5,又回答A,B两个问题正确与否相互独立,
所以仅答对其中一个问题的概率为:
P=P(A)[1﹣P(B)]+[1﹣P(A)]P(B)=0.6×(1﹣0.5)+(1﹣0.6)×0.5=0.5.
(2)设甲先回答A问题所获得的奖金总额为X,
则X的所有可能取值为0,10,10+x;
易知P(X=0)=1﹣0.6=0.4,P(X=10)=0.6×(1﹣0.5)=0.3,
P(X=10+x)=1﹣P(X=0)﹣P(X=10)=0.3,
则E(X)=0×0.4+10×0.3+(10+x)×0.3=6+0.3x;
设甲先回答B问题所获得的奖金总额为Y,
则Y的所有可能取值为0,x,10+x,
所以P(Y=0)=1﹣0.5=0.5,P(Y=x)=0.5×(1﹣0.6)=0.2,
P(Y=10+x)=1﹣P(Y=0)﹣P(Y=x),
则E(Y)=0×0.5+0.2x+(10+x)×0.3=3+0.5x,
因为甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,
所以6+0.3x=3+0.5x,
解得:x=15.
【点评】本题考查了相互独立事件的概率,离散型随机变量的分布列和期望,属于中档题.
15.(2025 东昌府区校级模拟)2024年2月27日,电动垂直起降航空器eVTOL“盛世龙”成功飞越深圳至珠海的航线,实现了“飞行汽车”的首飞,打开了未来城际通勤的巨大想象空间,某市教育局为了培养学生的科技创新素养,在全市高一.高二年级举办了一次科技知识竞赛,两个年级的学生人数基本相同.已知高一年级学生成绩的优秀率为0.24(优秀:竞赛成绩∈(80,100],单位:分),现从高二年级随机抽取100名学生的竞赛成绩,制成如图所示的频率分布直方图.
(1)从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,现从这6人中随机抽取3人,记成绩优秀的学生人数为X,求X的分布列和数学期望E(X);
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,求这名学生竞赛成绩优秀的概率;
(3)若从参与竞赛的学生中随机抽取n(n≥8)人,求n为何值时,竞赛成绩优秀的人数为8的概率最大.
【考点】离散型随机变量的均值(数学期望);离散型随机变量及其分布列.
【专题】转化思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】(1)分布列见解析,E(X)=1;
(2);
(3)n=31或n=32或33时,竞赛成绩优秀的人数为8的概率最大.
【分析】(1)结合频率分布直方图和分层抽样,可得在(70,80]中抽4人,在(80,90]中抽2人,进而可得随机变量的取值,列出分布列,求得期望;
(2)由全概率公式,即可求解;
(3)由题设得,利用二项分布概率公式及不等性质解决最大概率问题.
【解答】解:(1)由直方图可知,分数在(70,80]中的学生有32人,分数在(80,90]中的学生有16人,
从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,
∴根据分层抽样,在(70,80]中抽64人,在(80,90]中抽62人,
则成绩优秀的学生人数X可取0,1,2,
∴,
,
.
∴随机变量X的分布列为:
X 0 1 2
p
则期望.
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,
记事件A:成绩优秀的学生,事件B:高一年级的学生,
由已知条件可知,,
所以.
(3)记随机抽取n人中竞赛成绩优秀的人数为Y,
由题意可知,,
∴,令,
则,
令,则n<31,所以n≤30时,an+1>an,
令,则n>31,所以n≥32时,an+1<an,
令,则n=31,所以a32=a31,
∴当n=31或n=32或33时,an最大,即n=31或n=32或33时,竞赛成绩优秀的人数为8的概率最大.
【点评】本题考查离散型随机变量的分布列、数学期望、二项分布等基础知识,考查运算求解能力,是中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 离散型随机变量的数字特征
一.选择题(共7小题)
1.(2025 四川模拟)若随机变量X的分布列如表,表中数列{pn}是公比为2的等比数列,则E(X)=( )
X 1 2 3
P p1 p2 p3
A. B. C. D.
2.(2025春 九龙坡区校级期中)高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小球从通道口落下,第一次与第2层中间的小木块碰撞,以的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉入编号(从左至右)为1,2,3,4,5,6,7,8,9,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分an,否则不得分.若,为使所得积分的数学期望最大,每次试验前选定的球槽编号为( )
A.5 B.6 C.7 D.8
3.(2025 江苏校级三模)设正数a,b,随机变量X的分布列,若随机变量X的期望为1,则最小值为( )
X 0 a b
P c
A.1 B. C.4 D.2
4.(2025春 沙坪坝区校级期中)随机变量X的分布列如表,则方差D(X)=( )
X 0 1 2
P a 3a
A. B. C. D.
5.(2025 西安校级模拟)盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,随机无放回的摸两次球,记Y为摸到黑球的个数,则( )
A.E(X)<E(Y),DX>DY
B.E(X)=E(Y),D(X)>D(Y)
C.E(X)<E(Y),DX<DY
D.E(X)=E(Y),D(X)<D(Y)
6.(2025春 周口期中)2025年2月深圳福田区推出基于DeepSeek开发的AI数智员工,并上线福田区政务大模型2.0版,该模型能进一步驱动政务效能全面跃升.某地也准备推出20名AI数智员工(假定这20名AI数智员工没有区别),分别从事A,B,C三个服务项目,若每个项目至少需要5名AI数智员工,则不同的分配方法种数为( )
A.21 B.18 C.15 D.12
7.(2025春 周口期中)若随机变量X的分布列为,则a=( )
A.12 B.10 C.9 D.8
二.多选题(共3小题)
(多选)8.(2025春 如皋市期中)某高校强基计划分面试和笔试两部分,500名参加的考生面试成绩Y近似服从正态分布N(15,σ2),.笔试一共两道题,第1题答对得4分,第2题答对得6分,每道题答错得0分,考生每道题答对与否互不影响.某考生笔试第1题答对的概率为,第2题答对的概率为,则( )
A.
B.500名考生中面试成绩不低于20分约有125人
C.该考生笔试成绩未达6分的概率为
D.该考生笔试成绩的期望为
(多选)9.(2025 凉山州模拟)下列说法正确的有( )
A.69,63,65,55,71,73,77,78,83,82这组数据的第80百分位数是80
B.若一组数据x1,x2, ,xn的方差为,则2x1,2x2, ,2xn的方差为1
C.若变量X~B(4,),则E(X)=2
D.若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,则P(ξ<87)=0.2
(多选)10.(2025 吉林模拟)已知集合M={1,2,3, ,19},现随机选取集合M中3个元素组成子集(简称3元子集),记该子集中的最小数为k.( )
A.k的最小取值为1,最大取值为19
B.集合M中以k为最小数的3元子集共有个
C.取到“集合M中以k为最小数的3元子集”的概率为
D.E(k)=5
三.填空题(共3小题)
11.(2025春 浙江期中)老师从10篇课文中随机抽3篇让学生背诵,背诵篇数没达到2篇的为不合格,不合格者积分扣1分;能背诵篇数2篇的为合格,不扣分也不加分;3篇都能背诵的为优秀,优秀者积分加2分,某位同学只能背诵其中的6篇课文,记该同学的得分为X,则E(X)= .
12.(2025 重庆模拟)甲同学有3本故事书和1本科普书,乙同学有1本故事书和3本科普书,若甲、乙两位同学各取出i(i=1,2,3)本书进行交换,记交换后甲同学有故事书的本数为X,X的均值为Ei(X),则E1(X)+E3(X)= .
13.(2025 河西区校级模拟)对某实验项目进行测试,测试方法:①共进行3轮测试;②每轮测试2次,若至少合格1次,则本轮通过,否则不通过.已知测试1次合格的概率为,如果各次测试合格与否互不影响,则在一轮测试中,通过的概率为 ;在3轮测试中,通过的次数X的期望是 .
四.解答题(共2小题)
14.(2025 滨州二模)某学校组织“一带一路”有奖知识竞赛,有A,B两个问题,已知甲同学答对问题A的概率为0.6,回答正确得奖金10元,回答错误得奖金0元;答对问题B的概率为0.5,回答正确得奖金x元,回答错误得奖金0元,甲同学回答A,B两个问题正确与否相互独立,
(1)若甲同学对两个问题都作答,求他仅答对其中一个问题的概率;
(2)若规定只有在答对第一个问题的情况下,才能回答下一个问题,若甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,求x的值.
15.(2025 东昌府区校级模拟)2024年2月27日,电动垂直起降航空器eVTOL“盛世龙”成功飞越深圳至珠海的航线,实现了“飞行汽车”的首飞,打开了未来城际通勤的巨大想象空间,某市教育局为了培养学生的科技创新素养,在全市高一.高二年级举办了一次科技知识竞赛,两个年级的学生人数基本相同.已知高一年级学生成绩的优秀率为0.24(优秀:竞赛成绩∈(80,100],单位:分),现从高二年级随机抽取100名学生的竞赛成绩,制成如图所示的频率分布直方图.
(1)从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,现从这6人中随机抽取3人,记成绩优秀的学生人数为X,求X的分布列和数学期望E(X);
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,求这名学生竞赛成绩优秀的概率;
(3)若从参与竞赛的学生中随机抽取n(n≥8)人,求n为何值时,竞赛成绩优秀的人数为8的概率最大.
期末核心考点 离散型随机变量的数字特征
参考答案与试题解析
一.选择题(共7小题)
1.(2025 四川模拟)若随机变量X的分布列如表,表中数列{pn}是公比为2的等比数列,则E(X)=( )
X 1 2 3
P p1 p2 p3
A. B. C. D.
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;综合法;概率与统计;运算求解.
【答案】D
【分析】因为数列{pn}是公比为2的等比数列,又p1+p2+p3=1,所以p1+2p1+4p1=1,即,p3=4,即可得出E(X).
【解答】解:由已知可得,,又p1+p2+p3=1,
∴p1+2p1+4p1=1,即,p3=4,
∴.
故选:D.
【点评】本题考查离散型随机变量的均值(数学期望),属于中档题.
2.(2025春 九龙坡区校级期中)高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小球从通道口落下,第一次与第2层中间的小木块碰撞,以的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉入编号(从左至右)为1,2,3,4,5,6,7,8,9,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分an,否则不得分.若,为使所得积分的数学期望最大,每次试验前选定的球槽编号为( )
A.5 B.6 C.7 D.8
【考点】离散型随机变量的均值(数学期望).
【专题】对应思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】D
【分析】根据给定条件,求出小球落入第k号格子的概率,进而求出其数学期望,再求出取得最大值的编号.
【解答】解:设选定的格子编号为k(1≤k≤10,k∈N),
此时小球碰撞过程中有k﹣1次向右边滚落,
落到该格子的概率为,
则数学期望为,
令,
此时,
当k>7.5时,;当k<7.5时,,
所以当k=8时,bk取得最大,
则每次试验前选定的球槽编号为8,故选项D正确.
故选:D.
【点评】本题考查离散型随机变量的期望,考查了逻辑推理和运算能力,属于基础题.
3.(2025 江苏校级三模)设正数a,b,随机变量X的分布列,若随机变量X的期望为1,则最小值为( )
X 0 a b
P c
A.1 B. C.4 D.2
【考点】离散型随机变量的均值(数学期望);运用基本不等式求最值;离散型随机变量及其分布列.
【专题】计算题;整体思想;综合法;概率与统计;运算求解.
【答案】D
【分析】根据离散型随机变量分布列的性质求出c的值,再利用期望公式得到a与b的关系,然后换元,将所求式子进行变形,结合m与n的关系,运用基本不等式求出其最小值.
【解答】解:设正数a,b,随机变量X的分布列,若随机变量X的期望为1,
根据离散型随机变量分布列的性质:所有概率之和为1,即,解得,
已知随机变量X的期望为1,根据随机变量的期望公式可得,
化简可得:,进一步变形为2a+b=4,
设a+1=m,b+2=n,则2m+n=8,
将进行变形,
根据“1”的代换得到,
展开式子:,
根据基本不等式,有,
所以,当且仅当,即m=2,n=4时等号成立,
则最小值为2.
故选:D.
【点评】本题考查了分布列的性质、随机变量的期望公式和基本不等式的应用,属于中档题.
4.(2025春 沙坪坝区校级期中)随机变量X的分布列如表,则方差D(X)=( )
X 0 1 2
P a 3a
A. B. C. D.
【考点】离散型随机变量的方差与标准差.
【专题】对应思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】C
【分析】由题意,根据分布列的性质求出a的值,利用期望和方差公式求解即可.
【解答】解:因为a3a=1,
所以a,
此时E(X)=012,
则D(X)=(0)2(1)2(2)2.
故选:C.
【点评】本题考查离散型随机变量的期望和方差,考查了逻辑推理和运算能力,属于基础题.
5.(2025 西安校级模拟)盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,随机无放回的摸两次球,记Y为摸到黑球的个数,则( )
A.E(X)<E(Y),DX>DY
B.E(X)=E(Y),D(X)>D(Y)
C.E(X)<E(Y),DX<DY
D.E(X)=E(Y),D(X)<D(Y)
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据二项分布求E(X),D(X),根据超几何分布求E(Y),D(Y),即可得结果.
【解答】解:盲盒中有大小相同的3个红球,2个黑球,随机有放回的摸两次球,记X为摸到黑球的个数,
则,
所以,
随机无放回的摸两次球,记Y为摸到黑球的个数,则Y的所有可能取值为0,1,2,
则,
所以,
,
所以E(X)=E(Y),D(X)>D(Y).
故选:B.
【点评】本题主要考查离散型随机变量的期望和方差,考查运算求解能力,属于中档题.
6.(2025春 周口期中)2025年2月深圳福田区推出基于DeepSeek开发的AI数智员工,并上线福田区政务大模型2.0版,该模型能进一步驱动政务效能全面跃升.某地也准备推出20名AI数智员工(假定这20名AI数智员工没有区别),分别从事A,B,C三个服务项目,若每个项目至少需要5名AI数智员工,则不同的分配方法种数为( )
A.21 B.18 C.15 D.12
【考点】离散型随机变量的均值(数学期望);排列组合的综合应用.
【专题】计算题;对应思想;综合法;排列组合;运算求解.
【答案】A
【分析】先每组分5名员工,然后剩余5名分成三组,采用隔板法即可.
【解答】解:先每组分5名员工,然后剩余5名分成三组,
采用隔板法,五名员工和两个板,共有七个位置,
∴不同的分配方法种数为21种.
故选:A.
【点评】本题主要考查组合的应用,考查运算求解能力,属于基础题.
7.(2025春 周口期中)若随机变量X的分布列为,则a=( )
A.12 B.10 C.9 D.8
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;方程思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据分布列中概率之和为1,列方程求得a的值.
【解答】解:由题意可得:,
即,解得a=10.
故选:B.
【点评】本题主要考查离散型随机变量分布列的性质,考查运算求解能力,属于基础题.
二.多选题(共3小题)
(多选)8.(2025春 如皋市期中)某高校强基计划分面试和笔试两部分,500名参加的考生面试成绩Y近似服从正态分布N(15,σ2),.笔试一共两道题,第1题答对得4分,第2题答对得6分,每道题答错得0分,考生每道题答对与否互不影响.某考生笔试第1题答对的概率为,第2题答对的概率为,则( )
A.
B.500名考生中面试成绩不低于20分约有125人
C.该考生笔试成绩未达6分的概率为
D.该考生笔试成绩的期望为
【考点】离散型随机变量的均值(数学期望);正态分布曲线的特点及曲线所表示的意义.
【专题】分类讨论;分类法;概率与统计;运算求解.
【答案】ABD
【分析】利用正态分布的对称性判断A,B选项;考生两道题都未答对,或只答对第1题时,笔试成绩未达6分,计算概率判断C选项;由题意X的可能取值为0,4,6,10,分别计算各概率,再求期望判断D选项.
【解答】解:对于A,因为考生面试成绩Y近似服从正态分布N(15,σ2),,
所以P(Y<10),故A正确;
对于B,P(Y≥20),
所以500名考生中面试成绩不低于20分约有500125人,故B正确;
对于C,考生两道题都未答对,或只答对第1题时,笔试成绩未达6分,
所以其概率为,故C错误;
对于D,由题意,X的可能取值为0,4,6,10,
且P(X=0),P(X=4),
P(X=6),P(X=10),
所以该考生笔试成绩的期望为04610,故D正确.
故选:ABD.
【点评】本题考查正态分布的对称性、离散型随机变量的数学期望,综合性较强,属于中档题.
(多选)9.(2025 凉山州模拟)下列说法正确的有( )
A.69,63,65,55,71,73,77,78,83,82这组数据的第80百分位数是80
B.若一组数据x1,x2, ,xn的方差为,则2x1,2x2, ,2xn的方差为1
C.若变量X~B(4,),则E(X)=2
D.若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,则P(ξ<87)=0.2
【考点】离散型随机变量的均值(数学期望);正态分布曲线的特点及曲线所表示的意义;方差;百分位数.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】利用百分位数的定义计算判断A;由方差的性质判断B;由二项分布期望公式判断C;由正态分布曲线的对称性判断D.
【解答】解:对于A,将数据从小到大排序为55,63,65,69,71,73,77,78,82,83,
因为10×80%=8,所以这组数据的第80百分位数是80,A正确;
对于B,若一组数据x1,x2, ,xn的方差为,
则2x1,2x2, ,2xn的方差为222,故B错误;
对于C,若变量X~B(4,),则E(X)=42,故C正确;
对于D,若变量ξ~N(100,σ2),P(100<ξ≤113)=0.3,
则由对称性可知,P(87≤ξ<100)=0.3,所以P(ξ<87)=0.5﹣0.3=0.2,故D正确.
故选:ACD.
【点评】本题考查百分位数的定义、方差的性质、二项分布的期望公式、正态分布等知识点,属于基础题.
(多选)10.(2025 吉林模拟)已知集合M={1,2,3, ,19},现随机选取集合M中3个元素组成子集(简称3元子集),记该子集中的最小数为k.( )
A.k的最小取值为1,最大取值为19
B.集合M中以k为最小数的3元子集共有个
C.取到“集合M中以k为最小数的3元子集”的概率为
D.E(k)=5
【考点】离散型随机变量的均值(数学期望);子集的个数;古典概型及其概率计算公式.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】BCD
【分析】A最小为17;B问题转化为在k+1,k+2, ,19中选出2个数即可;C利用古典概型的概率公式可求;D以模型“随机选取集合N={1,2, ,20}中4个元素组成子集的种类数”证明即可求得.
【解答】解:对于A,由题意可知,k的最小取值为1,最大取值为17,故A错误;
对于B,以k为最小元的子集只需在k+1,k+2, ,19中选出2个数与k共同组成一个集合,
所以有个,故B正确;
对于C,集合M共有个3元子集,由B选项可知集合M中以k为最小数的3元子集共有个,
所以取到“集合M中以k为最小数的3元子集”的概率为,故C正确;
对于D,随机选取集合N={1,2, ,20}中4个元素组成子集共有种,
由于N={1, ,k}∪{k+1}∪{k+2, ,20},k=1, ,17,
其中k为集合{1, ,k}中的最大数,k+2是集合{k+2, ,20}中的最小数,
则从{1, ,k}中任取1个元素有种,从{k+2, ,20}中任取2个元素有种,
再取k+1,则从集合N中任取4个元素共有种,
则,
则,故D正确.
故选:BCD.
【点评】本题主要考查了古典概型的概率公式,考查了离散型随机变量的期望,属于中档题.
三.填空题(共3小题)
11.(2025春 浙江期中)老师从10篇课文中随机抽3篇让学生背诵,背诵篇数没达到2篇的为不合格,不合格者积分扣1分;能背诵篇数2篇的为合格,不扣分也不加分;3篇都能背诵的为优秀,优秀者积分加2分,某位同学只能背诵其中的6篇课文,记该同学的得分为X,则E(X)= 0 .
【考点】离散型随机变量的均值(数学期望).
【专题】分类讨论;分类法;概率与统计;逻辑思维.
【答案】0
【分析】由题意,X的可能取值为﹣1,0,1,分别求出每种取值对应的概率,可得X的分布列,进而计算E(X).
【解答】解:由题意,X的可能取值为﹣1,0,2,
所以,
,,
则X的分布列为:
X ﹣1 0 2
P
所以.
故答案为:0.
【点评】本题考查离散型随机变量的分布列与数学期望,结合超几何分布等相关知识,属于基础题.
12.(2025 重庆模拟)甲同学有3本故事书和1本科普书,乙同学有1本故事书和3本科普书,若甲、乙两位同学各取出i(i=1,2,3)本书进行交换,记交换后甲同学有故事书的本数为X,X的均值为Ei(X),则E1(X)+E3(X)= 4 .
【考点】离散型随机变量的均值(数学期望).
【专题】计算题;综合法;概率与统计;运算求解.
【答案】4.
【分析】分别计算交换1本书和3本书时甲同学故事书数量的期望值E1(X)和E3(X),再求和.解题分为两步:先分析交换1本书的情况,再分析交换3本书的情况.
【解答】解:当i=1时,X的取值可能是2,3,4,
且,
,
,
则,
当i=3时,X的取值可能是0,1,2,
且,
,
,
则.
故E1(X)+E3(X)=4.
故答案为:4.
【点评】本题考查离散型随机变量的均值(数学期望),属于中档题.
13.(2025 河西区校级模拟)对某实验项目进行测试,测试方法:①共进行3轮测试;②每轮测试2次,若至少合格1次,则本轮通过,否则不通过.已知测试1次合格的概率为,如果各次测试合格与否互不影响,则在一轮测试中,通过的概率为 ;在3轮测试中,通过的次数X的期望是 .
【考点】离散型随机变量的均值(数学期望).
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】;.
【分析】根据已知条件,结合相互独立事件的概率乘法公式,以及二项分布的期望公式,即可求解.
【解答】解:由题意可得,一轮测试2次都不合格的概率,
故在一轮测试中,通过的概率为1,
在3轮测试中,通过的次数X的所有可能取值为0,1,2,3,
各次测试合格与否互不影响,通过的次数X服从二项分布,即X~B(3,).
E(X)=3.
故答案为:;.
【点评】本题主要考查相互独立事件的概率乘法公式,以及二项分布的期望公式,属于基础题.
四.解答题(共2小题)
14.(2025 滨州二模)某学校组织“一带一路”有奖知识竞赛,有A,B两个问题,已知甲同学答对问题A的概率为0.6,回答正确得奖金10元,回答错误得奖金0元;答对问题B的概率为0.5,回答正确得奖金x元,回答错误得奖金0元,甲同学回答A,B两个问题正确与否相互独立,
(1)若甲同学对两个问题都作答,求他仅答对其中一个问题的概率;
(2)若规定只有在答对第一个问题的情况下,才能回答下一个问题,若甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,求x的值.
【考点】离散型随机变量的均值(数学期望);相互独立事件的概率乘法公式.
【专题】对应思想;综合法;概率与统计;运算求解.
【答案】(1)0.5;
(2)15.
【分析】(1)根据独立事件的乘法公式计算可得结果;
(2)求出甲先回答A问题和先回答B问题所获得的奖金总额的分布列,再由期望值相等解方程求得x=15.
【解答】解:(1)设甲同学答对问题A的概率为P(A),答对问题B的概率为P(B);
易知P(A)=0.6,P(B)=0.5,又回答A,B两个问题正确与否相互独立,
所以仅答对其中一个问题的概率为:
P=P(A)[1﹣P(B)]+[1﹣P(A)]P(B)=0.6×(1﹣0.5)+(1﹣0.6)×0.5=0.5.
(2)设甲先回答A问题所获得的奖金总额为X,
则X的所有可能取值为0,10,10+x;
易知P(X=0)=1﹣0.6=0.4,P(X=10)=0.6×(1﹣0.5)=0.3,
P(X=10+x)=1﹣P(X=0)﹣P(X=10)=0.3,
则E(X)=0×0.4+10×0.3+(10+x)×0.3=6+0.3x;
设甲先回答B问题所获得的奖金总额为Y,
则Y的所有可能取值为0,x,10+x,
所以P(Y=0)=1﹣0.5=0.5,P(Y=x)=0.5×(1﹣0.6)=0.2,
P(Y=10+x)=1﹣P(Y=0)﹣P(Y=x),
则E(Y)=0×0.5+0.2x+(10+x)×0.3=3+0.5x,
因为甲先回答A问题和先回答B问题所获得的奖金总额的期望相同,
所以6+0.3x=3+0.5x,
解得:x=15.
【点评】本题考查了相互独立事件的概率,离散型随机变量的分布列和期望,属于中档题.
15.(2025 东昌府区校级模拟)2024年2月27日,电动垂直起降航空器eVTOL“盛世龙”成功飞越深圳至珠海的航线,实现了“飞行汽车”的首飞,打开了未来城际通勤的巨大想象空间,某市教育局为了培养学生的科技创新素养,在全市高一.高二年级举办了一次科技知识竞赛,两个年级的学生人数基本相同.已知高一年级学生成绩的优秀率为0.24(优秀:竞赛成绩∈(80,100],单位:分),现从高二年级随机抽取100名学生的竞赛成绩,制成如图所示的频率分布直方图.
(1)从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,现从这6人中随机抽取3人,记成绩优秀的学生人数为X,求X的分布列和数学期望E(X);
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,求这名学生竞赛成绩优秀的概率;
(3)若从参与竞赛的学生中随机抽取n(n≥8)人,求n为何值时,竞赛成绩优秀的人数为8的概率最大.
【考点】离散型随机变量的均值(数学期望);离散型随机变量及其分布列.
【专题】转化思想;综合法;概率与统计;逻辑思维;运算求解.
【答案】(1)分布列见解析,E(X)=1;
(2);
(3)n=31或n=32或33时,竞赛成绩优秀的人数为8的概率最大.
【分析】(1)结合频率分布直方图和分层抽样,可得在(70,80]中抽4人,在(80,90]中抽2人,进而可得随机变量的取值,列出分布列,求得期望;
(2)由全概率公式,即可求解;
(3)由题设得,利用二项分布概率公式及不等性质解决最大概率问题.
【解答】解:(1)由直方图可知,分数在(70,80]中的学生有32人,分数在(80,90]中的学生有16人,
从高二年级竞赛分数在(70,90]中的学生中,采用分层抽样的方法抽取了6人,
∴根据分层抽样,在(70,80]中抽64人,在(80,90]中抽62人,
则成绩优秀的学生人数X可取0,1,2,
∴,
,
.
∴随机变量X的分布列为:
X 0 1 2
p
则期望.
(2)以样本的频率估计概率,从参与竞赛的学生中随机抽取1人,
记事件A:成绩优秀的学生,事件B:高一年级的学生,
由已知条件可知,,
所以.
(3)记随机抽取n人中竞赛成绩优秀的人数为Y,
由题意可知,,
∴,令,
则,
令,则n<31,所以n≤30时,an+1>an,
令,则n>31,所以n≥32时,an+1<an,
令,则n=31,所以a32=a31,
∴当n=31或n=32或33时,an最大,即n=31或n=32或33时,竞赛成绩优秀的人数为8的概率最大.
【点评】本题考查离散型随机变量的分布列、数学期望、二项分布等基础知识,考查运算求解能力,是中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
