江西省吉安市第一中学2024-2025学年高三下学期数学月考试卷(二)(含解析)
文档属性
| 名称 | 江西省吉安市第一中学2024-2025学年高三下学期数学月考试卷(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 09:44:47 | ||
图片预览



文档简介
江西省吉安市第一中学2024 2025学年高三下学期数学月考试卷(二)
一、单选题
1.设集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|12.已知复数z满足,其中i是虚数单位,则的虚部为( )
A.-1 B.1 C.0 D.2
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
4.基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A.1.2天 B.1.8天
C.2.5天 D.3.5天
5.已知平面向量均为单位向量,且,则的最大值为( )
A. B. C.1 D.
6.已知是函数的一个极大值点,若方程在上有且仅有一个实数根,则实数的取值范围是( )
A. B. C. D.
7.已知双曲线的右顶点为,直线与双曲线相交,从引双曲线的两条渐近线的平行线,与直线分别交于点、.若为坐标原点,,则双曲线的离心率为( )
A. B.或 C. D.或
8.已知函数,且,则的最小值为( )
A. B. C. D.
二、多选题
9.关于,则( )
A.
B.
C.
D.
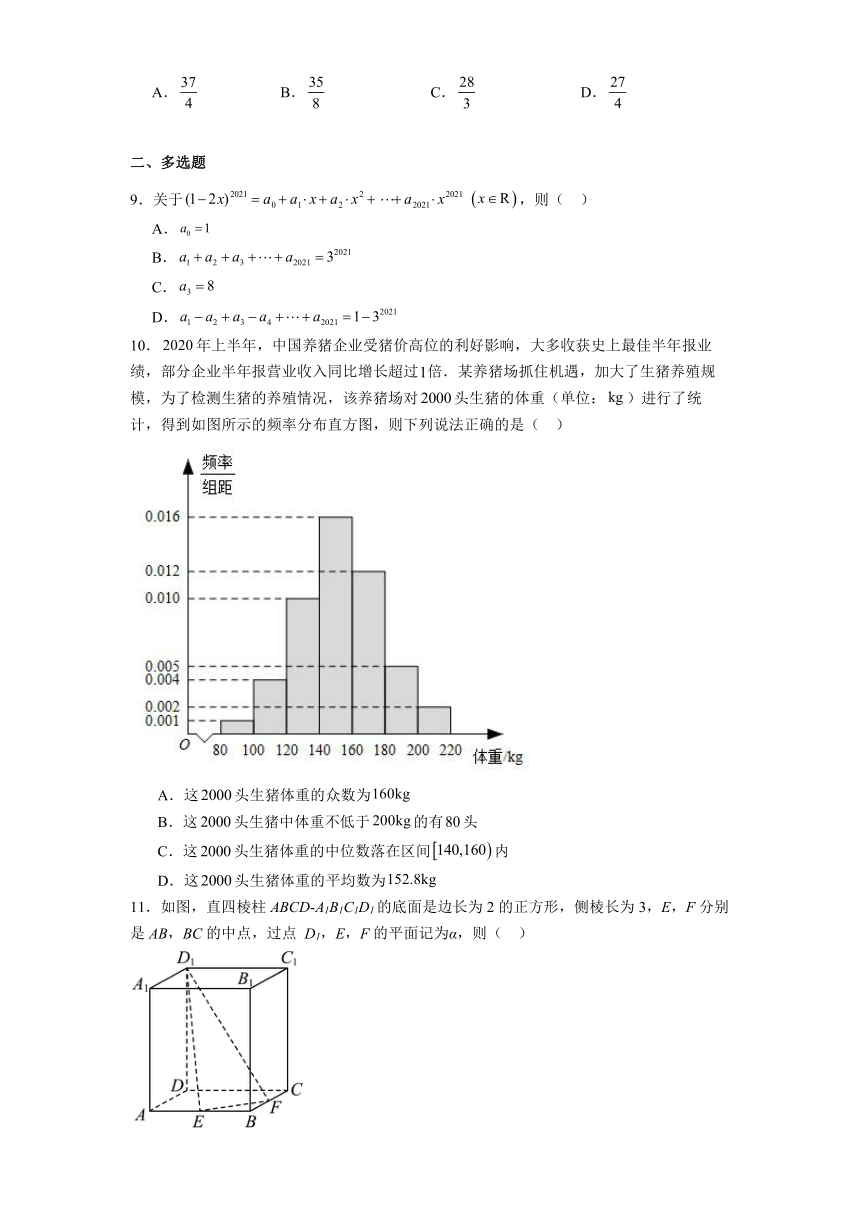
10.年上半年,中国养猪企业受猪价高位的利好影响,大多收获史上最佳半年报业绩,部分企业半年报营业收入同比增长超过倍.某养猪场抓住机遇,加大了生猪养殖规模,为了检测生猪的养殖情况,该养猪场对头生猪的体重(单位:)进行了统计,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.这头生猪体重的众数为
B.这头生猪中体重不低于的有头
C.这头生猪体重的中位数落在区间内
D.这头生猪体重的平均数为
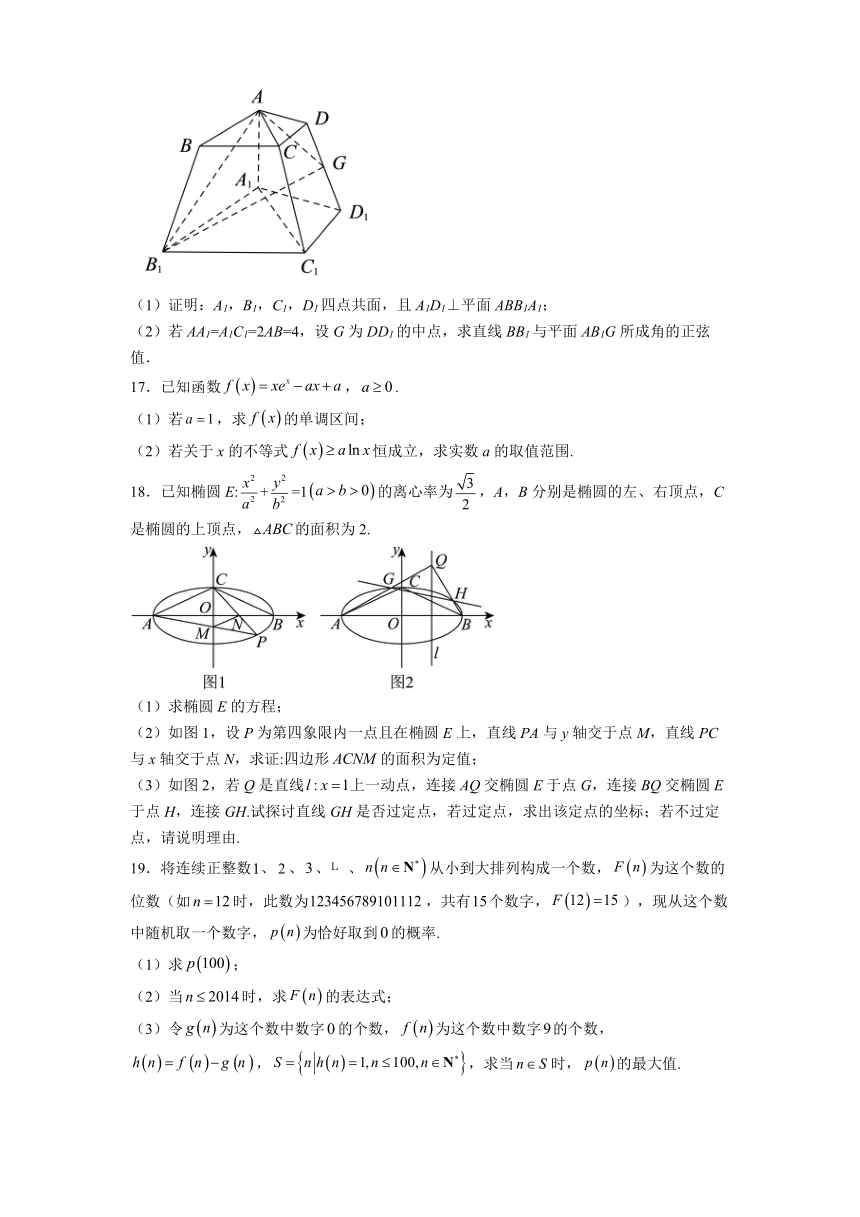
11.如图,直四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱长为3,E,F分别是AB,BC的中点,过点 D1,E,F的平面记为α,则( )
A.平面α截直四棱柱ABCD-A1B1C1D1所得截面的形状为四边形
B.平面α截直四棱柱ABCD-A1B1C1D1所得截面的面积为
C.平面α将直四棱柱分割成的上、下两部分的体积之比为47∶25
D.点B到平面α的距离与点A1到平面α的距离之比为1∶3
三、填空题
12.已知随机变量X服从正态分布,且,则 .
13.关于函数f(x)=有如下四个命题:
①f(x)的图象关于y轴对称.
②f(x)的图象关于原点对称.
③f(x)的图象关于直线x=对称.
④f(x)的最小值为2.
其中所有真命题的序号是 .
14.已知椭圆的右焦点为,离心率为.设A,B为椭圆上关于原点对称的两点,的中点为M,的中点为N,原点在以线段为直径的圆上.设直线AB的斜率为k,若,则的取值范围为
四、解答题
15.已知锐角的内角A,B,C的对边分别为a,b,c,,的面积为.
(1)求C;
(2)求面积的取值范围.
16.如图,在三棱台ABC A1B1C1中,△ABC为等边三角形,AA1⊥平面ABC,将梯形AA1C1C绕AA1旋转至AA1D1D位置,二面角D1 AA1 C1的大小为30°.
(1)证明:A1,B1,C1,D1四点共面,且A1D1⊥平面ABB1A1;
(2)若AA1=A1C1=2AB=4,设G为DD1的中点,求直线BB1与平面AB1G所成角的正弦值.
17.已知函数,.
(1)若,求的单调区间;
(2)若关于x的不等式恒成立,求实数a的取值范围.
18.已知椭圆E:+=1的离心率为,A,B分别是椭圆的左、右顶点,C是椭圆的上顶点,的面积为2.
(1)求椭圆E的方程;
(2)如图1,设P为第四象限内一点且在椭圆E上,直线PA与y轴交于点M,直线PC与x轴交于点N,求证:四边形的面积为定值;
(3)如图2,若Q是直线上一动点,连接AQ交椭圆E于点G,连接BQ交椭圆E于点H,连接GH.试探讨直线GH是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
19.将连续正整数、、、、从小到大排列构成一个数,为这个数的位数(如时,此数为,共有个数字,),现从这个数中随机取一个数字,为恰好取到的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字的个数,为这个数中数字的个数,,,求当时,的最大值.
参考答案
1.【答案】C
【详解】故选C
2.【答案】B
【详解】因为,
,
,
故选B.
3.【答案】A
【详解】因为可得:
当时,,充分性成立;
当时,,必要性不成立;
所以当,是的充分不必要条件.
故选A.
4.【答案】B
【详解】因为,,,所以,所以,
设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为天,
则,所以,所以,
所以天.
故选B.
5.【答案】B
【详解】,
,
,
,
,
即的最大值为.
故选B.
6.【答案】A
【详解】由题意知,则,,又,
所以,所以,方程在上有且仅有一个实数根,即函数的图象与直线有且仅有一个交点,
作出的图象,如图所示,由图易知满足题意的实数的取值范围是或,
故选A.
7.【答案】C
【详解】由题意可令直线的方程为,
联立得,解得,即,同理可得,
则.
由于直线与双曲线相交,则,
所以,整理得,
解得或(舍去),所以,
故选C.
8.【答案】A
【详解】解:因为函数的对称轴为,故由题意可得,
即,即,解得或(舍去),
则,即有.
记,令,则,
故,
又(当且仅当取等号),由于,则或时取最小值,
又,,
由于,故当时原式取最小值.
故选A.
9.【答案】AD
【详解】对于A,令,得,A正确;
对于B,令,得,B错误;
对于C,,C错误;
对于D,令,得,
因此,D正确.
故选AD
10.【答案】BCD
【详解】由频率分布直方图可知,这一组的数据对应的小长方形最高,所以这头生猪的体重的众数为,A错误;
这头生猪中体重不低于的有(头),B正确;
因为生猪的体重在内的频率为,
在内的频率为,且,
所以这头生猪体重的中位数落在区间内,C正确;
这头生猪体重的平均数为,
D正确.
故选BCD.
11.【答案】BC
【详解】如图,
延长EF分别与DA,DC的延长线交于点P,Q,连接D1P,交AA1于点M,连接D1Q,交CC1于点N,
连接ME,NF,则平面α截直四棱柱ABCD-A1B1C1D1所得截面为五边形D1MEFN,故A错误;
由平行线分线段成比例可得,AP=BF=1,故DP=DD1=3,则△DD1P为等腰直角三角形,
由相似三角形可知AM=AP=1,故A1M=2,则D1M=D1N=2,ME=EF=FN=,连接MN,易知MN=2,
因此五边形D1MEFN可以分成等边三角形D1MN和等腰梯形MEFN,等腰梯形MEFN的高h=,
则等腰梯形MEFN的面积为,又×2=2,
所以五边形D1MEFN的面积为2,故B正确;
记平面α将直四棱柱分割成的上、下两部分的体积分别为V1,V2,
则V2= V三棱锥M-PAE V三棱锥N-CFQ=×3×3×3 ×1×1×1 ×1×1×1=,所以V1= V1=12,
则V1∶V2=47∶25,故C正确;
因为平面α过线段AB的中点E,所以点A到平面α的距离与点B到平面α的距离相等,
由平面α过A1A的三等分点M可知,点A1到平面α的距离是点A到平面α的距离的2倍,
因此点A1到平面α的距离是点B到平面α的距离的2倍,故D错误.
故选BC
12.【答案】/.
【详解】因为,所以,因此.
13.【答案】②③
【详解】对于命题①,,,则,
所以,函数的图象不关于轴对称,命题①错误;
对于命题②,函数的定义域为,定义域关于原点对称,
,
所以,函数的图象关于原点对称,命题②正确;
对于命题③,,
,则,
所以,函数的图象关于直线对称,命题③正确;
对于命题④,当时,,则,
命题④错误.
14.【答案】
【详解】试题分析:由题知, ,又因为 是 的中点,所以;所以点 在原点为圆心,半径为的圆上,即
设联立 ,解得因为 ,所以,即,又因为 ,解得,,所以,即
所以
考点:直线与圆锥曲线的综合问题,求离心率取值范围
15.【答案】(1)
(2)
【详解】(1)的面积为,
则,则
又,则
(2)由(1)可知,又
则,则
则的面积
锐角中,,则,解之得
则,则,
则,则面积的取值范围为
16.【答案】(1)证明见解析
(2)
【详解】(1)证明:因为平面,所以,
又因为,,所以平面,
假设,,,四点不共面,因为平面,
平面,所以平面平面,
与平面平面矛盾,
故,,,四点共面,
又因为,,
所以二面角的平面角,
所以,又,
所以;又,,
所以平面;
(2)以为坐标原点,,,的方向为x,y,z轴正方向建立如图所示的空间直角坐标系;
则,,,,
,,,,
所以,则,,,
设平面的法向量为,
则,
令,得,
设与平面所成角为,
则.
所以与平面所成角的正弦值为.
17.【答案】(1)单调递减区间为,单调递增区间为;
(2).
【详解】(1)当时,,
则.
当时,因为,且,
所以,
所以,单调递减.
当时,因为,且,
所以,
所以,单调递增.
所以当时,的单调递减区间为,单调递增区间为.
(2)恒成立等价于恒成立,
令,
则.
①当时,在区间上恒成立,符合题意;
②当时,,
令,,即在上单调递增,,则存在,使得,此时,即,
则当时,,单调递减;当时,,单调递增.
所以.
令,得.
因为,所以.
综上,实数a的取值范围为.
18.【答案】(1)
(2)证明见解析
(3)是,
【详解】(1)由题意得,解得,
所以椭圆E的方程为.
(2)设 ,则,
又,所以直线PA的方程为.
令 ,得,从而.
直线PC的方程为.
令,得,从而.
所以四边形的面积
=2.
从而四边形的面积为定值.
(3)直线GH过定点,理由如下:
①当点Q在x轴上时,直线GH为x轴,过点.
②当点Q不在x轴上时,由题意可设,,,直线 ,
将直线方程代入椭圆E的方程得,
则,则点,
设直线 ,同理得点.
又点 为直线AG与直线BH的交点,则.
由两点式得直线GH的方程为:,
令 ,得,
故直线GH过定点.
19.【答案】(1)
(2)
(3)
【详解】(1)当时,一位数有,二位数个,三位数个,
这个数中总共有个数字,
其中数字的数有、、、、、,数字的个数为,
所以恰好取到的概率为.
(2)当时,全是一位数,;
当时,一位数个数为,二位数的个数为,;
当时,一位数的个数为,二位数的个数为,三位数的个数为,
;
当时,一位数的个数为,二位数的个数为,三位数的个数为,
四位数的个数为,.
综上所述,.
(3)当时,;
当时,;
当时,,
所以,,
同理可得,
由可知,
所以当时,,
当时,,
当时,;
当时,,
由随着的增大而增大,故当时,的最大值为,
又,所以当时,的最大值为.
一、单选题
1.设集合A={x|1≤x≤3},B={x|2
A.-1 B.1 C.0 D.2
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
4.基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A.1.2天 B.1.8天
C.2.5天 D.3.5天
5.已知平面向量均为单位向量,且,则的最大值为( )
A. B. C.1 D.
6.已知是函数的一个极大值点,若方程在上有且仅有一个实数根,则实数的取值范围是( )
A. B. C. D.
7.已知双曲线的右顶点为,直线与双曲线相交,从引双曲线的两条渐近线的平行线,与直线分别交于点、.若为坐标原点,,则双曲线的离心率为( )
A. B.或 C. D.或
8.已知函数,且,则的最小值为( )
A. B. C. D.
二、多选题
9.关于,则( )
A.
B.
C.
D.
10.年上半年,中国养猪企业受猪价高位的利好影响,大多收获史上最佳半年报业绩,部分企业半年报营业收入同比增长超过倍.某养猪场抓住机遇,加大了生猪养殖规模,为了检测生猪的养殖情况,该养猪场对头生猪的体重(单位:)进行了统计,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.这头生猪体重的众数为
B.这头生猪中体重不低于的有头
C.这头生猪体重的中位数落在区间内
D.这头生猪体重的平均数为
11.如图,直四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱长为3,E,F分别是AB,BC的中点,过点 D1,E,F的平面记为α,则( )
A.平面α截直四棱柱ABCD-A1B1C1D1所得截面的形状为四边形
B.平面α截直四棱柱ABCD-A1B1C1D1所得截面的面积为
C.平面α将直四棱柱分割成的上、下两部分的体积之比为47∶25
D.点B到平面α的距离与点A1到平面α的距离之比为1∶3
三、填空题
12.已知随机变量X服从正态分布,且,则 .
13.关于函数f(x)=有如下四个命题:
①f(x)的图象关于y轴对称.
②f(x)的图象关于原点对称.
③f(x)的图象关于直线x=对称.
④f(x)的最小值为2.
其中所有真命题的序号是 .
14.已知椭圆的右焦点为,离心率为.设A,B为椭圆上关于原点对称的两点,的中点为M,的中点为N,原点在以线段为直径的圆上.设直线AB的斜率为k,若,则的取值范围为
四、解答题
15.已知锐角的内角A,B,C的对边分别为a,b,c,,的面积为.
(1)求C;
(2)求面积的取值范围.
16.如图,在三棱台ABC A1B1C1中,△ABC为等边三角形,AA1⊥平面ABC,将梯形AA1C1C绕AA1旋转至AA1D1D位置,二面角D1 AA1 C1的大小为30°.
(1)证明:A1,B1,C1,D1四点共面,且A1D1⊥平面ABB1A1;
(2)若AA1=A1C1=2AB=4,设G为DD1的中点,求直线BB1与平面AB1G所成角的正弦值.
17.已知函数,.
(1)若,求的单调区间;
(2)若关于x的不等式恒成立,求实数a的取值范围.
18.已知椭圆E:+=1的离心率为,A,B分别是椭圆的左、右顶点,C是椭圆的上顶点,的面积为2.
(1)求椭圆E的方程;
(2)如图1,设P为第四象限内一点且在椭圆E上,直线PA与y轴交于点M,直线PC与x轴交于点N,求证:四边形的面积为定值;
(3)如图2,若Q是直线上一动点,连接AQ交椭圆E于点G,连接BQ交椭圆E于点H,连接GH.试探讨直线GH是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
19.将连续正整数、、、、从小到大排列构成一个数,为这个数的位数(如时,此数为,共有个数字,),现从这个数中随机取一个数字,为恰好取到的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字的个数,为这个数中数字的个数,,,求当时,的最大值.
参考答案
1.【答案】C
【详解】故选C
2.【答案】B
【详解】因为,
,
,
故选B.
3.【答案】A
【详解】因为可得:
当时,,充分性成立;
当时,,必要性不成立;
所以当,是的充分不必要条件.
故选A.
4.【答案】B
【详解】因为,,,所以,所以,
设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为天,
则,所以,所以,
所以天.
故选B.
5.【答案】B
【详解】,
,
,
,
,
即的最大值为.
故选B.
6.【答案】A
【详解】由题意知,则,,又,
所以,所以,方程在上有且仅有一个实数根,即函数的图象与直线有且仅有一个交点,
作出的图象,如图所示,由图易知满足题意的实数的取值范围是或,
故选A.
7.【答案】C
【详解】由题意可令直线的方程为,
联立得,解得,即,同理可得,
则.
由于直线与双曲线相交,则,
所以,整理得,
解得或(舍去),所以,
故选C.
8.【答案】A
【详解】解:因为函数的对称轴为,故由题意可得,
即,即,解得或(舍去),
则,即有.
记,令,则,
故,
又(当且仅当取等号),由于,则或时取最小值,
又,,
由于,故当时原式取最小值.
故选A.
9.【答案】AD
【详解】对于A,令,得,A正确;
对于B,令,得,B错误;
对于C,,C错误;
对于D,令,得,
因此,D正确.
故选AD
10.【答案】BCD
【详解】由频率分布直方图可知,这一组的数据对应的小长方形最高,所以这头生猪的体重的众数为,A错误;
这头生猪中体重不低于的有(头),B正确;
因为生猪的体重在内的频率为,
在内的频率为,且,
所以这头生猪体重的中位数落在区间内,C正确;
这头生猪体重的平均数为,
D正确.
故选BCD.
11.【答案】BC
【详解】如图,
延长EF分别与DA,DC的延长线交于点P,Q,连接D1P,交AA1于点M,连接D1Q,交CC1于点N,
连接ME,NF,则平面α截直四棱柱ABCD-A1B1C1D1所得截面为五边形D1MEFN,故A错误;
由平行线分线段成比例可得,AP=BF=1,故DP=DD1=3,则△DD1P为等腰直角三角形,
由相似三角形可知AM=AP=1,故A1M=2,则D1M=D1N=2,ME=EF=FN=,连接MN,易知MN=2,
因此五边形D1MEFN可以分成等边三角形D1MN和等腰梯形MEFN,等腰梯形MEFN的高h=,
则等腰梯形MEFN的面积为,又×2=2,
所以五边形D1MEFN的面积为2,故B正确;
记平面α将直四棱柱分割成的上、下两部分的体积分别为V1,V2,
则V2= V三棱锥M-PAE V三棱锥N-CFQ=×3×3×3 ×1×1×1 ×1×1×1=,所以V1= V1=12,
则V1∶V2=47∶25,故C正确;
因为平面α过线段AB的中点E,所以点A到平面α的距离与点B到平面α的距离相等,
由平面α过A1A的三等分点M可知,点A1到平面α的距离是点A到平面α的距离的2倍,
因此点A1到平面α的距离是点B到平面α的距离的2倍,故D错误.
故选BC
12.【答案】/.
【详解】因为,所以,因此.
13.【答案】②③
【详解】对于命题①,,,则,
所以,函数的图象不关于轴对称,命题①错误;
对于命题②,函数的定义域为,定义域关于原点对称,
,
所以,函数的图象关于原点对称,命题②正确;
对于命题③,,
,则,
所以,函数的图象关于直线对称,命题③正确;
对于命题④,当时,,则,
命题④错误.
14.【答案】
【详解】试题分析:由题知, ,又因为 是 的中点,所以;所以点 在原点为圆心,半径为的圆上,即
设联立 ,解得因为 ,所以,即,又因为 ,解得,,所以,即
所以
考点:直线与圆锥曲线的综合问题,求离心率取值范围
15.【答案】(1)
(2)
【详解】(1)的面积为,
则,则
又,则
(2)由(1)可知,又
则,则
则的面积
锐角中,,则,解之得
则,则,
则,则面积的取值范围为
16.【答案】(1)证明见解析
(2)
【详解】(1)证明:因为平面,所以,
又因为,,所以平面,
假设,,,四点不共面,因为平面,
平面,所以平面平面,
与平面平面矛盾,
故,,,四点共面,
又因为,,
所以二面角的平面角,
所以,又,
所以;又,,
所以平面;
(2)以为坐标原点,,,的方向为x,y,z轴正方向建立如图所示的空间直角坐标系;
则,,,,
,,,,
所以,则,,,
设平面的法向量为,
则,
令,得,
设与平面所成角为,
则.
所以与平面所成角的正弦值为.
17.【答案】(1)单调递减区间为,单调递增区间为;
(2).
【详解】(1)当时,,
则.
当时,因为,且,
所以,
所以,单调递减.
当时,因为,且,
所以,
所以,单调递增.
所以当时,的单调递减区间为,单调递增区间为.
(2)恒成立等价于恒成立,
令,
则.
①当时,在区间上恒成立,符合题意;
②当时,,
令,,即在上单调递增,,则存在,使得,此时,即,
则当时,,单调递减;当时,,单调递增.
所以.
令,得.
因为,所以.
综上,实数a的取值范围为.
18.【答案】(1)
(2)证明见解析
(3)是,
【详解】(1)由题意得,解得,
所以椭圆E的方程为.
(2)设 ,则,
又,所以直线PA的方程为.
令 ,得,从而.
直线PC的方程为.
令,得,从而.
所以四边形的面积
=2.
从而四边形的面积为定值.
(3)直线GH过定点,理由如下:
①当点Q在x轴上时,直线GH为x轴,过点.
②当点Q不在x轴上时,由题意可设,,,直线 ,
将直线方程代入椭圆E的方程得,
则,则点,
设直线 ,同理得点.
又点 为直线AG与直线BH的交点,则.
由两点式得直线GH的方程为:,
令 ,得,
故直线GH过定点.
19.【答案】(1)
(2)
(3)
【详解】(1)当时,一位数有,二位数个,三位数个,
这个数中总共有个数字,
其中数字的数有、、、、、,数字的个数为,
所以恰好取到的概率为.
(2)当时,全是一位数,;
当时,一位数个数为,二位数的个数为,;
当时,一位数的个数为,二位数的个数为,三位数的个数为,
;
当时,一位数的个数为,二位数的个数为,三位数的个数为,
四位数的个数为,.
综上所述,.
(3)当时,;
当时,;
当时,,
所以,,
同理可得,
由可知,
所以当时,,
当时,,
当时,;
当时,,
由随着的增大而增大,故当时,的最大值为,
又,所以当时,的最大值为.
同课章节目录
