甘肃省兰州市第四片区2024-2025学年高二下学期期中数学试卷(含答案)
文档属性
| 名称 | 甘肃省兰州市第四片区2024-2025学年高二下学期期中数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 521.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 17:40:02 | ||
图片预览


文档简介
甘肃省兰州市第四片区2024-2025学年高二下学期期中考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若向量在空间的一组基底下的坐标是,则在基底下的坐标是( )
A. B. C. D.
2.设点,点,点,若的中点为,则等于( )
A. B. C. D.3
3.已知非零空间向量,,且,则一定共线的三点是( )
A.A,B,D B.A,B,C C.B,C,D D.A,C,D
4.设正四面体的棱长为,,分别是,的中点,则的值为( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.函数在区间上是( )
A.单调增函数
B.单调减函数
C.在上是单调减函数,在上是单调增函数
D.在上是单调增函数,在上是单调减函数
7.已知的三个顶点坐标分别为,,,则的重心坐标为( )
A. B. C. D.
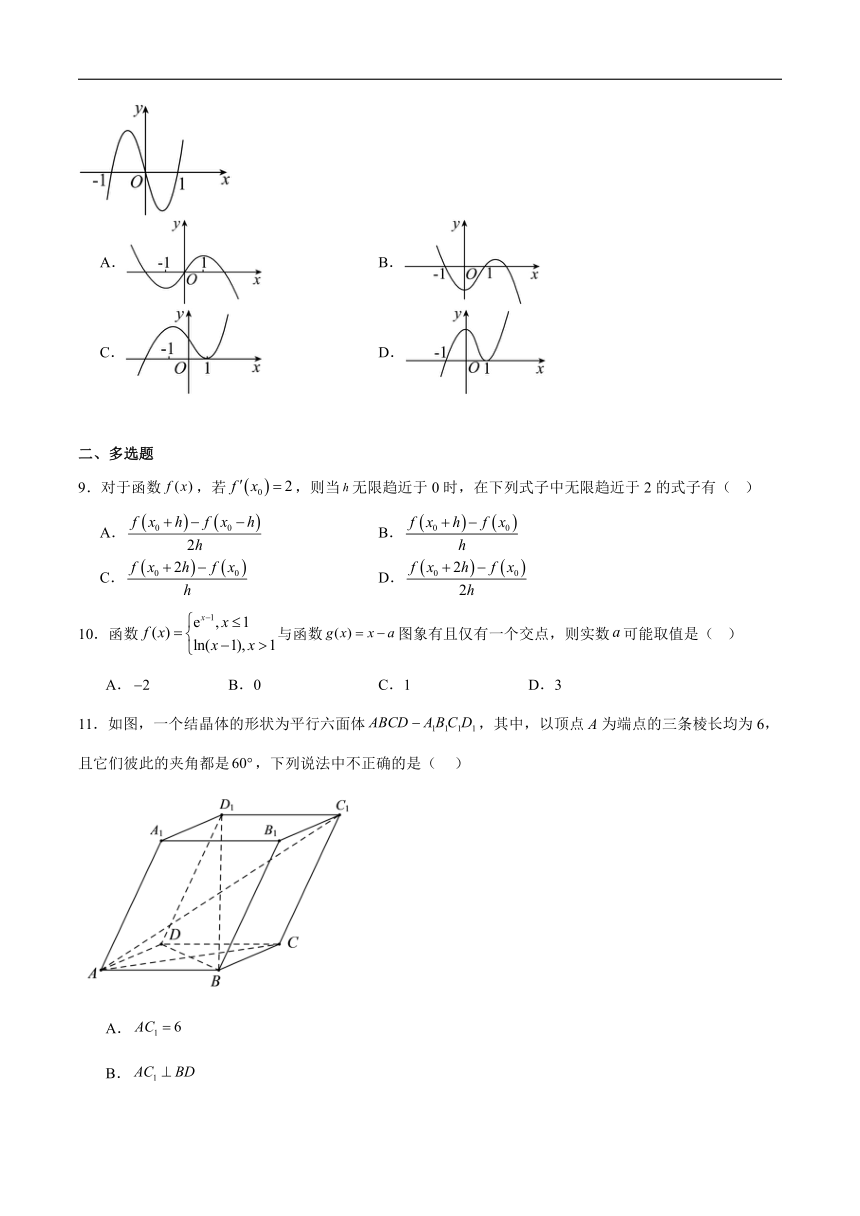
8.已知函数的图象如图所示(其中是函数的导函数),则下面四个图象中,的图象大致是( )
A. B.
C. D.
二、多选题
9.对于函数,若,则当无限趋近于0时,在下列式子中无限趋近于2的式子有( )
A. B.
C. D.
10.函数与函数图象有且仅有一个交点,则实数可能取值是( )
A. B.0 C.1 D.3
11.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是,下列说法中不正确的是( )
A.
B.
C.向量与的夹角是
D.与AC所成角的余弦值为
三、填空题
12.已知,,若与的夹角为钝角,则实数t的取值范围是 .
13.已知函数在上总是单调函数,则a的取值范围是
14.已知点P在曲线上,为曲线在点P处的切线的倾斜角,则的取值范围是 .
四、解答题
15.求下列函数的导数:
(1)
(2)
(3)
16.已知函数.
(1)若,求函数的极值;
(2)若函数有三个零点,求实数的取值范围.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设,
(I)若,且,求向量c;
(II)已知向量与互相垂直,求k的值;
(III)求的面积.
18.如图,在直三棱柱中,,棱,点分别是的中点.
(1)求
的模;
(2)求
;
(3)求证:
.
19.设函数,为正整数,为常数,曲线在处的切线方程为.
(1)求的值; (2)求函数的最大值; (3)证明:.
甘肃省兰州市第四片区2024-2025学年高二下学期期中考试数学试卷参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D A C B C ABD AB
题号 11
答案 ACD
12.
13.
14.
15.(1).
(2)
.
(3),则.
16.(1)当时,函数,所以,
令解得:或.
当时,,即函数在上是减函数.当时,,函数在上是增函数.
当时,,函数在上是减函数.
所以当时,函数取得极小值;当时,函数取得极大值为.
(2)函数有三个零点等价于函数与函数的图像有三个公共点.
由(1)可知:当时,,当时,,并且函数的极小值为,极大值为,函数图象如下所示:
所以.即实数的取值范围是.
17.(I),由于,故可设,故,解得,故为或.
(II),,由于与垂直,则.
(III)依题意,,,故由余弦定理得,所以.故三角形面积为.
18.(1)如图,建立以点为坐标原点,、、所在直线分别为轴、轴、轴的空间直角坐标系.
依题意得、,;
(2)依题意得、、、,
,,,,,
所以,;
(3)依题意,得、,
,,
,,即;
19.(1)因为,由点在上,可得
因为,所以
又因为切线的斜率为,所以,所以
(2)由(1)可知,
令,即在上有唯一的零点.
在上,,故单调递增;而在上,,单调递减,故在的最大值为.
(3)令,则
在上,,故单调递减,而在上,,单调递增,
故在上的最小值为,所以即,令,得,即所以,即由(2)知,,故所证不等式成立.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若向量在空间的一组基底下的坐标是,则在基底下的坐标是( )
A. B. C. D.
2.设点,点,点,若的中点为,则等于( )
A. B. C. D.3
3.已知非零空间向量,,且,则一定共线的三点是( )
A.A,B,D B.A,B,C C.B,C,D D.A,C,D
4.设正四面体的棱长为,,分别是,的中点,则的值为( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.函数在区间上是( )
A.单调增函数
B.单调减函数
C.在上是单调减函数,在上是单调增函数
D.在上是单调增函数,在上是单调减函数
7.已知的三个顶点坐标分别为,,,则的重心坐标为( )
A. B. C. D.
8.已知函数的图象如图所示(其中是函数的导函数),则下面四个图象中,的图象大致是( )
A. B.
C. D.
二、多选题
9.对于函数,若,则当无限趋近于0时,在下列式子中无限趋近于2的式子有( )
A. B.
C. D.
10.函数与函数图象有且仅有一个交点,则实数可能取值是( )
A. B.0 C.1 D.3
11.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是,下列说法中不正确的是( )
A.
B.
C.向量与的夹角是
D.与AC所成角的余弦值为
三、填空题
12.已知,,若与的夹角为钝角,则实数t的取值范围是 .
13.已知函数在上总是单调函数,则a的取值范围是
14.已知点P在曲线上,为曲线在点P处的切线的倾斜角,则的取值范围是 .
四、解答题
15.求下列函数的导数:
(1)
(2)
(3)
16.已知函数.
(1)若,求函数的极值;
(2)若函数有三个零点,求实数的取值范围.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设,
(I)若,且,求向量c;
(II)已知向量与互相垂直,求k的值;
(III)求的面积.
18.如图,在直三棱柱中,,棱,点分别是的中点.
(1)求
的模;
(2)求
;
(3)求证:
.
19.设函数,为正整数,为常数,曲线在处的切线方程为.
(1)求的值; (2)求函数的最大值; (3)证明:.
甘肃省兰州市第四片区2024-2025学年高二下学期期中考试数学试卷参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D A C B C ABD AB
题号 11
答案 ACD
12.
13.
14.
15.(1).
(2)
.
(3),则.
16.(1)当时,函数,所以,
令解得:或.
当时,,即函数在上是减函数.当时,,函数在上是增函数.
当时,,函数在上是减函数.
所以当时,函数取得极小值;当时,函数取得极大值为.
(2)函数有三个零点等价于函数与函数的图像有三个公共点.
由(1)可知:当时,,当时,,并且函数的极小值为,极大值为,函数图象如下所示:
所以.即实数的取值范围是.
17.(I),由于,故可设,故,解得,故为或.
(II),,由于与垂直,则.
(III)依题意,,,故由余弦定理得,所以.故三角形面积为.
18.(1)如图,建立以点为坐标原点,、、所在直线分别为轴、轴、轴的空间直角坐标系.
依题意得、,;
(2)依题意得、、、,
,,,,,
所以,;
(3)依题意,得、,
,,
,,即;
19.(1)因为,由点在上,可得
因为,所以
又因为切线的斜率为,所以,所以
(2)由(1)可知,
令,即在上有唯一的零点.
在上,,故单调递增;而在上,,单调递减,故在的最大值为.
(3)令,则
在上,,故单调递减,而在上,,单调递增,
故在上的最小值为,所以即,令,得,即所以,即由(2)知,,故所证不等式成立.
同课章节目录
