【中考押题卷】广东省广州市2024-2025学年九年级下学期数学中考模拟押题预测卷一人教版(含解析)
文档属性
| 名称 | 【中考押题卷】广东省广州市2024-2025学年九年级下学期数学中考模拟押题预测卷一人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 20:57:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东省广州市2024-2025学年九年级下学期数学中考模拟押题预测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2024 杭州模拟)某品牌酸奶外包装上标明“净含量:200±5ml”.随机抽取四种口味的这种酸奶分别称重如下表.其中,净含量不合格的是( )
种类 原味 草莓味 香草味 巧克力味
净含量/ml 190 195 203 200
A.原味 B.草莓味 C.香草味 D.巧克力味
2.(3分)(2023春 兴宁区校级月考)如图图形中,既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
3.(3分)(2022秋 易县期中)中国的陆地面积约为9600000km2,领水面积约为370000km2,用科学记数法表示上述两个数字的和为( )
A.9.97×106 B.9.637×106 C.9.97×105 D.9.637×105
4.(3分)(2024春 二七区月考)下列说法中,正确的是( )
A.不相交的两条直线平行
B.相等的角是对顶角
C.如果∠a=48°32′,那么∠a余角的度数为41.28°
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小
5.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
6.(3分)甲、乙两位同学在一次试验中统计了某一结果出现的频率,给出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现6点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同其他都相同的2个红球和1个黄球,从中任意取出一个球是黄球的概率
7.(3分)(2024春 惠阳区期中)连接对角线相等四边形各边的中点得到的是什么四边形?( )
A.平行四边形 B.矩形
C.菱形 D.正方形
8.(3分)(2023秋 义乌市期末)已知二次函数y=﹣mx2+2mx+4(m>0)经过点A(﹣2,y1),点B(1,y2),点C(3,y3),那么y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
9.(3分)(2017秋 华容县期末)方程:1的解是( )
A.x=1 B.x=﹣4
C.x1=1,x2=﹣4 D.x=4
10.(3分)(2023春 太原期中)如图,一次函数y=kx﹣1与y=﹣x+3的图象都经过点P(2,1),则不等式kx﹣1≥﹣x+3的解集为( )
A.x≥2 B.x≤2 C.x≥1 D.x≤1
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)(2022 台山市校级一模)小王统计了一周家庭用水量,绘制了如图的统计图,那么这周用水量的众数是 ,中位数是 .
12.(3分)已知关于x的不等式4x﹣a≥﹣5的解集如图所示,则a的值是 .
13.(3分)(2024 江西模拟)若关于x的一元二次方程x2﹣x+m=0有实数根,则m的取值范围是 .
14.(3分)已知两个分式A,B,那么A+B= .
15.(3分)(2024 溧阳市一模)如图,以菱形ABCD的顶点B为圆心,边长AB为半径作圆,经过顶点D,点E、F分别在弧AD、弧DC上,且∠EBF=60°,AB=4,则图中阴影部分的面积为 .
三.解答题(共8小题,满分75分)
16.(9分)计算:()﹣1﹣20210+|﹣4|﹣tan60°.
17.(9分)(2024春 嘉定区期末)已知∠α、∠β.
(1)作∠AOB,使∠AOB=∠α﹣2∠β;
(2)作∠AOB的平分线OC.
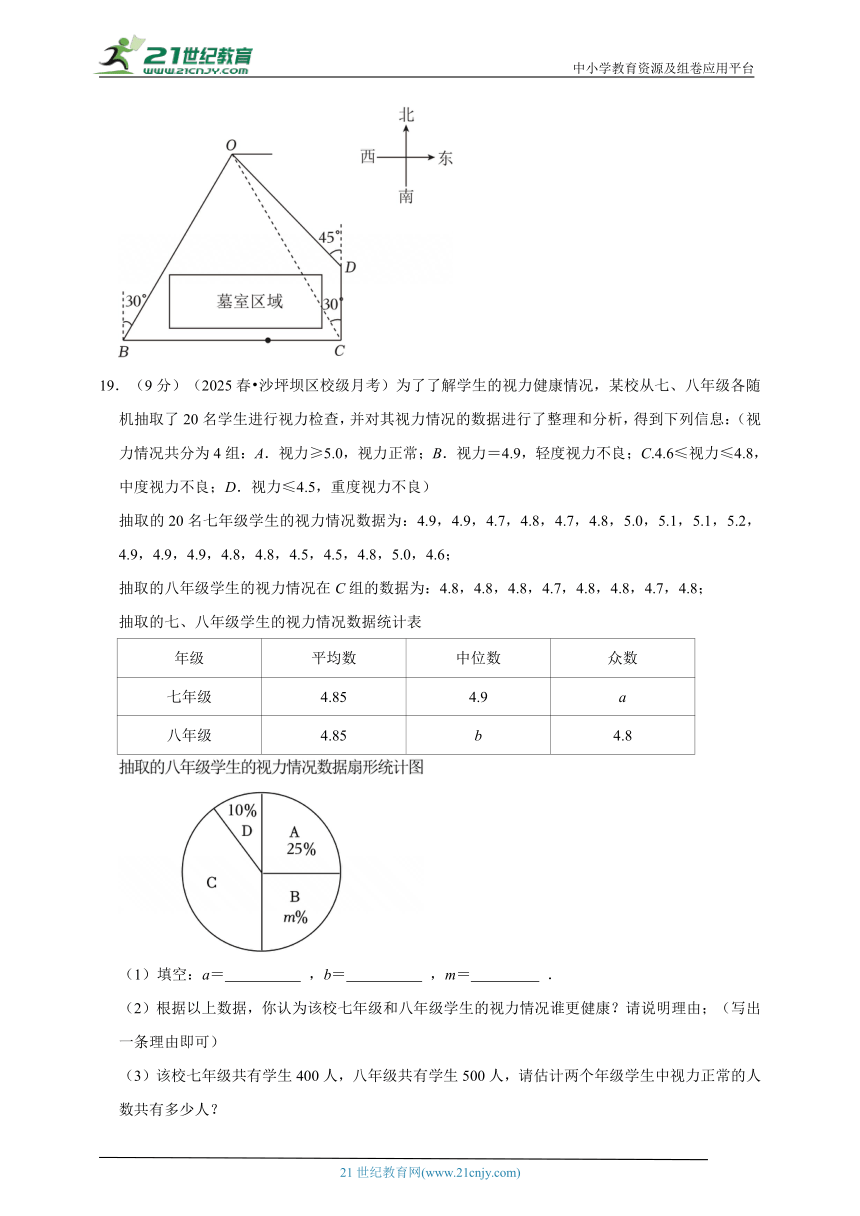
18.(9分)(2024春 沙坪坝区校级期中)如图,考古人员在古墓大门A处探测到一青铜古物O,由于大门A正北方向有间墓室,考古人员无法沿直线AO直接挖掘前往.经勘测,考古人员发现有两条线路可以挖掘前往青铜古物O:线路①A﹣C﹣D﹣O;线路②A﹣B﹣O.其中点C在点A的正东方10米处,点O在点C北偏西30°方向,点D在点C正北方,点O在点D西北方向20米处,点B在点A正西方向,点O在点B北偏东30°方向.(参考数据:,)
(1)求CD的长度;(结果保留根号)
(2)受周围环境的影响,考古人员在线路①挖掘的平均速度为3米/小时,在线路②挖掘的平均速度为3.2米/小时,请通过计算说明选择哪条线路能更快挖掘到古物O.
19.(9分)(2025春 沙坪坝区校级月考)为了了解学生的视力健康情况,某校从七、八年级各随机抽取了20名学生进行视力检查,并对其视力情况的数据进行了整理和分析,得到下列信息:(视力情况共分为4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,
中度视力不良;D.视力≤4.5,重度视力不良)
抽取的20名七年级学生的视力情况数据为:4.9,4.9,4.7,4.8,4.7,4.8,5.0,5.1,5.1,5.2,4.9,4.9,4.9,4.8,4.8,4.5,4.5,4.8,5.0,4.6;
抽取的八年级学生的视力情况在C组的数据为:4.8,4.8,4.8,4.7,4.8,4.8,4.7,4.8;
抽取的七、八年级学生的视力情况数据统计表
年级 平均数 中位数 众数
七年级 4.85 4.9 a
八年级 4.85 b 4.8
(1)填空:a= ,b= ,m= .
(2)根据以上数据,你认为该校七年级和八年级学生的视力情况谁更健康?请说明理由;(写出一条理由即可)
(3)该校七年级共有学生400人,八年级共有学生500人,请估计两个年级学生中视力正常的人数共有多少人?
20.(9分)(2024秋 西城区校级期中)甲,乙两名同学进行羽毛球比赛,羽毛球发出后的飞行路线可以看作是抛物线的一部分.如图建立平面直角坐标系,羽毛球从O点的正上方发出,飞行过程中羽毛球的竖直高度y(单位:m)与水平距离x(单位:m)之间近似满足函数关系y=a(x﹣h)2+k(a<0).
比赛中,甲同学连续进行了两次发球.
(1)甲同学第一次发球时,羽毛球的水平距离x与竖直高度y的七组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6
竖直高度y/m 1 2.75 4 4.75 5 4.75 4
根据以上数据,回答下列问题:
①当羽毛球飞行到最高点时,水平距离是 m;
②在水平距离5m处,放置一个高1.55m的球网,羽毛球 (填“是”或“否”)可以过网;
③求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)甲同学第二次发球时,羽毛球的竖直高度y与水平距离x之间近似满足函数关系y=﹣0.2(x﹣4.5)2+5.2.乙同学在两次接球中,都是原地起跳后使得球拍达到最大高度2.75m时刚好接到球,记乙同学第一次接球的起跳点的水平距离为d1,第二次接球的起跳点的水平距离为d2,则d2﹣d1 0(填“>”“<”或“=”).
21.(9分)(2024 济宁一模)如图,⊙O是△ABD的外接圆,AB是⊙O的直径,点C在⊙O上,连接AC,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P.
(1)求证:BD∥CP;
(2)若 cosP,BD=24,求BP的长.
22.(9分)(2023秋 开平市校级期中)如图1,在矩形ABCD中,AB=4,AD=6,E是边CD的中点,P(与点B,C不重合)是边BC上一动点,连接AP,PE,延长PE交AD的延长线于点Q.
(1)求证:△PCE≌△QDE.
(2)当△QDE∽△ABP时,求BP的长.
(3)如图2,分别取PA,PE,AD的中点F,G,H,连接FG,FH,GH,当FG⊥FH时,求BP的长和△FGH的面积.
23.(12分)(2024 驿城区模拟)如图,在平面直角坐标系中,以反比例函数图象上的点A和点B(1,﹣2)为顶点,分别作矩形ACOD和矩形BEOF,点C,E在x轴上,点D,F在y轴上,以点O为圆心,OF的长为半径作,交BE于点G,连接AO,OG.
(1)求k的值;
(2)求∠FOG的度数;
(3)求图中阴影部分的面积.
广东省广州市2024-2025学年九年级下学期数学中考押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2024 杭州模拟)某品牌酸奶外包装上标明“净含量:200±5ml”.随机抽取四种口味的这种酸奶分别称重如下表.其中,净含量不合格的是( )
种类 原味 草莓味 香草味 巧克力味
净含量/ml 190 195 203 200
A.原味 B.草莓味 C.香草味 D.巧克力味
【考点】正数和负数;有理数的加法;有理数的减法.
【专题】实数;运算能力.
【答案】A
【分析】根据题意,可得取值范围为(200﹣5)ml~(200+5)ml,即195ml~205ml,由此即可求解.
【解答】解:根据包装上标明“净含量:200±5ml”可得,最少为200﹣5=195ml,最多为200+5=205ml,
∴净含量的取值范围为195ml~205ml,
∴原味190<195,不合格,
故选:A.
【点评】本题考查了正负数,有理数的加减运算,结合已知条件列得正确的算式是解题的关键.
2.(3分)(2023春 兴宁区校级月考)如图图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】观察四个选项中的图形,判断轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合,找出既是轴对称图形又是中心对称图形的那个即可得出结论.
【解答】解:A、本选项图形是轴对称图形,不是中心对称图形,不符合题意;
B、本选项图形是中心对称图形,不是轴对称图形,不符合题意;
C、本选项图形是轴对称图形,不是中心对称图形,不符合题意;
D、本选项图形既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
【点评】本题考查了轴对称图形和中心对称图形的定义,仔细观察图形根据定义正确判断是解答本题的关键.
3.(3分)(2022秋 易县期中)中国的陆地面积约为9600000km2,领水面积约为370000km2,用科学记数法表示上述两个数字的和为( )
A.9.97×106 B.9.637×106 C.9.97×105 D.9.637×105
【考点】科学记数法—表示较大的数;有理数的加法.
【专题】实数;数感;符号意识.
【答案】A
【分析】先求和9600000+370000,再用科学记数法表示即可.
【解答】解:∵9600000+370000=9970000,
∴9970000=9.97×106;
故选:A.
【点评】此题考查了科学记数法与有理数的加法运算,熟练掌握科学记数法的表示形式(a×10n,其中1≤|a|<10,n为整数)是解答此题的关键.
4.(3分)(2024春 二七区月考)下列说法中,正确的是( )
A.不相交的两条直线平行
B.相等的角是对顶角
C.如果∠a=48°32′,那么∠a余角的度数为41.28°
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小
【考点】平行线的判定与性质;度分秒的换算;余角和补角;对顶角、邻补角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据平面内直线的位置关系,对顶角的定义,度分秒的进制,余角与补角的定义,逐一判断即可解答.
【解答】解:A.同一平面内,不相交的两条直线平行,故A不符合题意;
B.相等的角不一定是对顶角,故B不符合题意;
C.如果∠a=48°32′,那么∠a余角的度数为41°28′,故C不符合题意;
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小,故D符合题意;
故选:D.
【点评】本题考查了平面内直线的位置关系,对顶角的定义,度分秒的换算,余角与补角,熟练掌握这些数学概念是解题的关键.
5.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【专题】整式;运算能力.
【答案】C
【分析】各式计算得到结果,即可作出判断.
【解答】解:A、原式=a2﹣2ab+b2,不符合题意;
B、原式=﹣8a6,不符合题意;
C、原式=a,符合题意;
D、原式=3a2,不符合题意.
故选:C.
【点评】此题考查了完全平方公式,合并同类项,幂的乘方与积的乘方,同底数幂的除法,熟练掌握运算法则及公式是解本题的关键.
6.(3分)甲、乙两位同学在一次试验中统计了某一结果出现的频率,给出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现6点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同其他都相同的2个红球和1个黄球,从中任意取出一个球是黄球的概率
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【解答】解:A、掷一枚正六面体的骰子,出现6点的概率为,故此选不符合题意;
B、掷一枚硬币,出现正面朝上的概率为,故此选不符合题意;
C、任意写出一个整数,能被2整除的概率为,故此选不符合题意;
D、从一装有2个红球和1个黄球的袋子中任取一球,取到黄球的概率是:0.33,故此选项符合题意.
故选:D.
【点评】本题考查了列表法与树状图法和概率公式,解题关键是掌握i频率=所求情况数与总情况数之比.
7.(3分)(2024春 惠阳区期中)连接对角线相等四边形各边的中点得到的是什么四边形?( )
A.平行四边形 B.矩形
C.菱形 D.正方形
【考点】正方形的性质;平行四边形的性质;菱形的性质;矩形的性质.
【专题】多边形与平行四边形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】作四边形ABCD中,使AC=BD,令E、F、G、H分别是AB、BC、CD、DA的中点,由三角形的中位线定理得EF∥AC,EFAC,GH∥AC,GHAC,则EF∥GH,EF=GH,可证明四边形EFGH是平行四边形,由EFAC,EHBD,且AC=BD得EF=EG,则四边形EFGH是菱形,于是得到问题的答案.
【解答】解:如图,四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,
∵E、F分别是AB、BC的中点,
∴EF∥AC,EFAC,
同理GH∥AC,GHAC,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形,
∵E、H分别是AB、DA的中点,
∴EHBD,
∵AC=BD,
∴EF=EH,
∴四边形EFGH是菱形,
故选:C.
【点评】此题重点考查三角形的中位线定理、平行四边形的判定、菱形的判定等知识,根据三角形的中位线定理及AC=BD推导出EF=GH是解题的关键.
8.(3分)(2023秋 义乌市期末)已知二次函数y=﹣mx2+2mx+4(m>0)经过点A(﹣2,y1),点B(1,y2),点C(3,y3),那么y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【考点】二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;应用意识.
【答案】B
【分析】根据函数解析式求出抛物线对称轴和开口方向,再根据二次函数的性质求判断即可.
【解答】解:二次函数y=﹣mx2+2mx+4的对称轴为直线x1,
∵m>0,
∴抛物线开口向下,
∴x=1时,y2最大,
∵1﹣(﹣2)=3>3﹣1=2,
∴y3>y1,
∴y1,y2,y3的大小关y1<y3<y2.
故选:B.
【点评】本题考查了二次函数图象上点的坐标特征,关键是掌握二次函数的性质.
9.(3分)(2017秋 华容县期末)方程:1的解是( )
A.x=1 B.x=﹣4
C.x1=1,x2=﹣4 D.x=4
【考点】解分式方程.
【专题】分式方程及应用;运算能力.
【答案】B
【分析】按照解分式方程的步骤,进行计算即可解答.
【解答】解:1,
6﹣3(x+1)=x2﹣1,
解得:x=﹣4或x=1,
检验:当x=1时,x2﹣1=0,
∴x=1是原方程的增根,
当x=﹣4时,x2﹣1≠0,
∴x=﹣4是原方程的根,
故选:B.
【点评】本题考查了解分式方程,一定要注意解分式方程必须检验.
10.(3分)(2023春 太原期中)如图,一次函数y=kx﹣1与y=﹣x+3的图象都经过点P(2,1),则不等式kx﹣1≥﹣x+3的解集为( )
A.x≥2 B.x≤2 C.x≥1 D.x≤1
【考点】一次函数与一元一次不等式;两条直线相交或平行问题.
【专题】一元一次不等式(组)及应用;一次函数及其应用;几何直观.
【答案】A
【分析】根据函数图象可知:当x>2时,一次函数y=kx﹣1的图象在y=﹣x+3的图象的上方,然后即可写出不等式kx﹣1≥﹣x+3的解集.
【解答】解:由图象可得,
当x>2时,一次函数y=kx﹣1的图象在y=﹣x+3的图象的上方,
∴不等式kx﹣1≥﹣x+3的解集为x≥2,
故选:A.
【点评】本题考查一次函数与一元一次不等式,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)(2022 台山市校级一模)小王统计了一周家庭用水量,绘制了如图的统计图,那么这周用水量的众数是 1 ,中位数是 1 .
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】1;1.
【分析】根据众数和中位数的定义即可求解.
【解答】解:从统计图中得知:从星期日到星期六的每天用水量分别为:2,1,0.5,1.5,1,1.5,1(单位:t).
出现次数最多的数字是1,即可众数是1.
将其按从小到大顺序排列为:0.5,1,1,1,1.5,1.5,2,
位于中间的数字为1,即中位数是1.
故答案为:1;1.
【点评】本题考查的是众数和中位数.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
12.(3分)已知关于x的不等式4x﹣a≥﹣5的解集如图所示,则a的值是 ﹣3 .
【考点】解一元一次不等式;在数轴上表示不等式的解集.
【专题】一元一次不等式(组)及应用;运算能力.
【答案】﹣3.
【分析】本题是关于x的不等式,应先只把x看成未知数,求得x的解集,再根据x≥﹣2,求得a的值.
【解答】解:移项得,4x≥a﹣5,
化系数为1得,x,
由数轴知x≥﹣2,所以2,
解得a=﹣3.
故答案为:﹣3.
【点评】当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据解集进行判断,求得另一个字母的值.
13.(3分)(2024 江西模拟)若关于x的一元二次方程x2﹣x+m=0有实数根,则m的取值范围是 m .
【考点】根的判别式.
【专题】一元二次方程及应用;运算能力.
【答案】见试题解答内容
【分析】根据一元二次方程根的判别式求解即可.
【解答】解:∵关于x的一元二次方程x2﹣x+m=0有实数根,
∴Δ=b2﹣4ac=1﹣4m≥0,
∴m,
故答案为:m.
【点评】本题主要考查了一元二次方程根的判别式,熟知一元二次方程有实数根,则Δ=b2﹣4ac≥0是解题的关键.
14.(3分)已知两个分式A,B,那么A+B= 0 .
【考点】分式的加减法.
【专题】分式;运算能力.
【答案】0.
【分析】利用分式的加减运算的法则进行运算即可.
【解答】解:∵A,B,
∴A+B
=0.
故答案为:0.
【点评】本题主要考查分式的加减法,解答的关键是对相应的运算法则的掌握.
15.(3分)(2024 溧阳市一模)如图,以菱形ABCD的顶点B为圆心,边长AB为半径作圆,经过顶点D,点E、F分别在弧AD、弧DC上,且∠EBF=60°,AB=4,则图中阴影部分的面积为 4 .
【考点】扇形面积的计算;菱形的性质;圆周角定理.
【专题】矩形 菱形 正方形;与圆有关的计算;运算能力;推理能力.
【答案】4.
【分析】根据菱形的性质,正三角形的判断和性质以及扇形面积的计算方法进行计算即可.
【解答】解:如图,连接BD,
∵四边形ABCD是菱形,AB=DB=BE=FB=CB,
∴△ABD,△BCD是正三角形,
∴∠ABD=60°=∠EBF,即∠ABE+∠DBE=∠DBF+∠DBE,
∴∠AOE=∠DBF,
S阴影部分=S扇形ABD﹣S△ABD
4×(4)
4.
故答案为:4.
【点评】本题考查扇形面积的计算,菱形的性质,掌握扇形面积的计算方法,菱形的性质以及正三角形的判断和性质是正确解答的关键.
三.解答题(共8小题,满分75分)
16.(9分)计算:()﹣1﹣20210+|﹣4|﹣tan60°.
【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
【专题】实数;运算能力.
【答案】2+3.
【分析】先化简各式,然后再进行计算即可解答.
【解答】解:()﹣1﹣20210+|﹣4|﹣tan60°
=3﹣1+4
=2+3.
【点评】本题考查了实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.(9分)(2024春 嘉定区期末)已知∠α、∠β.
(1)作∠AOB,使∠AOB=∠α﹣2∠β;
(2)作∠AOB的平分线OC.
【考点】作图—复杂作图.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)见解析.
【分析】(1)先作射线OD,再作∠AOD=∠α,然后作∠EOD=∠β,∠BOE=∠β,则∠AOB即为所求;
(2)根据角平分线的尺规作图方法作图即可.
【解答】解:(1)如图所示,∠AOB即为所求;
(2)解:如图所示,OC即为所求.
【点评】本题主要考查了基本作图,掌握基本作图是解题的关键.
18.(9分)(2024春 沙坪坝区校级期中)如图,考古人员在古墓大门A处探测到一青铜古物O,由于大门A正北方向有间墓室,考古人员无法沿直线AO直接挖掘前往.经勘测,考古人员发现有两条线路可以挖掘前往青铜古物O:线路①A﹣C﹣D﹣O;线路②A﹣B﹣O.其中点C在点A的正东方10米处,点O在点C北偏西30°方向,点D在点C正北方,点O在点D西北方向20米处,点B在点A正西方向,点O在点B北偏东30°方向.(参考数据:,)
(1)求CD的长度;(结果保留根号)
(2)受周围环境的影响,考古人员在线路①挖掘的平均速度为3米/小时,在线路②挖掘的平均速度为3.2米/小时,请通过计算说明选择哪条线路能更快挖掘到古物O.
【考点】解直角三角形的应用﹣方向角问题;勾股定理的应用.
【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)CD的长度为(1010)米;
(2)选择线路①能更快挖掘到古物O.
【分析】(1)过点O作OE⊥CD交CD的延长线于点E,在RtODE中求出OE,DE,再在RtOCE中求出CE,OC,进而求出CD的抽到;
(2)由(1)可求出AC+CD+OD,证明△OBC是等边三角形,从而可求出AB+BO的长度,进而根据路程÷速度求出选择两条线路挖掘所用的时间,再比较即可解决问题.
【解答】解:(1)过点O作OE⊥CD交CD的延长线于点E,如图,
在Rt△ODE中,
∵OD=20米,∠ODE=45°,
∴OE=OD sin45°=2010(米),
DE=OD cos45°=2010(米),
在Rt△OCE中,
∵OE=10米,∠OCE=30°,
∴OC20(米),
CE(米),
∴CD=CE﹣DE=1010(米),
答:CD的长度为(1010)米;
(2)由题意,知∠OBC=∠OCB=60°,
∴△OBC是等边三角形,
∴OB=BC=OC=20米≈28.2米,
∴AC+CD+OD=10+101020≈40.4(米),
AB+BO=BC﹣AC+BO≈28.2﹣10+28.2=46.4(米),
∵线路①挖掘的平均速度为3米/小时,
∴线路①挖掘需要时间为:40.4÷3≈13.47(小时),
∵线路②挖掘的平均速度为3.2米/小时,
∴线路②挖掘需要时间为:46.4÷3.2=14.5(小时),
∵13.47<14.5,
∴选择线路①能更快挖掘到古物O.
【点评】本题考查解直角三角形的应用﹣方向角问题,理解题意,将问题转化为解直角三角形问题是解题的关键.
19.(9分)(2025春 沙坪坝区校级月考)为了了解学生的视力健康情况,某校从七、八年级各随机抽取了20名学生进行视力检查,并对其视力情况的数据进行了整理和分析,得到下列信息:(视力情况共分为4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,
中度视力不良;D.视力≤4.5,重度视力不良)
抽取的20名七年级学生的视力情况数据为:4.9,4.9,4.7,4.8,4.7,4.8,5.0,5.1,5.1,5.2,4.9,4.9,4.9,4.8,4.8,4.5,4.5,4.8,5.0,4.6;
抽取的八年级学生的视力情况在C组的数据为:4.8,4.8,4.8,4.7,4.8,4.8,4.7,4.8;
抽取的七、八年级学生的视力情况数据统计表
年级 平均数 中位数 众数
七年级 4.85 4.9 a
八年级 4.85 b 4.8
(1)填空:a= 4.9 ,b= 4.8 ,m= 25 .
(2)根据以上数据,你认为该校七年级和八年级学生的视力情况谁更健康?请说明理由;(写出一条理由即可)
(3)该校七年级共有学生400人,八年级共有学生500人,请估计两个年级学生中视力正常的人数共有多少人?
【考点】众数;用样本估计总体;扇形统计图;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)4.9,4.8,25;(2)七年级学生的视力情况谁更健康,理由见解答;(3)225人.
【分析】(1)根据众数和中位数的定义即可求出a和b的值,根据扇形统计图分别求出A、C、D组人数,然后计算m即可;
(2)分别根据平均数,中位数和众数的意义分析即可;
(3)用样本估计总体即可.
【解答】解:(1)被抽取的20名七年级学生的视力情况中,4.9出现的次数最多,故众数a=4.9;
把被抽取的20名八年级学生的视力从小到大排列,排在中间的两个数分别是4.8,4.8,故中位数b4.8;
八年级C组所占百分比为:40%,故m%=1﹣10%﹣40%﹣25%=25%,即m=25.
故答案为:4.9,4.8,25;
(2)七年级学生的视力情况谁更健康,理由如下:
从平均数来看,两个班一样,从众数和中位数来看,七年级学生的视力健康情况总体更好一些,综上,七年级学生的视力情况谁更健康;
(3)400500×25%=225(人),
答:估计两个年级学生中视力正常的人数大约共有225人.
【点评】本题考查了扇形统计图,众数,中位数,算术平均数以及用样本估计总体,掌握众数、中位数、平均数定义是解题的关键.
20.(9分)(2024秋 西城区校级期中)甲,乙两名同学进行羽毛球比赛,羽毛球发出后的飞行路线可以看作是抛物线的一部分.如图建立平面直角坐标系,羽毛球从O点的正上方发出,飞行过程中羽毛球的竖直高度y(单位:m)与水平距离x(单位:m)之间近似满足函数关系y=a(x﹣h)2+k(a<0).
比赛中,甲同学连续进行了两次发球.
(1)甲同学第一次发球时,羽毛球的水平距离x与竖直高度y的七组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6
竖直高度y/m 1 2.75 4 4.75 5 4.75 4
根据以上数据,回答下列问题:
①当羽毛球飞行到最高点时,水平距离是 4 m;
②在水平距离5m处,放置一个高1.55m的球网,羽毛球 是 (填“是”或“否”)可以过网;
③求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)甲同学第二次发球时,羽毛球的竖直高度y与水平距离x之间近似满足函数关系y=﹣0.2(x﹣4.5)2+5.2.乙同学在两次接球中,都是原地起跳后使得球拍达到最大高度2.75m时刚好接到球,记乙同学第一次接球的起跳点的水平距离为d1,第二次接球的起跳点的水平距离为d2,则d2﹣d1 > 0(填“>”“<”或“=”).
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)①4;②是;③y=﹣0.25(x﹣4)2+5;
(2)>.
【分析】(1)①由表中数据直接可以得出结论;
②由表中数据直接可以得出结论;
③用待定系数法求函数解析式;
(2)把y=2.4分别代入(1)、(2)解析式求出d1和d2即可.
【解答】解:(1)①由表格中数据知,当x=3和x=5时,y=4.75,
∴对称轴为x=4,顶点坐标为(4,5),
∴当羽毛球飞行到最高点时,水平距离是4m,
故答案为:4;
②∵当x=5时,y=4.75>1.55,
∴羽毛球是可以过网,
故答案为:是;
③∵h=4,k=5,
∴y=a(x﹣4)2+5,
把x=0,y=1代入解析式得,a(0﹣4)2+5=1,
解得a=﹣0.25,
∴y=﹣0.25(x﹣4)2+5;
(2)在第一次接球中,当y=2.75时,
则﹣0.25(x﹣4)2+5=2.75,
解得x1=7,x2=1,
∵接球时球越过球网,
∴d1=7,
在第二次接球中,当y=2.75时,
则﹣0.2(x﹣4.5)2+5.2=2.75,
解得x1=1,x2=8,
∵接球时球越过球网,
∴d2=8,
∴d2﹣d1=8﹣7=1>0.
故答案为:>.
【点评】本题考查了二次函数在实际生活中的应用.解题的关键是熟练掌握二次函数图象上点的坐标特征,用待定系数法求出函数解析式.
21.(9分)(2024 济宁一模)如图,⊙O是△ABD的外接圆,AB是⊙O的直径,点C在⊙O上,连接AC,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P.
(1)求证:BD∥CP;
(2)若 cosP,BD=24,求BP的长.
【考点】切线的性质;解直角三角形;垂径定理;圆周角定理;三角形的外接圆与外心.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)见解答;
(2)10.
【分析】(1)连接OC,如图,先利用圆周角定理得到,再根据垂径定理得到OC⊥BD,接着利用切线的性质得OC⊥PC,然后根据平行线的性质得到结论;
(2)先利用BD∥PC得到∠ABD=∠P,所以cos∠ABD=cosP,再根据圆周角定理得∠ADB=90°,则利用余弦的定义可求出AB=30,所以OB=OC=15,接着在Rt△OCP中利用余弦的定义得到cosP,于是设PC=4x,PO=5x,则OC=3x=15,求出x得到OP=25,然后计算OP﹣OB即可.
【解答】(1)证明:连接OC,如图,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴,
∴OC⊥BD,
∵CP为⊙O的切线,
∴OC⊥PC,
∴BD∥CP;
(2)解:∵BD∥PC,
∴∠ABD=∠P,
∴cos∠ABD=cosP,
∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△ABD中,∵cos∠ABD,
∴ABBD24=30,
∴OB=OC=15,
∵OC⊥PC,
∴∠OCP=90°,
在Rt△OCP中,∵cosP,
∴设PC=4x,PO=5x,
∴OC=3x,
即3x=15,
解得x=5,
∴OP=5x=25,
∴BP=OP﹣OB=25﹣15=10.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和解直角三角形.
22.(9分)(2023秋 开平市校级期中)如图1,在矩形ABCD中,AB=4,AD=6,E是边CD的中点,P(与点B,C不重合)是边BC上一动点,连接AP,PE,延长PE交AD的延长线于点Q.
(1)求证:△PCE≌△QDE.
(2)当△QDE∽△ABP时,求BP的长.
(3)如图2,分别取PA,PE,AD的中点F,G,H,连接FG,FH,GH,当FG⊥FH时,求BP的长和△FGH的面积.
【考点】相似形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)证明见解答过程;
(2)BP=4或2;
(3)BP;S△PGH.
【分析】(1)根据中点的定义和ASA证明△PCE与△QDE全等即可;
(2)根据相似三角形的性质和全等三角形的性质得出比例式解答即可;
(3)根据三角形中位线定理得出FGAE,FG∥AE,FH∥PD,FHPD,进而利用相似三角形的判定和性质以及勾股定理解答即可.
【解答】(1)证明:∵E是边CD的中点,
∴CE=DE,
点Q在AD的延长线上,
∴∠CDQ=∠ADC=∠C=90°,
∵∠CEP=∠DEQ,
在△PCE与△QDE中,
,
∴△PCE≌△QDE(ASA);
(2)解:∵△QDE∽△ABP,
∴,
∵△PCE≌△QDE,
∴PC=QD,CE=DE,
∴,
设BP=x,则CP=6﹣x,
即,
解得:x=4或2,
∴BP=4或2;
(3)解:连接AE,PD,交点为O,如图2,
∵F、G、H分别为PA、PE、AD的中点,
∴FGAE,FG∥AE,FH∥PD,FHPD,
∵FG⊥FH,
∴AE⊥PD,
在△AOD中,∠EAD+∠ADO=90°,
∵∠CDP+∠ADO=90°,
∴∠EAD=∠CDP,
∵∠ADC=∠BCD,
∴△ADE∽△DCP,
∴,
即,
可得:DPAE,
在Rt△ADE中,AD=6,DE=2,
∴,
∴DP,
∴
,
在△DPC中,DP2=CD2+CP2,
即,
解得:PC,
∴BP=BC﹣CP=6.
【点评】此题考查相似三角形的综合题,关键是根据相似三角形的判定和性质以及勾股定理解答.
23.(12分)(2024 驿城区模拟)如图,在平面直角坐标系中,以反比例函数图象上的点A和点B(1,﹣2)为顶点,分别作矩形ACOD和矩形BEOF,点C,E在x轴上,点D,F在y轴上,以点O为圆心,OF的长为半径作,交BE于点G,连接AO,OG.
(1)求k的值;
(2)求∠FOG的度数;
(3)求图中阴影部分的面积.
【考点】反比例函数综合题.
【专题】反比例函数及其应用;与圆有关的计算;解直角三角形及其应用;运算能力.
【答案】(1)﹣2;
(2)30°;
(3)3.
【分析】(1)把点B的坐标代入反比例函数的解析式,进而求得结果;
(2)在Rt△EOG中,OE=1,OG=OF=2,从而求得∠OGE的度数,进而求得结果;
(3)求出矩形的面积和扇形FOG的面积,进一步求得结果.
【解答】解:(1)把x=1,y=﹣2代入y得,
﹣2,
∴k=﹣2;
(2)在Rt△EOG中,OE=1,OG=OF=2,
∴sin∠EGO,
∴∠EGO=30°,
∵四边形OEBF是矩形,
∴OF∥EB,
∴∠FOG=∠EGO=30°;
(3)∵S矩形BFOE=OE OF=2,S扇形FOG,S△AOD=1,
∴S阴影=21=3.
【点评】本题考查了反比例函数的性质,扇形的面积公式,锐角三角函数函数的定义等知识,解决问题的关键是熟练掌握有关基础知识.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东省广州市2024-2025学年九年级下学期数学中考模拟押题预测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2024 杭州模拟)某品牌酸奶外包装上标明“净含量:200±5ml”.随机抽取四种口味的这种酸奶分别称重如下表.其中,净含量不合格的是( )
种类 原味 草莓味 香草味 巧克力味
净含量/ml 190 195 203 200
A.原味 B.草莓味 C.香草味 D.巧克力味
2.(3分)(2023春 兴宁区校级月考)如图图形中,既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
3.(3分)(2022秋 易县期中)中国的陆地面积约为9600000km2,领水面积约为370000km2,用科学记数法表示上述两个数字的和为( )
A.9.97×106 B.9.637×106 C.9.97×105 D.9.637×105
4.(3分)(2024春 二七区月考)下列说法中,正确的是( )
A.不相交的两条直线平行
B.相等的角是对顶角
C.如果∠a=48°32′,那么∠a余角的度数为41.28°
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小
5.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
6.(3分)甲、乙两位同学在一次试验中统计了某一结果出现的频率,给出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现6点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同其他都相同的2个红球和1个黄球,从中任意取出一个球是黄球的概率
7.(3分)(2024春 惠阳区期中)连接对角线相等四边形各边的中点得到的是什么四边形?( )
A.平行四边形 B.矩形
C.菱形 D.正方形
8.(3分)(2023秋 义乌市期末)已知二次函数y=﹣mx2+2mx+4(m>0)经过点A(﹣2,y1),点B(1,y2),点C(3,y3),那么y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
9.(3分)(2017秋 华容县期末)方程:1的解是( )
A.x=1 B.x=﹣4
C.x1=1,x2=﹣4 D.x=4
10.(3分)(2023春 太原期中)如图,一次函数y=kx﹣1与y=﹣x+3的图象都经过点P(2,1),则不等式kx﹣1≥﹣x+3的解集为( )
A.x≥2 B.x≤2 C.x≥1 D.x≤1
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)(2022 台山市校级一模)小王统计了一周家庭用水量,绘制了如图的统计图,那么这周用水量的众数是 ,中位数是 .
12.(3分)已知关于x的不等式4x﹣a≥﹣5的解集如图所示,则a的值是 .
13.(3分)(2024 江西模拟)若关于x的一元二次方程x2﹣x+m=0有实数根,则m的取值范围是 .
14.(3分)已知两个分式A,B,那么A+B= .
15.(3分)(2024 溧阳市一模)如图,以菱形ABCD的顶点B为圆心,边长AB为半径作圆,经过顶点D,点E、F分别在弧AD、弧DC上,且∠EBF=60°,AB=4,则图中阴影部分的面积为 .
三.解答题(共8小题,满分75分)
16.(9分)计算:()﹣1﹣20210+|﹣4|﹣tan60°.
17.(9分)(2024春 嘉定区期末)已知∠α、∠β.
(1)作∠AOB,使∠AOB=∠α﹣2∠β;
(2)作∠AOB的平分线OC.
18.(9分)(2024春 沙坪坝区校级期中)如图,考古人员在古墓大门A处探测到一青铜古物O,由于大门A正北方向有间墓室,考古人员无法沿直线AO直接挖掘前往.经勘测,考古人员发现有两条线路可以挖掘前往青铜古物O:线路①A﹣C﹣D﹣O;线路②A﹣B﹣O.其中点C在点A的正东方10米处,点O在点C北偏西30°方向,点D在点C正北方,点O在点D西北方向20米处,点B在点A正西方向,点O在点B北偏东30°方向.(参考数据:,)
(1)求CD的长度;(结果保留根号)
(2)受周围环境的影响,考古人员在线路①挖掘的平均速度为3米/小时,在线路②挖掘的平均速度为3.2米/小时,请通过计算说明选择哪条线路能更快挖掘到古物O.
19.(9分)(2025春 沙坪坝区校级月考)为了了解学生的视力健康情况,某校从七、八年级各随机抽取了20名学生进行视力检查,并对其视力情况的数据进行了整理和分析,得到下列信息:(视力情况共分为4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,
中度视力不良;D.视力≤4.5,重度视力不良)
抽取的20名七年级学生的视力情况数据为:4.9,4.9,4.7,4.8,4.7,4.8,5.0,5.1,5.1,5.2,4.9,4.9,4.9,4.8,4.8,4.5,4.5,4.8,5.0,4.6;
抽取的八年级学生的视力情况在C组的数据为:4.8,4.8,4.8,4.7,4.8,4.8,4.7,4.8;
抽取的七、八年级学生的视力情况数据统计表
年级 平均数 中位数 众数
七年级 4.85 4.9 a
八年级 4.85 b 4.8
(1)填空:a= ,b= ,m= .
(2)根据以上数据,你认为该校七年级和八年级学生的视力情况谁更健康?请说明理由;(写出一条理由即可)
(3)该校七年级共有学生400人,八年级共有学生500人,请估计两个年级学生中视力正常的人数共有多少人?
20.(9分)(2024秋 西城区校级期中)甲,乙两名同学进行羽毛球比赛,羽毛球发出后的飞行路线可以看作是抛物线的一部分.如图建立平面直角坐标系,羽毛球从O点的正上方发出,飞行过程中羽毛球的竖直高度y(单位:m)与水平距离x(单位:m)之间近似满足函数关系y=a(x﹣h)2+k(a<0).
比赛中,甲同学连续进行了两次发球.
(1)甲同学第一次发球时,羽毛球的水平距离x与竖直高度y的七组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6
竖直高度y/m 1 2.75 4 4.75 5 4.75 4
根据以上数据,回答下列问题:
①当羽毛球飞行到最高点时,水平距离是 m;
②在水平距离5m处,放置一个高1.55m的球网,羽毛球 (填“是”或“否”)可以过网;
③求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)甲同学第二次发球时,羽毛球的竖直高度y与水平距离x之间近似满足函数关系y=﹣0.2(x﹣4.5)2+5.2.乙同学在两次接球中,都是原地起跳后使得球拍达到最大高度2.75m时刚好接到球,记乙同学第一次接球的起跳点的水平距离为d1,第二次接球的起跳点的水平距离为d2,则d2﹣d1 0(填“>”“<”或“=”).
21.(9分)(2024 济宁一模)如图,⊙O是△ABD的外接圆,AB是⊙O的直径,点C在⊙O上,连接AC,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P.
(1)求证:BD∥CP;
(2)若 cosP,BD=24,求BP的长.
22.(9分)(2023秋 开平市校级期中)如图1,在矩形ABCD中,AB=4,AD=6,E是边CD的中点,P(与点B,C不重合)是边BC上一动点,连接AP,PE,延长PE交AD的延长线于点Q.
(1)求证:△PCE≌△QDE.
(2)当△QDE∽△ABP时,求BP的长.
(3)如图2,分别取PA,PE,AD的中点F,G,H,连接FG,FH,GH,当FG⊥FH时,求BP的长和△FGH的面积.
23.(12分)(2024 驿城区模拟)如图,在平面直角坐标系中,以反比例函数图象上的点A和点B(1,﹣2)为顶点,分别作矩形ACOD和矩形BEOF,点C,E在x轴上,点D,F在y轴上,以点O为圆心,OF的长为半径作,交BE于点G,连接AO,OG.
(1)求k的值;
(2)求∠FOG的度数;
(3)求图中阴影部分的面积.
广东省广州市2024-2025学年九年级下学期数学中考押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2024 杭州模拟)某品牌酸奶外包装上标明“净含量:200±5ml”.随机抽取四种口味的这种酸奶分别称重如下表.其中,净含量不合格的是( )
种类 原味 草莓味 香草味 巧克力味
净含量/ml 190 195 203 200
A.原味 B.草莓味 C.香草味 D.巧克力味
【考点】正数和负数;有理数的加法;有理数的减法.
【专题】实数;运算能力.
【答案】A
【分析】根据题意,可得取值范围为(200﹣5)ml~(200+5)ml,即195ml~205ml,由此即可求解.
【解答】解:根据包装上标明“净含量:200±5ml”可得,最少为200﹣5=195ml,最多为200+5=205ml,
∴净含量的取值范围为195ml~205ml,
∴原味190<195,不合格,
故选:A.
【点评】本题考查了正负数,有理数的加减运算,结合已知条件列得正确的算式是解题的关键.
2.(3分)(2023春 兴宁区校级月考)如图图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】观察四个选项中的图形,判断轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合,找出既是轴对称图形又是中心对称图形的那个即可得出结论.
【解答】解:A、本选项图形是轴对称图形,不是中心对称图形,不符合题意;
B、本选项图形是中心对称图形,不是轴对称图形,不符合题意;
C、本选项图形是轴对称图形,不是中心对称图形,不符合题意;
D、本选项图形既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
【点评】本题考查了轴对称图形和中心对称图形的定义,仔细观察图形根据定义正确判断是解答本题的关键.
3.(3分)(2022秋 易县期中)中国的陆地面积约为9600000km2,领水面积约为370000km2,用科学记数法表示上述两个数字的和为( )
A.9.97×106 B.9.637×106 C.9.97×105 D.9.637×105
【考点】科学记数法—表示较大的数;有理数的加法.
【专题】实数;数感;符号意识.
【答案】A
【分析】先求和9600000+370000,再用科学记数法表示即可.
【解答】解:∵9600000+370000=9970000,
∴9970000=9.97×106;
故选:A.
【点评】此题考查了科学记数法与有理数的加法运算,熟练掌握科学记数法的表示形式(a×10n,其中1≤|a|<10,n为整数)是解答此题的关键.
4.(3分)(2024春 二七区月考)下列说法中,正确的是( )
A.不相交的两条直线平行
B.相等的角是对顶角
C.如果∠a=48°32′,那么∠a余角的度数为41.28°
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小
【考点】平行线的判定与性质;度分秒的换算;余角和补角;对顶角、邻补角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据平面内直线的位置关系,对顶角的定义,度分秒的进制,余角与补角的定义,逐一判断即可解答.
【解答】解:A.同一平面内,不相交的两条直线平行,故A不符合题意;
B.相等的角不一定是对顶角,故B不符合题意;
C.如果∠a=48°32′,那么∠a余角的度数为41°28′,故C不符合题意;
D.如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小,故D符合题意;
故选:D.
【点评】本题考查了平面内直线的位置关系,对顶角的定义,度分秒的换算,余角与补角,熟练掌握这些数学概念是解题的关键.
5.(3分)下列计算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(﹣2a2)3=8a4
C.a3÷a2=a D.2a2+a2=3a4
【考点】完全平方公式;合并同类项;幂的乘方与积的乘方;同底数幂的除法.
【专题】整式;运算能力.
【答案】C
【分析】各式计算得到结果,即可作出判断.
【解答】解:A、原式=a2﹣2ab+b2,不符合题意;
B、原式=﹣8a6,不符合题意;
C、原式=a,符合题意;
D、原式=3a2,不符合题意.
故选:C.
【点评】此题考查了完全平方公式,合并同类项,幂的乘方与积的乘方,同底数幂的除法,熟练掌握运算法则及公式是解本题的关键.
6.(3分)甲、乙两位同学在一次试验中统计了某一结果出现的频率,给出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现6点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同其他都相同的2个红球和1个黄球,从中任意取出一个球是黄球的概率
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】D
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【解答】解:A、掷一枚正六面体的骰子,出现6点的概率为,故此选不符合题意;
B、掷一枚硬币,出现正面朝上的概率为,故此选不符合题意;
C、任意写出一个整数,能被2整除的概率为,故此选不符合题意;
D、从一装有2个红球和1个黄球的袋子中任取一球,取到黄球的概率是:0.33,故此选项符合题意.
故选:D.
【点评】本题考查了列表法与树状图法和概率公式,解题关键是掌握i频率=所求情况数与总情况数之比.
7.(3分)(2024春 惠阳区期中)连接对角线相等四边形各边的中点得到的是什么四边形?( )
A.平行四边形 B.矩形
C.菱形 D.正方形
【考点】正方形的性质;平行四边形的性质;菱形的性质;矩形的性质.
【专题】多边形与平行四边形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】作四边形ABCD中,使AC=BD,令E、F、G、H分别是AB、BC、CD、DA的中点,由三角形的中位线定理得EF∥AC,EFAC,GH∥AC,GHAC,则EF∥GH,EF=GH,可证明四边形EFGH是平行四边形,由EFAC,EHBD,且AC=BD得EF=EG,则四边形EFGH是菱形,于是得到问题的答案.
【解答】解:如图,四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,
∵E、F分别是AB、BC的中点,
∴EF∥AC,EFAC,
同理GH∥AC,GHAC,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形,
∵E、H分别是AB、DA的中点,
∴EHBD,
∵AC=BD,
∴EF=EH,
∴四边形EFGH是菱形,
故选:C.
【点评】此题重点考查三角形的中位线定理、平行四边形的判定、菱形的判定等知识,根据三角形的中位线定理及AC=BD推导出EF=GH是解题的关键.
8.(3分)(2023秋 义乌市期末)已知二次函数y=﹣mx2+2mx+4(m>0)经过点A(﹣2,y1),点B(1,y2),点C(3,y3),那么y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【考点】二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;应用意识.
【答案】B
【分析】根据函数解析式求出抛物线对称轴和开口方向,再根据二次函数的性质求判断即可.
【解答】解:二次函数y=﹣mx2+2mx+4的对称轴为直线x1,
∵m>0,
∴抛物线开口向下,
∴x=1时,y2最大,
∵1﹣(﹣2)=3>3﹣1=2,
∴y3>y1,
∴y1,y2,y3的大小关y1<y3<y2.
故选:B.
【点评】本题考查了二次函数图象上点的坐标特征,关键是掌握二次函数的性质.
9.(3分)(2017秋 华容县期末)方程:1的解是( )
A.x=1 B.x=﹣4
C.x1=1,x2=﹣4 D.x=4
【考点】解分式方程.
【专题】分式方程及应用;运算能力.
【答案】B
【分析】按照解分式方程的步骤,进行计算即可解答.
【解答】解:1,
6﹣3(x+1)=x2﹣1,
解得:x=﹣4或x=1,
检验:当x=1时,x2﹣1=0,
∴x=1是原方程的增根,
当x=﹣4时,x2﹣1≠0,
∴x=﹣4是原方程的根,
故选:B.
【点评】本题考查了解分式方程,一定要注意解分式方程必须检验.
10.(3分)(2023春 太原期中)如图,一次函数y=kx﹣1与y=﹣x+3的图象都经过点P(2,1),则不等式kx﹣1≥﹣x+3的解集为( )
A.x≥2 B.x≤2 C.x≥1 D.x≤1
【考点】一次函数与一元一次不等式;两条直线相交或平行问题.
【专题】一元一次不等式(组)及应用;一次函数及其应用;几何直观.
【答案】A
【分析】根据函数图象可知:当x>2时,一次函数y=kx﹣1的图象在y=﹣x+3的图象的上方,然后即可写出不等式kx﹣1≥﹣x+3的解集.
【解答】解:由图象可得,
当x>2时,一次函数y=kx﹣1的图象在y=﹣x+3的图象的上方,
∴不等式kx﹣1≥﹣x+3的解集为x≥2,
故选:A.
【点评】本题考查一次函数与一元一次不等式,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)(2022 台山市校级一模)小王统计了一周家庭用水量,绘制了如图的统计图,那么这周用水量的众数是 1 ,中位数是 1 .
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】1;1.
【分析】根据众数和中位数的定义即可求解.
【解答】解:从统计图中得知:从星期日到星期六的每天用水量分别为:2,1,0.5,1.5,1,1.5,1(单位:t).
出现次数最多的数字是1,即可众数是1.
将其按从小到大顺序排列为:0.5,1,1,1,1.5,1.5,2,
位于中间的数字为1,即中位数是1.
故答案为:1;1.
【点评】本题考查的是众数和中位数.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
12.(3分)已知关于x的不等式4x﹣a≥﹣5的解集如图所示,则a的值是 ﹣3 .
【考点】解一元一次不等式;在数轴上表示不等式的解集.
【专题】一元一次不等式(组)及应用;运算能力.
【答案】﹣3.
【分析】本题是关于x的不等式,应先只把x看成未知数,求得x的解集,再根据x≥﹣2,求得a的值.
【解答】解:移项得,4x≥a﹣5,
化系数为1得,x,
由数轴知x≥﹣2,所以2,
解得a=﹣3.
故答案为:﹣3.
【点评】当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据解集进行判断,求得另一个字母的值.
13.(3分)(2024 江西模拟)若关于x的一元二次方程x2﹣x+m=0有实数根,则m的取值范围是 m .
【考点】根的判别式.
【专题】一元二次方程及应用;运算能力.
【答案】见试题解答内容
【分析】根据一元二次方程根的判别式求解即可.
【解答】解:∵关于x的一元二次方程x2﹣x+m=0有实数根,
∴Δ=b2﹣4ac=1﹣4m≥0,
∴m,
故答案为:m.
【点评】本题主要考查了一元二次方程根的判别式,熟知一元二次方程有实数根,则Δ=b2﹣4ac≥0是解题的关键.
14.(3分)已知两个分式A,B,那么A+B= 0 .
【考点】分式的加减法.
【专题】分式;运算能力.
【答案】0.
【分析】利用分式的加减运算的法则进行运算即可.
【解答】解:∵A,B,
∴A+B
=0.
故答案为:0.
【点评】本题主要考查分式的加减法,解答的关键是对相应的运算法则的掌握.
15.(3分)(2024 溧阳市一模)如图,以菱形ABCD的顶点B为圆心,边长AB为半径作圆,经过顶点D,点E、F分别在弧AD、弧DC上,且∠EBF=60°,AB=4,则图中阴影部分的面积为 4 .
【考点】扇形面积的计算;菱形的性质;圆周角定理.
【专题】矩形 菱形 正方形;与圆有关的计算;运算能力;推理能力.
【答案】4.
【分析】根据菱形的性质,正三角形的判断和性质以及扇形面积的计算方法进行计算即可.
【解答】解:如图,连接BD,
∵四边形ABCD是菱形,AB=DB=BE=FB=CB,
∴△ABD,△BCD是正三角形,
∴∠ABD=60°=∠EBF,即∠ABE+∠DBE=∠DBF+∠DBE,
∴∠AOE=∠DBF,
S阴影部分=S扇形ABD﹣S△ABD
4×(4)
4.
故答案为:4.
【点评】本题考查扇形面积的计算,菱形的性质,掌握扇形面积的计算方法,菱形的性质以及正三角形的判断和性质是正确解答的关键.
三.解答题(共8小题,满分75分)
16.(9分)计算:()﹣1﹣20210+|﹣4|﹣tan60°.
【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
【专题】实数;运算能力.
【答案】2+3.
【分析】先化简各式,然后再进行计算即可解答.
【解答】解:()﹣1﹣20210+|﹣4|﹣tan60°
=3﹣1+4
=2+3.
【点评】本题考查了实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.(9分)(2024春 嘉定区期末)已知∠α、∠β.
(1)作∠AOB,使∠AOB=∠α﹣2∠β;
(2)作∠AOB的平分线OC.
【考点】作图—复杂作图.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)见解析.
【分析】(1)先作射线OD,再作∠AOD=∠α,然后作∠EOD=∠β,∠BOE=∠β,则∠AOB即为所求;
(2)根据角平分线的尺规作图方法作图即可.
【解答】解:(1)如图所示,∠AOB即为所求;
(2)解:如图所示,OC即为所求.
【点评】本题主要考查了基本作图,掌握基本作图是解题的关键.
18.(9分)(2024春 沙坪坝区校级期中)如图,考古人员在古墓大门A处探测到一青铜古物O,由于大门A正北方向有间墓室,考古人员无法沿直线AO直接挖掘前往.经勘测,考古人员发现有两条线路可以挖掘前往青铜古物O:线路①A﹣C﹣D﹣O;线路②A﹣B﹣O.其中点C在点A的正东方10米处,点O在点C北偏西30°方向,点D在点C正北方,点O在点D西北方向20米处,点B在点A正西方向,点O在点B北偏东30°方向.(参考数据:,)
(1)求CD的长度;(结果保留根号)
(2)受周围环境的影响,考古人员在线路①挖掘的平均速度为3米/小时,在线路②挖掘的平均速度为3.2米/小时,请通过计算说明选择哪条线路能更快挖掘到古物O.
【考点】解直角三角形的应用﹣方向角问题;勾股定理的应用.
【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)CD的长度为(1010)米;
(2)选择线路①能更快挖掘到古物O.
【分析】(1)过点O作OE⊥CD交CD的延长线于点E,在RtODE中求出OE,DE,再在RtOCE中求出CE,OC,进而求出CD的抽到;
(2)由(1)可求出AC+CD+OD,证明△OBC是等边三角形,从而可求出AB+BO的长度,进而根据路程÷速度求出选择两条线路挖掘所用的时间,再比较即可解决问题.
【解答】解:(1)过点O作OE⊥CD交CD的延长线于点E,如图,
在Rt△ODE中,
∵OD=20米,∠ODE=45°,
∴OE=OD sin45°=2010(米),
DE=OD cos45°=2010(米),
在Rt△OCE中,
∵OE=10米,∠OCE=30°,
∴OC20(米),
CE(米),
∴CD=CE﹣DE=1010(米),
答:CD的长度为(1010)米;
(2)由题意,知∠OBC=∠OCB=60°,
∴△OBC是等边三角形,
∴OB=BC=OC=20米≈28.2米,
∴AC+CD+OD=10+101020≈40.4(米),
AB+BO=BC﹣AC+BO≈28.2﹣10+28.2=46.4(米),
∵线路①挖掘的平均速度为3米/小时,
∴线路①挖掘需要时间为:40.4÷3≈13.47(小时),
∵线路②挖掘的平均速度为3.2米/小时,
∴线路②挖掘需要时间为:46.4÷3.2=14.5(小时),
∵13.47<14.5,
∴选择线路①能更快挖掘到古物O.
【点评】本题考查解直角三角形的应用﹣方向角问题,理解题意,将问题转化为解直角三角形问题是解题的关键.
19.(9分)(2025春 沙坪坝区校级月考)为了了解学生的视力健康情况,某校从七、八年级各随机抽取了20名学生进行视力检查,并对其视力情况的数据进行了整理和分析,得到下列信息:(视力情况共分为4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,
中度视力不良;D.视力≤4.5,重度视力不良)
抽取的20名七年级学生的视力情况数据为:4.9,4.9,4.7,4.8,4.7,4.8,5.0,5.1,5.1,5.2,4.9,4.9,4.9,4.8,4.8,4.5,4.5,4.8,5.0,4.6;
抽取的八年级学生的视力情况在C组的数据为:4.8,4.8,4.8,4.7,4.8,4.8,4.7,4.8;
抽取的七、八年级学生的视力情况数据统计表
年级 平均数 中位数 众数
七年级 4.85 4.9 a
八年级 4.85 b 4.8
(1)填空:a= 4.9 ,b= 4.8 ,m= 25 .
(2)根据以上数据,你认为该校七年级和八年级学生的视力情况谁更健康?请说明理由;(写出一条理由即可)
(3)该校七年级共有学生400人,八年级共有学生500人,请估计两个年级学生中视力正常的人数共有多少人?
【考点】众数;用样本估计总体;扇形统计图;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)4.9,4.8,25;(2)七年级学生的视力情况谁更健康,理由见解答;(3)225人.
【分析】(1)根据众数和中位数的定义即可求出a和b的值,根据扇形统计图分别求出A、C、D组人数,然后计算m即可;
(2)分别根据平均数,中位数和众数的意义分析即可;
(3)用样本估计总体即可.
【解答】解:(1)被抽取的20名七年级学生的视力情况中,4.9出现的次数最多,故众数a=4.9;
把被抽取的20名八年级学生的视力从小到大排列,排在中间的两个数分别是4.8,4.8,故中位数b4.8;
八年级C组所占百分比为:40%,故m%=1﹣10%﹣40%﹣25%=25%,即m=25.
故答案为:4.9,4.8,25;
(2)七年级学生的视力情况谁更健康,理由如下:
从平均数来看,两个班一样,从众数和中位数来看,七年级学生的视力健康情况总体更好一些,综上,七年级学生的视力情况谁更健康;
(3)400500×25%=225(人),
答:估计两个年级学生中视力正常的人数大约共有225人.
【点评】本题考查了扇形统计图,众数,中位数,算术平均数以及用样本估计总体,掌握众数、中位数、平均数定义是解题的关键.
20.(9分)(2024秋 西城区校级期中)甲,乙两名同学进行羽毛球比赛,羽毛球发出后的飞行路线可以看作是抛物线的一部分.如图建立平面直角坐标系,羽毛球从O点的正上方发出,飞行过程中羽毛球的竖直高度y(单位:m)与水平距离x(单位:m)之间近似满足函数关系y=a(x﹣h)2+k(a<0).
比赛中,甲同学连续进行了两次发球.
(1)甲同学第一次发球时,羽毛球的水平距离x与竖直高度y的七组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6
竖直高度y/m 1 2.75 4 4.75 5 4.75 4
根据以上数据,回答下列问题:
①当羽毛球飞行到最高点时,水平距离是 4 m;
②在水平距离5m处,放置一个高1.55m的球网,羽毛球 是 (填“是”或“否”)可以过网;
③求出满足的函数关系y=a(x﹣h)2+k(a<0);
(2)甲同学第二次发球时,羽毛球的竖直高度y与水平距离x之间近似满足函数关系y=﹣0.2(x﹣4.5)2+5.2.乙同学在两次接球中,都是原地起跳后使得球拍达到最大高度2.75m时刚好接到球,记乙同学第一次接球的起跳点的水平距离为d1,第二次接球的起跳点的水平距离为d2,则d2﹣d1 > 0(填“>”“<”或“=”).
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)①4;②是;③y=﹣0.25(x﹣4)2+5;
(2)>.
【分析】(1)①由表中数据直接可以得出结论;
②由表中数据直接可以得出结论;
③用待定系数法求函数解析式;
(2)把y=2.4分别代入(1)、(2)解析式求出d1和d2即可.
【解答】解:(1)①由表格中数据知,当x=3和x=5时,y=4.75,
∴对称轴为x=4,顶点坐标为(4,5),
∴当羽毛球飞行到最高点时,水平距离是4m,
故答案为:4;
②∵当x=5时,y=4.75>1.55,
∴羽毛球是可以过网,
故答案为:是;
③∵h=4,k=5,
∴y=a(x﹣4)2+5,
把x=0,y=1代入解析式得,a(0﹣4)2+5=1,
解得a=﹣0.25,
∴y=﹣0.25(x﹣4)2+5;
(2)在第一次接球中,当y=2.75时,
则﹣0.25(x﹣4)2+5=2.75,
解得x1=7,x2=1,
∵接球时球越过球网,
∴d1=7,
在第二次接球中,当y=2.75时,
则﹣0.2(x﹣4.5)2+5.2=2.75,
解得x1=1,x2=8,
∵接球时球越过球网,
∴d2=8,
∴d2﹣d1=8﹣7=1>0.
故答案为:>.
【点评】本题考查了二次函数在实际生活中的应用.解题的关键是熟练掌握二次函数图象上点的坐标特征,用待定系数法求出函数解析式.
21.(9分)(2024 济宁一模)如图,⊙O是△ABD的外接圆,AB是⊙O的直径,点C在⊙O上,连接AC,且AC平分∠DAB,过点C作⊙O的切线交AB的延长线于点P.
(1)求证:BD∥CP;
(2)若 cosP,BD=24,求BP的长.
【考点】切线的性质;解直角三角形;垂径定理;圆周角定理;三角形的外接圆与外心.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)见解答;
(2)10.
【分析】(1)连接OC,如图,先利用圆周角定理得到,再根据垂径定理得到OC⊥BD,接着利用切线的性质得OC⊥PC,然后根据平行线的性质得到结论;
(2)先利用BD∥PC得到∠ABD=∠P,所以cos∠ABD=cosP,再根据圆周角定理得∠ADB=90°,则利用余弦的定义可求出AB=30,所以OB=OC=15,接着在Rt△OCP中利用余弦的定义得到cosP,于是设PC=4x,PO=5x,则OC=3x=15,求出x得到OP=25,然后计算OP﹣OB即可.
【解答】(1)证明:连接OC,如图,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴,
∴OC⊥BD,
∵CP为⊙O的切线,
∴OC⊥PC,
∴BD∥CP;
(2)解:∵BD∥PC,
∴∠ABD=∠P,
∴cos∠ABD=cosP,
∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△ABD中,∵cos∠ABD,
∴ABBD24=30,
∴OB=OC=15,
∵OC⊥PC,
∴∠OCP=90°,
在Rt△OCP中,∵cosP,
∴设PC=4x,PO=5x,
∴OC=3x,
即3x=15,
解得x=5,
∴OP=5x=25,
∴BP=OP﹣OB=25﹣15=10.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和解直角三角形.
22.(9分)(2023秋 开平市校级期中)如图1,在矩形ABCD中,AB=4,AD=6,E是边CD的中点,P(与点B,C不重合)是边BC上一动点,连接AP,PE,延长PE交AD的延长线于点Q.
(1)求证:△PCE≌△QDE.
(2)当△QDE∽△ABP时,求BP的长.
(3)如图2,分别取PA,PE,AD的中点F,G,H,连接FG,FH,GH,当FG⊥FH时,求BP的长和△FGH的面积.
【考点】相似形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)证明见解答过程;
(2)BP=4或2;
(3)BP;S△PGH.
【分析】(1)根据中点的定义和ASA证明△PCE与△QDE全等即可;
(2)根据相似三角形的性质和全等三角形的性质得出比例式解答即可;
(3)根据三角形中位线定理得出FGAE,FG∥AE,FH∥PD,FHPD,进而利用相似三角形的判定和性质以及勾股定理解答即可.
【解答】(1)证明:∵E是边CD的中点,
∴CE=DE,
点Q在AD的延长线上,
∴∠CDQ=∠ADC=∠C=90°,
∵∠CEP=∠DEQ,
在△PCE与△QDE中,
,
∴△PCE≌△QDE(ASA);
(2)解:∵△QDE∽△ABP,
∴,
∵△PCE≌△QDE,
∴PC=QD,CE=DE,
∴,
设BP=x,则CP=6﹣x,
即,
解得:x=4或2,
∴BP=4或2;
(3)解:连接AE,PD,交点为O,如图2,
∵F、G、H分别为PA、PE、AD的中点,
∴FGAE,FG∥AE,FH∥PD,FHPD,
∵FG⊥FH,
∴AE⊥PD,
在△AOD中,∠EAD+∠ADO=90°,
∵∠CDP+∠ADO=90°,
∴∠EAD=∠CDP,
∵∠ADC=∠BCD,
∴△ADE∽△DCP,
∴,
即,
可得:DPAE,
在Rt△ADE中,AD=6,DE=2,
∴,
∴DP,
∴
,
在△DPC中,DP2=CD2+CP2,
即,
解得:PC,
∴BP=BC﹣CP=6.
【点评】此题考查相似三角形的综合题,关键是根据相似三角形的判定和性质以及勾股定理解答.
23.(12分)(2024 驿城区模拟)如图,在平面直角坐标系中,以反比例函数图象上的点A和点B(1,﹣2)为顶点,分别作矩形ACOD和矩形BEOF,点C,E在x轴上,点D,F在y轴上,以点O为圆心,OF的长为半径作,交BE于点G,连接AO,OG.
(1)求k的值;
(2)求∠FOG的度数;
(3)求图中阴影部分的面积.
【考点】反比例函数综合题.
【专题】反比例函数及其应用;与圆有关的计算;解直角三角形及其应用;运算能力.
【答案】(1)﹣2;
(2)30°;
(3)3.
【分析】(1)把点B的坐标代入反比例函数的解析式,进而求得结果;
(2)在Rt△EOG中,OE=1,OG=OF=2,从而求得∠OGE的度数,进而求得结果;
(3)求出矩形的面积和扇形FOG的面积,进一步求得结果.
【解答】解:(1)把x=1,y=﹣2代入y得,
﹣2,
∴k=﹣2;
(2)在Rt△EOG中,OE=1,OG=OF=2,
∴sin∠EGO,
∴∠EGO=30°,
∵四边形OEBF是矩形,
∴OF∥EB,
∴∠FOG=∠EGO=30°;
(3)∵S矩形BFOE=OE OF=2,S扇形FOG,S△AOD=1,
∴S阴影=21=3.
【点评】本题考查了反比例函数的性质,扇形的面积公式,锐角三角函数函数的定义等知识,解决问题的关键是熟练掌握有关基础知识.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
