沪科版数学九年级上册 22.3 第1课时 相似三角形的性质定理1及应用 课件(共23张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 第1课时 相似三角形的性质定理1及应用 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 238.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.3 相似三角形的性质
第一课时 相似三角形的性质定理1及应用
前 言
1.理解掌握相似三角形对应线段(高、中线、角平分线)的比及相似三角形的面积的比、周长比与相似比之间的关系;(重点)
2.明确相似三角形中对应线段与相似比的关系.(难点)
学习目标及重难点
A
C
B
A1
C1
B1
课程导入
A
C
B
A1
C1
B1
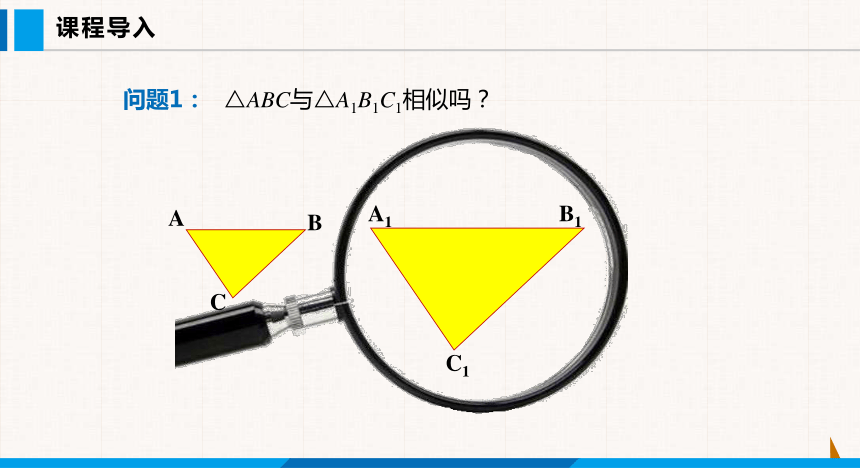
问题1: △ABC与△A1B1C1相似吗?
课程导入
A
C
B
A1
C1
B1
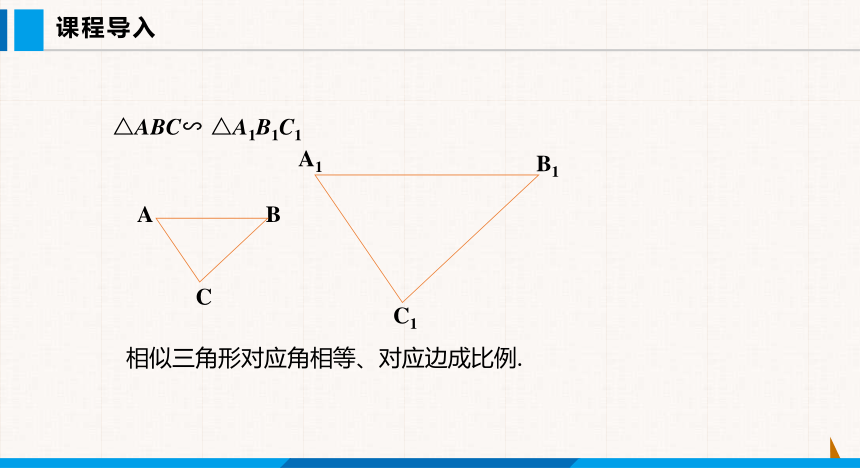
相似三角形对应角相等、对应边成比例.
△ABC∽ △A1B1C1
课程导入
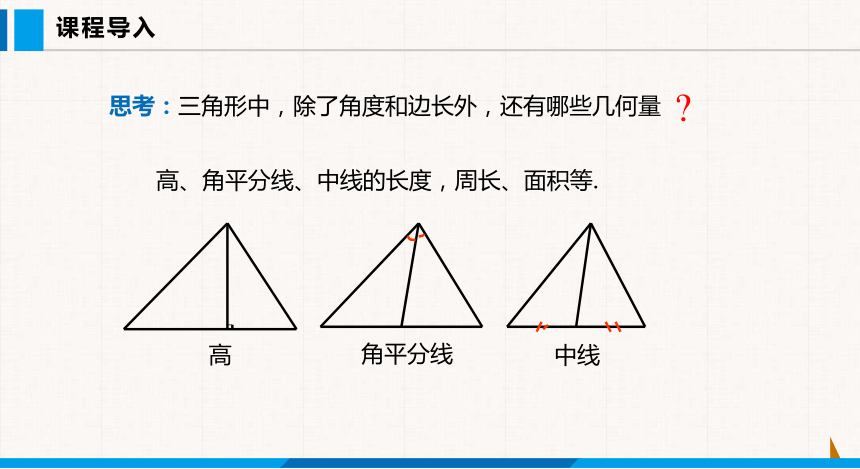
思考:三角形中,除了角度和边长外,还有哪些几何量
高、角平分线、中线的长度,周长、面积等.
高
角平分线
中线
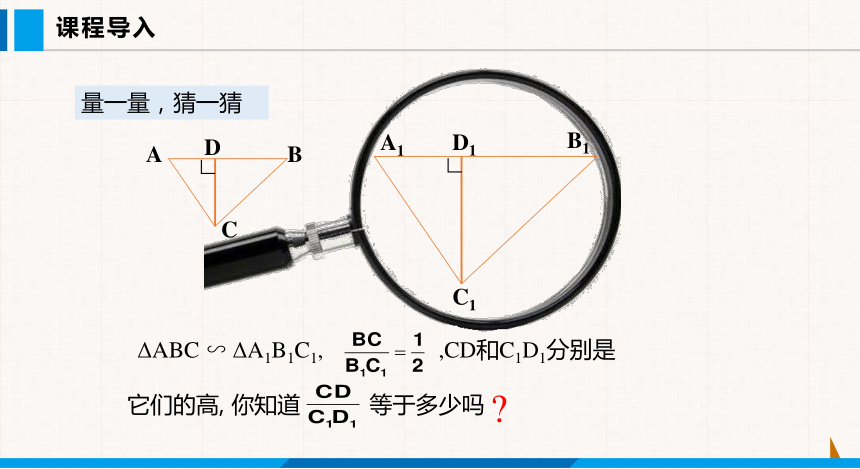
量一量,猜一猜
D1
A1
C1
B1
∟
A
C
B
D
∟
ΔABC ∽ ΔA1B1C1, ,CD和C1D1分别是它们的高, 你知道 等于多少吗
课程导入
课程讲授
新课推进
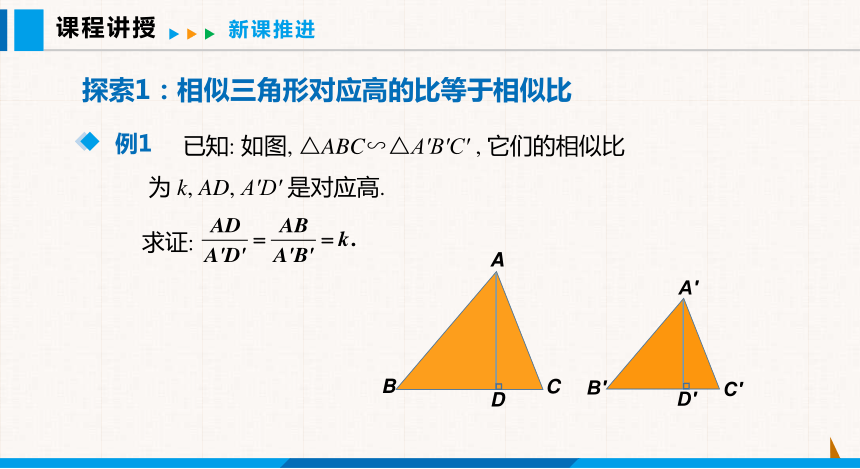
探索1:相似三角形对应高的比等于相似比
已知: 如图, △ABC∽△A′B′C′ , 它们的相似比为 k, AD, A′D′ 是对应高.
求证:
A
B
C
D
C′
B′
A′
D′
例1
课程讲授
新课推进
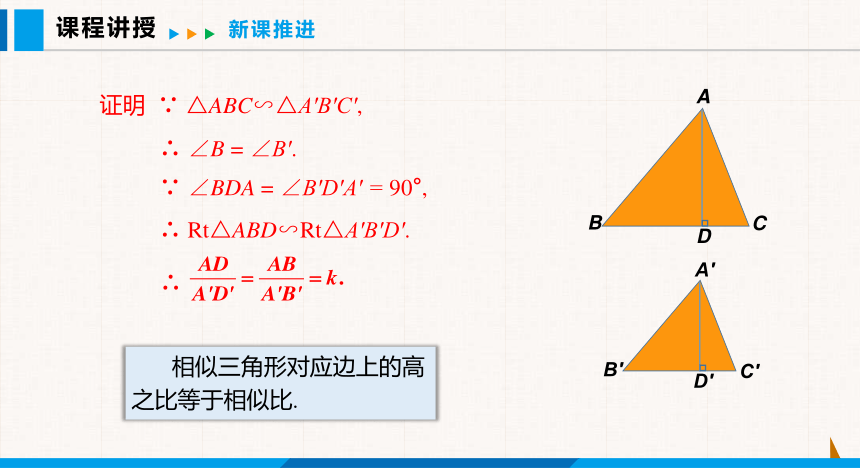
证明 ∵ △ABC∽△A′B′C′,
∴ ∠B = ∠B′.
∵ ∠BDA = ∠B′D′A′ = 90°,
∴ Rt△ABD∽Rt△A′B′D′.
∴
A
B
C
D
C′
B′
A′
D′
相似三角形对应边上的高之比等于相似比.
如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)AE是ΔASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
例2
课程讲授
新课推进
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由:
∵AD是ΔABC的高
∴ ∠ADC=90°
∵四边形PQRS是正方形
∴SR // BC
∴∠AER=∠ADC=90°
∴ AE是ΔASR的高.
BC=60cm,AD=40cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60cm,AD=40cm,四边形PQRS是正方形.
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似. 理由:
∵ SR // BC
∴ ∠ASR=∠B, ∠ARS=∠C
∴ ΔASR与ΔABC相似.
课程讲授
新课推进
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
如图,一块铁皮呈锐角三角形,它的边长BC=80cm,高AD=60cm,要把该铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形的边长.
S
R
Q
P
E
D
C
B
A
例3
课程讲授
新课推进
解: 如图,矩形PQRS为加工后的零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.设PS=xcm,则PQ为2xcm.
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC.
解方程,得x=24,2x=48.
答:这个矩形的零件的边长分别是48cm和24cm.
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
例4
相似三角形对应边上的中线有什么关系呢?
(1)如图, △ABC, AE为BC边上的中线, 则把三角形扩大 2 倍后得 △A′B′C′ , A′E′ 为 BC 边上的中线. △ABC 与△A′B′C′ 的相似比是多少?AE与A′E′ 的比是多少?
A
B
C
E
E′
A′
B′
C′
探索2:相似三角形对应角平分线的比、对应中线的比都
等于相似比
课程讲授
新课推进
(2)如右图两个相似三角形的比为 k, 则对应边上的中线的比是多少呢?说说你判断的理由是什么?
A
B
C
E
E′
A′
B′
C′
相似三角形对应边上的中线之比等于相似比.
B′
A′
C′
D′
B
A
C
D
已知: 如图, △ABC∽△A′B′C′ , 它们的相似比为 k, AD, A′D′ 分别是 ∠BAC, ∠B′A′C′ 的角平分线.
求证:
课程讲授
新课推进
探索3:相似三角形对应角的角平分线有什么关系呢?
例5
课程讲授
新课推进
证明 ∵ △ABC∽△A′B′C′,
∴ ∠BAC = ∠B′A′C′,
∴ ∠DAC = ∠D′A′C′ ,
∴ △DAC∽△D′A′C′.
∴
∠C = ∠C′.
又∵AD, A′D′ 分别是 ∠BAC, ∠B′A′C′ 的角平分线.
相似三角形对应角的角平分线之比等于相似比.
B′
A′
C′
D′
B
A
C
D
课程讲授
新课推进
两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
例6
A
B
C
D
E
F
A′
B′
C′
D′
E′
F′
小结
课程讲授
相似三角形的性质定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
习题解析
习题1
1. 判断题
(1)相似三角形的中线比等于相似比 . ( )
(2)两个相似三角形的边长之比等于高之比. ( )
×
×
2. 填空.
(1)相似三角形对应边的比为 2∶3, 那么相似比为_______, 对应角的角平分线的比为______.
(2)两个相似三角形的相似比为 1∶4, 则对应高的比为______, 对应角的角平分线的比为______.
2∶3
2∶3
1∶4
1∶4
习题解析
习题2
如图 , 梯形ABCD中, AB∥CD, 点F在BC上, 连DF与AB的延长线交于点G .
(1)求证: △CDF∽△BGF;
(2)当点F是BC的中点时, 过F作EF∥CD交AD于点E, 若AB=6cm, EF=4cm, 求CD的长.
习题解析
(1)证明: ∵在梯形ABCD中, AB∥CD,
∴∠CDF=∠FGB, ∠DCF=∠GBF,
∴△CDF∽△BGF.
(2) 由(1)知△CDF∽△BGF, 又F是BC的中点,
∴ BF = FC,
∴ △CDF≌△BGF,
∴ DF = FG, CD = BG.
又∵ EF∥CD, AB∥CD,
∴ EF∥AG, 得 2EF = AB+BG.
∴ BG = 2EF-AB = 2×4-6 = 2,
∴ CD = BG = 2cm.
课程总结
小结
对应高的比
对应角平分线的比
相似三角形
对应中线的比
都等于相似比
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.3 相似三角形的性质
第一课时 相似三角形的性质定理1及应用
前 言
1.理解掌握相似三角形对应线段(高、中线、角平分线)的比及相似三角形的面积的比、周长比与相似比之间的关系;(重点)
2.明确相似三角形中对应线段与相似比的关系.(难点)
学习目标及重难点
A
C
B
A1
C1
B1
课程导入
A
C
B
A1
C1
B1
问题1: △ABC与△A1B1C1相似吗?
课程导入
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
△ABC∽ △A1B1C1
课程导入
思考:三角形中,除了角度和边长外,还有哪些几何量
高、角平分线、中线的长度,周长、面积等.
高
角平分线
中线
量一量,猜一猜
D1
A1
C1
B1
∟
A
C
B
D
∟
ΔABC ∽ ΔA1B1C1, ,CD和C1D1分别是它们的高, 你知道 等于多少吗
课程导入
课程讲授
新课推进
探索1:相似三角形对应高的比等于相似比
已知: 如图, △ABC∽△A′B′C′ , 它们的相似比为 k, AD, A′D′ 是对应高.
求证:
A
B
C
D
C′
B′
A′
D′
例1
课程讲授
新课推进
证明 ∵ △ABC∽△A′B′C′,
∴ ∠B = ∠B′.
∵ ∠BDA = ∠B′D′A′ = 90°,
∴ Rt△ABD∽Rt△A′B′D′.
∴
A
B
C
D
C′
B′
A′
D′
相似三角形对应边上的高之比等于相似比.
如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)AE是ΔASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
例2
课程讲授
新课推进
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由:
∵AD是ΔABC的高
∴ ∠ADC=90°
∵四边形PQRS是正方形
∴SR // BC
∴∠AER=∠ADC=90°
∴ AE是ΔASR的高.
BC=60cm,AD=40cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60cm,AD=40cm,四边形PQRS是正方形.
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似. 理由:
∵ SR // BC
∴ ∠ASR=∠B, ∠ARS=∠C
∴ ΔASR与ΔABC相似.
课程讲授
新课推进
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
如图,一块铁皮呈锐角三角形,它的边长BC=80cm,高AD=60cm,要把该铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形的边长.
S
R
Q
P
E
D
C
B
A
例3
课程讲授
新课推进
解: 如图,矩形PQRS为加工后的零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.设PS=xcm,则PQ为2xcm.
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC.
解方程,得x=24,2x=48.
答:这个矩形的零件的边长分别是48cm和24cm.
S
R
Q
P
E
D
C
B
A
课程讲授
新课推进
例4
相似三角形对应边上的中线有什么关系呢?
(1)如图, △ABC, AE为BC边上的中线, 则把三角形扩大 2 倍后得 △A′B′C′ , A′E′ 为 BC 边上的中线. △ABC 与△A′B′C′ 的相似比是多少?AE与A′E′ 的比是多少?
A
B
C
E
E′
A′
B′
C′
探索2:相似三角形对应角平分线的比、对应中线的比都
等于相似比
课程讲授
新课推进
(2)如右图两个相似三角形的比为 k, 则对应边上的中线的比是多少呢?说说你判断的理由是什么?
A
B
C
E
E′
A′
B′
C′
相似三角形对应边上的中线之比等于相似比.
B′
A′
C′
D′
B
A
C
D
已知: 如图, △ABC∽△A′B′C′ , 它们的相似比为 k, AD, A′D′ 分别是 ∠BAC, ∠B′A′C′ 的角平分线.
求证:
课程讲授
新课推进
探索3:相似三角形对应角的角平分线有什么关系呢?
例5
课程讲授
新课推进
证明 ∵ △ABC∽△A′B′C′,
∴ ∠BAC = ∠B′A′C′,
∴ ∠DAC = ∠D′A′C′ ,
∴ △DAC∽△D′A′C′.
∴
∠C = ∠C′.
又∵AD, A′D′ 分别是 ∠BAC, ∠B′A′C′ 的角平分线.
相似三角形对应角的角平分线之比等于相似比.
B′
A′
C′
D′
B
A
C
D
课程讲授
新课推进
两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
例6
A
B
C
D
E
F
A′
B′
C′
D′
E′
F′
小结
课程讲授
相似三角形的性质定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
习题解析
习题1
1. 判断题
(1)相似三角形的中线比等于相似比 . ( )
(2)两个相似三角形的边长之比等于高之比. ( )
×
×
2. 填空.
(1)相似三角形对应边的比为 2∶3, 那么相似比为_______, 对应角的角平分线的比为______.
(2)两个相似三角形的相似比为 1∶4, 则对应高的比为______, 对应角的角平分线的比为______.
2∶3
2∶3
1∶4
1∶4
习题解析
习题2
如图 , 梯形ABCD中, AB∥CD, 点F在BC上, 连DF与AB的延长线交于点G .
(1)求证: △CDF∽△BGF;
(2)当点F是BC的中点时, 过F作EF∥CD交AD于点E, 若AB=6cm, EF=4cm, 求CD的长.
习题解析
(1)证明: ∵在梯形ABCD中, AB∥CD,
∴∠CDF=∠FGB, ∠DCF=∠GBF,
∴△CDF∽△BGF.
(2) 由(1)知△CDF∽△BGF, 又F是BC的中点,
∴ BF = FC,
∴ △CDF≌△BGF,
∴ DF = FG, CD = BG.
又∵ EF∥CD, AB∥CD,
∴ EF∥AG, 得 2EF = AB+BG.
∴ BG = 2EF-AB = 2×4-6 = 2,
∴ CD = BG = 2cm.
课程总结
小结
对应高的比
对应角平分线的比
相似三角形
对应中线的比
都等于相似比
