人教版2025年五年级下学期数学期末专题分类训练:解方程或比例(含解析)
文档属性
| 名称 | 人教版2025年五年级下学期数学期末专题分类训练:解方程或比例(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 12:33:58 | ||
图片预览

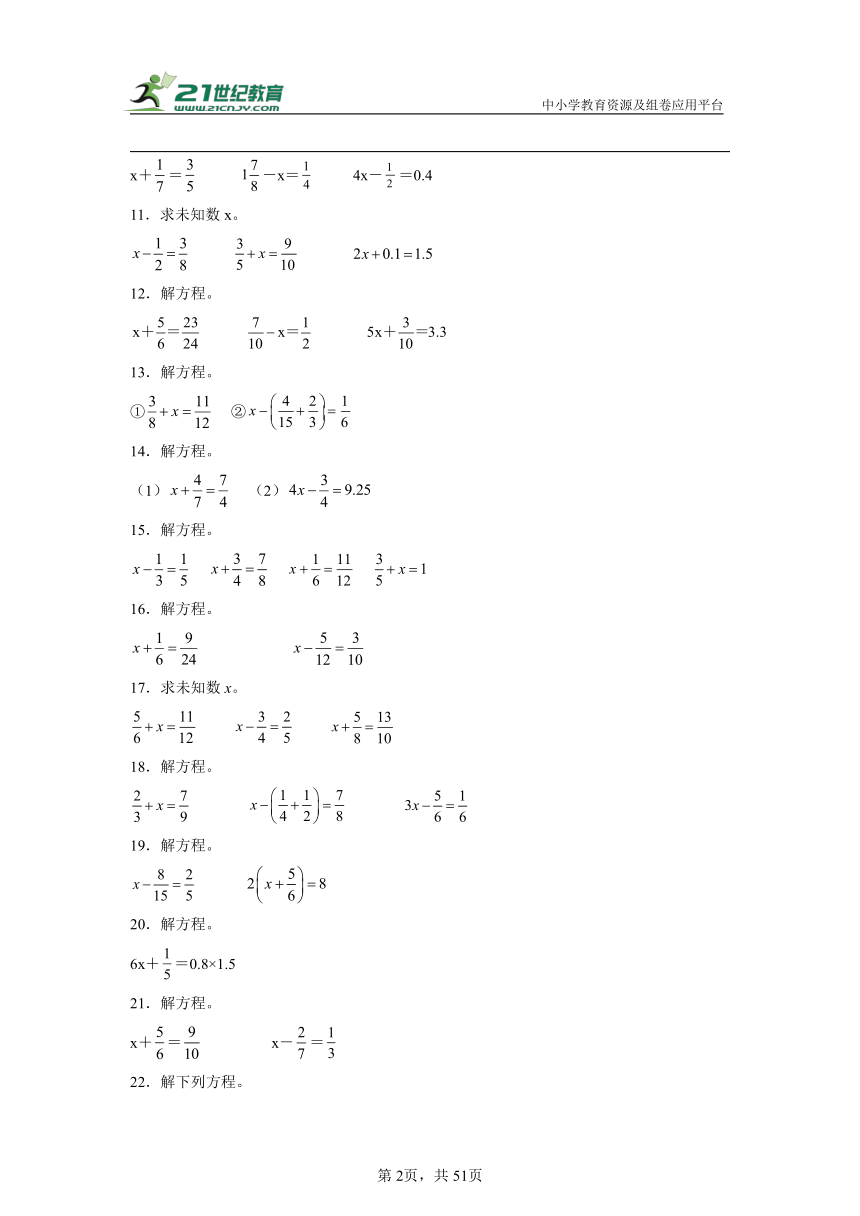
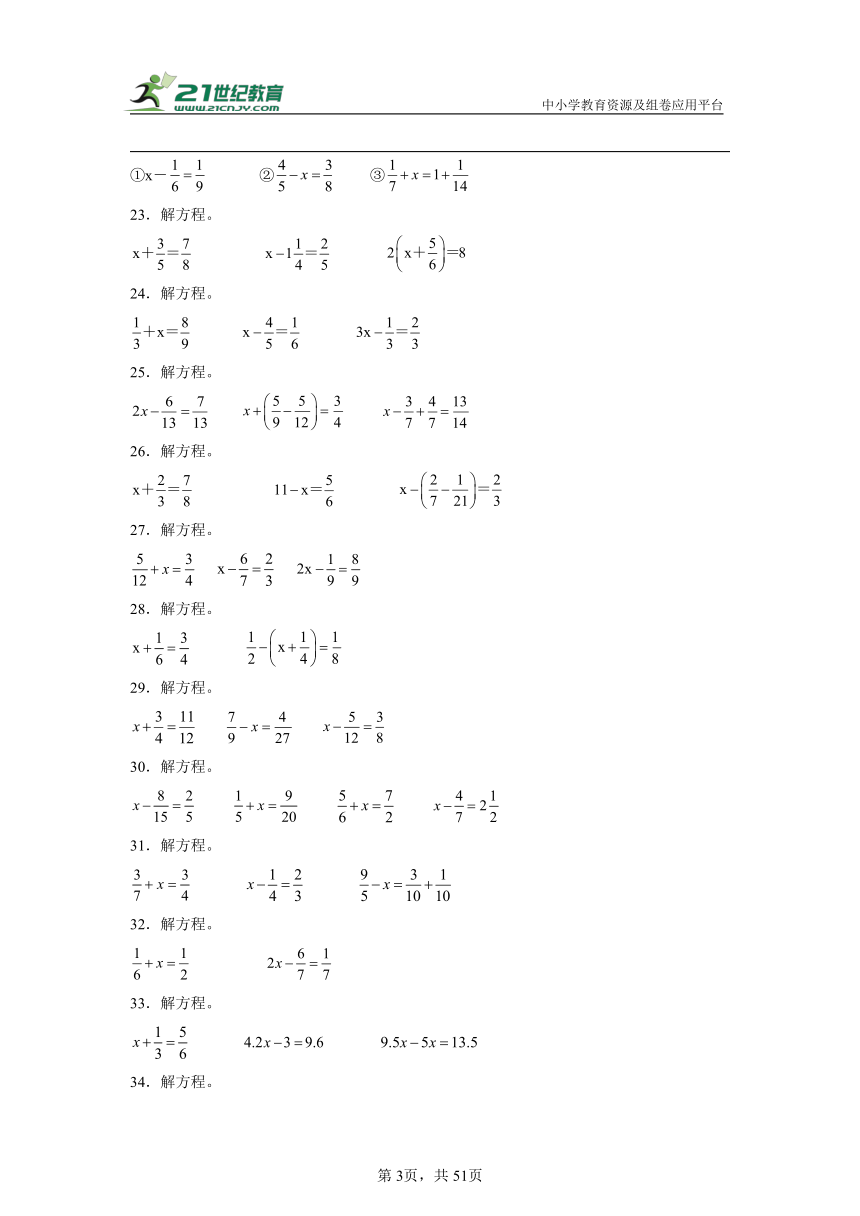
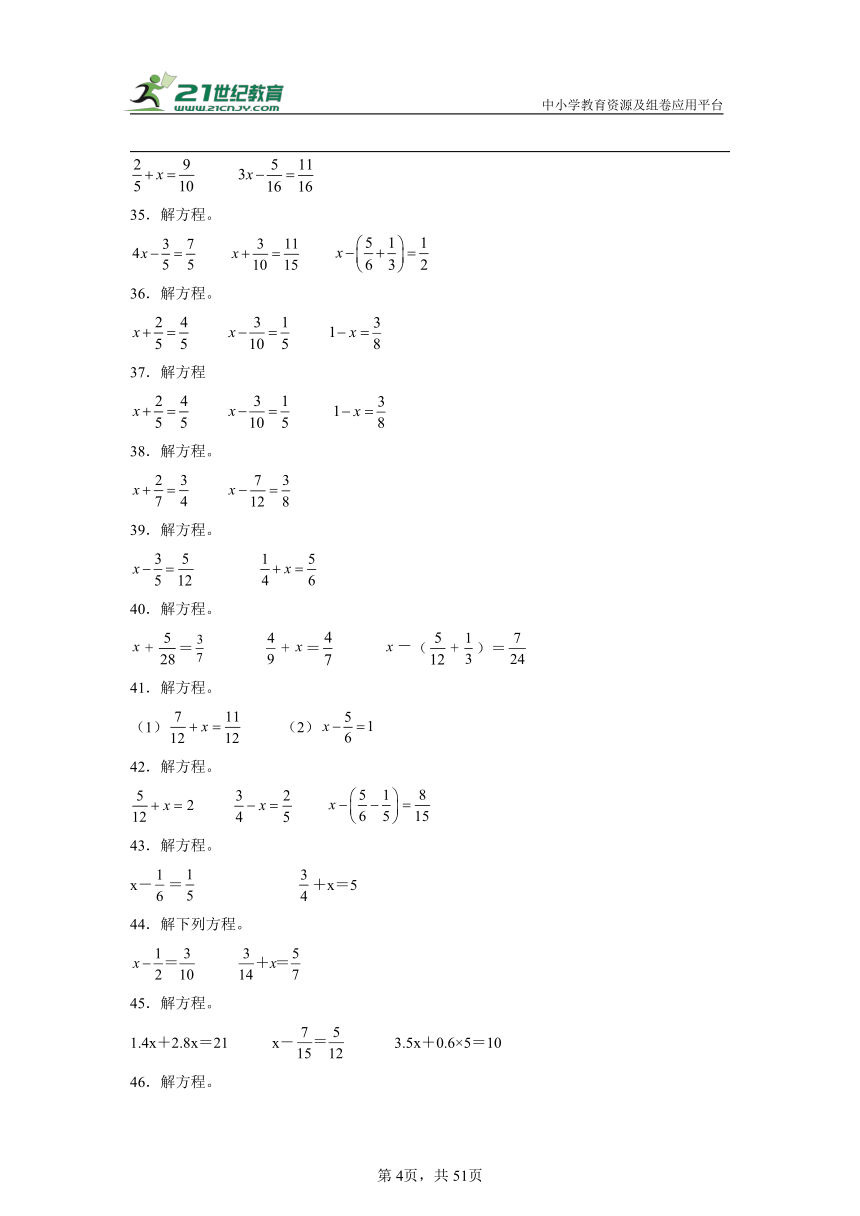
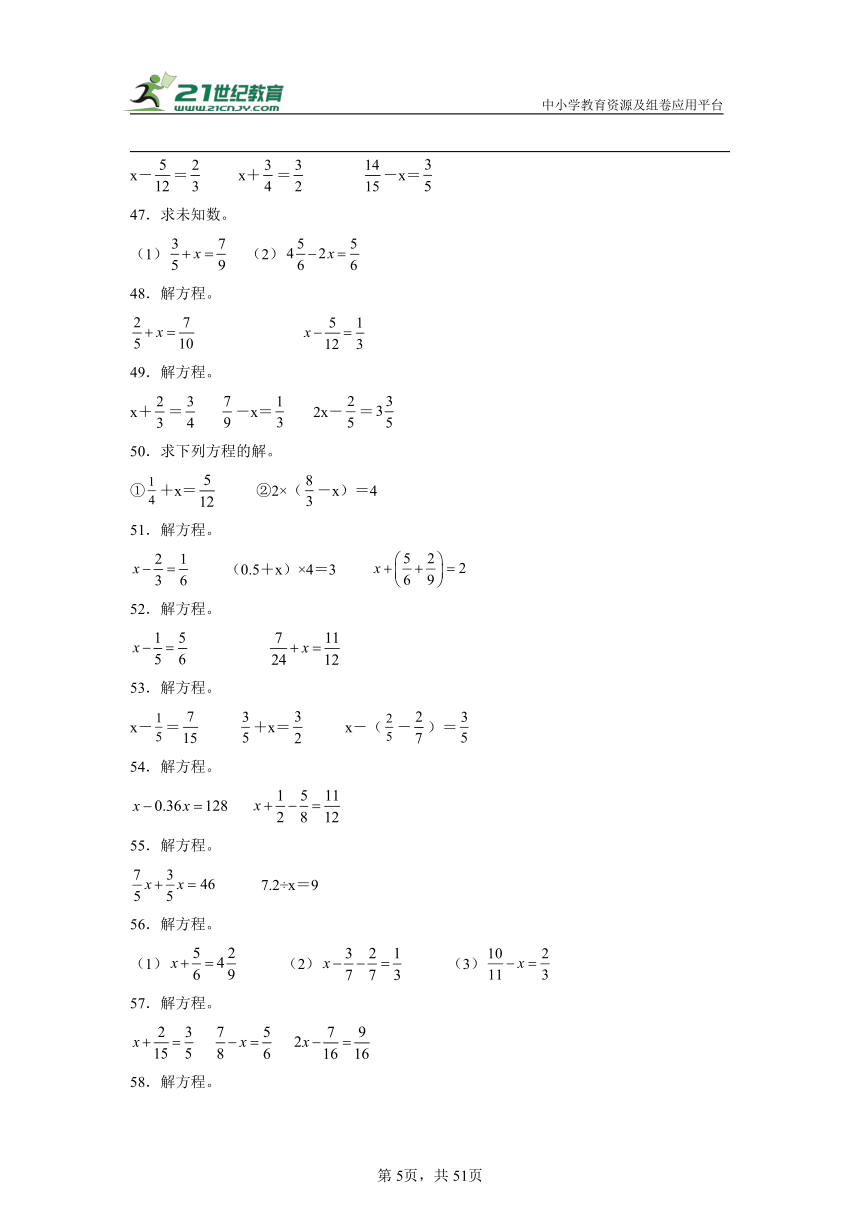
文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版2025年五年级下学期数学期末专题分类训练
解方程或比例
学校:___________姓名:___________班级:___________
1.解方程。
+= -=
2.解方程。
3.解方程。
4.解方程。
(1) (2)x-2×0.15=
5.解方程。
6.解方程。
7.解方程。
8.解方程。
+x= -x= 2x-97=34.2
9.解方程。
① ②7.6x+1.4x=12.6 ③8x+2.7=7.5
10.解方程。
x+= -x= 4x-=0.4
11.求未知数x。
12.解方程。
13.解方程。
① ②
14.解方程。
(1) (2)
15.解方程。
16.解方程。
17.求未知数x。
18.解方程。
19.解方程。
20.解方程。
6x+=0.8×1.5
21.解方程。
x+= x-=
22.解下列方程。
①x- ② ③
23.解方程。
24.解方程。
25.解方程。
26.解方程。
27.解方程。
28.解方程。
29.解方程。
30.解方程。
31.解方程。
32.解方程。
33.解方程。
34.解方程。
35.解方程。
36.解方程。
37.解方程
38.解方程。
39.解方程。
40.解方程。
= = ()=
41.解方程。
(1) (2)
42.解方程。
43.解方程。
x-= +x=5
44.解下列方程。
45.解方程。
1.4x+2.8x=21 x- 3.5x+0.6×5=10
46.解方程。
x-= x+= -x=
47.求未知数。
(1) (2)
48.解方程。
49.解方程。
x+= -x= 2x-=
50.求下列方程的解。
①+x= ②2×(-x)=4
51.解方程。
(0.5+x)×4=3
52.解方程。
53.解方程。
x-= +x= x-(-)=
54.解方程。
55.解方程。
7.2÷x=9
56.解方程。
(1) (2) (3)
57.解方程。
58.解方程。
+x= -x= x-=
59.解方程。
60.解下列方程。
(1) (2)
参考答案
1.=;=
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,方程变成+=,然后方程两边同时减去,求出方程的解。
【详解】(1)+=
解:+-=-
=-
=
(2)-=
解:-+=+
+=
+-=-
=-
=
2.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
3.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,把方程变成,然后方程两边同时减去,求出方程的解;
(3)先把方程化简成,然后方程两边同时加上,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
4.(1);(2)x=0.95
【分析】(1)根据等式的基本性质1,方程两边同时减,求出方程的解即可;
(2)先计算方程左边的算式,再根据等式的基本性质1,方程两边同时加0.3,求出方程的解即可。
【详解】(1)
解:
(2)
解:x-0.3=0.65
x-0.3+0.3=0.65+0.3
x=0.95
5.;;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
6.;;
【分析】,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时-即可;
,将左边合并成,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
7.;;
;;
【分析】,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上即可;
,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上,再同时减去即可;
,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上即可。
【详解】
解:
解:
解:
解:
解:
解:
8.x=;x=;x=65.6
【分析】(1)根据等式的基本性质,方程两边同时减去即可;
(2)根据减数=被减数-差可知x=-,进一步解方程即可;
(3)根据等式的基本性质,方程两边先同时加上97,再同时除以2即可。
【详解】+x=
解:x=-
x=-
x=
-x=
解:x=-
x=-
x=
2x-97=34.2
解:2x=34.2+97
2x=131.2
x=131.2÷2
x=65.6
9.;x=1.4;x=0.6
【分析】①根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加,计算即可得解。
②先计算左边的加法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以9,计算即可得解;
③根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时减2.7。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以8,计算即可得解。
【详解】①
解:
②7.6x+1.4x=12.6
解:9x=12.6
9x÷9=12.6÷9
x=1.4
③8x+2.7=7.5
解:8x+2.7-2.7=7.5-2.7
8x=4.8
8x÷8=4.8÷8
x=0.6
10.x=;x=;x=0.225
【分析】x+=,根据等式的性质1,方程两边同时减去即可。
-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可。
4x-=0.4,把分数化成小数,=0.5,方程化为:4x-0.5=0.4,再根据等式的性质1,方程两边同时加上0.5,再根据等式的性质2,方程两边同时除以4即可。
【详解】x+=
解:x+-=-
x=-
x=
-x=
解:-x+x-=-+x
x=-
x=-
x=
4x-=0.4
解:4x-0.5=0.4
4x-0.5+0.5=0.4+0.5
4x=0.9
4x÷4=0.9÷4
x=0.225
11.;;
【分析】(1)根据等式的性质1,方程两边同时加上,即可求解。
(2)根据等式的性质1,方程两边同时减去,即可求解。
(3)根据等式的性质1,方程两边同时减去0.1,再根据等式的性质2,方程两边同时除以2,即可求解。
【详解】
解:
解:
解:
12.x=;x=;x=0.6
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可;
5+=3.3,先把分数化成小数,=0.3,再根据等式的性质1,方程两边同时减去3.3,再根据等式的性质2,方程两边同时除以5即可。
【详解】x+=
解:x+-=-
x=-
x=
-x=
解:-x+x-=-+x
x=-
x=
5x+=3.3
解:5x+0.3=3.3
5x+0.3-0.3=3.3-0.3
5x=3
5x÷5=3÷5
x=0.6
13.①;②
【分析】①根据等式性质1,方程两边同时减去即可;
②先根据异分母分数的加法法则计算出的和,再根据等式的性质1,方程两边同时加上的和即可;
【详解】
解:
解:
14.;
【分析】(1)方程两边同时减去;
(2)方程两边同时加上,再在两边同时除以4;
【详解】
15.;;;
【分析】,根据等式的性质一,等式两边同时加上,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
【详解】
解:
解:
解:
解:
16.;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,即可求解;
(2)方程两边同时加上,即可求解。
【详解】(1)
解:
(2)
解:
17.;;
【分析】(1)根据等式的性质,等式两边同时减去,再进行通分求解;
(2)根据等式的性质,等式两边同时加上,再进行通分求解;
(3)根据等式的性质,等式两边同时减去,再进行通分求解。
【详解】
解:
解:
解:
18.x=;x= ;x=
【分析】(1)根据方程性质1,两边同时减去,计算出结果即可。
(2)先计算小括号内的+=+=,然后依据方程性质1,两边同时加上,然后计算出结果即可。
(3)根据方程性质1,两边同时加上,然后依据方程性质2,两边同时÷3,计算出结果即可。
【详解】
解;+x-=-
x=-
x=-
x=
解:x-=
x-+=+
x=+
x=+
x=
解:3x-+=+
3x=+
3x=1
3x÷3=1÷3
3x×=1×
x=
19.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边先同时除以2,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
20.
【分析】先化简方程的右边,再根据等式的基本性质,方程两边先同时减去,再同时除以6求解。
【详解】
解:
21.x=;x=
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
x-=,根据等式的性质1,方程两边同时加上即可。
【详解】x+=
解:x+-=-
x=-
x=
x-=
解:x-+=+
x=+
x=
22.①;②;③
【分析】(1)根据等式的性质,方程两边同时加上求解;
(2)根据等式的性质,方程两边同时加x,然后根据等式的性质,方程两边同时减去求解;
(3)根据等式的性质,方程两边同时减去求解。
【详解】(1)解:
(2)
(3)
【点睛】此题考查了解方程的方法,主要是利用等式的性质来求解,所以要掌握好基本的知识。
23.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,先把带分数化为假分数,然后根据等式的性质1,将方程左右两边同时加上即可;
,根据等式的性质1和2,将方程左右两边同时除以2,再同时减去即可。
【详解】
解:
解:
解:
24.x=;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可;
,根据等式的性质1和2,将方程左右两边同时加上,再同时除以3即可。
【详解】
解:
解:
解:
25.;;
【分析】根据等式的性质解方程。
(1)方程两边先同时加上,再同时除以2,求出方程的解;
(1)先把方程化简成,然后方程两边同时减去,求出方程的解;
(3)方程两边先同时减去,再同时加上,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
26.x=;x=;x=
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
11-x=,根据等式的性质1,方程两边同时加上x,再减去即可;
x-(-)=,先计算出-的差,再根据等式的性质1,方程两边同时加上-的差即可。
【详解】x+=
解:x+-=-
x=-
x=
11-x=
解:11-x+x-=-+x
x=11-
x=
x-(-)=
解:x-(-)=
x-=
x-+=+
x=+
x=
27.;;
【分析】(1)根据等式的性质,在方程两边同时减去即可;
(2)根据等式的性质,在方程两边同时加上即可;
(3)根据等式的性质,先在方程两边同时加上,再同时除以2即可。
【详解】
解:
解:
解:
28.x=;x=
【分析】第一个:根据等式的性质1:等式两边同时减去即可求解;
第二个:根据等式的性质1,方程两边同时加下x+,再根据等式的性质1,方程左右两边同时减去再减去即可。
【详解】
解:
x=
解:
x=
29.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上x,然后交换左右两边的位置,再根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可。
【详解】
解:
解:
解:
30.;;;
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
异分母分数相加减通分转化为同分母分数相加减。
根据等式的性质1,将等式的两边同时加上;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时加上。
【详解】
解:
解:
解:
解:
31.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边同时加上,求出方程的解;
(3)先把方程化简成,然后方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
32.;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,再同时除以2,求出方程的解。
【详解】(1)
解:
(2)
解:
33.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1和2,两边同时+3,再同时÷4.2即可;
,先将左边合并成,根据等式的性质2,两边同时÷4.2即可。
【详解】
解:
解:
解:
34.;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1和2,将方程左右两边同时加上,再同时除以3即可。
【详解】
解:
解:
35.;;
【分析】,根据等式的性质1和2,两边同时+,再同时÷4即可;
,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+的和即可。
【详解】
解:
解:
解:
36.;;
【分析】根据等式性质1,方程两边同时减去,即可求解。
根据等式性质1,方程两边同时加上,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
解:
37.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
38.;
【分析】(1)根据等式的性质,方程两边同时减去即可解答;
(2)根据等式的性质,方程两边同时加上即可解答。
【详解】
解:
解:
39.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
40.;;
【分析】(1)根据等式的基本性质,方程两边同时减去求解;
(2)根据等式的基本性质,方程两边同时减去求解;
(3)先化简(),再根据等式的基本性质,方程两边同时加上()求解。
【详解】(1)
解:
(2)
解:
(3)
解:
41.(1);(2)
【分析】(1)根据等式的性质1,方程两边同时减去即可;
(2)根据等式的性质1,方程两边同时加上即可。
【详解】(1)
解:
(2)
解:
42.;;
【分析】根据等式的性质1,方程的两边同时减去,即可求解;
根据等式的性质1,方程的两边同时加上,再同时减去,即可求解;
先化简为,再根据等式的性质1,方程的两边同时加上,即可求解。
【详解】
解:
解:
解:
43.x=;x=
【分析】x-=,根据等式的性质1,两边同时+即可;
+x=5,根据1,两边同时-即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=5
解:+x-=5-
x=
44.x=;x=
【分析】(1)根据等式的性质1,方程两边同时加即可;
(2)根据等式的性质1,方程两边同时减即可。
【详解】
解:=
x=
解:=
x=
45.x=5;x=;x=2
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘或除以同一个不为0的数,左右两边仍然相等。
(1)先化简方程得到4.2x=21,等号左右两边同时除以4.2,即可解出方程;
(2)方程等号左右两边同时加上,即可解出方程;
(3)先化简方程得到3.5x+3=10,方程等号左右两边同时减去3,等号左右两边同时除以3.5,即可解出方程。
【详解】(1)1.4x+2.8x=21
解:4.2x=21
4.2x÷4.2=21÷4.2
x=5
(2)
解:
(3)3.5x+0.6×5=10
解:3.5x+3=10
3.5x+3-3=10-3
3.5x=7
3.5x÷3.5=7÷3.5
x=2
46.x=;x=;x=
【分析】x-=,根据等式的性质1,两边同时+即可;
x+=,根据等式的性质1,两边同时-即可;
-x=,根据等式的性质1,两边同时+x,再同时-即可。
【详解】x-=
解:x-+=+
x=+
x=
x+=
解:x+-=-
x=-
x=
-x=
解:-x+x=+x
+x=
+x-=-
x=-
x=
x=
47.(1);(2)
【分析】(1)根据等式的性质,方程两边同时减去即可;
(2)根据等式的性质,方程两边同时加上2,再同时减去,最后同时除以2即可。
【详解】(1)
解:
(2)
解:
48.;
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
(1)方程等号左右两边同时减去,即可解出方程;
(2)方程等号左右两边同时加上,即可解出方程。
【详解】(1)
解:
(2)
解:
49.x=;x=;x=2
【分析】根据等式的性质1,方程两边同时减去;
根据等式的性质1,方程两边同时加上x,两边再同时减去;
方程两边同时加上,两边再同时除以2。
【详解】x+=
解:x+-=-
x=
x=
-x=
解:-x+x=+x
+x-=-
x=
2x-=
解:2x-+=+
2x=4
2x÷2=4÷2
x=2
50.①x=;②x=
【分析】①+x=,根据等式的性质1,方程两边同时减去即可;
②2×(-x)=4,根据等式的性质2,方程两边同时除以2,再根据等式的性质1,方程两同时加上x,再减去4÷2的商即可。
【详解】①+x=
解:+x-=-
x=-
x=
②2×(-x)=4
解:2×(-x)÷2=4÷2
-x=2
-x+x-2=2-2+x
x=-2
x=
51.;x=0.25;
【分析】“”将等式两边同时加上,解出;
“(0.5+x)×4=3”先将等式两边同时除以4,再同时减去0.5,解出x;
“”先计算小括号内的加法,再将等式两边同时减去,解出。
【详解】
解:
(0.5+x)×4=3
解:(0.5+x)×4÷4=3÷4
0.5+x=0.75
0.5+x-0.5=0.75-0.5
x=0.25
解:
52.;
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
(1)方程等号左右两边同时加上,即可解出方程;
(2)方程等号左右两边同时减去,即可解出方程。
【详解】(1)
解:
(2)
解:
53.x=;x=;x=
【分析】x-=,根据等式的性质1,方程两边同时加上即可;
+x=,根据等式的性质1,方程两边同时减去即可;
x-(-)=,先计算出括号里的减法,即求出-的差,再根据等式的性质1,方程两边同时加上-的差即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=-
x=
x-(-)=
解:x-(-)=
x-=
x-+=+
x=+
x=
54.;
【分析】先将方程化简为,再根据等式性质2,方程两边同时除以0.64,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
55.x=23;x=0.8
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘或除以同一个不为0的数,左右两边仍然相等。
(1)先求方程左边的加法,根据等式的性质,两边同时除以2即可;
(2)首先根据等式的性质,两边同时乘x,然后两边再同时除以9即可。
【详解】(1)x+x=46
解:2x=46
2x÷2=46÷2
x=23
(2)7.2÷x=9
解:7.2÷x×x=9×x
7.2=9x
9x=7.2
9x÷9=7.2÷9
x=0.8
56.(1)x=;(2)x=;(3)x=
【分析】(1)根据等式的性质,方程两边同时减去即可;
(2)根据等式的性质,方程两边同时加上,再同时加上即可;
(3)根据等式的性质,方程两边同时加上x,再同时减去即可。
【详解】(1)
解:x+-=-
x=
(2)
解:x--+=+
x-=
x-+=+
x=
(3)
解:-x+x=+x
+x=
+x-=-
x=
57.x=;x=;x=0.5
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
等式的基本性质2:等式的两边同时乘或者除以一个不为0的数,等式仍然成立。
利用等式的性质1,将等式的两边同时减,异分母分数的加法将异分母分数通分转化为同分母分数再相减。
将x看成减数,在一道减法算式里面,减数=被减数-差。
利用等式的性质1,将等式的两边同时加上,再利用等式的性质2,两边同时除以2。
【详解】
解:
解:
解:
58.x=;x=;x=
【分析】方程两边同时减去,进行解答;
方程两边同时加上x,转化成新方程+x=,方程两边再同时减去,进行解答;
方程两边同时加上,进行解答。
【详解】+x=
解:+x-=-
x=
-x=
解:-x+x=+x
+x=
+x-=-
x=
x-=
解:x-+=+
x=
59.;;
【分析】根据等式的性质1,方程的两边先同时加上,再同时减去即可求解。
先计算括号里的加法,得,再根据等式的性质1,方程的两边同时加上即可求解。
根据等式的性质1,方程的两边先同时加上 ,再同时减去即可求解。
【详解】
解:
解:
解:
60.(1)x=;(2)x=
【分析】(1)根据等式的性质1,将方程两边同时减去即可求解;
(2)根据等式的性质1,将方程的两边同时加上即可求解。
【详解】(1)
解:
(2)
解:
第1页,共2页
第1页,共2页
中小学教育资源及组卷应用平台
人教版2025年五年级下学期数学期末专题分类训练
解方程或比例
学校:___________姓名:___________班级:___________
1.解方程。
+= -=
2.解方程。
3.解方程。
4.解方程。
(1) (2)x-2×0.15=
5.解方程。
6.解方程。
7.解方程。
8.解方程。
+x= -x= 2x-97=34.2
9.解方程。
① ②7.6x+1.4x=12.6 ③8x+2.7=7.5
10.解方程。
x+= -x= 4x-=0.4
11.求未知数x。
12.解方程。
13.解方程。
① ②
14.解方程。
(1) (2)
15.解方程。
16.解方程。
17.求未知数x。
18.解方程。
19.解方程。
20.解方程。
6x+=0.8×1.5
21.解方程。
x+= x-=
22.解下列方程。
①x- ② ③
23.解方程。
24.解方程。
25.解方程。
26.解方程。
27.解方程。
28.解方程。
29.解方程。
30.解方程。
31.解方程。
32.解方程。
33.解方程。
34.解方程。
35.解方程。
36.解方程。
37.解方程
38.解方程。
39.解方程。
40.解方程。
= = ()=
41.解方程。
(1) (2)
42.解方程。
43.解方程。
x-= +x=5
44.解下列方程。
45.解方程。
1.4x+2.8x=21 x- 3.5x+0.6×5=10
46.解方程。
x-= x+= -x=
47.求未知数。
(1) (2)
48.解方程。
49.解方程。
x+= -x= 2x-=
50.求下列方程的解。
①+x= ②2×(-x)=4
51.解方程。
(0.5+x)×4=3
52.解方程。
53.解方程。
x-= +x= x-(-)=
54.解方程。
55.解方程。
7.2÷x=9
56.解方程。
(1) (2) (3)
57.解方程。
58.解方程。
+x= -x= x-=
59.解方程。
60.解下列方程。
(1) (2)
参考答案
1.=;=
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,方程变成+=,然后方程两边同时减去,求出方程的解。
【详解】(1)+=
解:+-=-
=-
=
(2)-=
解:-+=+
+=
+-=-
=-
=
2.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
3.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,把方程变成,然后方程两边同时减去,求出方程的解;
(3)先把方程化简成,然后方程两边同时加上,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
4.(1);(2)x=0.95
【分析】(1)根据等式的基本性质1,方程两边同时减,求出方程的解即可;
(2)先计算方程左边的算式,再根据等式的基本性质1,方程两边同时加0.3,求出方程的解即可。
【详解】(1)
解:
(2)
解:x-0.3=0.65
x-0.3+0.3=0.65+0.3
x=0.95
5.;;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
6.;;
【分析】,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时-即可;
,将左边合并成,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
7.;;
;;
【分析】,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上即可;
,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上,再同时减去即可;
,根据等式的性质1,两边同时减去即可;
,根据等式的性质1,两边同时加上即可。
【详解】
解:
解:
解:
解:
解:
解:
8.x=;x=;x=65.6
【分析】(1)根据等式的基本性质,方程两边同时减去即可;
(2)根据减数=被减数-差可知x=-,进一步解方程即可;
(3)根据等式的基本性质,方程两边先同时加上97,再同时除以2即可。
【详解】+x=
解:x=-
x=-
x=
-x=
解:x=-
x=-
x=
2x-97=34.2
解:2x=34.2+97
2x=131.2
x=131.2÷2
x=65.6
9.;x=1.4;x=0.6
【分析】①根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加,计算即可得解。
②先计算左边的加法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以9,计算即可得解;
③根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时减2.7。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以8,计算即可得解。
【详解】①
解:
②7.6x+1.4x=12.6
解:9x=12.6
9x÷9=12.6÷9
x=1.4
③8x+2.7=7.5
解:8x+2.7-2.7=7.5-2.7
8x=4.8
8x÷8=4.8÷8
x=0.6
10.x=;x=;x=0.225
【分析】x+=,根据等式的性质1,方程两边同时减去即可。
-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可。
4x-=0.4,把分数化成小数,=0.5,方程化为:4x-0.5=0.4,再根据等式的性质1,方程两边同时加上0.5,再根据等式的性质2,方程两边同时除以4即可。
【详解】x+=
解:x+-=-
x=-
x=
-x=
解:-x+x-=-+x
x=-
x=-
x=
4x-=0.4
解:4x-0.5=0.4
4x-0.5+0.5=0.4+0.5
4x=0.9
4x÷4=0.9÷4
x=0.225
11.;;
【分析】(1)根据等式的性质1,方程两边同时加上,即可求解。
(2)根据等式的性质1,方程两边同时减去,即可求解。
(3)根据等式的性质1,方程两边同时减去0.1,再根据等式的性质2,方程两边同时除以2,即可求解。
【详解】
解:
解:
解:
12.x=;x=;x=0.6
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
-x=,根据等式的性质1,方程两边同时加上x,再同时减去即可;
5+=3.3,先把分数化成小数,=0.3,再根据等式的性质1,方程两边同时减去3.3,再根据等式的性质2,方程两边同时除以5即可。
【详解】x+=
解:x+-=-
x=-
x=
-x=
解:-x+x-=-+x
x=-
x=
5x+=3.3
解:5x+0.3=3.3
5x+0.3-0.3=3.3-0.3
5x=3
5x÷5=3÷5
x=0.6
13.①;②
【分析】①根据等式性质1,方程两边同时减去即可;
②先根据异分母分数的加法法则计算出的和,再根据等式的性质1,方程两边同时加上的和即可;
【详解】
解:
解:
14.;
【分析】(1)方程两边同时减去;
(2)方程两边同时加上,再在两边同时除以4;
【详解】
15.;;;
【分析】,根据等式的性质一,等式两边同时加上,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
,根据等式的性质一,等式两边同时减去,即可解答。
【详解】
解:
解:
解:
解:
16.;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,即可求解;
(2)方程两边同时加上,即可求解。
【详解】(1)
解:
(2)
解:
17.;;
【分析】(1)根据等式的性质,等式两边同时减去,再进行通分求解;
(2)根据等式的性质,等式两边同时加上,再进行通分求解;
(3)根据等式的性质,等式两边同时减去,再进行通分求解。
【详解】
解:
解:
解:
18.x=;x= ;x=
【分析】(1)根据方程性质1,两边同时减去,计算出结果即可。
(2)先计算小括号内的+=+=,然后依据方程性质1,两边同时加上,然后计算出结果即可。
(3)根据方程性质1,两边同时加上,然后依据方程性质2,两边同时÷3,计算出结果即可。
【详解】
解;+x-=-
x=-
x=-
x=
解:x-=
x-+=+
x=+
x=+
x=
解:3x-+=+
3x=+
3x=1
3x÷3=1÷3
3x×=1×
x=
19.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边先同时除以2,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
20.
【分析】先化简方程的右边,再根据等式的基本性质,方程两边先同时减去,再同时除以6求解。
【详解】
解:
21.x=;x=
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
x-=,根据等式的性质1,方程两边同时加上即可。
【详解】x+=
解:x+-=-
x=-
x=
x-=
解:x-+=+
x=+
x=
22.①;②;③
【分析】(1)根据等式的性质,方程两边同时加上求解;
(2)根据等式的性质,方程两边同时加x,然后根据等式的性质,方程两边同时减去求解;
(3)根据等式的性质,方程两边同时减去求解。
【详解】(1)解:
(2)
(3)
【点睛】此题考查了解方程的方法,主要是利用等式的性质来求解,所以要掌握好基本的知识。
23.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,先把带分数化为假分数,然后根据等式的性质1,将方程左右两边同时加上即可;
,根据等式的性质1和2,将方程左右两边同时除以2,再同时减去即可。
【详解】
解:
解:
解:
24.x=;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可;
,根据等式的性质1和2,将方程左右两边同时加上,再同时除以3即可。
【详解】
解:
解:
解:
25.;;
【分析】根据等式的性质解方程。
(1)方程两边先同时加上,再同时除以2,求出方程的解;
(1)先把方程化简成,然后方程两边同时减去,求出方程的解;
(3)方程两边先同时减去,再同时加上,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
26.x=;x=;x=
【分析】x+=,根据等式的性质1,方程两边同时减去即可;
11-x=,根据等式的性质1,方程两边同时加上x,再减去即可;
x-(-)=,先计算出-的差,再根据等式的性质1,方程两边同时加上-的差即可。
【详解】x+=
解:x+-=-
x=-
x=
11-x=
解:11-x+x-=-+x
x=11-
x=
x-(-)=
解:x-(-)=
x-=
x-+=+
x=+
x=
27.;;
【分析】(1)根据等式的性质,在方程两边同时减去即可;
(2)根据等式的性质,在方程两边同时加上即可;
(3)根据等式的性质,先在方程两边同时加上,再同时除以2即可。
【详解】
解:
解:
解:
28.x=;x=
【分析】第一个:根据等式的性质1:等式两边同时减去即可求解;
第二个:根据等式的性质1,方程两边同时加下x+,再根据等式的性质1,方程左右两边同时减去再减去即可。
【详解】
解:
x=
解:
x=
29.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上x,然后交换左右两边的位置,再根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可。
【详解】
解:
解:
解:
30.;;;
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
异分母分数相加减通分转化为同分母分数相加减。
根据等式的性质1,将等式的两边同时加上;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时加上。
【详解】
解:
解:
解:
解:
31.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边同时加上,求出方程的解;
(3)先把方程化简成,然后方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
32.;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边先同时加上,再同时除以2,求出方程的解。
【详解】(1)
解:
(2)
解:
33.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1和2,两边同时+3,再同时÷4.2即可;
,先将左边合并成,根据等式的性质2,两边同时÷4.2即可。
【详解】
解:
解:
解:
34.;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1和2,将方程左右两边同时加上,再同时除以3即可。
【详解】
解:
解:
35.;;
【分析】,根据等式的性质1和2,两边同时+,再同时÷4即可;
,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+的和即可。
【详解】
解:
解:
解:
36.;;
【分析】根据等式性质1,方程两边同时减去,即可求解。
根据等式性质1,方程两边同时加上,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
解:
37.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
38.;
【分析】(1)根据等式的性质,方程两边同时减去即可解答;
(2)根据等式的性质,方程两边同时加上即可解答。
【详解】
解:
解:
39.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
40.;;
【分析】(1)根据等式的基本性质,方程两边同时减去求解;
(2)根据等式的基本性质,方程两边同时减去求解;
(3)先化简(),再根据等式的基本性质,方程两边同时加上()求解。
【详解】(1)
解:
(2)
解:
(3)
解:
41.(1);(2)
【分析】(1)根据等式的性质1,方程两边同时减去即可;
(2)根据等式的性质1,方程两边同时加上即可。
【详解】(1)
解:
(2)
解:
42.;;
【分析】根据等式的性质1,方程的两边同时减去,即可求解;
根据等式的性质1,方程的两边同时加上,再同时减去,即可求解;
先化简为,再根据等式的性质1,方程的两边同时加上,即可求解。
【详解】
解:
解:
解:
43.x=;x=
【分析】x-=,根据等式的性质1,两边同时+即可;
+x=5,根据1,两边同时-即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=5
解:+x-=5-
x=
44.x=;x=
【分析】(1)根据等式的性质1,方程两边同时加即可;
(2)根据等式的性质1,方程两边同时减即可。
【详解】
解:=
x=
解:=
x=
45.x=5;x=;x=2
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘或除以同一个不为0的数,左右两边仍然相等。
(1)先化简方程得到4.2x=21,等号左右两边同时除以4.2,即可解出方程;
(2)方程等号左右两边同时加上,即可解出方程;
(3)先化简方程得到3.5x+3=10,方程等号左右两边同时减去3,等号左右两边同时除以3.5,即可解出方程。
【详解】(1)1.4x+2.8x=21
解:4.2x=21
4.2x÷4.2=21÷4.2
x=5
(2)
解:
(3)3.5x+0.6×5=10
解:3.5x+3=10
3.5x+3-3=10-3
3.5x=7
3.5x÷3.5=7÷3.5
x=2
46.x=;x=;x=
【分析】x-=,根据等式的性质1,两边同时+即可;
x+=,根据等式的性质1,两边同时-即可;
-x=,根据等式的性质1,两边同时+x,再同时-即可。
【详解】x-=
解:x-+=+
x=+
x=
x+=
解:x+-=-
x=-
x=
-x=
解:-x+x=+x
+x=
+x-=-
x=-
x=
x=
47.(1);(2)
【分析】(1)根据等式的性质,方程两边同时减去即可;
(2)根据等式的性质,方程两边同时加上2,再同时减去,最后同时除以2即可。
【详解】(1)
解:
(2)
解:
48.;
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
(1)方程等号左右两边同时减去,即可解出方程;
(2)方程等号左右两边同时加上,即可解出方程。
【详解】(1)
解:
(2)
解:
49.x=;x=;x=2
【分析】根据等式的性质1,方程两边同时减去;
根据等式的性质1,方程两边同时加上x,两边再同时减去;
方程两边同时加上,两边再同时除以2。
【详解】x+=
解:x+-=-
x=
x=
-x=
解:-x+x=+x
+x-=-
x=
2x-=
解:2x-+=+
2x=4
2x÷2=4÷2
x=2
50.①x=;②x=
【分析】①+x=,根据等式的性质1,方程两边同时减去即可;
②2×(-x)=4,根据等式的性质2,方程两边同时除以2,再根据等式的性质1,方程两同时加上x,再减去4÷2的商即可。
【详解】①+x=
解:+x-=-
x=-
x=
②2×(-x)=4
解:2×(-x)÷2=4÷2
-x=2
-x+x-2=2-2+x
x=-2
x=
51.;x=0.25;
【分析】“”将等式两边同时加上,解出;
“(0.5+x)×4=3”先将等式两边同时除以4,再同时减去0.5,解出x;
“”先计算小括号内的加法,再将等式两边同时减去,解出。
【详解】
解:
(0.5+x)×4=3
解:(0.5+x)×4÷4=3÷4
0.5+x=0.75
0.5+x-0.5=0.75-0.5
x=0.25
解:
52.;
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
(1)方程等号左右两边同时加上,即可解出方程;
(2)方程等号左右两边同时减去,即可解出方程。
【详解】(1)
解:
(2)
解:
53.x=;x=;x=
【分析】x-=,根据等式的性质1,方程两边同时加上即可;
+x=,根据等式的性质1,方程两边同时减去即可;
x-(-)=,先计算出括号里的减法,即求出-的差,再根据等式的性质1,方程两边同时加上-的差即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=-
x=
x-(-)=
解:x-(-)=
x-=
x-+=+
x=+
x=
54.;
【分析】先将方程化简为,再根据等式性质2,方程两边同时除以0.64,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
55.x=23;x=0.8
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘或除以同一个不为0的数,左右两边仍然相等。
(1)先求方程左边的加法,根据等式的性质,两边同时除以2即可;
(2)首先根据等式的性质,两边同时乘x,然后两边再同时除以9即可。
【详解】(1)x+x=46
解:2x=46
2x÷2=46÷2
x=23
(2)7.2÷x=9
解:7.2÷x×x=9×x
7.2=9x
9x=7.2
9x÷9=7.2÷9
x=0.8
56.(1)x=;(2)x=;(3)x=
【分析】(1)根据等式的性质,方程两边同时减去即可;
(2)根据等式的性质,方程两边同时加上,再同时加上即可;
(3)根据等式的性质,方程两边同时加上x,再同时减去即可。
【详解】(1)
解:x+-=-
x=
(2)
解:x--+=+
x-=
x-+=+
x=
(3)
解:-x+x=+x
+x=
+x-=-
x=
57.x=;x=;x=0.5
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
等式的基本性质2:等式的两边同时乘或者除以一个不为0的数,等式仍然成立。
利用等式的性质1,将等式的两边同时减,异分母分数的加法将异分母分数通分转化为同分母分数再相减。
将x看成减数,在一道减法算式里面,减数=被减数-差。
利用等式的性质1,将等式的两边同时加上,再利用等式的性质2,两边同时除以2。
【详解】
解:
解:
解:
58.x=;x=;x=
【分析】方程两边同时减去,进行解答;
方程两边同时加上x,转化成新方程+x=,方程两边再同时减去,进行解答;
方程两边同时加上,进行解答。
【详解】+x=
解:+x-=-
x=
-x=
解:-x+x=+x
+x=
+x-=-
x=
x-=
解:x-+=+
x=
59.;;
【分析】根据等式的性质1,方程的两边先同时加上,再同时减去即可求解。
先计算括号里的加法,得,再根据等式的性质1,方程的两边同时加上即可求解。
根据等式的性质1,方程的两边先同时加上 ,再同时减去即可求解。
【详解】
解:
解:
解:
60.(1)x=;(2)x=
【分析】(1)根据等式的性质1,将方程两边同时减去即可求解;
(2)根据等式的性质1,将方程的两边同时加上即可求解。
【详解】(1)
解:
(2)
解:
第1页,共2页
第1页,共2页
同课章节目录
