浙江省杭州市2024-2025学年第二学期八年级期末数学模拟卷(含答案)
文档属性
| 名称 | 浙江省杭州市2024-2025学年第二学期八年级期末数学模拟卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 489.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:06:48 | ||
图片预览





文档简介
浙江省杭州市2024学年第二学期八年级期末模拟卷
数学试题卷
全卷共24题,满分120分,考试时间120分钟.
一、选择题(共10小题,每小题3分,共30分)
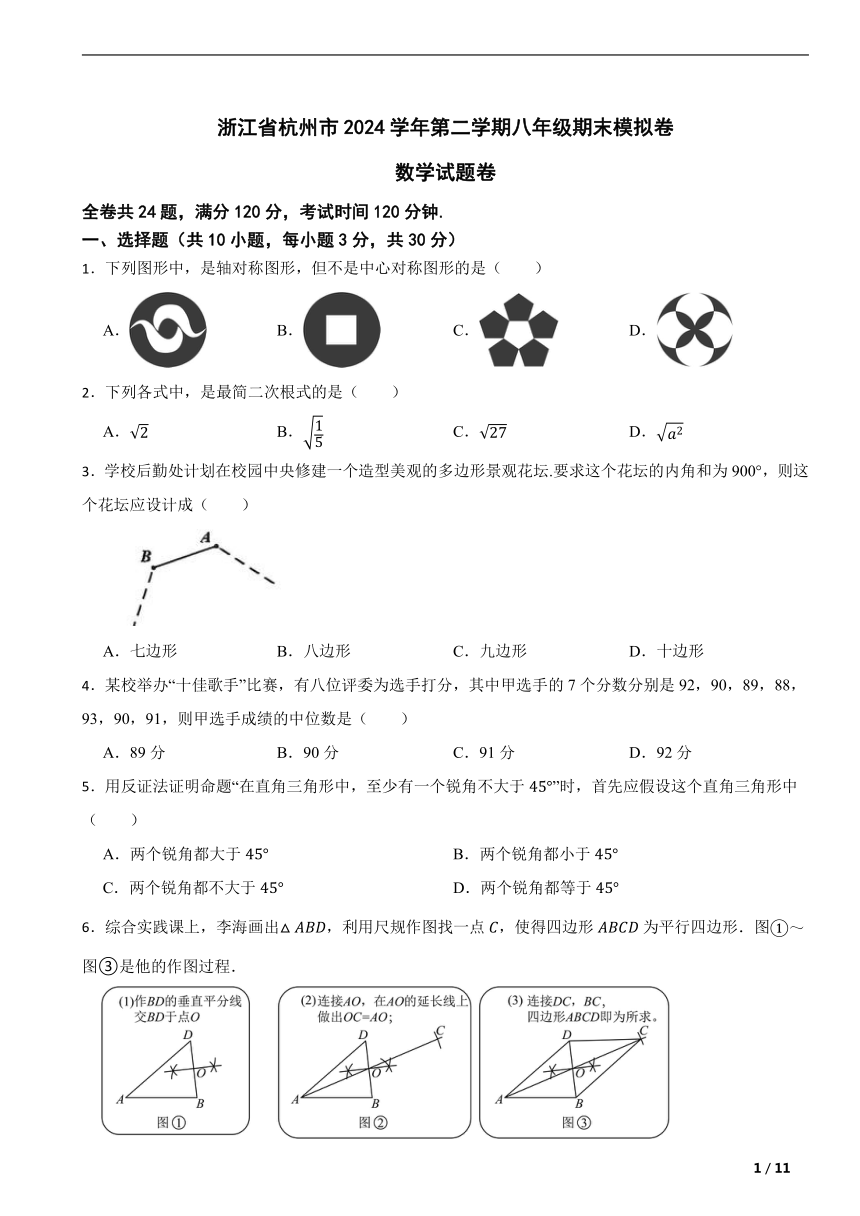
1.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
2.下列各式中,是最简二次根式的是( )
A. B. C. D.
3.学校后勤处计划在校园中央修建一个造型美观的多边形景观花坛.要求这个花坛的内角和为900°,则这个花坛应设计成( )
A.七边形 B.八边形 C.九边形 D.十边形
4.某校举办“十佳歌手”比赛,有八位评委为选手打分,其中甲选手的7个分数分别是92,90,89,88,93,90,91,则甲选手成绩的中位数是( )
A.89分 B.90分 C.91分 D.92分
5.用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,首先应假设这个直角三角形中( )
A.两个锐角都大于 B.两个锐角都小于
C.两个锐角都不大于 D.两个锐角都等于
6.综合实践课上,李海画出,利用尺规作图找一点,使得四边形为平行四边形.图图③是他的作图过程.
李海的作法中,可直接判定四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
7.方程配方后的结果是( )
A. B. C. D.
8.电影《哪吒2》于2025年1月上映,第一天票房约5亿,以后每天票房按相同的增长率增长,第三天票房约6亿,若把增长率记作x,则方程可以列为( )
A.5(1+x)=6 B.5+5(1+x)=6
C.5(1+x)2 =6 D.5+5(1+x)+5(1+x)2 =6
9. 已知点 在双曲线上,若,且,则 ,的大小关系是( )
A. B. C. D.
10.如图,在正方形中,P为上一点(点P不与点B,C重合),于G,并交于点H,过C作交AH延长线于点F,则的值为( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.若使代数式有意义的的取值范围是 .
12.某工厂两位工人(甲、乙)生产同一型号的精密零件,设计要求长度为.质检部门抽样检测发现,他们生产的零件长度的方差分别是:,,其中生产的零件的质量比较稳定的是 (填“甲”或“乙”).
13.若分式的值为0,则的值为 .
14.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
15.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是 .
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
三、解答题(共8题,共52分)
17.(本题8分)
(1)计算;.
(2)解方程:.
18.(本题6分)如图,在的正方形网格中,每个小正方形顶点称为格点,例如线段的端点在格点上,已知每个小正方形边长均为1,请完成下列各小题.
图① 图②
(1)在图①中,作菱形,其中点,为格点(只需作出一种情况);
(2)在图②中,作一个面积为3的菱形,其中点,为格点(只需作出一种情况).
19.(本题6分)为了解某校学生阅读的情况,现从各年级随机抽取了部分学生,对他们一周阅读的总时间进行了调查,并将调查结果绘制成如图所示的统计图:
(1)抽取的学生一周阅读总时间的众数为 ,学生一周阅读的总时间条形统计图中位数为 ;
(2)求抽取的学生一周阅读总时间的平均数;
(3)若该校有1500名学生,根据抽样调查的结果,请你估计该校一周阅读的总时间小于6小时的学生有多少名.
20.(本题7分)如图,E,F是的对角线AC上的两点,且。
(1)求证:四边形AFCE是平行四边形。
(2)若,求四边形ABCD的面积。
21.(本题7分)定义:如果关于x的一元二次方程ax2+bx+c=0(ac≠0)有一个根是c,那么我们称这个方程为“C方程”.
(1)判断一元二次方程x2-4x+3=0是否为“C方程”,请说明理由;
(2)已知关于x的一元二次方程4x2+bx+c=0(c≠0)是“C方程”,求代数式b2﹣4c﹣1的最小值.
22.(本题8分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,与反比例函数的图象分别交于点C、D,点C坐标为,点D坐标为.
(1)求一次函数与反比例函数的表达式;
(2)求的面积;
(3)直接写出当时,自变量x的取值范围.
23.(本题10分)折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为完美矩形.
(1)操作发现:
如图①,将纸片按所示折叠成完美矩形,若的面积为,,则此完美矩形的边长 ,面积为 .
(2)类比探究:
如图②,将平行四边形纸片按所示折叠成完美矩形,若平行四边形的面积为,,则完美矩形的周长为 .
(3)拓展延伸:
如图③,将平行四边形纸片按所示折叠成完美矩形,若,,求此完美矩形的周长为多少.
参考答案
1.C
2.A
3.A
4.B
5.A
6.C
7.B
8.C
9.B
10.C
11.
12.甲
13.
14..
15.(6,).
16.
17.(1)原式.
(2)移项,得,配方,得,
开方,得,
解得.
18.(1)解:
如图①中,菱形即为所求;
图①
(2)解:如图②中,菱形即为所求.
图②
19.(1)6;6
(2)解:总时间=4小时×5人 +5小时×5人+6小时×25人+7小时×15人=20+25+150+105=300小时,
∴平均数=总时间÷总人数=300÷60=6小时
(3)解: 小于6小时的人数为5+5=10人,占总样本60人的,
∴名
20.(1)解:四边形ABCD是平行四边形,
,
在和中,
四边形AFCE是平行四边形(证明方法不唯一)
(2)四边形AFCE是平行四边形,,
,
在中,
21.(1)是“C方程”,理由如下:(解法不唯一)
∵x2-4x+3=0,
∴(x-3)(x-1)=0,
∴x-3=0或x-1=0,
∴x1=3,x2=1,
∵c=3,
∴一元二次方程x2-4x+3=0是“C方程”;
(2)∵关于x的一元二次方程4x2+bx+c=0(c≠0)是“C方程”,
∴4c2+bc+c=0,
∵c≠0,
∴4c=-b-1,
∴b2-4c-1=b2+b=,
∵≥0,
∴b2-4c-1的最小值为.
22.(1)解:∵反比例函数的图象过点,
∴,解得,
即反比例函数解析式为:;
∵点D坐标为.
∴,
∴点D坐标为.
∵一次函数的图象过点,,
∴,
解得:,
∴一次函数解析式为;
(2)解:∵一次函数解析式为与x轴、y轴分别交于点A、B,
∴当时,则,
∴,
∴,
∵,,
则的面积,
(3)解:根据图象可得,当时,自变量的取值范围为或.
23.(1);
(2)16
(3)解:连接,如图所示:
由折叠可得:点E和G分别是AB和CD的中点,
∴AE=DG,AE∥DG,
∴四边形AEGD是平行四边形,
∴AD=EG=HF,
∵EF:EH=3:4,
∴设,则,
∴在中,,
∴,
解得:,
∴,,
∴矩形的周长.
1 / 1
数学试题卷
全卷共24题,满分120分,考试时间120分钟.
一、选择题(共10小题,每小题3分,共30分)
1.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
2.下列各式中,是最简二次根式的是( )
A. B. C. D.
3.学校后勤处计划在校园中央修建一个造型美观的多边形景观花坛.要求这个花坛的内角和为900°,则这个花坛应设计成( )
A.七边形 B.八边形 C.九边形 D.十边形
4.某校举办“十佳歌手”比赛,有八位评委为选手打分,其中甲选手的7个分数分别是92,90,89,88,93,90,91,则甲选手成绩的中位数是( )
A.89分 B.90分 C.91分 D.92分
5.用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,首先应假设这个直角三角形中( )
A.两个锐角都大于 B.两个锐角都小于
C.两个锐角都不大于 D.两个锐角都等于
6.综合实践课上,李海画出,利用尺规作图找一点,使得四边形为平行四边形.图图③是他的作图过程.
李海的作法中,可直接判定四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
7.方程配方后的结果是( )
A. B. C. D.
8.电影《哪吒2》于2025年1月上映,第一天票房约5亿,以后每天票房按相同的增长率增长,第三天票房约6亿,若把增长率记作x,则方程可以列为( )
A.5(1+x)=6 B.5+5(1+x)=6
C.5(1+x)2 =6 D.5+5(1+x)+5(1+x)2 =6
9. 已知点 在双曲线上,若,且,则 ,的大小关系是( )
A. B. C. D.
10.如图,在正方形中,P为上一点(点P不与点B,C重合),于G,并交于点H,过C作交AH延长线于点F,则的值为( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.若使代数式有意义的的取值范围是 .
12.某工厂两位工人(甲、乙)生产同一型号的精密零件,设计要求长度为.质检部门抽样检测发现,他们生产的零件长度的方差分别是:,,其中生产的零件的质量比较稳定的是 (填“甲”或“乙”).
13.若分式的值为0,则的值为 .
14.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
15.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是 .
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
三、解答题(共8题,共52分)
17.(本题8分)
(1)计算;.
(2)解方程:.
18.(本题6分)如图,在的正方形网格中,每个小正方形顶点称为格点,例如线段的端点在格点上,已知每个小正方形边长均为1,请完成下列各小题.
图① 图②
(1)在图①中,作菱形,其中点,为格点(只需作出一种情况);
(2)在图②中,作一个面积为3的菱形,其中点,为格点(只需作出一种情况).
19.(本题6分)为了解某校学生阅读的情况,现从各年级随机抽取了部分学生,对他们一周阅读的总时间进行了调查,并将调查结果绘制成如图所示的统计图:
(1)抽取的学生一周阅读总时间的众数为 ,学生一周阅读的总时间条形统计图中位数为 ;
(2)求抽取的学生一周阅读总时间的平均数;
(3)若该校有1500名学生,根据抽样调查的结果,请你估计该校一周阅读的总时间小于6小时的学生有多少名.
20.(本题7分)如图,E,F是的对角线AC上的两点,且。
(1)求证:四边形AFCE是平行四边形。
(2)若,求四边形ABCD的面积。
21.(本题7分)定义:如果关于x的一元二次方程ax2+bx+c=0(ac≠0)有一个根是c,那么我们称这个方程为“C方程”.
(1)判断一元二次方程x2-4x+3=0是否为“C方程”,请说明理由;
(2)已知关于x的一元二次方程4x2+bx+c=0(c≠0)是“C方程”,求代数式b2﹣4c﹣1的最小值.
22.(本题8分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,与反比例函数的图象分别交于点C、D,点C坐标为,点D坐标为.
(1)求一次函数与反比例函数的表达式;
(2)求的面积;
(3)直接写出当时,自变量x的取值范围.
23.(本题10分)折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为完美矩形.
(1)操作发现:
如图①,将纸片按所示折叠成完美矩形,若的面积为,,则此完美矩形的边长 ,面积为 .
(2)类比探究:
如图②,将平行四边形纸片按所示折叠成完美矩形,若平行四边形的面积为,,则完美矩形的周长为 .
(3)拓展延伸:
如图③,将平行四边形纸片按所示折叠成完美矩形,若,,求此完美矩形的周长为多少.
参考答案
1.C
2.A
3.A
4.B
5.A
6.C
7.B
8.C
9.B
10.C
11.
12.甲
13.
14..
15.(6,).
16.
17.(1)原式.
(2)移项,得,配方,得,
开方,得,
解得.
18.(1)解:
如图①中,菱形即为所求;
图①
(2)解:如图②中,菱形即为所求.
图②
19.(1)6;6
(2)解:总时间=4小时×5人 +5小时×5人+6小时×25人+7小时×15人=20+25+150+105=300小时,
∴平均数=总时间÷总人数=300÷60=6小时
(3)解: 小于6小时的人数为5+5=10人,占总样本60人的,
∴名
20.(1)解:四边形ABCD是平行四边形,
,
在和中,
四边形AFCE是平行四边形(证明方法不唯一)
(2)四边形AFCE是平行四边形,,
,
在中,
21.(1)是“C方程”,理由如下:(解法不唯一)
∵x2-4x+3=0,
∴(x-3)(x-1)=0,
∴x-3=0或x-1=0,
∴x1=3,x2=1,
∵c=3,
∴一元二次方程x2-4x+3=0是“C方程”;
(2)∵关于x的一元二次方程4x2+bx+c=0(c≠0)是“C方程”,
∴4c2+bc+c=0,
∵c≠0,
∴4c=-b-1,
∴b2-4c-1=b2+b=,
∵≥0,
∴b2-4c-1的最小值为.
22.(1)解:∵反比例函数的图象过点,
∴,解得,
即反比例函数解析式为:;
∵点D坐标为.
∴,
∴点D坐标为.
∵一次函数的图象过点,,
∴,
解得:,
∴一次函数解析式为;
(2)解:∵一次函数解析式为与x轴、y轴分别交于点A、B,
∴当时,则,
∴,
∴,
∵,,
则的面积,
(3)解:根据图象可得,当时,自变量的取值范围为或.
23.(1);
(2)16
(3)解:连接,如图所示:
由折叠可得:点E和G分别是AB和CD的中点,
∴AE=DG,AE∥DG,
∴四边形AEGD是平行四边形,
∴AD=EG=HF,
∵EF:EH=3:4,
∴设,则,
∴在中,,
∴,
解得:,
∴,,
∴矩形的周长.
1 / 1
同课章节目录
