人教版2025年五年级下学期数学期末专题分类训练:能力作图题(附答案)
文档属性
| 名称 | 人教版2025年五年级下学期数学期末专题分类训练:能力作图题(附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 12:34:30 | ||
图片预览

文档简介
人教版2025年五年级下学期数学期末专题分类训练
能力作图题
学校:___________姓名:___________班级:___________
作图题
1.如图是由若干个完全相同的小正方体堆成的几何体:
(1)画出该几何体的三视图。
(2)在该几何体的表面刷上黄色的漆,则在所有的小正方体中,有____个正方体的三个面是黄色。
(3)若现在你手头还有一个相同的小正方体,在不考虑颜色的情况下,该正方体应放在何处才能使堆成的几何体的三视图不变?直接在图中添上该正方体。
(4)若考虑颜色,要使三视图不变,则新添的正方体至少要在____个面上着色。
2.用同样的小正方体搭一个几何体,从上面看到的图形如图所示(方格中的数字表示该位置小正方体的个数),请你分别画出这个几何体从前面和左面看到的图形。
3.一个几何体由几个相同的小正方体搭成,从上面看到的图形如右图所示,小正方形上的数字表示在该位置上小正方体的个数。请分别画出从正面、左面看这个几何体得到的图形。
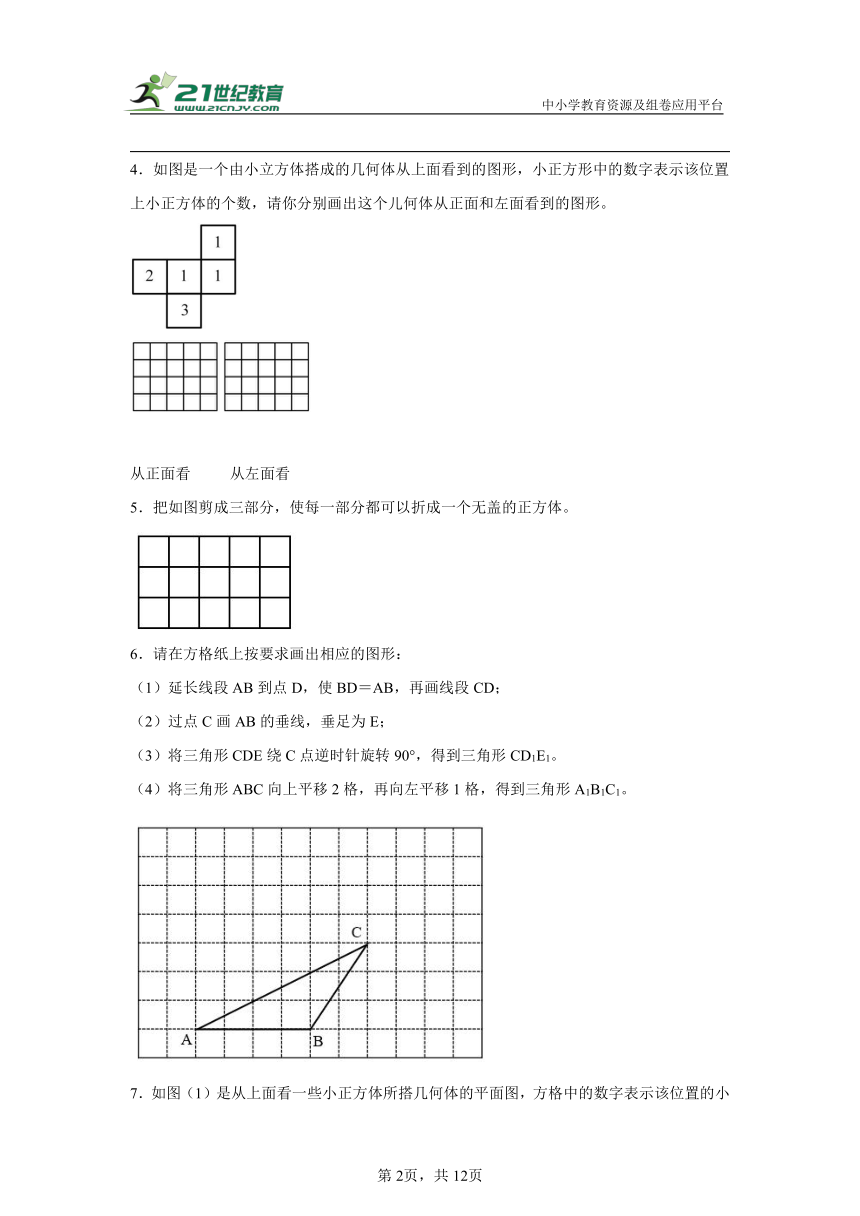
4.如图是一个由小立方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上小正方体的个数,请你分别画出这个儿何体从正面和左面看到的图形。
从正面看 从左面看
5.把如图剪成三部分,使每一部分都可以折成一个无盖的正方体。
6.请在方格纸上按要求画出相应的图形:
(1)延长线段AB到点D,使BD=AB,再画线段CD;
(2)过点C画AB的垂线,垂足为E;
(3)将三角形CDE绕C点逆时针旋转90°,得到三角形CD1E1。
(4)将三角形ABC向上平移2格,再向左平移1格,得到三角形A1B1C1。
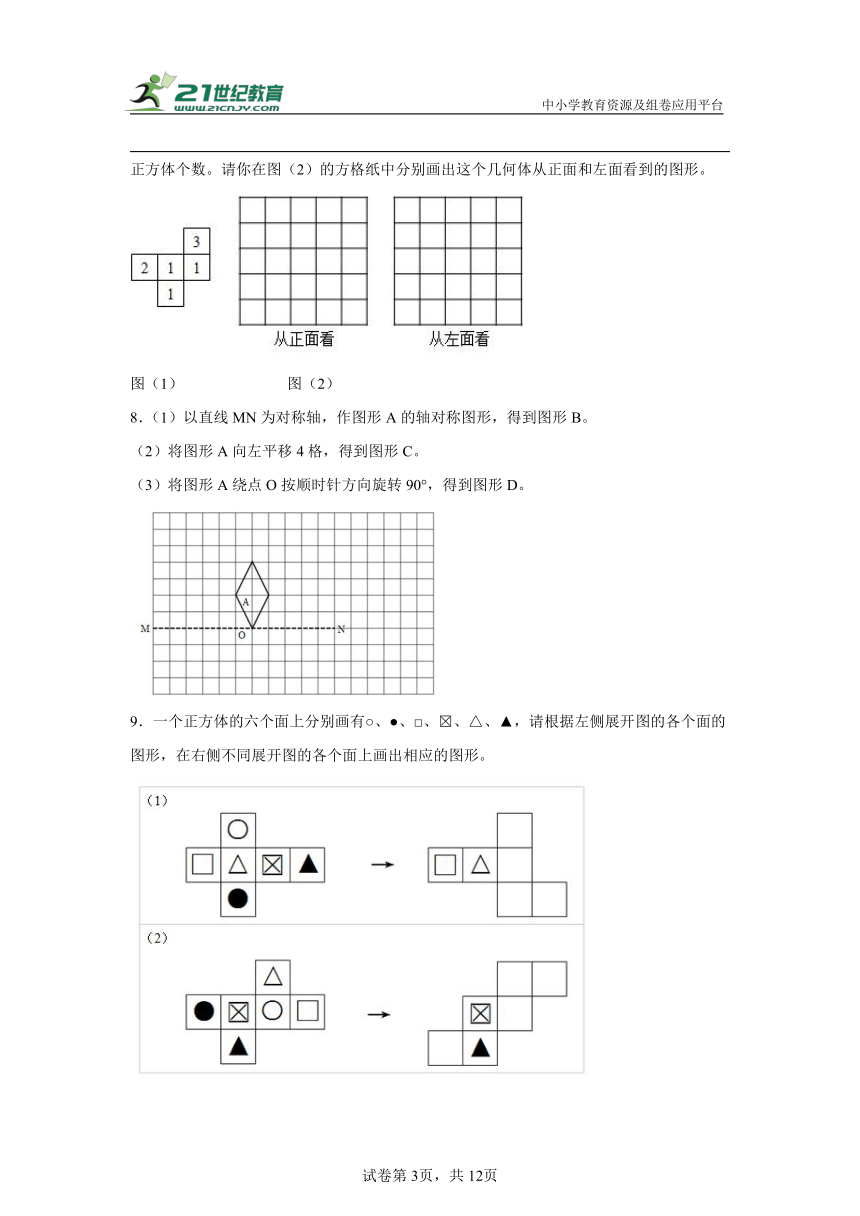
7.如图(1)是从上面看一些小正方体所搭几何体的平面图,方格中的数字表示该位置的小正方体个数。请你在图(2)的方格纸中分别画出这个几何体从正面和左面看到的图形。
图(1) 图(2)
8.(1)以直线MN为对称轴,作图形A的轴对称图形,得到图形B。
(2)将图形A向左平移4格,得到图形C。
(3)将图形A绕点O按顺时针方向旋转90°,得到图形D。
9.一个正方体的六个面上分别画有○、●、□、 、△、▲,请根据左侧展开图的各个面的图形,在右侧不同展开图的各个面上画出相应的图形。
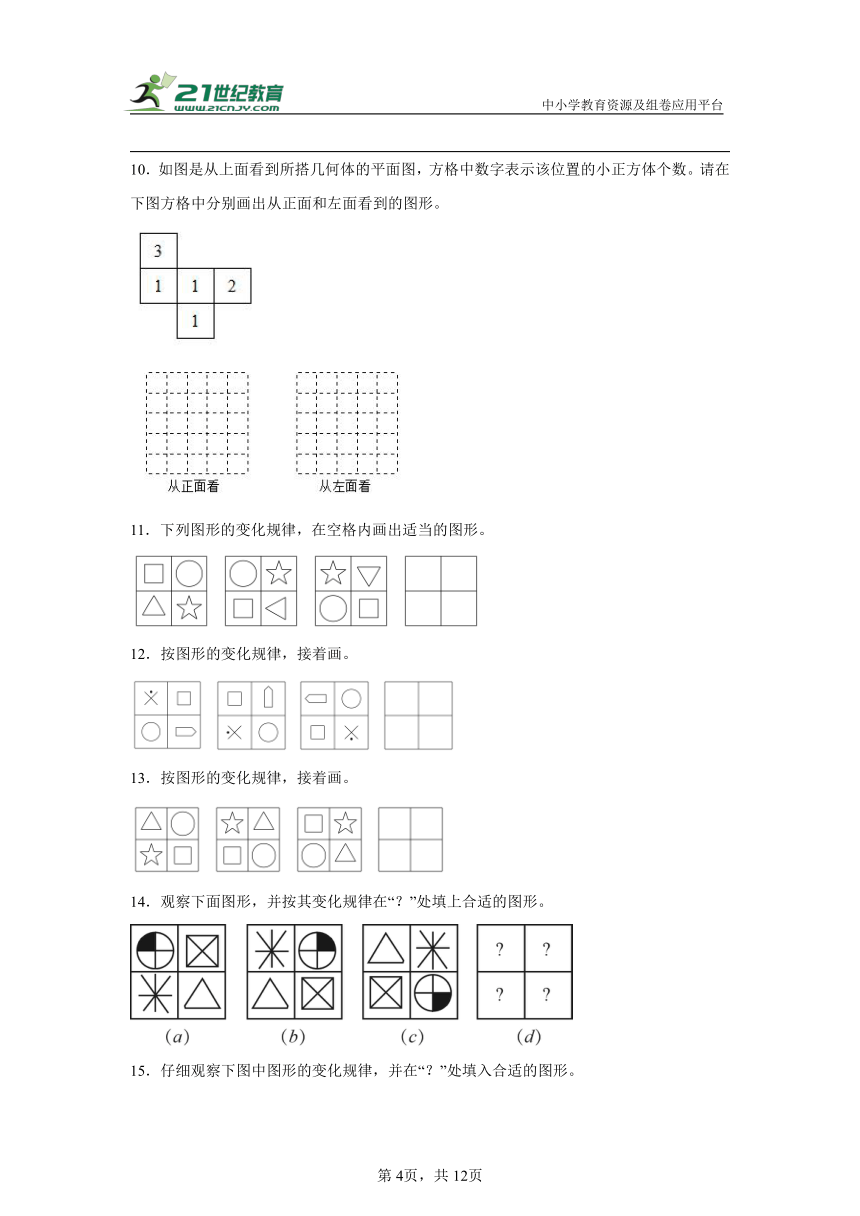
10.如图是从上面看到所搭几何体的平面图,方格中数字表示该位置的小正方体个数。请在下图方格中分别画出从正面和左面看到的图形。
11.下列图形的变化规律,在空格内画出适当的图形。
12.按图形的变化规律,接着画。
13.按图形的变化规律,接着画。
14.观察下面图形,并按其变化规律在“?”处填上合适的图形。
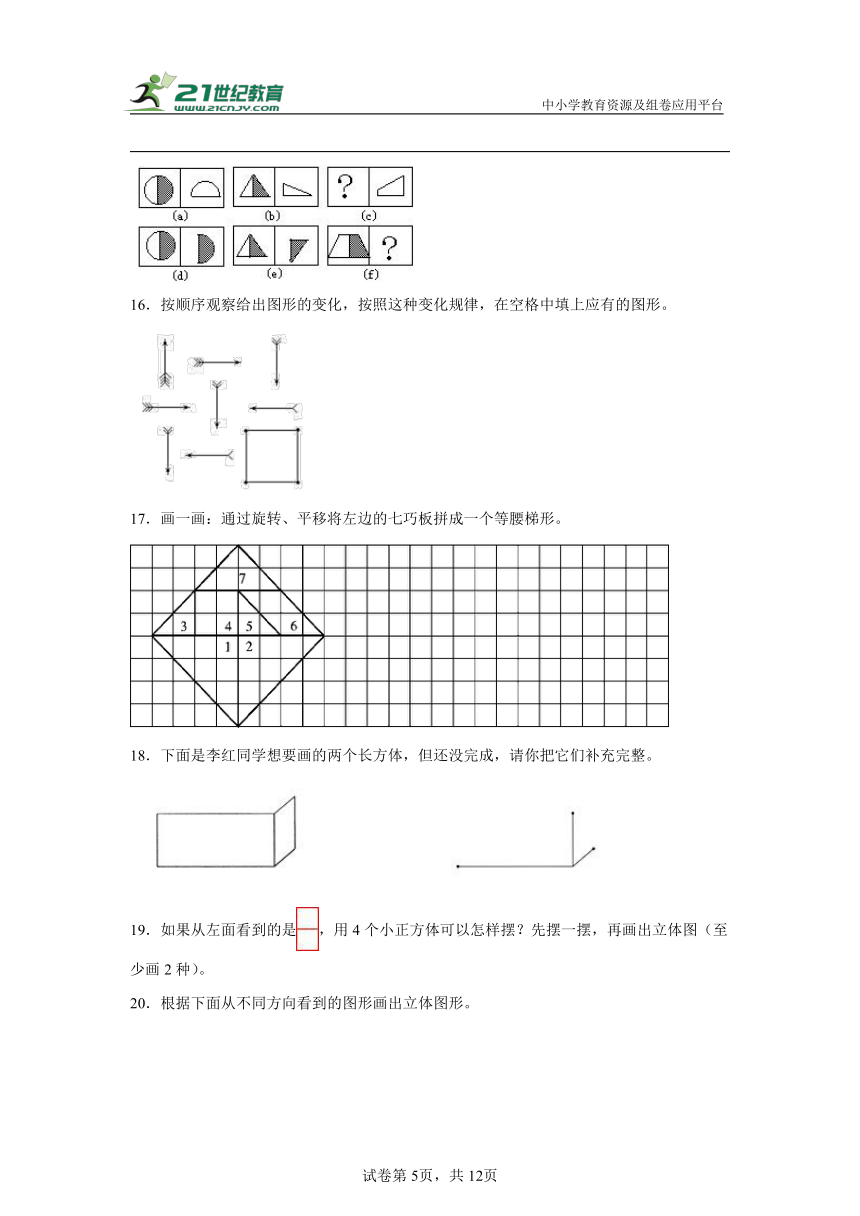
15.仔细观察下图中图形的变化规律,并在“?”处填入合适的图形。
16.按顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形。
17.画一画:通过旋转、平移将左边的七巧板拼成一个等腰梯形。
18.下面是李红同学想要画的两个长方体,但还没完成,请你把它们补充完整。
19.如果从左面看到的是,用4个小正方体可以怎样摆?先摆一摆,再画出立体图(至少画2种)。
20.根据下面从不同方向看到的图形画出立体图形。
从上面看 从正面看 从左面看
21.用正方体积木搭了一个几何体,从上面看到的图形是图1。图2中小正方形上面的数字表示在这个位置上所用的小正方体的个数。请画出从正面和左面看到的图形。
22.下面是从不同位置观察同一个物体所看到的图形,请把它摆出来。(画一画)
23.用6个正方体搭一搭3种使正面看到的形状是的图形,画出它们的三视图。
24.观察一个立体图形,从上面看到的图形如图所示,小正方形内的数字表示在这个位置上所用的小正方体的个数。请把从正面、左面看到的图形在方格纸上画出来。
25.根据从不同方向看到的平面图形,用小正方体摆出立体图形。
26.以O点为顶点画一个面积是4cm2的四边形(1小格为1cm2),再画出绕O点逆时针旋转90°后的图形.
27.(1)将图形A绕点O逆时针旋转90度,得到图形B。
(2)画一个和图形A面积相等的三角形。
28.有一张长方形硬纸,正好分成15个小正方形.数学老师想用这张硬纸做3个无盖的正方体盒子作为教具使用.请你用不同颜色的笔画出分割图,要求折成每个正方体的5个小正方形相连,折起来正好是一个无盖的正方体纸盒.请你试试看!
29.请你将下面的图形利用平移、旋转和轴对称变换分别设计图案。
30.请在格子里涂黑,使得上图成为一个轴对称图形
31.如图是一张长方形的硬纸板,请你沿着图中的线把这张硬纸板剪成三块,使每一块都可以折成一个无盖的正方体,该怎样剪?在图中画出来。
32.如图中有一个面积是6cm2的直角三角形ABC. (图中每个方格的面积代表1cm2).A点在(7,2),你认为B、C点可能在( , )和( , ).
①画出三角形ABC.②把这个三角形绕A点顺时针旋转90°,画出旋转后的图形.
③画一个和三角形ABC面积相等的梯形.
33.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
34.下图实线部分都是在白纸上面的无盖正方体的表面展开图,请你设计三种不同的方法,在图中添加一个正方形(涂色表示),使新图形剪下折叠后能够围成一个封闭的正方体。
35.(1)画出图①绕点O顺时针旋转90°后的图形,并在图中标出点A的对应点。
(2)将图②先绕点M( )时针旋转( )°,再向( )平移( )格得到图③。
36.下面是某地区7~13岁男、女生平均身高统计图。(单位:厘米)
年龄 7岁 8岁 9岁 10岁 11岁 12岁 13岁
男生 125 132 133 140 145 150 157
女生 123 127 135 141 145 152 156
(1)请根据统计表绘制复式折线统计图。
(2)比较男生与女生平均身高的变化情况,你能得出什么结论?
37.
(1)画出图①绕O点逆时针旋转90°后的图形。
(2)说一说,图①可以通过怎样的运动得到图②。
38.在下面展开图上用“上、下、左、右、前、后”标出长方体的各面。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第1页,共3页
试卷第1页,共3页
参考答案
1.(1)作图见详解;
(2)1;
(3)见详解;
(4)3
【分析】(1)主视图:从正面看,第一列最高是3层,第二列最高是2层,第三列最高是1层,所以主视图是三列,第一列3个正方形,第二列2个正方形,第三列1个正方形(从下往上对齐排列)。
左视图:从左面看,第一列最高是3层,第二列最高是2层,所以左视图是三列,第一列3个正方形,第二列2个正方形,第三列1个正方形(从下往上对齐排列)。
俯视图:从上面看,第一列3个正方形,第二列2个正方形,第三列1个正方形(从左往右对齐排列)。
(2)三个面是黄色的小正方体位置具有特定规律,通常在几何体的棱上且不处于顶点位置(顶点位置的小正方体是三个以上面外露) 。我们对该几何体的每一个小正方体进行位置分析。从底层开始看,再看中层和上层,逐一判断每个小正方体露出的面数。经过仔细观察,发现只有处于特定棱中间位置的小正方体才是三个面外露被刷成黄色。
(3)要使新添加一个小正方体后三视图不变,就意味着新添加的小正方体不能改变从正面、左面和上面观察到的形状。这就要求新添加的小正方体要放在原几何体中已有的小正方体能够遮挡住的位置,也就是放在原几何体的内部且不改变外部轮廓。比如放在特定棱中间位置的小正方体的上面,从正面看,挡住了原来的小正方体的但是不改变主视图形状;从左面看,被其他小正方体遮挡;从上面看,同样不会改变整体的形状布局。
(4)若考虑颜色且要使三视图不变,新添的正方体要与周围环境融合,不能因为颜色差异而改变从三个方向观察到的形状。如果新正方体有过多未着色的面,就可能在某个视图方向上显示出与原几何体不同的样子。当新正方体至少在3个面上着色时,无论从正面、左面还是上面看,都能与原几何体的颜色和形状布局相匹配,不会改变三视图。
【详解】(1)
(2)1个,如图所示,
在该几何体的表面刷上黄色的漆,则在所有的小正方体中,有1个正方体的三个面是黄色。
(3)在特定棱中间位置的小正方体的上面添加一个小正方体(可在图上对应位置画出)。
(4)要使三视图不变,则新添的正方体至少要在3个面上着色。
2.见详解
【分析】从前面看到三竖列,第一竖列有3个小正方形,第二竖列有1个小正方形,第三竖列有2个小正方形;
从左面看到三竖列,第一竖列有3个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形。
【详解】
【点睛】本题考查学生对立体物体分别从前、左、上面观察物体的能力,并能想象物体摆放的位置,发展空间想象力。
3.见详解
【分析】
分析:通过观察从上面看到的图形及所给条件发现,这个几何体分成上下两层。其中底层有4个小正方体,拼成的形状是,左列最前面的小正方体,上面摆放着1个小正方体,右列小正方体上面也摆放着1个小正方体,因此搭成的几何体是。进而可画出从正面、左面看到的图形。
【详解】
【点睛】本题是考查从不同方向观察物体,关键是培养学生的观察能力和空间想象能力。
4.图见详解
【分析】从正面看到3列小正方形,左面2个,中间3个,右面1个,下齐;从左面看到3列,左面1个,中间2个,右面3个,下齐。
【详解】如图:
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
5.见详解
【详解】正方体有6个面,无盖的正方体有5个面,图中给出了15个方格,要剪成3个无盖正方体,需要把这些方格都用上。根据正方体的展开图的11种形式来求解,如下图:
把这15个小正方形分成三部分,使每部分都是正方体展开图的上述样式之一,且少一个正方形即可,所以可以得到如下的方案:
【点睛】本题主要考查正方体的展开图形式。
6.(1)见详解
(2)见详解
(3)见详解
(4)见详解
【分析】(1)延长线段AB到点D,使BD=AB=4个格,再连接CD;
(2)把三角尺的一条直角边与AB重合,沿AB及AB的延长线移动三角尺,当另一直角边经过点C时,沿这条直角边画直线交AB的延长线于点E,E为垂足;
(3)根据旋转的特征,将三角形CDE绕C点逆时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的三角形CD1E1;
(4)根据平移的特征,将三角形ABC的各顶点分别先向上平移2格,再向左平移1格,依次连接即可得到三角形A1B1C1。
【详解】如图:
【点睛】掌握作垂线、作旋转后的图形、作平移后的图形的作图方法是解题的关键。
7.见详解。
【分析】根据方格中的数字,我们可以确定这个几何体的摆法如图:,这个几何体从正面看,分为3层,最下层有3个小正方形,中间层有2个小正方形,最左边和最右边各1个,最上层有1个小正方形,靠右对齐;从左面看,分为3层,最下层有3个小正方形,中间层有2个小正方形,靠左对齐,最上层有1个小正方形,靠左对齐。据此完成作图。
【详解】作图如下:
【点睛】此题的解题关键是先根据小正方体个数确定几何体的摆法,再通过三视图的画法,作出从正面和从左面看到的图形。
8.(1)见详解
(2)见详解
(3)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴MN的对称点后,依次连接各点得到图形B。
(2)根据平移的特征,将图形A的各顶点分别向左平移4格,依次连接即可得到图形C。
(3)根据旋转的特征,将图形A绕点O按顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形D。
【详解】如图:
【点睛】掌握补全轴对称图形、作旋转后的图形、作平移后的图形的作图方法是解题的关键。
9.见详解。
【分析】(1)(2)在一个正方体中,与一个面相邻的有四个面,相对的只有一个面。根据正方体展开图的类型,前一个正方体都属于1-4-1型,通过这种类型的特征可得,与相对的面上是;与相对的面上是;与相对的面上是;
观察右侧展开图,如图:1和3相对,和4相对,和2相对,所以2是,4是,1是,3是;7和8相对,和5相对,和6相对,所以5是,6是,7是,8是;据此在右侧不同展开图的各个面上画出相应的图形。
【详解】作图如下:
【点睛】此题主要考查正方体展开图的特征,图形有难度,可以实际试一试用折纸的形式解题。
10.见详解
【分析】根据从上面看到的几何体的平面图,可以得出:从正面看有3列,共6个小正方体;从左往右,分别是3个、1个、2个;从左面看有3行,从左往右,分别是3个、2个、1个;据此画出从正面看、从左面看的平面图形。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
可以画出从正面和左面看到的图形:
【点睛】具备根据部分视图还原立体图形的能力,从而画出其他视图。
11.
【分析】每个小图形的位置按照逆时针的方向转动,圆、正方形、五角星不需要考虑方向,而三角形要考虑方向。
【详解】如图:
【点睛】本题最难判断的是三角形的朝向问题,可以根据这四幅图中三角形的方向互不相同来判断。
12.
【分析】每一幅图可以看成是前一幅图逆时针旋转得到,其中圆和正方形不需要考虑方向,另外两个图形需要考虑方向。
【详解】如图:
【点睛】本题较为复杂,不仅仅要考虑位置,还要考虑由于旋转所造成的方向的改变。
13.
【分析】观察题目给出的三幅图,发现每个小图形都是按照左上角→右上角→右下角→左下角这样的顺时针方向转动的,并且这里不用考虑转动引起的方向问题。
【详解】如图:
【点睛】本题较为简单,只需要考虑图形的转动,而不用考虑方向,相对是比较容易的。
14.见详解
【分析】每一个图形都按照顺时针方向转动,并且圆中的阴影也按照顺时针方向转动。
【详解】如图所示:
【点睛】对于这种旋转型找规律问题,既要考虑图形的位置,也要考虑图形内部的旋转。
15.
【分析】每幅图中左侧的图形不考虑颜色都是轴对称图形,左侧空白,右侧阴影;第一行,每幅图的右半部分是左图的空白部分顺时针旋转得到;第二行,每幅图的右半部分是左图的阴影部分翻转得到,按照这样的规律补全图形。
【详解】如图所示:
【点睛】平移、旋转、轴对称是最基础的图形变换,其基本特征要非常熟悉。
16.
【分析】仔细观察,发现本题不只是箭方向上有变化,箭尾“羽毛”数量上也有变化,在同一行中,每旋转90°,箭尾上的“羽毛”将减少一对,依照这个规律,空格中的箭,其尾部应没有“羽毛”,成了光秃秃的一支箭。
【详解】空格中应填:
【点睛】在求解图形找规律的问题时,不仅要考虑数量的要求,还有考虑方向、颜色等要求。
17.见详解
【分析】平移:在平面内,将一个图形上所有的点都按照某个直线方向做相同距离的移动,这样的图形运动称为平移;
旋转:物体围绕着某一点或轴进行不改变其大小和形状的圆周运动的现象就是旋转;
七巧板中有平行四边形、等腰直角三角形、正方形,通过平移或旋转后得到等腰梯形;据此解答。
【详解】把①②旋转后平移,做等腰梯形的两腰部分;再将③④⑤⑥⑦旋转后平移,组成一个正方形,摆在①和②之间,就构成了一个完整的等腰梯形。
【点睛】本题图形的变换过程较复杂,可先变化图案得到等腰梯形,再按变换的过程描述即可。
18.
【分析】根据长方体的特征,12条棱分为互相平行(相对)的3组,每组4条棱的长度相等,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。长方体的长、宽、高决定了长方体的形状和大小。能看见的棱画实线,看不见的画虚线。由此作图即可。
【详解】根据长方体的特征作图如下:
【点睛】此题主要考查长方体的特征、长方体立体图形的画法,明确长方体的长、宽、高决定了长方体的形状和大小。
19.;
【分析】如果从左面看到的是,说明这个立体图形只有一排,并且最高不过两个小正方体。
【详解】①我们可以让这个立体图形只有两列,每列只有两层,这样2×2=4(个);②我们可以使这个立体图形有三列,第一列有两层,第二列、第三列只有一层,这样2+1+1=4(个)。两种方法都满足条件4个小正方体。
【点睛】动手画一画,也许复杂的题意就不再令人迷惑。此外,还要对三视图较为熟悉,懂得左视图就是从左面观察立体图形时看到的形状。
20.(答案不唯一)
【分析】从物体的前面、左面、上面这三个方向观看一个立体图形,就会得到描述这个立体图形的三张平面图形,简称为三视图。三视图可以完整地刻画一个立体图形的形状、大小、方位等所有特征信息。
【详解】作图如下:
【点睛】本题考查了从不同方向观察几何体,要综合分析。
21.见详解
【分析】结合图1、图2分析,从正面观察所给几何体,看到3列小正方形,左面一列3个,中间1个,右面2个;从左面看到两列小正方形,左面一列3个,右面一列2个,据此画图即可。
【详解】答案如图所示:
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
22.
【分析】观察图形可知,图形一共有3层,上层有1个正方体,中层有1个正方体,下层有5个正方体,由此即可解答。
【详解】从不同位置观察同一个物体所看到的图形。
【点睛】此题考查了从不同方向观察图形的方法,意在培养学生的空间想象的能力。
23.见详解
【详解】如下图:
24.
【解析】略
25.
【解析】略
26.
【详解】略
27.三角形画法不唯一
【详解】略
28.
【分析】正方体的展开图类型有四类:第一类:中间四连方,两侧各一个;第二类:中间三连方,两侧各一、二个;第三类:中间二连方,两侧各两个;第四类:两排各3个;
根据题意可知,一个无盖正方体展开图有5个正方形的面,15个小正方形刚好分成3个无盖的正方体的展开图,据此作图即可.
【详解】根据分析,解答如下:
.
29.见详解
【分析】平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移不改变图形的大小、形状和方向。平移两要素:方向和距离。
旋转:在平面内,将一个图形绕一个定点沿顺时针或逆时针方向转动一个角度,这样的图形运动称为旋转,这个固定点称为旋转中心,旋转的角度称为旋转角。旋转不改变图形的形状和大小。旋转三要素:旋转中心、方向和角度。
轴对称:如果两个图形沿着一条直线折叠后能够完全重合,那么称这两个图形关于这条直线对称,这条直线叫作它们的对称轴。
据此设计图案。
【详解】将这个图形往右平移一个宽度、两个宽度,得到的图形如下:
将这个图形沿锐角顶点顺时针旋转90°、180°、270°,得到的图形如下:
先确定对称轴,然后把图形沿着对称轴向右折叠或向下折叠,得到的图形如下图:
(答案不唯一)
【点睛】解决本题的关键是需要根据平移、旋转、轴对称的要素,作相对应的图形运动。
30.
【详解】考查了轴对称图形的画法
31.见解析
【分析】每个无盖正方体由五个面组成,根据正方体展开图的11种特征,即可这张硬纸板剪成三块,使每一块都可以折成一个无盖的正方体。
【详解】根据正方体展开图的11种特征,即可把这个长方形硬纸板分成三块(红、绿、蓝),每一块都可以折成一个无盖的正方体;如下图:
【点睛】要根据正方体展开图的特征来剪,意在培养学生的观察能力和空间想象能力。
32.(9,2)(9,8)
【详解】试题分析:①因为直角三角形ABC的面积是6平方厘米,即它的底乘高是12,按底乘高是12来找B、C点的坐标;(答案不唯一)
②把底是2,高是6的三角形的横的直角边绕点A顺时针转90°,变成竖的,竖边的直角边绕点A顺时针转90°变成横的,然后把两端点连接;
③只要这个梯形的上下底之和与高的积是12即可,如图:上底是1厘米,下底是3 厘米,高是3厘米,这个梯形的面积就是6平方厘米.
解答:解:画图如下:
点评:此题考查了直角三角形的面积算法,梯形面积的算法,及对坐标的表示方法.
33.(1)无数;画图见详解;
(2)见详解;
(3)见详解
【分析】(1)以线段AB为一条边,根据三角形的面积公式:三角形的面积=底×高÷2,面积为8平方厘米的三角形的底×高=8×2=16,据此可知这个三角形只要底和高的乘积是16即可,即点C的位置有无数种可能,已知AB是4cm,则可以在AB上方找出一个到AB的距离是4的点为点C,并画出图形①;
(2)根据旋转的性质,分别找出三角形ABC绕着点A逆时针旋转90°的对应点,顺次连接各点即可得到图②;
(3)如果一个图形沿着一条直线折叠,直线两边的部分能够完全重合,则这样的图形就是轴对称图形,据此先先画出一条直线作为对称轴,再画出对称图形即可。
【详解】(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(1)(2)(3)画图如下:
(画法不唯一)
34.见详解
【分析】正方体的展开图有11种特征,分四种类型。从题意可知:无盖正方体的表面展开图最接近正方体的展开图中的“231”型和“33” 型(如下图) :
据此添加一个正方形即可折叠后能够围成一个封闭的正方体。
【详解】根据分析可得:
35.(1)见详解
(2)顺;90;上;3
【分析】(1)根据旋转的三角形,旋转中心是点O,旋转角度是90°,旋转方向是顺时针,点O不变,图形的各个部分顺时针旋转90°,可作出旋转后的图形;
(2)图②可以以点M为旋转中心,各个部分按照顺时针90°或逆时针270°确定方向,再将各点向上移动3格再依次连接成图即可。
【详解】(1)由分析可作图:
(2)将图②先绕点M顺时针旋转90°,再向上平移3格得到图③。
36.见详解
【分析】(1)实线表示男生数据,虚线表示女生数据;根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来,标记数据即可。
(2)根据折线统计图的变化进行分析,折线往上表示上升趋势,折线往上坡度越陡表示长高越快,据此写出几条结论即可。
【详解】(1)某地区7~13岁男、女生平均身高统计图
(2)在7~13岁之间,男女生身高均呈现均匀上升的趋势,男生在9岁~13岁长高比较快,女生在8岁~13岁长高比较快,且男女生增长的情况相差不大(答案不唯一)。
37.(1)(2)见详解
【分析】(1)根据旋转的特征,图形①绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
(2)旋转的意义:在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。
决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),据此解答。
【详解】(1)如图:
(2)图形①绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形②。
38.见详解
【分析】长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,观察长方体可知,前后面最大,左右面其次,上下面最小,据此标出长方体的各面。
【详解】
第1页,共2页
第1页,共2页
能力作图题
学校:___________姓名:___________班级:___________
作图题
1.如图是由若干个完全相同的小正方体堆成的几何体:
(1)画出该几何体的三视图。
(2)在该几何体的表面刷上黄色的漆,则在所有的小正方体中,有____个正方体的三个面是黄色。
(3)若现在你手头还有一个相同的小正方体,在不考虑颜色的情况下,该正方体应放在何处才能使堆成的几何体的三视图不变?直接在图中添上该正方体。
(4)若考虑颜色,要使三视图不变,则新添的正方体至少要在____个面上着色。
2.用同样的小正方体搭一个几何体,从上面看到的图形如图所示(方格中的数字表示该位置小正方体的个数),请你分别画出这个几何体从前面和左面看到的图形。
3.一个几何体由几个相同的小正方体搭成,从上面看到的图形如右图所示,小正方形上的数字表示在该位置上小正方体的个数。请分别画出从正面、左面看这个几何体得到的图形。
4.如图是一个由小立方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上小正方体的个数,请你分别画出这个儿何体从正面和左面看到的图形。
从正面看 从左面看
5.把如图剪成三部分,使每一部分都可以折成一个无盖的正方体。
6.请在方格纸上按要求画出相应的图形:
(1)延长线段AB到点D,使BD=AB,再画线段CD;
(2)过点C画AB的垂线,垂足为E;
(3)将三角形CDE绕C点逆时针旋转90°,得到三角形CD1E1。
(4)将三角形ABC向上平移2格,再向左平移1格,得到三角形A1B1C1。
7.如图(1)是从上面看一些小正方体所搭几何体的平面图,方格中的数字表示该位置的小正方体个数。请你在图(2)的方格纸中分别画出这个几何体从正面和左面看到的图形。
图(1) 图(2)
8.(1)以直线MN为对称轴,作图形A的轴对称图形,得到图形B。
(2)将图形A向左平移4格,得到图形C。
(3)将图形A绕点O按顺时针方向旋转90°,得到图形D。
9.一个正方体的六个面上分别画有○、●、□、 、△、▲,请根据左侧展开图的各个面的图形,在右侧不同展开图的各个面上画出相应的图形。
10.如图是从上面看到所搭几何体的平面图,方格中数字表示该位置的小正方体个数。请在下图方格中分别画出从正面和左面看到的图形。
11.下列图形的变化规律,在空格内画出适当的图形。
12.按图形的变化规律,接着画。
13.按图形的变化规律,接着画。
14.观察下面图形,并按其变化规律在“?”处填上合适的图形。
15.仔细观察下图中图形的变化规律,并在“?”处填入合适的图形。
16.按顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形。
17.画一画:通过旋转、平移将左边的七巧板拼成一个等腰梯形。
18.下面是李红同学想要画的两个长方体,但还没完成,请你把它们补充完整。
19.如果从左面看到的是,用4个小正方体可以怎样摆?先摆一摆,再画出立体图(至少画2种)。
20.根据下面从不同方向看到的图形画出立体图形。
从上面看 从正面看 从左面看
21.用正方体积木搭了一个几何体,从上面看到的图形是图1。图2中小正方形上面的数字表示在这个位置上所用的小正方体的个数。请画出从正面和左面看到的图形。
22.下面是从不同位置观察同一个物体所看到的图形,请把它摆出来。(画一画)
23.用6个正方体搭一搭3种使正面看到的形状是的图形,画出它们的三视图。
24.观察一个立体图形,从上面看到的图形如图所示,小正方形内的数字表示在这个位置上所用的小正方体的个数。请把从正面、左面看到的图形在方格纸上画出来。
25.根据从不同方向看到的平面图形,用小正方体摆出立体图形。
26.以O点为顶点画一个面积是4cm2的四边形(1小格为1cm2),再画出绕O点逆时针旋转90°后的图形.
27.(1)将图形A绕点O逆时针旋转90度,得到图形B。
(2)画一个和图形A面积相等的三角形。
28.有一张长方形硬纸,正好分成15个小正方形.数学老师想用这张硬纸做3个无盖的正方体盒子作为教具使用.请你用不同颜色的笔画出分割图,要求折成每个正方体的5个小正方形相连,折起来正好是一个无盖的正方体纸盒.请你试试看!
29.请你将下面的图形利用平移、旋转和轴对称变换分别设计图案。
30.请在格子里涂黑,使得上图成为一个轴对称图形
31.如图是一张长方形的硬纸板,请你沿着图中的线把这张硬纸板剪成三块,使每一块都可以折成一个无盖的正方体,该怎样剪?在图中画出来。
32.如图中有一个面积是6cm2的直角三角形ABC. (图中每个方格的面积代表1cm2).A点在(7,2),你认为B、C点可能在( , )和( , ).
①画出三角形ABC.②把这个三角形绕A点顺时针旋转90°,画出旋转后的图形.
③画一个和三角形ABC面积相等的梯形.
33.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
34.下图实线部分都是在白纸上面的无盖正方体的表面展开图,请你设计三种不同的方法,在图中添加一个正方形(涂色表示),使新图形剪下折叠后能够围成一个封闭的正方体。
35.(1)画出图①绕点O顺时针旋转90°后的图形,并在图中标出点A的对应点。
(2)将图②先绕点M( )时针旋转( )°,再向( )平移( )格得到图③。
36.下面是某地区7~13岁男、女生平均身高统计图。(单位:厘米)
年龄 7岁 8岁 9岁 10岁 11岁 12岁 13岁
男生 125 132 133 140 145 150 157
女生 123 127 135 141 145 152 156
(1)请根据统计表绘制复式折线统计图。
(2)比较男生与女生平均身高的变化情况,你能得出什么结论?
37.
(1)画出图①绕O点逆时针旋转90°后的图形。
(2)说一说,图①可以通过怎样的运动得到图②。
38.在下面展开图上用“上、下、左、右、前、后”标出长方体的各面。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第1页,共3页
试卷第1页,共3页
参考答案
1.(1)作图见详解;
(2)1;
(3)见详解;
(4)3
【分析】(1)主视图:从正面看,第一列最高是3层,第二列最高是2层,第三列最高是1层,所以主视图是三列,第一列3个正方形,第二列2个正方形,第三列1个正方形(从下往上对齐排列)。
左视图:从左面看,第一列最高是3层,第二列最高是2层,所以左视图是三列,第一列3个正方形,第二列2个正方形,第三列1个正方形(从下往上对齐排列)。
俯视图:从上面看,第一列3个正方形,第二列2个正方形,第三列1个正方形(从左往右对齐排列)。
(2)三个面是黄色的小正方体位置具有特定规律,通常在几何体的棱上且不处于顶点位置(顶点位置的小正方体是三个以上面外露) 。我们对该几何体的每一个小正方体进行位置分析。从底层开始看,再看中层和上层,逐一判断每个小正方体露出的面数。经过仔细观察,发现只有处于特定棱中间位置的小正方体才是三个面外露被刷成黄色。
(3)要使新添加一个小正方体后三视图不变,就意味着新添加的小正方体不能改变从正面、左面和上面观察到的形状。这就要求新添加的小正方体要放在原几何体中已有的小正方体能够遮挡住的位置,也就是放在原几何体的内部且不改变外部轮廓。比如放在特定棱中间位置的小正方体的上面,从正面看,挡住了原来的小正方体的但是不改变主视图形状;从左面看,被其他小正方体遮挡;从上面看,同样不会改变整体的形状布局。
(4)若考虑颜色且要使三视图不变,新添的正方体要与周围环境融合,不能因为颜色差异而改变从三个方向观察到的形状。如果新正方体有过多未着色的面,就可能在某个视图方向上显示出与原几何体不同的样子。当新正方体至少在3个面上着色时,无论从正面、左面还是上面看,都能与原几何体的颜色和形状布局相匹配,不会改变三视图。
【详解】(1)
(2)1个,如图所示,
在该几何体的表面刷上黄色的漆,则在所有的小正方体中,有1个正方体的三个面是黄色。
(3)在特定棱中间位置的小正方体的上面添加一个小正方体(可在图上对应位置画出)。
(4)要使三视图不变,则新添的正方体至少要在3个面上着色。
2.见详解
【分析】从前面看到三竖列,第一竖列有3个小正方形,第二竖列有1个小正方形,第三竖列有2个小正方形;
从左面看到三竖列,第一竖列有3个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形。
【详解】
【点睛】本题考查学生对立体物体分别从前、左、上面观察物体的能力,并能想象物体摆放的位置,发展空间想象力。
3.见详解
【分析】
分析:通过观察从上面看到的图形及所给条件发现,这个几何体分成上下两层。其中底层有4个小正方体,拼成的形状是,左列最前面的小正方体,上面摆放着1个小正方体,右列小正方体上面也摆放着1个小正方体,因此搭成的几何体是。进而可画出从正面、左面看到的图形。
【详解】
【点睛】本题是考查从不同方向观察物体,关键是培养学生的观察能力和空间想象能力。
4.图见详解
【分析】从正面看到3列小正方形,左面2个,中间3个,右面1个,下齐;从左面看到3列,左面1个,中间2个,右面3个,下齐。
【详解】如图:
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
5.见详解
【详解】正方体有6个面,无盖的正方体有5个面,图中给出了15个方格,要剪成3个无盖正方体,需要把这些方格都用上。根据正方体的展开图的11种形式来求解,如下图:
把这15个小正方形分成三部分,使每部分都是正方体展开图的上述样式之一,且少一个正方形即可,所以可以得到如下的方案:
【点睛】本题主要考查正方体的展开图形式。
6.(1)见详解
(2)见详解
(3)见详解
(4)见详解
【分析】(1)延长线段AB到点D,使BD=AB=4个格,再连接CD;
(2)把三角尺的一条直角边与AB重合,沿AB及AB的延长线移动三角尺,当另一直角边经过点C时,沿这条直角边画直线交AB的延长线于点E,E为垂足;
(3)根据旋转的特征,将三角形CDE绕C点逆时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的三角形CD1E1;
(4)根据平移的特征,将三角形ABC的各顶点分别先向上平移2格,再向左平移1格,依次连接即可得到三角形A1B1C1。
【详解】如图:
【点睛】掌握作垂线、作旋转后的图形、作平移后的图形的作图方法是解题的关键。
7.见详解。
【分析】根据方格中的数字,我们可以确定这个几何体的摆法如图:,这个几何体从正面看,分为3层,最下层有3个小正方形,中间层有2个小正方形,最左边和最右边各1个,最上层有1个小正方形,靠右对齐;从左面看,分为3层,最下层有3个小正方形,中间层有2个小正方形,靠左对齐,最上层有1个小正方形,靠左对齐。据此完成作图。
【详解】作图如下:
【点睛】此题的解题关键是先根据小正方体个数确定几何体的摆法,再通过三视图的画法,作出从正面和从左面看到的图形。
8.(1)见详解
(2)见详解
(3)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴MN的对称点后,依次连接各点得到图形B。
(2)根据平移的特征,将图形A的各顶点分别向左平移4格,依次连接即可得到图形C。
(3)根据旋转的特征,将图形A绕点O按顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形D。
【详解】如图:
【点睛】掌握补全轴对称图形、作旋转后的图形、作平移后的图形的作图方法是解题的关键。
9.见详解。
【分析】(1)(2)在一个正方体中,与一个面相邻的有四个面,相对的只有一个面。根据正方体展开图的类型,前一个正方体都属于1-4-1型,通过这种类型的特征可得,与相对的面上是;与相对的面上是;与相对的面上是;
观察右侧展开图,如图:1和3相对,和4相对,和2相对,所以2是,4是,1是,3是;7和8相对,和5相对,和6相对,所以5是,6是,7是,8是;据此在右侧不同展开图的各个面上画出相应的图形。
【详解】作图如下:
【点睛】此题主要考查正方体展开图的特征,图形有难度,可以实际试一试用折纸的形式解题。
10.见详解
【分析】根据从上面看到的几何体的平面图,可以得出:从正面看有3列,共6个小正方体;从左往右,分别是3个、1个、2个;从左面看有3行,从左往右,分别是3个、2个、1个;据此画出从正面看、从左面看的平面图形。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
可以画出从正面和左面看到的图形:
【点睛】具备根据部分视图还原立体图形的能力,从而画出其他视图。
11.
【分析】每个小图形的位置按照逆时针的方向转动,圆、正方形、五角星不需要考虑方向,而三角形要考虑方向。
【详解】如图:
【点睛】本题最难判断的是三角形的朝向问题,可以根据这四幅图中三角形的方向互不相同来判断。
12.
【分析】每一幅图可以看成是前一幅图逆时针旋转得到,其中圆和正方形不需要考虑方向,另外两个图形需要考虑方向。
【详解】如图:
【点睛】本题较为复杂,不仅仅要考虑位置,还要考虑由于旋转所造成的方向的改变。
13.
【分析】观察题目给出的三幅图,发现每个小图形都是按照左上角→右上角→右下角→左下角这样的顺时针方向转动的,并且这里不用考虑转动引起的方向问题。
【详解】如图:
【点睛】本题较为简单,只需要考虑图形的转动,而不用考虑方向,相对是比较容易的。
14.见详解
【分析】每一个图形都按照顺时针方向转动,并且圆中的阴影也按照顺时针方向转动。
【详解】如图所示:
【点睛】对于这种旋转型找规律问题,既要考虑图形的位置,也要考虑图形内部的旋转。
15.
【分析】每幅图中左侧的图形不考虑颜色都是轴对称图形,左侧空白,右侧阴影;第一行,每幅图的右半部分是左图的空白部分顺时针旋转得到;第二行,每幅图的右半部分是左图的阴影部分翻转得到,按照这样的规律补全图形。
【详解】如图所示:
【点睛】平移、旋转、轴对称是最基础的图形变换,其基本特征要非常熟悉。
16.
【分析】仔细观察,发现本题不只是箭方向上有变化,箭尾“羽毛”数量上也有变化,在同一行中,每旋转90°,箭尾上的“羽毛”将减少一对,依照这个规律,空格中的箭,其尾部应没有“羽毛”,成了光秃秃的一支箭。
【详解】空格中应填:
【点睛】在求解图形找规律的问题时,不仅要考虑数量的要求,还有考虑方向、颜色等要求。
17.见详解
【分析】平移:在平面内,将一个图形上所有的点都按照某个直线方向做相同距离的移动,这样的图形运动称为平移;
旋转:物体围绕着某一点或轴进行不改变其大小和形状的圆周运动的现象就是旋转;
七巧板中有平行四边形、等腰直角三角形、正方形,通过平移或旋转后得到等腰梯形;据此解答。
【详解】把①②旋转后平移,做等腰梯形的两腰部分;再将③④⑤⑥⑦旋转后平移,组成一个正方形,摆在①和②之间,就构成了一个完整的等腰梯形。
【点睛】本题图形的变换过程较复杂,可先变化图案得到等腰梯形,再按变换的过程描述即可。
18.
【分析】根据长方体的特征,12条棱分为互相平行(相对)的3组,每组4条棱的长度相等,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。长方体的长、宽、高决定了长方体的形状和大小。能看见的棱画实线,看不见的画虚线。由此作图即可。
【详解】根据长方体的特征作图如下:
【点睛】此题主要考查长方体的特征、长方体立体图形的画法,明确长方体的长、宽、高决定了长方体的形状和大小。
19.;
【分析】如果从左面看到的是,说明这个立体图形只有一排,并且最高不过两个小正方体。
【详解】①我们可以让这个立体图形只有两列,每列只有两层,这样2×2=4(个);②我们可以使这个立体图形有三列,第一列有两层,第二列、第三列只有一层,这样2+1+1=4(个)。两种方法都满足条件4个小正方体。
【点睛】动手画一画,也许复杂的题意就不再令人迷惑。此外,还要对三视图较为熟悉,懂得左视图就是从左面观察立体图形时看到的形状。
20.(答案不唯一)
【分析】从物体的前面、左面、上面这三个方向观看一个立体图形,就会得到描述这个立体图形的三张平面图形,简称为三视图。三视图可以完整地刻画一个立体图形的形状、大小、方位等所有特征信息。
【详解】作图如下:
【点睛】本题考查了从不同方向观察几何体,要综合分析。
21.见详解
【分析】结合图1、图2分析,从正面观察所给几何体,看到3列小正方形,左面一列3个,中间1个,右面2个;从左面看到两列小正方形,左面一列3个,右面一列2个,据此画图即可。
【详解】答案如图所示:
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
22.
【分析】观察图形可知,图形一共有3层,上层有1个正方体,中层有1个正方体,下层有5个正方体,由此即可解答。
【详解】从不同位置观察同一个物体所看到的图形。
【点睛】此题考查了从不同方向观察图形的方法,意在培养学生的空间想象的能力。
23.见详解
【详解】如下图:
24.
【解析】略
25.
【解析】略
26.
【详解】略
27.三角形画法不唯一
【详解】略
28.
【分析】正方体的展开图类型有四类:第一类:中间四连方,两侧各一个;第二类:中间三连方,两侧各一、二个;第三类:中间二连方,两侧各两个;第四类:两排各3个;
根据题意可知,一个无盖正方体展开图有5个正方形的面,15个小正方形刚好分成3个无盖的正方体的展开图,据此作图即可.
【详解】根据分析,解答如下:
.
29.见详解
【分析】平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移不改变图形的大小、形状和方向。平移两要素:方向和距离。
旋转:在平面内,将一个图形绕一个定点沿顺时针或逆时针方向转动一个角度,这样的图形运动称为旋转,这个固定点称为旋转中心,旋转的角度称为旋转角。旋转不改变图形的形状和大小。旋转三要素:旋转中心、方向和角度。
轴对称:如果两个图形沿着一条直线折叠后能够完全重合,那么称这两个图形关于这条直线对称,这条直线叫作它们的对称轴。
据此设计图案。
【详解】将这个图形往右平移一个宽度、两个宽度,得到的图形如下:
将这个图形沿锐角顶点顺时针旋转90°、180°、270°,得到的图形如下:
先确定对称轴,然后把图形沿着对称轴向右折叠或向下折叠,得到的图形如下图:
(答案不唯一)
【点睛】解决本题的关键是需要根据平移、旋转、轴对称的要素,作相对应的图形运动。
30.
【详解】考查了轴对称图形的画法
31.见解析
【分析】每个无盖正方体由五个面组成,根据正方体展开图的11种特征,即可这张硬纸板剪成三块,使每一块都可以折成一个无盖的正方体。
【详解】根据正方体展开图的11种特征,即可把这个长方形硬纸板分成三块(红、绿、蓝),每一块都可以折成一个无盖的正方体;如下图:
【点睛】要根据正方体展开图的特征来剪,意在培养学生的观察能力和空间想象能力。
32.(9,2)(9,8)
【详解】试题分析:①因为直角三角形ABC的面积是6平方厘米,即它的底乘高是12,按底乘高是12来找B、C点的坐标;(答案不唯一)
②把底是2,高是6的三角形的横的直角边绕点A顺时针转90°,变成竖的,竖边的直角边绕点A顺时针转90°变成横的,然后把两端点连接;
③只要这个梯形的上下底之和与高的积是12即可,如图:上底是1厘米,下底是3 厘米,高是3厘米,这个梯形的面积就是6平方厘米.
解答:解:画图如下:
点评:此题考查了直角三角形的面积算法,梯形面积的算法,及对坐标的表示方法.
33.(1)无数;画图见详解;
(2)见详解;
(3)见详解
【分析】(1)以线段AB为一条边,根据三角形的面积公式:三角形的面积=底×高÷2,面积为8平方厘米的三角形的底×高=8×2=16,据此可知这个三角形只要底和高的乘积是16即可,即点C的位置有无数种可能,已知AB是4cm,则可以在AB上方找出一个到AB的距离是4的点为点C,并画出图形①;
(2)根据旋转的性质,分别找出三角形ABC绕着点A逆时针旋转90°的对应点,顺次连接各点即可得到图②;
(3)如果一个图形沿着一条直线折叠,直线两边的部分能够完全重合,则这样的图形就是轴对称图形,据此先先画出一条直线作为对称轴,再画出对称图形即可。
【详解】(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(1)(2)(3)画图如下:
(画法不唯一)
34.见详解
【分析】正方体的展开图有11种特征,分四种类型。从题意可知:无盖正方体的表面展开图最接近正方体的展开图中的“231”型和“33” 型(如下图) :
据此添加一个正方形即可折叠后能够围成一个封闭的正方体。
【详解】根据分析可得:
35.(1)见详解
(2)顺;90;上;3
【分析】(1)根据旋转的三角形,旋转中心是点O,旋转角度是90°,旋转方向是顺时针,点O不变,图形的各个部分顺时针旋转90°,可作出旋转后的图形;
(2)图②可以以点M为旋转中心,各个部分按照顺时针90°或逆时针270°确定方向,再将各点向上移动3格再依次连接成图即可。
【详解】(1)由分析可作图:
(2)将图②先绕点M顺时针旋转90°,再向上平移3格得到图③。
36.见详解
【分析】(1)实线表示男生数据,虚线表示女生数据;根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来,标记数据即可。
(2)根据折线统计图的变化进行分析,折线往上表示上升趋势,折线往上坡度越陡表示长高越快,据此写出几条结论即可。
【详解】(1)某地区7~13岁男、女生平均身高统计图
(2)在7~13岁之间,男女生身高均呈现均匀上升的趋势,男生在9岁~13岁长高比较快,女生在8岁~13岁长高比较快,且男女生增长的情况相差不大(答案不唯一)。
37.(1)(2)见详解
【分析】(1)根据旋转的特征,图形①绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
(2)旋转的意义:在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。
决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),据此解答。
【详解】(1)如图:
(2)图形①绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形②。
38.见详解
【分析】长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,观察长方体可知,前后面最大,左右面其次,上下面最小,据此标出长方体的各面。
【详解】
第1页,共2页
第1页,共2页
同课章节目录
