浙江省温州市2024-2025学年第二学期七年级期末数学模拟卷(含答案)
文档属性
| 名称 | 浙江省温州市2024-2025学年第二学期七年级期末数学模拟卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 228.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:11:52 | ||
图片预览




文档简介
浙江省温州市2024学年第二学期七年级期末模拟卷
数学试题卷
全卷共23题,满分100分,考试时间90分钟.
一、选择题(共10小题,每小题3分,共30分)
1.分式有意义,则x的取值范围为( )
A. B. C.且 D.x为一切实数
2. 计算的结果是( )
A.-9 B.-6 C. D.
3.下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
4.下列计算正确的是( )
A. B. C. D.
5.如图是“垃圾入桶”标志及垃圾桶的平面示意图,若,,则的度数是( )
A. B. C. D.
6.已知,,则的值为( )
A.5 B.7 C.11 D.13
7.照相机成像应用了一个重要原理,用公式表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离。已知f,v,则u=( )
A. B. C. D.
8.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重,问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
9.已知分式(a,b为常数),的部分取值及对应分式的值如下表,则的值是( )
-3 3
无意义 0 2
A.-2 B.-5 C.3 D.4
10.如图,将长方形ABCD的一角折叠,以CE(点在AB上,不与A,B重合)为折痕,得到,连结,设的度数分别为,若,则之间的关系是( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.分解因式:
12.如图,将边长为6的向右平移个单位得到,若,则 .
13.若关于x,y的二元一次方程组的解也是的解,则k的值为 .
14.《义务教育劳动课程标准年版》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有45名学生,其中学会炒菜的学生频率是,则该班学会炒菜的学生有 名.
15.已知,则 .
16.观察下列等式,解答后面的问题:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
(1)第5个等式是 ;
(2)根据上述规律猜想第n个等式是 (用含n的等式表示).
三、解答题(共8题,共52分)
17.(本题8分)
(1) (2)
18.(本题6分)先化简,再求值:,并从,,中选一个合适的数作为的值代入求值.
19.(本题6分)近年来,研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件。某校学生会负责该校学生的一次研学活动,为设计出同学们最感兴趣的研学路线,随机抽取了部分学生进行问卷调查,并将调查结果绘制成如下不完整的统计图。
调查问卷 1.你最感兴趣的研学类型是 ▲ (单选)。 A.研学+历史 B.研学+科学 C.研学+艺术 D.研学+农业 E.研学+外文 F.研学+工业
(1)请补全条形统计图,并写出扇形统计图中C,D的百分比。
(2)“B”与“C”所在的扇形圆心角的度数和为 °.
(3)若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数。
20.(本题7分)如图,已知AB//CD,AD平分∠EAC,∠B=∠D.
(1)请说明AD//BC:
(2)若∠DAC=(2x+15)°,∠B=(105-3x)°,求∠D的度数.
21.(本题7分)已知a,b均为不等于0的实数,我们定义新运算“※”:.例如:.
(1)验证新运算“※”是否满足乘法交换律?若满足,请写出推导过程;若不满足,请举反例说明.
(2)计算:.
(3)当时,若,尝试求出x的值.
22.(本题8分)根据以下信息,探索解决问题:
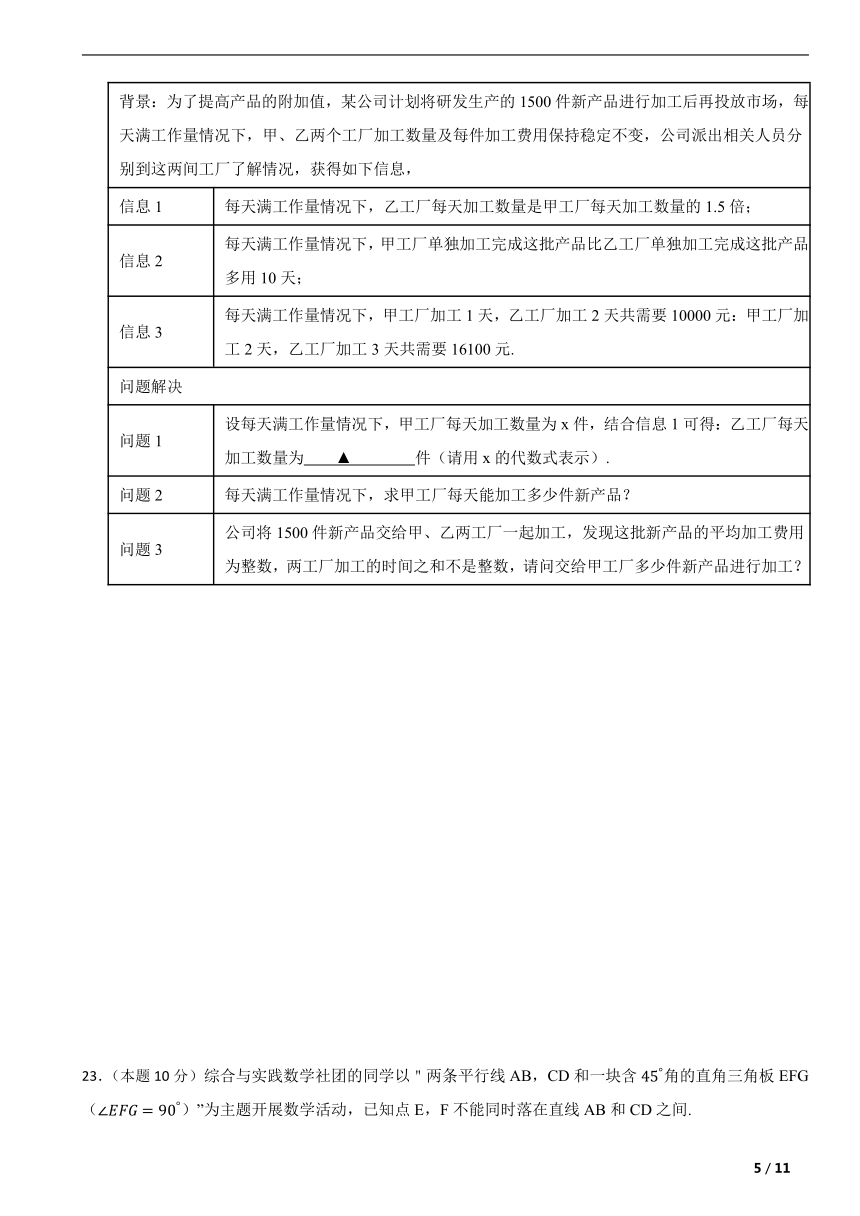
背景:为了提高产品的附加值,某公司计划将研发生产的1500件新产品进行加工后再投放市场,每天满工作量情况下,甲、乙两个工厂加工数量及每件加工费用保持稳定不变,公司派出相关人员分别到这两间工厂了解情况,获得如下信息,
信息1 每天满工作量情况下,乙工厂每天加工数量是甲工厂每天加工数量的1.5倍;
信息2 每天满工作量情况下,甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息3 每天满工作量情况下,甲工厂加工1天,乙工厂加工2天共需要10000元:甲工厂加工2天,乙工厂加工3天共需要16100元.
问题解决
问题1 设每天满工作量情况下,甲工厂每天加工数量为x件,结合信息1可得:乙工厂每天加工数量为 ▲ 件(请用x的代数式表示).
问题2 每天满工作量情况下,求甲工厂每天能加工多少件新产品?
问题3 公司将1500件新产品交给甲、乙两工厂一起加工,发现这批新产品的平均加工费用为整数,两工厂加工的时间之和不是整数,请问交给甲工厂多少件新产品进行加工?
23.(本题10分)综合与实践数学社团的同学以"两条平行线AB,CD和一块含角的直角三角板EFG()”为主题开展数学活动,已知点E,F不能同时落在直线AB和CD之间.
(1)观察猜想:如图1,把三角板的角的顶点E,G分别放在AB,CD上,若,则的度数为 ;(直接写出结论,不说明理由)
(2)类比探究:如图2,把三角板的锐角顶点放在CD上,且保持不动,绕点转动三角板,若点恰好落在AB和CD之间,且AB与EF所夹锐角为,求的度数;
(3)解决问题:把三角板的锐角顶点放在CD上,在绕点旋转三角板的过程中,若存在,请直接写出射线GF与AB相交所夹锐角的度数.
参考答案
1.B
2.D
3.C
4.C
5.B
6.D
7.A
8.A
9.B
10.B
11.(x+2)(x-2)
12.2
13.4
14.18
15.3
16.;
17.(1)解: ,
②-①得:4x=28,
x=7,
把 x=7代入①得y=5,
解得.
(2)解:去分母得: ,
去括号得:3x+3-4x=x-1,
移项得:3x-4x-x=-1-3,
合并同类项-2x=-4,
系数化为1得: ,
经检验 原方程的解.
18.解:
;
∵,
∴当时,原式.
19.(1)解:样本容量为:100÷25%=400,
∴C所占百分比为:,
∴D所占百分比为:1-25%-18%-20%-15%-12%=10%,
D的人数为:400×10%=40,
补全条形统计图如下:
(2)136.8
(3)解:4500×25%=1125(人),
答:估计该校对“研学+历史”最感兴趣的学生人数约1125名.
20.(1)证明:,
,
又,
,
(2)解:∵AD 平分∠EAC,
∴∠EAD=∠DAC=(2x+15)°
由(1) 可知: ∠EAD=∠B,
∴2x+15=105-3x,
解得:x=18,
∴∠B=(105-3x)° =(105-3×18)° =51°,
∴∠D=∠B=51°,
21.(1)解:新运算“※”满足乘法交换律,理由如下:,
,
;
(2)解:
;
(3)解:,
当时,,
即:,
解得:,
经检验,是原分式方程的解,
的值为.
22.解:问题1:1.5x;
问题2:根据题意得:,
解得:x=50,经检验,x=50是所列方程的解,其符合题意.
答:每天满工作量情况下,甲工厂每天能加工50件新产品;
问题3:设每天满工作量情况下,甲工厂加工1天所需费用为m元,乙工厂加工1天所需费用为n元,
根据题意得:,解得:,
∴每天满工作量情况下,甲工厂加工新产品的单价为2200÷50=44(元/件)
乙工厂加工新产品的单价为3900÷(1.5×50)=52(元/件).
设交给甲工厂y件新产品进行加工,则交给乙工厂(1500-y)件新产品进行加工,
根据题意得:,且n为整数)
∴.
∵y为正整数,
∴n可以为46, 48, 50,
当n=46时,y=(52-46)=1125,
此时(天),符合题意;
当时,,
此时(天),不符合题意,舍去;
当时,,
此时(天),符合题意.
答:交给甲工厂1125或375件新产品进行加工.
23.(1)100°
(2)解:过点E作EN//CD,如图1所示:
依题意得:∠BME=20°,∠FEG=∠FGE=45°,
∵AB//CD,EN//CD,
∴AB//EN//CD,
∴∠NEM=∠BME=20°,
∴∠NEG=∠FEG-∠NEM=45°-20°=25°,
∴∠DGE=∠NEG=25°,
∴∠FGD=∠FGE+∠DGE=45°+25°=70°,
∴∠FGC=180°-∠FGD=180°-70°=110°
(3)解:存在,射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
分两种情况讨论如下:
①当点E在CD上方时,设AB交GF于点H,如图2所示:
依题意得:∠FEG=∠FGE=45°,
设∠DGE=α,则∠FGC=5∠DGE=5α,
∵∠DGE+∠FGE+∠FGC=180°,
∴5α+45°+α=180,
解得:α=22.5°,
∴∠FGC=5α=112.5°,
∵AB//CD,
∴∠AHG=180°-∠FGC=180°-112.5°=67.5°
②当点E在CD下方时,延长GF交AB于点H,如图3所示:
依题意得:∠FGE=45°,
设∠EGD=β,则∠FGC=5∠DGE=5β,
∴∠FGD=∠FGE-∠EGD=45°-β,
∵∠FGC+∠FGD=180°,
∴5β+45°-β=180°,
解得:β=33.75°,
∴∠FGC=5β=168.75°
∵AB//CD,
∴∠AHG=180°-∠FGC=180°-168.75°=11.25°
综上所述:射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
1 / 1
数学试题卷
全卷共23题,满分100分,考试时间90分钟.
一、选择题(共10小题,每小题3分,共30分)
1.分式有意义,则x的取值范围为( )
A. B. C.且 D.x为一切实数
2. 计算的结果是( )
A.-9 B.-6 C. D.
3.下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
4.下列计算正确的是( )
A. B. C. D.
5.如图是“垃圾入桶”标志及垃圾桶的平面示意图,若,,则的度数是( )
A. B. C. D.
6.已知,,则的值为( )
A.5 B.7 C.11 D.13
7.照相机成像应用了一个重要原理,用公式表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离。已知f,v,则u=( )
A. B. C. D.
8.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重,问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
9.已知分式(a,b为常数),的部分取值及对应分式的值如下表,则的值是( )
-3 3
无意义 0 2
A.-2 B.-5 C.3 D.4
10.如图,将长方形ABCD的一角折叠,以CE(点在AB上,不与A,B重合)为折痕,得到,连结,设的度数分别为,若,则之间的关系是( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.分解因式:
12.如图,将边长为6的向右平移个单位得到,若,则 .
13.若关于x,y的二元一次方程组的解也是的解,则k的值为 .
14.《义务教育劳动课程标准年版》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有45名学生,其中学会炒菜的学生频率是,则该班学会炒菜的学生有 名.
15.已知,则 .
16.观察下列等式,解答后面的问题:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
(1)第5个等式是 ;
(2)根据上述规律猜想第n个等式是 (用含n的等式表示).
三、解答题(共8题,共52分)
17.(本题8分)
(1) (2)
18.(本题6分)先化简,再求值:,并从,,中选一个合适的数作为的值代入求值.
19.(本题6分)近年来,研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件。某校学生会负责该校学生的一次研学活动,为设计出同学们最感兴趣的研学路线,随机抽取了部分学生进行问卷调查,并将调查结果绘制成如下不完整的统计图。
调查问卷 1.你最感兴趣的研学类型是 ▲ (单选)。 A.研学+历史 B.研学+科学 C.研学+艺术 D.研学+农业 E.研学+外文 F.研学+工业
(1)请补全条形统计图,并写出扇形统计图中C,D的百分比。
(2)“B”与“C”所在的扇形圆心角的度数和为 °.
(3)若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数。
20.(本题7分)如图,已知AB//CD,AD平分∠EAC,∠B=∠D.
(1)请说明AD//BC:
(2)若∠DAC=(2x+15)°,∠B=(105-3x)°,求∠D的度数.
21.(本题7分)已知a,b均为不等于0的实数,我们定义新运算“※”:.例如:.
(1)验证新运算“※”是否满足乘法交换律?若满足,请写出推导过程;若不满足,请举反例说明.
(2)计算:.
(3)当时,若,尝试求出x的值.
22.(本题8分)根据以下信息,探索解决问题:
背景:为了提高产品的附加值,某公司计划将研发生产的1500件新产品进行加工后再投放市场,每天满工作量情况下,甲、乙两个工厂加工数量及每件加工费用保持稳定不变,公司派出相关人员分别到这两间工厂了解情况,获得如下信息,
信息1 每天满工作量情况下,乙工厂每天加工数量是甲工厂每天加工数量的1.5倍;
信息2 每天满工作量情况下,甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息3 每天满工作量情况下,甲工厂加工1天,乙工厂加工2天共需要10000元:甲工厂加工2天,乙工厂加工3天共需要16100元.
问题解决
问题1 设每天满工作量情况下,甲工厂每天加工数量为x件,结合信息1可得:乙工厂每天加工数量为 ▲ 件(请用x的代数式表示).
问题2 每天满工作量情况下,求甲工厂每天能加工多少件新产品?
问题3 公司将1500件新产品交给甲、乙两工厂一起加工,发现这批新产品的平均加工费用为整数,两工厂加工的时间之和不是整数,请问交给甲工厂多少件新产品进行加工?
23.(本题10分)综合与实践数学社团的同学以"两条平行线AB,CD和一块含角的直角三角板EFG()”为主题开展数学活动,已知点E,F不能同时落在直线AB和CD之间.
(1)观察猜想:如图1,把三角板的角的顶点E,G分别放在AB,CD上,若,则的度数为 ;(直接写出结论,不说明理由)
(2)类比探究:如图2,把三角板的锐角顶点放在CD上,且保持不动,绕点转动三角板,若点恰好落在AB和CD之间,且AB与EF所夹锐角为,求的度数;
(3)解决问题:把三角板的锐角顶点放在CD上,在绕点旋转三角板的过程中,若存在,请直接写出射线GF与AB相交所夹锐角的度数.
参考答案
1.B
2.D
3.C
4.C
5.B
6.D
7.A
8.A
9.B
10.B
11.(x+2)(x-2)
12.2
13.4
14.18
15.3
16.;
17.(1)解: ,
②-①得:4x=28,
x=7,
把 x=7代入①得y=5,
解得.
(2)解:去分母得: ,
去括号得:3x+3-4x=x-1,
移项得:3x-4x-x=-1-3,
合并同类项-2x=-4,
系数化为1得: ,
经检验 原方程的解.
18.解:
;
∵,
∴当时,原式.
19.(1)解:样本容量为:100÷25%=400,
∴C所占百分比为:,
∴D所占百分比为:1-25%-18%-20%-15%-12%=10%,
D的人数为:400×10%=40,
补全条形统计图如下:
(2)136.8
(3)解:4500×25%=1125(人),
答:估计该校对“研学+历史”最感兴趣的学生人数约1125名.
20.(1)证明:,
,
又,
,
(2)解:∵AD 平分∠EAC,
∴∠EAD=∠DAC=(2x+15)°
由(1) 可知: ∠EAD=∠B,
∴2x+15=105-3x,
解得:x=18,
∴∠B=(105-3x)° =(105-3×18)° =51°,
∴∠D=∠B=51°,
21.(1)解:新运算“※”满足乘法交换律,理由如下:,
,
;
(2)解:
;
(3)解:,
当时,,
即:,
解得:,
经检验,是原分式方程的解,
的值为.
22.解:问题1:1.5x;
问题2:根据题意得:,
解得:x=50,经检验,x=50是所列方程的解,其符合题意.
答:每天满工作量情况下,甲工厂每天能加工50件新产品;
问题3:设每天满工作量情况下,甲工厂加工1天所需费用为m元,乙工厂加工1天所需费用为n元,
根据题意得:,解得:,
∴每天满工作量情况下,甲工厂加工新产品的单价为2200÷50=44(元/件)
乙工厂加工新产品的单价为3900÷(1.5×50)=52(元/件).
设交给甲工厂y件新产品进行加工,则交给乙工厂(1500-y)件新产品进行加工,
根据题意得:,且n为整数)
∴.
∵y为正整数,
∴n可以为46, 48, 50,
当n=46时,y=(52-46)=1125,
此时(天),符合题意;
当时,,
此时(天),不符合题意,舍去;
当时,,
此时(天),符合题意.
答:交给甲工厂1125或375件新产品进行加工.
23.(1)100°
(2)解:过点E作EN//CD,如图1所示:
依题意得:∠BME=20°,∠FEG=∠FGE=45°,
∵AB//CD,EN//CD,
∴AB//EN//CD,
∴∠NEM=∠BME=20°,
∴∠NEG=∠FEG-∠NEM=45°-20°=25°,
∴∠DGE=∠NEG=25°,
∴∠FGD=∠FGE+∠DGE=45°+25°=70°,
∴∠FGC=180°-∠FGD=180°-70°=110°
(3)解:存在,射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
分两种情况讨论如下:
①当点E在CD上方时,设AB交GF于点H,如图2所示:
依题意得:∠FEG=∠FGE=45°,
设∠DGE=α,则∠FGC=5∠DGE=5α,
∵∠DGE+∠FGE+∠FGC=180°,
∴5α+45°+α=180,
解得:α=22.5°,
∴∠FGC=5α=112.5°,
∵AB//CD,
∴∠AHG=180°-∠FGC=180°-112.5°=67.5°
②当点E在CD下方时,延长GF交AB于点H,如图3所示:
依题意得:∠FGE=45°,
设∠EGD=β,则∠FGC=5∠DGE=5β,
∴∠FGD=∠FGE-∠EGD=45°-β,
∵∠FGC+∠FGD=180°,
∴5β+45°-β=180°,
解得:β=33.75°,
∴∠FGC=5β=168.75°
∵AB//CD,
∴∠AHG=180°-∠FGC=180°-168.75°=11.25°
综上所述:射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
1 / 1
同课章节目录
