北师大版数学九年级上 第1章 特殊的平行四边形 单元测试(含答案)
文档属性
| 名称 | 北师大版数学九年级上 第1章 特殊的平行四边形 单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 115.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:29:39 | ||
图片预览



文档简介
北师大版九年级上 第1章 特殊的平行四边形 单元测试
一.选择题(共12小题)
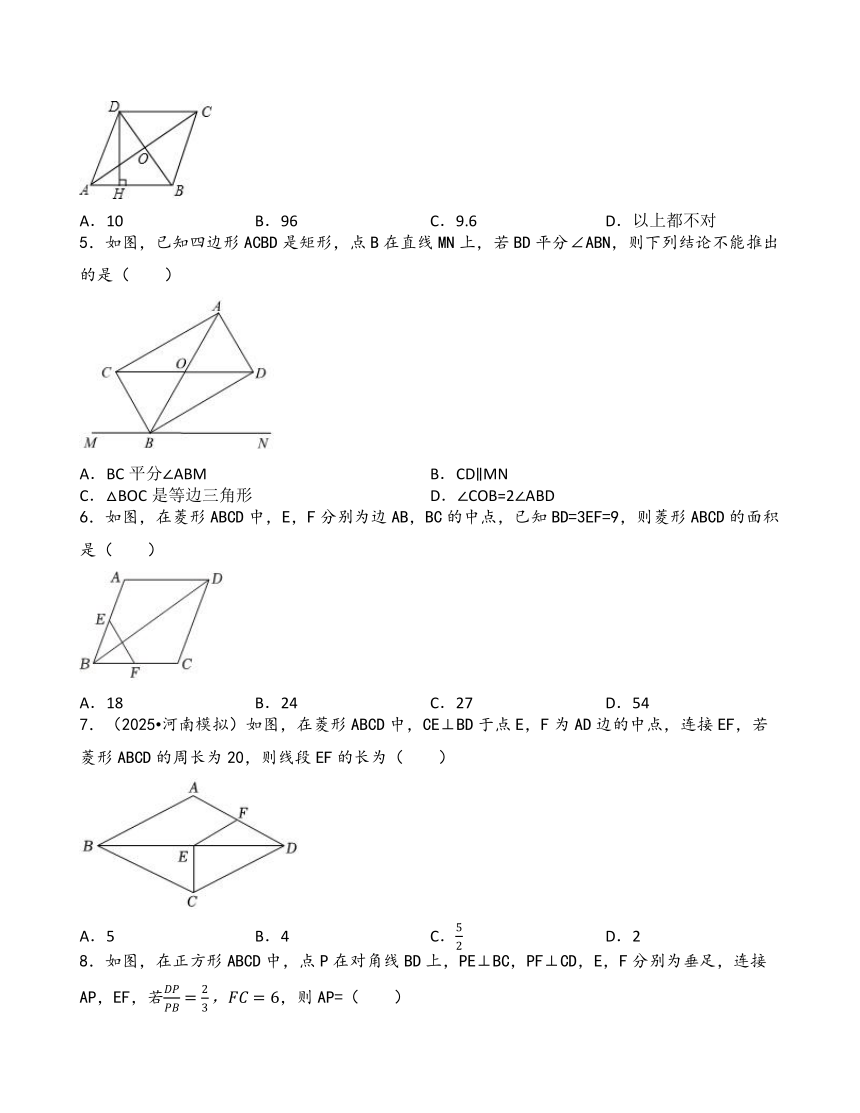
1.(2025 西峡县二模)如图,矩形ABCD的两条对角线相交于点O,AD=6,OD=5,点E是BC的中点,连接OE,则OE的长是( )
A.6 B.5 C.4 D.3
2.(2025 辽宁模拟)如图,在正方形ABCD中,点E为正方形ABCD内一点,连接BE、CE、AE、DE.若△BCE为等边三角形,则∠EAD的度数为( )
A.15° B.30° C.45° D.60°
3.如图所示,含30°的直角三角尺摆放在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若∠FGC=16°,则∠AEF等于( )
A.106° B.114° C.126° D.134°
4.如图:菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,求菱形ABCD的高DH的长是( )
A.10 B.96 C.9.6 D.以上都不对
5.如图,已知四边形ACBD是矩形,点B在直线MN上,若BD平分∠ABN,则下列结论不能推出的是( )
A.BC平分∠ABM B.CD∥MN
C.△BOC是等边三角形 D.∠COB=2∠ABD
6.如图,在菱形ABCD中,E,F分别为边AB,BC的中点,已知BD=3EF=9,则菱形ABCD的面积是( )
A.18 B.24 C.27 D.54
7.(2025 河南模拟)如图,在菱形ABCD中,CE⊥BD于点E,F为AD边的中点,连接EF,若菱形ABCD的周长为20,则线段EF的长为( )
A.5 B.4 C. D.2
8.如图,在正方形ABCD中,点P在对角线BD上,PE⊥BC,PF⊥CD,E,F分别为垂足,连接AP,EF,若,则AP=( )
A. B. C. D.5
9.(2025春 苍溪县期中)如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AD的中点,且OE=4,则菱形ABCD的周长为( )
A.8 B.16 C.24 D.32
10.如图,在正方形ABCD中,AB=4,E,F分别是边CD和AD上的动点,且AF=DE,BE与CF交于点G,连接AG,则AG的最小值是( )
A. B.3 C. D.
11.如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则△DEF的面积为( )
A.4 B.6 C.8 D.10
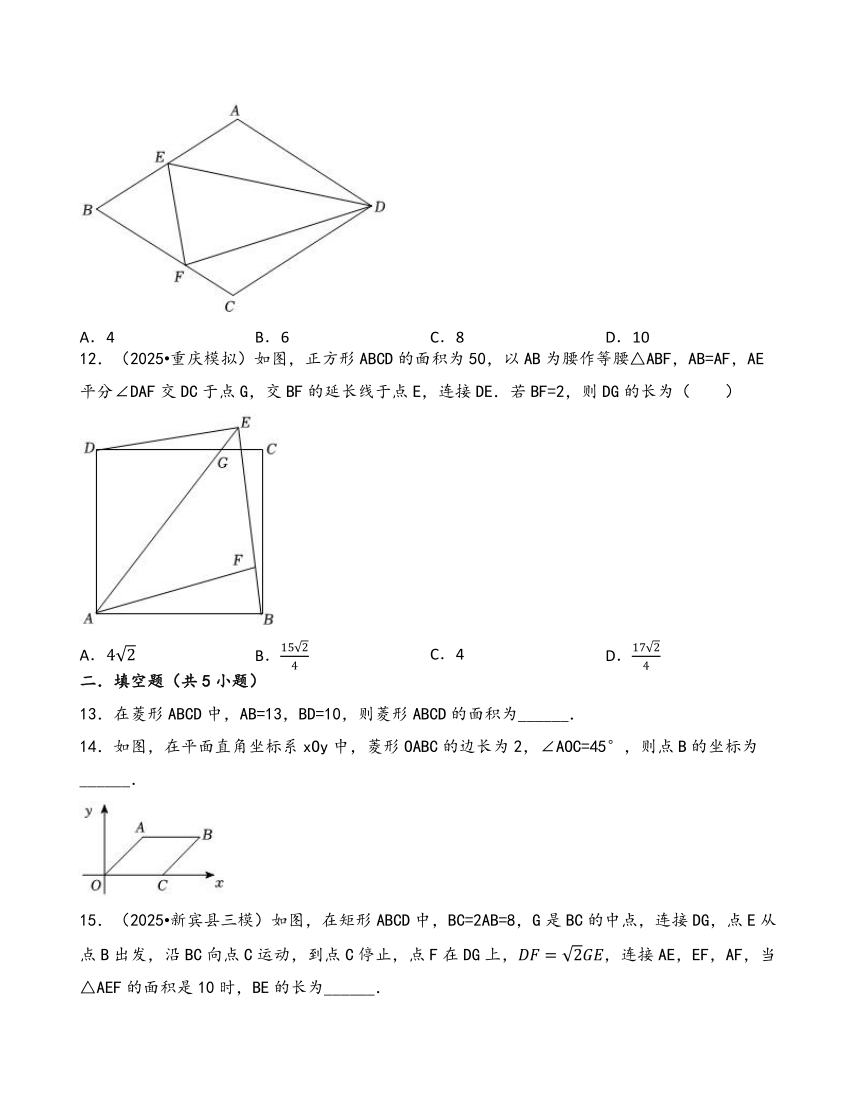
12.(2025 重庆模拟)如图,正方形ABCD的面积为50,以AB为腰作等腰△ABF,AB=AF,AE平分∠DAF交DC于点G,交BF的延长线于点E,连接DE.若BF=2,则DG的长为( )
A. B. C.4 D.
二.填空题(共5小题)
13.在菱形ABCD中,AB=13,BD=10,则菱形ABCD的面积为______.
14.如图,在平面直角坐标系xOy中,菱形OABC的边长为2,∠AOC=45°,则点B的坐标为 ______.
15.(2025 新宾县三模)如图,在矩形ABCD中,BC=2AB=8,G是BC的中点,连接DG,点E从点B出发,沿BC向点C运动,到点C停止,点F在DG上,,连接AE,EF,AF,当△AEF的面积是10时,BE的长为______.
16.如图,在菱形ABCD中,M,N分别为AC,CD的中点.若MN=1,则菱形ABCD的周长是 ______.
17.如图,在矩形OAHC中,,OA=12,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动,动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是1个单位长度/秒,连接CM,CN,MN,以运动时间为t(0<t<12)秒,则t=______时,△CMN为直角三角形.
三.解答题(共5小题)
18.如图,在矩形ABCD中(AB>BC),对角线AC,BD相交于点O,延长BC到点E,使得CE=BC,连接DE,点F是DE的中点,连接CF.
(1)求证:四边形DOCF是菱形;
(2)若矩形ABCD的周长为20,AC=8,求四边形DOCF的面积.
19.如图,在△ABC中,AD是BC边上的中线,BE是AC边上的高,EF⊥AD,垂足为F,且AF=DF.
(1)求证:AE=CD;
(2)若AE=5,CE=6,求△ABC的面积.
20.如图,在等腰△ABC中,AB=BC,BO平分∠ABC,过点A作AD∥BC交BO的延长线于D,连接CD,过点D作DE⊥BD交BC的延长线于E.
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB=6,∠ABC=120°,求DE的长.
21.如图,点A是菱形BDEF对角线的交点,BC∥FD,CD∥BE,连接AC,交BD于O.
(1)求证:四边形ABCD是矩形;
(2)若BE=6,DF=8,求AC的长.
22.如图,EF经过正方形ABCD的顶点D,BE⊥EF,BE与AD相交于点G,BG=DF,连接BF交CD于M.
(1)如图1,求证:BM=FM;
(2)如图2,连接AC,O为AC的中点,连接OM,OE,若,,直接写出OE+OM的值.
北师大版九年级上 第1章 特殊的平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、D 4、C 5、C 6、C 7、C 8、A 9、D 10、A 11、D 12、B
二.填空题(共5小题)
13、120; 14、; 15、2或; 16、8; 17、2或6;
三.解答题(共5小题)
18、(1)证明:由题意可得:AC=BD,,,∠BCD=90°,
∴OC=OD,
∵CE=BC,
∴点C是线段BE的中点,
∴CF是△EBD的中位线,
∴,CF∥BD,
∴四边形DOCF是平行四边形,
∵OC=OD,
∴四边形DOCF是菱形;
(2)解:由题意可得:AB=CD,AD=BC,∠ABC=90°,
∵矩形ABCD的周长为20,
∴2(AB+BC)=20,
∴AB+BC=10,
∴BC=10-AB,
在Rt△ABC中,AB2+BC2=AC2,即AB2+(10-AB)2=82,
解得或,
∵AB>BC,
∴,,
∴,
∴菱形DOCF的面积=2S△OCD=(5+)×(5-)=(25-7)=9.
19、(1)证明:如图,连接DE,
∵BE是AC边上的高,
∴BE⊥AC,
在△ABC中,AD是BC边上的中线,
∴BD=CD,
∴DE=BC=CD,
∵EF⊥AD,AF=DF,
∴EF垂直平分AD,
∴AE=DE,
∴AE=CD;
(2)解:∵AE=CD=5,BC=2CD,
∴BC=10,
∵BE⊥AC,CE=6,
∴BE===8,
∵AC=AE+CE=5+6=11,
∴△ABC的面积=AC BE=×11×8=44.
20、解:(1)四边形ABCD是菱形,
理由:由条件可得AO=CO,
∵AD∥BC
∴∠DAO=∠ACB,∠ADO=∠CBO,
∴△ADO≌△CBO(AAS),
∴DO=BO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)由条件可知∠DBC=∠ABE=60°,
∵四边形ABCD是菱形,
∴BC=CD=AB=6,
∴△BCD是等边三角形,
∴BD=BC=6,
∵BD⊥DE,
∴∠BDE=90°,
∴∠E=90°-∠DBC=30°,
∴BE=2BD=12,
∴.
21、(1)证明:∵BC∥FD,CD∥BE,
∴四边形ABCD是矩形,
∵四边形BDEF是菱形,
∴FD⊥BE,
∴∠BAD=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形BDEF是菱形,
∴AF=AD,AB=AE,∠BAD=90°,
∵BE=6,DF=8,
∴AB=3,AD=4,
根据勾股定理得:BD===5,
∵四边形ABCD是矩形,
∴AC=BD=5.
22、(1)证明:过点F作FH⊥CD,
∵四边形ABCD是正方形,BE⊥EF,FH⊥CD,
∴∠A=∠ADC=∠E=90°,HF∥AD,
∴∠DFH=∠EDG,
∵∠AGB=∠DGE,
∴∠ABG=∠EDG,
∴∠ABG=∠DFH,
∵∠A=∠DHF=90°,BG=DF,
∴△GAB≌△DHF(AAS),
∴HF=AB,
∵BC=AB,
∴HF=BC,
∵∠C=∠MHF=90°,∠BMC=∠FMH,
∴△BMC≌△FMH(AAS),
∴BM=FM;
(2)如图,连接BD,
∵,,
∴,
∵四边形ABCD是正方形,O为AC的中点,
∴OB=OD,
∵Rt△BDE中,OE是斜边上的中线,
∴,
∵OB=OD,BM=MF,
∴,
∴.
一.选择题(共12小题)
1.(2025 西峡县二模)如图,矩形ABCD的两条对角线相交于点O,AD=6,OD=5,点E是BC的中点,连接OE,则OE的长是( )
A.6 B.5 C.4 D.3
2.(2025 辽宁模拟)如图,在正方形ABCD中,点E为正方形ABCD内一点,连接BE、CE、AE、DE.若△BCE为等边三角形,则∠EAD的度数为( )
A.15° B.30° C.45° D.60°
3.如图所示,含30°的直角三角尺摆放在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若∠FGC=16°,则∠AEF等于( )
A.106° B.114° C.126° D.134°
4.如图:菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,求菱形ABCD的高DH的长是( )
A.10 B.96 C.9.6 D.以上都不对
5.如图,已知四边形ACBD是矩形,点B在直线MN上,若BD平分∠ABN,则下列结论不能推出的是( )
A.BC平分∠ABM B.CD∥MN
C.△BOC是等边三角形 D.∠COB=2∠ABD
6.如图,在菱形ABCD中,E,F分别为边AB,BC的中点,已知BD=3EF=9,则菱形ABCD的面积是( )
A.18 B.24 C.27 D.54
7.(2025 河南模拟)如图,在菱形ABCD中,CE⊥BD于点E,F为AD边的中点,连接EF,若菱形ABCD的周长为20,则线段EF的长为( )
A.5 B.4 C. D.2
8.如图,在正方形ABCD中,点P在对角线BD上,PE⊥BC,PF⊥CD,E,F分别为垂足,连接AP,EF,若,则AP=( )
A. B. C. D.5
9.(2025春 苍溪县期中)如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AD的中点,且OE=4,则菱形ABCD的周长为( )
A.8 B.16 C.24 D.32
10.如图,在正方形ABCD中,AB=4,E,F分别是边CD和AD上的动点,且AF=DE,BE与CF交于点G,连接AG,则AG的最小值是( )
A. B.3 C. D.
11.如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则△DEF的面积为( )
A.4 B.6 C.8 D.10
12.(2025 重庆模拟)如图,正方形ABCD的面积为50,以AB为腰作等腰△ABF,AB=AF,AE平分∠DAF交DC于点G,交BF的延长线于点E,连接DE.若BF=2,则DG的长为( )
A. B. C.4 D.
二.填空题(共5小题)
13.在菱形ABCD中,AB=13,BD=10,则菱形ABCD的面积为______.
14.如图,在平面直角坐标系xOy中,菱形OABC的边长为2,∠AOC=45°,则点B的坐标为 ______.
15.(2025 新宾县三模)如图,在矩形ABCD中,BC=2AB=8,G是BC的中点,连接DG,点E从点B出发,沿BC向点C运动,到点C停止,点F在DG上,,连接AE,EF,AF,当△AEF的面积是10时,BE的长为______.
16.如图,在菱形ABCD中,M,N分别为AC,CD的中点.若MN=1,则菱形ABCD的周长是 ______.
17.如图,在矩形OAHC中,,OA=12,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动,动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是1个单位长度/秒,连接CM,CN,MN,以运动时间为t(0<t<12)秒,则t=______时,△CMN为直角三角形.
三.解答题(共5小题)
18.如图,在矩形ABCD中(AB>BC),对角线AC,BD相交于点O,延长BC到点E,使得CE=BC,连接DE,点F是DE的中点,连接CF.
(1)求证:四边形DOCF是菱形;
(2)若矩形ABCD的周长为20,AC=8,求四边形DOCF的面积.
19.如图,在△ABC中,AD是BC边上的中线,BE是AC边上的高,EF⊥AD,垂足为F,且AF=DF.
(1)求证:AE=CD;
(2)若AE=5,CE=6,求△ABC的面积.
20.如图,在等腰△ABC中,AB=BC,BO平分∠ABC,过点A作AD∥BC交BO的延长线于D,连接CD,过点D作DE⊥BD交BC的延长线于E.
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB=6,∠ABC=120°,求DE的长.
21.如图,点A是菱形BDEF对角线的交点,BC∥FD,CD∥BE,连接AC,交BD于O.
(1)求证:四边形ABCD是矩形;
(2)若BE=6,DF=8,求AC的长.
22.如图,EF经过正方形ABCD的顶点D,BE⊥EF,BE与AD相交于点G,BG=DF,连接BF交CD于M.
(1)如图1,求证:BM=FM;
(2)如图2,连接AC,O为AC的中点,连接OM,OE,若,,直接写出OE+OM的值.
北师大版九年级上 第1章 特殊的平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、D 4、C 5、C 6、C 7、C 8、A 9、D 10、A 11、D 12、B
二.填空题(共5小题)
13、120; 14、; 15、2或; 16、8; 17、2或6;
三.解答题(共5小题)
18、(1)证明:由题意可得:AC=BD,,,∠BCD=90°,
∴OC=OD,
∵CE=BC,
∴点C是线段BE的中点,
∴CF是△EBD的中位线,
∴,CF∥BD,
∴四边形DOCF是平行四边形,
∵OC=OD,
∴四边形DOCF是菱形;
(2)解:由题意可得:AB=CD,AD=BC,∠ABC=90°,
∵矩形ABCD的周长为20,
∴2(AB+BC)=20,
∴AB+BC=10,
∴BC=10-AB,
在Rt△ABC中,AB2+BC2=AC2,即AB2+(10-AB)2=82,
解得或,
∵AB>BC,
∴,,
∴,
∴菱形DOCF的面积=2S△OCD=(5+)×(5-)=(25-7)=9.
19、(1)证明:如图,连接DE,
∵BE是AC边上的高,
∴BE⊥AC,
在△ABC中,AD是BC边上的中线,
∴BD=CD,
∴DE=BC=CD,
∵EF⊥AD,AF=DF,
∴EF垂直平分AD,
∴AE=DE,
∴AE=CD;
(2)解:∵AE=CD=5,BC=2CD,
∴BC=10,
∵BE⊥AC,CE=6,
∴BE===8,
∵AC=AE+CE=5+6=11,
∴△ABC的面积=AC BE=×11×8=44.
20、解:(1)四边形ABCD是菱形,
理由:由条件可得AO=CO,
∵AD∥BC
∴∠DAO=∠ACB,∠ADO=∠CBO,
∴△ADO≌△CBO(AAS),
∴DO=BO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)由条件可知∠DBC=∠ABE=60°,
∵四边形ABCD是菱形,
∴BC=CD=AB=6,
∴△BCD是等边三角形,
∴BD=BC=6,
∵BD⊥DE,
∴∠BDE=90°,
∴∠E=90°-∠DBC=30°,
∴BE=2BD=12,
∴.
21、(1)证明:∵BC∥FD,CD∥BE,
∴四边形ABCD是矩形,
∵四边形BDEF是菱形,
∴FD⊥BE,
∴∠BAD=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形BDEF是菱形,
∴AF=AD,AB=AE,∠BAD=90°,
∵BE=6,DF=8,
∴AB=3,AD=4,
根据勾股定理得:BD===5,
∵四边形ABCD是矩形,
∴AC=BD=5.
22、(1)证明:过点F作FH⊥CD,
∵四边形ABCD是正方形,BE⊥EF,FH⊥CD,
∴∠A=∠ADC=∠E=90°,HF∥AD,
∴∠DFH=∠EDG,
∵∠AGB=∠DGE,
∴∠ABG=∠EDG,
∴∠ABG=∠DFH,
∵∠A=∠DHF=90°,BG=DF,
∴△GAB≌△DHF(AAS),
∴HF=AB,
∵BC=AB,
∴HF=BC,
∵∠C=∠MHF=90°,∠BMC=∠FMH,
∴△BMC≌△FMH(AAS),
∴BM=FM;
(2)如图,连接BD,
∵,,
∴,
∵四边形ABCD是正方形,O为AC的中点,
∴OB=OD,
∵Rt△BDE中,OE是斜边上的中线,
∴,
∵OB=OD,BM=MF,
∴,
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
