北师大版数学九年级上 第4章 图形的相似 单元测试(含答案)
文档属性
| 名称 | 北师大版数学九年级上 第4章 图形的相似 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:30:42 | ||
图片预览




文档简介
北师大版九年级上 第4章 图形的相似 单元测试
一.选择题(共12小题)
1.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.1cm B.4cm C.2cm D.9cm
2.已知a:b=4:5,则下列式子正确的是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△DAF的面积之比为( )
A.2:5 B.3:5 C.4:25 D.9:25
4.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
5.如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
6.如图,在 ABCD中,点E在DC上,BE与AC相交于点F,若=,则的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,△ABC∽△ODC,且AB=3OD,若点A的坐标为(-2,0),则点C的坐标为( )
A.(0,1) B. C.(1,0) D.
8.如图,在△ABC中,D,E为边AB上的三等分点,点F,G在边BC上,AC∥DG∥EF,H为AF与DG的交点.若EF=4,则HG的长为( )
A.6 B.5 C.4 D.3
9.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是小孔成像实验图,抽象为数学模型如图2所示.已知AC与BD交于点O,AB∥CD.若点O到AB的距离为10cm,点O到CD的距离为15cm,蜡烛火焰AB的高度是2cm,则蜡烛火焰倒立的像CD的高度是( )
A.2cm B. C.3cm D.4cm
10.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=36cm,A′B′=24cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为( )cm.
A.20 B.22 C.24 D.26
11.如图,△ABC是等边三角形,点E,F在AB上,点H,G在AC上,AE=EF=FB,EH∥FG∥BC,△ABC的面积为27cm2,则四边形EFGH的面积为( )
A.9cm2 B.3cm2 C.12cm2 D.15cm2
12.(2025 温州模拟)如图,在正方形ABCD中,AB=14,点G,H在BD上,E为GH上一点,过点E作EF⊥CD于点F,连结AE,记,若,则GH的长为( )
A.2 B. C.4 D.
二.填空题(共5小题)
13.已知a,b,c,d是成比例线段,其中a=6cm,b=4cm,c=3cm,则线段d= ______cm.
14.如图,AE=5,AC=8,AB=10,当BD= ______时,DE∥BC.
15.如图,将腰长为12cm的等腰三角形纸片,沿与底边平行的方向剪去一个小的等腰三角形纸片,剩下一个等腰梯形纸片,如图所示.若剪去纸片面积是剩下的纸片面积的,则剪去等腰三角形纸片的腰长为 ______.
16.如图,直线l1∥l2∥l3,直线AC、DF被l1、l2、l3所截,若AB:BC=2:3,DF=10,则DE的长为 ______.
17.(2025 朝阳区校级一模)如图,在矩形纸片ABCD中,AB=6,BC=10.点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的点H处.给出下列四个结论:
①∠EBG=45°;
②△DEF∽△ABG;
③;
④AG+DF=FG.
上述结论中,正确结论的序号有______.
三.解答题(共5小题)
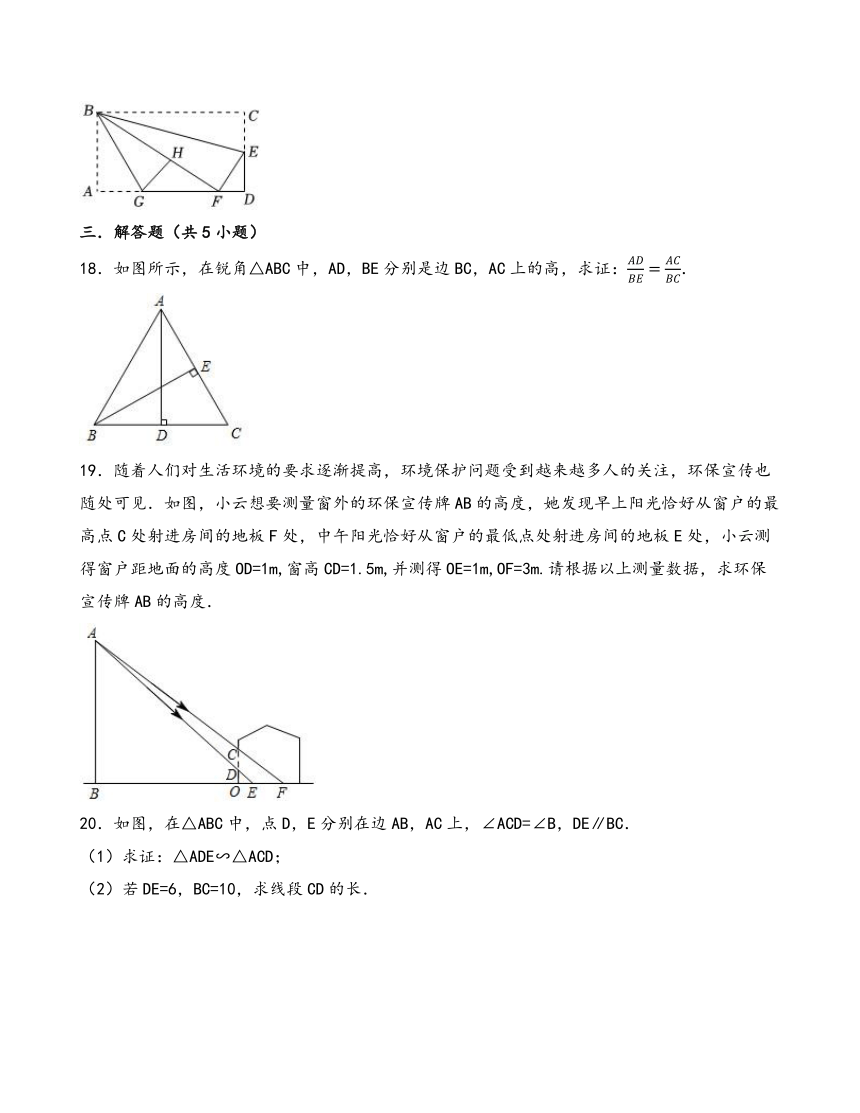
18.如图所示,在锐角△ABC中,AD,BE分别是边BC,AC上的高,求证:.
19.随着人们对生活环境的要求逐渐提高,环境保护问题受到越来越多人的关注,环保宣传也随处可见.如图,小云想要测量窗外的环保宣传牌AB的高度,她发现早上阳光恰好从窗户的最高点C处射进房间的地板F处,中午阳光恰好从窗户的最低点处射进房间的地板E处,小云测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求环保宣传牌AB的高度.
20.如图,在△ABC中,点D,E分别在边AB,AC上,∠ACD=∠B,DE∥BC.
(1)求证:△ADE∽△ACD;
(2)若DE=6,BC=10,求线段CD的长.
21.如图,在等边三角形ABC中,点P是边BC上一动点(P点不与端点重合),作∠DPE=60°,PE交边AC于点E,PD交边AB于点D.
(1)求证:△BPD∽△CEP;
(2)若AB=10,BD=3,CP:BP=1:4,求CE的长.
22.在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
(1)如图1,点D在BC边上,=,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,易得的值为 ______.
(2)如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,=,求的值.
北师大版九年级上 第4章 图形的相似 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、C 3、B 4、D 5、B 6、A 7、C 8、A 9、C 10、A 11、A 12、B
二.填空题(共5小题)
13、2; 14、; 15、4cm; 16、4; 17、①③④;
三.解答题(共5小题)
18、证明:∵AD,BE分别是边BC,AC上的高,
∴∠ADC=∠BEC=90°,
又∠C=∠C,
∴△ADC∽△BEC,
∴.
19、解:∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=10.
经检验:x=10是原方程的解.
答:AB的高度是10m.
20、(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠ACD=∠B,
∴∠ADE=∠ACD,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)解:∵DE∥BC,
∴∠BCD=∠EDC,
∵∠B=∠DCE,
∴△CDE∽△BCD,
∴,
∴,
∴CD=2.
21、(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BDC=180°-∠B-∠BPD=120°-∠BPD,
∵∠DPE=60°,
∴∠CPE=180°-∠DPE-∠BPD=120°-∠BPD,
∴∠BPD=∠CEP,
∴△BPD∽△CEP.
(2)解:∵AB=10,BD=3,CP:BP=1:4,
∴BC=AB=10,
∴BP=BC=BC=×10=8,CP=BC=BC=×10=2,
∵△BPD∽△CEP,
∴=,
∴CE===,
∴CE的长是.
22、解:(1)如图1中,∵AF∥BC,
∴∠F=∠EBC,
∵∠AEF=∠BEC,AE=EC,
∴△AEF≌△CEB(AAS),
∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
∵AF∥BC,
∴△APF∽△DPB,
∴==.
故答案为:;
(2)如图:过点A作AF∥DB,交BE的延长线于点F,
设DC=k,则BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠PBD
在△AEF和△CEB中,
,
∴△AEF≌△CEB(AAS),
∴EF=BE,AF=BC=2k.
∵AF∥BC,
∴△APF∽△DPB,
∴====.
一.选择题(共12小题)
1.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.1cm B.4cm C.2cm D.9cm
2.已知a:b=4:5,则下列式子正确的是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△DAF的面积之比为( )
A.2:5 B.3:5 C.4:25 D.9:25
4.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
5.如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
6.如图,在 ABCD中,点E在DC上,BE与AC相交于点F,若=,则的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,△ABC∽△ODC,且AB=3OD,若点A的坐标为(-2,0),则点C的坐标为( )
A.(0,1) B. C.(1,0) D.
8.如图,在△ABC中,D,E为边AB上的三等分点,点F,G在边BC上,AC∥DG∥EF,H为AF与DG的交点.若EF=4,则HG的长为( )
A.6 B.5 C.4 D.3
9.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.图1是小孔成像实验图,抽象为数学模型如图2所示.已知AC与BD交于点O,AB∥CD.若点O到AB的距离为10cm,点O到CD的距离为15cm,蜡烛火焰AB的高度是2cm,则蜡烛火焰倒立的像CD的高度是( )
A.2cm B. C.3cm D.4cm
10.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=36cm,A′B′=24cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为( )cm.
A.20 B.22 C.24 D.26
11.如图,△ABC是等边三角形,点E,F在AB上,点H,G在AC上,AE=EF=FB,EH∥FG∥BC,△ABC的面积为27cm2,则四边形EFGH的面积为( )
A.9cm2 B.3cm2 C.12cm2 D.15cm2
12.(2025 温州模拟)如图,在正方形ABCD中,AB=14,点G,H在BD上,E为GH上一点,过点E作EF⊥CD于点F,连结AE,记,若,则GH的长为( )
A.2 B. C.4 D.
二.填空题(共5小题)
13.已知a,b,c,d是成比例线段,其中a=6cm,b=4cm,c=3cm,则线段d= ______cm.
14.如图,AE=5,AC=8,AB=10,当BD= ______时,DE∥BC.
15.如图,将腰长为12cm的等腰三角形纸片,沿与底边平行的方向剪去一个小的等腰三角形纸片,剩下一个等腰梯形纸片,如图所示.若剪去纸片面积是剩下的纸片面积的,则剪去等腰三角形纸片的腰长为 ______.
16.如图,直线l1∥l2∥l3,直线AC、DF被l1、l2、l3所截,若AB:BC=2:3,DF=10,则DE的长为 ______.
17.(2025 朝阳区校级一模)如图,在矩形纸片ABCD中,AB=6,BC=10.点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的点H处.给出下列四个结论:
①∠EBG=45°;
②△DEF∽△ABG;
③;
④AG+DF=FG.
上述结论中,正确结论的序号有______.
三.解答题(共5小题)
18.如图所示,在锐角△ABC中,AD,BE分别是边BC,AC上的高,求证:.
19.随着人们对生活环境的要求逐渐提高,环境保护问题受到越来越多人的关注,环保宣传也随处可见.如图,小云想要测量窗外的环保宣传牌AB的高度,她发现早上阳光恰好从窗户的最高点C处射进房间的地板F处,中午阳光恰好从窗户的最低点处射进房间的地板E处,小云测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求环保宣传牌AB的高度.
20.如图,在△ABC中,点D,E分别在边AB,AC上,∠ACD=∠B,DE∥BC.
(1)求证:△ADE∽△ACD;
(2)若DE=6,BC=10,求线段CD的长.
21.如图,在等边三角形ABC中,点P是边BC上一动点(P点不与端点重合),作∠DPE=60°,PE交边AC于点E,PD交边AB于点D.
(1)求证:△BPD∽△CEP;
(2)若AB=10,BD=3,CP:BP=1:4,求CE的长.
22.在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
(1)如图1,点D在BC边上,=,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,易得的值为 ______.
(2)如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,=,求的值.
北师大版九年级上 第4章 图形的相似 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、C 3、B 4、D 5、B 6、A 7、C 8、A 9、C 10、A 11、A 12、B
二.填空题(共5小题)
13、2; 14、; 15、4cm; 16、4; 17、①③④;
三.解答题(共5小题)
18、证明:∵AD,BE分别是边BC,AC上的高,
∴∠ADC=∠BEC=90°,
又∠C=∠C,
∴△ADC∽△BEC,
∴.
19、解:∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=10.
经检验:x=10是原方程的解.
答:AB的高度是10m.
20、(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠ACD=∠B,
∴∠ADE=∠ACD,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)解:∵DE∥BC,
∴∠BCD=∠EDC,
∵∠B=∠DCE,
∴△CDE∽△BCD,
∴,
∴,
∴CD=2.
21、(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BDC=180°-∠B-∠BPD=120°-∠BPD,
∵∠DPE=60°,
∴∠CPE=180°-∠DPE-∠BPD=120°-∠BPD,
∴∠BPD=∠CEP,
∴△BPD∽△CEP.
(2)解:∵AB=10,BD=3,CP:BP=1:4,
∴BC=AB=10,
∴BP=BC=BC=×10=8,CP=BC=BC=×10=2,
∵△BPD∽△CEP,
∴=,
∴CE===,
∴CE的长是.
22、解:(1)如图1中,∵AF∥BC,
∴∠F=∠EBC,
∵∠AEF=∠BEC,AE=EC,
∴△AEF≌△CEB(AAS),
∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
∵AF∥BC,
∴△APF∽△DPB,
∴==.
故答案为:;
(2)如图:过点A作AF∥DB,交BE的延长线于点F,
设DC=k,则BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠PBD
在△AEF和△CEB中,
,
∴△AEF≌△CEB(AAS),
∴EF=BE,AF=BC=2k.
∵AF∥BC,
∴△APF∽△DPB,
∴====.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
