高中数学人教A版必修一第二章《2.3 幂函数》课件(27张PPT)
文档属性
| 名称 | 高中数学人教A版必修一第二章《2.3 幂函数》课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 895.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 00:00:00 | ||
图片预览








文档简介
课件27张PPT。2.3 幂函数金台高级中学 解宏涛理解幂函数的概念.会画 y=x y=x-1 y=x2 y=x3及
的函数图像.了解以上五个函数的性质.学习目标考情:
1.高考主要考查幂函数的概念、图像与性质,单独考
查的概率较低.
2.常与二次函数、指数函数、对数函数等知识交汇命题.
3.题型多以选择题、填空题的形式出现,属低中档题. 如果一个函数,底数是自变量x,
指数是常量 ,这样的函数称为幂函数.即【注意】判断一个函数是否为幂函数的依据:
①该函数是否为形如y=xα的形式.
②指数α为常数.底数为自变量x.系数为1.即时应用:1. 判断下列函数是否为幂函数√×××××√√即时应用:2.已知点 在幂函数f(x)
的图像上,则f(x)的表达式为________.解假设画出右边幂函数的图像 y=x y=x2 y=x -1 y=x3幂函数的图像
幂函数y=x、 y=x2、y=x-1、y=x3的图像如下:y=xy=x2y=x3y=x2y=x-1y=x-1笔记时请同学们分开画5个图像
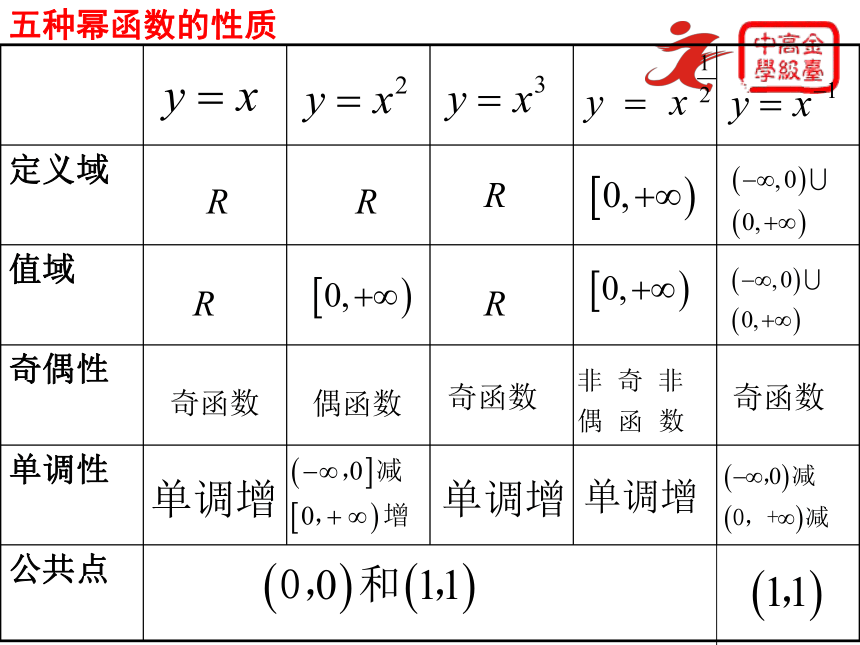
五种幂函数的性质 在第一象限的图象,可分为如图中的三类:
幂函数图像的特点
(1)幂函数的图像一定会出现在第一象限,一定不会出现
在第四象限,是否出现在第二、三象限,要看函数的
奇偶性。
(2)幂函数的图像最多只能出现在两个象限内。
(3)如果幂函数的图像与坐标轴相交,则交点一定是原点。 在第一象限的图象,可分为如图中的三类:
【即时应用】
(1)判断下列命题是否正确.(请在括号内填“√”或“×”)
①幂函数的图像都经过点(1,1)和点(0,0); ( )
②幂函数的图像不可能在第四象限; ( )
③n=0时,函数y=xn的图像是一条直线; ( )
④幂函数y=xn,当n>0时是增函数; ( )
⑤幂函数y=xn,当n<0时,在第一象限内函数值随x值的增大而减小. ( )×√××√(2)图中所示的曲线为幂函数y=xn在第一象限的图像,则c1、c2、c3、c4的大小关系是____________________.优化设计P26 例1解(1)∵f(x)是幂函数(2)∵f(x)是幂函数,且又是(0,+∞)上的增函数解之,得优化设计P26 例1解(3)∵f(x)是正比例函数解之,得(4)∵f(x)是反比例函数解之,得优化设计P27 举一反三 1解(1)∵f(x)是正比例函数解之,得(2)∵f(x)是反比例函数解之,得解(3)∵f(x)是二次函数优化设计P27 举一反三 1解之,得(4)∵f(x)是幂函数优化设计P27 例2解(1)∵ 在R上是增函数.(2)∵ 在R上是增函数.(3)建立中间量∵ 在R上是减函数.∵ 在(0,+∞)上的增加的.优化设计P27 举一反三 21.函数 的图像可能是下面四个图中的( )ABCDD巩固提升2.当0 关系是__________.
【解析】画出三个函数的图像易判断
f(x)答案:f(x)【解析】选B.因为当x>1时,x> 当x=1时,x= 所以A、C、
D错误,故选B.【例3】若点( 2)在幂函数f(x)的图像上,点(-2, )在幂
函数g(x)的图像上,定义
试求函数h(x)的最大值以及单调区间.【规范解答】设幂函数为f(x)=xα,因为点( 2)在f(x)的图
像上,所以 所以α=2,即f(x)=x2;又设g(x)=xβ,
点(-2, )在g(x)的图像上,所以(-2)β= 所以β=-2,
即g(x)=x-2.在同一直角坐标系中画出函数f(x)与g(x)的图像,如图所示:
则有:
结合图像可知:函数的最大值等于1,单调递增区间是
(-∞,-1)和(0,1),单调递减区间是(-1,0)和(1,+∞).f(x)f(x)g(x)g(x)1-11oxy【易错误区】幂函数图像与性质应用中的误区
【例5】已知幂函数
的图像与x轴、y轴都无公共点,且关于y轴对称,则m的值为
______________,幂函数的解析式为____________________.【规范解答】因为幂函数 的图像与x轴、y轴
都无公共点.
所以m2-2m-3≤0,解得-1≤m≤3.
又m∈Z,∴m=-1,0,1,2,3,
又 的图像关于y轴对称,
∴m2-2m-3为偶数.-1或1或3 作业
的函数图像.了解以上五个函数的性质.学习目标考情:
1.高考主要考查幂函数的概念、图像与性质,单独考
查的概率较低.
2.常与二次函数、指数函数、对数函数等知识交汇命题.
3.题型多以选择题、填空题的形式出现,属低中档题. 如果一个函数,底数是自变量x,
指数是常量 ,这样的函数称为幂函数.即【注意】判断一个函数是否为幂函数的依据:
①该函数是否为形如y=xα的形式.
②指数α为常数.底数为自变量x.系数为1.即时应用:1. 判断下列函数是否为幂函数√×××××√√即时应用:2.已知点 在幂函数f(x)
的图像上,则f(x)的表达式为________.解假设画出右边幂函数的图像 y=x y=x2 y=x -1 y=x3幂函数的图像
幂函数y=x、 y=x2、y=x-1、y=x3的图像如下:y=xy=x2y=x3y=x2y=x-1y=x-1笔记时请同学们分开画5个图像
五种幂函数的性质 在第一象限的图象,可分为如图中的三类:
幂函数图像的特点
(1)幂函数的图像一定会出现在第一象限,一定不会出现
在第四象限,是否出现在第二、三象限,要看函数的
奇偶性。
(2)幂函数的图像最多只能出现在两个象限内。
(3)如果幂函数的图像与坐标轴相交,则交点一定是原点。 在第一象限的图象,可分为如图中的三类:
【即时应用】
(1)判断下列命题是否正确.(请在括号内填“√”或“×”)
①幂函数的图像都经过点(1,1)和点(0,0); ( )
②幂函数的图像不可能在第四象限; ( )
③n=0时,函数y=xn的图像是一条直线; ( )
④幂函数y=xn,当n>0时是增函数; ( )
⑤幂函数y=xn,当n<0时,在第一象限内函数值随x值的增大而减小. ( )×√××√(2)图中所示的曲线为幂函数y=xn在第一象限的图像,则c1、c2、c3、c4的大小关系是____________________.优化设计P26 例1解(1)∵f(x)是幂函数(2)∵f(x)是幂函数,且又是(0,+∞)上的增函数解之,得优化设计P26 例1解(3)∵f(x)是正比例函数解之,得(4)∵f(x)是反比例函数解之,得优化设计P27 举一反三 1解(1)∵f(x)是正比例函数解之,得(2)∵f(x)是反比例函数解之,得解(3)∵f(x)是二次函数优化设计P27 举一反三 1解之,得(4)∵f(x)是幂函数优化设计P27 例2解(1)∵ 在R上是增函数.(2)∵ 在R上是增函数.(3)建立中间量∵ 在R上是减函数.∵ 在(0,+∞)上的增加的.优化设计P27 举一反三 21.函数 的图像可能是下面四个图中的( )ABCDD巩固提升2.当0
【解析】画出三个函数的图像易判断
f(x)
D错误,故选B.【例3】若点( 2)在幂函数f(x)的图像上,点(-2, )在幂
函数g(x)的图像上,定义
试求函数h(x)的最大值以及单调区间.【规范解答】设幂函数为f(x)=xα,因为点( 2)在f(x)的图
像上,所以 所以α=2,即f(x)=x2;又设g(x)=xβ,
点(-2, )在g(x)的图像上,所以(-2)β= 所以β=-2,
即g(x)=x-2.在同一直角坐标系中画出函数f(x)与g(x)的图像,如图所示:
则有:
结合图像可知:函数的最大值等于1,单调递增区间是
(-∞,-1)和(0,1),单调递减区间是(-1,0)和(1,+∞).f(x)f(x)g(x)g(x)1-11oxy【易错误区】幂函数图像与性质应用中的误区
【例5】已知幂函数
的图像与x轴、y轴都无公共点,且关于y轴对称,则m的值为
______________,幂函数的解析式为____________________.【规范解答】因为幂函数 的图像与x轴、y轴
都无公共点.
所以m2-2m-3≤0,解得-1≤m≤3.
又m∈Z,∴m=-1,0,1,2,3,
又 的图像关于y轴对称,
∴m2-2m-3为偶数.-1或1或3 作业
