冀教版数学八年级下 第21章 一次函数 单元测试(含答案)
文档属性
| 名称 | 冀教版数学八年级下 第21章 一次函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:31:28 | ||
图片预览




文档简介
冀教版八年级下 第21章 一次函数 单元测试
一.选择题(共12小题)
1.下列四点中,在函数y=3x+2的图象上的点是( )
A.(-1,1) B.(-1,-1) C.(2,0) D.(0,-1.5)
2.函数y=x+2的图象如图所示,当y>0时,x的值是( )
A.x<-2 B.x>-2 C.x>2 D.x<2
3.已知一次函数y=kx+k+1,y随x的增大而减小,且图象与y轴交于正半轴,则k的取值范围是( )
A.k<-1或k>1 B.-1<k<1 C.0<k<1 D.-1<k<0
4.若点A(-2,y1),B(3,y2),C(1,y3)在一次函数y=-3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
5.点P(a,b)在函数y=3x+2的图象上,则代数式3a-b+1的值等于( )
A.-1 B.1 C.-3 D.3
6.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3200米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,下列说法正确的是( )
A.乙用16分钟追上甲
B.乙的速度是60米/分钟
C.乙到达终点时,甲离终点还有800米
D.当乙出发40分钟时,甲、乙两人的距离最远
7.A(x1,y1)、B(x2,y2)是直线y=(m-2)x+5图象上相异的两点,若,则m的取值范围( )
A.m>2 B.m<2 C.m≥2 D.m≤2
8.能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且mn≠0)的图象的是( )
A. B. C. D.
9.已知直线y=kx+3经过点(2,m)和(4,n),其中mn<0,则k的值可能为( )
A.-2 B.-1 C.1 D.2
10.要将直线y=2x+3平移后过点(2,8),下列平移方法正确的是( )
A.向上平移1个单位长度 B.向下平移1个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
11.小南和小凯进行百米赛跑,因小南比小凯跑得快,若两人同时起跑,小南肯定赢.现小南让小凯先跑,结果两人同时到达终点,图中l1,l2分别表示小凯、小南两人的路程y(米)和小凯出发的时间x(秒)之间的函数关系,则小南让小凯先跑的时间是( )
A.3秒 B.秒 C.秒 D.5秒
12.如图,已知直线l1:y=-3x+6与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
A.-3<k<0 B.-3<k<3 C.0<k<3 D.0<k<6
二.填空题(共5小题)
13.若点P(m,5)在函数y=2x-1的图象上,则m的值为 ______.
14.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.-1.5)两点,那么当y<0时,自变量x的取值范围是 ______.
15.某水果店销售某种水果,销售额y(元)与一次销售量x(kg)与之间的函数关系如图所示.若王叔叔从该水果店一次性购买25kg该种水果,需要付款 ______元.
16.如图,直线y=-x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 ______.
17.如图,四边形ABCD的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3).
(1)四边形ABCD的面积为 ______;
(2)当过点B的直线l将四边形ABCD的面积分成面积相等的两部分时,则直线l的函数表达式为 ______.
三.解答题(共5小题)
18.跳绳项目在中考体考中易得分,是大多数学生首选的项目,在中考体考来临前,某文具店看准商机购进甲、乙两种跳绳.已知甲、乙两种跳绳进价单价之和为32元;甲种跳绳每根获利4元,乙种跳绳每根获利5元;店主第一批购买甲种跳绳25根、乙种跳绳30根一共花费885元.
(1)甲、乙两种跳绳的单价分别是多少元?
(2)若该文具店预备第二批购进甲、乙两种跳绳共60根,在费用不超过1000元的情况下,如何进货才能保证利润W最大?
19.甲、乙两车分别从相距360km的沈阳、大连两地出发,匀速行驶,先相向而行,乙车在甲车出发1h后出发,到达沈阳后停止行驶,甲车到达大连后,立即按原路原速返回沈阳(甲车调头的时间忽略不计),甲、乙两车距大连的路程与甲车出发时间x(单位:h)之间的图象如图所示,请结合图象信息解答下列问题:
(1)乙车的行驶速度是 ______km/h,a=______;甲车的行驶速度是 ______km/h;
(2)甲车与乙车第一次相遇时,距离沈阳的路程是 ______km.
(3)甲车出发多少小时后两车相距为100km?
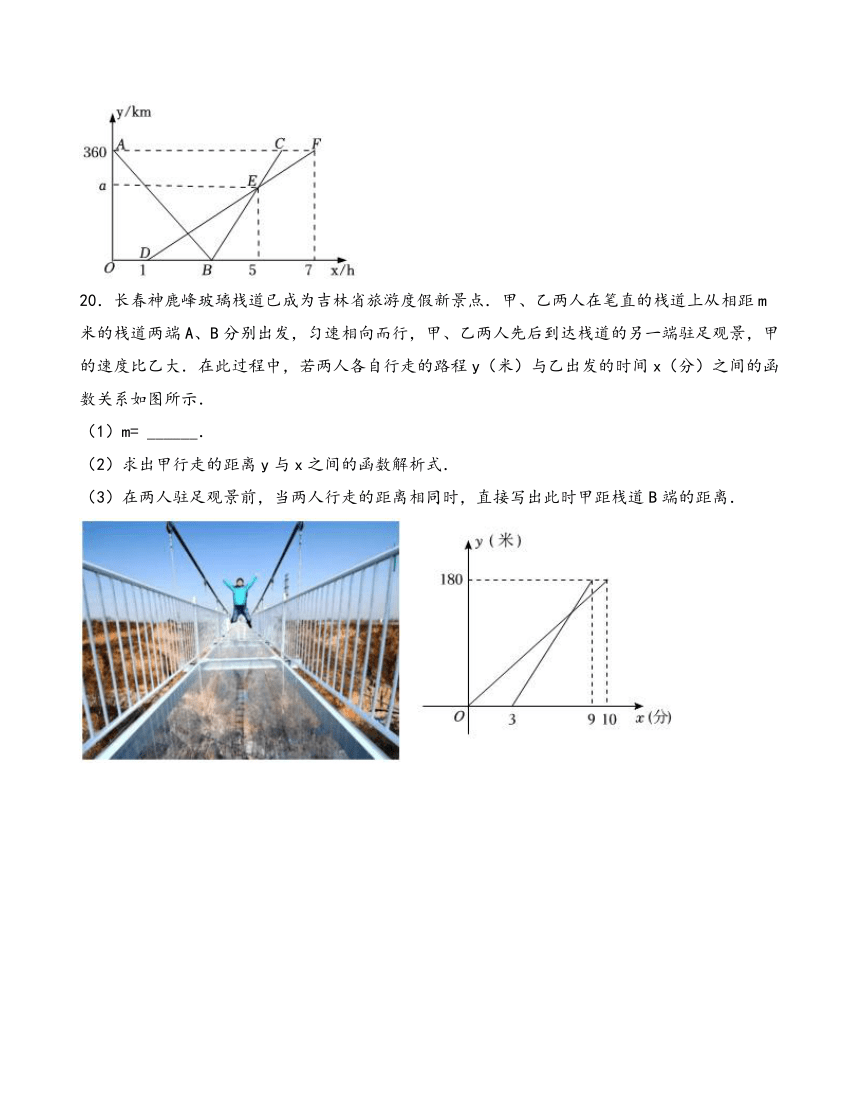
20.长春神鹿峰玻璃栈道已成为吉林省旅游度假新景点.甲、乙两人在笔直的栈道上从相距m米的栈道两端A、B分别出发,匀速相向而行,甲、乙两人先后到达栈道的另一端驻足观景,甲的速度比乙大.在此过程中,若两人各自行走的路程y(米)与乙出发的时间x(分)之间的函数关系如图所示.
(1)m= ______.
(2)求出甲行走的距离y与x之间的函数解析式.
(3)在两人驻足观景前,当两人行走的距离相同时,直接写出此时甲距栈道B端的距离.
21.如图1,直线AB:y=2x+2与直线AC交于y轴上一点A,点C在x轴正半轴上,.
(1)求直线AC的函数表达式;
(2)如图2,将直线AC绕点C逆时针旋转与射线AB交于点D,若△ACD面积是,求点D的坐标;
(3)点E是直线AC上的一个动点,在坐标轴上找一点F,连接BE,EF,FB,当△BEF是以EF为底边的等腰直角三角形时,直接写出F点的坐标.
22.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
冀教版八年级下 第21章 一次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、D 4、C 5、A 6、D 7、A 8、C 9、B 10、A 11、D 12、C
二.填空题(共5小题)
13、3; 14、x<2; 15、220; 16、; 17、14;;
三.解答题(共5小题)
18、解:(1)设甲、乙两种跳绳的单价分别是x元和y元,根据题意得,
,
解得:,
答:甲、乙两种跳绳的单价分别是15元和17元;
(2)解:设第二批购进甲种跳绳a根,乙种跳绳(60-a)根,由题意得,
W=4a+5(60-a)=-a+300,
∵-1<0,
∴W随a的增大而减小,
∵费用不超过1000元,
∴15a+17(60-a)≤1000,
解得:a≥10,
∴60-a=50(根),
∴当购进甲种跳绳10根,购进乙种跳绳50根,利润W最大.
19、解:(1)乙车的速度为360÷(7-1)=60(km/h),
a=60×(5-1)=240,
乙车距哈市的路程y2与甲车出发时间x之间的函数解析式是y2=60(x-1)=60x-60,
甲车的速度为(360+240)÷5=120(km/h).
故答案为:60,240,120;
(2)根据题意得:AB段的解析式为y=360-120x(0≤x≤3);
DF段的解析式为y=60(x-1)=60x-60(1≤x≤7).
当y=360-120x=60x-60时,x=,
此时120x=120×=280(km).
答:甲车与乙车第一次相遇时,距离沈阳的路程是280千米;
故答案为:280;
(3)设甲车出发t小时后,两车相距100km时,由题意可得:
①第一次相遇前,有120t+100+60(t-1)=360,解得 ,
②第一次相遇后,有20t+60(t-1)-100=360,解得 ;
③第二次相遇前,有120rt-360+100=60(t-1),解得 ,
综上所述:甲车出发 、 或小时后两车相距为100km.
20、解:(1)由图象可知,m的值为180,
故答案为:180;
(2)设直线解析式为y=kx+b,把(3,0),(9,180)代入得:,
解得,
∴直线解析式为y=30x-90(3≤x≤9);
(3)由图象可知,乙行走的速度为=18(米/分),
根据题意得:18x=30(x-3),
解得x=7.5,
此时甲距栈道B端的距离为180-30×(7.5-3)=180-135=45(米).
21、解:(1)直线AB:y=2x+2分别与x轴,y轴交于B、A两点,
∴A点坐标为(0,2),
∵点C在x轴正半轴上,OC=,
∴C(,0),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的函数表达式为y=-x+2;
(2)∵B(-1,0),OC=,A(0,2),
∴BC=1+=,
∴S△ABC=BC AO=×2=,
由题意知,点D在x轴下方,
∵S△ACD=S△ABC+S△BCD,
∴|=,
∴yD=-1,
把y=-1代入y=2x+2,
∴2x+2=-1,
解得x=-,
∴D(-,-1);
(3)若点F在x轴的正半轴,如图,
∵直线AC的解析式为y=-x+2,
∴x=-1时,y=-×(-1)+2=,
∴BE=BF=,
∴OF=BF-OB=,
∴F(,0);
若点F在x轴的负半轴,如图,
OF=BF+OB=+1=,
∴F(-,0);
若点F在y轴的负半轴,如图,
过点E作EH⊥x轴于点H,
∵△EBF是等腰直角三角形,
∴∠EBF=90°,EB=BF,
∵∠EBH+∠OBF=∠OBF+∠BFO=90°,
∴∠EBH=∠BFO,
∴△EBH≌△BFO(AAS),
∴EH=OB,BH=OF,
设E(m,-m+2),
∴-m+2=1,
解得m=,
∴BH=OB+OH=1+=,
∴OF=BF=,
∴F(0,-);
若点F在y轴的正半轴,如图,
过点E作EG⊥x轴于点G,
同理可得EG=OB,
∴m-2=1,
∴m=,
∴BG=,
∴OF=,
∴F(0,).
综上所述,点F的坐标为(,0)或(-,0)或(0,-)或(0,).
22、解:(1)设y乙与t之间的函数关系式是y乙=kt+b,
,
解得,
即y乙与t之间的函数关系式是y乙=120t-600(5≤t≤8);
(2)由图象可得,
甲的工作效率为120÷3=40(个/时),
a=120+40×(8-4)=280,
即a的值是280,实际意义是当甲加工8小时时,一共加工了280个零件;
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480个,
120+40(c-4)+(120c-600)=480,
解得c=7,
即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
一.选择题(共12小题)
1.下列四点中,在函数y=3x+2的图象上的点是( )
A.(-1,1) B.(-1,-1) C.(2,0) D.(0,-1.5)
2.函数y=x+2的图象如图所示,当y>0时,x的值是( )
A.x<-2 B.x>-2 C.x>2 D.x<2
3.已知一次函数y=kx+k+1,y随x的增大而减小,且图象与y轴交于正半轴,则k的取值范围是( )
A.k<-1或k>1 B.-1<k<1 C.0<k<1 D.-1<k<0
4.若点A(-2,y1),B(3,y2),C(1,y3)在一次函数y=-3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
5.点P(a,b)在函数y=3x+2的图象上,则代数式3a-b+1的值等于( )
A.-1 B.1 C.-3 D.3
6.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3200米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,下列说法正确的是( )
A.乙用16分钟追上甲
B.乙的速度是60米/分钟
C.乙到达终点时,甲离终点还有800米
D.当乙出发40分钟时,甲、乙两人的距离最远
7.A(x1,y1)、B(x2,y2)是直线y=(m-2)x+5图象上相异的两点,若,则m的取值范围( )
A.m>2 B.m<2 C.m≥2 D.m≤2
8.能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且mn≠0)的图象的是( )
A. B. C. D.
9.已知直线y=kx+3经过点(2,m)和(4,n),其中mn<0,则k的值可能为( )
A.-2 B.-1 C.1 D.2
10.要将直线y=2x+3平移后过点(2,8),下列平移方法正确的是( )
A.向上平移1个单位长度 B.向下平移1个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
11.小南和小凯进行百米赛跑,因小南比小凯跑得快,若两人同时起跑,小南肯定赢.现小南让小凯先跑,结果两人同时到达终点,图中l1,l2分别表示小凯、小南两人的路程y(米)和小凯出发的时间x(秒)之间的函数关系,则小南让小凯先跑的时间是( )
A.3秒 B.秒 C.秒 D.5秒
12.如图,已知直线l1:y=-3x+6与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
A.-3<k<0 B.-3<k<3 C.0<k<3 D.0<k<6
二.填空题(共5小题)
13.若点P(m,5)在函数y=2x-1的图象上,则m的值为 ______.
14.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.-1.5)两点,那么当y<0时,自变量x的取值范围是 ______.
15.某水果店销售某种水果,销售额y(元)与一次销售量x(kg)与之间的函数关系如图所示.若王叔叔从该水果店一次性购买25kg该种水果,需要付款 ______元.
16.如图,直线y=-x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 ______.
17.如图,四边形ABCD的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3).
(1)四边形ABCD的面积为 ______;
(2)当过点B的直线l将四边形ABCD的面积分成面积相等的两部分时,则直线l的函数表达式为 ______.
三.解答题(共5小题)
18.跳绳项目在中考体考中易得分,是大多数学生首选的项目,在中考体考来临前,某文具店看准商机购进甲、乙两种跳绳.已知甲、乙两种跳绳进价单价之和为32元;甲种跳绳每根获利4元,乙种跳绳每根获利5元;店主第一批购买甲种跳绳25根、乙种跳绳30根一共花费885元.
(1)甲、乙两种跳绳的单价分别是多少元?
(2)若该文具店预备第二批购进甲、乙两种跳绳共60根,在费用不超过1000元的情况下,如何进货才能保证利润W最大?
19.甲、乙两车分别从相距360km的沈阳、大连两地出发,匀速行驶,先相向而行,乙车在甲车出发1h后出发,到达沈阳后停止行驶,甲车到达大连后,立即按原路原速返回沈阳(甲车调头的时间忽略不计),甲、乙两车距大连的路程与甲车出发时间x(单位:h)之间的图象如图所示,请结合图象信息解答下列问题:
(1)乙车的行驶速度是 ______km/h,a=______;甲车的行驶速度是 ______km/h;
(2)甲车与乙车第一次相遇时,距离沈阳的路程是 ______km.
(3)甲车出发多少小时后两车相距为100km?
20.长春神鹿峰玻璃栈道已成为吉林省旅游度假新景点.甲、乙两人在笔直的栈道上从相距m米的栈道两端A、B分别出发,匀速相向而行,甲、乙两人先后到达栈道的另一端驻足观景,甲的速度比乙大.在此过程中,若两人各自行走的路程y(米)与乙出发的时间x(分)之间的函数关系如图所示.
(1)m= ______.
(2)求出甲行走的距离y与x之间的函数解析式.
(3)在两人驻足观景前,当两人行走的距离相同时,直接写出此时甲距栈道B端的距离.
21.如图1,直线AB:y=2x+2与直线AC交于y轴上一点A,点C在x轴正半轴上,.
(1)求直线AC的函数表达式;
(2)如图2,将直线AC绕点C逆时针旋转与射线AB交于点D,若△ACD面积是,求点D的坐标;
(3)点E是直线AC上的一个动点,在坐标轴上找一点F,连接BE,EF,FB,当△BEF是以EF为底边的等腰直角三角形时,直接写出F点的坐标.
22.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
冀教版八年级下 第21章 一次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、D 4、C 5、A 6、D 7、A 8、C 9、B 10、A 11、D 12、C
二.填空题(共5小题)
13、3; 14、x<2; 15、220; 16、; 17、14;;
三.解答题(共5小题)
18、解:(1)设甲、乙两种跳绳的单价分别是x元和y元,根据题意得,
,
解得:,
答:甲、乙两种跳绳的单价分别是15元和17元;
(2)解:设第二批购进甲种跳绳a根,乙种跳绳(60-a)根,由题意得,
W=4a+5(60-a)=-a+300,
∵-1<0,
∴W随a的增大而减小,
∵费用不超过1000元,
∴15a+17(60-a)≤1000,
解得:a≥10,
∴60-a=50(根),
∴当购进甲种跳绳10根,购进乙种跳绳50根,利润W最大.
19、解:(1)乙车的速度为360÷(7-1)=60(km/h),
a=60×(5-1)=240,
乙车距哈市的路程y2与甲车出发时间x之间的函数解析式是y2=60(x-1)=60x-60,
甲车的速度为(360+240)÷5=120(km/h).
故答案为:60,240,120;
(2)根据题意得:AB段的解析式为y=360-120x(0≤x≤3);
DF段的解析式为y=60(x-1)=60x-60(1≤x≤7).
当y=360-120x=60x-60时,x=,
此时120x=120×=280(km).
答:甲车与乙车第一次相遇时,距离沈阳的路程是280千米;
故答案为:280;
(3)设甲车出发t小时后,两车相距100km时,由题意可得:
①第一次相遇前,有120t+100+60(t-1)=360,解得 ,
②第一次相遇后,有20t+60(t-1)-100=360,解得 ;
③第二次相遇前,有120rt-360+100=60(t-1),解得 ,
综上所述:甲车出发 、 或小时后两车相距为100km.
20、解:(1)由图象可知,m的值为180,
故答案为:180;
(2)设直线解析式为y=kx+b,把(3,0),(9,180)代入得:,
解得,
∴直线解析式为y=30x-90(3≤x≤9);
(3)由图象可知,乙行走的速度为=18(米/分),
根据题意得:18x=30(x-3),
解得x=7.5,
此时甲距栈道B端的距离为180-30×(7.5-3)=180-135=45(米).
21、解:(1)直线AB:y=2x+2分别与x轴,y轴交于B、A两点,
∴A点坐标为(0,2),
∵点C在x轴正半轴上,OC=,
∴C(,0),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的函数表达式为y=-x+2;
(2)∵B(-1,0),OC=,A(0,2),
∴BC=1+=,
∴S△ABC=BC AO=×2=,
由题意知,点D在x轴下方,
∵S△ACD=S△ABC+S△BCD,
∴|=,
∴yD=-1,
把y=-1代入y=2x+2,
∴2x+2=-1,
解得x=-,
∴D(-,-1);
(3)若点F在x轴的正半轴,如图,
∵直线AC的解析式为y=-x+2,
∴x=-1时,y=-×(-1)+2=,
∴BE=BF=,
∴OF=BF-OB=,
∴F(,0);
若点F在x轴的负半轴,如图,
OF=BF+OB=+1=,
∴F(-,0);
若点F在y轴的负半轴,如图,
过点E作EH⊥x轴于点H,
∵△EBF是等腰直角三角形,
∴∠EBF=90°,EB=BF,
∵∠EBH+∠OBF=∠OBF+∠BFO=90°,
∴∠EBH=∠BFO,
∴△EBH≌△BFO(AAS),
∴EH=OB,BH=OF,
设E(m,-m+2),
∴-m+2=1,
解得m=,
∴BH=OB+OH=1+=,
∴OF=BF=,
∴F(0,-);
若点F在y轴的正半轴,如图,
过点E作EG⊥x轴于点G,
同理可得EG=OB,
∴m-2=1,
∴m=,
∴BG=,
∴OF=,
∴F(0,).
综上所述,点F的坐标为(,0)或(-,0)或(0,-)或(0,).
22、解:(1)设y乙与t之间的函数关系式是y乙=kt+b,
,
解得,
即y乙与t之间的函数关系式是y乙=120t-600(5≤t≤8);
(2)由图象可得,
甲的工作效率为120÷3=40(个/时),
a=120+40×(8-4)=280,
即a的值是280,实际意义是当甲加工8小时时,一共加工了280个零件;
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480个,
120+40(c-4)+(120c-600)=480,
解得c=7,
即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
