冀教版数学九年级下 第29章 直线与圆的位置关系 单元测试(含答案)
文档属性
| 名称 | 冀教版数学九年级下 第29章 直线与圆的位置关系 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 126.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 00:00:00 | ||
图片预览



文档简介
冀教版九年级下 第29章 直线与圆的位置关系 单元测试
一.选择题(共12小题)
1.已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
2.如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则tan∠APO等于( )
A. B. C. D.
3.如图,已知AB,BC,CD是正n边形的三条边,在同一平面内,在BC边上以B为顶点作正方形BEMN,若∠ABN=45°,则该n边形的内角和为( )
A.900° B.1080° C.1260° D.1440°
4.如图,AB是⊙O的直径,BM与⊙O相切于点B,∠A=27°,半径OE的延长线交BM于点M,则∠M的度数是( )
A.36° B.38° C.40° D.43°
5.半径为5的四个圆按如图所示位置摆放,若其中有一个圆的圆心到直线l的距离为4,则这个圆可以是( )
A.⊙O1 B.⊙O2 C.⊙O3 D.⊙O4
6.已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于点C,AB=4,PB=3.CD⊥AB,垂足为D.E是弧AC上一点,AE=5EC.延长AE,与DC,BP的延长线分别交于点F,G,则的值( )
A. B. C. D.
7.如图,AB是⊙O的直径,点C,D在⊙O上且关于直径AB对称,MN是⊙O切线,切点为B,若∠CBO=50°,则∠DBN的大小为( )
A.50° B.40° C.35° D.25°
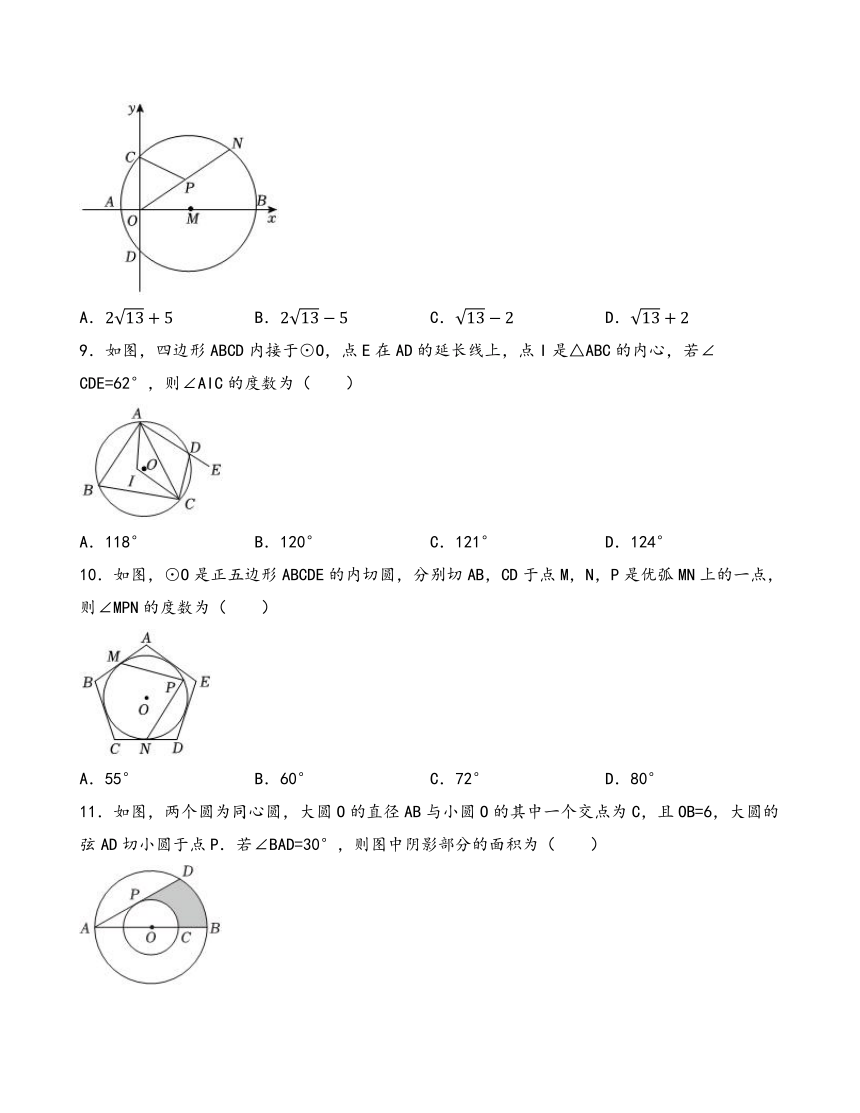
8.如图所示,M是x轴的正半轴上一点,⊙M与x轴交于A、B两点,与y轴交于C、D两点,A(-2,0),C(0,6),点N是⊙M上任意一点,点P是ON的中点,则CP的最小值为( )
A. B. C. D.
9.如图,四边形ABCD内接于⊙O,点E在AD的延长线上,点I是△ABC的内心,若∠CDE=62°,则∠AIC的度数为( )
A.118° B.120° C.121° D.124°
10.如图,⊙O是正五边形ABCDE的内切圆,分别切AB,CD于点M,N,P是优弧MN上的一点,则∠MPN的度数为( )
A.55° B.60° C.72° D.80°
11.如图,两个圆为同心圆,大圆O的直径AB与小圆O的其中一个交点为C,且OB=6,大圆的弦AD切小圆于点P.若∠BAD=30°,则图中阴影部分的面积为( )
A. B. C. D.
12.如图,⊙O内切于正方形ABCD,边AD、CD分别与⊙O切于点E、F,点M、N分别在线段DE、DF上,且MN与⊙O相切.若△MBN的面积为6,则⊙O的半径为( )
A.2 B. C.2 D.
二.填空题(共5小题)
13.如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD.若∠AOD=80°,则∠C的度数为______.
14.如图,AB是⊙O的内接正n边形的一边,点C在⊙O上,∠ACB=22.5°,则n= ______.
15.如图,△ABO为等边三角形,A,B在⊙O的圆周上,AO=1,P为圆周上一动点,C为BP的中点,当P在圆周上运动时,AC的最小值为______.
16.如图,以AB为直径的⊙O与AE相切于点A,以AE为边作菱形ACDE,点C在⊙O上,CD与AB交于点F,连接CE,与⊙O交于点G,连接GF,若AB=8,,则CF= ______,GF= ______.
17.如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以A为圆心,半径为1作⊙A,P为⊙A上的一个动点,连接PD,PO,则△PDO的面积的最大值为 ______.
三.解答题(共5小题)
18.如图,⊙O中,AB为直径,BC与⊙O相切于点B,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
(1)求证:OD⊥AE;
(2)若,OA=3,求AE的长.
19.如图,在△ABC中,AC=4,BC=20,∠C=90°,点O为AB边上一点,⊙O切边AC于点D,设CD=x,⊙O的半径为y.
(1)求y关于x的函数解析式;
(2)当y=5时,求⊙O在BC边上截得的线段EF的长.
20.如图,△ABC中,∠B=∠ACB=30°,点O在线段BC上,连接AO,AO=OC,过点C作CD∥AB交AO的延长线于点D,以O为圆心,OD为半径作⊙O.
(1)求证:AC为⊙O的切线;
(2)若AD=6,求图中阴影部分的面积.
21.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B.
(1)求证:CD是⊙O的切线;
(2)过点D作DE⊥AB,垂足为E,DE交AC于点F.
①求证:AF CF=2DF EF;
②若CD=20,sinA=,求CF的长.
22.如图,△ABC内接于⊙O,AB是⊙O的直径,CE是⊙O的切线,D是⊙O上的一点,CE⊥AD,垂足为点E,AB与CD相交于点F.
(1)求证:CO平分∠BCD;
(2)若AE=4,AB=9,求AC的长.
冀教版九年级下 第29章 直线与圆的位置关系 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、D 3、B 4、A 5、C 6、C 7、B 8、B 9、C 10、C 11、B 12、D
二.填空题(共5小题)
13、50°; 14、8; 15、; 16、;; 17、;
三.解答题(共5小题)
18、(1)证明:∵BC与⊙O相切于点B,
∴AB⊥BC,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵∠AOD=∠C,
∴∠A+∠AOD=90°,
∴∠ADO=90°,
∴OD⊥AE;
(2)解:如图,连接BE,
∵OA=3,
∴AB=6,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵cosA==,
∴AE=4.
19、解:(1)连接OD,如图,
∵⊙O切边AC于点D,
∴OD⊥AC,
∵∠C=90°,
∴BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴=,即=,
∴y=-5x+20;
(2)当y=5时,-5x+20=5,解得x=3,即CD=3,
作OH⊥BC于H,连接OE,如图,则EH=FH,
∵∠ODC=∠C=∠OHC=90°,
∴四边形ODCH为矩形,
∴OH=CD=3,
在Rt△OEH中,HE===4,
∴EF=2HE=8.
20、(1)证明:如图,过点O作OE⊥AC于点E,
∵∠B=∠ACB=30°,
∴∠BAC=180°-30°-30°=120°,
∵AO=OC,
∴∠CAO=∠ACB=30°,
∴∠BAD=∠BAC-∠CAO=90°,
∵CD∥AB,
∴∠ODC=∠BAD=90°,∠DCO=∠B=30°=∠ECO,
∵OE⊥AC,
∴∠OEC=90°=∠ODC,
在△OCE和△OCD中,
,
∴△OCE≌△OCD(AAS),
∴OE=OD,
∵⊙O是以O为圆心,OD为半径,
∴OE为半径,
又OE⊥AC,
∴AC为⊙O的切线;
(2)解:由(1)得,∠ODC=90°,∠DAC=30°,
∵AD=6,
∴CD=AD tan30°=6×=2,
∵∠OCD=30°,
∴OD=CD tan30°=2×=2,
∵△OCE≌△OCD,
∴四边形ODCE的面积=2S△OCD=2×CD OD=4,
∵S扇形ODE==π,
∴阴影部分的面积=四边形ODCE的面积-S扇形ODE=4-π.
21、(1)证明:如图,连接OC,
∵OC=OA,
∴∠OCA=∠OAC,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠OAC+∠B=90°,
∵∠DCA=∠B,
∴∠OCA+∠DCA=∠OCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)①证明:如图,过点D作DM⊥CF于点M,则∠DMF=90°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠DMF=∠AEF=90°,
∵∠DFM=∠AFE(对顶角相等),
∴△DFM∽△AFE,
∴,
∴AF FM=DF EF,
∵∠OCA+∠DCA=90°,∠OCA=∠OAC,
∴∠OAC+∠DCA=90°,
∵∠OAC+∠EFA=90°,
∴∠DCA=∠EFA,
∵∠EFA=∠DFC,
∴∠DCA=∠DFC,
∴△CDF是等腰三角形,
∵DM⊥CF,
∴CM=FM,
∴,
∴,
∴AF CF=2DF EF;
②解:∵∠CDM=∠MDF=∠OCA=∠OAC,
∴,
∴,
∵CD=20,
∴,
∴CF=2CM=2×12=24.
22、(1)证明:∵CE⊥AD,
∴∠E=90°,
由题意可得:∠OCE=90°,
∴∠OCE+∠E=180°,
∴OC∥DE,
∴∠D=∠OCD,
∴∠B=∠OCB=∠D,
∴∠OCB=∠OCD,
∴CO平分∠BCD;
(2)解:由题意可得:∠ACB=90°.
∵∠OCE=∠ACO+∠ACE=90°,∠ACB=∠ACO+∠OCB=90°,
∴∠ACE=∠OCB,
∵∠B=∠OCB,
∴∠ACE=∠B,
又∵∠ACB=∠AEC=90°,
∴△ACE∽△ABC,
∴,
即AC2=AE AB=4×9=36.
∴AC=6.
一.选择题(共12小题)
1.已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
2.如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则tan∠APO等于( )
A. B. C. D.
3.如图,已知AB,BC,CD是正n边形的三条边,在同一平面内,在BC边上以B为顶点作正方形BEMN,若∠ABN=45°,则该n边形的内角和为( )
A.900° B.1080° C.1260° D.1440°
4.如图,AB是⊙O的直径,BM与⊙O相切于点B,∠A=27°,半径OE的延长线交BM于点M,则∠M的度数是( )
A.36° B.38° C.40° D.43°
5.半径为5的四个圆按如图所示位置摆放,若其中有一个圆的圆心到直线l的距离为4,则这个圆可以是( )
A.⊙O1 B.⊙O2 C.⊙O3 D.⊙O4
6.已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于点C,AB=4,PB=3.CD⊥AB,垂足为D.E是弧AC上一点,AE=5EC.延长AE,与DC,BP的延长线分别交于点F,G,则的值( )
A. B. C. D.
7.如图,AB是⊙O的直径,点C,D在⊙O上且关于直径AB对称,MN是⊙O切线,切点为B,若∠CBO=50°,则∠DBN的大小为( )
A.50° B.40° C.35° D.25°
8.如图所示,M是x轴的正半轴上一点,⊙M与x轴交于A、B两点,与y轴交于C、D两点,A(-2,0),C(0,6),点N是⊙M上任意一点,点P是ON的中点,则CP的最小值为( )
A. B. C. D.
9.如图,四边形ABCD内接于⊙O,点E在AD的延长线上,点I是△ABC的内心,若∠CDE=62°,则∠AIC的度数为( )
A.118° B.120° C.121° D.124°
10.如图,⊙O是正五边形ABCDE的内切圆,分别切AB,CD于点M,N,P是优弧MN上的一点,则∠MPN的度数为( )
A.55° B.60° C.72° D.80°
11.如图,两个圆为同心圆,大圆O的直径AB与小圆O的其中一个交点为C,且OB=6,大圆的弦AD切小圆于点P.若∠BAD=30°,则图中阴影部分的面积为( )
A. B. C. D.
12.如图,⊙O内切于正方形ABCD,边AD、CD分别与⊙O切于点E、F,点M、N分别在线段DE、DF上,且MN与⊙O相切.若△MBN的面积为6,则⊙O的半径为( )
A.2 B. C.2 D.
二.填空题(共5小题)
13.如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD.若∠AOD=80°,则∠C的度数为______.
14.如图,AB是⊙O的内接正n边形的一边,点C在⊙O上,∠ACB=22.5°,则n= ______.
15.如图,△ABO为等边三角形,A,B在⊙O的圆周上,AO=1,P为圆周上一动点,C为BP的中点,当P在圆周上运动时,AC的最小值为______.
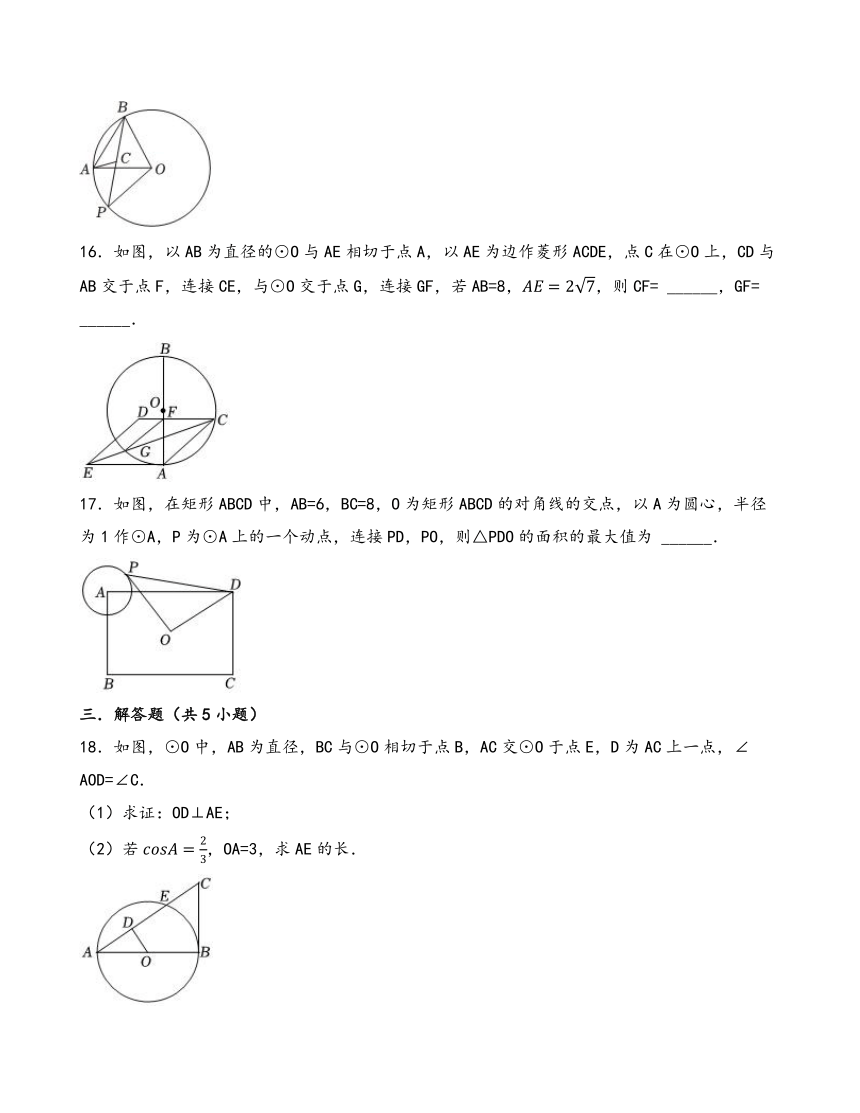
16.如图,以AB为直径的⊙O与AE相切于点A,以AE为边作菱形ACDE,点C在⊙O上,CD与AB交于点F,连接CE,与⊙O交于点G,连接GF,若AB=8,,则CF= ______,GF= ______.
17.如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以A为圆心,半径为1作⊙A,P为⊙A上的一个动点,连接PD,PO,则△PDO的面积的最大值为 ______.
三.解答题(共5小题)
18.如图,⊙O中,AB为直径,BC与⊙O相切于点B,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
(1)求证:OD⊥AE;
(2)若,OA=3,求AE的长.
19.如图,在△ABC中,AC=4,BC=20,∠C=90°,点O为AB边上一点,⊙O切边AC于点D,设CD=x,⊙O的半径为y.
(1)求y关于x的函数解析式;
(2)当y=5时,求⊙O在BC边上截得的线段EF的长.
20.如图,△ABC中,∠B=∠ACB=30°,点O在线段BC上,连接AO,AO=OC,过点C作CD∥AB交AO的延长线于点D,以O为圆心,OD为半径作⊙O.
(1)求证:AC为⊙O的切线;
(2)若AD=6,求图中阴影部分的面积.
21.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B.
(1)求证:CD是⊙O的切线;
(2)过点D作DE⊥AB,垂足为E,DE交AC于点F.
①求证:AF CF=2DF EF;
②若CD=20,sinA=,求CF的长.
22.如图,△ABC内接于⊙O,AB是⊙O的直径,CE是⊙O的切线,D是⊙O上的一点,CE⊥AD,垂足为点E,AB与CD相交于点F.
(1)求证:CO平分∠BCD;
(2)若AE=4,AB=9,求AC的长.
冀教版九年级下 第29章 直线与圆的位置关系 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、D 3、B 4、A 5、C 6、C 7、B 8、B 9、C 10、C 11、B 12、D
二.填空题(共5小题)
13、50°; 14、8; 15、; 16、;; 17、;
三.解答题(共5小题)
18、(1)证明:∵BC与⊙O相切于点B,
∴AB⊥BC,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵∠AOD=∠C,
∴∠A+∠AOD=90°,
∴∠ADO=90°,
∴OD⊥AE;
(2)解:如图,连接BE,
∵OA=3,
∴AB=6,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵cosA==,
∴AE=4.
19、解:(1)连接OD,如图,
∵⊙O切边AC于点D,
∴OD⊥AC,
∵∠C=90°,
∴BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴=,即=,
∴y=-5x+20;
(2)当y=5时,-5x+20=5,解得x=3,即CD=3,
作OH⊥BC于H,连接OE,如图,则EH=FH,
∵∠ODC=∠C=∠OHC=90°,
∴四边形ODCH为矩形,
∴OH=CD=3,
在Rt△OEH中,HE===4,
∴EF=2HE=8.
20、(1)证明:如图,过点O作OE⊥AC于点E,
∵∠B=∠ACB=30°,
∴∠BAC=180°-30°-30°=120°,
∵AO=OC,
∴∠CAO=∠ACB=30°,
∴∠BAD=∠BAC-∠CAO=90°,
∵CD∥AB,
∴∠ODC=∠BAD=90°,∠DCO=∠B=30°=∠ECO,
∵OE⊥AC,
∴∠OEC=90°=∠ODC,
在△OCE和△OCD中,
,
∴△OCE≌△OCD(AAS),
∴OE=OD,
∵⊙O是以O为圆心,OD为半径,
∴OE为半径,
又OE⊥AC,
∴AC为⊙O的切线;
(2)解:由(1)得,∠ODC=90°,∠DAC=30°,
∵AD=6,
∴CD=AD tan30°=6×=2,
∵∠OCD=30°,
∴OD=CD tan30°=2×=2,
∵△OCE≌△OCD,
∴四边形ODCE的面积=2S△OCD=2×CD OD=4,
∵S扇形ODE==π,
∴阴影部分的面积=四边形ODCE的面积-S扇形ODE=4-π.
21、(1)证明:如图,连接OC,
∵OC=OA,
∴∠OCA=∠OAC,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠OAC+∠B=90°,
∵∠DCA=∠B,
∴∠OCA+∠DCA=∠OCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)①证明:如图,过点D作DM⊥CF于点M,则∠DMF=90°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠DMF=∠AEF=90°,
∵∠DFM=∠AFE(对顶角相等),
∴△DFM∽△AFE,
∴,
∴AF FM=DF EF,
∵∠OCA+∠DCA=90°,∠OCA=∠OAC,
∴∠OAC+∠DCA=90°,
∵∠OAC+∠EFA=90°,
∴∠DCA=∠EFA,
∵∠EFA=∠DFC,
∴∠DCA=∠DFC,
∴△CDF是等腰三角形,
∵DM⊥CF,
∴CM=FM,
∴,
∴,
∴AF CF=2DF EF;
②解:∵∠CDM=∠MDF=∠OCA=∠OAC,
∴,
∴,
∵CD=20,
∴,
∴CF=2CM=2×12=24.
22、(1)证明:∵CE⊥AD,
∴∠E=90°,
由题意可得:∠OCE=90°,
∴∠OCE+∠E=180°,
∴OC∥DE,
∴∠D=∠OCD,
∴∠B=∠OCB=∠D,
∴∠OCB=∠OCD,
∴CO平分∠BCD;
(2)解:由题意可得:∠ACB=90°.
∵∠OCE=∠ACO+∠ACE=90°,∠ACB=∠ACO+∠OCB=90°,
∴∠ACE=∠OCB,
∵∠B=∠OCB,
∴∠ACE=∠B,
又∵∠ACB=∠AEC=90°,
∴△ACE∽△ABC,
∴,
即AC2=AE AB=4×9=36.
∴AC=6.
