冀教版数学九年级下 第30章 二次函数 单元测试(含答案)
文档属性
| 名称 | 冀教版数学九年级下 第30章 二次函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.0KB | ||
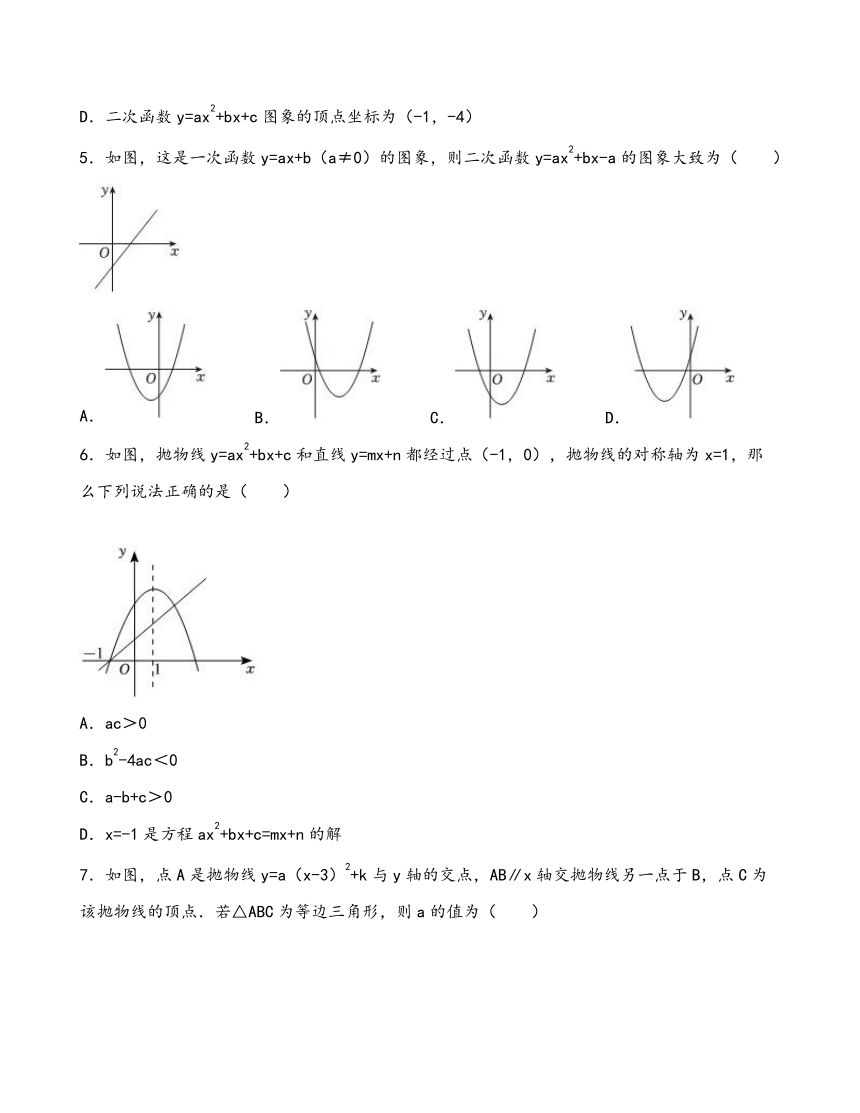
| 资源类型 | 教案 | ||
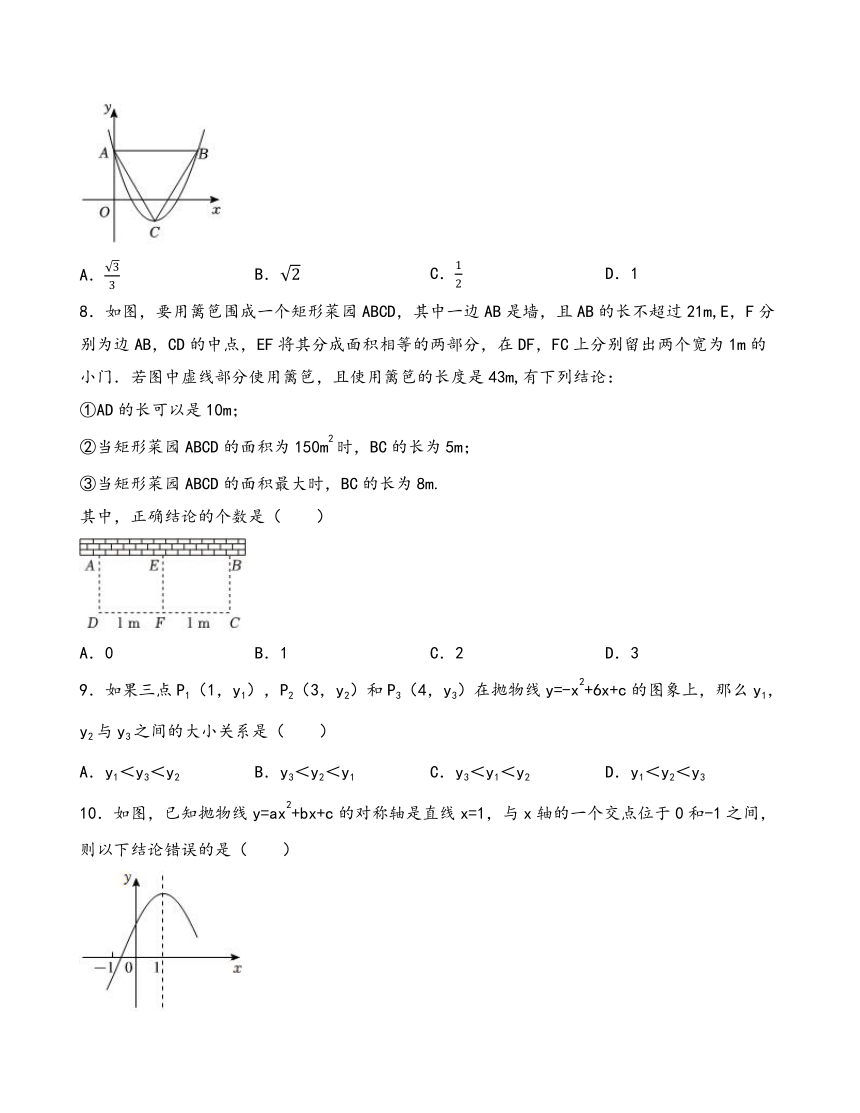
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:32:10 | ||
图片预览



文档简介
冀教版九年级下 第30章 二次函数 单元测试
一.选择题(共12小题)
1.抛物线y=x2+4x-4的对称轴为直线( )
A.x=2 B.x=-2 C.x=-4 D.x=4
2.抛物线的函数表达式为y=3(x-2)2+1,将函数图象向上平移2个单位长度,向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )
A.y=3(x-5)2+3 B.y=3(x+1)2+3
C.y=3(x-5)2-1 D.y=3(x+1)2-1
3.已知二次函数y=ax2+bx+c的图象如图所示,P1(x1,y1),P2(x2,y2)是函数图象上的两点,下列结论正确的是( )
A.a+b+c<0 B.b+2a=0
C.x1>x2,则y1>y2 D.若y1=y2,则x1+x2=1
4.某同学用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
x … -1 0 1 2 3 …
y … -4 -3 0 5 12 …
A.对称轴为x=1
B.关于x的一元二次方程ax2+bx+c=0只有一个根x=1
C.当x<3时,y随x的减小而减小
D.二次函数y=ax2+bx+c图象的顶点坐标为(-1,-4)
5.如图,这是一次函数y=ax+b(a≠0)的图象,则二次函数y=ax2+bx-a的图象大致为( )
A. B. C. D.
6.如图,抛物线y=ax2+bx+c和直线y=mx+n都经过点(-1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.a-b+c>0
D.x=-1是方程ax2+bx+c=mx+n的解
7.如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
8.如图,要用篱笆围成一个矩形菜园ABCD,其中一边AB是墙,且AB的长不超过21m,E,F分别为边AB,CD的中点,EF将其分成面积相等的两部分,在DF,FC上分别留出两个宽为1m的小门.若图中虚线部分使用篱笆,且使用篱笆的长度是43m,有下列结论:
①AD的长可以是10m;
②当矩形菜园ABCD的面积为150m2时,BC的长为5m;
③当矩形菜园ABCD的面积最大时,BC的长为8m.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
9.如果三点P1(1,y1),P2(3,y2)和P3(4,y3)在抛物线y=-x2+6x+c的图象上,那么y1,y2与y3之间的大小关系是( )
A.y1<y3<y2 B.y3<y2<y1 C.y3<y1<y2 D.y1<y2<y3
10.如图,已知抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点位于0和-1之间,则以下结论错误的是( )
A.abc<0
B.2a+b=0
C.若点(-3,y1)和(4,y2)在该抛物线上,则y1>y2
D.若c-a>1,则关于x的一元二次方程ax2+bx+c=1有两个不相等实数根
11.如图,二次函数y=ax2+bx+c的图象过点A(m,0)和B(1,0),下列结论:①abc<0;②9a+c<-3b;③;④am2-(3a-b)m+a+b+c<0;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
12.如图,抛物线l1:与交于点A(1,-2),以下结论:
①无论x取何值,y2总是负数;
②l2可由l1向右平移3个单位,再向下平移3个单位得到;
③当-3<x<1时,随着x的增大,y1-y2的值先增大后减小.
下列说法正确的是( )
A.只有①正确 B.只有②正确
C.只有③不正确 D.①②③都正确
二.填空题(共5小题)
13.二次函数y=3(x+2)2+1的图象的顶点坐标是 ______.
14.如图,若y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为______.
15.已知点P(0,m2-4),Q(m,0),若线段PQ与抛物线y=x2+3x-4恰有一个交点,则m的取值范围是______.
16.我们把a,b,c三个数的中位数记作Z{a,b,c},直线y=kx+(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为______.
17.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2-4ac>0)的函数叫做“鹊桥”函数.某数学兴趣小组画出了“鹊桥”函数G:y=|x2-x-6|的图象(如图所示),并写出了下列结论:
①图象与坐标轴的交点为A(-2,0),B(3,0),C(0,6);
②当时,函数取得最大值;
③若(x0,y0)在函数图象上,则(1-x0,y0)也在函数图象上;
④当直线y=-x+m与函数G的图象有4个交点时,则m的取值范围是3<m<7.其中正确的结论有______.(填写所有正确结论的序号)
三.解答题(共5小题)
18.在平面直角坐标系xOy中,抛物线y=ax2-3ax-3a+1(a<0)与y轴交于点A,过点A作AB∥x轴,与抛物线交于点B.
(1)若抛物线经过点(-1,0);
①求点B的坐标;
②当t-1≤x≤t时,抛物线取得最大值为,求t的值;
(2)已知点G(1,3),H(3,3),若抛物线与线段GH有且只有一个交点(不含端点G、H),求a的取值范围.
19.已知二次函数y=ax2-(a-2)x+2(a≠0).
(1)若函数图象经过点(3,2),求抛物线的对称轴.
(2)若a>0,当x≥-1时,y随x的增大而增大,求a的取值范围.
(3)若,两点都在二次函数的图象上,试比较b与c的大小,并说明理由.
20.已知二次函数y=ax2+(2-a)x-1(a为常数,a≠0).
(1)求证:该二次函数图象与x轴有两个公共点;
(2)若A(1,y1)、B(3,y2)是该函数图象上的两个点,若y1<y2,求a的取值范围;
(3)当-1<x<1时,y随x的增大而增大,结合函数图象,则a的取值范围是 ______.
21.在平面直角坐标系中,定义两个函数y1=(x-a)(x-b),.
(1)如果函数y1的图象经过点(0,3),函数y2的图象经过点(1,5),求a2+b2的值;
(2)如果1<a<b<4,判断函数y2的图象与x轴的交点情况;
(3)若点P(-1,c)在y1上,点Q(a,c)在y2上,求ab的最小值.
22.毛乌素沙漠是中国四大沙地之一,位于陕西省榆林市长城一线以北,如图1是该沙漠边缘地区常见的抛物线状沙丘(一种风积地貌),其平面轮廓呈抛物线状.如图2,已知某一抛物线状沙丘OPA两翼端点的水平距离OA=200m,沙丘弧顶最高点P到OA的距离为80m,抛物线的对称轴垂直于OA,以OA所在直线为x轴,过点O且垂直于OA的直线为y轴建立平面直角坐标系,现计划从点M到点N种植一排柠条(M、N在抛物线上,点M在点N的左侧).
(1)求抛物线状沙丘OPA的函数表达式;
(2)ME⊥x轴于点E,NF⊥x轴于点F,若,求M、N两点之间的距离.
冀教版九年级下 第30章 二次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、B 4、D 5、C 6、D 7、A 8、C 9、A 10、C 11、B 12、C
二.填空题(共5小题)
13、(-2,1); 14、x=-1; 15、m=0或m≥1或m≤-4; 16、<k≤1或k=; 17、①③④;
三.解答题(共5小题)
18、解:(1)①∵抛物线y=ax2-3ax-3a+1(a<0)过点(-1,0),
∴a+3a-3a+1=0,
∴a=-1,
∴抛物线解析式为:y=-x2+3x+4,
∴点A坐标为(0,4),
当y=4时,即y=-x2+3x+4=4,
∴x1=0,x2=3,
∴点B(3,4),
②∵,
∴抛物线开口向下,顶点坐标为,
分以下两种情况讨论:
Ⅰ.当时,t-1≤x≤t在对称轴左侧,y随x增大而增大,
∴x=t时,为最大值,即,
解得或(舍);
Ⅱ.当即时,t-1≤x≤t在对称轴右侧,y随x增大而减小,
x=t-1时,为最大值,即,
解得或(舍),
综上所述,t的值为或;
(2)∵抛物线,
∴抛物线,
对称轴为,顶点为,
∵点G(1,3),H(3,3),若抛物线与线段GH有且只有一个交点,
分以下两种情况讨论:
Ⅰ.当抛物线y=ax2-3ax-3a+1的顶点在线段GH上时,
即:,
解得:;
Ⅱ.当抛物线顶点落在GH上方时,
当x=1时,y=a-3a-3a+1=-5a+1,
当x=3时,y=9a-9a-3a+1=-3a+1,
∵a<0,对称轴为,
∴-5a+1<-3a+1,
∵抛物线y=ax2-3ax-3a+1与线段GH有且只有一个交点(不含端点G、H),
∴与线段GH有且只有一个交点,一定在对称轴右侧,
∴,
解得:,
综上,a的取值范围是或.
19、解:(1)由条件可得9a-3(a-2)+2=2,
解得a=-1,
∴抛物线的表达式为y=-x2+3x+2,
∴抛物线的对称轴为直线.
(2)由条件可得抛物线在对称轴右侧y随x的增大而增大,
∵抛物线的对称轴为直线,
∴,
解得:,
∴;
(3)∵抛物线的对称轴为直线,
∴,
∵,,
∴点A,点B在对称轴的右侧,
①当a>0时,在对称轴右侧,y随x的增大而增大,
∵,
∴b<c.
②当a<0时,在对称轴右侧,y随x的增大而减小,
∵,
∴b>c.
综上,当a>0时,b<c;当a<0时,b>c.
20、解:(1)∵Δ=(2-a)2-4×a×(-1)=a2+4>0,
∴该二次函数图象与x轴有两个公共点;
(2)当x=1时,y=1,当x=3时,y=6a+5,
∵y1<y2,
∴6a+5>1,
解得,
又∵a≠0,
∴a的取值范围为且a≠0;
(3)∵二次函数y=ax2+(2-a)x-1,
∴抛物线的对称轴为直线,
当a>0时,抛物线开口向上,
∵当-1<x<1时,y随x的增大而增大,
∴,
解得;
当a<0时,抛物线开口向下,
∵当-1<x<1时,y随x的增大而增大,
∴,
解得a≥-2;
∴,
∵a≠0,
∴a的取值范围是,
故答案为:.
21、解:(1)把(0,3),(1,5)分别代入中,
得ab=3,a+b=4,∴a2+b2=(a+b)2-2ab=10,
∴a2+b2=(a+b)2-2ab=42-2×3=10;
(2)由题意得Δ=a2-4b,
∵1<a<b<4,
∴a2<b2<42,b2<4b,
∴a2<4b,
即Δ=a2-4b<0,
∴y2的图象与x轴没有交点;
(3)把P(-1,c),Q(a,c)分别代入中,得:
由题意得(-1-a)(-1-b)=c,a2+a2+b=c,
(-1-a)(-1-b)=c,a2+a2+b=c,
∴ab+a+b+1=2a2+b,
即ab=2a2-a-1,
设y=2a2-a-1,
图象开口向上,
∴在对称轴处取得最小值,
把代入y=2a2-a-1中得,
,
∴y=2a2-a-1的最小值为,
∵ab=2a2-a-1,
∴当时,ab的最小值为.
22、解:(1)根据题意可设抛物线的函数表达式为y=a(x-100)2+80.
将点A(200,0)代入,得a(200-100)2+80=0,
解得,
∴抛物线状沙丘OPA的函数表达式为.
(2)令,得,
解得x1=20,x2=180,
∴,,
∴M、N两点之间的距离为160m.
一.选择题(共12小题)
1.抛物线y=x2+4x-4的对称轴为直线( )
A.x=2 B.x=-2 C.x=-4 D.x=4
2.抛物线的函数表达式为y=3(x-2)2+1,将函数图象向上平移2个单位长度,向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )
A.y=3(x-5)2+3 B.y=3(x+1)2+3
C.y=3(x-5)2-1 D.y=3(x+1)2-1
3.已知二次函数y=ax2+bx+c的图象如图所示,P1(x1,y1),P2(x2,y2)是函数图象上的两点,下列结论正确的是( )
A.a+b+c<0 B.b+2a=0
C.x1>x2,则y1>y2 D.若y1=y2,则x1+x2=1
4.某同学用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
x … -1 0 1 2 3 …
y … -4 -3 0 5 12 …
A.对称轴为x=1
B.关于x的一元二次方程ax2+bx+c=0只有一个根x=1
C.当x<3时,y随x的减小而减小
D.二次函数y=ax2+bx+c图象的顶点坐标为(-1,-4)
5.如图,这是一次函数y=ax+b(a≠0)的图象,则二次函数y=ax2+bx-a的图象大致为( )
A. B. C. D.
6.如图,抛物线y=ax2+bx+c和直线y=mx+n都经过点(-1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.a-b+c>0
D.x=-1是方程ax2+bx+c=mx+n的解
7.如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
8.如图,要用篱笆围成一个矩形菜园ABCD,其中一边AB是墙,且AB的长不超过21m,E,F分别为边AB,CD的中点,EF将其分成面积相等的两部分,在DF,FC上分别留出两个宽为1m的小门.若图中虚线部分使用篱笆,且使用篱笆的长度是43m,有下列结论:
①AD的长可以是10m;
②当矩形菜园ABCD的面积为150m2时,BC的长为5m;
③当矩形菜园ABCD的面积最大时,BC的长为8m.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
9.如果三点P1(1,y1),P2(3,y2)和P3(4,y3)在抛物线y=-x2+6x+c的图象上,那么y1,y2与y3之间的大小关系是( )
A.y1<y3<y2 B.y3<y2<y1 C.y3<y1<y2 D.y1<y2<y3
10.如图,已知抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点位于0和-1之间,则以下结论错误的是( )
A.abc<0
B.2a+b=0
C.若点(-3,y1)和(4,y2)在该抛物线上,则y1>y2
D.若c-a>1,则关于x的一元二次方程ax2+bx+c=1有两个不相等实数根
11.如图,二次函数y=ax2+bx+c的图象过点A(m,0)和B(1,0),下列结论:①abc<0;②9a+c<-3b;③;④am2-(3a-b)m+a+b+c<0;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
12.如图,抛物线l1:与交于点A(1,-2),以下结论:
①无论x取何值,y2总是负数;
②l2可由l1向右平移3个单位,再向下平移3个单位得到;
③当-3<x<1时,随着x的增大,y1-y2的值先增大后减小.
下列说法正确的是( )
A.只有①正确 B.只有②正确
C.只有③不正确 D.①②③都正确
二.填空题(共5小题)
13.二次函数y=3(x+2)2+1的图象的顶点坐标是 ______.
14.如图,若y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为______.
15.已知点P(0,m2-4),Q(m,0),若线段PQ与抛物线y=x2+3x-4恰有一个交点,则m的取值范围是______.
16.我们把a,b,c三个数的中位数记作Z{a,b,c},直线y=kx+(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为______.
17.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2-4ac>0)的函数叫做“鹊桥”函数.某数学兴趣小组画出了“鹊桥”函数G:y=|x2-x-6|的图象(如图所示),并写出了下列结论:
①图象与坐标轴的交点为A(-2,0),B(3,0),C(0,6);
②当时,函数取得最大值;
③若(x0,y0)在函数图象上,则(1-x0,y0)也在函数图象上;
④当直线y=-x+m与函数G的图象有4个交点时,则m的取值范围是3<m<7.其中正确的结论有______.(填写所有正确结论的序号)
三.解答题(共5小题)
18.在平面直角坐标系xOy中,抛物线y=ax2-3ax-3a+1(a<0)与y轴交于点A,过点A作AB∥x轴,与抛物线交于点B.
(1)若抛物线经过点(-1,0);
①求点B的坐标;
②当t-1≤x≤t时,抛物线取得最大值为,求t的值;
(2)已知点G(1,3),H(3,3),若抛物线与线段GH有且只有一个交点(不含端点G、H),求a的取值范围.
19.已知二次函数y=ax2-(a-2)x+2(a≠0).
(1)若函数图象经过点(3,2),求抛物线的对称轴.
(2)若a>0,当x≥-1时,y随x的增大而增大,求a的取值范围.
(3)若,两点都在二次函数的图象上,试比较b与c的大小,并说明理由.
20.已知二次函数y=ax2+(2-a)x-1(a为常数,a≠0).
(1)求证:该二次函数图象与x轴有两个公共点;
(2)若A(1,y1)、B(3,y2)是该函数图象上的两个点,若y1<y2,求a的取值范围;
(3)当-1<x<1时,y随x的增大而增大,结合函数图象,则a的取值范围是 ______.
21.在平面直角坐标系中,定义两个函数y1=(x-a)(x-b),.
(1)如果函数y1的图象经过点(0,3),函数y2的图象经过点(1,5),求a2+b2的值;
(2)如果1<a<b<4,判断函数y2的图象与x轴的交点情况;
(3)若点P(-1,c)在y1上,点Q(a,c)在y2上,求ab的最小值.
22.毛乌素沙漠是中国四大沙地之一,位于陕西省榆林市长城一线以北,如图1是该沙漠边缘地区常见的抛物线状沙丘(一种风积地貌),其平面轮廓呈抛物线状.如图2,已知某一抛物线状沙丘OPA两翼端点的水平距离OA=200m,沙丘弧顶最高点P到OA的距离为80m,抛物线的对称轴垂直于OA,以OA所在直线为x轴,过点O且垂直于OA的直线为y轴建立平面直角坐标系,现计划从点M到点N种植一排柠条(M、N在抛物线上,点M在点N的左侧).
(1)求抛物线状沙丘OPA的函数表达式;
(2)ME⊥x轴于点E,NF⊥x轴于点F,若,求M、N两点之间的距离.
冀教版九年级下 第30章 二次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、B 4、D 5、C 6、D 7、A 8、C 9、A 10、C 11、B 12、C
二.填空题(共5小题)
13、(-2,1); 14、x=-1; 15、m=0或m≥1或m≤-4; 16、<k≤1或k=; 17、①③④;
三.解答题(共5小题)
18、解:(1)①∵抛物线y=ax2-3ax-3a+1(a<0)过点(-1,0),
∴a+3a-3a+1=0,
∴a=-1,
∴抛物线解析式为:y=-x2+3x+4,
∴点A坐标为(0,4),
当y=4时,即y=-x2+3x+4=4,
∴x1=0,x2=3,
∴点B(3,4),
②∵,
∴抛物线开口向下,顶点坐标为,
分以下两种情况讨论:
Ⅰ.当时,t-1≤x≤t在对称轴左侧,y随x增大而增大,
∴x=t时,为最大值,即,
解得或(舍);
Ⅱ.当即时,t-1≤x≤t在对称轴右侧,y随x增大而减小,
x=t-1时,为最大值,即,
解得或(舍),
综上所述,t的值为或;
(2)∵抛物线,
∴抛物线,
对称轴为,顶点为,
∵点G(1,3),H(3,3),若抛物线与线段GH有且只有一个交点,
分以下两种情况讨论:
Ⅰ.当抛物线y=ax2-3ax-3a+1的顶点在线段GH上时,
即:,
解得:;
Ⅱ.当抛物线顶点落在GH上方时,
当x=1时,y=a-3a-3a+1=-5a+1,
当x=3时,y=9a-9a-3a+1=-3a+1,
∵a<0,对称轴为,
∴-5a+1<-3a+1,
∵抛物线y=ax2-3ax-3a+1与线段GH有且只有一个交点(不含端点G、H),
∴与线段GH有且只有一个交点,一定在对称轴右侧,
∴,
解得:,
综上,a的取值范围是或.
19、解:(1)由条件可得9a-3(a-2)+2=2,
解得a=-1,
∴抛物线的表达式为y=-x2+3x+2,
∴抛物线的对称轴为直线.
(2)由条件可得抛物线在对称轴右侧y随x的增大而增大,
∵抛物线的对称轴为直线,
∴,
解得:,
∴;
(3)∵抛物线的对称轴为直线,
∴,
∵,,
∴点A,点B在对称轴的右侧,
①当a>0时,在对称轴右侧,y随x的增大而增大,
∵,
∴b<c.
②当a<0时,在对称轴右侧,y随x的增大而减小,
∵,
∴b>c.
综上,当a>0时,b<c;当a<0时,b>c.
20、解:(1)∵Δ=(2-a)2-4×a×(-1)=a2+4>0,
∴该二次函数图象与x轴有两个公共点;
(2)当x=1时,y=1,当x=3时,y=6a+5,
∵y1<y2,
∴6a+5>1,
解得,
又∵a≠0,
∴a的取值范围为且a≠0;
(3)∵二次函数y=ax2+(2-a)x-1,
∴抛物线的对称轴为直线,
当a>0时,抛物线开口向上,
∵当-1<x<1时,y随x的增大而增大,
∴,
解得;
当a<0时,抛物线开口向下,
∵当-1<x<1时,y随x的增大而增大,
∴,
解得a≥-2;
∴,
∵a≠0,
∴a的取值范围是,
故答案为:.
21、解:(1)把(0,3),(1,5)分别代入中,
得ab=3,a+b=4,∴a2+b2=(a+b)2-2ab=10,
∴a2+b2=(a+b)2-2ab=42-2×3=10;
(2)由题意得Δ=a2-4b,
∵1<a<b<4,
∴a2<b2<42,b2<4b,
∴a2<4b,
即Δ=a2-4b<0,
∴y2的图象与x轴没有交点;
(3)把P(-1,c),Q(a,c)分别代入中,得:
由题意得(-1-a)(-1-b)=c,a2+a2+b=c,
(-1-a)(-1-b)=c,a2+a2+b=c,
∴ab+a+b+1=2a2+b,
即ab=2a2-a-1,
设y=2a2-a-1,
图象开口向上,
∴在对称轴处取得最小值,
把代入y=2a2-a-1中得,
,
∴y=2a2-a-1的最小值为,
∵ab=2a2-a-1,
∴当时,ab的最小值为.
22、解:(1)根据题意可设抛物线的函数表达式为y=a(x-100)2+80.
将点A(200,0)代入,得a(200-100)2+80=0,
解得,
∴抛物线状沙丘OPA的函数表达式为.
(2)令,得,
解得x1=20,x2=180,
∴,,
∴M、N两点之间的距离为160m.
