人教版数学九年级上 第24章 圆 单元测试(含答案)
文档属性
| 名称 | 人教版数学九年级上 第24章 圆 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:28:45 | ||
图片预览

文档简介
人教版九年级上 第24章 圆 单元测试
一.选择题(共12小题)
1.如图,BC是⊙O的弦,点A是圆上一点,OA⊥BC于点D.若OA=5,BC=8,则AD的长是( )
A.3 B.2 C. D.
2.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,并且CD=4m,EM=6m.则⊙O的半径为( )
A.3m B. C.4m D.
3.如图,⊙O的半径为1,点A、B、C都在⊙O上,∠B=45°,则的长为( )
A.π B.π C.π D.π
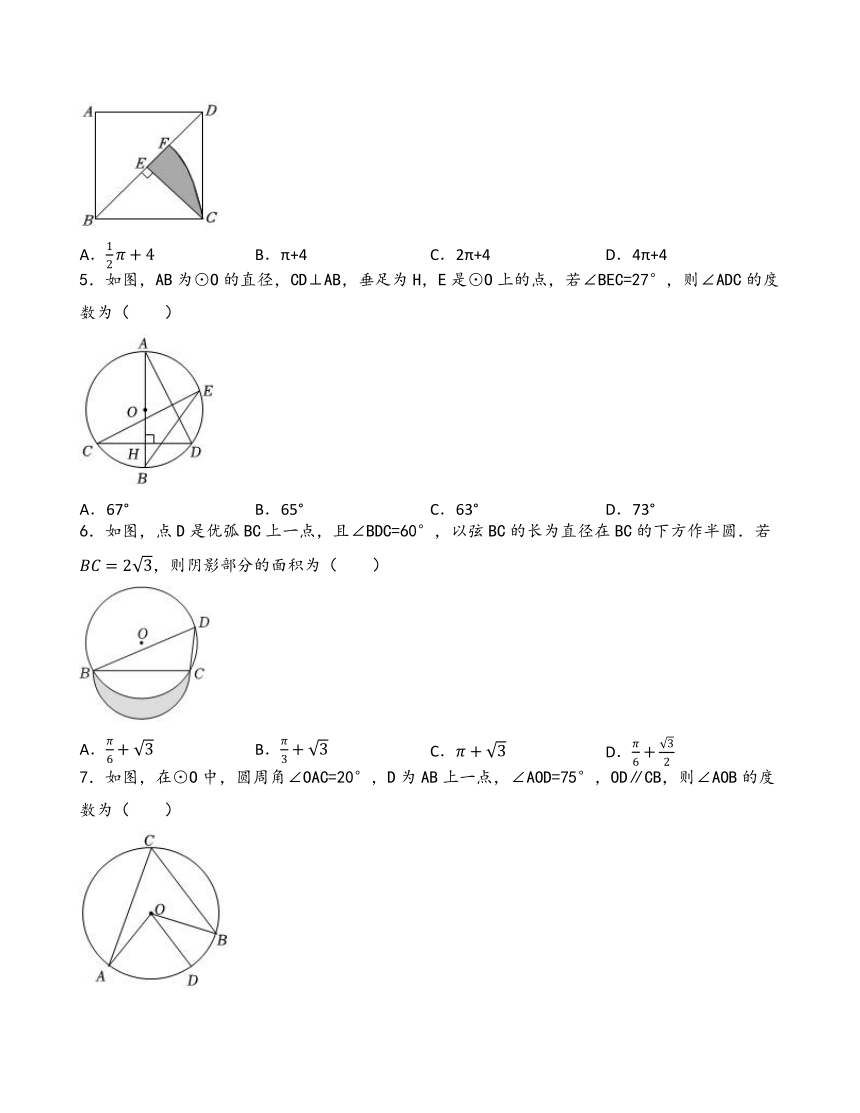
4.如图,在正方形ABCD中,AB=4,以点B为圆心,BC为半径画弧交BD于点F,过点C作CE⊥BD于点E,则阴影部分的周长为( )
A. B.π+4 C.2π+4 D.4π+4
5.如图,AB为⊙O的直径,CD⊥AB,垂足为H,E是⊙O上的点,若∠BEC=27°,则∠ADC的度数为( )
A.67° B.65° C.63° D.73°
6.如图,点D是优弧BC上一点,且∠BDC=60°,以弦BC的长为直径在BC的下方作半圆.若,则阴影部分的面积为( )
A. B. C. D.
7.如图,在⊙O中,圆周角∠OAC=20°,D为AB上一点,∠AOD=75°,OD∥CB,则∠AOB的度数为( )
A.100° B.110° C.55° D.120°
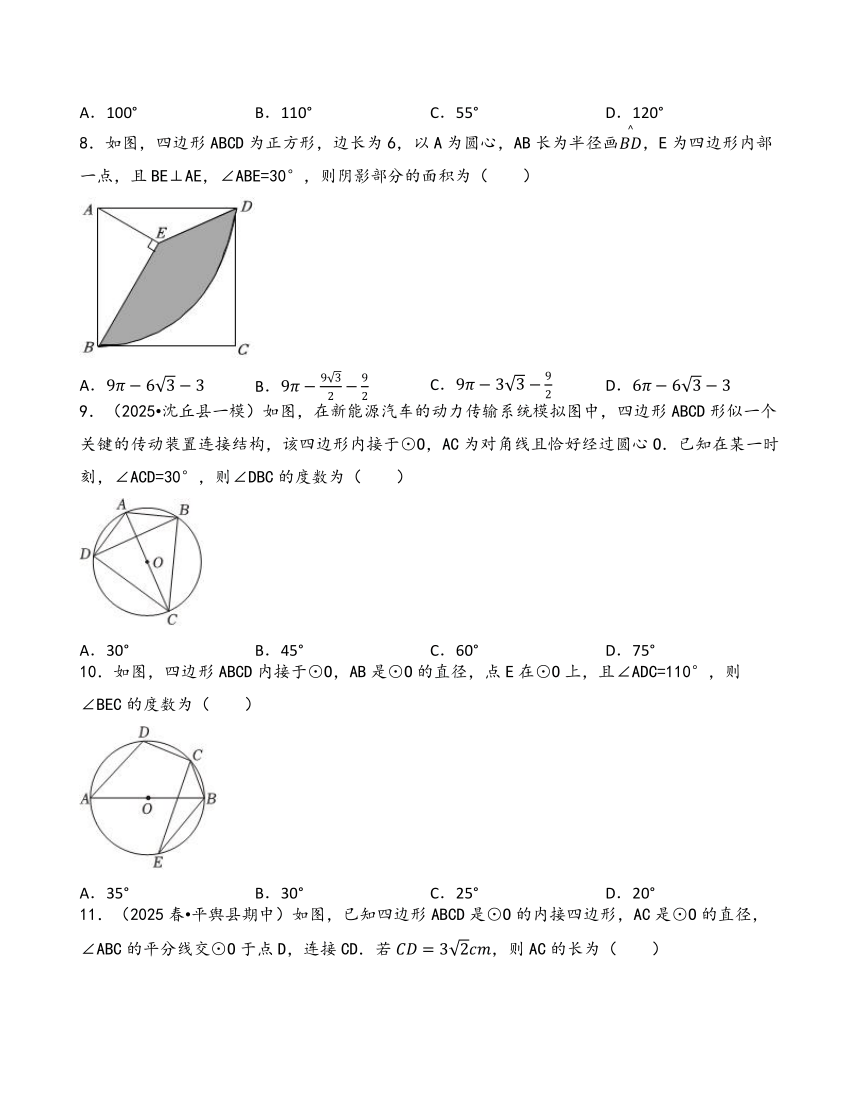
8.如图,四边形ABCD为正方形,边长为6,以A为圆心,AB长为半径画,E为四边形内部一点,且BE⊥AE,∠ABE=30°,则阴影部分的面积为( )
A. B. C. D.
9.(2025 沈丘县一模)如图,在新能源汽车的动力传输系统模拟图中,四边形ABCD形似一个关键的传动装置连接结构,该四边形内接于⊙O,AC为对角线且恰好经过圆心O.已知在某一时刻,∠ACD=30°,则∠DBC的度数为( )
A.30° B.45° C.60° D.75°
10.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点E在⊙O上,且∠ADC=110°,则∠BEC的度数为( )
A.35° B.30° C.25° D.20°
11.(2025春 平舆县期中)如图,已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,∠ABC的平分线交⊙O于点D,连接CD.若,则AC的长为( )
A.3cm B. C.6cm D.12cm
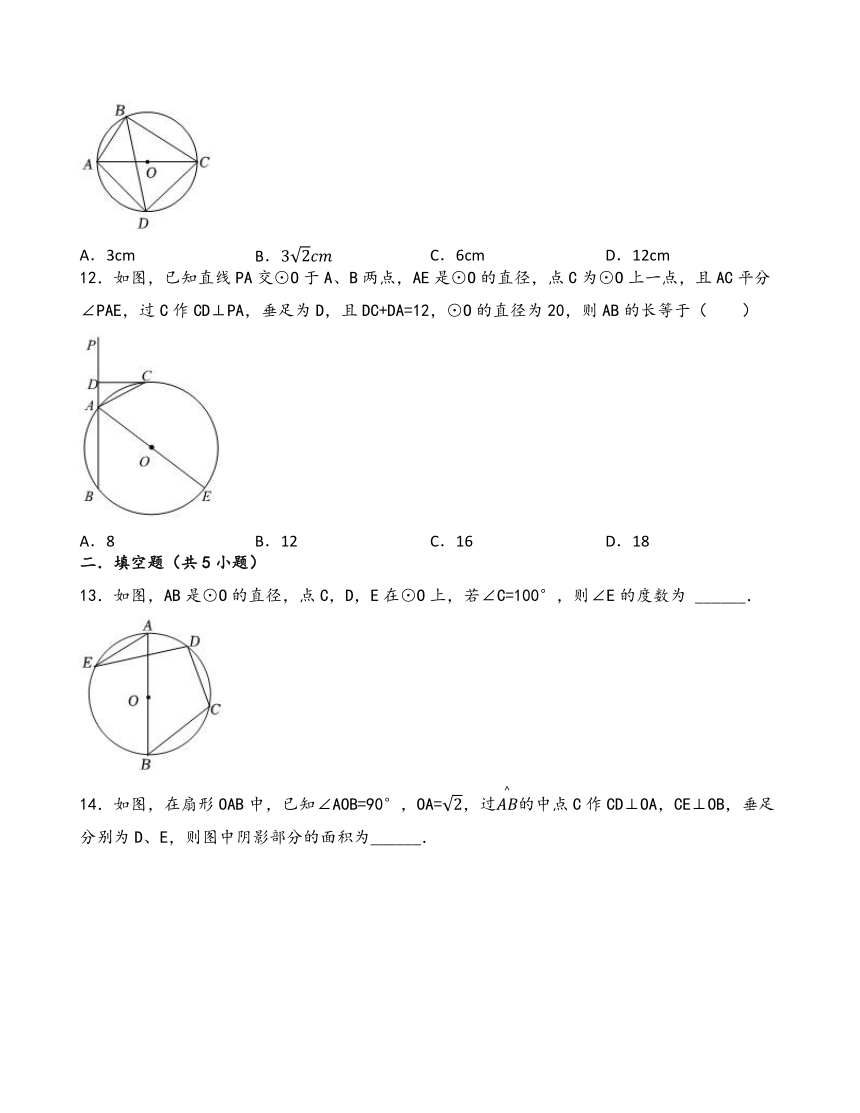
12.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D,且DC+DA=12,⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
二.填空题(共5小题)
13.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 ______.
14.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为______.
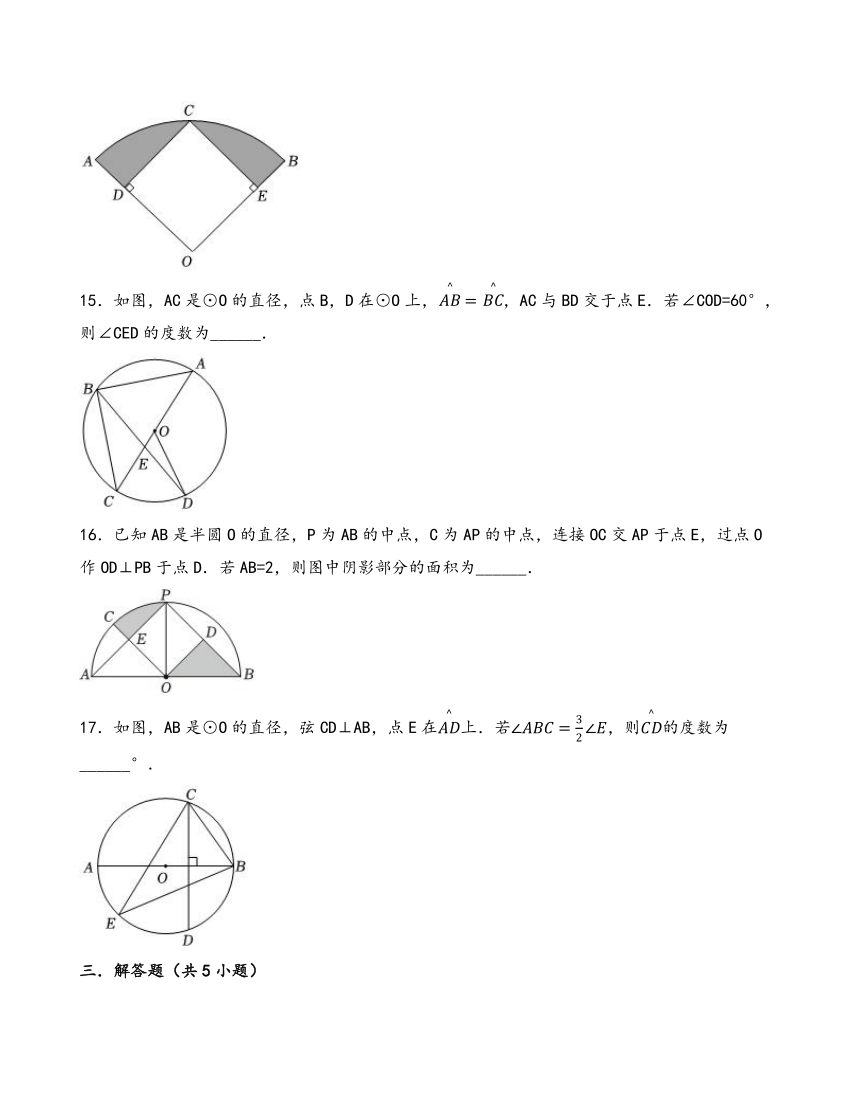
15.如图,AC是⊙O的直径,点B,D在⊙O上,,AC与BD交于点E.若∠COD=60°,则∠CED的度数为______.
16.已知AB是半圆O的直径,P为AB的中点,C为AP的中点,连接OC交AP于点E,过点O作OD⊥PB于点D.若AB=2,则图中阴影部分的面积为______.
17.如图,AB是⊙O的直径,弦CD⊥AB,点E在上.若,则的度数为 ______°.
三.解答题(共5小题)
18.如图,四边形ABCD内接于⊙O,对角线AC是直径,延长边BA,CD交于点P,过点D作DE⊥AP于点E,已知PA=AC;
(1)求证:DE是⊙O的切线;
(2)若∠ACD=30°,DE=3,求⊙O的半径.
19.如图,CD是⊙O的直径,点B是⊙O上一点,延长CD到点A,连接AB,CB,BD,OB,若∠ABD=∠CBO.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为1,D是AO的中点,求劣弧的长(结果用π表示).
20.一个弓形桥洞截面示意图如图所示,弦AB是水底,弦CD表示水面,EF过圆心O且EF⊥AB,EF=AB=24米,CD∥AB.
(1)当水深GF为19米时,求此时水面CD的宽;
(2)若水面下降,当水面CD的宽为12米时,求此时水深.
21.如图,AB是⊙O的直径,过点B作⊙O的切线BM,点A,C,D分别为⊙O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.
22.如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O、切线PA相交于C、Q两点.
(1)求证:PB是⊙O的切线;
(2)QD为PB边上的中线,若AQ=4,CQ=2,求QD的值.
人教版九年级上 第24章 圆 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、C 4、B 5、C 6、A 7、B 8、B 9、C 10、D 11、C 12、B
二.填空题(共5小题)
13、10°; 14、; 15、75°; 16、; 17、144;
三.解答题(共5小题)
18、(1)证明:连接OD,
由题意可得:∠P=∠PCO=∠CDO,
∴OD∥AP,
又∵DE⊥AP,
∴∠DEA=∠ODE=90°,而OD为半径,
∴DE是⊙O的切线;
(2)解:∵∠ADC=∠ADP=90°,PA=AC,
∴∠P=∠ACD=30°,
又∵DE⊥AP,DE=3,
∴PD=2DE=6,
,
∴,
∴⊙O的半径为.
19、(1)证明:∵CD是⊙O的直径,
∴∠CBD=90°,
∴∠CBO+∠OBD=90°,
由条件可知∠ABD+∠OBD=90°,即∠ABO=90°,
∴OB⊥AB,
又∵OB是⊙O的半径,
∴AB是⊙O的切线.
(2)解:∵⊙O的半径为1,
∴OB=OC=OD=1,
由(1)已得:∠ABO=90°,
由条件可得BD=OD=1,
∴OB=OD=BD,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=180°-∠BOD=120°,
∴劣弧的长.
20、解:(1)如图,连接OA、OC,
∵EF⊥AB,EF过圆心O,
∴AB=24,
∴AF=AB=12,
设圆O的半径为r,则OF=24-r,
在Rt△AOF中,OF2+AF2=OA2,
∴122+(24-r)2=r2,
解得r=15,
∵∵GF=19,
∴OF=9,OG=10,
∵CD∥AB,
∴∠CGO=∠BFO=90°,
∴CG===5,
∴CD=2CG=10,
∴当水深GF为19米时,求此时水面CD的宽为10米.
(2)若水面下降,当水面CD的宽为12米时,CG=6米,
∴OG===3米,
∵OF=9米,
∴当CD在O点上方时,水深GF=9+3=12米,
当CD在O点下方时,水深GF=9-3=6米,
答:若水面下降,当水面CD的宽为12米时,此时水深为12米或6米.
21、(1)证明:∵点A、C、D为⊙O的三等分点,
∴,
∴AD=DC=AC.
∴△ACD为等边三角形,
而点O为△ACD的外心,
∴AB⊥CD.
∵BM为⊙O的切线,
∴BE⊥AB.
∴CD∥BM;
(2)解:连接DB,如图,
∵△ACD为等边三角形,
∴∠C=60°,
∴∠ABD=∠C=60°,
∴∠DBE=30°,
在Rt△DBE中,BE=2DE=2m,DB=DE=m.
在Rt△ADB中,AB=2BD=2m,则OB=m,
在Rt△OBE中,OE==m,
∴△OBE周长为2m+m+m=(2++)m.
22、(1)证明:连接OA,
在△OBP和△OAP中,
,
∴△OBP≌△OAP(SSS),
∴∠OBP=∠OAP,
∵PA是⊙O的切线,A是切点,
∴∠OAP=90°,
∴∠OBP=90°,
∵OB是半径,
∴PB是⊙O的切线;
(2)连接OC
∵AQ=4,CQ=2,∠OAQ=90°,
设OA=r,
则r2+42=(r+2)2,
解得,r=3,
则OA=3,BC=6,
设BP=x,则 AP=x,
∵PB是圆O的切线,
∴∠PBQ=90°,
∴x2+(6+2)2=(x+4)2,
解得,x=6,
∴BP=6,
∴BD=3,
∴QD=,
即QD的值是.
一.选择题(共12小题)
1.如图,BC是⊙O的弦,点A是圆上一点,OA⊥BC于点D.若OA=5,BC=8,则AD的长是( )
A.3 B.2 C. D.
2.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心交⊙O于点E,并且CD=4m,EM=6m.则⊙O的半径为( )
A.3m B. C.4m D.
3.如图,⊙O的半径为1,点A、B、C都在⊙O上,∠B=45°,则的长为( )
A.π B.π C.π D.π
4.如图,在正方形ABCD中,AB=4,以点B为圆心,BC为半径画弧交BD于点F,过点C作CE⊥BD于点E,则阴影部分的周长为( )
A. B.π+4 C.2π+4 D.4π+4
5.如图,AB为⊙O的直径,CD⊥AB,垂足为H,E是⊙O上的点,若∠BEC=27°,则∠ADC的度数为( )
A.67° B.65° C.63° D.73°
6.如图,点D是优弧BC上一点,且∠BDC=60°,以弦BC的长为直径在BC的下方作半圆.若,则阴影部分的面积为( )
A. B. C. D.
7.如图,在⊙O中,圆周角∠OAC=20°,D为AB上一点,∠AOD=75°,OD∥CB,则∠AOB的度数为( )
A.100° B.110° C.55° D.120°
8.如图,四边形ABCD为正方形,边长为6,以A为圆心,AB长为半径画,E为四边形内部一点,且BE⊥AE,∠ABE=30°,则阴影部分的面积为( )
A. B. C. D.
9.(2025 沈丘县一模)如图,在新能源汽车的动力传输系统模拟图中,四边形ABCD形似一个关键的传动装置连接结构,该四边形内接于⊙O,AC为对角线且恰好经过圆心O.已知在某一时刻,∠ACD=30°,则∠DBC的度数为( )
A.30° B.45° C.60° D.75°
10.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点E在⊙O上,且∠ADC=110°,则∠BEC的度数为( )
A.35° B.30° C.25° D.20°
11.(2025春 平舆县期中)如图,已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,∠ABC的平分线交⊙O于点D,连接CD.若,则AC的长为( )
A.3cm B. C.6cm D.12cm
12.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D,且DC+DA=12,⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
二.填空题(共5小题)
13.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠C=100°,则∠E的度数为 ______.
14.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为______.
15.如图,AC是⊙O的直径,点B,D在⊙O上,,AC与BD交于点E.若∠COD=60°,则∠CED的度数为______.
16.已知AB是半圆O的直径,P为AB的中点,C为AP的中点,连接OC交AP于点E,过点O作OD⊥PB于点D.若AB=2,则图中阴影部分的面积为______.
17.如图,AB是⊙O的直径,弦CD⊥AB,点E在上.若,则的度数为 ______°.
三.解答题(共5小题)
18.如图,四边形ABCD内接于⊙O,对角线AC是直径,延长边BA,CD交于点P,过点D作DE⊥AP于点E,已知PA=AC;
(1)求证:DE是⊙O的切线;
(2)若∠ACD=30°,DE=3,求⊙O的半径.
19.如图,CD是⊙O的直径,点B是⊙O上一点,延长CD到点A,连接AB,CB,BD,OB,若∠ABD=∠CBO.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为1,D是AO的中点,求劣弧的长(结果用π表示).
20.一个弓形桥洞截面示意图如图所示,弦AB是水底,弦CD表示水面,EF过圆心O且EF⊥AB,EF=AB=24米,CD∥AB.
(1)当水深GF为19米时,求此时水面CD的宽;
(2)若水面下降,当水面CD的宽为12米时,求此时水深.
21.如图,AB是⊙O的直径,过点B作⊙O的切线BM,点A,C,D分别为⊙O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.
22.如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O、切线PA相交于C、Q两点.
(1)求证:PB是⊙O的切线;
(2)QD为PB边上的中线,若AQ=4,CQ=2,求QD的值.
人教版九年级上 第24章 圆 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、B 3、C 4、B 5、C 6、A 7、B 8、B 9、C 10、D 11、C 12、B
二.填空题(共5小题)
13、10°; 14、; 15、75°; 16、; 17、144;
三.解答题(共5小题)
18、(1)证明:连接OD,
由题意可得:∠P=∠PCO=∠CDO,
∴OD∥AP,
又∵DE⊥AP,
∴∠DEA=∠ODE=90°,而OD为半径,
∴DE是⊙O的切线;
(2)解:∵∠ADC=∠ADP=90°,PA=AC,
∴∠P=∠ACD=30°,
又∵DE⊥AP,DE=3,
∴PD=2DE=6,
,
∴,
∴⊙O的半径为.
19、(1)证明:∵CD是⊙O的直径,
∴∠CBD=90°,
∴∠CBO+∠OBD=90°,
由条件可知∠ABD+∠OBD=90°,即∠ABO=90°,
∴OB⊥AB,
又∵OB是⊙O的半径,
∴AB是⊙O的切线.
(2)解:∵⊙O的半径为1,
∴OB=OC=OD=1,
由(1)已得:∠ABO=90°,
由条件可得BD=OD=1,
∴OB=OD=BD,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=180°-∠BOD=120°,
∴劣弧的长.
20、解:(1)如图,连接OA、OC,
∵EF⊥AB,EF过圆心O,
∴AB=24,
∴AF=AB=12,
设圆O的半径为r,则OF=24-r,
在Rt△AOF中,OF2+AF2=OA2,
∴122+(24-r)2=r2,
解得r=15,
∵∵GF=19,
∴OF=9,OG=10,
∵CD∥AB,
∴∠CGO=∠BFO=90°,
∴CG===5,
∴CD=2CG=10,
∴当水深GF为19米时,求此时水面CD的宽为10米.
(2)若水面下降,当水面CD的宽为12米时,CG=6米,
∴OG===3米,
∵OF=9米,
∴当CD在O点上方时,水深GF=9+3=12米,
当CD在O点下方时,水深GF=9-3=6米,
答:若水面下降,当水面CD的宽为12米时,此时水深为12米或6米.
21、(1)证明:∵点A、C、D为⊙O的三等分点,
∴,
∴AD=DC=AC.
∴△ACD为等边三角形,
而点O为△ACD的外心,
∴AB⊥CD.
∵BM为⊙O的切线,
∴BE⊥AB.
∴CD∥BM;
(2)解:连接DB,如图,
∵△ACD为等边三角形,
∴∠C=60°,
∴∠ABD=∠C=60°,
∴∠DBE=30°,
在Rt△DBE中,BE=2DE=2m,DB=DE=m.
在Rt△ADB中,AB=2BD=2m,则OB=m,
在Rt△OBE中,OE==m,
∴△OBE周长为2m+m+m=(2++)m.
22、(1)证明:连接OA,
在△OBP和△OAP中,
,
∴△OBP≌△OAP(SSS),
∴∠OBP=∠OAP,
∵PA是⊙O的切线,A是切点,
∴∠OAP=90°,
∴∠OBP=90°,
∵OB是半径,
∴PB是⊙O的切线;
(2)连接OC
∵AQ=4,CQ=2,∠OAQ=90°,
设OA=r,
则r2+42=(r+2)2,
解得,r=3,
则OA=3,BC=6,
设BP=x,则 AP=x,
∵PB是圆O的切线,
∴∠PBQ=90°,
∴x2+(6+2)2=(x+4)2,
解得,x=6,
∴BP=6,
∴BD=3,
∴QD=,
即QD的值是.
同课章节目录
