人教版数学九年级下 第27章 相似 单元测试(含答案)
文档属性
| 名称 | 人教版数学九年级下 第27章 相似 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 87.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:35:36 | ||
图片预览



文档简介
人教版九年级下 第27章 相似 单元测试
一.选择题(共12小题)
1.下列各组多边形中,一定相似的是( )
A.两个矩形 B.两个等边三角形
C.两个菱形 D.两个等腰三角形
2.若两个相似三角形的相似比为3:5,则它们的周长之比为( )
A.3:5 B.9:25 C.25:9 D.3:8
3.若2a-b=0(ab≠0),则的值为( )
A.-1 B.-2 C.1 D.
4.如图,在平面直角坐标系中,△ABC∽△ODC,其中点A的坐标为(-2,0),点C的坐标为(1,0),则△ABC与△ODC的面积比是 ( )
A.9:1 B.3:1 C.4:1 D.2:1
5.如图,在Rt△ABC中(∠C=90°)放置边长分别为1,2,x的三个正方形,则x的值为( )
A.3 B.4 C. D.
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠PCB的度数是( )
A.60° B.50° C.40° D.30°
7.如图,点D是△ABC的边BC的中点,过点D作DE∥AB交AC于点E,点F在AE上,AF=,连接DF并延长,与BA的延长线交于点G.若AB=6,则线段BG的长为( )
A. B.7 C. D.8
8.如图,在△ABC中,AB=AC,∠BAC>90°,AD∥BC,∠BDC=90°,记AB=x,AD=y,当BC不变,AB改变的过程中,下列代数式的值不变的是( )
A.x+y B.xy C.x2+y2 D.x2-y2
9.如图,在平行四边形ABCD中,点O是BD的中点,AE⊥BC于点E,CF⊥AD于点F,AE、CF分别交BD于点G、H.若,则为( )
A. B. C. D.
10.如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,且不与A,D重合,过点P作PE⊥CP交AB于点E,设PD=x,AE=y,则y于x的函数关系式是( )
A. B.
C. D.
11.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=4,BC=6,点E在CD边上,且CE=1,连接OE并延长与BC的延长线相交于点F,则CF的长为( ).
A.3 B.4 C.5 D.6
12.如图,在矩形ABCD中,点E在边AB上,且AE=3BE,F是AD中点,BF与CE,DE分别相交于点M,N.当AB=4,BC=6时,MN的长为( )
A. B. C. D.
二.填空题(共5小题)
13.若△ABC∽△DEF,∠A=30°,∠B=60°,则∠D=______.
14.如果3a=5b(a、b均不为0),那么a:b=______.(填比值)
15.(2025 调兵山市三模)玻璃瓶中装入不同量的水,敲击时能发出不同的音符.实验发现,当液面高度AC与瓶高AB之比为黄金比(约等于0.618)时(如图),可以敲击出音符“sol”的声音.若AB=10cm,且敲击时发出音符“sol”的声音,则液面高度AC约为______.
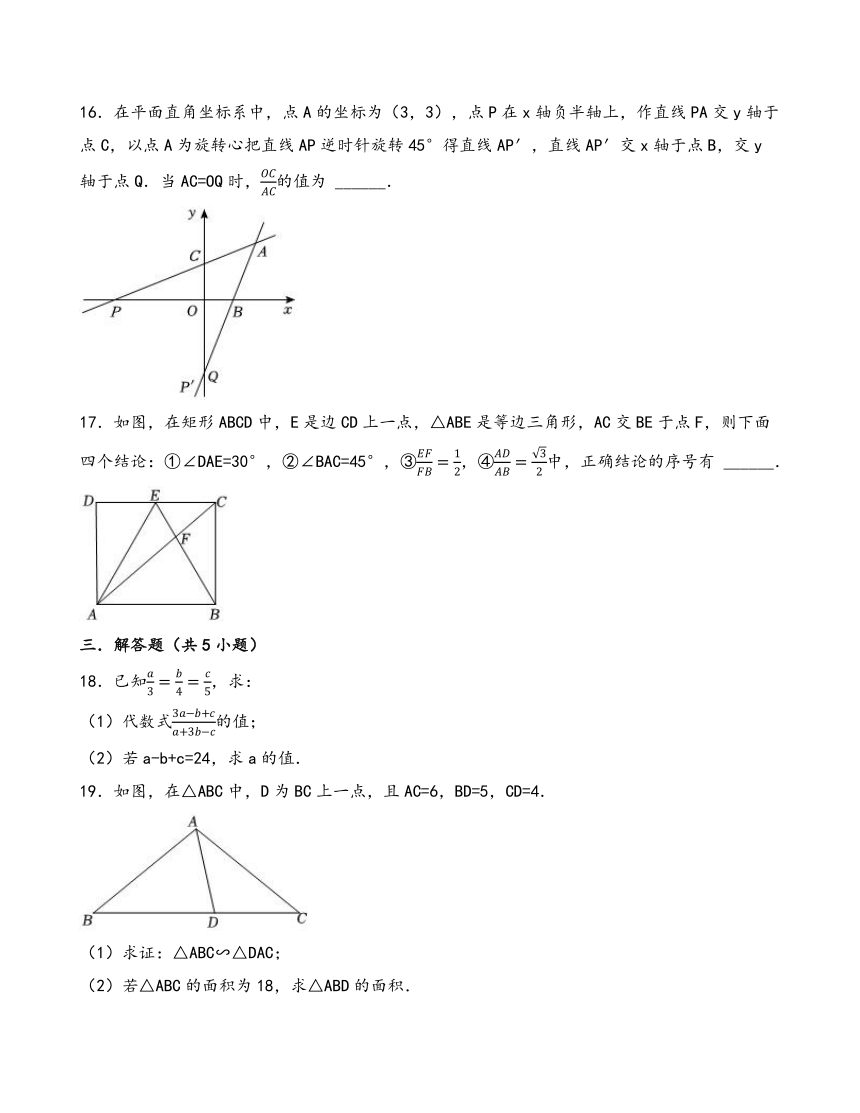
16.在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 ______.
17.如图,在矩形ABCD中,E是边CD上一点,△ABE是等边三角形,AC交BE于点F,则下面四个结论:①∠DAE=30°,②∠BAC=45°,③,④中,正确结论的序号有 ______.
三.解答题(共5小题)
18.已知,求:
(1)代数式的值;
(2)若a-b+c=24,求a的值.
19.如图,在△ABC中,D为BC上一点,且AC=6,BD=5,CD=4.
(1)求证:△ABC∽△DAC;
(2)若△ABC的面积为18,求△ABD的面积.
20.如图,△ABC,△GCD,△FDE是三个全等的等腰三角形,点B、C、D、E在一条直线上,且,BC=1,BF交AC于点P.
(1)求证:△BFE∽△FDE;
(2)求CP的长.
21.如图,在平行四边形ABCD中,E是边AD的延长线上一点,连接BE交CD于点F,交对角线AC于点G.
(1)若DE=1,AD=2,求的值;
(2)求证:△BCF∽△EAB.
22.如图,在菱形ABCD中,点M是BC上一点,连接AM并延长分别交BD和DC的延长线于点Q和点N,连接CQ.
(1)求证:;
(2)连接AC,若AM⊥BC,且 QN=8,MN=6,求BD的长.
人教版九年级下 第27章 相似 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、A 3、B 4、A 5、A 6、C 7、C 8、C 9、B 10、A 11、A 12、D
二.填空题(共5小题)
13、30°; 14、; 15、6.18cm; 16、; 17、①③④;
三.解答题(共5小题)
18、解:(1)设,
则a=3k,b=4k,c=5k,
∴;
(2)∵a-b+c=24,
∴3k-4k+5k=24,
解得:k=6,
则a=3k=3×6=18,
∴a的值为18.
19、(1)证明:∵BD=5,CD=4,
∴BC=BD+CD=9,
∵AC=6,
∴,,
∴,
∵∠C=∠C,
∴△ABC∽△DAC;
(2)解:∵△ABC∽△DAC,
∴,
∵S△ABC=18,
∴,
∴S△ABD=S△ABC-S△DAC=18-8=10.
20、(1)证明:由题意可知:BC=CD=DE=1,BE=3,,
∴,,
∴,
又∵∠E=∠E,
∴△BFE∽△FDE;
(2)解:∵△BFE∽△FDE,
∴∠EBF=∠DFE=∠A,
∵∠ACB=∠ACB,
∴△ABC∽△BCP,
∴,
即,
∴.
21、(1)解:∵四边形ABCD是平行四边形,
∴BC∥AE,BC=AD=2,
∴△CBF∽△DEF,
∴==2;
(2)证明:∵四边形ABCD是平行四边形,
∴BC∥AE,∠BAE=∠FCB,
∴∠E=∠CBF,
∴△BCF∽△EAB.
22、(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,
在△ABQ和△CBQ中,
,
∴△ABQ≌△CBQ(SAS),
∴∠BAQ=∠BCQ,
∵AB∥CD,
∴∠BAQ=∠N,
∴BCQ=∠N,
∵∠CQM=∠NQB,
∴△CQM∽△NQC,
∴;
(2)解∵QN=8,MN=6,
∴QM=2,
由(1)知,,
∴,
∴CQ=4,
由(1)知,△ABQ≌△CBQ,
∴AQ=CQ=4,
∴AM=AQ+QM=4+2=6,
在Rt△CQM中,
CM===2,
设BM=x,则AB=BC=BM+CM=2+x,
在Rt△ABM中,AB2=AM2+BM2,
即(x+2)2=62+x2,
解得x=2,
即BM=2,
∴BM=CM,
∵AM⊥BC,
∴△ABC是等边三角形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴BD=2AM=12.
一.选择题(共12小题)
1.下列各组多边形中,一定相似的是( )
A.两个矩形 B.两个等边三角形
C.两个菱形 D.两个等腰三角形
2.若两个相似三角形的相似比为3:5,则它们的周长之比为( )
A.3:5 B.9:25 C.25:9 D.3:8
3.若2a-b=0(ab≠0),则的值为( )
A.-1 B.-2 C.1 D.
4.如图,在平面直角坐标系中,△ABC∽△ODC,其中点A的坐标为(-2,0),点C的坐标为(1,0),则△ABC与△ODC的面积比是 ( )
A.9:1 B.3:1 C.4:1 D.2:1
5.如图,在Rt△ABC中(∠C=90°)放置边长分别为1,2,x的三个正方形,则x的值为( )
A.3 B.4 C. D.
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠PCB的度数是( )
A.60° B.50° C.40° D.30°
7.如图,点D是△ABC的边BC的中点,过点D作DE∥AB交AC于点E,点F在AE上,AF=,连接DF并延长,与BA的延长线交于点G.若AB=6,则线段BG的长为( )
A. B.7 C. D.8
8.如图,在△ABC中,AB=AC,∠BAC>90°,AD∥BC,∠BDC=90°,记AB=x,AD=y,当BC不变,AB改变的过程中,下列代数式的值不变的是( )
A.x+y B.xy C.x2+y2 D.x2-y2
9.如图,在平行四边形ABCD中,点O是BD的中点,AE⊥BC于点E,CF⊥AD于点F,AE、CF分别交BD于点G、H.若,则为( )
A. B. C. D.
10.如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,且不与A,D重合,过点P作PE⊥CP交AB于点E,设PD=x,AE=y,则y于x的函数关系式是( )
A. B.
C. D.
11.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=4,BC=6,点E在CD边上,且CE=1,连接OE并延长与BC的延长线相交于点F,则CF的长为( ).
A.3 B.4 C.5 D.6
12.如图,在矩形ABCD中,点E在边AB上,且AE=3BE,F是AD中点,BF与CE,DE分别相交于点M,N.当AB=4,BC=6时,MN的长为( )
A. B. C. D.
二.填空题(共5小题)
13.若△ABC∽△DEF,∠A=30°,∠B=60°,则∠D=______.
14.如果3a=5b(a、b均不为0),那么a:b=______.(填比值)
15.(2025 调兵山市三模)玻璃瓶中装入不同量的水,敲击时能发出不同的音符.实验发现,当液面高度AC与瓶高AB之比为黄金比(约等于0.618)时(如图),可以敲击出音符“sol”的声音.若AB=10cm,且敲击时发出音符“sol”的声音,则液面高度AC约为______.
16.在平面直角坐标系中,点A的坐标为(3,3),点P在x轴负半轴上,作直线PA交y轴于点C,以点A为旋转心把直线AP逆时针旋转45°得直线AP′,直线AP′交x轴于点B,交y轴于点Q.当AC=OQ时,的值为 ______.
17.如图,在矩形ABCD中,E是边CD上一点,△ABE是等边三角形,AC交BE于点F,则下面四个结论:①∠DAE=30°,②∠BAC=45°,③,④中,正确结论的序号有 ______.
三.解答题(共5小题)
18.已知,求:
(1)代数式的值;
(2)若a-b+c=24,求a的值.
19.如图,在△ABC中,D为BC上一点,且AC=6,BD=5,CD=4.
(1)求证:△ABC∽△DAC;
(2)若△ABC的面积为18,求△ABD的面积.
20.如图,△ABC,△GCD,△FDE是三个全等的等腰三角形,点B、C、D、E在一条直线上,且,BC=1,BF交AC于点P.
(1)求证:△BFE∽△FDE;
(2)求CP的长.
21.如图,在平行四边形ABCD中,E是边AD的延长线上一点,连接BE交CD于点F,交对角线AC于点G.
(1)若DE=1,AD=2,求的值;
(2)求证:△BCF∽△EAB.
22.如图,在菱形ABCD中,点M是BC上一点,连接AM并延长分别交BD和DC的延长线于点Q和点N,连接CQ.
(1)求证:;
(2)连接AC,若AM⊥BC,且 QN=8,MN=6,求BD的长.
人教版九年级下 第27章 相似 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、A 3、B 4、A 5、A 6、C 7、C 8、C 9、B 10、A 11、A 12、D
二.填空题(共5小题)
13、30°; 14、; 15、6.18cm; 16、; 17、①③④;
三.解答题(共5小题)
18、解:(1)设,
则a=3k,b=4k,c=5k,
∴;
(2)∵a-b+c=24,
∴3k-4k+5k=24,
解得:k=6,
则a=3k=3×6=18,
∴a的值为18.
19、(1)证明:∵BD=5,CD=4,
∴BC=BD+CD=9,
∵AC=6,
∴,,
∴,
∵∠C=∠C,
∴△ABC∽△DAC;
(2)解:∵△ABC∽△DAC,
∴,
∵S△ABC=18,
∴,
∴S△ABD=S△ABC-S△DAC=18-8=10.
20、(1)证明:由题意可知:BC=CD=DE=1,BE=3,,
∴,,
∴,
又∵∠E=∠E,
∴△BFE∽△FDE;
(2)解:∵△BFE∽△FDE,
∴∠EBF=∠DFE=∠A,
∵∠ACB=∠ACB,
∴△ABC∽△BCP,
∴,
即,
∴.
21、(1)解:∵四边形ABCD是平行四边形,
∴BC∥AE,BC=AD=2,
∴△CBF∽△DEF,
∴==2;
(2)证明:∵四边形ABCD是平行四边形,
∴BC∥AE,∠BAE=∠FCB,
∴∠E=∠CBF,
∴△BCF∽△EAB.
22、(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,
在△ABQ和△CBQ中,
,
∴△ABQ≌△CBQ(SAS),
∴∠BAQ=∠BCQ,
∵AB∥CD,
∴∠BAQ=∠N,
∴BCQ=∠N,
∵∠CQM=∠NQB,
∴△CQM∽△NQC,
∴;
(2)解∵QN=8,MN=6,
∴QM=2,
由(1)知,,
∴,
∴CQ=4,
由(1)知,△ABQ≌△CBQ,
∴AQ=CQ=4,
∴AM=AQ+QM=4+2=6,
在Rt△CQM中,
CM===2,
设BM=x,则AB=BC=BM+CM=2+x,
在Rt△ABM中,AB2=AM2+BM2,
即(x+2)2=62+x2,
解得x=2,
即BM=2,
∴BM=CM,
∵AM⊥BC,
∴△ABC是等边三角形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴BD=2AM=12.
