【期末真题汇编】期末核心考点 平行四边形(含解析)-2024-2025学年八年级下册数学人教版
文档属性
| 名称 | 【期末真题汇编】期末核心考点 平行四边形(含解析)-2024-2025学年八年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 平行四边形
一.选择题(共10小题)
1.(2025春 平乡县期中)如图,在3×3的小正方形网格中,以线段MN为对角线作平行四边形,使另两个顶点均在网格的格点(网格线的交点)上,这样的平行四边形最多可画n个,则n的值为( )
A.3 B.4 C.5 D.6
2.(2025春 武威期中)已知△ABC,现有四条信息:①D为AB中点;②E为AC中点;③DE∥BC;④BC=2DE,若从中任选两条信息作为条件,再从余下的两条信息中任选一条信息作为结论,一共能组成真命题的个数为( )
A.6个 B.8个 C.10个 D.12个
3.(2025 江北区校级二模)如图,正方形ABCD中,E、F、H分别在AD、DC、BC边上,BF⊥EH于G,连接EB、DG,若DF=DE=2CF,则的值为( )
A. B. C. D.
4.(2025春 离石区期中)如图,在 ABCD中,E,F是对角线AC上的两点(不与点A,C重合),且AE=CF,连接BE,BF,DE,DF,下列结论错误的是( )
A.四边形BEDF是平行四边形
B.若四边形ABCD是菱形,则四边形BEDF是菱形
C.若四边形ABCD是正方形,则四边形BEDF是菱形
D.若四边形ABCD是矩形,则四边形BEDF也是矩形
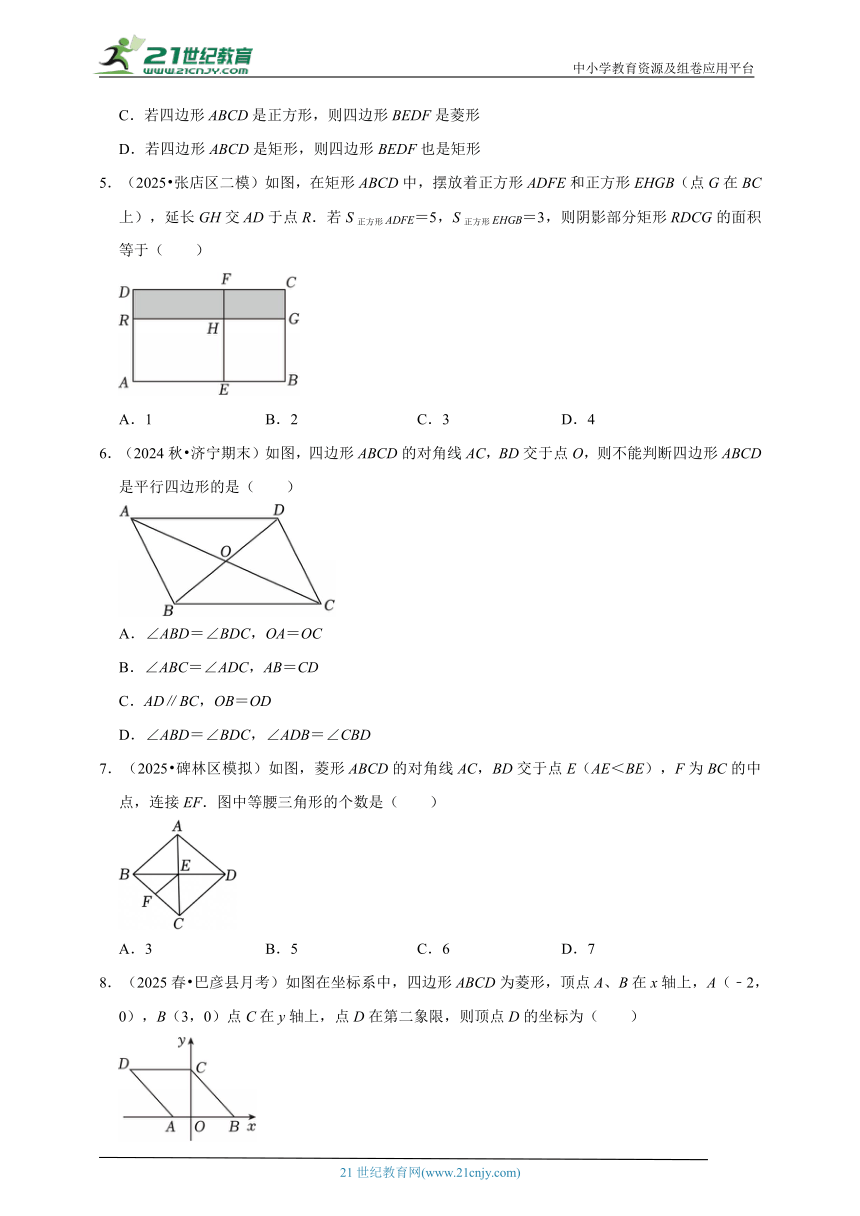
5.(2025 张店区二模)如图,在矩形ABCD中,摆放着正方形ADFE和正方形EHGB(点G在BC上),延长GH交AD于点R.若S正方形ADFE=5,S正方形EHGB=3,则阴影部分矩形RDCG的面积等于( )
A.1 B.2 C.3 D.4
6.(2024秋 济宁期末)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC
B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD
D.∠ABD=∠BDC,∠ADB=∠CBD
7.(2025 碑林区模拟)如图,菱形ABCD的对角线AC,BD交于点E(AE<BE),F为BC的中点,连接EF.图中等腰三角形的个数是( )
A.3 B.5 C.6 D.7
8.(2025春 巴彦县月考)如图在坐标系中,四边形ABCD为菱形,顶点A、B在x轴上,A(﹣2,0),B(3,0)点C在y轴上,点D在第二象限,则顶点D的坐标为( )
A.(4,5) B.(5,4) C.(﹣5,4) D.(﹣4,5)
9.(2025春 确山县期中)若正方形的一条对角线长为8cm,则这个正方形的面积是_____cm2.( )
A.64 B.32 C.48 D.36
10.(2025春 汶上县期中)如图, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.4
二.填空题(共6小题)
11.(2025 柳林县二模)如图,在菱形ABCD中,AE⊥BC于点E,AC=6,BD=8,则AE的长是 .
12.(2025春 济南月考)如图,平行四边形ABCD中,BE、CF分别平分∠ABC、∠BCD交AD于点E、点F,已知AB=6,BC=10,则EF的长为 .
13.(2025春 巴彦县月考)如图,已知矩形ABCD中,AB=4,AD=7,AE平分∠BAD交BC于E,点F、N分别为AE、AD的中点,则FN的长度为 .
14.(2025春 确山县期中)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=3,BC=4,则EF的长为 .
15.(2025春 临颍县期中)已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,则ED= .
16.(2025春 东平县期中)菱形的面积为24cm2,一条对角线是6cm,那么菱形的另一条对角线长为 .
三.解答题(共8小题)
17.(2025春 兴宾区期中)如图,在Rt△ABC中,∠BAC=90°,点E,点F分别是BC,AC的中点,延长BA到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE的交点为点O.
(1)判断AE与DF有什么数量关系,并说明理由.
(2)当AB=6,BC=10,求OD的长.
18.(2025 西安模拟)如图,四边形ABCD是矩形,点E在BC边上,AF⊥DE,垂足为F,AF=DC.证明AD=DE.
19.(2025春 淮滨县期中)如图,E,F是平行四边形ABCD的对角线AC上的点,AE=CF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
20.(2025 秦淮区二模)如图,△ABC与△ADC关于直线AC对称,∠BAD=∠BCD.求证:四边形ABCD是菱形.
21.(2025 无锡校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
22.(2025 惠阳区二模)如图,在 ABCD中,对角线AC,BD相交于点O,AO=BO.
(1)求证: ABCD是矩形;
(2)点E在BC边上,满足CE=CO.若AB=6,BC=8,求BE的长.
23.(2025 建湖县三模)在平行四边形ABCD中,E为BC上一点,点F为AE的中点,连接DF并延长,交CB的延长线于点G.
(1)求证:△ADF≌△EGF;
(2)求证:BG=CE.
24.(2025 泰州二模)如图,在 ABCD中,连接对角线AC,分别作△ABC和△ACD的中线AE、CF.
(1)求证:AE=CF;
(2)从下列条件中任选一个作为已知条件,判断四边形AECF的形状,并证明你的结论.
①AC=AB;②AC⊥AB.
我选择的条件: ,(填写序号).(注:如果选择①,②分别进行解答,按第一个解答计分)
期末核心考点 平行四边形
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 平乡县期中)如图,在3×3的小正方形网格中,以线段MN为对角线作平行四边形,使另两个顶点均在网格的格点(网格线的交点)上,这样的平行四边形最多可画n个,则n的值为( )
A.3 B.4 C.5 D.6
【答案】C
【分析】由所作的平行四边形以MN为对角线,可知该平行四边形另两个顶点关于MN的中点I对称,不重复且无遗漏的找出所给网格的格点中,关于点I对称的每一组对称点,再画出相应的平行四边形,即可得到问题的答案.
【解答】解:∵所作的平行四边形以MN为对角线,
∴该平行四边形另两个顶点关于MN的中点I对称,
如图1,点A与点B关于点I对称,连接AB,作四边形AMBN,
∵MI=NI,AI=BI,
∴四边形AMBN是平行四边形,
如图2,点C与点D关于点I对称,则四边形CMDN是平行四边形;
如图3,点E与点F关于点I对称,则四边形EMFN是平行四边形;
如图4,点G与点L关于点I对称,则四边形BMLN是平行四边形;
如图5,点P与点T关于点I对称,则四边形PMTN是平行四边形,
∴以线段MN为对角线作平行四边形,使另两个顶点均在格点上,这样的平行四边形最多可画5个,
∴n的值是5,
故选:C.
【点评】此题重点考查平行四边形的判定,在所给网格的格点中找出关于MN的中点对称的两个点是解题的关键.
2.(2025春 武威期中)已知△ABC,现有四条信息:①D为AB中点;②E为AC中点;③DE∥BC;④BC=2DE,若从中任选两条信息作为条件,再从余下的两条信息中任选一条信息作为结论,一共能组成真命题的个数为( )
A.6个 B.8个 C.10个 D.12个
【答案】A
【分析】根据三角形相关以及三角形中位线定理判断所有可能的命题组合.
【解答】解:条件①②,结论③:根据中位线定理,成立;
条件①②,结论④:根据中位线定理,成立;
条件①③,结论②:由DE∥BC和D为中点,可推E为AC中点,成立;
条件①③,结论④:由DE∥BC和D为中点,可得E为中点,进而BC=2DE,成立;
条件①④,结论②:由BC=2DE和D为中点,不可推E为AC中点,不成立;
条件①④,结论③:由BC=2DE和D为中点,不可推DE∥BC,不成立;
条件②③,结论①:同理,由DE∥BC和E为中点,可推D为AB中点,成立;
条件②③,结论④:成立;
条件②④,结论①:同理,由BC=2DE和E为中点,不可推D为AB中点,不成立;
条件②④,结论③:不成立;
条件③④,结论①:需同时满足DE∥BC和BC=2DE,但仅此无法确定D是否为中点,可能不成立(如DE非中位线但满足比例);
条件③④,结论②:同理,无法确定E是否为中点,可能不成立;
上述组合中共计6个真命题.
故选:A.
【点评】本题主要考查了三角形中位线定理和命题与定理,解题的关键在于确认哪些组合能通过定理或逆推成立,最终排除不成立的情况,得出正确得情况.
3.(2025 江北区校级二模)如图,正方形ABCD中,E、F、H分别在AD、DC、BC边上,BF⊥EH于G,连接EB、DG,若DF=DE=2CF,则的值为( )
A. B. C. D.
【答案】A
【分析】过点A作AM∥EH交BC于点M,过点G作GN⊥CD于点N,设CF=a,则DF=DE=2CF=2a,AB=BC=CD=AD=3a,AE=a,证明四边形AEHM是平行四边形得AE=MH=a,证明△BAM和△CBF全等得BM=CF=a,则BH=2a,由勾股定理求出BF=,再证明△BGH和△BCF全等得BG=,GH=,则GF=,然后证明△GNF和△BCF相似得GN=,FN=,则DN=,进而由勾股定理求出DG=,由此即可得出的值.
【解答】解:过点A作AM∥EH交BC于点M,过点G作GN⊥CD于点N,如图所示:
设CF=a,
∴DF=DE=2CF=2a,
∴CD=DF+CF=3a,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3a,∠ABC=∠C=90°,AD∥BC,
∴AE=AD﹣DE=a,
∵AM∥EH,AD∥BC,BF⊥EH,
∴四边形AEHM是平行四边形,BF⊥AM
∴AE=MH=a,∠BAM+∠ABF=90°,
∵∠ABC=∠ABF+∠CBF=90°,
∴∠BAM=∠CBF,
在△BAM和△CBF中,
,
∴△BAM≌△CBF(ASA),
∴BM=CF=a,
∴BH=BM+MH=2a,
在Rt△BCF中,由勾股定理得:BF===,
∵BF⊥EH,
∴∠BGH=∠C=90°,
又∵∠GBH=∠CBF,
∴△BGH∽△BCF,
∴==,
∴==,
∴BG=,GH=,
∴GF=BF﹣BG==,
∵GN⊥BC,
∴∠GNF=∠C=90°,
∴GN∥BC,
∴△GNF∽△BCF,
∴==,
∴==,
∴GN=,FN=,
∴DN=DF+FN==,
在Rt△DNG中,由勾股定理得:DG===,
∴==.
故选:A.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,理解正方形的性质,熟练掌握全等三角形的判定和性质,相似三角形的判定和性质,勾股定理是解决问题的关键.
4.(2025春 离石区期中)如图,在 ABCD中,E,F是对角线AC上的两点(不与点A,C重合),且AE=CF,连接BE,BF,DE,DF,下列结论错误的是( )
A.四边形BEDF是平行四边形
B.若四边形ABCD是菱形,则四边形BEDF是菱形
C.若四边形ABCD是正方形,则四边形BEDF是菱形
D.若四边形ABCD是矩形,则四边形BEDF也是矩形
【答案】D
【分析】连接BD交AC于点O,根据平行四边形的性质可得OA=OC,OB=OD,再根据E、F是对角线AC上的两点(不与点A、C重合),AE=CF,可得OE=OF,进一步即可判断A选项;根据菱形的性质可得BD⊥AC,进一步即可判断B选项;根据正方形的性质可得 BD⊥AC,进一步即可判断C选项;根据矩形的性质可得 AC=BD,再根据E、F是对角线AC上的两点(不与点A、C重合),可得EF≠BD,进一步可判断D选项.
【解答】解:连接BD交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是对角线AC上的两点(不与点A、C重合),AE=CF,
∴OE=OF,
∵OB=OD,
∴四边形BFDE是平行四边形,故A不符合题意;
当四边形ABCD是菱形时,BD⊥AC,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形,故B不符合题意;
当四边形ABCD是正方形时,BD⊥AC,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形,故C不符合题意;
当四边形ABCD是矩形时,AC=BD,
∵E、F是对角线AC上的两点(不与点A、C重合),
∴EF≠BD,
∴四边形BFDE不是矩形,故D符合题意,
故选:D.
【点评】本题考查了平行四边形的判定和性质,菱形的判定和性质,矩形的判定和性质,正方形的性质,熟练掌握这些知识是解题的关键.
5.(2025 张店区二模)如图,在矩形ABCD中,摆放着正方形ADFE和正方形EHGB(点G在BC上),延长GH交AD于点R.若S正方形ADFE=5,S正方形EHGB=3,则阴影部分矩形RDCG的面积等于( )
A.1 B.2 C.3 D.4
【答案】B
【分析】设正方形ADFE边长为a,正方形EHGB边长为b,则a2=5,b2=3,根据正方形和矩形的性质得CD=a+b,RD=a﹣b,则阴影部分矩形RDCG的面积为:CD RD=(a+b)(a﹣b)=a2﹣b2=2,由此即可得出答案.
【解答】解:设正方形ADFE的边长为a,正方形EHGB边长为b,
∵S正方形ADFE=5,S正方形EHGB=3,
∴a2=5,b2=3,
根据正方形和矩形的性质得:CD=a+b,RD=a﹣b,
∴阴影部分矩形RDCG的面积为:CD RD=(a+b)(a﹣b)=a2﹣b2=2.
故选:B.
【点评】此题主要考查了正方形和矩形的性质,熟练掌握正方形和矩形的性质是解决问题的关键.
6.(2024秋 济宁期末)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC
B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD
D.∠ABD=∠BDC,∠ADB=∠CBD
【答案】B
【分析】由∠ABD=∠BDC,∠AOB=∠COD,OA=OC,证明△AOB≌△COD,得OB=OD,则四边形ABCD是平行四边形,可判断A不符合题意;由∠ABC=∠ADC,AB=CD,不能证明△ABC≌△CDA,所以不能确定BC与AD是否相等,则不能判断四边形ABCD是平行四边形,可判断B符合题意;AD∥BC,得∠OCB=∠OAD,而∠COB=∠AOD,OB=OD,可根据“AAS”证明△COB≌△AOD,得OC=OA,则四边形ABCD是平行四边形,可判断C不符合题意;由∠ABD=∠BDC,得AB∥CD,由∠ADB=∠CBD,得AD∥CB,则四边形ABCD是平行四边形,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵∠ABD=∠BDC,
∴∠ABO=∠CDO,
在△AOB和△COD中,
,
∴△AOB≌△COD(AAS),
∴OB=OD,
∴四边形ABCD是平行四边形,
故A不符合题意;
∵由∠ABC=∠ADC,AB=CD,不能证明△ABC≌△CDA,
∴不能确定BC与AD是否相等,
∴不能判断四边形ABCD是平行四边形,
故B符合题意;
∵AD∥BC,
∴∠OCB=∠OAD,
在△COB和△AOD中,
,
∴△COB≌△AOD(AAS),
∴OC=OA,
∴四边形ABCD是平行四边形,
故C不符合题意;
∵∠ABD=∠BDC,
∴AB∥CD,
∵∠ADB=∠CBD,
∴AD∥CB,
四边形ABCD是平行四边形,
故D不符合题意,
故选:B.
【点评】此题重点考查平行四边形的定义和判定定理,根据所给的条件,适当选择平行四边形的定义或判定定理证明四边形ABCD是平行四边形是解题的关键.
7.(2025 碑林区模拟)如图,菱形ABCD的对角线AC,BD交于点E(AE<BE),F为BC的中点,连接EF.图中等腰三角形的个数是( )
A.3 B.5 C.6 D.7
【答案】C
【分析】由菱形的性质推出AB=AD=CD=BC,AC⊥BD,由直角三角形斜边中线的性质推出EF=BF=FC,即可得到图中等腰三角形的个数.
【解答】解:∵四边形ABCD是菱形,
∴AB=AD=CD=BC,AC⊥BD,
∴∠BEC=90°,
∵F为BC的中点,
∴EF=BC,
∴EF=BF=FC,
∴△ABD、△DAC、△CBD、△BAC、△FBE、△FEC是等腰三角形,
∴图中等腰三角形的个数是6个.
故选:C.
【点评】本题考查菱形的性质,等腰三角形的判定,直角三角形斜边的中线,关键是掌握菱形的四条边相等,对角线互相垂直;直角三角形斜边的中线等于斜边的一半.
8.(2025春 巴彦县月考)如图在坐标系中,四边形ABCD为菱形,顶点A、B在x轴上,A(﹣2,0),B(3,0)点C在y轴上,点D在第二象限,则顶点D的坐标为( )
A.(4,5) B.(5,4) C.(﹣5,4) D.(﹣4,5)
【答案】C
【分析】由A、B的坐标求出OA=2,OB=3,得到AB=OA+OB=5,由菱形的性质推出DC=BC=AB=5,DC∥AB,由勾股定理求出OC=4,即可得到D的坐标.
【解答】解:∵A(﹣2,0),B(3,0),
∴OA=2,OB=3,
∴AB=OA+OB=5,
∵四边形ABCD是菱形,
∴DC=BC=AB=5,DC∥AB,
∵∠BOC=90°,
∴OC==4,
∵DC∥AB,AB⊥y轴,
∴DC⊥y轴,
∴D的坐标是(﹣5,4).
故选:C.
【点评】本题考查菱形的性质,坐标与图形的性质,勾股定理,关键是由菱形的性质推出DC=BC=AB=5,DC∥AB.
9.(2025春 确山县期中)若正方形的一条对角线长为8cm,则这个正方形的面积是_____cm2.( )
A.64 B.32 C.48 D.36
【答案】B
【分析】正方形对角线是边长的倍,求出正方形的边长即可求出面积.
【解答】解:∵正方形对角线=8cm,正方形对角线是边长的倍,
∴正方形边长=4(cm),
∴正方形面积==32(cm2).
故选:B.
【点评】本题考查正方形的性质,解题的关键是关键是相关知识.
10.(2025春 汶上县期中)如图, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.4
【答案】B
【分析】因为四边形ABCD是平行四边形,所以OA=OC;再根据点E是BC的中点,得出OE是△ABC的中位线,即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴OE是△ABC的中位线,
∴根据三角形的中位线定理可得:AB=2OE=4.
则OE=2,
故选:B.
【点评】此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线的性质:三角形的中位线平行且等于三角形第三边的一半.
二.填空题(共6小题)
11.(2025 柳林县二模)如图,在菱形ABCD中,AE⊥BC于点E,AC=6,BD=8,则AE的长是 .
【答案】.
【分析】由菱形的性质推出AC⊥BD,OC=AC=3,OB=BD=4,由勾股定理求出BC=5,由菱形ABCD的面积=BC AE=AC BD,即可求出AE的长.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OC=AC,OB=BD,
∵AC=6,BD=8,
∴OC=3,OB=4,
∴BC==5,
∵AE⊥BC,
∴菱形ABCD的面积=BC AE=AC BD,
∴5×AE=×6×8,
∴AE=.
故答案为:.
【点评】本题考查菱形的性质,关键是由菱形的面积公式得到BC AE=AC BD.
12.(2025春 济南月考)如图,平行四边形ABCD中,BE、CF分别平分∠ABC、∠BCD交AD于点E、点F,已知AB=6,BC=10,则EF的长为 2 .
【答案】2.
【分析】结合平行四边形的性质,先证∠ABE=∠AEB,则AB=AE=6,同理可证FD=CD=6,进而得出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=6,AD∥BC,AD=BC=10,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AE=AB=6,
同理可证:DF=CD=6,
∴EF=AE+FD﹣AD=6+6﹣10=2.
故答案为:2.
【点评】本题主要考查了平行四边形的性质等知识,熟练掌握平行四边形的性质,证明AE=AB是解题的关键.
13.(2025春 巴彦县月考)如图,已知矩形ABCD中,AB=4,AD=7,AE平分∠BAD交BC于E,点F、N分别为AE、AD的中点,则FN的长度为 2.5 .
【答案】2.5.
【分析】连接DE,由矩形的性质推出DC=AB=4,BC=AD=7,AD∥BC,∠C=90°,由平行线的性质和角平分线定义推出∠AEB=∠BAE,得到BE=AB=4,求出CE=3,由勾股定理求出DE=5,判定FN是△ADE的中位线,推出FN=DE=2.5.
【解答】解:连接DE,
∵四边形ABCD是矩形,
∴DC=AB=4,BC=AD=7,AD∥BC,∠C=90°,
∴∠AEB=∠DAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠AEB=∠BAE,
∴BE=AB=4,
∴CE=BC﹣BE=7﹣4=3,
∴DE==5,
∵点F、N分别为AE、AD的中点,
∴FN是△ADE的中位线,
∴FN=DE=2.5.
故答案为:2.5.
【点评】本题考查矩形的性质,勾股定理,三角形中位线定理,角平分线定义,关键是由三角形中位线定理推出FN=DE.
14.(2025春 确山县期中)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=3,BC=4,则EF的长为 1 .
【答案】1.
【分析】根据勾股定理得到AB=5,根据三角形中位线定理得到DE∥AB,DE=,根据平行线的性质和角平分线的定义得到得到∠DAF=∠DFA,根据等腰三角形的判定得到结论.
【解答】解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB==5,
∵D、E分别为CA、CB的中点,
∴DE是△ABC的中位线,
∴DE∥AB,DE=AB=,
∴∠DFA=∠FAB,
∵AF平分∠BAC,
∴∠DAF=∠BAF,
∴∠DAF=∠DFA,
∴DF=AD=AC=×3=.
∴EF=DE﹣DF=1,
故答案为:1.
【点评】本题考查的是三角形中位线定理、勾股定理、平行线的性质,等腰三角形的判定,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
15.(2025春 临颍县期中)已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,则ED= 1 .
【答案】1.
【分析】延长BE交AC于F,由已知条件可得△BAF是等腰三角形,由等腰三角形的性质可得BE=EF,又因为BD=CD是,所以DE是△BCF的中位线,由三角形中位线定理即可求出DE的长.
【解答】解:延长BE交AC于F,
∵AE平分∠BAC,BE⊥AE,
∴∠BAE=∠CAE,∠AEB=∠AEF=90°,
在△ABE与△AFE中,
,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC﹣AF=7﹣5=2,
∵D为BC中点
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=CF=1,
故答案为:1.
【点评】本题考查了三角形中位线定理以及等腰三角形的判定,解题的关键是正确作出辅助线,得到△BAF是等腰三角形.
16.(2025春 东平县期中)菱形的面积为24cm2,一条对角线是6cm,那么菱形的另一条对角线长为 8cm .
【答案】8cm.
【分析】根据菱形的面积等于对角线乘积的一半,设另一条对角线为x,即可得出一个一元一次方程,解出即可得出结论.
【解答】解:设另一条对角线为x cm,
∵菱形的面积为24cm2,一条对角线是6cm,
∴,
解得:x=8,
∴菱形的另一条对角线长为8cm.
故答案为:8cm.
【点评】本题考查了菱形的性质、解一元一次方程,解本题的关键在熟练掌握菱形的面积等于对角线乘积的一半.
三.解答题(共8小题)
17.(2025春 兴宾区期中)如图,在Rt△ABC中,∠BAC=90°,点E,点F分别是BC,AC的中点,延长BA到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE的交点为点O.
(1)判断AE与DF有什么数量关系,并说明理由.
(2)当AB=6,BC=10,求OD的长.
【答案】(1)AE=DF,理由见解析;
(2).
【分析】(1)根据三角形中位线定理得到EF∥AB,AB=2EF,则可证明EF∥AD,AD=EF,进一步可证明四边形AEFD是平行四边形,得到AE=DF.
(2)由勾股定理求出AC=8,利用平行四边形对角线互相平分和线段中点的定义求出OA的长,再利用勾股定理即可求出OD的长.
【解答】解:(1)AE=DF,理由如下:
∵E,F分别是BC,AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB,AB=2EF,
∵AB=2AD,
∴EF∥AD,AD=EF,
∴四边形AEFD是平行四边形.
∴AE=DF;
(2)∵∠BAC=90°,AB=6,BC=10,
∴,.
由(1)知四边形AEFD是平行四边形,F是AC的中点,
∴OA=OF,AF=CF.
∴,
∵∠BAC=90°,
∴∠DAO=90°,
∴.
【点评】本题考查的是直角三角形斜边上的中线,三角形中位线定理,平行四边形的判定与性质,熟知以上知识是解题的关键.
18.(2025 西安模拟)如图,四边形ABCD是矩形,点E在BC边上,AF⊥DE,垂足为F,AF=DC.证明AD=DE.
【答案】见试题解答内容
【分析】由矩形的性质推出∠C=90°,AD∥BC,由平行线的性质推出∠ADF=∠CED,由垂直的定义得到∠AFD=∠C=90°,又AF=DC,由AAS证明△ADF≌△DEC,推出AD=DE.
【解答】解:∵四边形ABCD是矩形,
∴∠C=90°,AD∥BC,
∴∠ADF=∠CED,
∵AF⊥DE,
∴∠AFD=∠C=90°,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AD=DE.
【点评】本题考查矩形的性质,全等三角形的判定和性质,关键是由矩形的性质推出△ADF≌△DEC(AAS).
19.(2025春 淮滨县期中)如图,E,F是平行四边形ABCD的对角线AC上的点,AE=CF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
【答案】BE∥DF,BE=DF,证明见解答.
【分析】由平行四边形的性质得CB=AD,CB∥AD,则∠BCE=∠DAF,由AE=CF,推导出AF=CE,即可根据“SAS”证明△BCE≌△DAF,则BE=DF,∠CEB=∠AFD,所以BE∥DF.
【解答】解:BE∥DF,BE=DF,
证明:∵四边形ABCD是平行四边形,
∴CB=AD,CB∥AD,
∴∠BCE=∠DAF,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△BCE和△DAF中,
,
∴△BCE≌△DAF(SAS),
∴BE=DF,∠CEB=∠AFD,
∴BE∥DF.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质等知识,证明△BCE≌△DAF是解题的关键.
20.(2025 秦淮区二模)如图,△ABC与△ADC关于直线AC对称,∠BAD=∠BCD.求证:四边形ABCD是菱形.
【答案】证明见解答过程.
【分析】根据轴对称的性质求出AB=AD,CB=CD,∠BAC=∠DAC=∠BAD,∠BCA=∠DCA=∠BCD,进而求出∠BAC=∠BCA,结合等腰三角形的判定求出AB=AD=CB=CD,再根据“四边相等的四边形是菱形”即可得证.
【解答】证明:∵△ABC与△ADC关于直线AC对称,
∴AB=AD,CB=CD,∠BAC=∠DAC=∠BAD,∠BCA=∠DCA=∠BCD,
∵∠BAD=∠BCD,
∴∠BAC=∠BCA,
∴AB=CB,
∴AB=AD=CB=CD,
∴四边形ABCD是菱形.
【点评】此题考查了菱形的判定、轴对称的性质,熟记菱形的判定定理、轴对称的性质是解题的关键.
21.(2025 无锡校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
【答案】见试题解答内容
【分析】(1)由正方形的性质得AB=DC,∠ABC=∠DCB=90°,由等边三角形的性质得BE=CE,∠EBC=∠ECB=60°,则∠ABE=∠DCE,即可证明△ABE≌△DCE,得AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得180﹣2x=360﹣60﹣2(90﹣x),求出x,再用180﹣2x即可.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
∴∠ABC﹣∠EBC=∠ECB﹣∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得
180﹣2x=360﹣60﹣2(90﹣x),
x=15,
180﹣2×15=150,
∴∠AED为150度.
【点评】此题重点考查正方形的性质、等边三角形的性质、全等三角形的判定与性质等知识,证明△ABE≌△DCE是解题的关键.
22.(2025 惠阳区二模)如图,在 ABCD中,对角线AC,BD相交于点O,AO=BO.
(1)求证: ABCD是矩形;
(2)点E在BC边上,满足CE=CO.若AB=6,BC=8,求BE的长.
【答案】(1)证明见解答过程;
(2)3.
【分析】(1)根据平行四边形性质得AC=2AO,BD=2BO,再根据AO=BO得AC=BD,然后根据对角线相等平行四边形是矩形即可得出结论;
(2)先由勾股定理求出AC=10,进而根据矩形行得CO=AO=5,则CE=CO=5,由此即可得出BE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,且AB=6,BC=8,
∴∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC===10,
∴CO=AO=AC=5,
∵CE=CO,
∴CE=5,
∴BE=BC﹣CE=8﹣5=3.
【点评】此题主要考查了矩形的判定和性质,平行四边形的性质,勾股定理,熟练掌握矩形的判定和性质,平行四边形的性质,勾股定理是解决问题的关键.
23.(2025 建湖县三模)在平行四边形ABCD中,E为BC上一点,点F为AE的中点,连接DF并延长,交CB的延长线于点G.
(1)求证:△ADF≌△EGF;
(2)求证:BG=CE.
【答案】(1)证明见解析;
(2)证明见解析.
【分析】(1)先由平行四边形性质得到AD∥BC,再由平行线性质和中点定义确定相关角度与边长,再由全等三角形的判定定理即可得证;
(2)由全等三角形的性质和平行四边形的性质得到GE=CB,数形结合表示出BG、CE即可得证.
【解答】(1)证明:在平行四边形ABCD中,AD∥BC,点F为AE的中点,
∴∠DAF=∠GEF,AF=EF,
在△ADF和△EGF中,
∴△ADF≌△EGF(ASA);
(2)解:由(1)知△ADF≌△EGF,
∴GE=DA,
∵四边形ABCD是平行四边形,AD=BC,
∴GE=CB,
∵GE=GB+BE,CB=BE+CE,
∴BG=CE.
【点评】本题考查的是平行四边形的性质、全等三角形的判定与性质,熟练掌握以上知识是解决问题的关键.
24.(2025 泰州二模)如图,在 ABCD中,连接对角线AC,分别作△ABC和△ACD的中线AE、CF.
(1)求证:AE=CF;
(2)从下列条件中任选一个作为已知条件,判断四边形AECF的形状,并证明你的结论.
①AC=AB;②AC⊥AB.
我选择的条件: ① ,(填写序号).(注:如果选择①,②分别进行解答,按第一个解答计分)
【答案】(1)见解析;
(2)①,见解析.
【分析】(1)利用平行四边形的性质得到AD=BC,AD∥BC,由中线的定义得到,,得出AF=CE,再利用平行四边形的性质与判定即可证明;
(2)根据矩形、菱形的判定即可解答.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵△ABC和△ACD的中线分别为AE、CF.
∴,,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF;
(2)解:若选择条件①,则四边形AECF是矩形.理由如下:
∵AC=AB,AE是△ABC的中线,
∴AE⊥BC,
∴∠AEC=90°,
由(1)得,四边形AECF是平行四边形,
∴平行四边形AECF是矩形;
若选择条件②,则四边形AECF是菱形.理由如下:
∵AC⊥AB,AE是△ABC的中线,
∴,
由(1)得,四边形AECF是平行四边形,
∴平行四边形AECF是菱形.
故答案为:①.
【点评】本题考查了平行四边形的判定与性质、矩形的判定、菱形的判定、三角形中位线定理,熟练掌握相关知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 平行四边形
一.选择题(共10小题)
1.(2025春 平乡县期中)如图,在3×3的小正方形网格中,以线段MN为对角线作平行四边形,使另两个顶点均在网格的格点(网格线的交点)上,这样的平行四边形最多可画n个,则n的值为( )
A.3 B.4 C.5 D.6
2.(2025春 武威期中)已知△ABC,现有四条信息:①D为AB中点;②E为AC中点;③DE∥BC;④BC=2DE,若从中任选两条信息作为条件,再从余下的两条信息中任选一条信息作为结论,一共能组成真命题的个数为( )
A.6个 B.8个 C.10个 D.12个
3.(2025 江北区校级二模)如图,正方形ABCD中,E、F、H分别在AD、DC、BC边上,BF⊥EH于G,连接EB、DG,若DF=DE=2CF,则的值为( )
A. B. C. D.
4.(2025春 离石区期中)如图,在 ABCD中,E,F是对角线AC上的两点(不与点A,C重合),且AE=CF,连接BE,BF,DE,DF,下列结论错误的是( )
A.四边形BEDF是平行四边形
B.若四边形ABCD是菱形,则四边形BEDF是菱形
C.若四边形ABCD是正方形,则四边形BEDF是菱形
D.若四边形ABCD是矩形,则四边形BEDF也是矩形
5.(2025 张店区二模)如图,在矩形ABCD中,摆放着正方形ADFE和正方形EHGB(点G在BC上),延长GH交AD于点R.若S正方形ADFE=5,S正方形EHGB=3,则阴影部分矩形RDCG的面积等于( )
A.1 B.2 C.3 D.4
6.(2024秋 济宁期末)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC
B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD
D.∠ABD=∠BDC,∠ADB=∠CBD
7.(2025 碑林区模拟)如图,菱形ABCD的对角线AC,BD交于点E(AE<BE),F为BC的中点,连接EF.图中等腰三角形的个数是( )
A.3 B.5 C.6 D.7
8.(2025春 巴彦县月考)如图在坐标系中,四边形ABCD为菱形,顶点A、B在x轴上,A(﹣2,0),B(3,0)点C在y轴上,点D在第二象限,则顶点D的坐标为( )
A.(4,5) B.(5,4) C.(﹣5,4) D.(﹣4,5)
9.(2025春 确山县期中)若正方形的一条对角线长为8cm,则这个正方形的面积是_____cm2.( )
A.64 B.32 C.48 D.36
10.(2025春 汶上县期中)如图, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.4
二.填空题(共6小题)
11.(2025 柳林县二模)如图,在菱形ABCD中,AE⊥BC于点E,AC=6,BD=8,则AE的长是 .
12.(2025春 济南月考)如图,平行四边形ABCD中,BE、CF分别平分∠ABC、∠BCD交AD于点E、点F,已知AB=6,BC=10,则EF的长为 .
13.(2025春 巴彦县月考)如图,已知矩形ABCD中,AB=4,AD=7,AE平分∠BAD交BC于E,点F、N分别为AE、AD的中点,则FN的长度为 .
14.(2025春 确山县期中)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=3,BC=4,则EF的长为 .
15.(2025春 临颍县期中)已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,则ED= .
16.(2025春 东平县期中)菱形的面积为24cm2,一条对角线是6cm,那么菱形的另一条对角线长为 .
三.解答题(共8小题)
17.(2025春 兴宾区期中)如图,在Rt△ABC中,∠BAC=90°,点E,点F分别是BC,AC的中点,延长BA到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE的交点为点O.
(1)判断AE与DF有什么数量关系,并说明理由.
(2)当AB=6,BC=10,求OD的长.
18.(2025 西安模拟)如图,四边形ABCD是矩形,点E在BC边上,AF⊥DE,垂足为F,AF=DC.证明AD=DE.
19.(2025春 淮滨县期中)如图,E,F是平行四边形ABCD的对角线AC上的点,AE=CF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
20.(2025 秦淮区二模)如图,△ABC与△ADC关于直线AC对称,∠BAD=∠BCD.求证:四边形ABCD是菱形.
21.(2025 无锡校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
22.(2025 惠阳区二模)如图,在 ABCD中,对角线AC,BD相交于点O,AO=BO.
(1)求证: ABCD是矩形;
(2)点E在BC边上,满足CE=CO.若AB=6,BC=8,求BE的长.
23.(2025 建湖县三模)在平行四边形ABCD中,E为BC上一点,点F为AE的中点,连接DF并延长,交CB的延长线于点G.
(1)求证:△ADF≌△EGF;
(2)求证:BG=CE.
24.(2025 泰州二模)如图,在 ABCD中,连接对角线AC,分别作△ABC和△ACD的中线AE、CF.
(1)求证:AE=CF;
(2)从下列条件中任选一个作为已知条件,判断四边形AECF的形状,并证明你的结论.
①AC=AB;②AC⊥AB.
我选择的条件: ,(填写序号).(注:如果选择①,②分别进行解答,按第一个解答计分)
期末核心考点 平行四边形
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 平乡县期中)如图,在3×3的小正方形网格中,以线段MN为对角线作平行四边形,使另两个顶点均在网格的格点(网格线的交点)上,这样的平行四边形最多可画n个,则n的值为( )
A.3 B.4 C.5 D.6
【答案】C
【分析】由所作的平行四边形以MN为对角线,可知该平行四边形另两个顶点关于MN的中点I对称,不重复且无遗漏的找出所给网格的格点中,关于点I对称的每一组对称点,再画出相应的平行四边形,即可得到问题的答案.
【解答】解:∵所作的平行四边形以MN为对角线,
∴该平行四边形另两个顶点关于MN的中点I对称,
如图1,点A与点B关于点I对称,连接AB,作四边形AMBN,
∵MI=NI,AI=BI,
∴四边形AMBN是平行四边形,
如图2,点C与点D关于点I对称,则四边形CMDN是平行四边形;
如图3,点E与点F关于点I对称,则四边形EMFN是平行四边形;
如图4,点G与点L关于点I对称,则四边形BMLN是平行四边形;
如图5,点P与点T关于点I对称,则四边形PMTN是平行四边形,
∴以线段MN为对角线作平行四边形,使另两个顶点均在格点上,这样的平行四边形最多可画5个,
∴n的值是5,
故选:C.
【点评】此题重点考查平行四边形的判定,在所给网格的格点中找出关于MN的中点对称的两个点是解题的关键.
2.(2025春 武威期中)已知△ABC,现有四条信息:①D为AB中点;②E为AC中点;③DE∥BC;④BC=2DE,若从中任选两条信息作为条件,再从余下的两条信息中任选一条信息作为结论,一共能组成真命题的个数为( )
A.6个 B.8个 C.10个 D.12个
【答案】A
【分析】根据三角形相关以及三角形中位线定理判断所有可能的命题组合.
【解答】解:条件①②,结论③:根据中位线定理,成立;
条件①②,结论④:根据中位线定理,成立;
条件①③,结论②:由DE∥BC和D为中点,可推E为AC中点,成立;
条件①③,结论④:由DE∥BC和D为中点,可得E为中点,进而BC=2DE,成立;
条件①④,结论②:由BC=2DE和D为中点,不可推E为AC中点,不成立;
条件①④,结论③:由BC=2DE和D为中点,不可推DE∥BC,不成立;
条件②③,结论①:同理,由DE∥BC和E为中点,可推D为AB中点,成立;
条件②③,结论④:成立;
条件②④,结论①:同理,由BC=2DE和E为中点,不可推D为AB中点,不成立;
条件②④,结论③:不成立;
条件③④,结论①:需同时满足DE∥BC和BC=2DE,但仅此无法确定D是否为中点,可能不成立(如DE非中位线但满足比例);
条件③④,结论②:同理,无法确定E是否为中点,可能不成立;
上述组合中共计6个真命题.
故选:A.
【点评】本题主要考查了三角形中位线定理和命题与定理,解题的关键在于确认哪些组合能通过定理或逆推成立,最终排除不成立的情况,得出正确得情况.
3.(2025 江北区校级二模)如图,正方形ABCD中,E、F、H分别在AD、DC、BC边上,BF⊥EH于G,连接EB、DG,若DF=DE=2CF,则的值为( )
A. B. C. D.
【答案】A
【分析】过点A作AM∥EH交BC于点M,过点G作GN⊥CD于点N,设CF=a,则DF=DE=2CF=2a,AB=BC=CD=AD=3a,AE=a,证明四边形AEHM是平行四边形得AE=MH=a,证明△BAM和△CBF全等得BM=CF=a,则BH=2a,由勾股定理求出BF=,再证明△BGH和△BCF全等得BG=,GH=,则GF=,然后证明△GNF和△BCF相似得GN=,FN=,则DN=,进而由勾股定理求出DG=,由此即可得出的值.
【解答】解:过点A作AM∥EH交BC于点M,过点G作GN⊥CD于点N,如图所示:
设CF=a,
∴DF=DE=2CF=2a,
∴CD=DF+CF=3a,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3a,∠ABC=∠C=90°,AD∥BC,
∴AE=AD﹣DE=a,
∵AM∥EH,AD∥BC,BF⊥EH,
∴四边形AEHM是平行四边形,BF⊥AM
∴AE=MH=a,∠BAM+∠ABF=90°,
∵∠ABC=∠ABF+∠CBF=90°,
∴∠BAM=∠CBF,
在△BAM和△CBF中,
,
∴△BAM≌△CBF(ASA),
∴BM=CF=a,
∴BH=BM+MH=2a,
在Rt△BCF中,由勾股定理得:BF===,
∵BF⊥EH,
∴∠BGH=∠C=90°,
又∵∠GBH=∠CBF,
∴△BGH∽△BCF,
∴==,
∴==,
∴BG=,GH=,
∴GF=BF﹣BG==,
∵GN⊥BC,
∴∠GNF=∠C=90°,
∴GN∥BC,
∴△GNF∽△BCF,
∴==,
∴==,
∴GN=,FN=,
∴DN=DF+FN==,
在Rt△DNG中,由勾股定理得:DG===,
∴==.
故选:A.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,理解正方形的性质,熟练掌握全等三角形的判定和性质,相似三角形的判定和性质,勾股定理是解决问题的关键.
4.(2025春 离石区期中)如图,在 ABCD中,E,F是对角线AC上的两点(不与点A,C重合),且AE=CF,连接BE,BF,DE,DF,下列结论错误的是( )
A.四边形BEDF是平行四边形
B.若四边形ABCD是菱形,则四边形BEDF是菱形
C.若四边形ABCD是正方形,则四边形BEDF是菱形
D.若四边形ABCD是矩形,则四边形BEDF也是矩形
【答案】D
【分析】连接BD交AC于点O,根据平行四边形的性质可得OA=OC,OB=OD,再根据E、F是对角线AC上的两点(不与点A、C重合),AE=CF,可得OE=OF,进一步即可判断A选项;根据菱形的性质可得BD⊥AC,进一步即可判断B选项;根据正方形的性质可得 BD⊥AC,进一步即可判断C选项;根据矩形的性质可得 AC=BD,再根据E、F是对角线AC上的两点(不与点A、C重合),可得EF≠BD,进一步可判断D选项.
【解答】解:连接BD交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是对角线AC上的两点(不与点A、C重合),AE=CF,
∴OE=OF,
∵OB=OD,
∴四边形BFDE是平行四边形,故A不符合题意;
当四边形ABCD是菱形时,BD⊥AC,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形,故B不符合题意;
当四边形ABCD是正方形时,BD⊥AC,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形,故C不符合题意;
当四边形ABCD是矩形时,AC=BD,
∵E、F是对角线AC上的两点(不与点A、C重合),
∴EF≠BD,
∴四边形BFDE不是矩形,故D符合题意,
故选:D.
【点评】本题考查了平行四边形的判定和性质,菱形的判定和性质,矩形的判定和性质,正方形的性质,熟练掌握这些知识是解题的关键.
5.(2025 张店区二模)如图,在矩形ABCD中,摆放着正方形ADFE和正方形EHGB(点G在BC上),延长GH交AD于点R.若S正方形ADFE=5,S正方形EHGB=3,则阴影部分矩形RDCG的面积等于( )
A.1 B.2 C.3 D.4
【答案】B
【分析】设正方形ADFE边长为a,正方形EHGB边长为b,则a2=5,b2=3,根据正方形和矩形的性质得CD=a+b,RD=a﹣b,则阴影部分矩形RDCG的面积为:CD RD=(a+b)(a﹣b)=a2﹣b2=2,由此即可得出答案.
【解答】解:设正方形ADFE的边长为a,正方形EHGB边长为b,
∵S正方形ADFE=5,S正方形EHGB=3,
∴a2=5,b2=3,
根据正方形和矩形的性质得:CD=a+b,RD=a﹣b,
∴阴影部分矩形RDCG的面积为:CD RD=(a+b)(a﹣b)=a2﹣b2=2.
故选:B.
【点评】此题主要考查了正方形和矩形的性质,熟练掌握正方形和矩形的性质是解决问题的关键.
6.(2024秋 济宁期末)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC
B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD
D.∠ABD=∠BDC,∠ADB=∠CBD
【答案】B
【分析】由∠ABD=∠BDC,∠AOB=∠COD,OA=OC,证明△AOB≌△COD,得OB=OD,则四边形ABCD是平行四边形,可判断A不符合题意;由∠ABC=∠ADC,AB=CD,不能证明△ABC≌△CDA,所以不能确定BC与AD是否相等,则不能判断四边形ABCD是平行四边形,可判断B符合题意;AD∥BC,得∠OCB=∠OAD,而∠COB=∠AOD,OB=OD,可根据“AAS”证明△COB≌△AOD,得OC=OA,则四边形ABCD是平行四边形,可判断C不符合题意;由∠ABD=∠BDC,得AB∥CD,由∠ADB=∠CBD,得AD∥CB,则四边形ABCD是平行四边形,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵∠ABD=∠BDC,
∴∠ABO=∠CDO,
在△AOB和△COD中,
,
∴△AOB≌△COD(AAS),
∴OB=OD,
∴四边形ABCD是平行四边形,
故A不符合题意;
∵由∠ABC=∠ADC,AB=CD,不能证明△ABC≌△CDA,
∴不能确定BC与AD是否相等,
∴不能判断四边形ABCD是平行四边形,
故B符合题意;
∵AD∥BC,
∴∠OCB=∠OAD,
在△COB和△AOD中,
,
∴△COB≌△AOD(AAS),
∴OC=OA,
∴四边形ABCD是平行四边形,
故C不符合题意;
∵∠ABD=∠BDC,
∴AB∥CD,
∵∠ADB=∠CBD,
∴AD∥CB,
四边形ABCD是平行四边形,
故D不符合题意,
故选:B.
【点评】此题重点考查平行四边形的定义和判定定理,根据所给的条件,适当选择平行四边形的定义或判定定理证明四边形ABCD是平行四边形是解题的关键.
7.(2025 碑林区模拟)如图,菱形ABCD的对角线AC,BD交于点E(AE<BE),F为BC的中点,连接EF.图中等腰三角形的个数是( )
A.3 B.5 C.6 D.7
【答案】C
【分析】由菱形的性质推出AB=AD=CD=BC,AC⊥BD,由直角三角形斜边中线的性质推出EF=BF=FC,即可得到图中等腰三角形的个数.
【解答】解:∵四边形ABCD是菱形,
∴AB=AD=CD=BC,AC⊥BD,
∴∠BEC=90°,
∵F为BC的中点,
∴EF=BC,
∴EF=BF=FC,
∴△ABD、△DAC、△CBD、△BAC、△FBE、△FEC是等腰三角形,
∴图中等腰三角形的个数是6个.
故选:C.
【点评】本题考查菱形的性质,等腰三角形的判定,直角三角形斜边的中线,关键是掌握菱形的四条边相等,对角线互相垂直;直角三角形斜边的中线等于斜边的一半.
8.(2025春 巴彦县月考)如图在坐标系中,四边形ABCD为菱形,顶点A、B在x轴上,A(﹣2,0),B(3,0)点C在y轴上,点D在第二象限,则顶点D的坐标为( )
A.(4,5) B.(5,4) C.(﹣5,4) D.(﹣4,5)
【答案】C
【分析】由A、B的坐标求出OA=2,OB=3,得到AB=OA+OB=5,由菱形的性质推出DC=BC=AB=5,DC∥AB,由勾股定理求出OC=4,即可得到D的坐标.
【解答】解:∵A(﹣2,0),B(3,0),
∴OA=2,OB=3,
∴AB=OA+OB=5,
∵四边形ABCD是菱形,
∴DC=BC=AB=5,DC∥AB,
∵∠BOC=90°,
∴OC==4,
∵DC∥AB,AB⊥y轴,
∴DC⊥y轴,
∴D的坐标是(﹣5,4).
故选:C.
【点评】本题考查菱形的性质,坐标与图形的性质,勾股定理,关键是由菱形的性质推出DC=BC=AB=5,DC∥AB.
9.(2025春 确山县期中)若正方形的一条对角线长为8cm,则这个正方形的面积是_____cm2.( )
A.64 B.32 C.48 D.36
【答案】B
【分析】正方形对角线是边长的倍,求出正方形的边长即可求出面积.
【解答】解:∵正方形对角线=8cm,正方形对角线是边长的倍,
∴正方形边长=4(cm),
∴正方形面积==32(cm2).
故选:B.
【点评】本题考查正方形的性质,解题的关键是关键是相关知识.
10.(2025春 汶上县期中)如图, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.4
【答案】B
【分析】因为四边形ABCD是平行四边形,所以OA=OC;再根据点E是BC的中点,得出OE是△ABC的中位线,即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴OE是△ABC的中位线,
∴根据三角形的中位线定理可得:AB=2OE=4.
则OE=2,
故选:B.
【点评】此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线的性质:三角形的中位线平行且等于三角形第三边的一半.
二.填空题(共6小题)
11.(2025 柳林县二模)如图,在菱形ABCD中,AE⊥BC于点E,AC=6,BD=8,则AE的长是 .
【答案】.
【分析】由菱形的性质推出AC⊥BD,OC=AC=3,OB=BD=4,由勾股定理求出BC=5,由菱形ABCD的面积=BC AE=AC BD,即可求出AE的长.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OC=AC,OB=BD,
∵AC=6,BD=8,
∴OC=3,OB=4,
∴BC==5,
∵AE⊥BC,
∴菱形ABCD的面积=BC AE=AC BD,
∴5×AE=×6×8,
∴AE=.
故答案为:.
【点评】本题考查菱形的性质,关键是由菱形的面积公式得到BC AE=AC BD.
12.(2025春 济南月考)如图,平行四边形ABCD中,BE、CF分别平分∠ABC、∠BCD交AD于点E、点F,已知AB=6,BC=10,则EF的长为 2 .
【答案】2.
【分析】结合平行四边形的性质,先证∠ABE=∠AEB,则AB=AE=6,同理可证FD=CD=6,进而得出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=6,AD∥BC,AD=BC=10,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AE=AB=6,
同理可证:DF=CD=6,
∴EF=AE+FD﹣AD=6+6﹣10=2.
故答案为:2.
【点评】本题主要考查了平行四边形的性质等知识,熟练掌握平行四边形的性质,证明AE=AB是解题的关键.
13.(2025春 巴彦县月考)如图,已知矩形ABCD中,AB=4,AD=7,AE平分∠BAD交BC于E,点F、N分别为AE、AD的中点,则FN的长度为 2.5 .
【答案】2.5.
【分析】连接DE,由矩形的性质推出DC=AB=4,BC=AD=7,AD∥BC,∠C=90°,由平行线的性质和角平分线定义推出∠AEB=∠BAE,得到BE=AB=4,求出CE=3,由勾股定理求出DE=5,判定FN是△ADE的中位线,推出FN=DE=2.5.
【解答】解:连接DE,
∵四边形ABCD是矩形,
∴DC=AB=4,BC=AD=7,AD∥BC,∠C=90°,
∴∠AEB=∠DAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠AEB=∠BAE,
∴BE=AB=4,
∴CE=BC﹣BE=7﹣4=3,
∴DE==5,
∵点F、N分别为AE、AD的中点,
∴FN是△ADE的中位线,
∴FN=DE=2.5.
故答案为:2.5.
【点评】本题考查矩形的性质,勾股定理,三角形中位线定理,角平分线定义,关键是由三角形中位线定理推出FN=DE.
14.(2025春 确山县期中)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=3,BC=4,则EF的长为 1 .
【答案】1.
【分析】根据勾股定理得到AB=5,根据三角形中位线定理得到DE∥AB,DE=,根据平行线的性质和角平分线的定义得到得到∠DAF=∠DFA,根据等腰三角形的判定得到结论.
【解答】解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB==5,
∵D、E分别为CA、CB的中点,
∴DE是△ABC的中位线,
∴DE∥AB,DE=AB=,
∴∠DFA=∠FAB,
∵AF平分∠BAC,
∴∠DAF=∠BAF,
∴∠DAF=∠DFA,
∴DF=AD=AC=×3=.
∴EF=DE﹣DF=1,
故答案为:1.
【点评】本题考查的是三角形中位线定理、勾股定理、平行线的性质,等腰三角形的判定,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
15.(2025春 临颍县期中)已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,则ED= 1 .
【答案】1.
【分析】延长BE交AC于F,由已知条件可得△BAF是等腰三角形,由等腰三角形的性质可得BE=EF,又因为BD=CD是,所以DE是△BCF的中位线,由三角形中位线定理即可求出DE的长.
【解答】解:延长BE交AC于F,
∵AE平分∠BAC,BE⊥AE,
∴∠BAE=∠CAE,∠AEB=∠AEF=90°,
在△ABE与△AFE中,
,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC﹣AF=7﹣5=2,
∵D为BC中点
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=CF=1,
故答案为:1.
【点评】本题考查了三角形中位线定理以及等腰三角形的判定,解题的关键是正确作出辅助线,得到△BAF是等腰三角形.
16.(2025春 东平县期中)菱形的面积为24cm2,一条对角线是6cm,那么菱形的另一条对角线长为 8cm .
【答案】8cm.
【分析】根据菱形的面积等于对角线乘积的一半,设另一条对角线为x,即可得出一个一元一次方程,解出即可得出结论.
【解答】解:设另一条对角线为x cm,
∵菱形的面积为24cm2,一条对角线是6cm,
∴,
解得:x=8,
∴菱形的另一条对角线长为8cm.
故答案为:8cm.
【点评】本题考查了菱形的性质、解一元一次方程,解本题的关键在熟练掌握菱形的面积等于对角线乘积的一半.
三.解答题(共8小题)
17.(2025春 兴宾区期中)如图,在Rt△ABC中,∠BAC=90°,点E,点F分别是BC,AC的中点,延长BA到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE的交点为点O.
(1)判断AE与DF有什么数量关系,并说明理由.
(2)当AB=6,BC=10,求OD的长.
【答案】(1)AE=DF,理由见解析;
(2).
【分析】(1)根据三角形中位线定理得到EF∥AB,AB=2EF,则可证明EF∥AD,AD=EF,进一步可证明四边形AEFD是平行四边形,得到AE=DF.
(2)由勾股定理求出AC=8,利用平行四边形对角线互相平分和线段中点的定义求出OA的长,再利用勾股定理即可求出OD的长.
【解答】解:(1)AE=DF,理由如下:
∵E,F分别是BC,AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB,AB=2EF,
∵AB=2AD,
∴EF∥AD,AD=EF,
∴四边形AEFD是平行四边形.
∴AE=DF;
(2)∵∠BAC=90°,AB=6,BC=10,
∴,.
由(1)知四边形AEFD是平行四边形,F是AC的中点,
∴OA=OF,AF=CF.
∴,
∵∠BAC=90°,
∴∠DAO=90°,
∴.
【点评】本题考查的是直角三角形斜边上的中线,三角形中位线定理,平行四边形的判定与性质,熟知以上知识是解题的关键.
18.(2025 西安模拟)如图,四边形ABCD是矩形,点E在BC边上,AF⊥DE,垂足为F,AF=DC.证明AD=DE.
【答案】见试题解答内容
【分析】由矩形的性质推出∠C=90°,AD∥BC,由平行线的性质推出∠ADF=∠CED,由垂直的定义得到∠AFD=∠C=90°,又AF=DC,由AAS证明△ADF≌△DEC,推出AD=DE.
【解答】解:∵四边形ABCD是矩形,
∴∠C=90°,AD∥BC,
∴∠ADF=∠CED,
∵AF⊥DE,
∴∠AFD=∠C=90°,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AD=DE.
【点评】本题考查矩形的性质,全等三角形的判定和性质,关键是由矩形的性质推出△ADF≌△DEC(AAS).
19.(2025春 淮滨县期中)如图,E,F是平行四边形ABCD的对角线AC上的点,AE=CF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
【答案】BE∥DF,BE=DF,证明见解答.
【分析】由平行四边形的性质得CB=AD,CB∥AD,则∠BCE=∠DAF,由AE=CF,推导出AF=CE,即可根据“SAS”证明△BCE≌△DAF,则BE=DF,∠CEB=∠AFD,所以BE∥DF.
【解答】解:BE∥DF,BE=DF,
证明:∵四边形ABCD是平行四边形,
∴CB=AD,CB∥AD,
∴∠BCE=∠DAF,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△BCE和△DAF中,
,
∴△BCE≌△DAF(SAS),
∴BE=DF,∠CEB=∠AFD,
∴BE∥DF.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质等知识,证明△BCE≌△DAF是解题的关键.
20.(2025 秦淮区二模)如图,△ABC与△ADC关于直线AC对称,∠BAD=∠BCD.求证:四边形ABCD是菱形.
【答案】证明见解答过程.
【分析】根据轴对称的性质求出AB=AD,CB=CD,∠BAC=∠DAC=∠BAD,∠BCA=∠DCA=∠BCD,进而求出∠BAC=∠BCA,结合等腰三角形的判定求出AB=AD=CB=CD,再根据“四边相等的四边形是菱形”即可得证.
【解答】证明:∵△ABC与△ADC关于直线AC对称,
∴AB=AD,CB=CD,∠BAC=∠DAC=∠BAD,∠BCA=∠DCA=∠BCD,
∵∠BAD=∠BCD,
∴∠BAC=∠BCA,
∴AB=CB,
∴AB=AD=CB=CD,
∴四边形ABCD是菱形.
【点评】此题考查了菱形的判定、轴对称的性质,熟记菱形的判定定理、轴对称的性质是解题的关键.
21.(2025 无锡校级一模)如图,四边形ABCD是正方形,△BCE是等边三角形,连接AE、DE.
(1)求证:AE=DE;
(2)求∠AED的度数.
【答案】见试题解答内容
【分析】(1)由正方形的性质得AB=DC,∠ABC=∠DCB=90°,由等边三角形的性质得BE=CE,∠EBC=∠ECB=60°,则∠ABE=∠DCE,即可证明△ABE≌△DCE,得AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得180﹣2x=360﹣60﹣2(90﹣x),求出x,再用180﹣2x即可.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
∴∠ABC﹣∠EBC=∠ECB﹣∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE;
(2)由(1)得△ABE、△CDE、△ADE是等腰三角形,设∠DAE=x°,依题意得
180﹣2x=360﹣60﹣2(90﹣x),
x=15,
180﹣2×15=150,
∴∠AED为150度.
【点评】此题重点考查正方形的性质、等边三角形的性质、全等三角形的判定与性质等知识,证明△ABE≌△DCE是解题的关键.
22.(2025 惠阳区二模)如图,在 ABCD中,对角线AC,BD相交于点O,AO=BO.
(1)求证: ABCD是矩形;
(2)点E在BC边上,满足CE=CO.若AB=6,BC=8,求BE的长.
【答案】(1)证明见解答过程;
(2)3.
【分析】(1)根据平行四边形性质得AC=2AO,BD=2BO,再根据AO=BO得AC=BD,然后根据对角线相等平行四边形是矩形即可得出结论;
(2)先由勾股定理求出AC=10,进而根据矩形行得CO=AO=5,则CE=CO=5,由此即可得出BE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,且AB=6,BC=8,
∴∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC===10,
∴CO=AO=AC=5,
∵CE=CO,
∴CE=5,
∴BE=BC﹣CE=8﹣5=3.
【点评】此题主要考查了矩形的判定和性质,平行四边形的性质,勾股定理,熟练掌握矩形的判定和性质,平行四边形的性质,勾股定理是解决问题的关键.
23.(2025 建湖县三模)在平行四边形ABCD中,E为BC上一点,点F为AE的中点,连接DF并延长,交CB的延长线于点G.
(1)求证:△ADF≌△EGF;
(2)求证:BG=CE.
【答案】(1)证明见解析;
(2)证明见解析.
【分析】(1)先由平行四边形性质得到AD∥BC,再由平行线性质和中点定义确定相关角度与边长,再由全等三角形的判定定理即可得证;
(2)由全等三角形的性质和平行四边形的性质得到GE=CB,数形结合表示出BG、CE即可得证.
【解答】(1)证明:在平行四边形ABCD中,AD∥BC,点F为AE的中点,
∴∠DAF=∠GEF,AF=EF,
在△ADF和△EGF中,
∴△ADF≌△EGF(ASA);
(2)解:由(1)知△ADF≌△EGF,
∴GE=DA,
∵四边形ABCD是平行四边形,AD=BC,
∴GE=CB,
∵GE=GB+BE,CB=BE+CE,
∴BG=CE.
【点评】本题考查的是平行四边形的性质、全等三角形的判定与性质,熟练掌握以上知识是解决问题的关键.
24.(2025 泰州二模)如图,在 ABCD中,连接对角线AC,分别作△ABC和△ACD的中线AE、CF.
(1)求证:AE=CF;
(2)从下列条件中任选一个作为已知条件,判断四边形AECF的形状,并证明你的结论.
①AC=AB;②AC⊥AB.
我选择的条件: ① ,(填写序号).(注:如果选择①,②分别进行解答,按第一个解答计分)
【答案】(1)见解析;
(2)①,见解析.
【分析】(1)利用平行四边形的性质得到AD=BC,AD∥BC,由中线的定义得到,,得出AF=CE,再利用平行四边形的性质与判定即可证明;
(2)根据矩形、菱形的判定即可解答.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵△ABC和△ACD的中线分别为AE、CF.
∴,,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF;
(2)解:若选择条件①,则四边形AECF是矩形.理由如下:
∵AC=AB,AE是△ABC的中线,
∴AE⊥BC,
∴∠AEC=90°,
由(1)得,四边形AECF是平行四边形,
∴平行四边形AECF是矩形;
若选择条件②,则四边形AECF是菱形.理由如下:
∵AC⊥AB,AE是△ABC的中线,
∴,
由(1)得,四边形AECF是平行四边形,
∴平行四边形AECF是菱形.
故答案为:①.
【点评】本题考查了平行四边形的判定与性质、矩形的判定、菱形的判定、三角形中位线定理,熟练掌握相关知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
