吉林省白城市三校联考2025届九年级下学期中考模拟考试数学试卷(含答案)
文档属性
| 名称 | 吉林省白城市三校联考2025届九年级下学期中考模拟考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 07:10:26 | ||
图片预览



文档简介
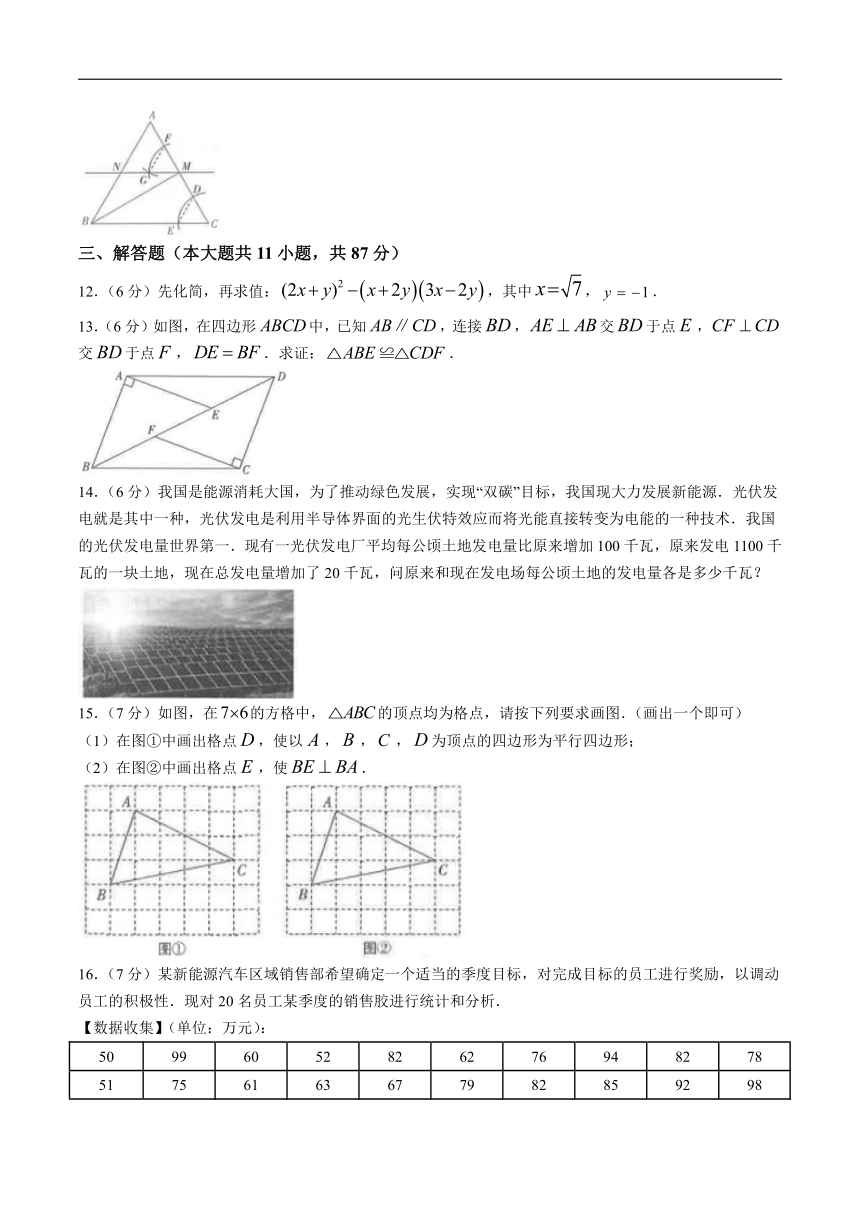
初中学业水平考试数学模拟试题
数学试卷包括三道大题,共22道小题。全卷满分120分。考试时间为120分钟。考琙结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数中,比小的数是( )
A. B. C.0 D.1
2.如图是:2024年巴黎奥运会公布的一些视觉标识和体育图标,既展示了法国的风情,又体现了体育项目本身的美感,达到了宣传国家特色及赛事主旨的效果.其文字上方的图案既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.若使算式“”的运算结果最小,则“”表示的运算符号是( )
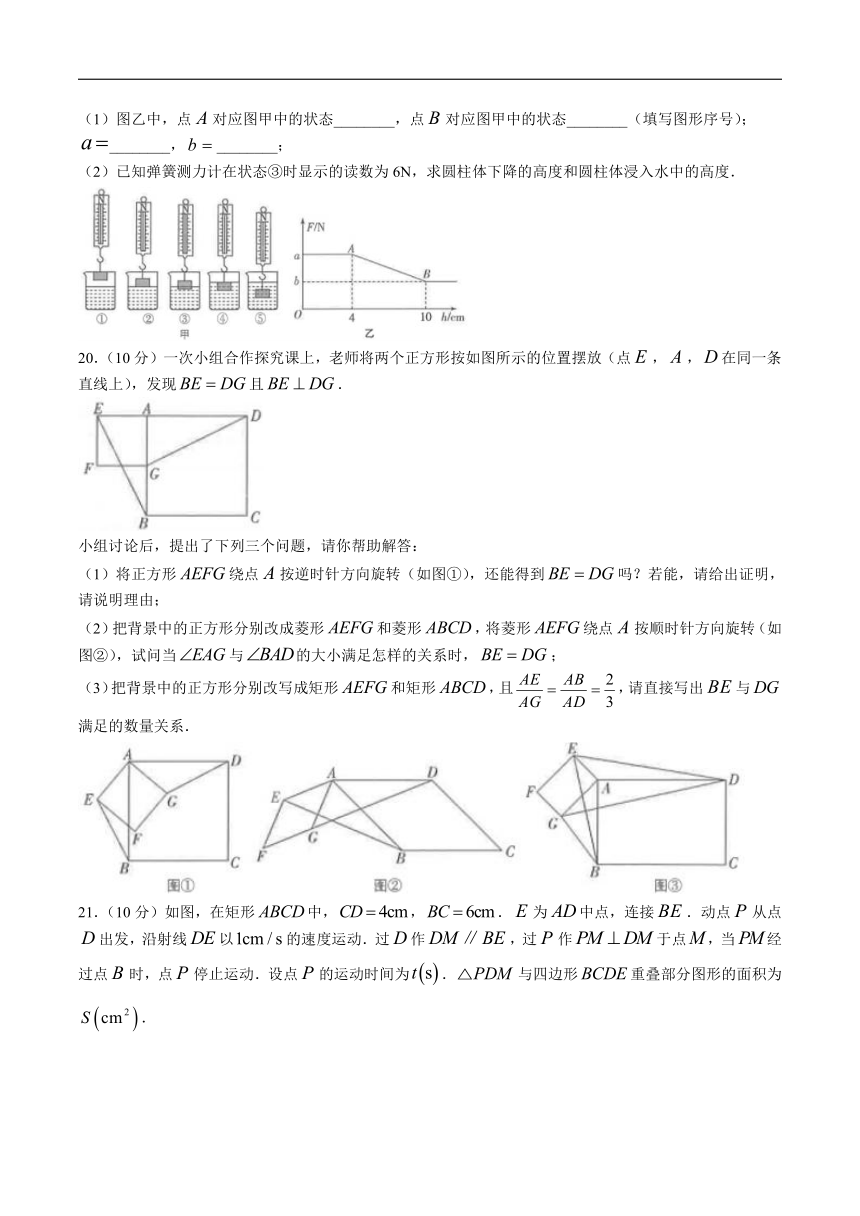
A. B. C. D.
4.如图①,是由五个边长都是1的正方形纸片拼接而成的,现将图①沿虚线折成一个无盖的正方体纸盒(图②)后,与线段重合的线段是( )
A. B. C. D.
5.如图,菱形与菱形为位似图形,位似中心为点,相似比为.若,则菱形的周长为( )
A.9 B.16 C.24 D.36
6.如图,切于点,交于点且为的直径,点是上异于点,的一点.若,则的度数为( )
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
7.写出不等式的一个正整数解:________.
8.已知,,则________.
9.在平面直角坐标系中,矩形位置如图放置,点,分别在,轴上,将逆时针旋转到,使得点落在轴的负半轴上.若,,则点的坐标是________.
10.如图①,中国美食讲究色香味美,优雅的摆盘造型能让美食锦上添花.图②是部分扇形摆盘的平面几何示意图(阴影部分为摆盘).通过测量,得到,若,两点之间的距离是,,则阴影部分的面积为________.
11.如图,在中,平分,按下列要求作图:(1)以点为圆心,适当长为半径画弧,交于点,交于点;(2)以点为圆心,长为半径画弧,交于点;(3)以点为圆心,长为半径画弧,交前一条弧于点,点与点在直线同侧;(4)作直线交于点.
给出下面四个结论:
①;②;③若,则是等边三角形;④若,则.
上述结论中,正确结论的序号有________.
三、解答题(本大题共11小题,共87分)
12.(6分)先化简,再求值:,其中,.
13.(6分)如图,在四边形中,已知,连接,交于点,交于点,.求证:.
14.(6分)我国是能源消耗大国,为了推动绿色发展,实现“双碳”目标,我国现大力发展新能源.光伏发电就是其中一种,光伏发电是利用半导体界面的光生伏特效应而将光能直接转变为电能的一种技术.我国的光伏发电量世界第一.现有一光伏发电厂平均每公顷土地发电量比原来增加100千瓦,原来发电1100千瓦的一块土地,现在总发电量增加了20千瓦,问原来和现在发电场每公顷土地的发电量各是多少千瓦?
15.(7分)如图,在的方格中,的顶点均为格点,请按下列要求画图.(画出一个即可)
(1)在图①中画出格点,使以,,,为顶点的四边形为平行四边形;
(2)在图②中画出格点,使.
16.(7分)某新能源汽车区域销售部希望确定一个适当的季度目标,对完成目标的员工进行奖励,以调动员工的积极性.现对20名员工某季度的销售 进行统计和分析.
【数据收集】(单位:万元):
50 99 60 52 82 62 76 94 82 78
51 75 61 63 67 79 82 85 92 98
【数据整理】
销售额/万元
频数 3 5 4 4
【数据分析】
平均数 众数 中位数
74.4 82
【问题解决】
(1)填空:________,________;
(2)销售部对数据分析以后,最终对一半的员工进行了奖励.某员工反映:“我这个季度的销售额是75万元”,请问该员工是否能获得奖励________(填“是”或“否”);
(3)若季度的销售额不低于70万元为合格,该销售部共有员工200名,请估计该销售部这个季度有多少员工达到合格?
17.(7分)根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示.
(1)求关于的函数解析式;
(2)当时,求受力面积的变化范围.
18.(8分)图①是某款电动平衡车,图②是其简化示意图,该款平衡车的座位和底盘均平行于地面,座位可沿射线方向调节,当座位的位置最低时,支架,,支架与座位的夹角,与支架的夹角,底盘到地面的距离为,求此时座位到地面的高度.(结果精确到,参考数据:,,)
19.(8分)如图甲,在测浮力的实验中,下方为盛水的烧杯,上方有弹簧测力计悬挂的圆柱体,将圆柱体缓僈下降,直至圆柱体完全浸入水中,各种状态如图甲所示.其中,弹簧测力计在状态②和④显示的读数分别为10N和5N.整个过程中,弹簧测力计读数与圆柱体下降高度的关系图象如图乙所示.
(1)图乙中,点对应图甲中的状态________,点对应图甲中的状态________(填写图形序号);________,________;
(2)已知弹簧测力计在状态③时显示的读数为6N,求圆柱体下降的高度和圆柱体浸入水中的高度.
20.(10分)一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点,,在同一条直线上),发现且.
小组讨论后,提出了下列三个问题,请你帮助解答:
(1)将正方形绕点按逆时针方向旋转(如图①),还能得到吗?若能,请给出证明,请说明理由;
(2)把背景中的正方形分别改成菱形和菱形,将菱形绕点按顺时针方向旋转(如图②),试问当与的大小满足怎样的关系时,;
(3)把背景中的正方形分别改写成矩形和矩形,且,请直接写出与满足的数量关系.
21.(10分)如图,在矩形中,,.为中点,连接.动点从点出发,沿射线以的速度运动.过作,过作于点,当经过点时,点停止运动.设点的运动时间为.与四边形重叠部分图形的面积为.
(1)当点落在边上时,的值为________;
(2)当经过点时,的值为________;
(3)求关于的函数解析式,并直接写出自变量的取值范围.
22.(12分)如图,抛物线与轴交于,两点(点在点的左侧),点的坐标为.将抛物线在轴下方的部分沿轴翻折,图象的其余部分保持不变,得到新的函数的图象.
(1)求抛物线的解析式;
(2)当函数的图象与直线有两个交点时,则的取值范围是________;
(3)若点在函数的图象上,求出的值;
(4)当时,函数的最大值与最小值的差是2时,直接写出的取值范围.
参考答案
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.A 2.D 3.B 4.C 5.D 6.B
二、填空题(本大题共5小题,每小题3分,共15分)
7.2(答案不唯一) 8.18 9. 10. 11.①②④
三、解答题(本大题共11小题,共87分)
12.解:原式
.
当,时,
原式.
13.证明:,
,即.
,,
.
又,
.
在和中,
.
14.解:设光伏发电厂原来平均每公顷土地发电量为千瓦.
由题意,得.
解得.
经检验,是原分式方程的解.
(千瓦).
答:原来和现在发电场每公顷土地的发电量各是5500千瓦、5600千瓦.
15.解:(1)如图①,点,即为所求.
(2)如图②,点即为所求.
16.解:(1)4 77.
(2)否.
(3)20名员工某季度的销售额不低于70万元的有12名,
名.
答:该销售部这个季度有120名员工达到合格.
17.解:(1)设.
点在这个函数的图象上,
.
.
关于的函数解析式为.
(2)令,,
令,,
当时,.
18.解:过点作,垂足为,延长交的延长线于点.
,
.
在中,,,
,
.
,
.
在中,,
.
底盘到地面的距离为,
此时座位到地面的高度
.
19.解:(1)② ④ 10N 5N.
(2)设线段段对应的函数解析式为:.
把,,代入,得:解得
.
当时,.解得.
圆柱体下降的高度为,
圆柱体浸入水中的高度为.
20.解:(1)能得到.
理由:四边形为正方形,
,.
又四边形为正方形,
,.
.
在和中,
.
.
(2)当时,.
理由:,
,
又四边形和四边形均为菱形,
,.
在和中,
.
.
(3).
21.解:(1).
(2).
(3)I.当时,,如图①,
此时,
根据,可得
,即.
,.
.
.
II.当时,如图②,过作交于点.
,
为中点,
.
,,
,四边形为矩形.
.
.
,
即.
,.
.
此时,,,
,
.
,
即.
.
III.当时,如图③,
22.解:(1)将代入,得.
解得或(舍去).
.
(2)或.
提示:,
顶点坐标为,对称轴为直线.
.
将抛物线在轴下方的部分沿轴翻折,
在部分的图象的顶点坐标为,解析式为.
的解析式为
观察函数图象可得,函数的图象与直线有两个交点时,则的取值范围是或.
(3)当,时,.
解得或.
当时,.
解得或.
点在函数的图象上,
(4)的取值范围为或.
提示:①当时即时,依题意
.
解得(舍去)或(舍去).
②当即时,依题意
.
解得或(舍去).
③令,.
解得或.
当时,函数值的最大值为2,最小值为0,符合题意,
解得.
数学试卷包括三道大题,共22道小题。全卷满分120分。考试时间为120分钟。考琙结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数中,比小的数是( )
A. B. C.0 D.1
2.如图是:2024年巴黎奥运会公布的一些视觉标识和体育图标,既展示了法国的风情,又体现了体育项目本身的美感,达到了宣传国家特色及赛事主旨的效果.其文字上方的图案既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.若使算式“”的运算结果最小,则“”表示的运算符号是( )
A. B. C. D.
4.如图①,是由五个边长都是1的正方形纸片拼接而成的,现将图①沿虚线折成一个无盖的正方体纸盒(图②)后,与线段重合的线段是( )
A. B. C. D.
5.如图,菱形与菱形为位似图形,位似中心为点,相似比为.若,则菱形的周长为( )
A.9 B.16 C.24 D.36
6.如图,切于点,交于点且为的直径,点是上异于点,的一点.若,则的度数为( )
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
7.写出不等式的一个正整数解:________.
8.已知,,则________.
9.在平面直角坐标系中,矩形位置如图放置,点,分别在,轴上,将逆时针旋转到,使得点落在轴的负半轴上.若,,则点的坐标是________.
10.如图①,中国美食讲究色香味美,优雅的摆盘造型能让美食锦上添花.图②是部分扇形摆盘的平面几何示意图(阴影部分为摆盘).通过测量,得到,若,两点之间的距离是,,则阴影部分的面积为________.
11.如图,在中,平分,按下列要求作图:(1)以点为圆心,适当长为半径画弧,交于点,交于点;(2)以点为圆心,长为半径画弧,交于点;(3)以点为圆心,长为半径画弧,交前一条弧于点,点与点在直线同侧;(4)作直线交于点.
给出下面四个结论:
①;②;③若,则是等边三角形;④若,则.
上述结论中,正确结论的序号有________.
三、解答题(本大题共11小题,共87分)
12.(6分)先化简,再求值:,其中,.
13.(6分)如图,在四边形中,已知,连接,交于点,交于点,.求证:.
14.(6分)我国是能源消耗大国,为了推动绿色发展,实现“双碳”目标,我国现大力发展新能源.光伏发电就是其中一种,光伏发电是利用半导体界面的光生伏特效应而将光能直接转变为电能的一种技术.我国的光伏发电量世界第一.现有一光伏发电厂平均每公顷土地发电量比原来增加100千瓦,原来发电1100千瓦的一块土地,现在总发电量增加了20千瓦,问原来和现在发电场每公顷土地的发电量各是多少千瓦?
15.(7分)如图,在的方格中,的顶点均为格点,请按下列要求画图.(画出一个即可)
(1)在图①中画出格点,使以,,,为顶点的四边形为平行四边形;
(2)在图②中画出格点,使.
16.(7分)某新能源汽车区域销售部希望确定一个适当的季度目标,对完成目标的员工进行奖励,以调动员工的积极性.现对20名员工某季度的销售 进行统计和分析.
【数据收集】(单位:万元):
50 99 60 52 82 62 76 94 82 78
51 75 61 63 67 79 82 85 92 98
【数据整理】
销售额/万元
频数 3 5 4 4
【数据分析】
平均数 众数 中位数
74.4 82
【问题解决】
(1)填空:________,________;
(2)销售部对数据分析以后,最终对一半的员工进行了奖励.某员工反映:“我这个季度的销售额是75万元”,请问该员工是否能获得奖励________(填“是”或“否”);
(3)若季度的销售额不低于70万元为合格,该销售部共有员工200名,请估计该销售部这个季度有多少员工达到合格?
17.(7分)根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示.
(1)求关于的函数解析式;
(2)当时,求受力面积的变化范围.
18.(8分)图①是某款电动平衡车,图②是其简化示意图,该款平衡车的座位和底盘均平行于地面,座位可沿射线方向调节,当座位的位置最低时,支架,,支架与座位的夹角,与支架的夹角,底盘到地面的距离为,求此时座位到地面的高度.(结果精确到,参考数据:,,)
19.(8分)如图甲,在测浮力的实验中,下方为盛水的烧杯,上方有弹簧测力计悬挂的圆柱体,将圆柱体缓僈下降,直至圆柱体完全浸入水中,各种状态如图甲所示.其中,弹簧测力计在状态②和④显示的读数分别为10N和5N.整个过程中,弹簧测力计读数与圆柱体下降高度的关系图象如图乙所示.
(1)图乙中,点对应图甲中的状态________,点对应图甲中的状态________(填写图形序号);________,________;
(2)已知弹簧测力计在状态③时显示的读数为6N,求圆柱体下降的高度和圆柱体浸入水中的高度.
20.(10分)一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点,,在同一条直线上),发现且.
小组讨论后,提出了下列三个问题,请你帮助解答:
(1)将正方形绕点按逆时针方向旋转(如图①),还能得到吗?若能,请给出证明,请说明理由;
(2)把背景中的正方形分别改成菱形和菱形,将菱形绕点按顺时针方向旋转(如图②),试问当与的大小满足怎样的关系时,;
(3)把背景中的正方形分别改写成矩形和矩形,且,请直接写出与满足的数量关系.
21.(10分)如图,在矩形中,,.为中点,连接.动点从点出发,沿射线以的速度运动.过作,过作于点,当经过点时,点停止运动.设点的运动时间为.与四边形重叠部分图形的面积为.
(1)当点落在边上时,的值为________;
(2)当经过点时,的值为________;
(3)求关于的函数解析式,并直接写出自变量的取值范围.
22.(12分)如图,抛物线与轴交于,两点(点在点的左侧),点的坐标为.将抛物线在轴下方的部分沿轴翻折,图象的其余部分保持不变,得到新的函数的图象.
(1)求抛物线的解析式;
(2)当函数的图象与直线有两个交点时,则的取值范围是________;
(3)若点在函数的图象上,求出的值;
(4)当时,函数的最大值与最小值的差是2时,直接写出的取值范围.
参考答案
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.A 2.D 3.B 4.C 5.D 6.B
二、填空题(本大题共5小题,每小题3分,共15分)
7.2(答案不唯一) 8.18 9. 10. 11.①②④
三、解答题(本大题共11小题,共87分)
12.解:原式
.
当,时,
原式.
13.证明:,
,即.
,,
.
又,
.
在和中,
.
14.解:设光伏发电厂原来平均每公顷土地发电量为千瓦.
由题意,得.
解得.
经检验,是原分式方程的解.
(千瓦).
答:原来和现在发电场每公顷土地的发电量各是5500千瓦、5600千瓦.
15.解:(1)如图①,点,即为所求.
(2)如图②,点即为所求.
16.解:(1)4 77.
(2)否.
(3)20名员工某季度的销售额不低于70万元的有12名,
名.
答:该销售部这个季度有120名员工达到合格.
17.解:(1)设.
点在这个函数的图象上,
.
.
关于的函数解析式为.
(2)令,,
令,,
当时,.
18.解:过点作,垂足为,延长交的延长线于点.
,
.
在中,,,
,
.
,
.
在中,,
.
底盘到地面的距离为,
此时座位到地面的高度
.
19.解:(1)② ④ 10N 5N.
(2)设线段段对应的函数解析式为:.
把,,代入,得:解得
.
当时,.解得.
圆柱体下降的高度为,
圆柱体浸入水中的高度为.
20.解:(1)能得到.
理由:四边形为正方形,
,.
又四边形为正方形,
,.
.
在和中,
.
.
(2)当时,.
理由:,
,
又四边形和四边形均为菱形,
,.
在和中,
.
.
(3).
21.解:(1).
(2).
(3)I.当时,,如图①,
此时,
根据,可得
,即.
,.
.
.
II.当时,如图②,过作交于点.
,
为中点,
.
,,
,四边形为矩形.
.
.
,
即.
,.
.
此时,,,
,
.
,
即.
.
III.当时,如图③,
22.解:(1)将代入,得.
解得或(舍去).
.
(2)或.
提示:,
顶点坐标为,对称轴为直线.
.
将抛物线在轴下方的部分沿轴翻折,
在部分的图象的顶点坐标为,解析式为.
的解析式为
观察函数图象可得,函数的图象与直线有两个交点时,则的取值范围是或.
(3)当,时,.
解得或.
当时,.
解得或.
点在函数的图象上,
(4)的取值范围为或.
提示:①当时即时,依题意
.
解得(舍去)或(舍去).
②当即时,依题意
.
解得或(舍去).
③令,.
解得或.
当时,函数值的最大值为2,最小值为0,符合题意,
解得.
同课章节目录
