【期末真题汇编】期末题型培优 计算题(含解析)-2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 【期末真题汇编】期末题型培优 计算题(含解析)-2024-2025学年六年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 20:05:19 | ||
图片预览

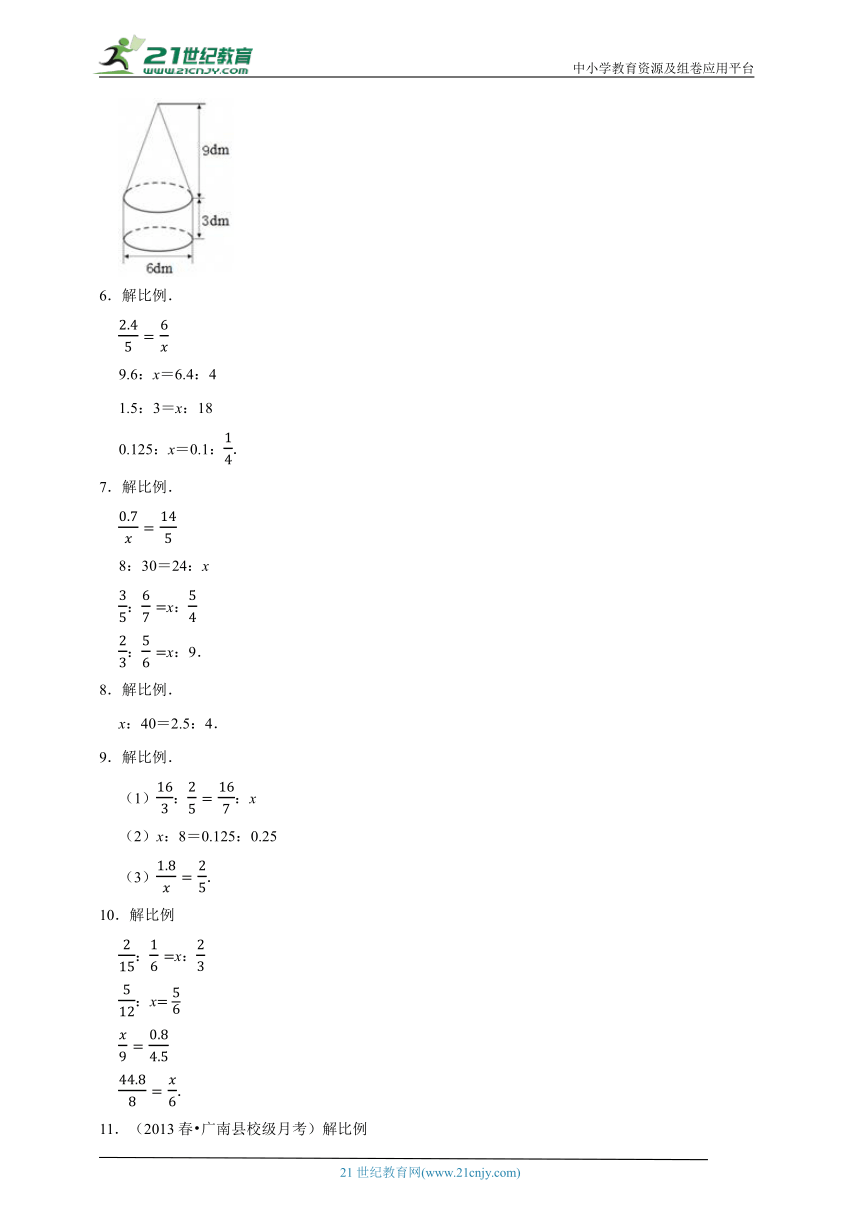

文档简介
中小学教育资源及组卷应用平台
期末题型培优 计算题
一.计算题(共36小题)
1.(2024 海拉尔区校级期中)求下面图形的体积。(单位:cm)
2.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
3.(2024 武穴市校级期中)求如图的表面积.
4.(2024 虎林市校级期中)(1)计算圆柱的表面积和体积。
(2)计算圆锥的体积。
5.(2024 东川区期中)计算下面图形的体积。
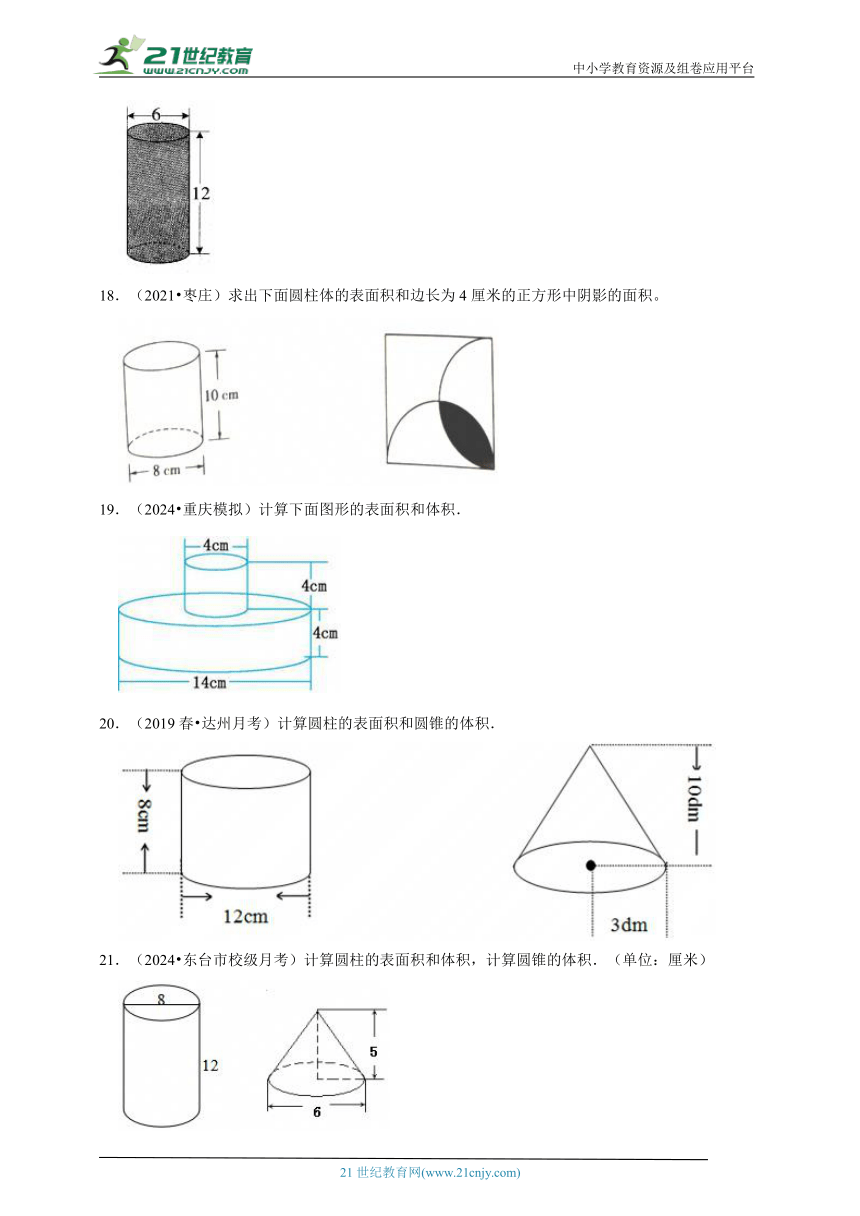
6.解比例.
9.6:x=6.4:4
1.5:3=x:18
0.125:x=0.1:.
7.解比例.
8:30=24:x
:x:
:x:9.
8.解比例.
x:40=2.5:4.
9.解比例.
(1)::x
(2)x:8=0.125:0.25
(3).
10.解比例
:x:
:x
.
11.(2013春 广南县校级月考)解比例
3:8=24:x 34:910=x:35 12.5:2.5=8:x
: x:1.6=12:
12.(2023 甘州区)解方程或解比例。
13.(2024 青岛期末)脱式计算.
13﹣(61)
9(1.25)
7.85﹣(43.37)
2.4+(712)
14.(2024 成都期末)竖式计算,慢慢算.
15﹣11.2=
1.2+12.8=
218×7=
1000﹣472=
15.(2012秋 香坊区月考)简便运算
0.3÷0.25÷0.4
7.12×9.9+0.712
27×1.25+1.25×73
12.5×1.6×0.8.
16.能简算的要简算.
[(87.5%﹣37.5%)]
7﹣().
17.(2020 清丰县)计算下面图形的体积。(单位:厘米)
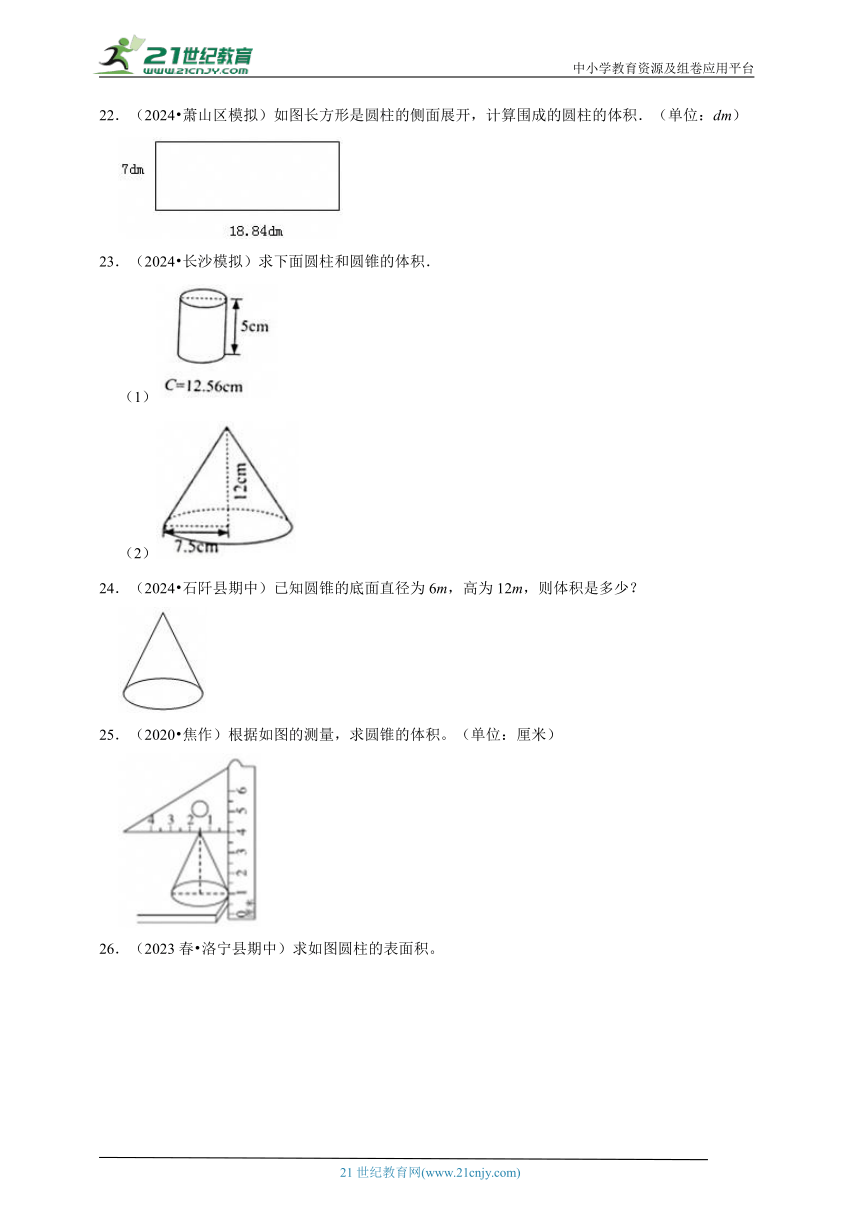
18.(2021 枣庄)求出下面圆柱体的表面积和边长为4厘米的正方形中阴影的面积。
19.(2024 重庆模拟)计算下面图形的表面积和体积.
20.(2019春 达州月考)计算圆柱的表面积和圆锥的体积.
21.(2024 东台市校级月考)计算圆柱的表面积和体积,计算圆锥的体积.(单位:厘米)
22.(2024 萧山区模拟)如图长方形是圆柱的侧面展开,计算围成的圆柱的体积.(单位:dm)
23.(2024 长沙模拟)求下面圆柱和圆锥的体积.
(1)
(2)
24.(2024 石阡县期中)已知圆锥的底面直径为6m,高为12m,则体积是多少?
25.(2020 焦作)根据如图的测量,求圆锥的体积。(单位:厘米)
26.(2023春 洛宁县期中)求如图圆柱的表面积。
27.(2024 澄江市期中)计算下面圆锥的体积。(单位:cm)
28.(2024 澄江市期中)计算下面圆柱的表面积。(单位:dm)
29.(2024 镇安县期末)计算如图所示图形的表面积。
30.(2024 北票市期中)求下面零件的体积。(单位:cm)
31.(2023 伊犁州)把一张铁皮按如图所示展开,正好能制成一只铁皮汽油桶,求所制铁皮汽油桶的容积.
32.(2024 郑州模拟)求如图的表面积和体积.单位(dm)
33.(2019春 潘集区期中)看图列式计算.
(1)求如图图形体的表面积.(单位:厘米)
(2)计算圆锥的体积.(单位:分米)
34.(2024 沙湾县)计算以长方形AB为轴旋转一周所形成的立体图形的体积.
35.(2024 长春期中)按要求计算:
(1)求表面积. (2)求圆锥的体积.
36.(2024 邵阳模拟)计算下面图形的体积.(单位:cm)
期末题型培优 计算题
参考答案与试题解析
一.计算题(共36小题)
1.(2024 海拉尔区校级期中)求下面图形的体积。(单位:cm)
【答案】1406.72立方厘米。
【分析】圆锥的体积:VShπr2h,已知高是21厘米,底面半径是8厘米,据此代入公式计算即可解答。
【解答】解:3.14×82×21
3.14×64×21
=1406.72(立方厘米)
答:圆锥的体积是1406.72立方厘米。
【点评】此题考查了圆锥的体积公式的计算应用,熟记公式是解答本题的关键。
2.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
【答案】1700平方厘米。
【分析】由图意可知:这个物体的表面积=长方体的表面积﹣圆柱的底面积×2+圆柱的侧面积,据此代入数据即可求解。
【解答】解:(30×5+30×20+5×20)×2
=850×2
=1700(平方厘米)
1700﹣3.14×(10÷2)2×2+3.14×10×5
=1700﹣157+157
=1700(平方厘米)
答:这个物体的表面积是1700平方厘米。
【点评】本题考查圆柱表面积和长方体表面积的计算及应用。理解题意,找出数量关系,列式计算即可。
3.(2024 武穴市校级期中)求如图的表面积.
【答案】见试题解答内容
【分析】圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,再根据圆的面积公式,把数据分别代入公式解答即可.
【解答】解:2×3.14×3×10+3.14×32×2
=18.84×10+3.14×9×2
=188.4+56.52
=244.92(平方分米);
答:它的表面积是244.92平方分米.
【点评】此题主要考查圆柱的表面积公式的灵活运用.
4.(2024 虎林市校级期中)(1)计算圆柱的表面积和体积。
(2)计算圆锥的体积。
【答案】(1)1884平方厘米,6280立方厘米;(2)314立方厘米。
【分析】(1)根据圆柱的表面积=侧面积+2个底面积=底面周长×高+π×半径的平方×2,以及圆柱的体积=底面积×高=πr2h,代入数据解答即可;
(2)根据圆锥的体积公式:圆锥的体积=底面积×高÷3=πr2h÷3,代入数据解答即可。
【解答】解:(1)2×3.14×10×20+3.14×102×2
=3.14×400+3.14×200
=3.14×600
=1884(平方厘米)
3.14×102×20
=314×20
=6280(立方厘米)
(2)3.14×(10÷2)2×12÷3
=3.14×25×4
=3.14×(25×4)
=3.14×100
=314(立方厘米)
【点评】熟练掌握圆柱的表面积公式和圆柱的体积公式以及圆锥的体积公式是解题的关键,圆柱的表面积公式:圆柱的表面积=底面周长×高+π×半径的平方×2,圆柱的体积=πr2h,圆锥的体积=πr2h÷3。
5.(2024 东川区期中)计算下面图形的体积。
【答案】169.56立方分米。
【分析】该图形由一个圆柱和一个圆锥组成,利用圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,计算即可。
【解答】解:3.14×(6÷2)2×3+3.14×(6÷2)2×9
=3.14×32×3+3.14×32×9
=84.78+84.78
=169.56(立方分米)
答:这个几何体的体积是169.56立方分米。
【点评】本题主要考查组合图形的体积,关键是把不规则几何体分成规则几何体,利用规则几何体的体积公式计算。
6.解比例.
9.6:x=6.4:4
1.5:3=x:18
0.125:x=0.1:.
【答案】见试题解答内容
【分析】(1)先根据比例的基本性质,把原式转化为2.4x=5×6,再根据等式的性质,在方程两边同时除以2.4求解;
(2)先根据比例的基本性质,把原式转化为6.4x=9.6×4,再根据等式的性质,在方程两边同时除以6.4求解;
(3)先根据比例的基本性质,把原式转化为3x=1.5×18,再根据等式的性质,在方程两边同时除以3求解;
(4)先根据比例的基本性质,把原式转化为0.1x=0.125,再根据等式的性质,在方程两边同时除以0.1求解.
【解答】解:(1)
2.4x=5×6
2.4x÷2.4=5×6÷2.4
x=12.5;
(2)9.6:x=6.4:4
6.4x=9.6×4
6.4x÷6.4=9.6×4÷6.4
x=6;
(3)1.5:3=x:18
3x=1.5×18
3x÷3=1.5×18÷3
x=9;
(4)0.125:x=0.1:
0.1x=0.125
0.1x÷0.1=0.1250.1
x=0.3125.
【点评】本题考查了学生根据等式的性质和比例的基本性质解方程的能力,注意等号对齐.
7.解比例.
8:30=24:x
:x:
:x:9.
【答案】见试题解答内容
【分析】根据比例的基本性质“两外项的积等于两内项的积”,先把比例式改写成已学过的简易方程,再利用等式的性质解简易方程即可.
【解答】解:
14x=0.7×5
14x÷14=3.5÷14
x=0.25
8:30=24:x
8x=30×24
8x÷8=720÷8
x=90
:x:
x
x
x
:x:9
x9
x=6
x6
x
【点评】此题主要考查学生根据比例的性质解比例和根据等式的性质解方程的能力,注意等号对齐.
8.解比例.
x:40=2.5:4.
【答案】见试题解答内容
【分析】根据比例基本性质,两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以4求解.
【解答】解:x:40=2.5:4
4x=40×2.5
4x=100
4x÷4=100÷4
x=25.
【点评】本题主要考查学生依据等式的性质,以及比例的基本性质解方程的能力,解方程时注意对齐等号;知识点:比例基本的性质是:两内项之积等于两外项之积.
9.解比例.
(1)::x
(2)x:8=0.125:0.25
(3).
【答案】见试题解答内容
【分析】(1)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解;
(2)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以0.25求解;
(3)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以2求解.
【解答】解:(1)::x
x
x
x;
(2)x:8=0.125:0.25
0.25x=8×0.125
0.25x÷0.25=8×0.125÷0.25
x=4;
(3)
2x=5×1.8
2x÷2=5×1.8÷2
x=4.5.
【点评】本题主要考查学生依据等式的性质,以及比例基本性质解方程的能力,解方程时注意对齐等号.
10.解比例
:x:
:x
.
【答案】见试题解答内容
【分析】(1)根据比例的基本性质,把原式化为x,然后等式的两边同时除以;
(2)根据比例的基本性质,把原式化为5x6,然后等式的两边同时除以5;
(3)根据比例的基本性质,把原式化为4.5x=9×0.8,然后等式的两边同时除以4.5;
(4)根据比例的基本性质,把原式化为8x=44.8×6,然后等式的两边同时除以8.
【解答】解:(1):x:
x
x
x;
(2):x
5x6
5x÷56÷5
x;
(3)
4.5x=9×0.8
4.5x÷4.5=9×0.8÷4.5
x=1.6;
(4)
8x=44.8×6
8x÷8=44.8×6÷8
x=33.6.
【点评】解比例是利用比例的基本性质,即比例的两个内项的积等于两个外项的积.
11.(2013春 广南县校级月考)解比例
3:8=24:x 34:910=x:35 12.5:2.5=8:x
: x:1.6=12:
【答案】见试题解答内容
【分析】(1)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以3求解;
(2)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以910求解;
(3)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以12.5求解;
(4)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以0.4求解;
(5)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解;
(6)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解.
【解答】解:(1)3:8=24:x
3x=8×24
3x÷3=8×24÷3
x=64;
(2)34:910=x:35
910x=34×35
910x÷910=34×35÷910
x;
(3)12.5:2.5=8:x
12.5x=2.5×8
12.5x÷12.5=2.5×8÷12.5
x=1.6;
(4)
0.4x=0.5×0.6
0.4x÷0.4=0.5×0.6÷0.4
x=0.75;
(5):
x0.4
x0.4
x;
(6)x:1.6=12:
x=1.6×12
x1.6×12
x=24.
【点评】等式的性质以及比例的基本性质是解比例的依据,解答时注意对齐等号.
12.(2023 甘州区)解方程或解比例。
【答案】x=32.4;x=12.25;x。
【分析】1、先计算出的结果,再根据等式的性质,方程两端同时除以,算出方程的解。
2、先计算出20×0.5的结果,再根据等式的性质,方程两端同时减去,再同时除以,算出方程的解。
3、根据比例的基本性质,把比例改写成1.75x的形式,再根据等式的性质,算出比例的解。
【解答】解:
x=10.8
x=32.4
0.8x=9.8
0.8x÷0.8=9.8÷0.8
x=12.25
1.75x
1.75x
x
【点评】本题解题的关键是熟练掌握解方程、解比例的方法。
13.(2024 青岛期末)脱式计算.
13﹣(61)
9(1.25)
7.85﹣(43.37)
2.4+(712)
【答案】见试题解答内容
【分析】①首先计算括号内的减法,然后计算括号外的减法;
②根据加法结合律,计算即可;
③首先计算括号内的加法,然后计算括号外的减法;
④首先计算括号内的加法,然后计算括号外的加法;即可得解.
【解答】解:①13﹣(61)
=13﹣4
=8
②9( 1.25)
=9()
=9
=9
=9
③7.85﹣(43.37)
=7.85﹣(4.12+3.37)
=7.85﹣7.49
=0.36
④2.4+(712)
=2.4+(712)
=2.4+20
=220
=22
【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.
14.(2024 成都期末)竖式计算,慢慢算.
15﹣11.2=
1.2+12.8=
218×7=
1000﹣472=
【答案】见试题解答内容
【分析】根据小数加减法和整数乘法与减法的计算方法进行计算.
【解答】解:15﹣11.2=3.8
1.2+12.8=14
218×7=1526
1000﹣472=528
【点评】考查了小数加减法和整数乘法与减法的笔算,根据各自的计算方法进行计算.
15.(2012秋 香坊区月考)简便运算
0.3÷0.25÷0.4
7.12×9.9+0.712
27×1.25+1.25×73
12.5×1.6×0.8.
【答案】见试题解答内容
【分析】①根据除法性质进行计算;
②把7.12×9.9写成0.712×99,根据乘法分配律进行计算.
③根据乘法分配律进行计算.
④根据乘法交换律及结合律计算.
【解答】解:①0.3÷0.25÷0.4
=0.3÷(0.25×0.4)
=0.3÷0.1
=3
②7.12×9.9+0.712
=0.712×99+0.712
=0.712×(99+1)
=0.712×100
=71.2
③27×1.25+1.25×73
=1.25×(27+73)
=1.25×100
=125
④12.5×1.6×0.8
=1.6×(12.5×0.8)
=1.6×10
=16
【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律简便计算.
16.能简算的要简算.
[(87.5%﹣37.5%)]
7﹣().
【答案】见试题解答内容
【分析】(1)运用乘法的分配律进行简算;
(2)先算小括号里的减法,再算中括号里的乘法,最后算括号外的除法;
(3)先算小括号里的除法,再算小括号里的减法,然后算括号外的乘法,最后算减法.
【解答】解:(1)
=()
=2
;
(2)[(87.5%﹣37.5%)]
[50%]
;
(3)7﹣()
=7﹣()
=7﹣0
=7﹣0
=7.
【点评】本题考查分数的四则混合运算,注意应用运算定律及其简便方法.
17.(2020 清丰县)计算下面图形的体积。(单位:厘米)
【答案】339.12。
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(6÷2)2×12
=3.14×9×12
=28.26×12
=339.12(立方厘米)
答:它的体积是339.12立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
18.(2021 枣庄)求出下面圆柱体的表面积和边长为4厘米的正方形中阴影的面积。
【答案】351.68平方厘米,2.28平方厘米。
【分析】(1)根据圆柱的表面积:S=2πrh+2πr2,据此列式解答。
(2),如图所示阴影面积=图形①+图形②;图形①=图形②;图形①的面积=圆面积的三角形的面积。三角形面积=底×高÷2;圆的面积:πr2。代入数据计算。
【解答】解:(1)3.14×8×10+2×3.14×(8÷2)2
=251.2+2×50.24
=251.2+100.48
=351.68(平方厘米)
答:表面积是351.68平方厘米。
(2)4÷2=2(厘米)
3.14×2×22×2÷2
=3.14﹣2
=1.14(平方厘米)
1.14×2=2.28(平方厘米)
答:面积是2.28平方厘米。
【点评】本题考查圆柱的表面积以及圆的面积的灵活运用。
19.(2024 重庆模拟)计算下面图形的表面积和体积.
【答案】见试题解答内容
【分析】根据圆柱的体积公式:V=Sh,把数据代入公式求出大小圆柱的体积和就是这个组合图形的体积,由于大小两个圆柱结合在一起,所以它的表面积等于小圆柱的侧面积加上大圆柱的表面积,根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2.把数据代入公式解答.
【解答】解:3.14×4×4+3.14×14×4+3.14×(14÷2)2×2
=3.14×16+3.14×56+3.14×72×2
=3.14×16+3.14×56+3.14×98
=3.14×170
=533.8(平方厘米)
3.14×(4÷2)2×4+3.14×(14÷2)2×4
=3.14×4×4+3.14×49×4
=3.14×212
=665.68(立方厘米)
答:图形的表面积是533.8平方厘米,体积是665.68立方厘米.
【点评】此题主要考查圆柱的侧面积公式、表面积公式、体积公式的灵活运用,关键是熟记公式.
20.(2019春 达州月考)计算圆柱的表面积和圆锥的体积.
【答案】见试题解答内容
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积搜狗:S=πr2,把数据代入公式解答;
根据圆锥的体积公式:Vr2h,把数据代入公式解答.
【解答】解:3.14×12×8+3.14×(12÷2)2×2
=37.68×8+3.14×36×2
=301.44+113.04×2
=301.44+226.08
=527.52(平方厘米);
答:这个圆柱的表面积是527.52平方厘米.
3.14×32×10
3.14×9×10
=94.2(立方分米);
答:这个圆锥的体积是94.2立方分米.
【点评】此题主要考查圆柱的表面积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
21.(2024 东台市校级月考)计算圆柱的表面积和体积,计算圆锥的体积.(单位:厘米)
【答案】见试题解答内容
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,把数据分别代入公式解答.
(2)根据圆锥的体积公式:VSh,把数据代入公式解答.
【解答】解:(1)3.14×8×12+3.14×()2×2
=301.44+100.48
=401.92(平方厘米)
3.14×()2×12
=3.14×16×12
=602.88(立方厘米)
答:这个圆柱的表面积是401.92平方厘米,体积是602.88立方厘米.
(2)3.14×(6÷2)2×5
3.14×9×5
=47.1(立方厘米)
答:这个圆锥的体积是47.1立方厘米.
【点评】此题主要考查圆柱的表面积公式、体积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
22.(2024 萧山区模拟)如图长方形是圆柱的侧面展开,计算围成的圆柱的体积.(单位:dm)
【答案】见试题解答内容
【分析】根据圆柱侧面展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高.根据圆柱的体积公式V=πr2h,把数据代入公式解答即可.
【解答】解:3.14×(18.84÷3.14÷2)2×7
=3.14×32×7
=3.14×9×7
=197.82(立方厘米)
答:围成的圆柱的体积是197.82立方厘米.
【点评】主要考查圆柱的体积公式的灵活运用,关键是熟记公式.
23.(2024 长沙模拟)求下面圆柱和圆锥的体积.
(1)
(2)
【答案】见试题解答内容
【分析】(1)已知圆柱的底面周长,先求出圆柱的底面半径,用C÷2÷π=r,然后用公式:V=πr2h,据此列式解答;
(2)已知圆锥的底面半径和高,求圆锥的体积,用公式:Vπr2h,据此列式解答.
【解答】解:(1)圆柱的底面半径:
12.56÷2÷3.14=2(cm);
圆柱的体积:
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(cm3)
答:圆柱的体积设计62.8立方厘米.
(2)圆锥的体积:
3.14×7.52×12
3.14×56.25×12
=3.14×56.25×4
=176.625×4
=706.5(cm3)
答:圆锥的体积时706.5立方厘米.
【点评】本题主要考查了对圆柱体积和圆锥体积公式的理解和灵活运用情况.
24.(2024 石阡县期中)已知圆锥的底面直径为6m,高为12m,则体积是多少?
【答案】见试题解答内容
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式解答.
【解答】解:3.14×(6÷2)2×12
3.14×9×12
=113.04(立方米),
答:圆锥的体积是113.04立方米.
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式.
25.(2020 焦作)根据如图的测量,求圆锥的体积。(单位:厘米)
【答案】7.065立方厘米。
【分析】观察图形可知,圆锥的底面半径是1.5厘米,高是4﹣1=3(厘米),圆锥的体积πr2h,代入数据即可解答。
【解答】解:观察图形可知,圆锥的底面半径是1.5厘米,高是4﹣1=3(厘米),
3.14×1.52×3
=3.14×2.25
=7.065(立方厘米)
答:圆锥的体积是7.065立方厘米。
【点评】本题主要考查了学生对圆锥体积公式的掌握情况,注意圆锥高的刻度从1厘米开始的。
26.(2023春 洛宁县期中)求如图圆柱的表面积。
【答案】表面积是200.96平方厘米。
【分析】该圆柱的表面积是两个底面的面积加上侧面积,计算即可。
【解答】解:3.14×4×14+3.14×(4÷2)2×2
=175.84+25.12
=200.96(平方厘米)
答:这个圆柱的表面积是200.96平方厘米。
【点评】本题主要考查圆柱表面积的计算。
27.(2024 澄江市期中)计算下面圆锥的体积。(单位:cm)
【答案】6280立方厘米。
【分析】根据圆锥的体积Vπr2h解答即可。
【解答】解:3.1415
=3.14×400×5
=6280(立方厘米)
答:圆锥的体积是6280立方厘米。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
28.(2024 澄江市期中)计算下面圆柱的表面积。(单位:dm)
【答案】1356.48平方分米。
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:3.14×18×15+3.14×(18÷2)2×2
=3.14×270+3.14×81×2
=847.8+508.68
=1356.48(平方分米)
答:这个圆柱的表面积是1356.48平方分米。
【点评】此题主要考查圆柱的表面积公式的灵活运用,关键是熟记公式。
29.(2024 镇安县期末)计算如图所示图形的表面积。
【答案】1411.2平方厘米。
【分析】根据图形的特点,因为上面的圆柱与下面的长方体粘合在一起,所以在计算它的表面积时,上面的圆柱只求侧面积,根据圆柱的侧面积公式:S=Ch将数据代入公式计算,下面的长方体求出它的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2将数据代入公式计算,然后合并起来。
【解答】解:3.14×10×8+(15×20+15×8+20×8)×2
=251.2+(300+120+160)×2
=251.2+1160
=1411.2(平方厘米)
答:图形的表面积是1411.2平方厘米。
【点评】此题主要考查圆柱的侧面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
30.(2024 北票市期中)求下面零件的体积。(单位:cm)
【答案】9.57立方厘米。
【分析】根据圆柱的体积公式:V=sh,正方体的体积公式:V=a3,把数据分别代入公式求出它们的体积和即可。
【解答】解:(1)2×2×2+3.14×(1÷2)2×2
=8+3.14×0.25×2
=8+1.57
=9.57(立方厘米)
答:这个组合图形的体积是9.57立方厘米。
【点评】解答求组合图形的体积,关键是观察分析图形是由哪几部分组成的,是求各部分的体积和、还是求各部分的体积差,再根据相应的体积公式解答。
31.(2023 伊犁州)把一张铁皮按如图所示展开,正好能制成一只铁皮汽油桶,求所制铁皮汽油桶的容积.
【答案】见试题解答内容
【分析】根据图意可知,这个长方形的宽这个圆柱形油桶的高,也是这两个圆的直径和,也就是4个半径,由此即可求出半径的长度,再利用圆柱的容积=πr2h,计算出答案.
【解答】解:3.14×(8÷4)2×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:所制铁皮汽油桶的容积是100.48升.
【点评】解答本道题的关键是利用圆柱的侧面展开图的特点得出圆柱的底面半径与圆柱的高,据此解决问题.
32.(2024 郑州模拟)求如图的表面积和体积.单位(dm)
【答案】见试题解答内容
【分析】根据图示可知,这个组合图形的表面积就是外面正方体的表面积加上里面圆柱的侧面积,利用正方体和圆柱表面积公式进行计算即可; 组合图形的体积等于正方体体积减去圆柱的体积,利用公式把数代入计算即可.
【解答】解:10×10×6+3.14×4×6
=600+75.36
=675.36(平方分米)
10×10×10﹣3.14×(4÷2)2×6
=1000﹣75.36
=924.64(立方分米)
答:这个图形的表面积为675.36平方分米,体积为924.64立方分米.
【点评】本题主要考查组合图形的体积和表面积的计算,关键把不规则图形转化为规则图形,再计算.
33.(2019春 潘集区期中)看图列式计算.
(1)求如图图形体的表面积.(单位:厘米)
(2)计算圆锥的体积.(单位:分米)
【答案】见试题解答内容
【分析】(1)观察图形可知,根据这个半圆柱的表面积等于直径6厘米的圆的面积与直径6厘米、高8厘米的侧面积的一半,再加上长8厘米、宽6厘米的长方形的面积之和,据此计算即可解答问题;
(2)根据圆锥的体积πr2h,代入数据计算即可解答问题.
【解答】解:(1)3.14×(6÷2)2+3.14×6×8÷2+6×8
=3.14×9+3.14×24+48
=28.26+75.36+48
=151.62(平方厘米)
答:这个半圆柱的表面积是151.62平方厘米.
(2)3.14×(10÷2)2×15
3.14×25×15
=3.14×125
=392.5(立方分米)
答:圆锥的体积是392.5立方分米.
【点评】此题主要考查了圆柱的表面积和圆锥的体积公式的计算应用,熟记公式即可解答问题.
34.(2024 沙湾县)计算以长方形AB为轴旋转一周所形成的立体图形的体积.
【答案】113.04。
【分析】根据题意可知,以长方形的长为轴旋转一周形成一个底面半径是3厘米,高是4厘米的圆柱,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×32×4
=3.14×9×4
=28.26×4
=113.04(立方厘米)
答:这个立体图形的体积是113.04立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
35.(2024 长春期中)按要求计算:
(1)求表面积. (2)求圆锥的体积.
【答案】见试题解答内容
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,把数据代入公式解答.
(2)根据圆锥的体积公式:Vsh,把数据代入公式解答.
【解答】解:(1)6.28×5+3.14×(6.28÷3.14÷2)2×2
=31.4+3.14×1×2
=31.4+6.28
=37.68(平方厘米);
答:这个圆柱的表面积是37.68平方厘米.
(2)3.14×(6÷2)2×4
3.14×9×4
=37.68(立方分米);
答:这个圆锥的体积是37.68立方分米.
【点评】此题主要考查圆柱的表面积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
36.(2024 邵阳模拟)计算下面图形的体积.(单位:cm)
【答案】见试题解答内容
【分析】根据圆柱的体积公式V=πr2h,圆锥的体积公式:Vπr2h即可解答.
【解答】解:(1)3.14×32×5.4
=3.14×9×5.4
=3.14×48.6
=152.604(立方厘米)
答:圆柱的体积是152.604立方厘米.
(2)3.14×(8÷2)2×6
=3.14×16×2
=3.14×32
=100.48(立方厘米)
答:圆锥的体积是100.48立方厘米.
【点评】本题主要考查了学生对圆柱和圆锥体积计算方法的掌握.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末题型培优 计算题
一.计算题(共36小题)
1.(2024 海拉尔区校级期中)求下面图形的体积。(单位:cm)
2.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
3.(2024 武穴市校级期中)求如图的表面积.
4.(2024 虎林市校级期中)(1)计算圆柱的表面积和体积。
(2)计算圆锥的体积。
5.(2024 东川区期中)计算下面图形的体积。
6.解比例.
9.6:x=6.4:4
1.5:3=x:18
0.125:x=0.1:.
7.解比例.
8:30=24:x
:x:
:x:9.
8.解比例.
x:40=2.5:4.
9.解比例.
(1)::x
(2)x:8=0.125:0.25
(3).
10.解比例
:x:
:x
.
11.(2013春 广南县校级月考)解比例
3:8=24:x 34:910=x:35 12.5:2.5=8:x
: x:1.6=12:
12.(2023 甘州区)解方程或解比例。
13.(2024 青岛期末)脱式计算.
13﹣(61)
9(1.25)
7.85﹣(43.37)
2.4+(712)
14.(2024 成都期末)竖式计算,慢慢算.
15﹣11.2=
1.2+12.8=
218×7=
1000﹣472=
15.(2012秋 香坊区月考)简便运算
0.3÷0.25÷0.4
7.12×9.9+0.712
27×1.25+1.25×73
12.5×1.6×0.8.
16.能简算的要简算.
[(87.5%﹣37.5%)]
7﹣().
17.(2020 清丰县)计算下面图形的体积。(单位:厘米)
18.(2021 枣庄)求出下面圆柱体的表面积和边长为4厘米的正方形中阴影的面积。
19.(2024 重庆模拟)计算下面图形的表面积和体积.
20.(2019春 达州月考)计算圆柱的表面积和圆锥的体积.
21.(2024 东台市校级月考)计算圆柱的表面积和体积,计算圆锥的体积.(单位:厘米)
22.(2024 萧山区模拟)如图长方形是圆柱的侧面展开,计算围成的圆柱的体积.(单位:dm)
23.(2024 长沙模拟)求下面圆柱和圆锥的体积.
(1)
(2)
24.(2024 石阡县期中)已知圆锥的底面直径为6m,高为12m,则体积是多少?
25.(2020 焦作)根据如图的测量,求圆锥的体积。(单位:厘米)
26.(2023春 洛宁县期中)求如图圆柱的表面积。
27.(2024 澄江市期中)计算下面圆锥的体积。(单位:cm)
28.(2024 澄江市期中)计算下面圆柱的表面积。(单位:dm)
29.(2024 镇安县期末)计算如图所示图形的表面积。
30.(2024 北票市期中)求下面零件的体积。(单位:cm)
31.(2023 伊犁州)把一张铁皮按如图所示展开,正好能制成一只铁皮汽油桶,求所制铁皮汽油桶的容积.
32.(2024 郑州模拟)求如图的表面积和体积.单位(dm)
33.(2019春 潘集区期中)看图列式计算.
(1)求如图图形体的表面积.(单位:厘米)
(2)计算圆锥的体积.(单位:分米)
34.(2024 沙湾县)计算以长方形AB为轴旋转一周所形成的立体图形的体积.
35.(2024 长春期中)按要求计算:
(1)求表面积. (2)求圆锥的体积.
36.(2024 邵阳模拟)计算下面图形的体积.(单位:cm)
期末题型培优 计算题
参考答案与试题解析
一.计算题(共36小题)
1.(2024 海拉尔区校级期中)求下面图形的体积。(单位:cm)
【答案】1406.72立方厘米。
【分析】圆锥的体积:VShπr2h,已知高是21厘米,底面半径是8厘米,据此代入公式计算即可解答。
【解答】解:3.14×82×21
3.14×64×21
=1406.72(立方厘米)
答:圆锥的体积是1406.72立方厘米。
【点评】此题考查了圆锥的体积公式的计算应用,熟记公式是解答本题的关键。
2.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
【答案】1700平方厘米。
【分析】由图意可知:这个物体的表面积=长方体的表面积﹣圆柱的底面积×2+圆柱的侧面积,据此代入数据即可求解。
【解答】解:(30×5+30×20+5×20)×2
=850×2
=1700(平方厘米)
1700﹣3.14×(10÷2)2×2+3.14×10×5
=1700﹣157+157
=1700(平方厘米)
答:这个物体的表面积是1700平方厘米。
【点评】本题考查圆柱表面积和长方体表面积的计算及应用。理解题意,找出数量关系,列式计算即可。
3.(2024 武穴市校级期中)求如图的表面积.
【答案】见试题解答内容
【分析】圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,再根据圆的面积公式,把数据分别代入公式解答即可.
【解答】解:2×3.14×3×10+3.14×32×2
=18.84×10+3.14×9×2
=188.4+56.52
=244.92(平方分米);
答:它的表面积是244.92平方分米.
【点评】此题主要考查圆柱的表面积公式的灵活运用.
4.(2024 虎林市校级期中)(1)计算圆柱的表面积和体积。
(2)计算圆锥的体积。
【答案】(1)1884平方厘米,6280立方厘米;(2)314立方厘米。
【分析】(1)根据圆柱的表面积=侧面积+2个底面积=底面周长×高+π×半径的平方×2,以及圆柱的体积=底面积×高=πr2h,代入数据解答即可;
(2)根据圆锥的体积公式:圆锥的体积=底面积×高÷3=πr2h÷3,代入数据解答即可。
【解答】解:(1)2×3.14×10×20+3.14×102×2
=3.14×400+3.14×200
=3.14×600
=1884(平方厘米)
3.14×102×20
=314×20
=6280(立方厘米)
(2)3.14×(10÷2)2×12÷3
=3.14×25×4
=3.14×(25×4)
=3.14×100
=314(立方厘米)
【点评】熟练掌握圆柱的表面积公式和圆柱的体积公式以及圆锥的体积公式是解题的关键,圆柱的表面积公式:圆柱的表面积=底面周长×高+π×半径的平方×2,圆柱的体积=πr2h,圆锥的体积=πr2h÷3。
5.(2024 东川区期中)计算下面图形的体积。
【答案】169.56立方分米。
【分析】该图形由一个圆柱和一个圆锥组成,利用圆柱的体积公式:V=πr2h,圆锥的体积公式:Vπr2h,计算即可。
【解答】解:3.14×(6÷2)2×3+3.14×(6÷2)2×9
=3.14×32×3+3.14×32×9
=84.78+84.78
=169.56(立方分米)
答:这个几何体的体积是169.56立方分米。
【点评】本题主要考查组合图形的体积,关键是把不规则几何体分成规则几何体,利用规则几何体的体积公式计算。
6.解比例.
9.6:x=6.4:4
1.5:3=x:18
0.125:x=0.1:.
【答案】见试题解答内容
【分析】(1)先根据比例的基本性质,把原式转化为2.4x=5×6,再根据等式的性质,在方程两边同时除以2.4求解;
(2)先根据比例的基本性质,把原式转化为6.4x=9.6×4,再根据等式的性质,在方程两边同时除以6.4求解;
(3)先根据比例的基本性质,把原式转化为3x=1.5×18,再根据等式的性质,在方程两边同时除以3求解;
(4)先根据比例的基本性质,把原式转化为0.1x=0.125,再根据等式的性质,在方程两边同时除以0.1求解.
【解答】解:(1)
2.4x=5×6
2.4x÷2.4=5×6÷2.4
x=12.5;
(2)9.6:x=6.4:4
6.4x=9.6×4
6.4x÷6.4=9.6×4÷6.4
x=6;
(3)1.5:3=x:18
3x=1.5×18
3x÷3=1.5×18÷3
x=9;
(4)0.125:x=0.1:
0.1x=0.125
0.1x÷0.1=0.1250.1
x=0.3125.
【点评】本题考查了学生根据等式的性质和比例的基本性质解方程的能力,注意等号对齐.
7.解比例.
8:30=24:x
:x:
:x:9.
【答案】见试题解答内容
【分析】根据比例的基本性质“两外项的积等于两内项的积”,先把比例式改写成已学过的简易方程,再利用等式的性质解简易方程即可.
【解答】解:
14x=0.7×5
14x÷14=3.5÷14
x=0.25
8:30=24:x
8x=30×24
8x÷8=720÷8
x=90
:x:
x
x
x
:x:9
x9
x=6
x6
x
【点评】此题主要考查学生根据比例的性质解比例和根据等式的性质解方程的能力,注意等号对齐.
8.解比例.
x:40=2.5:4.
【答案】见试题解答内容
【分析】根据比例基本性质,两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以4求解.
【解答】解:x:40=2.5:4
4x=40×2.5
4x=100
4x÷4=100÷4
x=25.
【点评】本题主要考查学生依据等式的性质,以及比例的基本性质解方程的能力,解方程时注意对齐等号;知识点:比例基本的性质是:两内项之积等于两外项之积.
9.解比例.
(1)::x
(2)x:8=0.125:0.25
(3).
【答案】见试题解答内容
【分析】(1)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解;
(2)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以0.25求解;
(3)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以2求解.
【解答】解:(1)::x
x
x
x;
(2)x:8=0.125:0.25
0.25x=8×0.125
0.25x÷0.25=8×0.125÷0.25
x=4;
(3)
2x=5×1.8
2x÷2=5×1.8÷2
x=4.5.
【点评】本题主要考查学生依据等式的性质,以及比例基本性质解方程的能力,解方程时注意对齐等号.
10.解比例
:x:
:x
.
【答案】见试题解答内容
【分析】(1)根据比例的基本性质,把原式化为x,然后等式的两边同时除以;
(2)根据比例的基本性质,把原式化为5x6,然后等式的两边同时除以5;
(3)根据比例的基本性质,把原式化为4.5x=9×0.8,然后等式的两边同时除以4.5;
(4)根据比例的基本性质,把原式化为8x=44.8×6,然后等式的两边同时除以8.
【解答】解:(1):x:
x
x
x;
(2):x
5x6
5x÷56÷5
x;
(3)
4.5x=9×0.8
4.5x÷4.5=9×0.8÷4.5
x=1.6;
(4)
8x=44.8×6
8x÷8=44.8×6÷8
x=33.6.
【点评】解比例是利用比例的基本性质,即比例的两个内项的积等于两个外项的积.
11.(2013春 广南县校级月考)解比例
3:8=24:x 34:910=x:35 12.5:2.5=8:x
: x:1.6=12:
【答案】见试题解答内容
【分析】(1)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以3求解;
(2)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以910求解;
(3)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以12.5求解;
(4)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以0.4求解;
(5)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解;
(6)根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以求解.
【解答】解:(1)3:8=24:x
3x=8×24
3x÷3=8×24÷3
x=64;
(2)34:910=x:35
910x=34×35
910x÷910=34×35÷910
x;
(3)12.5:2.5=8:x
12.5x=2.5×8
12.5x÷12.5=2.5×8÷12.5
x=1.6;
(4)
0.4x=0.5×0.6
0.4x÷0.4=0.5×0.6÷0.4
x=0.75;
(5):
x0.4
x0.4
x;
(6)x:1.6=12:
x=1.6×12
x1.6×12
x=24.
【点评】等式的性质以及比例的基本性质是解比例的依据,解答时注意对齐等号.
12.(2023 甘州区)解方程或解比例。
【答案】x=32.4;x=12.25;x。
【分析】1、先计算出的结果,再根据等式的性质,方程两端同时除以,算出方程的解。
2、先计算出20×0.5的结果,再根据等式的性质,方程两端同时减去,再同时除以,算出方程的解。
3、根据比例的基本性质,把比例改写成1.75x的形式,再根据等式的性质,算出比例的解。
【解答】解:
x=10.8
x=32.4
0.8x=9.8
0.8x÷0.8=9.8÷0.8
x=12.25
1.75x
1.75x
x
【点评】本题解题的关键是熟练掌握解方程、解比例的方法。
13.(2024 青岛期末)脱式计算.
13﹣(61)
9(1.25)
7.85﹣(43.37)
2.4+(712)
【答案】见试题解答内容
【分析】①首先计算括号内的减法,然后计算括号外的减法;
②根据加法结合律,计算即可;
③首先计算括号内的加法,然后计算括号外的减法;
④首先计算括号内的加法,然后计算括号外的加法;即可得解.
【解答】解:①13﹣(61)
=13﹣4
=8
②9( 1.25)
=9()
=9
=9
=9
③7.85﹣(43.37)
=7.85﹣(4.12+3.37)
=7.85﹣7.49
=0.36
④2.4+(712)
=2.4+(712)
=2.4+20
=220
=22
【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.
14.(2024 成都期末)竖式计算,慢慢算.
15﹣11.2=
1.2+12.8=
218×7=
1000﹣472=
【答案】见试题解答内容
【分析】根据小数加减法和整数乘法与减法的计算方法进行计算.
【解答】解:15﹣11.2=3.8
1.2+12.8=14
218×7=1526
1000﹣472=528
【点评】考查了小数加减法和整数乘法与减法的笔算,根据各自的计算方法进行计算.
15.(2012秋 香坊区月考)简便运算
0.3÷0.25÷0.4
7.12×9.9+0.712
27×1.25+1.25×73
12.5×1.6×0.8.
【答案】见试题解答内容
【分析】①根据除法性质进行计算;
②把7.12×9.9写成0.712×99,根据乘法分配律进行计算.
③根据乘法分配律进行计算.
④根据乘法交换律及结合律计算.
【解答】解:①0.3÷0.25÷0.4
=0.3÷(0.25×0.4)
=0.3÷0.1
=3
②7.12×9.9+0.712
=0.712×99+0.712
=0.712×(99+1)
=0.712×100
=71.2
③27×1.25+1.25×73
=1.25×(27+73)
=1.25×100
=125
④12.5×1.6×0.8
=1.6×(12.5×0.8)
=1.6×10
=16
【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律简便计算.
16.能简算的要简算.
[(87.5%﹣37.5%)]
7﹣().
【答案】见试题解答内容
【分析】(1)运用乘法的分配律进行简算;
(2)先算小括号里的减法,再算中括号里的乘法,最后算括号外的除法;
(3)先算小括号里的除法,再算小括号里的减法,然后算括号外的乘法,最后算减法.
【解答】解:(1)
=()
=2
;
(2)[(87.5%﹣37.5%)]
[50%]
;
(3)7﹣()
=7﹣()
=7﹣0
=7﹣0
=7.
【点评】本题考查分数的四则混合运算,注意应用运算定律及其简便方法.
17.(2020 清丰县)计算下面图形的体积。(单位:厘米)
【答案】339.12。
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×(6÷2)2×12
=3.14×9×12
=28.26×12
=339.12(立方厘米)
答:它的体积是339.12立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
18.(2021 枣庄)求出下面圆柱体的表面积和边长为4厘米的正方形中阴影的面积。
【答案】351.68平方厘米,2.28平方厘米。
【分析】(1)根据圆柱的表面积:S=2πrh+2πr2,据此列式解答。
(2),如图所示阴影面积=图形①+图形②;图形①=图形②;图形①的面积=圆面积的三角形的面积。三角形面积=底×高÷2;圆的面积:πr2。代入数据计算。
【解答】解:(1)3.14×8×10+2×3.14×(8÷2)2
=251.2+2×50.24
=251.2+100.48
=351.68(平方厘米)
答:表面积是351.68平方厘米。
(2)4÷2=2(厘米)
3.14×2×22×2÷2
=3.14﹣2
=1.14(平方厘米)
1.14×2=2.28(平方厘米)
答:面积是2.28平方厘米。
【点评】本题考查圆柱的表面积以及圆的面积的灵活运用。
19.(2024 重庆模拟)计算下面图形的表面积和体积.
【答案】见试题解答内容
【分析】根据圆柱的体积公式:V=Sh,把数据代入公式求出大小圆柱的体积和就是这个组合图形的体积,由于大小两个圆柱结合在一起,所以它的表面积等于小圆柱的侧面积加上大圆柱的表面积,根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2.把数据代入公式解答.
【解答】解:3.14×4×4+3.14×14×4+3.14×(14÷2)2×2
=3.14×16+3.14×56+3.14×72×2
=3.14×16+3.14×56+3.14×98
=3.14×170
=533.8(平方厘米)
3.14×(4÷2)2×4+3.14×(14÷2)2×4
=3.14×4×4+3.14×49×4
=3.14×212
=665.68(立方厘米)
答:图形的表面积是533.8平方厘米,体积是665.68立方厘米.
【点评】此题主要考查圆柱的侧面积公式、表面积公式、体积公式的灵活运用,关键是熟记公式.
20.(2019春 达州月考)计算圆柱的表面积和圆锥的体积.
【答案】见试题解答内容
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积搜狗:S=πr2,把数据代入公式解答;
根据圆锥的体积公式:Vr2h,把数据代入公式解答.
【解答】解:3.14×12×8+3.14×(12÷2)2×2
=37.68×8+3.14×36×2
=301.44+113.04×2
=301.44+226.08
=527.52(平方厘米);
答:这个圆柱的表面积是527.52平方厘米.
3.14×32×10
3.14×9×10
=94.2(立方分米);
答:这个圆锥的体积是94.2立方分米.
【点评】此题主要考查圆柱的表面积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
21.(2024 东台市校级月考)计算圆柱的表面积和体积,计算圆锥的体积.(单位:厘米)
【答案】见试题解答内容
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,把数据分别代入公式解答.
(2)根据圆锥的体积公式:VSh,把数据代入公式解答.
【解答】解:(1)3.14×8×12+3.14×()2×2
=301.44+100.48
=401.92(平方厘米)
3.14×()2×12
=3.14×16×12
=602.88(立方厘米)
答:这个圆柱的表面积是401.92平方厘米,体积是602.88立方厘米.
(2)3.14×(6÷2)2×5
3.14×9×5
=47.1(立方厘米)
答:这个圆锥的体积是47.1立方厘米.
【点评】此题主要考查圆柱的表面积公式、体积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
22.(2024 萧山区模拟)如图长方形是圆柱的侧面展开,计算围成的圆柱的体积.(单位:dm)
【答案】见试题解答内容
【分析】根据圆柱侧面展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高.根据圆柱的体积公式V=πr2h,把数据代入公式解答即可.
【解答】解:3.14×(18.84÷3.14÷2)2×7
=3.14×32×7
=3.14×9×7
=197.82(立方厘米)
答:围成的圆柱的体积是197.82立方厘米.
【点评】主要考查圆柱的体积公式的灵活运用,关键是熟记公式.
23.(2024 长沙模拟)求下面圆柱和圆锥的体积.
(1)
(2)
【答案】见试题解答内容
【分析】(1)已知圆柱的底面周长,先求出圆柱的底面半径,用C÷2÷π=r,然后用公式:V=πr2h,据此列式解答;
(2)已知圆锥的底面半径和高,求圆锥的体积,用公式:Vπr2h,据此列式解答.
【解答】解:(1)圆柱的底面半径:
12.56÷2÷3.14=2(cm);
圆柱的体积:
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(cm3)
答:圆柱的体积设计62.8立方厘米.
(2)圆锥的体积:
3.14×7.52×12
3.14×56.25×12
=3.14×56.25×4
=176.625×4
=706.5(cm3)
答:圆锥的体积时706.5立方厘米.
【点评】本题主要考查了对圆柱体积和圆锥体积公式的理解和灵活运用情况.
24.(2024 石阡县期中)已知圆锥的底面直径为6m,高为12m,则体积是多少?
【答案】见试题解答内容
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式解答.
【解答】解:3.14×(6÷2)2×12
3.14×9×12
=113.04(立方米),
答:圆锥的体积是113.04立方米.
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式.
25.(2020 焦作)根据如图的测量,求圆锥的体积。(单位:厘米)
【答案】7.065立方厘米。
【分析】观察图形可知,圆锥的底面半径是1.5厘米,高是4﹣1=3(厘米),圆锥的体积πr2h,代入数据即可解答。
【解答】解:观察图形可知,圆锥的底面半径是1.5厘米,高是4﹣1=3(厘米),
3.14×1.52×3
=3.14×2.25
=7.065(立方厘米)
答:圆锥的体积是7.065立方厘米。
【点评】本题主要考查了学生对圆锥体积公式的掌握情况,注意圆锥高的刻度从1厘米开始的。
26.(2023春 洛宁县期中)求如图圆柱的表面积。
【答案】表面积是200.96平方厘米。
【分析】该圆柱的表面积是两个底面的面积加上侧面积,计算即可。
【解答】解:3.14×4×14+3.14×(4÷2)2×2
=175.84+25.12
=200.96(平方厘米)
答:这个圆柱的表面积是200.96平方厘米。
【点评】本题主要考查圆柱表面积的计算。
27.(2024 澄江市期中)计算下面圆锥的体积。(单位:cm)
【答案】6280立方厘米。
【分析】根据圆锥的体积Vπr2h解答即可。
【解答】解:3.1415
=3.14×400×5
=6280(立方厘米)
答:圆锥的体积是6280立方厘米。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
28.(2024 澄江市期中)计算下面圆柱的表面积。(单位:dm)
【答案】1356.48平方分米。
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:3.14×18×15+3.14×(18÷2)2×2
=3.14×270+3.14×81×2
=847.8+508.68
=1356.48(平方分米)
答:这个圆柱的表面积是1356.48平方分米。
【点评】此题主要考查圆柱的表面积公式的灵活运用,关键是熟记公式。
29.(2024 镇安县期末)计算如图所示图形的表面积。
【答案】1411.2平方厘米。
【分析】根据图形的特点,因为上面的圆柱与下面的长方体粘合在一起,所以在计算它的表面积时,上面的圆柱只求侧面积,根据圆柱的侧面积公式:S=Ch将数据代入公式计算,下面的长方体求出它的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2将数据代入公式计算,然后合并起来。
【解答】解:3.14×10×8+(15×20+15×8+20×8)×2
=251.2+(300+120+160)×2
=251.2+1160
=1411.2(平方厘米)
答:图形的表面积是1411.2平方厘米。
【点评】此题主要考查圆柱的侧面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
30.(2024 北票市期中)求下面零件的体积。(单位:cm)
【答案】9.57立方厘米。
【分析】根据圆柱的体积公式:V=sh,正方体的体积公式:V=a3,把数据分别代入公式求出它们的体积和即可。
【解答】解:(1)2×2×2+3.14×(1÷2)2×2
=8+3.14×0.25×2
=8+1.57
=9.57(立方厘米)
答:这个组合图形的体积是9.57立方厘米。
【点评】解答求组合图形的体积,关键是观察分析图形是由哪几部分组成的,是求各部分的体积和、还是求各部分的体积差,再根据相应的体积公式解答。
31.(2023 伊犁州)把一张铁皮按如图所示展开,正好能制成一只铁皮汽油桶,求所制铁皮汽油桶的容积.
【答案】见试题解答内容
【分析】根据图意可知,这个长方形的宽这个圆柱形油桶的高,也是这两个圆的直径和,也就是4个半径,由此即可求出半径的长度,再利用圆柱的容积=πr2h,计算出答案.
【解答】解:3.14×(8÷4)2×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:所制铁皮汽油桶的容积是100.48升.
【点评】解答本道题的关键是利用圆柱的侧面展开图的特点得出圆柱的底面半径与圆柱的高,据此解决问题.
32.(2024 郑州模拟)求如图的表面积和体积.单位(dm)
【答案】见试题解答内容
【分析】根据图示可知,这个组合图形的表面积就是外面正方体的表面积加上里面圆柱的侧面积,利用正方体和圆柱表面积公式进行计算即可; 组合图形的体积等于正方体体积减去圆柱的体积,利用公式把数代入计算即可.
【解答】解:10×10×6+3.14×4×6
=600+75.36
=675.36(平方分米)
10×10×10﹣3.14×(4÷2)2×6
=1000﹣75.36
=924.64(立方分米)
答:这个图形的表面积为675.36平方分米,体积为924.64立方分米.
【点评】本题主要考查组合图形的体积和表面积的计算,关键把不规则图形转化为规则图形,再计算.
33.(2019春 潘集区期中)看图列式计算.
(1)求如图图形体的表面积.(单位:厘米)
(2)计算圆锥的体积.(单位:分米)
【答案】见试题解答内容
【分析】(1)观察图形可知,根据这个半圆柱的表面积等于直径6厘米的圆的面积与直径6厘米、高8厘米的侧面积的一半,再加上长8厘米、宽6厘米的长方形的面积之和,据此计算即可解答问题;
(2)根据圆锥的体积πr2h,代入数据计算即可解答问题.
【解答】解:(1)3.14×(6÷2)2+3.14×6×8÷2+6×8
=3.14×9+3.14×24+48
=28.26+75.36+48
=151.62(平方厘米)
答:这个半圆柱的表面积是151.62平方厘米.
(2)3.14×(10÷2)2×15
3.14×25×15
=3.14×125
=392.5(立方分米)
答:圆锥的体积是392.5立方分米.
【点评】此题主要考查了圆柱的表面积和圆锥的体积公式的计算应用,熟记公式即可解答问题.
34.(2024 沙湾县)计算以长方形AB为轴旋转一周所形成的立体图形的体积.
【答案】113.04。
【分析】根据题意可知,以长方形的长为轴旋转一周形成一个底面半径是3厘米,高是4厘米的圆柱,根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×32×4
=3.14×9×4
=28.26×4
=113.04(立方厘米)
答:这个立体图形的体积是113.04立方厘米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
35.(2024 长春期中)按要求计算:
(1)求表面积. (2)求圆锥的体积.
【答案】见试题解答内容
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,把数据代入公式解答.
(2)根据圆锥的体积公式:Vsh,把数据代入公式解答.
【解答】解:(1)6.28×5+3.14×(6.28÷3.14÷2)2×2
=31.4+3.14×1×2
=31.4+6.28
=37.68(平方厘米);
答:这个圆柱的表面积是37.68平方厘米.
(2)3.14×(6÷2)2×4
3.14×9×4
=37.68(立方分米);
答:这个圆锥的体积是37.68立方分米.
【点评】此题主要考查圆柱的表面积公式、圆锥的体积公式的灵活运用,关键是熟记公式.
36.(2024 邵阳模拟)计算下面图形的体积.(单位:cm)
【答案】见试题解答内容
【分析】根据圆柱的体积公式V=πr2h,圆锥的体积公式:Vπr2h即可解答.
【解答】解:(1)3.14×32×5.4
=3.14×9×5.4
=3.14×48.6
=152.604(立方厘米)
答:圆柱的体积是152.604立方厘米.
(2)3.14×(8÷2)2×6
=3.14×16×2
=3.14×32
=100.48(立方厘米)
答:圆锥的体积是100.48立方厘米.
【点评】本题主要考查了学生对圆柱和圆锥体积计算方法的掌握.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
