【期末押题卷】2024-2025学年六年级下学期期末素养评价数学押题预测卷 人教版(含解析)
文档属性
| 名称 | 【期末押题卷】2024-2025学年六年级下学期期末素养评价数学押题预测卷 人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 722.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-11 22:31:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下学期期末素养评价数学押题预测卷
一、单选题
1.把一个鸡蛋放入水杯中(如图),这个鸡蛋的体积是( )cm 。
A.62 B.882 C.42
2.能与∶组成比例的是( )。
A.2∶1 B.1∶2 C.∶ D.8∶2
3.计算如图三角形的面积,选择数据正确的是( )。
A.10cm和13 cm B.11 cm和14.3 cm
C.10 cm和14.3cm D.10 cm和11 cm
4. 一副象棋棋盘上的棋子摆放如图所示,如果“馬”的下一步可能走到(1,3),那么“相”的下一步不可能走到( )
A.(2,4) B.(6,4) C.(3,3)
5.将一个长方体铸成一个正方体(没有损耗),( )不变。
A.体积 B.表面积 C.棱长的和 D.面积
6.在△ABC中,阴影部分是由各边的四等分点连结形成的,那么阴影部分与△ABC的面积之比为( )。
A. B. C. D.
E.以上都不对
二、判断题
7.一个不等于0的数乘假分数的积一定大于这个数.( )
8.6× = = 。( )
9.甲数比乙数多,则乙数比甲数少。( )
10.比的前项和后项都扩大为原来的2倍,得到一个新的比,这两个比能组成比例。( )
11.将一个5毫米长的零件画在图上长为5厘米,这幅图的比例尺是1:10.( )
12.小数5.2365精确到千分位是5.236。( )
13.一个数的倒数是 ,这个数的 是 。( )
14.500克的水减少了 后再增加 千克,结果还是500克。
15.把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书.( )
三、填空题
16.小明用一根绳子测量一个水井深度,绳子两折时,露出井外50厘米;绳子三折时,还差40厘米.那么井深 厘米.
17. (比的应用) 如图,一个瓶身为圆柱体的玻璃瓶内装有高 3 厘米的墨水, 将瓶盖盖好后倒置, 墨水水面高为 4 厘米, 则瓶内的墨水的体积与玻璃 容积之比为 。
18.把一块底面积是24cm2,高是3cm的圆柱形橡皮泥捏成同样底面大小的圆锥,圆锥的高是 cm。如果把它捏成同样高的圆锥,圆锥的底面积是 分米。
19.天天家在东东家东偏北40°方向500 m处,则东东家在天天家 偏 方向 m处。
20.绿地中心千玺广场,又名“大玉米”,位于郑州市郑东新区,被誉为“中原第一高楼”。如果把第20层记作0层,那么第15层应记作 层,记作+38层的那一层实际为第 层。
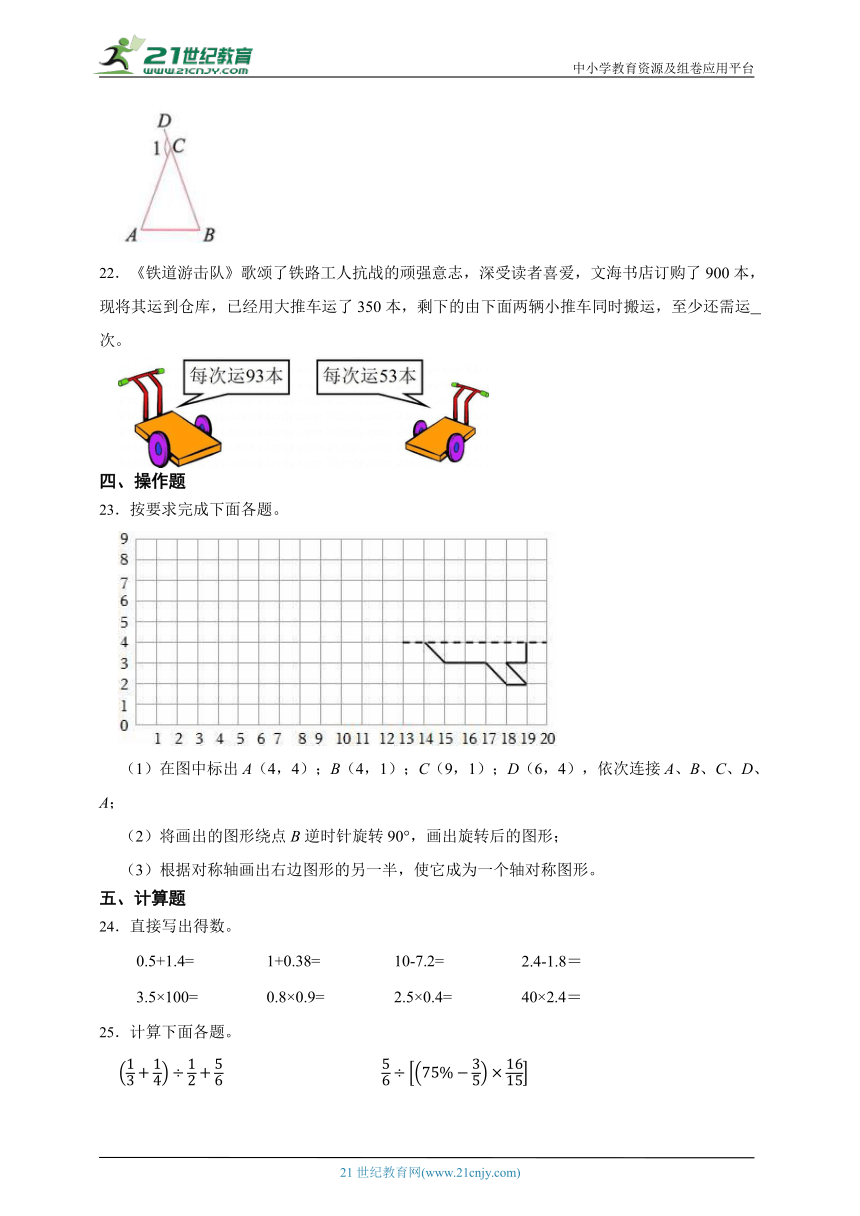
21.桑梯是我国古代发明的一种采桑工具。如图所示为明朝科学家许光启在《农政启书》中用图画描绘的桑梯示意图。已知BC=AC,∠BAC=70°,则∠1的度数为 °。
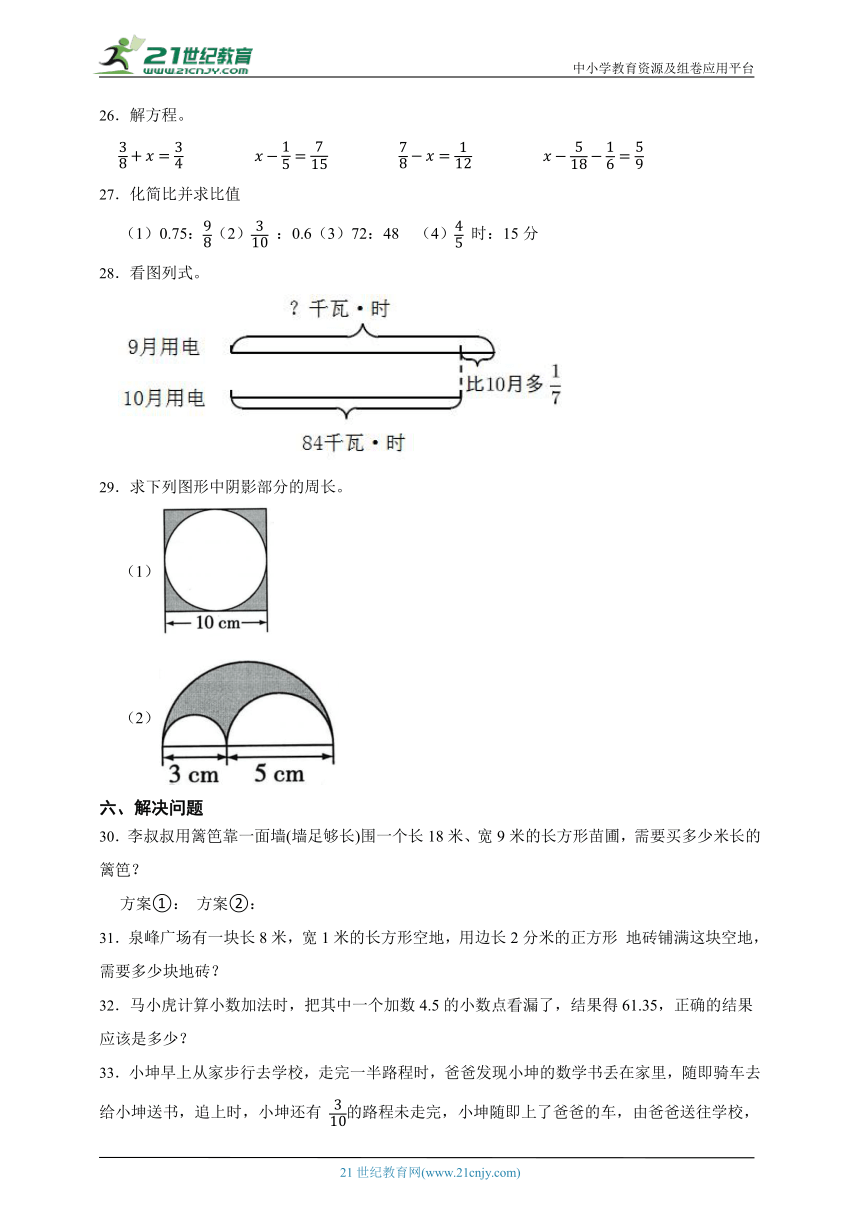
22.《铁道游击队》歌颂了铁路工人抗战的顽强意志,深受读者喜爱,文海书店订购了900本,现将其运到仓库,已经用大推车运了350本,剩下的由下面两辆小推车同时搬运,至少还需运 次。
四、操作题
23.按要求完成下面各题。
(1)在图中标出A(4,4);B(4,1);C(9,1);D(6,4),依次连接A、B、C、D、A;
(2)将画出的图形绕点B逆时针旋转90°,画出旋转后的图形;
(3)根据对称轴画出右边图形的另一半,使它成为一个轴对称图形。
五、计算题
24.直接写出得数。
0.5+1.4= 1+0.38= 10-7.2= 2.4-1.8=
3.5×100= 0.8×0.9= 2.5×0.4= 40×2.4=
25.计算下面各题。
26.解方程。
27.化简比并求比值
(1)0.75:(2) :0.6(3)72:48 (4) 时:15分
28.看图列式。
29.求下列图形中阴影部分的周长。
(1)
(2)
六、解决问题
30.李叔叔用篱笆靠一面墙(墙足够长)围一个长18米、宽9米的长方形苗圃,需要买多少米长的篱笆?
方案①: 方案②:
31.泉峰广场有一块长8米,宽1米的长方形空地,用边长2分米的正方形 地砖铺满这块空地,需要多少块地砖?
32.马小虎计算小数加法时,把其中一个加数4.5的小数点看漏了,结果得61.35,正确的结果应该是多少?
33.小坤早上从家步行去学校,走完一半路程时,爸爸发现小坤的数学书丢在家里,随即骑车去给小坤送书,追上时,小坤还有 的路程未走完,小坤随即上了爸爸的车,由爸爸送往学校,这样小坤比独自步行提早6分钟到校,小坤从家到学校全部步行需要多少时间?
34.中国是世界上最早养蚕织绸的国家。“丝绸之路”就是因丝绸外销而得名的重要贸易通道。蚕桑养殖每年五月初开始,十月末结束,一年可养10批蚕。一只雌蛾一生可产400-500粒蚕卵,10000粒蚕卵重约5g。贵州省某县去年第一批共收获295吨蚕茧,其中一等茧每千克售价53元,二等茧每千克售价17元。蚕茧的丰收给蚕农生活带来了巨大改变。今年李伯伯家一等蚕和二等蚕各产出60千克,王伯伯的这些蚕一共能卖多少钱?(用两种方法解答)
35.A,B两地相距1800米,甲、乙二人分别从A,B两地同时出发,相向而行。相遇后甲又走了8分到达B地,乙又走了18分到达A地。甲、乙二人每分钟各走多少米?
36.六(1)班有学生60人,男生人数是全班的,又转来几名女生后,这时男生人数是全班的,又转来几名女生?
答案解析
1.【答案】C
【解析】【解答】解:462-420=42(立方厘米)。
故答案为:C。
【分析】这个鸡蛋的体积=放入鸡蛋后的体积-放入鸡蛋前的体积。
2.【答案】A
3.【答案】C
【解析】【解答】解:计算面积时,选取的底和高要对应,10 cm和14.3cm相对应,13cm 和11 cm相对应;所以C正确。
故答案为:C。
【分析】三角形中对应的一组底和高形成垂直的,垂足有90度角,据此找出对应的高和底即可。
4.【答案】C
【解析】【解答】解: “相”的下一步可能走到:(2,0)、(2,4)、(6,0)、(6,4);
不可能走到(3,3)。
故答案为:C。
【分析】根据“相”走“田”,把可能的位置用数对表示出来,再进行选择即可。
5.【答案】A
6.【答案】C
【解析】【解答】解:设的面积为S。
因为,,且为公共角,
所以。
根据相似三角形的性质(相似三角形面积比等于相似比的平方),可得,即。
同理,可得到其他类似小三角形的面积与面积的关系:
、与也相似,且它们与的面积比同样为,即。
以为例,,,为公共角,
所以,
则,即。
那么的面积为,
其中与相似,相似比为,面积比为,
所以,则。
同理可得、的面积也都为。
阴影部分面积S阴影=S-S AJQ-S BME-SCNF-3×(S JQD-S AKD)
将上述面积关系代入可得:
所以阴影部分与的面积之比为。
故答案为:C
【分析】本题可通过利用三角形的面积公式以及相似三角形的性质,求出阴影部分面积与ABC面积的关系,进而得出它们的面积之比。先利用相似三角形性质求相关线段比例,再求由两个小三角形组成的大一些三角形的面积,最后根据阴影部分面积S阴影=S-S AJQ-S BME-SCNF-3×(S JQD-S AKD)代入即可得到答案。
7.【答案】错误
【解析】【解答】 一个不等于0的数乘假分数的积等于或大于这个数,例如:3×=3,3×>3,原题说法错误。
故答案为:错误。
【分析】假分数等于或大于1,一个不等于0的数乘假分数的积等于或大于这个数,据此举例判断。
8.【答案】错误
【解析】【解答】解:6×==。
故答案为:错误。
【分析】分数乘整数,分母不变,用分子乘整数,能约份的要约分。
9.【答案】错误
【解析】【解答】解:1×(1+)=,(-1)÷=,所以乙数比甲数少。
故答案为:错误。
【分析】甲数=乙数×(1+甲数比乙数多几分之几),那么乙数比甲数少几分之几=(甲数-乙数)÷甲数。
10.【答案】正确
【解析】【解答】解: 设原比为a:b,其中a、b为比的前项和后项。
根据比的性质,比的前项和后项都扩大为原来的2倍后,新的比为2a:2b。
由于2a∶2b = a∶b,说明新的比与原比的比值相等,即新的比与原比能组成比例。
因此,题目中的判断是正确的。
故答案为:正确。
【分析】比的性质指出,比的前项和后项同时乘以或除以同一个非零数,比值不变。而比例是指两个比相等的关系。因此,本题需要判断比的前项和后项都扩大为原来的2倍后,新的比与原比是否能组成比例。
11.【答案】错误
【解析】【解答】解:5÷10=0.5(厘米)
5厘米:0.5厘米=10:1;
所以这幅图的比例尺是10:1。
故答案为:错误。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
12.【答案】错误
【解析】【解答】解:小数5.2365精确到千分位是5.237。
故答案为:错误。
【分析】小数的近似数:精确到哪一位,就看那一位的下一位,再利用“四舍五入”法解答即可。
13.【答案】错误
【解析】【解答】这个数是1÷=,
×=。
所以的是。
故答案为:错误。
【分析】乘积为1的两个数互为倒数,根据倒数的概念求出这个数,再用这个数乘以,计算出来的结果与比较即可。
14.【答案】错误
【解析】【解答】500×(1-)+×1000
=500×+×1000
=375+250
=625(克)
原题说法错误.
故答案为:错误.
【分析】根据题意可知,把原来水的质量看作单位“1”,用单位“1”×(1-)+增加的水的质量=现在的水的质量,注意:千克化成克,乘进率1000,据此列式解答.
15.【答案】正确
【解析】【解答】7÷3=2(本)……1(本)
2+1=3(本)
所以总有一个抽屉至少会放进3本书,原题说法正确。
故答案为:正确。
【分析】此题主要考查了抽屉原理的应用,抽屉原理的公式:a个物体放入n个抽屉,如果a÷n=b……c,那么有一个抽屉至少放(b+1)个物体,据此列式解答。
16.【答案】220
【解析】【解答】解:(2×50+3×40)÷(3-2)
=(100+120)÷1
=220÷1
=220(厘米)。
故答案为:220。
【分析】绳子两折时,露出井外50厘米,多出来的绳子长度=50×2=100厘米,绳子三折时,还差40厘米,则绳子差了3×40=120厘米,井深=(多出的绳长+还差的绳长) ÷ (3-2)。
17.【答案】
【解析】【解答】解:设玻璃瓶正立时下底面积为,则有墨水部分的体积为;
玻璃瓶倒立时空余部分的体积为,则玻璃瓶容积为,所以瓶内的墨水的体积与玻璃 容积之比为。
故答案为:。
【分析】设玻璃瓶正立时下底面积为,根据图一求得墨水的容积,根据图二求得空白部分的容积,从而得瓶子的容积,再计算瓶内的墨水的体积与玻璃 容积之比即可。
18.【答案】9;72
【解析】【解答】解:3×3=9(cm),
24×3=72(cm2);
故答案为:9;72。
【分析】等底等高的圆锥的体积是圆柱体积的三分之一,所以当圆柱与圆柱的体积相等、底面积相等时,圆锥的高是圆柱高的3倍,当圆柱与圆柱的体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
19.【答案】西;南;40°;500
【解析】【解答】解:天天家在东东家东偏北40°方向500m处,则东东家在天天家西偏南40°方向500m处。
故答案为:西;南;40°;500
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
20.【答案】-5;58
【解析】【解答】解:20-15=5, 第15层应记作-5层
20+38=58(层)
故答案为:-5;58。
【分析】用正负数来表示具有意义相反的两种量:选20层作为标准记为0,超过部分为正,不足的部分为负,直接得出结论即可
21.【答案】140
【解析】【解答】解:∠ACB=180°-70°-70°=40°,∠1=180°-40°=140°。
故答案为:140。
【分析】BC=AC,则∠A=∠B,用三角形内角和减去∠A的度数,再减去∠B的度数即可求出∠ACB的度数。∠ACB与∠1组成平角,用180°减去∠ACB的度数即可求出∠1的度数。
22.【答案】4
【解析】【解答】900-350=550(本),93+53=146(本),550-146=404(本),404-146=258(本),258-146=112(本),112<146,至少还需运4次
故答案为:4.
【分析】先计算出还剩多少本没有运,再计算两个小车每次可以运走多少本,依次去减,则可计算出至少需要多少次.
23.【答案】(1)解:
(2)解:
(3)解:
【解析】【分析】(1)数对的表示方法:先列后行。括号里的第一个数表示列数,第二个数表示行数,列数和行数相交的地方就是这个数对表示的位置,据此先描点,再连线;
(2)做旋转后的图形:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图;
(3)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点或关键线段的对称线段,然后再连线。
24.【答案】
0.5+1.4=1.9 1+0.38=1.38 10-7.2=2.8 2.4-1.8=0.6
3.5×100=350 0.8×0.9=0.72 2.5×0.4=1 40×2.4=96
【解析】【分析】 一个数乘10、100、1000,就是把这个数的小数点向右分别移动一位、两位、三位;
0乘任何数都得0;
小数的加法和减法计算法则: 计算小数加、减法,先把各数的小数点对齐(也就是把相同数位上的数对齐),再按照整数加、减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点。得数的小数部分末尾有0,一般要把0去掉。
小数乘小数的计算法则:先按照整数乘法法则计算;然后根据因数中小数位的数量,从积的右边起数出相应的位数,点上小数点;如果积的位数不够,要在前面补0。
25.【答案】2;或
26.【答案】
解: x=-
x= 解: x=+
x= 解: x=-
x= 解: x=+
x=1
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
应用等式的性质1解方程。
27.【答案】(1)解: 0.75:=(0.75×8) :(×8)=2:3
0.75:=×=
(2)解: :0.6=(×10) :(0.6×10)=1:2
:0.6= ÷0.6=0.5
(3)解:72:48=(72:24) :(48÷24)=3:2
72:48=72÷48=1.5
(4)解: 时:15分=(48÷3) :(15÷3)=16:5
时:15分=48÷15=3.2
【解析】【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,以及比的基本性质化简比;求比值,用比的前项÷比的后项。
28.【答案】解:84×(1+)
=84×
=96(千瓦时)
【解析】【分析】9月份的用电量=10月份的用电量×(单位“1”+多的分率)。
29.【答案】(1)解:10×4+3.14×10=71.4(cm)
(2)解:3+5=8(cm)
×(3.14×8+3.14×3+3.14×5)=25.12(cm)
【解析】【分析】(1)阴影部分的周长=圆的周长+正方形的周长
(2)阴影部分的周长=三个不同直径的半圆的弧长+3+5
30.【答案】解:
方案①:
18+9×2
=18+18
=36(米)
方案②:
18×2+9
=36+9
=45(米)
答:需要买36米或者45米长的篱笆。
【解析】【分析】方案①:当长边靠墙时,篱笆的长=长+宽×2;方案②:当宽边靠墙时,篱笆的长=长×2+宽。
31.【答案】200块
32.【答案】解:61.35-45=16.35
16.35+4.5=20.85
答:正确的结果应该是20.85。
【解析】【分析】另一个加数=和-加数,因为另一个加数没有变化,因此用错误的结果减去45求出没有变化的加数,然后再加上正确的加数4.5即可求出正确结果。
33.【答案】解:根据题意,可得
=56(分钟)
答:小坤走完全程:56÷2=28(分钟)
【解析】【分析】从小坤家到学校的全程设为1,小坤走完一半路程时爸爸出发,两人在小坤还有路程未走完时相遇。因此,从爸爸出发到两人相遇,小坤走过的路程为,爸爸走过的路程为。因此,小坤与爸爸的路程比为= 2 : 7。由于小坤与爸爸的速度比为2:7,因此,他们完成剩余路程所需时间的比也为7:2。即,如果小坤步行剩余的路程需要7个单位时间,那么爸爸骑车完成这段路程则只需2个单位时间。小坤比独自步行提早了6分钟到校,这6分钟是由于剩余路程由爸爸骑车而非小坤步行节省的时间。根据时间比7:2,这6分钟对应于时间比中的5个单位时间,因此每个单位时间为= 1.2分钟。小坤步行剩余3/10路程需要7个单位时间,即7×1.2=8.4分钟。因此,步行全程的时间为分钟。
34.【答案】4200元
35.【答案】解:设甲每分钟走x米,乙每分钟走y米,
则由题意得:8x+18y=1800,…①
甲总共用时为,乙总共用时为,
甲比乙少用了18-8=10分钟,
即有:…②
由将①变形为x=代入②,
解得:x=90,y=60,
即甲每分钟走90米,乙每分钟走60米;
答:甲每分钟走90米,乙每分钟走60米.
【解析】【分析】本题中甲、乙的速度都是未知的,可分别设出来,根据“相遇后甲又走了8分到达B地,乙又走了18分到达A地”可得:相遇后甲8分钟行的路程+乙18分钟行的路程=1800米;由于甲乙在相遇时所用的时间是相同的,而在相遇后用的时间不同,所以都走完全程所用的时间相差18-8=10分钟;根据这两个等量关系可列方程解答即可.
36.【答案】解:60×÷-60
=35÷-60
=63-60
=3(名)
答:又转来3名女生。
【解析】【分析】又转来女生的人数=六(1)班原来有学生的人数×男生占的分率÷又转来几名女生后男生占的分率-六(1)班原来有学生的人数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下学期期末素养评价数学押题预测卷
一、单选题
1.把一个鸡蛋放入水杯中(如图),这个鸡蛋的体积是( )cm 。
A.62 B.882 C.42
2.能与∶组成比例的是( )。
A.2∶1 B.1∶2 C.∶ D.8∶2
3.计算如图三角形的面积,选择数据正确的是( )。
A.10cm和13 cm B.11 cm和14.3 cm
C.10 cm和14.3cm D.10 cm和11 cm
4. 一副象棋棋盘上的棋子摆放如图所示,如果“馬”的下一步可能走到(1,3),那么“相”的下一步不可能走到( )
A.(2,4) B.(6,4) C.(3,3)
5.将一个长方体铸成一个正方体(没有损耗),( )不变。
A.体积 B.表面积 C.棱长的和 D.面积
6.在△ABC中,阴影部分是由各边的四等分点连结形成的,那么阴影部分与△ABC的面积之比为( )。
A. B. C. D.
E.以上都不对
二、判断题
7.一个不等于0的数乘假分数的积一定大于这个数.( )
8.6× = = 。( )
9.甲数比乙数多,则乙数比甲数少。( )
10.比的前项和后项都扩大为原来的2倍,得到一个新的比,这两个比能组成比例。( )
11.将一个5毫米长的零件画在图上长为5厘米,这幅图的比例尺是1:10.( )
12.小数5.2365精确到千分位是5.236。( )
13.一个数的倒数是 ,这个数的 是 。( )
14.500克的水减少了 后再增加 千克,结果还是500克。
15.把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书.( )
三、填空题
16.小明用一根绳子测量一个水井深度,绳子两折时,露出井外50厘米;绳子三折时,还差40厘米.那么井深 厘米.
17. (比的应用) 如图,一个瓶身为圆柱体的玻璃瓶内装有高 3 厘米的墨水, 将瓶盖盖好后倒置, 墨水水面高为 4 厘米, 则瓶内的墨水的体积与玻璃 容积之比为 。
18.把一块底面积是24cm2,高是3cm的圆柱形橡皮泥捏成同样底面大小的圆锥,圆锥的高是 cm。如果把它捏成同样高的圆锥,圆锥的底面积是 分米。
19.天天家在东东家东偏北40°方向500 m处,则东东家在天天家 偏 方向 m处。
20.绿地中心千玺广场,又名“大玉米”,位于郑州市郑东新区,被誉为“中原第一高楼”。如果把第20层记作0层,那么第15层应记作 层,记作+38层的那一层实际为第 层。
21.桑梯是我国古代发明的一种采桑工具。如图所示为明朝科学家许光启在《农政启书》中用图画描绘的桑梯示意图。已知BC=AC,∠BAC=70°,则∠1的度数为 °。
22.《铁道游击队》歌颂了铁路工人抗战的顽强意志,深受读者喜爱,文海书店订购了900本,现将其运到仓库,已经用大推车运了350本,剩下的由下面两辆小推车同时搬运,至少还需运 次。
四、操作题
23.按要求完成下面各题。
(1)在图中标出A(4,4);B(4,1);C(9,1);D(6,4),依次连接A、B、C、D、A;
(2)将画出的图形绕点B逆时针旋转90°,画出旋转后的图形;
(3)根据对称轴画出右边图形的另一半,使它成为一个轴对称图形。
五、计算题
24.直接写出得数。
0.5+1.4= 1+0.38= 10-7.2= 2.4-1.8=
3.5×100= 0.8×0.9= 2.5×0.4= 40×2.4=
25.计算下面各题。
26.解方程。
27.化简比并求比值
(1)0.75:(2) :0.6(3)72:48 (4) 时:15分
28.看图列式。
29.求下列图形中阴影部分的周长。
(1)
(2)
六、解决问题
30.李叔叔用篱笆靠一面墙(墙足够长)围一个长18米、宽9米的长方形苗圃,需要买多少米长的篱笆?
方案①: 方案②:
31.泉峰广场有一块长8米,宽1米的长方形空地,用边长2分米的正方形 地砖铺满这块空地,需要多少块地砖?
32.马小虎计算小数加法时,把其中一个加数4.5的小数点看漏了,结果得61.35,正确的结果应该是多少?
33.小坤早上从家步行去学校,走完一半路程时,爸爸发现小坤的数学书丢在家里,随即骑车去给小坤送书,追上时,小坤还有 的路程未走完,小坤随即上了爸爸的车,由爸爸送往学校,这样小坤比独自步行提早6分钟到校,小坤从家到学校全部步行需要多少时间?
34.中国是世界上最早养蚕织绸的国家。“丝绸之路”就是因丝绸外销而得名的重要贸易通道。蚕桑养殖每年五月初开始,十月末结束,一年可养10批蚕。一只雌蛾一生可产400-500粒蚕卵,10000粒蚕卵重约5g。贵州省某县去年第一批共收获295吨蚕茧,其中一等茧每千克售价53元,二等茧每千克售价17元。蚕茧的丰收给蚕农生活带来了巨大改变。今年李伯伯家一等蚕和二等蚕各产出60千克,王伯伯的这些蚕一共能卖多少钱?(用两种方法解答)
35.A,B两地相距1800米,甲、乙二人分别从A,B两地同时出发,相向而行。相遇后甲又走了8分到达B地,乙又走了18分到达A地。甲、乙二人每分钟各走多少米?
36.六(1)班有学生60人,男生人数是全班的,又转来几名女生后,这时男生人数是全班的,又转来几名女生?
答案解析
1.【答案】C
【解析】【解答】解:462-420=42(立方厘米)。
故答案为:C。
【分析】这个鸡蛋的体积=放入鸡蛋后的体积-放入鸡蛋前的体积。
2.【答案】A
3.【答案】C
【解析】【解答】解:计算面积时,选取的底和高要对应,10 cm和14.3cm相对应,13cm 和11 cm相对应;所以C正确。
故答案为:C。
【分析】三角形中对应的一组底和高形成垂直的,垂足有90度角,据此找出对应的高和底即可。
4.【答案】C
【解析】【解答】解: “相”的下一步可能走到:(2,0)、(2,4)、(6,0)、(6,4);
不可能走到(3,3)。
故答案为:C。
【分析】根据“相”走“田”,把可能的位置用数对表示出来,再进行选择即可。
5.【答案】A
6.【答案】C
【解析】【解答】解:设的面积为S。
因为,,且为公共角,
所以。
根据相似三角形的性质(相似三角形面积比等于相似比的平方),可得,即。
同理,可得到其他类似小三角形的面积与面积的关系:
、与也相似,且它们与的面积比同样为,即。
以为例,,,为公共角,
所以,
则,即。
那么的面积为,
其中与相似,相似比为,面积比为,
所以,则。
同理可得、的面积也都为。
阴影部分面积S阴影=S-S AJQ-S BME-SCNF-3×(S JQD-S AKD)
将上述面积关系代入可得:
所以阴影部分与的面积之比为。
故答案为:C
【分析】本题可通过利用三角形的面积公式以及相似三角形的性质,求出阴影部分面积与ABC面积的关系,进而得出它们的面积之比。先利用相似三角形性质求相关线段比例,再求由两个小三角形组成的大一些三角形的面积,最后根据阴影部分面积S阴影=S-S AJQ-S BME-SCNF-3×(S JQD-S AKD)代入即可得到答案。
7.【答案】错误
【解析】【解答】 一个不等于0的数乘假分数的积等于或大于这个数,例如:3×=3,3×>3,原题说法错误。
故答案为:错误。
【分析】假分数等于或大于1,一个不等于0的数乘假分数的积等于或大于这个数,据此举例判断。
8.【答案】错误
【解析】【解答】解:6×==。
故答案为:错误。
【分析】分数乘整数,分母不变,用分子乘整数,能约份的要约分。
9.【答案】错误
【解析】【解答】解:1×(1+)=,(-1)÷=,所以乙数比甲数少。
故答案为:错误。
【分析】甲数=乙数×(1+甲数比乙数多几分之几),那么乙数比甲数少几分之几=(甲数-乙数)÷甲数。
10.【答案】正确
【解析】【解答】解: 设原比为a:b,其中a、b为比的前项和后项。
根据比的性质,比的前项和后项都扩大为原来的2倍后,新的比为2a:2b。
由于2a∶2b = a∶b,说明新的比与原比的比值相等,即新的比与原比能组成比例。
因此,题目中的判断是正确的。
故答案为:正确。
【分析】比的性质指出,比的前项和后项同时乘以或除以同一个非零数,比值不变。而比例是指两个比相等的关系。因此,本题需要判断比的前项和后项都扩大为原来的2倍后,新的比与原比是否能组成比例。
11.【答案】错误
【解析】【解答】解:5÷10=0.5(厘米)
5厘米:0.5厘米=10:1;
所以这幅图的比例尺是10:1。
故答案为:错误。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
12.【答案】错误
【解析】【解答】解:小数5.2365精确到千分位是5.237。
故答案为:错误。
【分析】小数的近似数:精确到哪一位,就看那一位的下一位,再利用“四舍五入”法解答即可。
13.【答案】错误
【解析】【解答】这个数是1÷=,
×=。
所以的是。
故答案为:错误。
【分析】乘积为1的两个数互为倒数,根据倒数的概念求出这个数,再用这个数乘以,计算出来的结果与比较即可。
14.【答案】错误
【解析】【解答】500×(1-)+×1000
=500×+×1000
=375+250
=625(克)
原题说法错误.
故答案为:错误.
【分析】根据题意可知,把原来水的质量看作单位“1”,用单位“1”×(1-)+增加的水的质量=现在的水的质量,注意:千克化成克,乘进率1000,据此列式解答.
15.【答案】正确
【解析】【解答】7÷3=2(本)……1(本)
2+1=3(本)
所以总有一个抽屉至少会放进3本书,原题说法正确。
故答案为:正确。
【分析】此题主要考查了抽屉原理的应用,抽屉原理的公式:a个物体放入n个抽屉,如果a÷n=b……c,那么有一个抽屉至少放(b+1)个物体,据此列式解答。
16.【答案】220
【解析】【解答】解:(2×50+3×40)÷(3-2)
=(100+120)÷1
=220÷1
=220(厘米)。
故答案为:220。
【分析】绳子两折时,露出井外50厘米,多出来的绳子长度=50×2=100厘米,绳子三折时,还差40厘米,则绳子差了3×40=120厘米,井深=(多出的绳长+还差的绳长) ÷ (3-2)。
17.【答案】
【解析】【解答】解:设玻璃瓶正立时下底面积为,则有墨水部分的体积为;
玻璃瓶倒立时空余部分的体积为,则玻璃瓶容积为,所以瓶内的墨水的体积与玻璃 容积之比为。
故答案为:。
【分析】设玻璃瓶正立时下底面积为,根据图一求得墨水的容积,根据图二求得空白部分的容积,从而得瓶子的容积,再计算瓶内的墨水的体积与玻璃 容积之比即可。
18.【答案】9;72
【解析】【解答】解:3×3=9(cm),
24×3=72(cm2);
故答案为:9;72。
【分析】等底等高的圆锥的体积是圆柱体积的三分之一,所以当圆柱与圆柱的体积相等、底面积相等时,圆锥的高是圆柱高的3倍,当圆柱与圆柱的体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
19.【答案】西;南;40°;500
【解析】【解答】解:天天家在东东家东偏北40°方向500m处,则东东家在天天家西偏南40°方向500m处。
故答案为:西;南;40°;500
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
20.【答案】-5;58
【解析】【解答】解:20-15=5, 第15层应记作-5层
20+38=58(层)
故答案为:-5;58。
【分析】用正负数来表示具有意义相反的两种量:选20层作为标准记为0,超过部分为正,不足的部分为负,直接得出结论即可
21.【答案】140
【解析】【解答】解:∠ACB=180°-70°-70°=40°,∠1=180°-40°=140°。
故答案为:140。
【分析】BC=AC,则∠A=∠B,用三角形内角和减去∠A的度数,再减去∠B的度数即可求出∠ACB的度数。∠ACB与∠1组成平角,用180°减去∠ACB的度数即可求出∠1的度数。
22.【答案】4
【解析】【解答】900-350=550(本),93+53=146(本),550-146=404(本),404-146=258(本),258-146=112(本),112<146,至少还需运4次
故答案为:4.
【分析】先计算出还剩多少本没有运,再计算两个小车每次可以运走多少本,依次去减,则可计算出至少需要多少次.
23.【答案】(1)解:
(2)解:
(3)解:
【解析】【分析】(1)数对的表示方法:先列后行。括号里的第一个数表示列数,第二个数表示行数,列数和行数相交的地方就是这个数对表示的位置,据此先描点,再连线;
(2)做旋转后的图形:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图;
(3)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点或关键线段的对称线段,然后再连线。
24.【答案】
0.5+1.4=1.9 1+0.38=1.38 10-7.2=2.8 2.4-1.8=0.6
3.5×100=350 0.8×0.9=0.72 2.5×0.4=1 40×2.4=96
【解析】【分析】 一个数乘10、100、1000,就是把这个数的小数点向右分别移动一位、两位、三位;
0乘任何数都得0;
小数的加法和减法计算法则: 计算小数加、减法,先把各数的小数点对齐(也就是把相同数位上的数对齐),再按照整数加、减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点。得数的小数部分末尾有0,一般要把0去掉。
小数乘小数的计算法则:先按照整数乘法法则计算;然后根据因数中小数位的数量,从积的右边起数出相应的位数,点上小数点;如果积的位数不够,要在前面补0。
25.【答案】2;或
26.【答案】
解: x=-
x= 解: x=+
x= 解: x=-
x= 解: x=+
x=1
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
应用等式的性质1解方程。
27.【答案】(1)解: 0.75:=(0.75×8) :(×8)=2:3
0.75:=×=
(2)解: :0.6=(×10) :(0.6×10)=1:2
:0.6= ÷0.6=0.5
(3)解:72:48=(72:24) :(48÷24)=3:2
72:48=72÷48=1.5
(4)解: 时:15分=(48÷3) :(15÷3)=16:5
时:15分=48÷15=3.2
【解析】【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,以及比的基本性质化简比;求比值,用比的前项÷比的后项。
28.【答案】解:84×(1+)
=84×
=96(千瓦时)
【解析】【分析】9月份的用电量=10月份的用电量×(单位“1”+多的分率)。
29.【答案】(1)解:10×4+3.14×10=71.4(cm)
(2)解:3+5=8(cm)
×(3.14×8+3.14×3+3.14×5)=25.12(cm)
【解析】【分析】(1)阴影部分的周长=圆的周长+正方形的周长
(2)阴影部分的周长=三个不同直径的半圆的弧长+3+5
30.【答案】解:
方案①:
18+9×2
=18+18
=36(米)
方案②:
18×2+9
=36+9
=45(米)
答:需要买36米或者45米长的篱笆。
【解析】【分析】方案①:当长边靠墙时,篱笆的长=长+宽×2;方案②:当宽边靠墙时,篱笆的长=长×2+宽。
31.【答案】200块
32.【答案】解:61.35-45=16.35
16.35+4.5=20.85
答:正确的结果应该是20.85。
【解析】【分析】另一个加数=和-加数,因为另一个加数没有变化,因此用错误的结果减去45求出没有变化的加数,然后再加上正确的加数4.5即可求出正确结果。
33.【答案】解:根据题意,可得
=56(分钟)
答:小坤走完全程:56÷2=28(分钟)
【解析】【分析】从小坤家到学校的全程设为1,小坤走完一半路程时爸爸出发,两人在小坤还有路程未走完时相遇。因此,从爸爸出发到两人相遇,小坤走过的路程为,爸爸走过的路程为。因此,小坤与爸爸的路程比为= 2 : 7。由于小坤与爸爸的速度比为2:7,因此,他们完成剩余路程所需时间的比也为7:2。即,如果小坤步行剩余的路程需要7个单位时间,那么爸爸骑车完成这段路程则只需2个单位时间。小坤比独自步行提早了6分钟到校,这6分钟是由于剩余路程由爸爸骑车而非小坤步行节省的时间。根据时间比7:2,这6分钟对应于时间比中的5个单位时间,因此每个单位时间为= 1.2分钟。小坤步行剩余3/10路程需要7个单位时间,即7×1.2=8.4分钟。因此,步行全程的时间为分钟。
34.【答案】4200元
35.【答案】解:设甲每分钟走x米,乙每分钟走y米,
则由题意得:8x+18y=1800,…①
甲总共用时为,乙总共用时为,
甲比乙少用了18-8=10分钟,
即有:…②
由将①变形为x=代入②,
解得:x=90,y=60,
即甲每分钟走90米,乙每分钟走60米;
答:甲每分钟走90米,乙每分钟走60米.
【解析】【分析】本题中甲、乙的速度都是未知的,可分别设出来,根据“相遇后甲又走了8分到达B地,乙又走了18分到达A地”可得:相遇后甲8分钟行的路程+乙18分钟行的路程=1800米;由于甲乙在相遇时所用的时间是相同的,而在相遇后用的时间不同,所以都走完全程所用的时间相差18-8=10分钟;根据这两个等量关系可列方程解答即可.
36.【答案】解:60×÷-60
=35÷-60
=63-60
=3(名)
答:又转来3名女生。
【解析】【分析】又转来女生的人数=六(1)班原来有学生的人数×男生占的分率÷又转来几名女生后男生占的分率-六(1)班原来有学生的人数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
