华东师大版八年级数学下册第18章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 华东师大版八年级数学下册第18章 平行四边形 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 101.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 00:00:00 | ||
图片预览



文档简介
华东师大版八年级下 第18章 平行四边形 单元测试
一.选择题(共12小题)
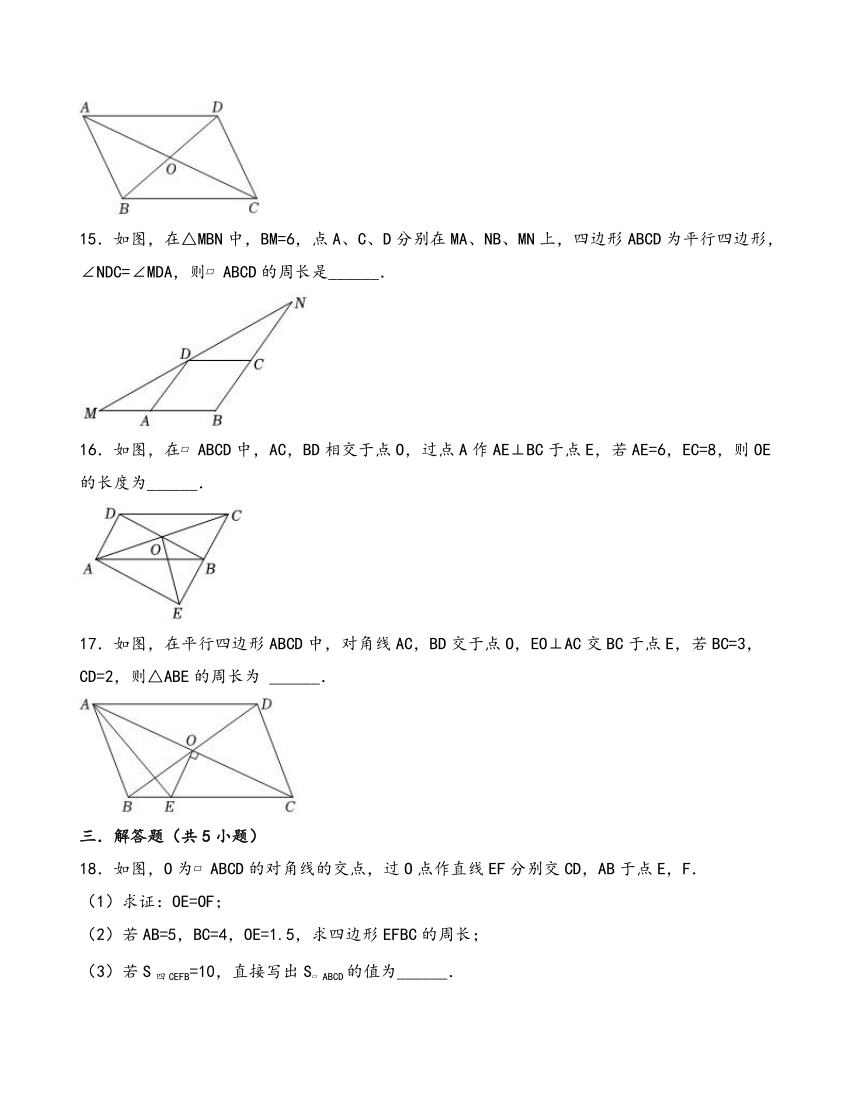
1.如图,在平行四边形ABCD中,∠A+∠C=120°,则∠D的度数是( )
A.60° B.70° C.110° D.120°
2.如图, ABCD的顶点A在 DEFG的边EF上, DEFG的顶点G在 ABCD的边BC上,若 ABCD的面积为8,则 DEFG的面积为( )
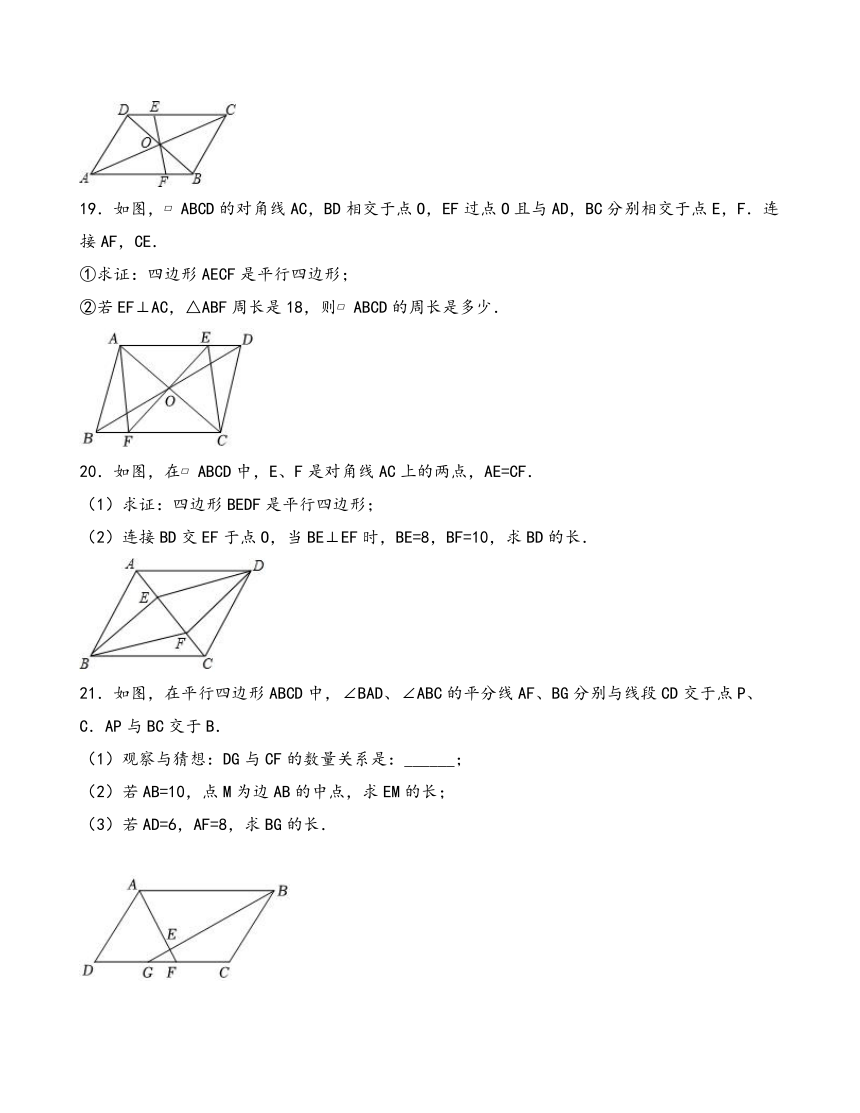
A.6 B.8 C.10 D.12
3.如图,在平行四边形ABCD中,点F是BC延长线上一点,连接AF交CD于点E,下列选项中与∠CEF相等的是( )
A.∠ADC B.∠DCF C.∠BAF D.∠AEC
4.如图在平行四边形中,AB=a,BC=b,对角线相交于O点,过O点作EO⊥BD交BC于E,则△CDE周长为( )
A.a+b B.ab C.2(a+b) D.2(b-a)
5.如图,在 ABCD中,AB=2,BF、CE分别是∠ABC与∠BCD的角平分线,交点为点O,EF=1,则OB2+OC2=( )
A.5 B.10 C.9 D.12
6.如图,在平行四边形ABCD中,AB=6cm,AD=10cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的值为( )
A.1cm B.2cm C.3cm D.4cm
7.在平行四边形ABCD中,∠A+∠C=210°,则∠B的度数为( )
A.30° B.75° C.95° D.105°
8.如图,在 ABCD中,∠BAD的平分线AE交CD于点E,AB=6,AD=4,则CE=( )
A.1 B.2 C.3 D.4
9.(2025春 西丰县期中)如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AB∥DC B.OA=OC,∠BAC=∠DCA
C.AB=DC,AD=BC D.OA=OC,AB=CD
10.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
11.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
12.如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当AD=CD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
二.填空题(共5小题)
13.(2025春 衡山县期中)在平行四边形ABCD中,AB=5cm,BC=4cm,则平行四边形ABCD的周长为______cm.
14.如图, ABCD的对角线交于点O,AB=10,AC+BD=22,则△COD的周长为 ______.
15.如图,在△MBN中,BM=6,点A、C、D分别在MA、NB、MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,则 ABCD的周长是______.
16.如图,在 ABCD中,AC,BD相交于点O,过点A作AE⊥BC于点E,若AE=6,EC=8,则OE的长度为______.
17.如图,在平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC交BC于点E,若BC=3,CD=2,则△ABE的周长为 ______.
三.解答题(共5小题)
18.如图,O为 ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.
(1)求证:OE=OF;
(2)若AB=5,BC=4,OE=1.5,求四边形EFBC的周长;
(3)若S四CEFB=10,直接写出S ABCD的值为______.
19.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.连接AF,CE.
①求证:四边形AECF是平行四边形;
②若EF⊥AC,△ABF周长是18,则 ABCD的周长是多少.
20.如图,在 ABCD中,E、F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)连接BD交EF于点O,当BE⊥EF时,BE=8,BF=10,求BD的长.
21.如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点P、C.AP与BC交于B.
(1)观察与猜想:DG与CF的数量关系是:______;
(2)若AB=10,点M为边AB的中点,求EM的长;
(3)若AD=6,AF=8,求BG的长.
22.如图,在△ABF中,E是AB的中点,延长BF至点D,使得DF=BF,连接AD,延长EF至点C,使得CF=AD,连接CD.
(1)求证:四边形AFCD为平行四边形;
(2)连接AC交DB于点O,若CE⊥DB,EF=1,,求AF的长.
华东师大版八年级下 第18章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、C 4、A 5、C 6、D 7、B 8、B 9、D 10、C 11、D 12、C
二.填空题(共5小题)
13、18; 14、21; 15、12; 16、5; 17、5;
三.解答题(共5小题)
18、(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,OD=OB
∴∠CDO=∠ABO,
在△DEO与△BFO中,
∴△DEO≌△BFO(ASA).
∴OE=OF;
(2)∵△DEO≌△BFO(ASA).
∴OE=OF=1.5,BF=DE,
∴EF=3,BF+CE=AB=5,
∴四边形EFBC的周长=3+5+4=12;
(3)∵△DEO≌△BFO,
同理△CEO≌△AFO,
∵△ADO≌△BCO,
∴S ABCD=2S四CEFB=10×2=20,
故答案为:20.
19、①证明:在 ABCD中,
∵AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠OFC,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=FC,
又∵AE∥FC,
∴四边形AECF是平行四边形;
②解;∵四边形AECF是平行四边形,AC⊥EF,
∴四边形AFCE是菱形,
∴AF=FC,
∵AB+AF+BF=18,即AB+FC+BF=18,
即AB+BC=18,
∴2AB+2BC=36,即 ABCD的周长是36.
20、(1)证明:连接BD交AC于O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,∵OB=OD,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥AC,
∴∠BEF=90°,
在Rt△BEF中,EF===6,
∴OE=OF=3,
在Rt△BEO中,OB===,
∴BD=2OB=2.
21、解:(1)DG=CF,理由如下:
∵AF平分∠BAD,
∴∠DAF=∠BAF=∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
故答案为:DF=CG;
(2)∵四边形ABCD平行四边形,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°-(∠BAF+∠ABG)=180°-90°=90°.
∴AF⊥BG,
∵AB=10,点M为边AB的中点,
∴EM=AB=5;
(3)∵DF=AD=6,
∴CG=DF=6.
如图,过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形,
∴BH=AF=8,
∵∠AFD=∠H,∠D=∠BCH,AD=BC,
∴△ADF≌△BCH(AAS),
∴DF=CH=6,
∴GH=CG+CH=6+6=12,
在Rt△BHG中,BG===4,
∴BG的长度为4.
22、(1)证明:∵DF=BF,
∴F是DB的中点,
∴E是AB的中点,
∴EF∥AD,
∵点C在EF的延长线上,
∴CF∥AD,
∵CF=AD,
∴四边形AFCD为平行四边形.
(2)解:∵DF=BF,AE=BE=,EF=1,
∴EF∥AD,且EF=AD,AB=2AE=2,
∴AD=2EF=2,
∵CE⊥DB于点F,
∴∠ADB=∠EFB=90°,
∴BD==6,
∴DF=BF=BD=3,
∴AF===.
一.选择题(共12小题)
1.如图,在平行四边形ABCD中,∠A+∠C=120°,则∠D的度数是( )
A.60° B.70° C.110° D.120°
2.如图, ABCD的顶点A在 DEFG的边EF上, DEFG的顶点G在 ABCD的边BC上,若 ABCD的面积为8,则 DEFG的面积为( )
A.6 B.8 C.10 D.12
3.如图,在平行四边形ABCD中,点F是BC延长线上一点,连接AF交CD于点E,下列选项中与∠CEF相等的是( )
A.∠ADC B.∠DCF C.∠BAF D.∠AEC
4.如图在平行四边形中,AB=a,BC=b,对角线相交于O点,过O点作EO⊥BD交BC于E,则△CDE周长为( )
A.a+b B.ab C.2(a+b) D.2(b-a)
5.如图,在 ABCD中,AB=2,BF、CE分别是∠ABC与∠BCD的角平分线,交点为点O,EF=1,则OB2+OC2=( )
A.5 B.10 C.9 D.12
6.如图,在平行四边形ABCD中,AB=6cm,AD=10cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的值为( )
A.1cm B.2cm C.3cm D.4cm
7.在平行四边形ABCD中,∠A+∠C=210°,则∠B的度数为( )
A.30° B.75° C.95° D.105°
8.如图,在 ABCD中,∠BAD的平分线AE交CD于点E,AB=6,AD=4,则CE=( )
A.1 B.2 C.3 D.4
9.(2025春 西丰县期中)如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AB∥DC B.OA=OC,∠BAC=∠DCA
C.AB=DC,AD=BC D.OA=OC,AB=CD
10.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
11.(2025 蜀山区三模)如图,平行四边形ABCD中,∠BAD的平分线AE交BC边于点E,BF⊥AE交AD边于点F,AB=5,AE=4,则BF的长为( )
A.3 B. C.6 D.
12.如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当AD=CD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
二.填空题(共5小题)
13.(2025春 衡山县期中)在平行四边形ABCD中,AB=5cm,BC=4cm,则平行四边形ABCD的周长为______cm.
14.如图, ABCD的对角线交于点O,AB=10,AC+BD=22,则△COD的周长为 ______.
15.如图,在△MBN中,BM=6,点A、C、D分别在MA、NB、MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,则 ABCD的周长是______.
16.如图,在 ABCD中,AC,BD相交于点O,过点A作AE⊥BC于点E,若AE=6,EC=8,则OE的长度为______.
17.如图,在平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC交BC于点E,若BC=3,CD=2,则△ABE的周长为 ______.
三.解答题(共5小题)
18.如图,O为 ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.
(1)求证:OE=OF;
(2)若AB=5,BC=4,OE=1.5,求四边形EFBC的周长;
(3)若S四CEFB=10,直接写出S ABCD的值为______.
19.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.连接AF,CE.
①求证:四边形AECF是平行四边形;
②若EF⊥AC,△ABF周长是18,则 ABCD的周长是多少.
20.如图,在 ABCD中,E、F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)连接BD交EF于点O,当BE⊥EF时,BE=8,BF=10,求BD的长.
21.如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点P、C.AP与BC交于B.
(1)观察与猜想:DG与CF的数量关系是:______;
(2)若AB=10,点M为边AB的中点,求EM的长;
(3)若AD=6,AF=8,求BG的长.
22.如图,在△ABF中,E是AB的中点,延长BF至点D,使得DF=BF,连接AD,延长EF至点C,使得CF=AD,连接CD.
(1)求证:四边形AFCD为平行四边形;
(2)连接AC交DB于点O,若CE⊥DB,EF=1,,求AF的长.
华东师大版八年级下 第18章 平行四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、B 3、C 4、A 5、C 6、D 7、B 8、B 9、D 10、C 11、D 12、C
二.填空题(共5小题)
13、18; 14、21; 15、12; 16、5; 17、5;
三.解答题(共5小题)
18、(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,OD=OB
∴∠CDO=∠ABO,
在△DEO与△BFO中,
∴△DEO≌△BFO(ASA).
∴OE=OF;
(2)∵△DEO≌△BFO(ASA).
∴OE=OF=1.5,BF=DE,
∴EF=3,BF+CE=AB=5,
∴四边形EFBC的周长=3+5+4=12;
(3)∵△DEO≌△BFO,
同理△CEO≌△AFO,
∵△ADO≌△BCO,
∴S ABCD=2S四CEFB=10×2=20,
故答案为:20.
19、①证明:在 ABCD中,
∵AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠OFC,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=FC,
又∵AE∥FC,
∴四边形AECF是平行四边形;
②解;∵四边形AECF是平行四边形,AC⊥EF,
∴四边形AFCE是菱形,
∴AF=FC,
∵AB+AF+BF=18,即AB+FC+BF=18,
即AB+BC=18,
∴2AB+2BC=36,即 ABCD的周长是36.
20、(1)证明:连接BD交AC于O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,∵OB=OD,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥AC,
∴∠BEF=90°,
在Rt△BEF中,EF===6,
∴OE=OF=3,
在Rt△BEO中,OB===,
∴BD=2OB=2.
21、解:(1)DG=CF,理由如下:
∵AF平分∠BAD,
∴∠DAF=∠BAF=∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
故答案为:DF=CG;
(2)∵四边形ABCD平行四边形,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°-(∠BAF+∠ABG)=180°-90°=90°.
∴AF⊥BG,
∵AB=10,点M为边AB的中点,
∴EM=AB=5;
(3)∵DF=AD=6,
∴CG=DF=6.
如图,过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形,
∴BH=AF=8,
∵∠AFD=∠H,∠D=∠BCH,AD=BC,
∴△ADF≌△BCH(AAS),
∴DF=CH=6,
∴GH=CG+CH=6+6=12,
在Rt△BHG中,BG===4,
∴BG的长度为4.
22、(1)证明:∵DF=BF,
∴F是DB的中点,
∴E是AB的中点,
∴EF∥AD,
∵点C在EF的延长线上,
∴CF∥AD,
∵CF=AD,
∴四边形AFCD为平行四边形.
(2)解:∵DF=BF,AE=BE=,EF=1,
∴EF∥AD,且EF=AD,AB=2AE=2,
∴AD=2EF=2,
∵CE⊥DB于点F,
∴∠ADB=∠EFB=90°,
∴BD==6,
∴DF=BF=BD=3,
∴AF===.
