华东师大版八年级下 第19章 矩形、菱形与正方形单元测试(含答案)
文档属性
| 名称 | 华东师大版八年级下 第19章 矩形、菱形与正方形单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 11:18:38 | ||
图片预览



文档简介
华东师大版八年级下 第19章 矩形、菱形与正方形 单元测试
一.选择题(共12小题)
1.(2025春 浦北县期中)平行四边形,矩形,菱形,正方形共有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线平分内角
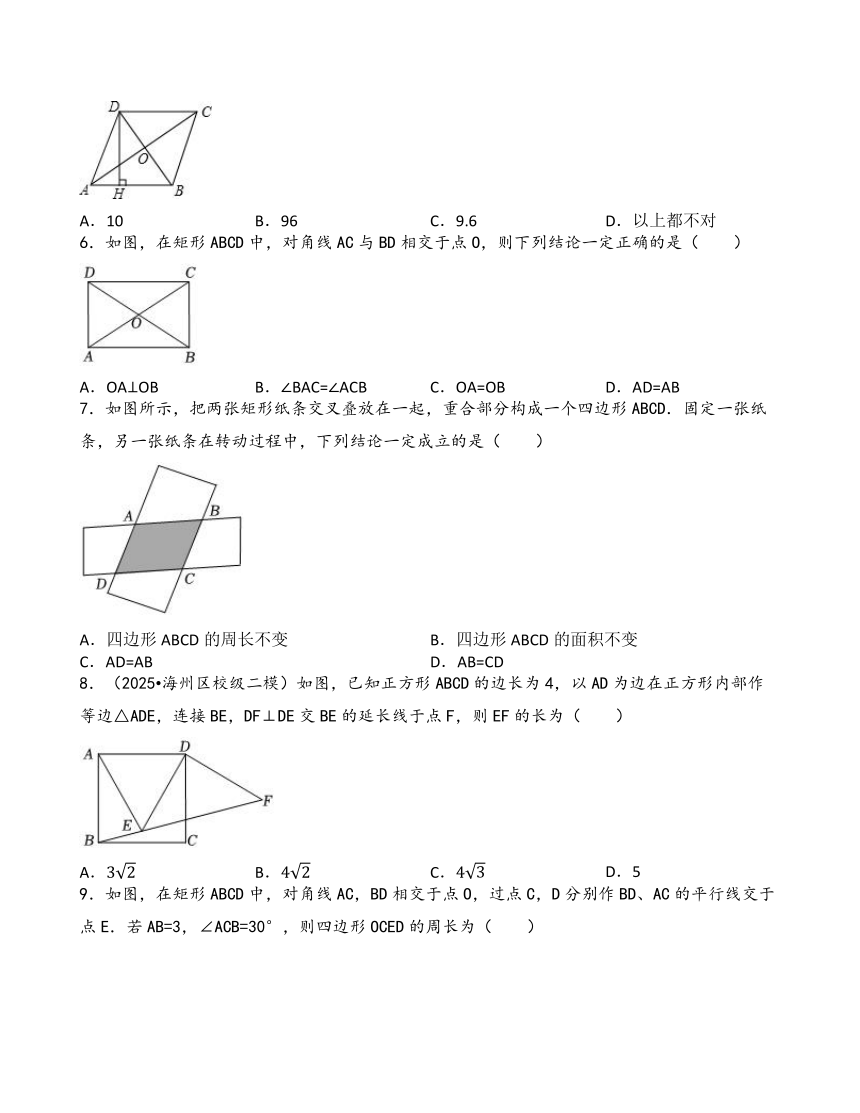
2.如图,在正方形ABCD中,点E为正方形ABCD内一点,连接BE、CE、AE、DE.若△BCE为等边三角形,则∠EAD的度数为( )
A.15° B.30° C.45° D.60°
3.如图,直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,若∠2=41°,则∠1的度数为( )
A.41° B.51° C.49° D.59°
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.如图:菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,求菱形ABCD的高DH的长是( )
A.10 B.96 C.9.6 D.以上都不对
6.如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.OA⊥OB B.∠BAC=∠ACB C.OA=OB D.AD=AB
7.如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形ABCD.固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD的周长不变 B.四边形ABCD的面积不变
C.AD=AB D.AB=CD
8.(2025 海州区校级二模)如图,已知正方形ABCD的边长为4,以AD为边在正方形内部作等边△ADE,连接BE,DF⊥DE交BE的延长线于点F,则EF的长为( )
A. B. C. D.5
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
10.如图,矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F,连接BE、DF.若AB=6,AD=8,则四边形EBFD的周长是( )
A. B.20 C.25 D.40
11.(2025春 灞桥区校级月考)如图,菱形ABCD中,∠B=60°,连结AC,点E和点F分别在边AC,AB上,BF=4,CE=2,若M、N分别为线段EF、BC的中点,则线段MN的长度等于( )
A. B. C. D.3
12.(2025春 开鲁县期中)如图,在菱形ABCD中,AB=4,∠BCD=60°,E为AD上一动点,连接BE,以BE为腰作等腰三角形BEE′,使得∠EBE′=120°,连结AE′.当AE=3时,△BCE′的面积为( )
A.2 B.3 C.6 D.6
二.填空题(共5小题)
13.在菱形ABCD中,AB=13,BD=10,则菱形ABCD的面积为______.
14.如图,已知菱形ABCD中,对角线AC与BD交于点O,BD=8,AC=4,则该菱形的面积是 ______.
15.如图,在正方形ABCD中,P,Q分别是边CD和对角线BD上的动点,且DP=BQ,当BP+CQ的最小值为时,则正方形的边长为 ______.
16.(2025 新宾县三模)如图,在矩形ABCD中,BC=2AB=8,G是BC的中点,连接DG,点E从点B出发,沿BC向点C运动,到点C停止,点F在DG上,,连接AE,EF,AF,当△AEF的面积是10时,BE的长为______.
17.如图,等腰直角三角形AEF的斜边EF经过正方形ABCD的顶点B,点G为EF的中点,连接DE,AG,DE与AG交于点H.
(1)若DH=5,则DE的长度为 ______.
(2)若B恰为EG的中点,则的值为 ______.
三.解答题(共5小题)
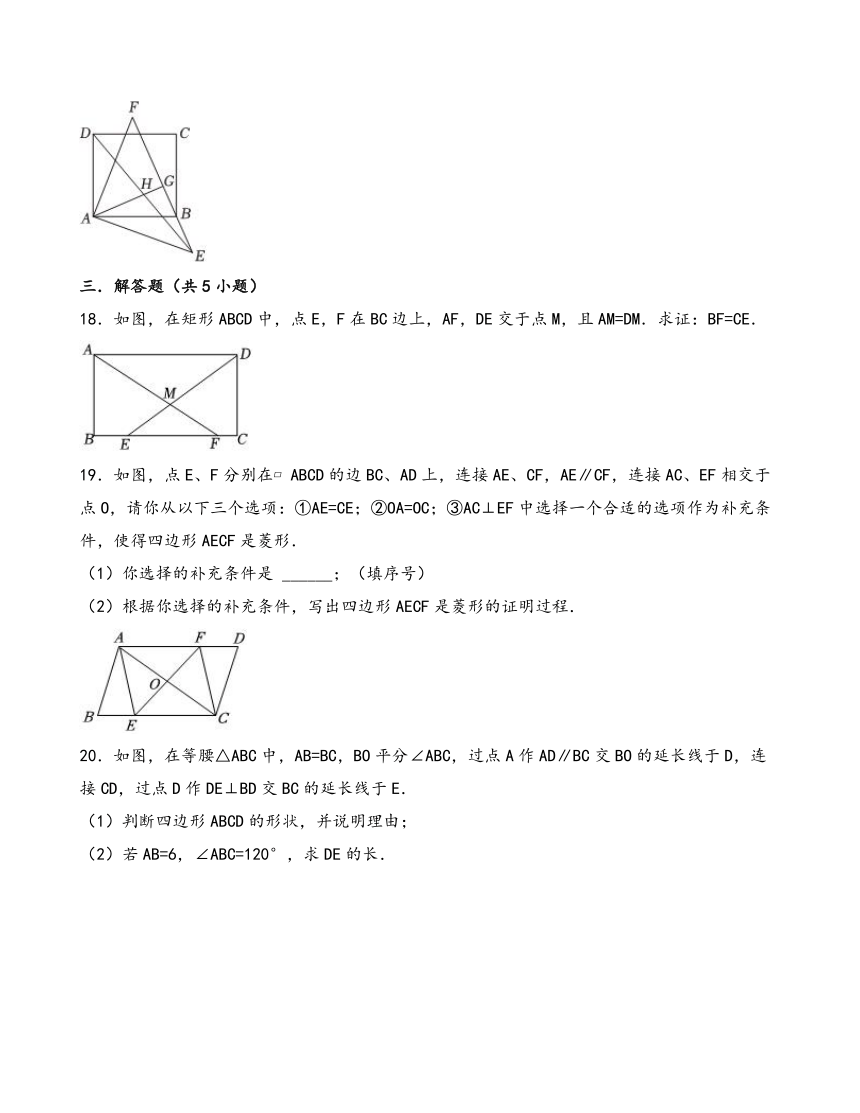
18.如图,在矩形ABCD中,点E,F在BC边上,AF,DE交于点M,且AM=DM.求证:BF=CE.
19.如图,点E、F分别在 ABCD的边BC、AD上,连接AE、CF,AE∥CF,连接AC、EF相交于点O,请你从以下三个选项:①AE=CE;②OA=OC;③AC⊥EF中选择一个合适的选项作为补充条件,使得四边形AECF是菱形.
(1)你选择的补充条件是 ______;(填序号)
(2)根据你选择的补充条件,写出四边形AECF是菱形的证明过程.
20.如图,在等腰△ABC中,AB=BC,BO平分∠ABC,过点A作AD∥BC交BO的延长线于D,连接CD,过点D作DE⊥BD交BC的延长线于E.
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB=6,∠ABC=120°,求DE的长.
21.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=6,OE=4,∠BAE=∠DEF,求BF、DF的长.
22.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
华东师大版八年级下 第19章 矩形、菱形与正方形 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、A 4、B 5、C 6、C 7、D 8、B 9、B 10、C 11、B 12、B
二.填空题(共5小题)
13、120; 14、16; 15、2; 16、2或; 17、10;;
三.解答题(共5小题)
18、证明:∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠B=∠C=∠ADC=90°,
∵AM=DM,
∴∠MAD=∠MDA,
∴∠BAD-∠MAD=∠ADC-∠MDA,即∠BAF=∠CDE,
∴△ABF≌△DCE(ASA),
∴BF=CE.
19、解:(1)补充条件①或③皆可,(答案不唯一);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥CE.
∵AE∥CF,
∴四边形AECF是平行四边形.
补充条件①:∵四边形ABCD是平行四边形,AE=CE,
∴四边形AECF是菱形.
补充条件③:∵四边形ABCD是平行四边形,AC⊥EF,
∴四边形AECF是菱形.
20、解:(1)四边形ABCD是菱形,
理由:由条件可得AO=CO,
∵AD∥BC
∴∠DAO=∠ACB,∠ADO=∠CBO,
∴△ADO≌△CBO(AAS),
∴DO=BO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)由条件可知∠DBC=∠ABE=60°,
∵四边形ABCD是菱形,
∴BC=CD=AB=6,
∴△BCD是等边三角形,
∴BD=BC=6,
∵BD⊥DE,
∴∠BDE=90°,
∴∠E=90°-∠DBC=30°,
∴BE=2BD=12,
∴.
21、(1)证明:∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:∵四边形AEFD为矩形,
∴,
∴AF=DE=2OE=8,OA=OF=OD=OE,
∴∠DEF=∠AFE,
又∵∠AEF=90°,
∴∠EAF+∠AFE=90°,
又∵∠BAE=∠DEF,∠DEF=∠AFE,
∴∠BAE+∠EAF=90°,
∴∠BAF=90°,
在Rt△BAF中,由勾股定理得:BF2=AB2+AF2=62+82=100,
∴BF=10,
∵,
∴,
解得AE=4.8,
∴DF=AE=4.8.
22、(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
一.选择题(共12小题)
1.(2025春 浦北县期中)平行四边形,矩形,菱形,正方形共有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线平分内角
2.如图,在正方形ABCD中,点E为正方形ABCD内一点,连接BE、CE、AE、DE.若△BCE为等边三角形,则∠EAD的度数为( )
A.15° B.30° C.45° D.60°
3.如图,直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,若∠2=41°,则∠1的度数为( )
A.41° B.51° C.49° D.59°
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.如图:菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,求菱形ABCD的高DH的长是( )
A.10 B.96 C.9.6 D.以上都不对
6.如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.OA⊥OB B.∠BAC=∠ACB C.OA=OB D.AD=AB
7.如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形ABCD.固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD的周长不变 B.四边形ABCD的面积不变
C.AD=AB D.AB=CD
8.(2025 海州区校级二模)如图,已知正方形ABCD的边长为4,以AD为边在正方形内部作等边△ADE,连接BE,DF⊥DE交BE的延长线于点F,则EF的长为( )
A. B. C. D.5
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,过点C,D分别作BD、AC的平行线交于点E.若AB=3,∠ACB=30°,则四边形OCED的周长为( )
A.6 B.12 C.18 D.24
10.如图,矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F,连接BE、DF.若AB=6,AD=8,则四边形EBFD的周长是( )
A. B.20 C.25 D.40
11.(2025春 灞桥区校级月考)如图,菱形ABCD中,∠B=60°,连结AC,点E和点F分别在边AC,AB上,BF=4,CE=2,若M、N分别为线段EF、BC的中点,则线段MN的长度等于( )
A. B. C. D.3
12.(2025春 开鲁县期中)如图,在菱形ABCD中,AB=4,∠BCD=60°,E为AD上一动点,连接BE,以BE为腰作等腰三角形BEE′,使得∠EBE′=120°,连结AE′.当AE=3时,△BCE′的面积为( )
A.2 B.3 C.6 D.6
二.填空题(共5小题)
13.在菱形ABCD中,AB=13,BD=10,则菱形ABCD的面积为______.
14.如图,已知菱形ABCD中,对角线AC与BD交于点O,BD=8,AC=4,则该菱形的面积是 ______.
15.如图,在正方形ABCD中,P,Q分别是边CD和对角线BD上的动点,且DP=BQ,当BP+CQ的最小值为时,则正方形的边长为 ______.
16.(2025 新宾县三模)如图,在矩形ABCD中,BC=2AB=8,G是BC的中点,连接DG,点E从点B出发,沿BC向点C运动,到点C停止,点F在DG上,,连接AE,EF,AF,当△AEF的面积是10时,BE的长为______.
17.如图,等腰直角三角形AEF的斜边EF经过正方形ABCD的顶点B,点G为EF的中点,连接DE,AG,DE与AG交于点H.
(1)若DH=5,则DE的长度为 ______.
(2)若B恰为EG的中点,则的值为 ______.
三.解答题(共5小题)
18.如图,在矩形ABCD中,点E,F在BC边上,AF,DE交于点M,且AM=DM.求证:BF=CE.
19.如图,点E、F分别在 ABCD的边BC、AD上,连接AE、CF,AE∥CF,连接AC、EF相交于点O,请你从以下三个选项:①AE=CE;②OA=OC;③AC⊥EF中选择一个合适的选项作为补充条件,使得四边形AECF是菱形.
(1)你选择的补充条件是 ______;(填序号)
(2)根据你选择的补充条件,写出四边形AECF是菱形的证明过程.
20.如图,在等腰△ABC中,AB=BC,BO平分∠ABC,过点A作AD∥BC交BO的延长线于D,连接CD,过点D作DE⊥BD交BC的延长线于E.
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB=6,∠ABC=120°,求DE的长.
21.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=6,OE=4,∠BAE=∠DEF,求BF、DF的长.
22.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
华东师大版八年级下 第19章 矩形、菱形与正方形 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、A 4、B 5、C 6、C 7、D 8、B 9、B 10、C 11、B 12、B
二.填空题(共5小题)
13、120; 14、16; 15、2; 16、2或; 17、10;;
三.解答题(共5小题)
18、证明:∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠B=∠C=∠ADC=90°,
∵AM=DM,
∴∠MAD=∠MDA,
∴∠BAD-∠MAD=∠ADC-∠MDA,即∠BAF=∠CDE,
∴△ABF≌△DCE(ASA),
∴BF=CE.
19、解:(1)补充条件①或③皆可,(答案不唯一);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥CE.
∵AE∥CF,
∴四边形AECF是平行四边形.
补充条件①:∵四边形ABCD是平行四边形,AE=CE,
∴四边形AECF是菱形.
补充条件③:∵四边形ABCD是平行四边形,AC⊥EF,
∴四边形AECF是菱形.
20、解:(1)四边形ABCD是菱形,
理由:由条件可得AO=CO,
∵AD∥BC
∴∠DAO=∠ACB,∠ADO=∠CBO,
∴△ADO≌△CBO(AAS),
∴DO=BO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)由条件可知∠DBC=∠ABE=60°,
∵四边形ABCD是菱形,
∴BC=CD=AB=6,
∴△BCD是等边三角形,
∴BD=BC=6,
∵BD⊥DE,
∴∠BDE=90°,
∴∠E=90°-∠DBC=30°,
∴BE=2BD=12,
∴.
21、(1)证明:∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:∵四边形AEFD为矩形,
∴,
∴AF=DE=2OE=8,OA=OF=OD=OE,
∴∠DEF=∠AFE,
又∵∠AEF=90°,
∴∠EAF+∠AFE=90°,
又∵∠BAE=∠DEF,∠DEF=∠AFE,
∴∠BAE+∠EAF=90°,
∴∠BAF=90°,
在Rt△BAF中,由勾股定理得:BF2=AB2+AF2=62+82=100,
∴BF=10,
∵,
∴,
解得AE=4.8,
∴DF=AE=4.8.
22、(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
