(期末考点培优)专题02 填空题2024-2025学年六年级数学下册期末复习专项青岛版(六三制)(含答案解析)
文档属性
| 名称 | (期末考点培优)专题02 填空题2024-2025学年六年级数学下册期末复习专项青岛版(六三制)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 588.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 10:44:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项青岛版(六三制)
(期末考点培优)专题02 填空题
学校:___________姓名:___________班级:___________考号:___________
1.一个刷油漆的滚筒形状是圆柱形(如图所示),长20厘米,底面直径为8厘米,滚筒滚动一周能刷漆的面积是( )平方厘米。
2.海边栈道提供3人脚踏车和2人脚踏车供游客骑行游览,26位游客乘坐10辆脚踏车正好坐满。其中3人脚踏车有( )辆,2人脚踏车有( )辆。
3.如图,容器中装有一定的水,现将容器倒置,此时,水面的高度为( )cm。
4.2024年2月份,小丽将自己的压岁钱2000元存入银行3年,年利率是1.5%,到期后她把钱全部取出捐给希望小学,她一共捐了( )元。
5.十七世纪,著名数学家莱布尼兹认为比号与除号有一种亲缘关系,把“÷”中的小横线去掉,于是“∶”就成为现在的样子了。根据式子9x=5y(x、y均不为0),写出一个比例为( )。
6.在一幅比例尺是1∶200000的地图上,量得北京到广州的距离是4.2厘米,两地的实际距离是( )千米。 ,把左边的线段比例尺改成数值比例尺是( )。
7.一个圆柱的底面半径是3分米,高是2分米,它的侧面积是( )平方分米,它的表面积是( )平方分米,体积是( )立方分米。
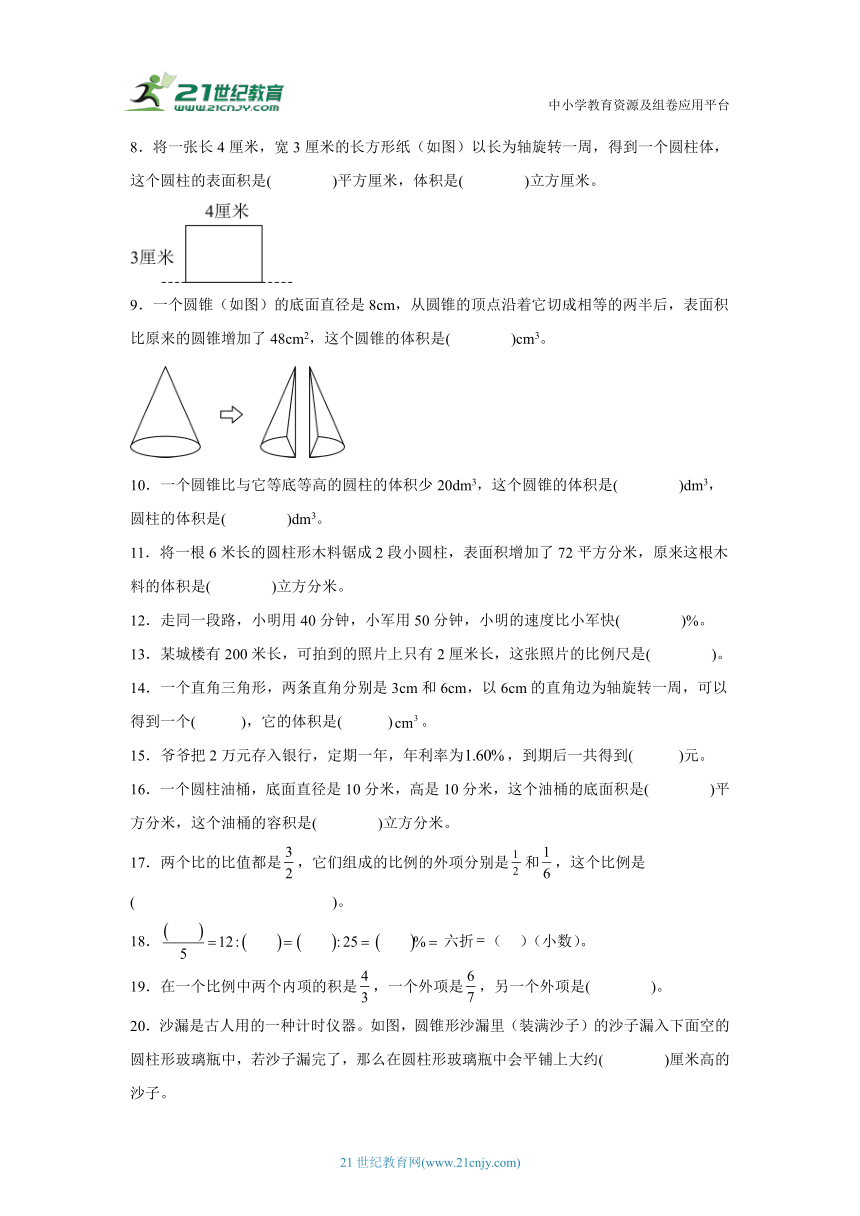
8.将一张长4厘米,宽3厘米的长方形纸(如图)以长为轴旋转一周,得到一个圆柱体,这个圆柱的表面积是( )平方厘米,体积是( )立方厘米。
9.一个圆锥(如图)的底面直径是8cm,从圆锥的顶点沿着它切成相等的两半后,表面积比原来的圆锥增加了48cm2,这个圆锥的体积是( )cm3。
10.一个圆锥比与它等底等高的圆柱的体积少20dm3,这个圆锥的体积是( )dm3,圆柱的体积是( )dm3。
11.将一根6米长的圆柱形木料锯成2段小圆柱,表面积增加了72平方分米,原来这根木料的体积是( )立方分米。
12.走同一段路,小明用40分钟,小军用50分钟,小明的速度比小军快( )%。
13.某城楼有200米长,可拍到的照片上只有2厘米长,这张照片的比例尺是( )。
14.一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个( ),它的体积是( )。
15.爷爷把2万元存入银行,定期一年,年利率为,到期后一共得到( )元。
16.一个圆柱油桶,底面直径是10分米,高是10分米,这个油桶的底面积是( )平方分米,这个油桶的容积是( )立方分米。
17.两个比的比值都是,它们组成的比例的外项分别是和,这个比例是( )。
18.六折( )(小数)。
19.在一个比例中两个内项的积是,一个外项是,另一个外项是( )。
20.沙漏是古人用的一种计时仪器。如图,圆锥形沙漏里(装满沙子)的沙子漏入下面空的圆柱形玻璃瓶中,若沙子漏完了,那么在圆柱形玻璃瓶中会平铺上大约( )厘米高的沙子。
21.一个圆锥的底面周长是62.8厘米,高是6厘米,它的体积是( )立方厘米。
22.甲数是乙数的20%,甲数与乙数的比是( ),乙数与甲、乙两数之和的比是( )。
23.两名工程师分别对同一个零件按照20∶1和30∶1的比例尺放大,结果图纸上两个零件的长度差是8厘米,那么这个零件的实际长度是( )厘米。
24.如图是小明哥哥在探究电流和电阻的关系时绘制的“电流——电阻”图像。由图象可知,可以看出电压一定时,电流和电阻成( )比例,理由是( )。
25.某小学举行数学竞赛,共10道题,每做对一道题得10分,每做错一道扣2分。乐乐得了64分。那么他做错了( )道题。
26.为缓解交通拥挤情况,某道路由原来的4车道变成了6车道(每条道的宽度不变),路面拓宽了( )%。
27.华为Mate60发售后,销量遥遥领先。其中使用的华为新麒麟芯片突破5纳米(1纳米=0.000001毫米)制程工艺。如果将5纳米的芯片画在图纸上,量的其长度为5毫米,这幅图的比例尺是( )。
28.在描述数据时,不仅能表示数量的多少,而且更能表示数量增减变化情况的是 统计图。
29.如图所示,把底面直径是8厘米,高是20厘米的圆柱切成若干等份,拼成一个近似的长方体。这个近似长方体的表面积是 平方厘米,体积是 立方厘米。
30.在比例尺为地图上,量得甲、乙两城的距离为2.5厘米。一辆汽车以每小时75千米的速度从甲城开往乙城, 小时可以到达;根据图中的线段比例尺写出数值比例尺是 。
31.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国存在最早的有系统的数学典籍,其中记载:有求“困盖”的术,“置如其周,令相乘也,又以高乘之,三十六成一”。意思是在求圆锥体积的时候,用圆锥底面周长乘周长再乘高,最后除以36,这种方法与现在的计算方法是一致的,只不过取π的近似值为3,如果一个圆锥的底面周长是12厘米,高是9厘米,那么请你用古人的方法和现在的方法分别计算后进行验证。
古人的方法: 。
现在的方法: 。
32.琪琪在书中了解到:宽与长的比值为0.618的长方形被称为“黄金长方形”。她画了一个长10cm、宽6.18cm的“黄金长方形”,若把这个长方形的长延长到15cm,使延长后的长方形仍为“黄金长方形”,那么宽应该延长到( )cm。
33.如图,一个圆柱形木料的底面积是10平方分米,高是6分米,把它削成顶点相对的两圆锥形体,那么削去部分的体积是 立方分米。
34.如图,小亮用小棒搭房子,他搭1间房子用了5根小棒,搭2间房子用了9根小棒,搭3间房子用了13根小棒……照这样的方式搭,用21根小棒能搭( )间房子;搭n间房子要用( )根小棒。
35.一个圆柱形的物品包装盒,将它的侧面沿虚线剪开,得到一个平行四边形(如图)。
(1)它的侧面积是( )平方厘米。
(2)这个包装盒最多能容纳( )立方厘米的物体。
36.一个晒盐场用100克海水可以晒出4克盐,照这样计算,要晒出8吨盐,需要( )吨海水。
37.小明家2025年2月份比3月份节约用水40%,2月份用水是3月份的( )%。
38.立竿见影。同一时间、同一地点,竿高和影长成( )比例。如果一棵小树的高度是1.2米,影长是0.6米,同一时间、同一地点,测得一棵大树的影长是4.5米,那么这棵大树的高度是( )米。
39.《九章算术》中记载的圆柱体积计算方法是“周自相乘,以高乘之,十二而一”也就是底面周长的平方乘高。再除以12(π取近似值3),如果一个圆柱的底面周长是4π分米,高是6分米,按照古人的方法计算出的圆柱的体积是( )立方分米。友情提示:。
40.《山东省中小学校园园林绿化管理办法》中规定:新建学校绿地率不得低于35%,绿化覆盖率应该在50%以上。某小学的占地面积约30000平方米,要想绿地率达标,至少需要( )平方米的绿地。
41.在开展“读书周”活动中,东东借了一本《童话书》阅读。第一天看了45页,第二天看了全书的25%,第二天看的页数比第一天多20%。这本书共有( )页。
42.房间里有4条腿的椅子和3条腿的凳子共18个,若椅子腿和凳子腿共68条,那么椅子有( )个。
43.潍坊科技市场搞促销活动,所有商品八五折出售。小明买一台电脑花了a元,这台电脑原价( )元。
44.儿童手表里的一种精密电子元件的实际长度是0.3毫米,画在图纸上是3厘米,这幅平面图的比例尺是( )。
45.一个圆柱和圆锥的底面半径和高分别相等,已知圆锥体积比圆柱的体积少16立方米,圆柱的体积是( )立方米,圆锥的体积比圆柱的体积少( )(填分数)。
46.已知银行的年利率是3.25%,王奶奶将50000元存入银行,存三年定期。三年后,王奶奶可以拿到利息多少元?只列式不计算( )。
47.
小军沿着直尺的方向将橡皮筋拉紧(如图),如果点A的位置固定不变,沿原来的方向将橡皮筋拉长,使点C的位置在21cm处,此时点B的位置在( )cm处。
48.一瓶盐水,盐和水的质量比是1∶24,如果再加入75克水,这时盐和水的质量比是1∶27,那么原来瓶内盐水重( )克。现有含盐率30%的盐水300克,要把它变成含盐率20%的盐水需要加水( )克。
49.张叔叔运送了250件瓷器,规定完整运一个到目的地可以得到运送费20元,损坏一个赔偿100元,运完这批瓷器张叔叔共得到运费4160元,张叔叔在运输过程中,完整运送了( )件瓷器,损坏了( )件瓷器。
50.天舟六号货运飞船于2023年5月10日21时22分成功发射,整船的载重能力提高到7.4吨, ,天舟五号货运飞船的载重能力是多少吨?如果列式为7.4÷(1+7%),那么应补充的信息是( )。
51.牛牛家养了鸡和兔子共8只,共有20条腿,鸡、兔各有几只?
先画8个圆圈代表8只动物,每只动物画两条腿,代表8只鸡。这样有2×8=( )条腿,还差20-( )=( )条腿。一只兔子比一只鸡多2条腿,再在上图中给每只兔子添上两条腿。可知鸡有( )只,兔子有( )只。
52.妈妈购买了30000元三年期国债,年利率3.35%。到期后妈妈一共能取出多少钱?解决“到期后妈妈一共能取出多少钱?”这个问题的正确列式是( )。
53.乒乓球馆里面有40人,同时在14张乒乓球台进行“1人对1人”的单打和“2人对2人”的双打比赛。单打比赛的共有( )人。
54.CPU(中央处理器)是一台计算机的运算核心和控制核心,相当于计算机的心脏。将一个长30mm的CPU零件画在图纸上,长为12cm,这张图纸的比例尺是( )。
55.一件外套标价500元,商场开展“每满200元减50元”的优惠促销活动,现在买这件外套实际花( )元,相当于打( )折出售。
56.一种长为2.5毫米的仪器零件,画在图纸上的长度是10厘米,这幅图纸的比例尺是( ),是( )(选填“缩小”或“放大”)比例尺。
57.乐乐把一块底面半径2厘米、高15厘米的圆锥形橡皮泥,捏成一个底面积与圆锥底面积相等的圆柱,圆柱的高是( ),体积是( )。
58.一幅地图,图上2厘米代表实际距离30千米。若实际距离是150千米,则图上距离是( )厘米。
59.一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要( )平方米的钢化玻璃。
60.圆柱形粮囤(如图),从里面量得底面半径是1m,高是2m,它的容积是( )。
61.六一儿童节期间一家超市所有儿童学习用品都优惠30%,也就是打( )折出售;其中一盒彩笔原价是20元,现价是( )元。
62.十七世纪,著名数学家莱布尼茨认为比号与除号有一种亲缘关系,把“÷”的小横线去掉,于是就成了“∶”现在的样子,那么5÷9=30÷54就可以改写成比例( );4×5=2×10可以改写成比例( )。
63.李老师将30000元存入银行,定期3年,如果年利率3.20%,到期后可得到利息( )元。
64.某地一个龙虾店铺使用“八两秤”被处罚。事件中消费者将500g的标准砝码放入到电子秤上,显示的克数却是625,这说明实际克数只是显示克数的( )%,如果该秤显示的克数是500,那么实际只有( )g。
65.“双十一”购物节来了,网上的商品迎来大减价,聪聪喜欢的一款耳机以原价的八五折出售,可以把( )看作单位“1”,现价比原价降低了( )%。
66.接种流感疫苗可以有效预防流感病毒感染。如果要统计上个月我市每周接种人数的多少情况,应选用( )统计图;如果要反应每周接种疫苗的人数增减变化情况,应选用( )统计图;如果要反映上个月我市各县区接种人数与我市接种总人数之间的关系,应选用( )统计图。
67.果园里桃树和梨树的棵数比是7∶8,桃树棵数是梨树棵数的( );桃树棵数比梨树棵数少( )%;梨树棵数比桃树棵数多( );梨树棵数占两种树总棵数的( )。
68.将3个完全相同的小圆柱,拼成一个高是30厘米的大圆柱,表面积减少了50平方厘米,原来每个小圆柱的体积是( )立方厘米。
69.王青把压岁钱4000元存入银行,定期5年,到期后王青取回4720元,该银行五年期的年利率是( )%。
70.学校自来水管的直径是2厘米,水管内水的流速是每秒10厘米,阳阳洗完手忘记关水龙头,3分钟后小欣发现并关掉了水龙头,共浪费了( )升水。
71.一个高是8cm的圆柱,如果把它的高截短3cm,那么它的表面积将减少94.2cm2,原来这个圆柱的体积是( )。
72.把一个圆柱形木料削成最大的圆锥,削去的体积是30立方厘米,圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
73.一个圆柱的侧面沿高展开后得到一个边长是15.7分米的正方形,原来圆柱的底面半径是( )分米。
74.把一个高6厘米的圆柱平均分成3段,变成了3个完全相同的小圆柱,这时表面积比原来增加了50.24平方厘米,那么原来圆柱的体积是( )。
75.一个圆柱的高是4厘米,沿直径垂直切开后,切面是一个正方形,这个圆柱的体积是( )立方厘米。
76.一个圆锥和一个圆柱的底面积相等。已知圆锥与圆柱的体积的比是1∶6,圆锥的高是8.4厘米,圆柱的高是( )厘米。
77.一个圆柱和一个圆锥等底等高,体积相差7.36立方米,圆柱的体积是( )立方米,圆锥的体积是( )立方米。
78.把一根圆柱形木料截成3段小圆木,表面积增加了314平方分米;若沿底面直径平均分成两个半圆柱体,表面积增加300平方分米,木料原来的体积是( )立方米。
79.一个圆柱形橡皮泥的高减少2厘米,底面积不变,表面积减少了12.56平方厘米,则这个圆柱形橡皮泥的底面周长是( )厘米,体积减少了( )立方厘米。
80.南山湖音乐喷泉是由48个内直径为2厘米的出水管围成的一个圆形。打开音乐喷泉时,水喷涌的速度是5米/秒,如果不实行水循环系统,那么一分钟会浪费( )吨水。(每立方米水的质量是1吨)
81.一个圆柱的底面半径和高都扩大到原来的3倍,底面周长扩大到原来的( )倍,底面积扩大到原来的( )倍,侧面积扩大到原来的( )倍,体积扩大到原来的( )倍。
82.在一个比例中,两个内项都是质数,且乘积是6,其中一个外项0.4,这个比例可以写成( )。
83.如果y=8x,那么x和y成( )比例;如果,那么x和y成( )比例。(x、y均不为0)
84.(1)图中甲、乙两个正方形的边长之比是( ),周长之比是( ),这两个比( )组成比例(填“能”或“不能”)。
(2)甲、乙两个正方形的面积之比是( ),这个比和边长之比( )组成比例(填“能”或“不能”)。
85.运输队运送一批物资,货车的载质量和所需货车的数量如下表。
货车的载质量(吨) 2.5 4 6 10
所需货车的数量(辆) 48 30 20 12
(1)货车的载质量与所需货车的数量成( )比例。
(2)如果改用每节车厢载质量为60吨的火车运输,需要( )节这样的车厢。
86.六年级同学排队做广播操,每行人数和排成的行数成( )比例;圆锥的底面半径一定,圆锥的体积和高成( )比例。
87.下面每题中的两个量,成正比例的有 ,成反比例的有 ,既不成正比例也不成反比例的有 。(填序号)
①汽车每千米耗油量一定,所行的路程和耗油总量。
②圆锥体的体积一定,它的底面积和高。
③出油率一定,花生油的质量和花生的质量
④优优读一本书,已读的页数与未读的页数。
⑤正方形的面积和边长。
⑥把一根绳子剪成同样长的小段,每段的长度和剪成的段数。
88.下面每题中的两种量是否成比例?如果成,成正比例还是反比例?在下面写一写。
(1)乒乓球总个数一定,每盒装的个数和需要的盒数。( )
(2)全班人数一定,男生人数和女生人数。( )
(3)每小时织布的米数一定,织布的总米数和时间。( )
(4)长方形的周长一定,长方形的长和宽。( )
89.据报道:目前5G以更快的速度、更稳定的连接与更大的容量,正在融入中原大地千行百业。用4G下载一部电影要5分钟,用5G下载时间是4G的1%,只需( )秒。
90.某种子站做种子发芽实验,结果发芽的48粒,没发芽的2粒,这批种子的发芽率是( )。照这样计算,要想保证有720粒种子发芽,至少要种( )粒。
91.营养学家研究提出:一个儿童每天需要90克的蛋白质。已知每100克鸡蛋中,含蛋白质14克,每100克面粉中含蛋白质10.1克,淘气的早餐吃了50克鸡蛋和100克面条,这顿饭淘气一共摄入蛋白质( )克,大约占一天所需蛋白质总量的( )%。
92.“妇女节”期间游乐园门票八五折优惠,现价是原价的( )%,今年的玉米产量比去年增产一成五,今年产量是去年的( )%。
93.一袋面粉,用去10千克,还剩15千克,用去这袋面粉的( )%,还剩这袋面粉的( )%,剩下的比用去的多( )%,用去的比剩下的少( )%。
94.北京冬奥会的成功举办,让我国冰上运动项目得到快速发展。学校组织滑冰比赛,在相同的比赛场地,莉莉滑完全场用了40秒,张华用了50秒,张华滑完全场所用的时间比莉莉多( )%。
95.15÷( )=0.75==30∶( )=( )%=( )(成数)。
96.“儿童节”期间游乐园门票八五折优惠,现价是原价的( )%,儿童文具店所有学习用品一律打九折出售,节省( )%。
97.将5000元人民币存入银行,整存整取两年,年利率是2.75%。到期后共可取回( )元。
98.国家鼓励二胎生育后,2023年恰逢一年级新生入学高峰年,某市2022年约有8万名一年级新生入学,2023年约有12万名新生入学,一年级新生入学增长率约 %。
99.王老师花43元,买了钢笔和圆珠笔共10支。圆珠笔每支3.5元,钢笔每支7.5元,买了 支圆珠笔。
100.用底面半径是6厘米,高是12厘米的空心圆锥和空心圆柱各一个,组成竖放的容器(如下图)。在这个容器内装入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2厘米。若将这个容器上面封住并倒立,细沙的高度是( )厘米。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.502.4
【分析】根据题意可知,求滚动一周能刷的面积,就是求圆柱的侧面积,根据圆柱侧面=π×直径×高,代入数据,即可解答。
【解析】3.14×8×20
=25.12×20
=502.4(平方厘米)
滚筒滚动一周能刷漆的面积是502.4平方厘米。
2.6 4
【分析】假设全是2人脚踏车,那么10辆车可坐人数为10×2=20人,比实际的26人少26-20=6人;每把一辆3人脚踏车看成2人脚踏车,就少算3-2=1人,所以3人脚踏车数量为6÷1=6辆;2人脚踏车数量为10-6=4辆。
【解析】2×10=20(人)
26-20=6(人)
6÷(3-2)
=6÷1
=6(辆)
10-6=4(辆)
即,3人脚踏车有6辆;2人脚踏车有4辆。
3.11
【分析】从图中可知,圆柱和圆锥的底面积相等,原来圆柱内水的高度为(23-18)cm;原来圆锥内水的高度为18cm;容器倒置后,圆锥内的水流入圆柱内,根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍,据此求出原来圆锥内的水流入圆柱内的高度为(18÷3)cm,再加上原来圆柱内水的高度,即是容器倒置后的水面高度。
【解析】原来圆柱内水的高度:23-18=5(cm)
原来圆锥内水流入圆柱后的高度:18÷3=6(cm)
5+6=11(cm)
现将容器倒置,此时,水面的高度为11cm。
4.2090
【分析】由题意知:本息=本金×年利率×时间+本金,由此将数据代入即可求得捐款钱数。
【解析】2000×1.5%×3+2000
=90+2000
=2090(元)
则她一共捐了2090元。
5.9∶5=y∶x
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。据此解答。
【解析】根据式子9x=5y(x、y均不为0),写出一个比例为9∶5=y∶x。
(答案不唯一)
6.8.4 1∶1000000/
【分析】已知一幅地图的比例尺和从北京到广州的图上距离,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出两地的实际距离。
线段比例尺表示图上1厘米相当于实际距离10千米,根据“比例尺=图上距离∶实际距离” 以及进率“1千米=100000厘米”,把线段比例尺改成数值比例尺。
【解析】4.2÷
=4.2×200000
=840000(厘米)
840000厘米=8.4千米
1厘米∶10千米
=1厘米∶(10×100000)厘米
=1∶1000000
填空如下:
在一幅比例尺是1∶200000的地图上,量得北京到广州的距离是4.2厘米,两地的实际距离是(8.4)千米。 ,把左边的线段比例尺改成数值比例尺是(1∶1000000)。
7.37.68 94.2 56.52
【分析】已知一个圆柱的底面半径是3分米,高是2分米,根据圆柱的侧面积公式计算出圆柱的侧面积;然后根据圆的面积公式计算出圆柱的底面积,因为圆柱有两个底面,所以底面积要乘2,根据圆柱的表面积公式计算出圆柱的表面积;最后根据圆柱的体积公式计算出圆柱的体积。
【解析】①2×3.14×3×2
=6.28×3×2
=18.84×2
=37.68(平方分米)
所以该圆柱的侧面积是37.68平方分米;
②3.14×32
=3.14×9
=28.26(平方分米)
37.68+28.26×2
=37.68+56.52
=94.2(平方分米)
所以该圆柱的表面积是94.2平方分米;
③3.14×32×2
=3.14×9×2
=28.26×2
=56.52(立方分米)
所以该圆柱的体积是56.52立方分米。
8.131.88 113.04
【分析】根据题意,把一个长方形纸以长为轴旋转一周,得到一个圆柱体,那么这个圆柱的高等于长方形的长,圆柱的底面半径等于长方形的宽;
根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,求出圆柱的表面积;
根据圆柱的体积公式V=πr2h,代入数据计算,求出圆柱的体积。
【解析】2×3.14×3×4+3.14×32×2
=2×3.14×3×4+3.14×9×2
=75.36+56.52
=131.88(平方厘米)
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
这个圆柱的表面积是131.88平方厘米,体积是113.04立方厘米。
9.100.48
【分析】根据题意,把一个圆锥从它的顶点沿底面直径切成相等的两半后,表面积比原来圆锥的表面积增加了2个切面的面积,切面是一个以圆锥的底面直径为底,以圆锥的高为高的三角形;
先用增加的表面积除以2,求出一个切面的面积;再根据三角形的高=面积×2÷底,求出圆锥的高;
再根据圆锥的体积公式V=πr2h,代入数据计算,求出这个圆锥的体积。
【解析】一个切面的面积:48÷2=24(cm2)
圆锥的高:24×2÷8=6(cm)
圆锥的体积:
×3.14×(8÷2)2×6
=×3.14×42×6
=×3.14×16×6
=100.48(cm3)
这个圆锥的体积是100.48cm3。
10.10 30
【分析】当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍;把圆锥的体积看作1份,圆柱的体积看作3份,相差(3-1)份;
用等底等高的圆锥与圆柱的体积差除以份数差,求出一份数,即圆锥的体积;再用圆锥的体积乘3,求出圆柱的体积。
【解析】圆锥的体积:
20÷(3-1)
=20÷2
=10(dm3)
圆柱的体积:
10×3=30(dm3)
这个圆锥的体积是10dm3,圆柱的体积是30dm3。
11.2160
【分析】根据题意,把一根圆柱形木料锯成2段小圆柱,那么增加的表面积是圆柱的2个底面圆的面积;先用增加的表面积除以2,求出圆柱的底面积;再根据圆柱的体积V=Sh,求出原来这根木料的体积。注意单位的换算:1米=10分米。
【解析】6米=60分米
72÷2=36(平方分米)
36×60=2160(立方分米)
原来这根木料的体积是2160立方分米。
12.25
【分析】将路程看作单位“1”,时间分之一可以看作速度,将小军速度看作单位“1”,小明与小军的速度差÷小军速度=小明的速度比小军快百分之几。
【解析】(-)÷
=×50
=0.25
=25%
小明的速度比小军快25%。
13.1∶10000
【分析】图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可。
【解析】2厘米∶200米=2厘米∶20000厘米=(2÷2)∶(20000÷2)=1∶10000
这张照片的比例尺是1∶10000。
14.圆锥 56.52
【分析】把一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个底面半径是3cm,高是6cm的圆锥,再根据圆锥的体积公式,代入数据计算即可得解。
【解析】
(cm3)
一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个圆锥,它的体积是56.52。
15.20320
【分析】已知本金是2万元,定期一年,利率为1.60%,根据利息的计算公式“利息=本金×利率×时间”算出利息,再加上本金,就可得到到期后一共得到的钱数,需要统一单位,2万元=20000元。
【解析】2万元=20000元
20000×1.60%×1
=20000×0.016×1
=320(元)
20000+320=20320(元)
所以到期后一共得到20320元。
16.78.5 785
【分析】圆柱的底面积=圆周率×底面半径的平方,根据圆柱体积=底面积×高,求出容积。
【解析】3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
78.5×10=785(立方分米)
这个油桶的底面积是78.5平方分米,这个油桶的容积是785立方分米。
17./
【分析】在两个外项中要先确定一个是第一个比的前项,另一个则是第二个比的后项,再根据比值求出两个比的后项和前项,比的后项等于比的前项除以比值,比的前项等于比值乘比的后项,即可得出答案。
【解析】当是第一个比的前项时,则是第二个比的后项。
这个比例是。
或当是第一个比的前项时,则是第二个比的后项。
这个比例是。
两个比的比值都是,它们组成的比例的外项分别是和,这个比例是(或)。
18.3;20;15;60;0.6
【分析】“六折”表示十分之六,写成分数是,约分后是;
分数可以写成比的形式3∶5,前项3变成12,相当于前项乘4,根据比的基本性质“比的前项和后项同时乘或除以一个相同的数(0除外)比值不变”,后项5也要乘4;
对于3∶5,后项5变为25,相当于后项乘5,根据比的基本性质前项3也要乘5;
“六折”也可以表示百分之六十,写成百分数就是60%;
将60%化为小数,去掉百分号,小数点向左移动两位。
【解析】==;
5×4=20;
3×5=15;
百分之六十写成百分数是60%;
60%=0.6。
所以=12∶20=15∶25=60%=六折=0.6。
19./
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
已知一个比例的两个内项的积是,根据比例的基本性质,那么这个比例的两个外项的积也是;用两个外项的积除以已知的一个外项,即可求出另一个外项。
【解析】÷
=×
=
另一个外项是。
20.4
【分析】先求出圆锥形沙漏里装的沙子体积,用公式:,当沙子漏到圆柱形玻璃瓶中时,圆柱形玻璃瓶里沙子的体积不变,用沙子的体积÷圆柱形玻璃瓶的底面积=沙子的高度,据此列式解答。
【解析】
(厘米)
故在圆柱形玻璃瓶中会平铺上大约4厘米高的沙子。
21.628
【分析】根据圆的周长=2r,用圆锥的底面周长除以,再除以2求出圆锥的底面半径,再根据圆锥的体积=h求出圆锥的体积即可。
【解析】62.8÷3.14÷2
=20÷2
=10(厘米)
×3.14××6
=3.14×100×2
=314×2
=628(立方厘米)
所以它的体积是628立方厘米。
22.1∶5 5∶6
【分析】假设乙数是100,根据求一个数的百分之几是多少,用乘法,则甲数是100×20%,据此求出甲数,再用甲数比乙数,再根据比的性质化简成最简比;用甲数加上乙数,求出甲、乙两数的和,用乙数比甲、乙两数之和,再根据比的性质化简成最简比,据此解答第二空。
【解析】假设乙数是100。
100×20%=20
20∶100
=(20÷20)∶(100÷20)
=1∶5
20+100=120
100∶120
=(100÷20)∶(120÷20)
=5∶6
所以甲数与乙数的比是1∶5,乙数与甲、乙两数之和的比是5∶6。
23.0.8/
【分析】由题可知,第一幅图是原零件的20倍,第二幅图是原零件的30倍,相差了原零件的10倍,相差8厘米,即可算出1倍是0.8厘米,从而计算得出答案。
【解析】8÷(30-20)
=8÷10
=0.8(厘米)
所以这个零件实际长度是0.8厘米。
24.反 电流×电阻=电压(一定)
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【解析】0.1×30=0.2×15=0.3×10=0.6×5=…=3(一定)
乘积一定,那么电流和电阻成反比例。
由图象可知,可以看出电压一定时,电流和电阻成反比例,理由是电流×电阻=电压(一定)。
25.3
【分析】分析题目,假设乐乐10道题全做对了,则他应得10×10=100(分),而实际得了64分,这是因为他每做错一题,不仅得不到10分,还要扣2分,就是做错一题要少得10+2=12(分),据此用总分之差除以(10+2)即可求出做错的题数。
【解析】假设乐乐10道题都做对了。
(10×10-64)÷(10+2)
=(100-64)÷12
=36÷12
=3(道)
某小学举行数学竞赛,共10道题,每做对一道题得10分,每做错一道扣2分。乐乐得了64分。那么他做错了3道题。
26.50
【分析】明确原来和现在的车道数:题目中直接给出原来道路是4车道,现在变为6车道。计算车道增加量:用现在车道数减去原来车道数,得到增加的车道数,即6-4=2车道。计算拓宽的百分比:求路面拓宽的百分比,就是求增加的车道数占原来车道数的百分比。根据求一个数是另一个数百分之几的方法,用增加的车道数除以原来的车道数再乘以100% 。
【解析】(6-4)÷4×100%
=2÷4×100%
=50%
路面拓宽了50%。
27.1000000∶1
【分析】已知将5纳米的芯片画在图纸上,量的其长度为5毫米,根据“比例尺=图上距离∶实际距离”,以及进率“1纳米=0.000001毫米”,据此求出这幅图的比例尺。
【解析】5毫米∶5纳米
=5毫米∶(5×0.000001)毫米
=5∶0.000005
=(5÷0.000005)∶(0.000005÷0.000005)
=1000000∶1
这幅图的比例尺是1000000∶1。
28.折线
【分析】理解三种统计图各自的特点,并能根据不同问题选择适当的统计图描述数据。
(1)条形统计图的特点:条形统计图能清楚地表示出每个项目的具体数量。
(2)折线统计图的特点:折线统计图不仅能表示每个项目的具体数量还能清楚地反映事物的增减变化情况。
(3)扇形统计图的特点:扇形统计图能清楚地表示出各部分在总体中所占的百分比。
【解析】据分析可得:在描述数据时,不仅能表示数量的多少,而且更能表示数量增减变化情况的是折线统计图。
29.762.88 1004.8
【分析】把一个圆柱切拼成一个近似长方体,长方体的体积等于圆柱的体积,长方体的长等于圆柱的底面周长的一半即πd÷2,长方体的宽等于圆柱的底面半径r,长方体的高等于圆柱的高h;
根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据计算,求出这个近似长方体的表面积和体积。
【解析】长方体的长:3.14×8÷2=12.56(厘米)
长方体的宽:8÷2=4(厘米)
长方体的表面积:
(12.56×4+12.56×20+4×20)×2
=(50.24+251.2+80)×2
=381.44×2
=762.88(平方厘米)
长方体的体积:
12.56×4×20
=50.24×20
=1004.8(立方厘米)
这个近似长方体的表面积是762.88平方厘米,体积是1004.8立方厘米。
30.2 1∶6000000/
【分析】线段比例尺的意思是,图上1厘米相当于实际距离60千米,图上甲、乙两城的距离为2.5厘米,那么实际距离是(2.5×60)千米;
已知一辆汽车以每小时75千米的速度从甲城开出,根据“时间=路程÷速度”求出汽车到达乙城的所需的时间;
根据“比例尺=图上距离∶实际距离”以及进率“1千米=100000厘米”,将线段比例尺改写成数值比例尺。
【解析】2.5×60÷75
=150÷75
=2(小时)
1厘米∶60千米
=1厘米∶(60×100000)厘米
=1∶6000000
一辆汽车以每小时75千米的速度从甲城开往乙城,(2)小时可以到达;根据图中的线段比例尺写出数值比例尺是(1∶6000000)。
31.12×12×9÷36=36(立方厘米) 12÷3÷2=2(厘米);3×22×9×=36(立方厘米)
【分析】古人的方法:用圆锥的底面周长×底面周长,再乘圆锥的高,再除以36,据此用古人方法计算出圆锥的体积。
现在的方法:根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆锥底面积的周长,再根据圆锥的体积公式:体积=底面积×高×,据此用现在方法,求出圆锥的体积。
【解析】古人的方法:
12×12×9÷36
=144×9÷36
=1296÷36
=36(立方厘米)
现在的方法:
12÷3÷2
=4÷2
=2(厘米)
3×22×9×
=3×4×9×
=12×9×
=108×
=36(立方厘米)
36=36
即,圆锥的体积是36立方厘米;不管用古人的方法还是现在的方法计算的结果都是一样的。
32.9.27
【分析】根据题意,宽与长的比值为0.618的长方形被称为“黄金长方形”,即宽∶长=0.618(一定),比值一定,那么长与宽成正比例关系,据此列出正比例方程,并求解。
【解析】解:设宽应该延长到cm。
10∶6.18=15∶
10=6.18×15
10=92.7
=92.7÷10
=9.27
宽应该延长到9.27cm。
33.40
【分析】因为将圆柱形木料削成两个的圆锥,所以两个圆锥的高之和等于圆柱的高,根据圆柱的体积=底面积×高,圆锥的体积=底面积×高×,分别求出圆柱的体积和两个圆锥的体积之和;再用圆柱的体积减去两个圆锥体的体积之和,计算即可求出削去部分的体积。
【解析】10×6-10×6×
=60-60×
=60-20
=40(立方分米)
所以削去部分的体积是40立方分米。
34.5 (4n+1)/(1+4n)
【分析】搭1个房子用5根小棒,搭2个房子用(5+4)根小棒,搭3个房子用(5+4+4)根小棒,也就是每多搭一个房子,需要用4根小棒,据此找到小棒根数与房子个数之间的规律,再根据规律求出21根小棒能搭几间房子,据此解答。
【解析】1个房子:5根
2个房子:5+4=9(根)
3个房子:
5+4+4
=9+4
=13(根)
n个房子:5+(n-1)×4
=5+4n-4
=(4n+1)根
当有21根小棒时,
(21-1)÷4
=20÷4
=5(间)
故用21根小棒能搭5间房子;搭n间房子要用(4n+1)根小棒。
35.(1)150.72
(2)226.08
【分析】(1)圆柱侧面沿虚线剪开得到平行四边形,圆柱侧面积就等于这个平行四边形面积,“平行四边形面积=底×高”,在此图中,平行四边形的底恰好是圆柱底面的周长18.84厘米,高为8厘米,所以用底18.84厘米乘高8厘米就能得出侧面积;
(2)要计算圆柱包装盒容积,需先求底面半径,已知底面周长18.84厘米,根据圆周长公式C=2πr,通过变形公式r=C÷π÷2可算出半径r ,得到半径后,再依据圆柱体积公式V=πr2h,将半径r和高h的值代入公式就能算出体积,也就是包装盒最多能容纳物体的体积。
【解析】(1)18.84×8=150.72(平方厘米)
所以它的侧面积是150.72平方厘米。
(2))18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×8
=3.14×9×8
=28.26×8
=226.08(立方厘米)
所以这个包装盒最多能容纳226.08立方厘米的物体。
36.200
【分析】本题可先求出海水与盐的比例关系,100克海水可以晒出4克盐,则海水与盐的比例为100÷4=25,即每晒出1克盐需要25克海水;再根据要晒出盐的重量求出所需海水的重量,因为要晒出8吨盐,且每晒出1克盐需要25克海水,所以需要海水8×25=200吨。
【解析】100÷4=25(克)
8吨=8000000克
8000000×25=200000000(克)
200000000克=200(吨)
所以要晒出8吨盐,需要200吨海水。
37.60
【分析】以3月份用水数量为单位“1”,2月份比3月份少40%,即相当于3月份的(1-40%)。据此解答。
【解析】1-40%=60%
2月份用水是3月份的60%。
38.正 9
【分析】同一时间、同一地点,物体的长度和它影子长度的比值一定,所以同一时间、同一地点,竿高和影长成正比例关系,大树的高度∶大树的影长=小树的高度∶小树的影长,据此列出正比例方程,并求解。
【解析】同一时间、同一地点,竿高和影长成正比例。
解:设这棵大树的高度是x米。
x∶4.5=1.2∶0.6
0.6x=4.5×1.2
0.6x=5.4
x=5.4÷0.6
x=9
所以,这棵大树的高度是9米。
39.8
【分析】按照古人的方法,需要先求出底面周长的平方,再乘高,最后除以12来计算圆柱体积。
【解析】×6÷12
=16×6÷12
=96÷12
=8(立方分米)
所以按照古人的方法计算出的圆柱的体积是8立方分米。
40.10500
【分析】根据绿地面积=占地面积×绿地率,代入数据计算即可。
【解析】30000×35%=10500(平方米)
所以至少需要10500平方米的绿地。
41.216
【分析】已知第一天看了45页,第二天看的页数比第一天多20%,把第一天看的页数看作单位“1”,则第二天看的页数是第一天的(1+20%),单位“1”已知,用第一天看的页数乘(1+20%),求出第二天看的页数。
已知第二天看了全书的25%,把这本书的总页数看作单位“1”,单位“1”未知,用第二天看的页数除以25%,即可求出这本书的总页数。
【解析】第二天看了:
45×(1+20%)
=45×(1+0.2)
=45×1.2
=54(页)
总页数:
54÷25%
=54÷0.25
=216(页)
这本书共有216页。
42.14
【分析】设4条腿的椅子有x个,则3条腿的凳子有(18-x)个;x个椅子有4x条腿,3条腿的凳子有3×(18-x)条腿,椅子腿和凳子腿共68条,列方程:4x+3×(18-x)=68,解方程,即可解答。
【解析】解:设4条腿的椅子有x个,则凳子有(18-x)个。
4x+3×(18-x)=68
4x+3×18-3x=68
4x+54-3x=68
x+54=68
x+54-54=68-54
x=14
房间里有4条腿的椅子和3条腿的凳子共18个,若椅子腿和凳子腿共68条,那么椅子有14个。
43.
【分析】八五折出售,就是现价是原价的85%,把原价看作单位“1”,原价×85%=现价,已知一个数的百分之几是多少,求这个数,用除法计算,所以:原价=现价÷折扣,代入数据计算即可。
【解析】八五折=85%
a÷85%=(元)
这台电脑原价元。
44.100∶1
【分析】已知一种精密电子元件的实际长度和图上的长度,根据“比例尺=图上距离∶实际距离”,以及进率“1厘米=10毫米”,求出这幅平面图的比例尺。
【解析】3厘米∶0.3毫米
=(3×10)毫米∶0.3毫米
=30∶0.3
=(30÷0.3)∶(0.3÷0.3)
=100∶1
这幅平面图的比例尺是100∶1。
45.24
【分析】由题可知,圆柱与圆锥底面半径和高分别相等,因此可得圆柱与圆锥是等底等高。在等底等高的情况下,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,那么圆锥体积比圆柱体积少(1-),已知圆锥体积比圆柱的体积少16立方米,根据已知一个数的几分之几是多少,求这个数,用除法计算,即可求出圆柱的体积,据此解答。
【解析】1-=
16÷=16×=24(立方米)
即圆柱的体积是24立方米,圆锥的体积比圆柱的体积少。
46.50000×3.25%×3
【分析】已知本金50000元,年利率是3.25%,存三年定期,根据“利息=本金×利率×存期”,求出到期时可得到的利息。
【解析】50000×3.25%×3
=50000×0.0325×3
=1625×3
=4875(元)
三年后,王奶奶可以拿到利息4875元。
列式为:50000×3.25%×3。
47.14
【分析】用比例解决问题只要比例两边的比统一即可,设此时点B的位置在xcm处,根据点C的位置∶点B的位置=9∶6,列出比例求出x的值即可。
【解析】解:设此时点B的位置在xcm处。
21∶x=9∶6
9x=21×6
9x÷9=126÷9
x=14
此时点B的位置在14cm处。
48.25 150
【分析】第一个空,盐的质量没变,再加入75克水,水增加了(27-24)份,将比的前后项看成份数,加入的水的质量÷对应份数=一份数,一份数×盐的对应份数=盐的质量;
第二个空,盐的质量没变,将原来盐水质量看作单位“1”,原来盐水质量×含盐率=盐的质量,再将含盐率20%的盐水质量看作单位“1”,盐的质量÷含盐率=含盐率20%的盐水质量,含盐率20%的盐水-原来盐水质量=需要加水的质量。
【解析】75÷(27-24)×1
=75÷3×1
=25(克)
300×30%÷20%-300
=300×0.3÷0.2-300
=450-300
=150(克)
一瓶盐水,盐和水的质量比是1∶24,如果再加入75克水,这时盐和水的质量比是1∶27,那么原来瓶内盐水重25克。现有含盐率30%的盐水300克,要把它变成含盐率20%的盐水需要加水150克。
49.243 7
【分析】根据题意,设损坏了件瓷器。已知运送瓷器250件,损坏了件瓷器,则完整运送 (250-)件瓷器,每件可得到运送费20元,根据“单价×数量=总价”可知,完整运送可得到运送费20×(250-)元;如果损坏一个赔偿100元,那么损坏了件瓷器,需赔偿100元;等量关系:完整运送瓷器得到的运送费-损坏瓷器的赔偿费=共得到的运费,据此列出方程,并求解。
【解析】解:设损坏了件瓷器,则完整运送了(250-)件瓷器。
20×(250-)-100=4160
20×250-20-100=4160
5000-(20+100)=4160
5000-120=4160
120=5000-4160
120=840
=840÷120
=7
250-7=243(件)
完整运送了243件瓷器,损坏了7件瓷器。
50.比天舟五号整船的载重能力提高了7%
【分析】如果列式为7.4÷(1+7%),则把天舟五号货运飞船的载重能力看作单位“1”,整船的载重能力提高到7.4吨,比天舟五号货运飞船的载重能力提高了7%,则整船的载重能力是天舟五号货运飞船的(1+7%),单位“1”未知,用整船的载重能力除以(1+7%),即是天舟五号货运飞船的载重能力。
【解析】列式为7.4÷(1+7%),那么应补充的信息是(比天舟五号整船的载重能力提高了7%)。
51.16 16 4 6 2
【分析】假设8只动物全是鸡,每只鸡有两条腿,一共有2×8=16条腿,与实际20条腿相差20-16=4条腿。因为一只兔子比一只鸡多2条腿,用相差的总腿数除以2,求出兔子的只数;再用总只数减去兔子的只数,求出鸡的只数。
【解析】假设8只动物全是鸡,则兔子有:
(20-2×8)÷(4-2)
=(20-16)÷2
=4÷2
=2(只)
鸡有:8-2=6(只)
填空如下:
先画8个圆圈代表8只动物,每只动物画两条腿,代表8只鸡。这样有2×8=(16)条腿,还差20-(16)=(4)条腿。一只兔子比一只鸡多2条腿,再在上图中给每只兔子添上两条腿。可知鸡有(6)只,兔子有(2)只。
52.30000×3.35%×3+30000
【分析】根据“利息=本金×利率×存期”求出到期后可得到的利息,再加上本金,即是到期后一共能取出的钱数。
【解析】30000×3.35%×3+30000
=30000×0.0335×3+30000
=3015+30000
=33015(元)
到期后妈妈一共能取出33015元。
这个问题的正确列式是30000×3.35%×3+30000。
53.16
【分析】假设所有桌都进行单打比赛,应有14×2=28人,而实际上却有40人,少出了40-28=12人;而每张单打桌比双打桌少了4-2=2人,看少的总人数里面有几个2,就有几张双打桌,再用总桌数减去双打桌,即是单打桌的张数;然后用单打桌的张数乘每张单打桌的人数,求出单打比赛的人数。
【解析】假设全是单打桌,则双打桌数有:
(40-14×2)÷(4-2)
=(40-28)÷2
=12÷2
=6(张)
单打桌数:14-6=8(张)
8×2=16(人)
单打比赛的有16人。
54.4∶1
【分析】图上距离与实际距离的比叫作比例尺。先要将单位换算成统一的单位,1厘米=10毫米,高级单位转化为低级单位用乘法,则30毫米=3厘米。再将两个数的比化简成为最简整数比,据此解答即可。
【解析】30毫米=3厘米
12∶3=4∶1
所以,这张图纸的比例尺是4∶1。
55.400 八
【分析】由题意可知,这件外套的价格是200元满50元,先看500元里有几个200元,实际价格需要减去几个50元,几折就表示现价占原价的十分之几,也就是百分之几十,据此解答。
【解析】500÷200=2(个)……100(元)
500-2×50
=500-100
=400(元)
400÷500×100%
=0.8×100%
=80%
80%就是八折。
现在买这件外套实际花400元,相当于打八折出售。
56.40∶1 放大
【分析】比例尺=图上距离∶实际距离,据此求出比例尺,把零件在图纸上放大时,是放大比例尺,据此解答即可。
【解析】比例尺:
10厘米∶2.5毫米
=10厘米∶0.25厘米
=1000∶25
=40∶1
所以这幅图纸的比例尺是40∶1,是放大比例尺。
57.5厘米/5cm 62.8立方厘米/62.8cm3
【分析】根据题意可知,圆锥和圆柱的体积相等,根据“”求出圆锥的体积,再除以圆柱的底面积即可解答。
【解析】
(立方厘米)
=62.8÷12.56
(厘米)
所以圆柱的高是5厘米,体积是62.8立方厘米。
58.10
【分析】先根据比例尺=图上距离∶实际距离,代入数据求出比例尺,再根据图上距离=实际距离×比例尺,即可得解,注意根据1千米=100000厘米,把单位千米转化为厘米。
【解析】30千米=3000000厘米
150千米=15000000厘米
(厘米)
因此,图上距离是10厘米。
59.18.84
【分析】圆柱的侧面积=底面周长×高=πdh,据此代入数据计算即可。
【解析】3.14×2×3
=6.28×3
=18.84(平方米)
则至少需要18.84平方米的钢化玻璃。
60.6.28m3/6.28立方米
【分析】根据圆柱的体积公式,代入数据计算即可得解。
【解析】
(m3)
它的容积是6.28m3。
61.七 14
【分析】把儿童学习用品的原价看作单位“1”,优惠30%,则现价是原价的1-30%=70%,70%就是打七折;打七折,表示现价是原价的70%,根据“求一个数的百分之几是多少,用乘法计算”,用彩笔的原价乘70%即可求出现价。
【解析】1-30%=70%,也就是打七折出售;
20×70%
=20×0.7
=14(元)
则现价是14元。
62.5∶9=30∶54 4∶2=10∶5
【分析】第一个空,直接将“÷”换成“∶”,即可改写成比例;第二个空,根据比例的基本性质,比例的两内项积=两外项积,只要4和5同时在比例的外项或内项,2和10同时在比例的内项或外项即可。
【解析】5÷9=30÷54就可以改写成比例5∶9=30∶54;4×5=2×10可以改写成比例4∶2=10∶5(答案不唯一)。
63.2880
【分析】根据利息=本金×利率×存期,代入数据求出她能取出来的利息。
【解析】由分析可得:
30000×3.20%×3
=960×3
=2880(元)
综上所述:李老师将30000元存入银行,定期3年,如果年利率3.20%,到期后可得到利息2880元。
64.80 400
【分析】用实际克数除以显示的克数,求出实际克数是显示克数的百分之几;再用显示克数乘实际克数占显示克数的百分率,即可求出如果该秤显示的克数是500,那么实际只有多少克。
【解析】500÷625×100%
=0.8×100%
=80%
500×80%=400(g)
实际克数只是显示克数的80%,如果该秤显示的克数是500,那么实际只有400g。
65.原价 15
【分析】一个整体可以用自然数1表示,我们通常把它叫做单位“1”。确定单位“1”,关键是看以谁为标准,谁是标准谁就是单位“1”,题中耳机以原价的八五折出售,是把原价看作单位“1”;打折就是按照折数低价出售商品,几折就是百分之几十,1-折扣=现价比原价降低了百分之几。
【解析】1-85%=15%
“双十一”购物节来了,网上的商品迎来大减价,聪聪喜欢的一款耳机以原价的八五折出售,可以把原价看作单位“1”,现价比原价降低了15%。
66.条形 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解析】如果要统计上个月我市每周接种人数的多少情况,应选用条形统计图;如果要反应每周接种疫苗的人数增减变化情况,应选用折线统计图;如果要反映上个月我市各县区接种人数与我市接种总人数之间的关系,应选用扇形统计图。
67. 12.5
【分析】根据比的意义,把桃树的棵数看作7份,梨树的棵数看作8份,根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用7÷8即可求出桃树棵树是梨树棵数的几分之几;用8÷(7+8)即可求出梨树棵数占两种树总棵数的几分之几;再根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用(8-7)÷8×100%即可求出桃树棵树比梨树棵数少百分之几;根据求一个数比另一个数多几分之几,用相差数除以另一个数,则用(8-7)÷7即可求出梨树棵数比桃树棵数多几分之几。
【解析】把桃树的棵数看作7份,梨树的棵数看作8份,
7÷8=
桃树棵数是梨树棵数的;
(8-7)÷8×100%
=1÷8×100%
=12.5%
桃树棵树比梨树棵数少12.5%。
(8-7)÷7
=1÷7
=
8÷(7+8)
=8÷15
=
梨树棵数占两种树总棵数的。
68.125
【分析】要求每个小圆柱的体积,需要求出这个小圆柱的底面积和高;3个完全相同的小圆柱拼成一个大圆柱时,高是30厘米,由此可知,用30÷3,求出小圆柱的高;表面积减少了50平方厘米,是指4个圆柱的底面的面积和,用50÷4,求出一个圆柱的底面积;再根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【解析】(50÷4)×(30÷3)
=12.5×10
=125(立方厘米)
将3个完全相同的小圆柱,拼成一个高是30厘米的大圆柱,表面积减少了50平方厘米,原来每个小圆柱的体积是125立方厘米。
69.3.6
【分析】用4720-4000,求出利息,再用利息÷本金÷时间×100%,即可求出年利率,即可解答。
【解析】(4720-4000)÷4000÷5×100%
=720÷4000÷5×100%
=0.18÷5×100%
=0.036×100%
=3.6%
王青把压岁钱4000元存入银行,定期5年,到期后王青取回4720元,该银行五年期的年利率是3.6%。
70.5.652
【分析】根据题意可知,水管的直径是2厘米,水管内水的流速是每秒10厘米,相等于底面直径是2厘米,高是10厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,求出高是10厘米的圆柱的体积,1分钟=60秒,把3分钟=180秒;再用高是10厘米的圆柱的体积×180,求出3分钟流出的水的体积,再化成升,即可解答。
【解析】3分钟=180秒
3.14×(2÷2)2×10×180
=3.14×12×10×180
=3.14×1×10×180
=3.14×10×180
=31.4×180
=5652(立方厘米)
5652立方厘米=5.652升
学校自来水管的直径是2厘米,水管内水的流速是每秒10厘米,阳阳洗完手忘记关水龙头,3分钟后小欣发现并关掉了水龙头,共浪费了5.652升水。
71.628cm3/628立方厘米
【分析】减少的表面积是圆柱的侧面积,减少的表面积÷截短的高=圆柱底面周长,圆柱底面半径=底面周长÷圆周率÷2,圆柱体积=底面积×高,据此列式计算。
【解析】94.2÷3=31.4(cm)
31.4÷3.14÷2=5(cm)
3.14×52×8
=3.14×25×8
=628(cm3)
原来这个圆柱的体积是628cm3。
72.45 15
【分析】把一个圆柱形木料削成最大的圆锥,这个圆锥和圆柱等底等高,则圆柱的体积与圆锥的体积比是3∶1,即圆柱的体积是3份,圆锥的体积是这样的1份,相差2份,就是30立方厘米,每一份就是15立方厘米,3份就是圆柱的体积,1份是圆锥的体积。
【解析】30÷(3-1)
=30÷2
=15(立方厘米)
15×3=45(立方厘米)
则圆柱的体积是45立方厘米,,圆锥的体积是15立方厘米。
73.2.5
【分析】根据题意可知,圆柱的侧面沿高展开得到一个边长是15.7分米的正方形,则圆柱的底面周长等于圆柱的高;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,即可解答。
【解析】15.7÷3.14÷2
=5÷2
=2.5(分米)
一个圆柱的侧面沿高展开后得到一个边长是15.7分米的正方形,原来圆柱的底面半径是2.5分米。
74.75.36立方厘米
【分析】根据题意,将圆柱截成3个完全相同的小圆柱,表面积增加了4个底面的面积,这时表面积比原来增加了50.24平方厘米,所以圆柱的底面积为平方厘米,圆柱的体积=底面积×高,据此即可算出原来圆柱的体积。
【解析】(平方厘米)
(立方厘米)
所以原来圆柱的体积是75.36立方厘米。
75.50.24
【分析】根据题意可知,圆柱沿直径垂直切开后是一个正方形,则圆柱的底面直径等于圆柱的高;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【解析】3.14×(4÷2)2×4
=3.14×22×4
=3.14×4×4
=12.56×4
=50.24(立方厘米)
一个圆柱的高是4厘米,沿直径垂直切开后,切面是一个正方形,这个圆柱的体积是50.24立方厘米。
76.16.8
【分析】根据圆柱的体积=底面积×高,可推出高=圆柱的体积÷底面积;根据圆锥的体积=底面积×高÷3,可推出高=圆锥的体积×3÷底面积;把底面积看成S,把圆锥的体积看作1,则圆柱的体积为6,那么圆柱的高为6÷S=,圆锥的高为1×3÷S=3÷S=,圆柱与圆锥高的比为:∶=2∶1,即圆柱的高是圆锥的2倍,圆柱的高为8.4×2=16.8(厘米),据此解答。
【解析】由分析可知:
把底面积看成S,把圆锥的体积看作1份,则圆柱的体积为6份
圆柱的高为:6÷S=
圆锥的高为:1×3÷S
=3÷S
=
圆柱与圆锥高的比为:∶
=∶
=6∶3
=2∶1
8.4×2=16.8(厘米)
所以圆柱的高为16.8厘米。
77.11.04 3.68
【分析】圆柱和圆锥等底等高,可知圆柱的体积是圆锥的体积的3倍,把圆锥的体积看作1份,则圆柱的体积就看作3份,它们的体积就相差了(3-1)份,而体积相差7.36立方米,从而可以求出平均1份是多少,即求出圆锥的体积,再求出圆柱的体积即可。
【解析】7.36÷(3-1)
=7.36÷2
=3.68(立方米)
3.68×3=11.04(立方米)
圆柱的体积是11.04立方米,圆锥的体积是3.68立方米。
78.1.1775
【分析】把一根圆柱形木料截成3段小圆木,表面积增加了314平方分米,那么增加的表面积是4个底面积,用增加的表面积除以4,即可求出圆柱的底面积;然后根据S底=πr2,得出圆柱的底面半径;
若沿底面直径平均分成两个半圆柱体,表面积增加300平方分米,那么增加的表面积是2个以底面直径和高分别为长、宽的长方形,用增加的表面积除以2,求出一个截面的面积,再除以直径,即可求出圆柱的高;
最后根据圆柱的体积公式V=Sh,求出木料原来的体积。注意单位的换算:1立方米=1000立方分米。
【解析】圆柱的底面积:314÷4=78.5(平方分米)
底面半径的平方:78.5÷3.14=25(平方分米)
因为25=5×5,所以圆柱的底面半径是5分米;
圆柱的底面直径:5×2=10(分米)
圆柱的高:
300÷2÷10
=150÷10
=15(分米)
圆柱的体积:
78.5×15=1177.5(立方分米)
1177.5立方分米=1.1775立方米
木料原来的体积是1.1775立方米。
79.6.28 6.28
【分析】从“高减少2厘米,底面积不变”可知,表面积减少了12.56平方厘米,就是侧面积减少了12.56平方厘米。根据侧面积=底面周长×高,可得底面周长=侧面积÷高,用12.56÷2即可求出底面周长,进而可求出底面半径。因为底面积不变,所以体积减少的部分的形状也是圆柱;根据圆柱的体积=底面积×高,代入数据,即可求出减少的体积。据此解答。
【解析】底面周长:12.56÷2=6.28(厘米)
减少的体积:
(6.28÷3.14÷2)2×3.14×2
=12×3.14×2
=1×3.14×2
=6.28(立方厘米)
这个圆柱形橡皮泥的底面周长是6.28厘米,体积减少了6.28立方厘米。
80.4.5216
【分析】先计算出一分钟每个出水管喷出水的体积,利用圆柱的体积=底面积×高;用出水管的底面积乘一分钟喷出水的长度;一分钟喷出水的长度=速度×时间,代入相应数值计算;再用每个出水管喷出水的体积乘48,求出一分钟一共会喷出水的体积,最后用水的体积乘每立方米水的质量,求出水的总质量,据此解答。
【解析】1分=60秒
2厘米=0.02米
3.14×(0.02÷2)2×(5×60)
=3.14×0.012×300
=3.14×0.0001×300
=0.0942(立方米)
48×0.0942=4.5216(立方米)
4.5216×1=4.5216(吨)
因此一分钟会浪费4.5216吨水。
81.3 9 9 27
【分析】设圆柱的底面半径是1,高是1,变化后的底面半径是3,高是3,根据C=2πr,S=πr2,S侧=2πrh,V=πr2h,用变化后的底面周长、底面积、侧面积、体积结果,除以变化前的结果就是扩大的倍数,据此解答。
【解析】设圆柱的底面半径是1,高是1,变化后的底面半径是3,高是3,
底面周长:(2π×3)÷(2π×1)=6π÷2π=3
底面积:(π×32)÷(π×12)=9π÷π=9
侧面积:(2π×3×3)÷(2π×1×1)=18π÷2π=9
体积:(π×32×3)÷(π×12×1)=(π×9×3)÷(π×1×1)=27π÷π=27
因此底面周长扩大到原来的3倍,底面积扩大到原来的9倍,侧面积扩大到原来的9倍,体积扩大到原来的27倍。
82.0.4∶2=3∶15
【分析】根据比例的基本性质:内项积=外项积,内项积是6,其中有一个外项是0.4,即用除法得出另外一个外项是15,内项两个质数相乘,6=2×3,则内项是2和3,写出相应的比例(答案不唯一)。
【解析】6÷0.4=15
6=2×3
这个比例可以写成0.4∶2=3∶15(答案不唯一)
83.正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解析】y=8x,则y∶x=8(一定),x和y成正比例;
x=,则xy=5(一定),x和y成反比例。
如果y=8x,那么x和y乘正比例;如果x=,那么x和y成反比例。
84.2∶3 2∶3 能 4∶9 不能
【分析】(1)两数相除又叫两个数的比,正方形周长=边长×4,据此写出甲、乙两个正方形的边长之比和周长之比,化简,并求出比值,根据表示两个比相等的式子叫比例,确定能否组成比例;
(2)正方形面积=边长×边长,写出甲、乙两个正方形的面积之比,并求出比值,根据比例的意义,确定面积之比和边长之比能否组成比例。
【解析】(1)边长之比:4∶6=(4÷2)∶(6÷2)=2∶3=2÷3=
周长之比:(4×4)∶(6×4)=16∶24=(16÷8)∶(24÷8)=2∶3=
图中甲、乙两个正方形的边长之比是2∶3,周长之比是2∶3,这两个比能组成比例。
(2)面积之比:(4×4)∶(6×6)=16∶36=(16÷4)∶(36÷4)=4∶9=4÷9=
甲、乙两个正方形的面积之比是4∶9,这个比和边长之比不能组成比例。
85.反 2
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(2)根据所成比例,进行解答。
【解析】(1)2.5×48=120
4×30=120
6×20=120
10×12=120
2.5×48=4×30=6×20=10×12=120(一定),所以货车的载质量与所需货车的数量成反比例。
(2)2.5×48÷60
=120÷60
=2(节)
如果改用每节车厢载质量为60吨的火车运输,需要2节这样的车厢。
86.反 正
【分析】由正比例与反比例的意义可知:两个相关联的量,当它们的比值(商)一定时,这两个量成正比例;当它们的乘积一定时,这两个量成反比例。
【解析】六年级同学排队做广播操,每行人数×排成的行数=六年级总人数(一定),所以每行人数和排成的行数成反比例;
圆锥的底面半径一定,即圆锥的底面积一定。根据圆锥的体积公式可知,圆锥的体积÷高=×底面积,圆锥的底面积一定,则圆锥的体积和高成正比例。
87.①③ ②⑥ ④⑤
【分析】第①个,每千米耗油量一定,路程越大,耗油总量越多,耗油总量除以路程,得到每千米耗油量,结果是定值,正比例关系;
第②个,圆锥体的体积一定,它的底面积和高乘积是定值,反比例关系;
第③个,出油率一定,花生油的质量和花生的质量的比值是定值,正比例关系;
第④个,已读的页数与未读的页数的乘积和比值都在变化,不是定值,不存在比例关系;
第⑤个,用正方形的面积S除以边长a,结果是变量,所以不构成正比例,而边长变大,面积变大,更不可能是反比例,所以二者不构成比例关系;
第⑥个,剪成同样长的小段,每段的长度越长,段数就越少,且每段的长度与剪成的段数的乘积是总长,是定值,典型的反比例关系。
【解析】成正比例的有①③,成反比例的有②⑥,既不成正比例也不成反比例的有④⑤。
88.成反比例 不成比例 成正比例 不成比例
【分析】x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
【解析】(1)每盒装的个数×需要的盒数=总个数,乒乓球总个数一定,每盒装的个数和需要的盒数。成反比例
(2)男生人数+女生人数=总人数,全班人数一定,男生人数和女生人数。不成比例
(3)织布总米数÷时间=每小时织布米数,每小时织布的米数一定,织布的总米数和时间。成正比例
(4)长+宽=长方形的周长÷2,长方形的周长一定,长方形的长和宽。不成比例
89.3
【分析】把5分钟看作单位“1”,根据百分数乘法的意义,用5×1%即可求出用5G下载的时间,再把单位换算成秒。
【解析】5×1%=0.05(分钟)
0.05×60=3(秒)
只需3秒。
90.96% 750
【分析】发芽路=发芽种子数÷种子总数×100%,据此求出发芽率;将种子总数看作单位“1”,发芽种子数÷发芽率=种子总数,据此列式计算。
【解析】48÷(48+2)×100%
=48÷50×100%
=0.96×100%
=96%
720÷96%=720÷0.96=750(粒)
这批种子的发芽率是96%。照这样计算,要想保证有720粒种子发芽,至少要种750粒。
91.17.1 19
【分析】由题目可知,每100克鸡蛋中含蛋白质14克,每100克面粉中含蛋白质10.1克,那么50克鸡蛋中含蛋白质的重量就是(14÷2)克,用50克鸡蛋和100克面条中含蛋白质的重量相加即可求出这顿饭淘气一共摄入蛋白质多少克;再用这顿饭淘气一共摄入蛋白质重量除以一个儿童每天需要的蛋白质重量,即可求出大约占一天所需蛋白质总量的百分之几。
【解析】(14÷2)+10.1
=7+10.1
=17.1(克)
17.1÷90×100%
=0.19×100%
=19%
这顿饭淘气一共摄入蛋白质17.1克,大约占一天所需蛋白质总量的19%。
92.85 115
【分析】把原价看作单位“1”,八五折就是现价是原价的85%。一成五就是15%,把去年的玉米的产量看作单位“1”,今年是去年的1+15%,据此解答。
【解析】八五折就是现价是原价的85%。
一成五就是15%。
1+15%=115%
“妇女节”期间游乐园门票八五折优惠,现价是原价的85%,今年的玉米产量比去年增产一成五,今年产量是去年的115%。
93.40 60 50 33.3
【分析】用这袋面粉用去的重量+剩下的重量,求出这袋面粉的总重量,再用用去面粉的重量÷这袋面粉的总重量×100%,求出用去这袋面粉的百分比;
把这袋面粉的总重量看作单位“1”,用1减去用去面粉占总重量的百分比,求出剩下面粉占总重量的百分比;
用用去面粉的重量与剩下面粉的重量差,除以用去面粉的重量,再乘100%,求出剩下的比用去的多的百分之几;
用用去面粉的重量与剩下面粉的重量差,除以剩下面粉的重量,再乘100%,求出用去的比剩下的少百分之几,据此解答。
【解析】10÷(10+15)×100%
=10÷25×100%
=0.4×100%
=40%
1-40%=60%
(15-10)÷10×100%
=5÷10×100%
=0.5×100%
=50%
(15-10)÷15×100%
=5÷15×100%
≈0.333×100%
=33.3%
一袋面粉,用去10千克,还剩15千克,用去这袋面粉的40%,还剩这袋面粉的60%,剩下的比用去的多50%,用去的比剩下的少33.3%
94.25
【分析】求张华滑完全场所用的时间比莉莉多百分之几,用张华滑完全场比莉莉多用的时间除以莉莉滑完全场用的时间,结果用百分数表示,据此解答。
【解析】
张华滑完全场所用的时间比莉莉多25%。
95.20;32;40;75;七成五
【分析】小数化成分数,两位小数先化成分母为100的分数,再化简成最简分数;
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号;
根据成数的意义,百分之几十几就是几成几。
【解析】0.75==
==,=15÷20
==
==,=30∶40
0.75=75%
75%=七成五
即15÷20=0.75==30∶40=75%=七成五。
96.85 10
【分析】把原价看作单位“1”,打八五折就是现价是原价的85%,打九折就是现价是原价的90%,节省了(1-90%),据此解答。
【解析】游乐园门票八五折优惠,也就是现价是原价的85%;学习用品一律打九折出售,也就是现价是原价的90%。
1-90%=10%,所以节省了10%。
因此“儿童节”期间游乐园门票八五折优惠,现价是原价的85%;儿童文具店所有学习用品一律打九折出售,节省10%。
97.5275
【分析】存入银行的钱叫做本金;取款时银行多支付的钱叫做利息;单位时间(如1年、1月、1日等)的利息与本金的比值叫做利率。根据利息=本金×年利率×年数,本金+利息即到期后能取回的钱数,据此解答。
【解析】5000×2.75%×2+5000
=5000×2×2.75%+5000
=275+5000
=5275(元)
到期后共可取回5275元。
98.50
【分析】已知2022年、2023年一年级新生入学人数,根据新生入学增长率=(2023年一年级新生入学人数-2022年一年级新生入学人数)÷2022年一年级新生入学人数×100%,据此计算得出答案。
【解析】一年级新生入学增长率约为:
99.8
【分析】设买了x支圆珠笔,则买了(10-x)支钢笔,根据圆珠笔单价×圆珠笔数量+钢笔单价×钢笔数量=花的总钱数,列出方程求出x的值即可。
【解析】解:设买了x支圆珠笔。
3.5x+7.5×(10-x)=43
3.5x+75-7.5x=43
75-4x=43
75-4x+4x=43+4x
43+4x=75
43+4x-43=75-43
4x=32
4x÷4=32÷4
x=8
买了8支圆珠笔。
100.6
【分析】根据等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,圆锥部分的高÷3=倒入圆柱部分的高,再加上圆柱部分原来的高即可。
【解析】12÷3+2
=4+2
=6(厘米)
细沙的高度是6厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项青岛版(六三制)
(期末考点培优)专题02 填空题
学校:___________姓名:___________班级:___________考号:___________
1.一个刷油漆的滚筒形状是圆柱形(如图所示),长20厘米,底面直径为8厘米,滚筒滚动一周能刷漆的面积是( )平方厘米。
2.海边栈道提供3人脚踏车和2人脚踏车供游客骑行游览,26位游客乘坐10辆脚踏车正好坐满。其中3人脚踏车有( )辆,2人脚踏车有( )辆。
3.如图,容器中装有一定的水,现将容器倒置,此时,水面的高度为( )cm。
4.2024年2月份,小丽将自己的压岁钱2000元存入银行3年,年利率是1.5%,到期后她把钱全部取出捐给希望小学,她一共捐了( )元。
5.十七世纪,著名数学家莱布尼兹认为比号与除号有一种亲缘关系,把“÷”中的小横线去掉,于是“∶”就成为现在的样子了。根据式子9x=5y(x、y均不为0),写出一个比例为( )。
6.在一幅比例尺是1∶200000的地图上,量得北京到广州的距离是4.2厘米,两地的实际距离是( )千米。 ,把左边的线段比例尺改成数值比例尺是( )。
7.一个圆柱的底面半径是3分米,高是2分米,它的侧面积是( )平方分米,它的表面积是( )平方分米,体积是( )立方分米。
8.将一张长4厘米,宽3厘米的长方形纸(如图)以长为轴旋转一周,得到一个圆柱体,这个圆柱的表面积是( )平方厘米,体积是( )立方厘米。
9.一个圆锥(如图)的底面直径是8cm,从圆锥的顶点沿着它切成相等的两半后,表面积比原来的圆锥增加了48cm2,这个圆锥的体积是( )cm3。
10.一个圆锥比与它等底等高的圆柱的体积少20dm3,这个圆锥的体积是( )dm3,圆柱的体积是( )dm3。
11.将一根6米长的圆柱形木料锯成2段小圆柱,表面积增加了72平方分米,原来这根木料的体积是( )立方分米。
12.走同一段路,小明用40分钟,小军用50分钟,小明的速度比小军快( )%。
13.某城楼有200米长,可拍到的照片上只有2厘米长,这张照片的比例尺是( )。
14.一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个( ),它的体积是( )。
15.爷爷把2万元存入银行,定期一年,年利率为,到期后一共得到( )元。
16.一个圆柱油桶,底面直径是10分米,高是10分米,这个油桶的底面积是( )平方分米,这个油桶的容积是( )立方分米。
17.两个比的比值都是,它们组成的比例的外项分别是和,这个比例是( )。
18.六折( )(小数)。
19.在一个比例中两个内项的积是,一个外项是,另一个外项是( )。
20.沙漏是古人用的一种计时仪器。如图,圆锥形沙漏里(装满沙子)的沙子漏入下面空的圆柱形玻璃瓶中,若沙子漏完了,那么在圆柱形玻璃瓶中会平铺上大约( )厘米高的沙子。
21.一个圆锥的底面周长是62.8厘米,高是6厘米,它的体积是( )立方厘米。
22.甲数是乙数的20%,甲数与乙数的比是( ),乙数与甲、乙两数之和的比是( )。
23.两名工程师分别对同一个零件按照20∶1和30∶1的比例尺放大,结果图纸上两个零件的长度差是8厘米,那么这个零件的实际长度是( )厘米。
24.如图是小明哥哥在探究电流和电阻的关系时绘制的“电流——电阻”图像。由图象可知,可以看出电压一定时,电流和电阻成( )比例,理由是( )。
25.某小学举行数学竞赛,共10道题,每做对一道题得10分,每做错一道扣2分。乐乐得了64分。那么他做错了( )道题。
26.为缓解交通拥挤情况,某道路由原来的4车道变成了6车道(每条道的宽度不变),路面拓宽了( )%。
27.华为Mate60发售后,销量遥遥领先。其中使用的华为新麒麟芯片突破5纳米(1纳米=0.000001毫米)制程工艺。如果将5纳米的芯片画在图纸上,量的其长度为5毫米,这幅图的比例尺是( )。
28.在描述数据时,不仅能表示数量的多少,而且更能表示数量增减变化情况的是 统计图。
29.如图所示,把底面直径是8厘米,高是20厘米的圆柱切成若干等份,拼成一个近似的长方体。这个近似长方体的表面积是 平方厘米,体积是 立方厘米。
30.在比例尺为地图上,量得甲、乙两城的距离为2.5厘米。一辆汽车以每小时75千米的速度从甲城开往乙城, 小时可以到达;根据图中的线段比例尺写出数值比例尺是 。
31.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国存在最早的有系统的数学典籍,其中记载:有求“困盖”的术,“置如其周,令相乘也,又以高乘之,三十六成一”。意思是在求圆锥体积的时候,用圆锥底面周长乘周长再乘高,最后除以36,这种方法与现在的计算方法是一致的,只不过取π的近似值为3,如果一个圆锥的底面周长是12厘米,高是9厘米,那么请你用古人的方法和现在的方法分别计算后进行验证。
古人的方法: 。
现在的方法: 。
32.琪琪在书中了解到:宽与长的比值为0.618的长方形被称为“黄金长方形”。她画了一个长10cm、宽6.18cm的“黄金长方形”,若把这个长方形的长延长到15cm,使延长后的长方形仍为“黄金长方形”,那么宽应该延长到( )cm。
33.如图,一个圆柱形木料的底面积是10平方分米,高是6分米,把它削成顶点相对的两圆锥形体,那么削去部分的体积是 立方分米。
34.如图,小亮用小棒搭房子,他搭1间房子用了5根小棒,搭2间房子用了9根小棒,搭3间房子用了13根小棒……照这样的方式搭,用21根小棒能搭( )间房子;搭n间房子要用( )根小棒。
35.一个圆柱形的物品包装盒,将它的侧面沿虚线剪开,得到一个平行四边形(如图)。
(1)它的侧面积是( )平方厘米。
(2)这个包装盒最多能容纳( )立方厘米的物体。
36.一个晒盐场用100克海水可以晒出4克盐,照这样计算,要晒出8吨盐,需要( )吨海水。
37.小明家2025年2月份比3月份节约用水40%,2月份用水是3月份的( )%。
38.立竿见影。同一时间、同一地点,竿高和影长成( )比例。如果一棵小树的高度是1.2米,影长是0.6米,同一时间、同一地点,测得一棵大树的影长是4.5米,那么这棵大树的高度是( )米。
39.《九章算术》中记载的圆柱体积计算方法是“周自相乘,以高乘之,十二而一”也就是底面周长的平方乘高。再除以12(π取近似值3),如果一个圆柱的底面周长是4π分米,高是6分米,按照古人的方法计算出的圆柱的体积是( )立方分米。友情提示:。
40.《山东省中小学校园园林绿化管理办法》中规定:新建学校绿地率不得低于35%,绿化覆盖率应该在50%以上。某小学的占地面积约30000平方米,要想绿地率达标,至少需要( )平方米的绿地。
41.在开展“读书周”活动中,东东借了一本《童话书》阅读。第一天看了45页,第二天看了全书的25%,第二天看的页数比第一天多20%。这本书共有( )页。
42.房间里有4条腿的椅子和3条腿的凳子共18个,若椅子腿和凳子腿共68条,那么椅子有( )个。
43.潍坊科技市场搞促销活动,所有商品八五折出售。小明买一台电脑花了a元,这台电脑原价( )元。
44.儿童手表里的一种精密电子元件的实际长度是0.3毫米,画在图纸上是3厘米,这幅平面图的比例尺是( )。
45.一个圆柱和圆锥的底面半径和高分别相等,已知圆锥体积比圆柱的体积少16立方米,圆柱的体积是( )立方米,圆锥的体积比圆柱的体积少( )(填分数)。
46.已知银行的年利率是3.25%,王奶奶将50000元存入银行,存三年定期。三年后,王奶奶可以拿到利息多少元?只列式不计算( )。
47.
小军沿着直尺的方向将橡皮筋拉紧(如图),如果点A的位置固定不变,沿原来的方向将橡皮筋拉长,使点C的位置在21cm处,此时点B的位置在( )cm处。
48.一瓶盐水,盐和水的质量比是1∶24,如果再加入75克水,这时盐和水的质量比是1∶27,那么原来瓶内盐水重( )克。现有含盐率30%的盐水300克,要把它变成含盐率20%的盐水需要加水( )克。
49.张叔叔运送了250件瓷器,规定完整运一个到目的地可以得到运送费20元,损坏一个赔偿100元,运完这批瓷器张叔叔共得到运费4160元,张叔叔在运输过程中,完整运送了( )件瓷器,损坏了( )件瓷器。
50.天舟六号货运飞船于2023年5月10日21时22分成功发射,整船的载重能力提高到7.4吨, ,天舟五号货运飞船的载重能力是多少吨?如果列式为7.4÷(1+7%),那么应补充的信息是( )。
51.牛牛家养了鸡和兔子共8只,共有20条腿,鸡、兔各有几只?
先画8个圆圈代表8只动物,每只动物画两条腿,代表8只鸡。这样有2×8=( )条腿,还差20-( )=( )条腿。一只兔子比一只鸡多2条腿,再在上图中给每只兔子添上两条腿。可知鸡有( )只,兔子有( )只。
52.妈妈购买了30000元三年期国债,年利率3.35%。到期后妈妈一共能取出多少钱?解决“到期后妈妈一共能取出多少钱?”这个问题的正确列式是( )。
53.乒乓球馆里面有40人,同时在14张乒乓球台进行“1人对1人”的单打和“2人对2人”的双打比赛。单打比赛的共有( )人。
54.CPU(中央处理器)是一台计算机的运算核心和控制核心,相当于计算机的心脏。将一个长30mm的CPU零件画在图纸上,长为12cm,这张图纸的比例尺是( )。
55.一件外套标价500元,商场开展“每满200元减50元”的优惠促销活动,现在买这件外套实际花( )元,相当于打( )折出售。
56.一种长为2.5毫米的仪器零件,画在图纸上的长度是10厘米,这幅图纸的比例尺是( ),是( )(选填“缩小”或“放大”)比例尺。
57.乐乐把一块底面半径2厘米、高15厘米的圆锥形橡皮泥,捏成一个底面积与圆锥底面积相等的圆柱,圆柱的高是( ),体积是( )。
58.一幅地图,图上2厘米代表实际距离30千米。若实际距离是150千米,则图上距离是( )厘米。
59.一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要( )平方米的钢化玻璃。
60.圆柱形粮囤(如图),从里面量得底面半径是1m,高是2m,它的容积是( )。
61.六一儿童节期间一家超市所有儿童学习用品都优惠30%,也就是打( )折出售;其中一盒彩笔原价是20元,现价是( )元。
62.十七世纪,著名数学家莱布尼茨认为比号与除号有一种亲缘关系,把“÷”的小横线去掉,于是就成了“∶”现在的样子,那么5÷9=30÷54就可以改写成比例( );4×5=2×10可以改写成比例( )。
63.李老师将30000元存入银行,定期3年,如果年利率3.20%,到期后可得到利息( )元。
64.某地一个龙虾店铺使用“八两秤”被处罚。事件中消费者将500g的标准砝码放入到电子秤上,显示的克数却是625,这说明实际克数只是显示克数的( )%,如果该秤显示的克数是500,那么实际只有( )g。
65.“双十一”购物节来了,网上的商品迎来大减价,聪聪喜欢的一款耳机以原价的八五折出售,可以把( )看作单位“1”,现价比原价降低了( )%。
66.接种流感疫苗可以有效预防流感病毒感染。如果要统计上个月我市每周接种人数的多少情况,应选用( )统计图;如果要反应每周接种疫苗的人数增减变化情况,应选用( )统计图;如果要反映上个月我市各县区接种人数与我市接种总人数之间的关系,应选用( )统计图。
67.果园里桃树和梨树的棵数比是7∶8,桃树棵数是梨树棵数的( );桃树棵数比梨树棵数少( )%;梨树棵数比桃树棵数多( );梨树棵数占两种树总棵数的( )。
68.将3个完全相同的小圆柱,拼成一个高是30厘米的大圆柱,表面积减少了50平方厘米,原来每个小圆柱的体积是( )立方厘米。
69.王青把压岁钱4000元存入银行,定期5年,到期后王青取回4720元,该银行五年期的年利率是( )%。
70.学校自来水管的直径是2厘米,水管内水的流速是每秒10厘米,阳阳洗完手忘记关水龙头,3分钟后小欣发现并关掉了水龙头,共浪费了( )升水。
71.一个高是8cm的圆柱,如果把它的高截短3cm,那么它的表面积将减少94.2cm2,原来这个圆柱的体积是( )。
72.把一个圆柱形木料削成最大的圆锥,削去的体积是30立方厘米,圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
73.一个圆柱的侧面沿高展开后得到一个边长是15.7分米的正方形,原来圆柱的底面半径是( )分米。
74.把一个高6厘米的圆柱平均分成3段,变成了3个完全相同的小圆柱,这时表面积比原来增加了50.24平方厘米,那么原来圆柱的体积是( )。
75.一个圆柱的高是4厘米,沿直径垂直切开后,切面是一个正方形,这个圆柱的体积是( )立方厘米。
76.一个圆锥和一个圆柱的底面积相等。已知圆锥与圆柱的体积的比是1∶6,圆锥的高是8.4厘米,圆柱的高是( )厘米。
77.一个圆柱和一个圆锥等底等高,体积相差7.36立方米,圆柱的体积是( )立方米,圆锥的体积是( )立方米。
78.把一根圆柱形木料截成3段小圆木,表面积增加了314平方分米;若沿底面直径平均分成两个半圆柱体,表面积增加300平方分米,木料原来的体积是( )立方米。
79.一个圆柱形橡皮泥的高减少2厘米,底面积不变,表面积减少了12.56平方厘米,则这个圆柱形橡皮泥的底面周长是( )厘米,体积减少了( )立方厘米。
80.南山湖音乐喷泉是由48个内直径为2厘米的出水管围成的一个圆形。打开音乐喷泉时,水喷涌的速度是5米/秒,如果不实行水循环系统,那么一分钟会浪费( )吨水。(每立方米水的质量是1吨)
81.一个圆柱的底面半径和高都扩大到原来的3倍,底面周长扩大到原来的( )倍,底面积扩大到原来的( )倍,侧面积扩大到原来的( )倍,体积扩大到原来的( )倍。
82.在一个比例中,两个内项都是质数,且乘积是6,其中一个外项0.4,这个比例可以写成( )。
83.如果y=8x,那么x和y成( )比例;如果,那么x和y成( )比例。(x、y均不为0)
84.(1)图中甲、乙两个正方形的边长之比是( ),周长之比是( ),这两个比( )组成比例(填“能”或“不能”)。
(2)甲、乙两个正方形的面积之比是( ),这个比和边长之比( )组成比例(填“能”或“不能”)。
85.运输队运送一批物资,货车的载质量和所需货车的数量如下表。
货车的载质量(吨) 2.5 4 6 10
所需货车的数量(辆) 48 30 20 12
(1)货车的载质量与所需货车的数量成( )比例。
(2)如果改用每节车厢载质量为60吨的火车运输,需要( )节这样的车厢。
86.六年级同学排队做广播操,每行人数和排成的行数成( )比例;圆锥的底面半径一定,圆锥的体积和高成( )比例。
87.下面每题中的两个量,成正比例的有 ,成反比例的有 ,既不成正比例也不成反比例的有 。(填序号)
①汽车每千米耗油量一定,所行的路程和耗油总量。
②圆锥体的体积一定,它的底面积和高。
③出油率一定,花生油的质量和花生的质量
④优优读一本书,已读的页数与未读的页数。
⑤正方形的面积和边长。
⑥把一根绳子剪成同样长的小段,每段的长度和剪成的段数。
88.下面每题中的两种量是否成比例?如果成,成正比例还是反比例?在下面写一写。
(1)乒乓球总个数一定,每盒装的个数和需要的盒数。( )
(2)全班人数一定,男生人数和女生人数。( )
(3)每小时织布的米数一定,织布的总米数和时间。( )
(4)长方形的周长一定,长方形的长和宽。( )
89.据报道:目前5G以更快的速度、更稳定的连接与更大的容量,正在融入中原大地千行百业。用4G下载一部电影要5分钟,用5G下载时间是4G的1%,只需( )秒。
90.某种子站做种子发芽实验,结果发芽的48粒,没发芽的2粒,这批种子的发芽率是( )。照这样计算,要想保证有720粒种子发芽,至少要种( )粒。
91.营养学家研究提出:一个儿童每天需要90克的蛋白质。已知每100克鸡蛋中,含蛋白质14克,每100克面粉中含蛋白质10.1克,淘气的早餐吃了50克鸡蛋和100克面条,这顿饭淘气一共摄入蛋白质( )克,大约占一天所需蛋白质总量的( )%。
92.“妇女节”期间游乐园门票八五折优惠,现价是原价的( )%,今年的玉米产量比去年增产一成五,今年产量是去年的( )%。
93.一袋面粉,用去10千克,还剩15千克,用去这袋面粉的( )%,还剩这袋面粉的( )%,剩下的比用去的多( )%,用去的比剩下的少( )%。
94.北京冬奥会的成功举办,让我国冰上运动项目得到快速发展。学校组织滑冰比赛,在相同的比赛场地,莉莉滑完全场用了40秒,张华用了50秒,张华滑完全场所用的时间比莉莉多( )%。
95.15÷( )=0.75==30∶( )=( )%=( )(成数)。
96.“儿童节”期间游乐园门票八五折优惠,现价是原价的( )%,儿童文具店所有学习用品一律打九折出售,节省( )%。
97.将5000元人民币存入银行,整存整取两年,年利率是2.75%。到期后共可取回( )元。
98.国家鼓励二胎生育后,2023年恰逢一年级新生入学高峰年,某市2022年约有8万名一年级新生入学,2023年约有12万名新生入学,一年级新生入学增长率约 %。
99.王老师花43元,买了钢笔和圆珠笔共10支。圆珠笔每支3.5元,钢笔每支7.5元,买了 支圆珠笔。
100.用底面半径是6厘米,高是12厘米的空心圆锥和空心圆柱各一个,组成竖放的容器(如下图)。在这个容器内装入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2厘米。若将这个容器上面封住并倒立,细沙的高度是( )厘米。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.502.4
【分析】根据题意可知,求滚动一周能刷的面积,就是求圆柱的侧面积,根据圆柱侧面=π×直径×高,代入数据,即可解答。
【解析】3.14×8×20
=25.12×20
=502.4(平方厘米)
滚筒滚动一周能刷漆的面积是502.4平方厘米。
2.6 4
【分析】假设全是2人脚踏车,那么10辆车可坐人数为10×2=20人,比实际的26人少26-20=6人;每把一辆3人脚踏车看成2人脚踏车,就少算3-2=1人,所以3人脚踏车数量为6÷1=6辆;2人脚踏车数量为10-6=4辆。
【解析】2×10=20(人)
26-20=6(人)
6÷(3-2)
=6÷1
=6(辆)
10-6=4(辆)
即,3人脚踏车有6辆;2人脚踏车有4辆。
3.11
【分析】从图中可知,圆柱和圆锥的底面积相等,原来圆柱内水的高度为(23-18)cm;原来圆锥内水的高度为18cm;容器倒置后,圆锥内的水流入圆柱内,根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍,据此求出原来圆锥内的水流入圆柱内的高度为(18÷3)cm,再加上原来圆柱内水的高度,即是容器倒置后的水面高度。
【解析】原来圆柱内水的高度:23-18=5(cm)
原来圆锥内水流入圆柱后的高度:18÷3=6(cm)
5+6=11(cm)
现将容器倒置,此时,水面的高度为11cm。
4.2090
【分析】由题意知:本息=本金×年利率×时间+本金,由此将数据代入即可求得捐款钱数。
【解析】2000×1.5%×3+2000
=90+2000
=2090(元)
则她一共捐了2090元。
5.9∶5=y∶x
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。据此解答。
【解析】根据式子9x=5y(x、y均不为0),写出一个比例为9∶5=y∶x。
(答案不唯一)
6.8.4 1∶1000000/
【分析】已知一幅地图的比例尺和从北京到广州的图上距离,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出两地的实际距离。
线段比例尺表示图上1厘米相当于实际距离10千米,根据“比例尺=图上距离∶实际距离” 以及进率“1千米=100000厘米”,把线段比例尺改成数值比例尺。
【解析】4.2÷
=4.2×200000
=840000(厘米)
840000厘米=8.4千米
1厘米∶10千米
=1厘米∶(10×100000)厘米
=1∶1000000
填空如下:
在一幅比例尺是1∶200000的地图上,量得北京到广州的距离是4.2厘米,两地的实际距离是(8.4)千米。 ,把左边的线段比例尺改成数值比例尺是(1∶1000000)。
7.37.68 94.2 56.52
【分析】已知一个圆柱的底面半径是3分米,高是2分米,根据圆柱的侧面积公式计算出圆柱的侧面积;然后根据圆的面积公式计算出圆柱的底面积,因为圆柱有两个底面,所以底面积要乘2,根据圆柱的表面积公式计算出圆柱的表面积;最后根据圆柱的体积公式计算出圆柱的体积。
【解析】①2×3.14×3×2
=6.28×3×2
=18.84×2
=37.68(平方分米)
所以该圆柱的侧面积是37.68平方分米;
②3.14×32
=3.14×9
=28.26(平方分米)
37.68+28.26×2
=37.68+56.52
=94.2(平方分米)
所以该圆柱的表面积是94.2平方分米;
③3.14×32×2
=3.14×9×2
=28.26×2
=56.52(立方分米)
所以该圆柱的体积是56.52立方分米。
8.131.88 113.04
【分析】根据题意,把一个长方形纸以长为轴旋转一周,得到一个圆柱体,那么这个圆柱的高等于长方形的长,圆柱的底面半径等于长方形的宽;
根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,求出圆柱的表面积;
根据圆柱的体积公式V=πr2h,代入数据计算,求出圆柱的体积。
【解析】2×3.14×3×4+3.14×32×2
=2×3.14×3×4+3.14×9×2
=75.36+56.52
=131.88(平方厘米)
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
这个圆柱的表面积是131.88平方厘米,体积是113.04立方厘米。
9.100.48
【分析】根据题意,把一个圆锥从它的顶点沿底面直径切成相等的两半后,表面积比原来圆锥的表面积增加了2个切面的面积,切面是一个以圆锥的底面直径为底,以圆锥的高为高的三角形;
先用增加的表面积除以2,求出一个切面的面积;再根据三角形的高=面积×2÷底,求出圆锥的高;
再根据圆锥的体积公式V=πr2h,代入数据计算,求出这个圆锥的体积。
【解析】一个切面的面积:48÷2=24(cm2)
圆锥的高:24×2÷8=6(cm)
圆锥的体积:
×3.14×(8÷2)2×6
=×3.14×42×6
=×3.14×16×6
=100.48(cm3)
这个圆锥的体积是100.48cm3。
10.10 30
【分析】当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍;把圆锥的体积看作1份,圆柱的体积看作3份,相差(3-1)份;
用等底等高的圆锥与圆柱的体积差除以份数差,求出一份数,即圆锥的体积;再用圆锥的体积乘3,求出圆柱的体积。
【解析】圆锥的体积:
20÷(3-1)
=20÷2
=10(dm3)
圆柱的体积:
10×3=30(dm3)
这个圆锥的体积是10dm3,圆柱的体积是30dm3。
11.2160
【分析】根据题意,把一根圆柱形木料锯成2段小圆柱,那么增加的表面积是圆柱的2个底面圆的面积;先用增加的表面积除以2,求出圆柱的底面积;再根据圆柱的体积V=Sh,求出原来这根木料的体积。注意单位的换算:1米=10分米。
【解析】6米=60分米
72÷2=36(平方分米)
36×60=2160(立方分米)
原来这根木料的体积是2160立方分米。
12.25
【分析】将路程看作单位“1”,时间分之一可以看作速度,将小军速度看作单位“1”,小明与小军的速度差÷小军速度=小明的速度比小军快百分之几。
【解析】(-)÷
=×50
=0.25
=25%
小明的速度比小军快25%。
13.1∶10000
【分析】图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可。
【解析】2厘米∶200米=2厘米∶20000厘米=(2÷2)∶(20000÷2)=1∶10000
这张照片的比例尺是1∶10000。
14.圆锥 56.52
【分析】把一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个底面半径是3cm,高是6cm的圆锥,再根据圆锥的体积公式,代入数据计算即可得解。
【解析】
(cm3)
一个直角三角形,两条直角分别是3cm和6cm,以6cm的直角边为轴旋转一周,可以得到一个圆锥,它的体积是56.52。
15.20320
【分析】已知本金是2万元,定期一年,利率为1.60%,根据利息的计算公式“利息=本金×利率×时间”算出利息,再加上本金,就可得到到期后一共得到的钱数,需要统一单位,2万元=20000元。
【解析】2万元=20000元
20000×1.60%×1
=20000×0.016×1
=320(元)
20000+320=20320(元)
所以到期后一共得到20320元。
16.78.5 785
【分析】圆柱的底面积=圆周率×底面半径的平方,根据圆柱体积=底面积×高,求出容积。
【解析】3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方分米)
78.5×10=785(立方分米)
这个油桶的底面积是78.5平方分米,这个油桶的容积是785立方分米。
17./
【分析】在两个外项中要先确定一个是第一个比的前项,另一个则是第二个比的后项,再根据比值求出两个比的后项和前项,比的后项等于比的前项除以比值,比的前项等于比值乘比的后项,即可得出答案。
【解析】当是第一个比的前项时,则是第二个比的后项。
这个比例是。
或当是第一个比的前项时,则是第二个比的后项。
这个比例是。
两个比的比值都是,它们组成的比例的外项分别是和,这个比例是(或)。
18.3;20;15;60;0.6
【分析】“六折”表示十分之六,写成分数是,约分后是;
分数可以写成比的形式3∶5,前项3变成12,相当于前项乘4,根据比的基本性质“比的前项和后项同时乘或除以一个相同的数(0除外)比值不变”,后项5也要乘4;
对于3∶5,后项5变为25,相当于后项乘5,根据比的基本性质前项3也要乘5;
“六折”也可以表示百分之六十,写成百分数就是60%;
将60%化为小数,去掉百分号,小数点向左移动两位。
【解析】==;
5×4=20;
3×5=15;
百分之六十写成百分数是60%;
60%=0.6。
所以=12∶20=15∶25=60%=六折=0.6。
19./
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
已知一个比例的两个内项的积是,根据比例的基本性质,那么这个比例的两个外项的积也是;用两个外项的积除以已知的一个外项,即可求出另一个外项。
【解析】÷
=×
=
另一个外项是。
20.4
【分析】先求出圆锥形沙漏里装的沙子体积,用公式:,当沙子漏到圆柱形玻璃瓶中时,圆柱形玻璃瓶里沙子的体积不变,用沙子的体积÷圆柱形玻璃瓶的底面积=沙子的高度,据此列式解答。
【解析】
(厘米)
故在圆柱形玻璃瓶中会平铺上大约4厘米高的沙子。
21.628
【分析】根据圆的周长=2r,用圆锥的底面周长除以,再除以2求出圆锥的底面半径,再根据圆锥的体积=h求出圆锥的体积即可。
【解析】62.8÷3.14÷2
=20÷2
=10(厘米)
×3.14××6
=3.14×100×2
=314×2
=628(立方厘米)
所以它的体积是628立方厘米。
22.1∶5 5∶6
【分析】假设乙数是100,根据求一个数的百分之几是多少,用乘法,则甲数是100×20%,据此求出甲数,再用甲数比乙数,再根据比的性质化简成最简比;用甲数加上乙数,求出甲、乙两数的和,用乙数比甲、乙两数之和,再根据比的性质化简成最简比,据此解答第二空。
【解析】假设乙数是100。
100×20%=20
20∶100
=(20÷20)∶(100÷20)
=1∶5
20+100=120
100∶120
=(100÷20)∶(120÷20)
=5∶6
所以甲数与乙数的比是1∶5,乙数与甲、乙两数之和的比是5∶6。
23.0.8/
【分析】由题可知,第一幅图是原零件的20倍,第二幅图是原零件的30倍,相差了原零件的10倍,相差8厘米,即可算出1倍是0.8厘米,从而计算得出答案。
【解析】8÷(30-20)
=8÷10
=0.8(厘米)
所以这个零件实际长度是0.8厘米。
24.反 电流×电阻=电压(一定)
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【解析】0.1×30=0.2×15=0.3×10=0.6×5=…=3(一定)
乘积一定,那么电流和电阻成反比例。
由图象可知,可以看出电压一定时,电流和电阻成反比例,理由是电流×电阻=电压(一定)。
25.3
【分析】分析题目,假设乐乐10道题全做对了,则他应得10×10=100(分),而实际得了64分,这是因为他每做错一题,不仅得不到10分,还要扣2分,就是做错一题要少得10+2=12(分),据此用总分之差除以(10+2)即可求出做错的题数。
【解析】假设乐乐10道题都做对了。
(10×10-64)÷(10+2)
=(100-64)÷12
=36÷12
=3(道)
某小学举行数学竞赛,共10道题,每做对一道题得10分,每做错一道扣2分。乐乐得了64分。那么他做错了3道题。
26.50
【分析】明确原来和现在的车道数:题目中直接给出原来道路是4车道,现在变为6车道。计算车道增加量:用现在车道数减去原来车道数,得到增加的车道数,即6-4=2车道。计算拓宽的百分比:求路面拓宽的百分比,就是求增加的车道数占原来车道数的百分比。根据求一个数是另一个数百分之几的方法,用增加的车道数除以原来的车道数再乘以100% 。
【解析】(6-4)÷4×100%
=2÷4×100%
=50%
路面拓宽了50%。
27.1000000∶1
【分析】已知将5纳米的芯片画在图纸上,量的其长度为5毫米,根据“比例尺=图上距离∶实际距离”,以及进率“1纳米=0.000001毫米”,据此求出这幅图的比例尺。
【解析】5毫米∶5纳米
=5毫米∶(5×0.000001)毫米
=5∶0.000005
=(5÷0.000005)∶(0.000005÷0.000005)
=1000000∶1
这幅图的比例尺是1000000∶1。
28.折线
【分析】理解三种统计图各自的特点,并能根据不同问题选择适当的统计图描述数据。
(1)条形统计图的特点:条形统计图能清楚地表示出每个项目的具体数量。
(2)折线统计图的特点:折线统计图不仅能表示每个项目的具体数量还能清楚地反映事物的增减变化情况。
(3)扇形统计图的特点:扇形统计图能清楚地表示出各部分在总体中所占的百分比。
【解析】据分析可得:在描述数据时,不仅能表示数量的多少,而且更能表示数量增减变化情况的是折线统计图。
29.762.88 1004.8
【分析】把一个圆柱切拼成一个近似长方体,长方体的体积等于圆柱的体积,长方体的长等于圆柱的底面周长的一半即πd÷2,长方体的宽等于圆柱的底面半径r,长方体的高等于圆柱的高h;
根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据计算,求出这个近似长方体的表面积和体积。
【解析】长方体的长:3.14×8÷2=12.56(厘米)
长方体的宽:8÷2=4(厘米)
长方体的表面积:
(12.56×4+12.56×20+4×20)×2
=(50.24+251.2+80)×2
=381.44×2
=762.88(平方厘米)
长方体的体积:
12.56×4×20
=50.24×20
=1004.8(立方厘米)
这个近似长方体的表面积是762.88平方厘米,体积是1004.8立方厘米。
30.2 1∶6000000/
【分析】线段比例尺的意思是,图上1厘米相当于实际距离60千米,图上甲、乙两城的距离为2.5厘米,那么实际距离是(2.5×60)千米;
已知一辆汽车以每小时75千米的速度从甲城开出,根据“时间=路程÷速度”求出汽车到达乙城的所需的时间;
根据“比例尺=图上距离∶实际距离”以及进率“1千米=100000厘米”,将线段比例尺改写成数值比例尺。
【解析】2.5×60÷75
=150÷75
=2(小时)
1厘米∶60千米
=1厘米∶(60×100000)厘米
=1∶6000000
一辆汽车以每小时75千米的速度从甲城开往乙城,(2)小时可以到达;根据图中的线段比例尺写出数值比例尺是(1∶6000000)。
31.12×12×9÷36=36(立方厘米) 12÷3÷2=2(厘米);3×22×9×=36(立方厘米)
【分析】古人的方法:用圆锥的底面周长×底面周长,再乘圆锥的高,再除以36,据此用古人方法计算出圆锥的体积。
现在的方法:根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆锥底面积的周长,再根据圆锥的体积公式:体积=底面积×高×,据此用现在方法,求出圆锥的体积。
【解析】古人的方法:
12×12×9÷36
=144×9÷36
=1296÷36
=36(立方厘米)
现在的方法:
12÷3÷2
=4÷2
=2(厘米)
3×22×9×
=3×4×9×
=12×9×
=108×
=36(立方厘米)
36=36
即,圆锥的体积是36立方厘米;不管用古人的方法还是现在的方法计算的结果都是一样的。
32.9.27
【分析】根据题意,宽与长的比值为0.618的长方形被称为“黄金长方形”,即宽∶长=0.618(一定),比值一定,那么长与宽成正比例关系,据此列出正比例方程,并求解。
【解析】解:设宽应该延长到cm。
10∶6.18=15∶
10=6.18×15
10=92.7
=92.7÷10
=9.27
宽应该延长到9.27cm。
33.40
【分析】因为将圆柱形木料削成两个的圆锥,所以两个圆锥的高之和等于圆柱的高,根据圆柱的体积=底面积×高,圆锥的体积=底面积×高×,分别求出圆柱的体积和两个圆锥的体积之和;再用圆柱的体积减去两个圆锥体的体积之和,计算即可求出削去部分的体积。
【解析】10×6-10×6×
=60-60×
=60-20
=40(立方分米)
所以削去部分的体积是40立方分米。
34.5 (4n+1)/(1+4n)
【分析】搭1个房子用5根小棒,搭2个房子用(5+4)根小棒,搭3个房子用(5+4+4)根小棒,也就是每多搭一个房子,需要用4根小棒,据此找到小棒根数与房子个数之间的规律,再根据规律求出21根小棒能搭几间房子,据此解答。
【解析】1个房子:5根
2个房子:5+4=9(根)
3个房子:
5+4+4
=9+4
=13(根)
n个房子:5+(n-1)×4
=5+4n-4
=(4n+1)根
当有21根小棒时,
(21-1)÷4
=20÷4
=5(间)
故用21根小棒能搭5间房子;搭n间房子要用(4n+1)根小棒。
35.(1)150.72
(2)226.08
【分析】(1)圆柱侧面沿虚线剪开得到平行四边形,圆柱侧面积就等于这个平行四边形面积,“平行四边形面积=底×高”,在此图中,平行四边形的底恰好是圆柱底面的周长18.84厘米,高为8厘米,所以用底18.84厘米乘高8厘米就能得出侧面积;
(2)要计算圆柱包装盒容积,需先求底面半径,已知底面周长18.84厘米,根据圆周长公式C=2πr,通过变形公式r=C÷π÷2可算出半径r ,得到半径后,再依据圆柱体积公式V=πr2h,将半径r和高h的值代入公式就能算出体积,也就是包装盒最多能容纳物体的体积。
【解析】(1)18.84×8=150.72(平方厘米)
所以它的侧面积是150.72平方厘米。
(2))18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×8
=3.14×9×8
=28.26×8
=226.08(立方厘米)
所以这个包装盒最多能容纳226.08立方厘米的物体。
36.200
【分析】本题可先求出海水与盐的比例关系,100克海水可以晒出4克盐,则海水与盐的比例为100÷4=25,即每晒出1克盐需要25克海水;再根据要晒出盐的重量求出所需海水的重量,因为要晒出8吨盐,且每晒出1克盐需要25克海水,所以需要海水8×25=200吨。
【解析】100÷4=25(克)
8吨=8000000克
8000000×25=200000000(克)
200000000克=200(吨)
所以要晒出8吨盐,需要200吨海水。
37.60
【分析】以3月份用水数量为单位“1”,2月份比3月份少40%,即相当于3月份的(1-40%)。据此解答。
【解析】1-40%=60%
2月份用水是3月份的60%。
38.正 9
【分析】同一时间、同一地点,物体的长度和它影子长度的比值一定,所以同一时间、同一地点,竿高和影长成正比例关系,大树的高度∶大树的影长=小树的高度∶小树的影长,据此列出正比例方程,并求解。
【解析】同一时间、同一地点,竿高和影长成正比例。
解:设这棵大树的高度是x米。
x∶4.5=1.2∶0.6
0.6x=4.5×1.2
0.6x=5.4
x=5.4÷0.6
x=9
所以,这棵大树的高度是9米。
39.8
【分析】按照古人的方法,需要先求出底面周长的平方,再乘高,最后除以12来计算圆柱体积。
【解析】×6÷12
=16×6÷12
=96÷12
=8(立方分米)
所以按照古人的方法计算出的圆柱的体积是8立方分米。
40.10500
【分析】根据绿地面积=占地面积×绿地率,代入数据计算即可。
【解析】30000×35%=10500(平方米)
所以至少需要10500平方米的绿地。
41.216
【分析】已知第一天看了45页,第二天看的页数比第一天多20%,把第一天看的页数看作单位“1”,则第二天看的页数是第一天的(1+20%),单位“1”已知,用第一天看的页数乘(1+20%),求出第二天看的页数。
已知第二天看了全书的25%,把这本书的总页数看作单位“1”,单位“1”未知,用第二天看的页数除以25%,即可求出这本书的总页数。
【解析】第二天看了:
45×(1+20%)
=45×(1+0.2)
=45×1.2
=54(页)
总页数:
54÷25%
=54÷0.25
=216(页)
这本书共有216页。
42.14
【分析】设4条腿的椅子有x个,则3条腿的凳子有(18-x)个;x个椅子有4x条腿,3条腿的凳子有3×(18-x)条腿,椅子腿和凳子腿共68条,列方程:4x+3×(18-x)=68,解方程,即可解答。
【解析】解:设4条腿的椅子有x个,则凳子有(18-x)个。
4x+3×(18-x)=68
4x+3×18-3x=68
4x+54-3x=68
x+54=68
x+54-54=68-54
x=14
房间里有4条腿的椅子和3条腿的凳子共18个,若椅子腿和凳子腿共68条,那么椅子有14个。
43.
【分析】八五折出售,就是现价是原价的85%,把原价看作单位“1”,原价×85%=现价,已知一个数的百分之几是多少,求这个数,用除法计算,所以:原价=现价÷折扣,代入数据计算即可。
【解析】八五折=85%
a÷85%=(元)
这台电脑原价元。
44.100∶1
【分析】已知一种精密电子元件的实际长度和图上的长度,根据“比例尺=图上距离∶实际距离”,以及进率“1厘米=10毫米”,求出这幅平面图的比例尺。
【解析】3厘米∶0.3毫米
=(3×10)毫米∶0.3毫米
=30∶0.3
=(30÷0.3)∶(0.3÷0.3)
=100∶1
这幅平面图的比例尺是100∶1。
45.24
【分析】由题可知,圆柱与圆锥底面半径和高分别相等,因此可得圆柱与圆锥是等底等高。在等底等高的情况下,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,那么圆锥体积比圆柱体积少(1-),已知圆锥体积比圆柱的体积少16立方米,根据已知一个数的几分之几是多少,求这个数,用除法计算,即可求出圆柱的体积,据此解答。
【解析】1-=
16÷=16×=24(立方米)
即圆柱的体积是24立方米,圆锥的体积比圆柱的体积少。
46.50000×3.25%×3
【分析】已知本金50000元,年利率是3.25%,存三年定期,根据“利息=本金×利率×存期”,求出到期时可得到的利息。
【解析】50000×3.25%×3
=50000×0.0325×3
=1625×3
=4875(元)
三年后,王奶奶可以拿到利息4875元。
列式为:50000×3.25%×3。
47.14
【分析】用比例解决问题只要比例两边的比统一即可,设此时点B的位置在xcm处,根据点C的位置∶点B的位置=9∶6,列出比例求出x的值即可。
【解析】解:设此时点B的位置在xcm处。
21∶x=9∶6
9x=21×6
9x÷9=126÷9
x=14
此时点B的位置在14cm处。
48.25 150
【分析】第一个空,盐的质量没变,再加入75克水,水增加了(27-24)份,将比的前后项看成份数,加入的水的质量÷对应份数=一份数,一份数×盐的对应份数=盐的质量;
第二个空,盐的质量没变,将原来盐水质量看作单位“1”,原来盐水质量×含盐率=盐的质量,再将含盐率20%的盐水质量看作单位“1”,盐的质量÷含盐率=含盐率20%的盐水质量,含盐率20%的盐水-原来盐水质量=需要加水的质量。
【解析】75÷(27-24)×1
=75÷3×1
=25(克)
300×30%÷20%-300
=300×0.3÷0.2-300
=450-300
=150(克)
一瓶盐水,盐和水的质量比是1∶24,如果再加入75克水,这时盐和水的质量比是1∶27,那么原来瓶内盐水重25克。现有含盐率30%的盐水300克,要把它变成含盐率20%的盐水需要加水150克。
49.243 7
【分析】根据题意,设损坏了件瓷器。已知运送瓷器250件,损坏了件瓷器,则完整运送 (250-)件瓷器,每件可得到运送费20元,根据“单价×数量=总价”可知,完整运送可得到运送费20×(250-)元;如果损坏一个赔偿100元,那么损坏了件瓷器,需赔偿100元;等量关系:完整运送瓷器得到的运送费-损坏瓷器的赔偿费=共得到的运费,据此列出方程,并求解。
【解析】解:设损坏了件瓷器,则完整运送了(250-)件瓷器。
20×(250-)-100=4160
20×250-20-100=4160
5000-(20+100)=4160
5000-120=4160
120=5000-4160
120=840
=840÷120
=7
250-7=243(件)
完整运送了243件瓷器,损坏了7件瓷器。
50.比天舟五号整船的载重能力提高了7%
【分析】如果列式为7.4÷(1+7%),则把天舟五号货运飞船的载重能力看作单位“1”,整船的载重能力提高到7.4吨,比天舟五号货运飞船的载重能力提高了7%,则整船的载重能力是天舟五号货运飞船的(1+7%),单位“1”未知,用整船的载重能力除以(1+7%),即是天舟五号货运飞船的载重能力。
【解析】列式为7.4÷(1+7%),那么应补充的信息是(比天舟五号整船的载重能力提高了7%)。
51.16 16 4 6 2
【分析】假设8只动物全是鸡,每只鸡有两条腿,一共有2×8=16条腿,与实际20条腿相差20-16=4条腿。因为一只兔子比一只鸡多2条腿,用相差的总腿数除以2,求出兔子的只数;再用总只数减去兔子的只数,求出鸡的只数。
【解析】假设8只动物全是鸡,则兔子有:
(20-2×8)÷(4-2)
=(20-16)÷2
=4÷2
=2(只)
鸡有:8-2=6(只)
填空如下:
先画8个圆圈代表8只动物,每只动物画两条腿,代表8只鸡。这样有2×8=(16)条腿,还差20-(16)=(4)条腿。一只兔子比一只鸡多2条腿,再在上图中给每只兔子添上两条腿。可知鸡有(6)只,兔子有(2)只。
52.30000×3.35%×3+30000
【分析】根据“利息=本金×利率×存期”求出到期后可得到的利息,再加上本金,即是到期后一共能取出的钱数。
【解析】30000×3.35%×3+30000
=30000×0.0335×3+30000
=3015+30000
=33015(元)
到期后妈妈一共能取出33015元。
这个问题的正确列式是30000×3.35%×3+30000。
53.16
【分析】假设所有桌都进行单打比赛,应有14×2=28人,而实际上却有40人,少出了40-28=12人;而每张单打桌比双打桌少了4-2=2人,看少的总人数里面有几个2,就有几张双打桌,再用总桌数减去双打桌,即是单打桌的张数;然后用单打桌的张数乘每张单打桌的人数,求出单打比赛的人数。
【解析】假设全是单打桌,则双打桌数有:
(40-14×2)÷(4-2)
=(40-28)÷2
=12÷2
=6(张)
单打桌数:14-6=8(张)
8×2=16(人)
单打比赛的有16人。
54.4∶1
【分析】图上距离与实际距离的比叫作比例尺。先要将单位换算成统一的单位,1厘米=10毫米,高级单位转化为低级单位用乘法,则30毫米=3厘米。再将两个数的比化简成为最简整数比,据此解答即可。
【解析】30毫米=3厘米
12∶3=4∶1
所以,这张图纸的比例尺是4∶1。
55.400 八
【分析】由题意可知,这件外套的价格是200元满50元,先看500元里有几个200元,实际价格需要减去几个50元,几折就表示现价占原价的十分之几,也就是百分之几十,据此解答。
【解析】500÷200=2(个)……100(元)
500-2×50
=500-100
=400(元)
400÷500×100%
=0.8×100%
=80%
80%就是八折。
现在买这件外套实际花400元,相当于打八折出售。
56.40∶1 放大
【分析】比例尺=图上距离∶实际距离,据此求出比例尺,把零件在图纸上放大时,是放大比例尺,据此解答即可。
【解析】比例尺:
10厘米∶2.5毫米
=10厘米∶0.25厘米
=1000∶25
=40∶1
所以这幅图纸的比例尺是40∶1,是放大比例尺。
57.5厘米/5cm 62.8立方厘米/62.8cm3
【分析】根据题意可知,圆锥和圆柱的体积相等,根据“”求出圆锥的体积,再除以圆柱的底面积即可解答。
【解析】
(立方厘米)
=62.8÷12.56
(厘米)
所以圆柱的高是5厘米,体积是62.8立方厘米。
58.10
【分析】先根据比例尺=图上距离∶实际距离,代入数据求出比例尺,再根据图上距离=实际距离×比例尺,即可得解,注意根据1千米=100000厘米,把单位千米转化为厘米。
【解析】30千米=3000000厘米
150千米=15000000厘米
(厘米)
因此,图上距离是10厘米。
59.18.84
【分析】圆柱的侧面积=底面周长×高=πdh,据此代入数据计算即可。
【解析】3.14×2×3
=6.28×3
=18.84(平方米)
则至少需要18.84平方米的钢化玻璃。
60.6.28m3/6.28立方米
【分析】根据圆柱的体积公式,代入数据计算即可得解。
【解析】
(m3)
它的容积是6.28m3。
61.七 14
【分析】把儿童学习用品的原价看作单位“1”,优惠30%,则现价是原价的1-30%=70%,70%就是打七折;打七折,表示现价是原价的70%,根据“求一个数的百分之几是多少,用乘法计算”,用彩笔的原价乘70%即可求出现价。
【解析】1-30%=70%,也就是打七折出售;
20×70%
=20×0.7
=14(元)
则现价是14元。
62.5∶9=30∶54 4∶2=10∶5
【分析】第一个空,直接将“÷”换成“∶”,即可改写成比例;第二个空,根据比例的基本性质,比例的两内项积=两外项积,只要4和5同时在比例的外项或内项,2和10同时在比例的内项或外项即可。
【解析】5÷9=30÷54就可以改写成比例5∶9=30∶54;4×5=2×10可以改写成比例4∶2=10∶5(答案不唯一)。
63.2880
【分析】根据利息=本金×利率×存期,代入数据求出她能取出来的利息。
【解析】由分析可得:
30000×3.20%×3
=960×3
=2880(元)
综上所述:李老师将30000元存入银行,定期3年,如果年利率3.20%,到期后可得到利息2880元。
64.80 400
【分析】用实际克数除以显示的克数,求出实际克数是显示克数的百分之几;再用显示克数乘实际克数占显示克数的百分率,即可求出如果该秤显示的克数是500,那么实际只有多少克。
【解析】500÷625×100%
=0.8×100%
=80%
500×80%=400(g)
实际克数只是显示克数的80%,如果该秤显示的克数是500,那么实际只有400g。
65.原价 15
【分析】一个整体可以用自然数1表示,我们通常把它叫做单位“1”。确定单位“1”,关键是看以谁为标准,谁是标准谁就是单位“1”,题中耳机以原价的八五折出售,是把原价看作单位“1”;打折就是按照折数低价出售商品,几折就是百分之几十,1-折扣=现价比原价降低了百分之几。
【解析】1-85%=15%
“双十一”购物节来了,网上的商品迎来大减价,聪聪喜欢的一款耳机以原价的八五折出售,可以把原价看作单位“1”,现价比原价降低了15%。
66.条形 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解析】如果要统计上个月我市每周接种人数的多少情况,应选用条形统计图;如果要反应每周接种疫苗的人数增减变化情况,应选用折线统计图;如果要反映上个月我市各县区接种人数与我市接种总人数之间的关系,应选用扇形统计图。
67. 12.5
【分析】根据比的意义,把桃树的棵数看作7份,梨树的棵数看作8份,根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用7÷8即可求出桃树棵树是梨树棵数的几分之几;用8÷(7+8)即可求出梨树棵数占两种树总棵数的几分之几;再根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用(8-7)÷8×100%即可求出桃树棵树比梨树棵数少百分之几;根据求一个数比另一个数多几分之几,用相差数除以另一个数,则用(8-7)÷7即可求出梨树棵数比桃树棵数多几分之几。
【解析】把桃树的棵数看作7份,梨树的棵数看作8份,
7÷8=
桃树棵数是梨树棵数的;
(8-7)÷8×100%
=1÷8×100%
=12.5%
桃树棵树比梨树棵数少12.5%。
(8-7)÷7
=1÷7
=
8÷(7+8)
=8÷15
=
梨树棵数占两种树总棵数的。
68.125
【分析】要求每个小圆柱的体积,需要求出这个小圆柱的底面积和高;3个完全相同的小圆柱拼成一个大圆柱时,高是30厘米,由此可知,用30÷3,求出小圆柱的高;表面积减少了50平方厘米,是指4个圆柱的底面的面积和,用50÷4,求出一个圆柱的底面积;再根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【解析】(50÷4)×(30÷3)
=12.5×10
=125(立方厘米)
将3个完全相同的小圆柱,拼成一个高是30厘米的大圆柱,表面积减少了50平方厘米,原来每个小圆柱的体积是125立方厘米。
69.3.6
【分析】用4720-4000,求出利息,再用利息÷本金÷时间×100%,即可求出年利率,即可解答。
【解析】(4720-4000)÷4000÷5×100%
=720÷4000÷5×100%
=0.18÷5×100%
=0.036×100%
=3.6%
王青把压岁钱4000元存入银行,定期5年,到期后王青取回4720元,该银行五年期的年利率是3.6%。
70.5.652
【分析】根据题意可知,水管的直径是2厘米,水管内水的流速是每秒10厘米,相等于底面直径是2厘米,高是10厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,求出高是10厘米的圆柱的体积,1分钟=60秒,把3分钟=180秒;再用高是10厘米的圆柱的体积×180,求出3分钟流出的水的体积,再化成升,即可解答。
【解析】3分钟=180秒
3.14×(2÷2)2×10×180
=3.14×12×10×180
=3.14×1×10×180
=3.14×10×180
=31.4×180
=5652(立方厘米)
5652立方厘米=5.652升
学校自来水管的直径是2厘米,水管内水的流速是每秒10厘米,阳阳洗完手忘记关水龙头,3分钟后小欣发现并关掉了水龙头,共浪费了5.652升水。
71.628cm3/628立方厘米
【分析】减少的表面积是圆柱的侧面积,减少的表面积÷截短的高=圆柱底面周长,圆柱底面半径=底面周长÷圆周率÷2,圆柱体积=底面积×高,据此列式计算。
【解析】94.2÷3=31.4(cm)
31.4÷3.14÷2=5(cm)
3.14×52×8
=3.14×25×8
=628(cm3)
原来这个圆柱的体积是628cm3。
72.45 15
【分析】把一个圆柱形木料削成最大的圆锥,这个圆锥和圆柱等底等高,则圆柱的体积与圆锥的体积比是3∶1,即圆柱的体积是3份,圆锥的体积是这样的1份,相差2份,就是30立方厘米,每一份就是15立方厘米,3份就是圆柱的体积,1份是圆锥的体积。
【解析】30÷(3-1)
=30÷2
=15(立方厘米)
15×3=45(立方厘米)
则圆柱的体积是45立方厘米,,圆锥的体积是15立方厘米。
73.2.5
【分析】根据题意可知,圆柱的侧面沿高展开得到一个边长是15.7分米的正方形,则圆柱的底面周长等于圆柱的高;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,即可解答。
【解析】15.7÷3.14÷2
=5÷2
=2.5(分米)
一个圆柱的侧面沿高展开后得到一个边长是15.7分米的正方形,原来圆柱的底面半径是2.5分米。
74.75.36立方厘米
【分析】根据题意,将圆柱截成3个完全相同的小圆柱,表面积增加了4个底面的面积,这时表面积比原来增加了50.24平方厘米,所以圆柱的底面积为平方厘米,圆柱的体积=底面积×高,据此即可算出原来圆柱的体积。
【解析】(平方厘米)
(立方厘米)
所以原来圆柱的体积是75.36立方厘米。
75.50.24
【分析】根据题意可知,圆柱沿直径垂直切开后是一个正方形,则圆柱的底面直径等于圆柱的高;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【解析】3.14×(4÷2)2×4
=3.14×22×4
=3.14×4×4
=12.56×4
=50.24(立方厘米)
一个圆柱的高是4厘米,沿直径垂直切开后,切面是一个正方形,这个圆柱的体积是50.24立方厘米。
76.16.8
【分析】根据圆柱的体积=底面积×高,可推出高=圆柱的体积÷底面积;根据圆锥的体积=底面积×高÷3,可推出高=圆锥的体积×3÷底面积;把底面积看成S,把圆锥的体积看作1,则圆柱的体积为6,那么圆柱的高为6÷S=,圆锥的高为1×3÷S=3÷S=,圆柱与圆锥高的比为:∶=2∶1,即圆柱的高是圆锥的2倍,圆柱的高为8.4×2=16.8(厘米),据此解答。
【解析】由分析可知:
把底面积看成S,把圆锥的体积看作1份,则圆柱的体积为6份
圆柱的高为:6÷S=
圆锥的高为:1×3÷S
=3÷S
=
圆柱与圆锥高的比为:∶
=∶
=6∶3
=2∶1
8.4×2=16.8(厘米)
所以圆柱的高为16.8厘米。
77.11.04 3.68
【分析】圆柱和圆锥等底等高,可知圆柱的体积是圆锥的体积的3倍,把圆锥的体积看作1份,则圆柱的体积就看作3份,它们的体积就相差了(3-1)份,而体积相差7.36立方米,从而可以求出平均1份是多少,即求出圆锥的体积,再求出圆柱的体积即可。
【解析】7.36÷(3-1)
=7.36÷2
=3.68(立方米)
3.68×3=11.04(立方米)
圆柱的体积是11.04立方米,圆锥的体积是3.68立方米。
78.1.1775
【分析】把一根圆柱形木料截成3段小圆木,表面积增加了314平方分米,那么增加的表面积是4个底面积,用增加的表面积除以4,即可求出圆柱的底面积;然后根据S底=πr2,得出圆柱的底面半径;
若沿底面直径平均分成两个半圆柱体,表面积增加300平方分米,那么增加的表面积是2个以底面直径和高分别为长、宽的长方形,用增加的表面积除以2,求出一个截面的面积,再除以直径,即可求出圆柱的高;
最后根据圆柱的体积公式V=Sh,求出木料原来的体积。注意单位的换算:1立方米=1000立方分米。
【解析】圆柱的底面积:314÷4=78.5(平方分米)
底面半径的平方:78.5÷3.14=25(平方分米)
因为25=5×5,所以圆柱的底面半径是5分米;
圆柱的底面直径:5×2=10(分米)
圆柱的高:
300÷2÷10
=150÷10
=15(分米)
圆柱的体积:
78.5×15=1177.5(立方分米)
1177.5立方分米=1.1775立方米
木料原来的体积是1.1775立方米。
79.6.28 6.28
【分析】从“高减少2厘米,底面积不变”可知,表面积减少了12.56平方厘米,就是侧面积减少了12.56平方厘米。根据侧面积=底面周长×高,可得底面周长=侧面积÷高,用12.56÷2即可求出底面周长,进而可求出底面半径。因为底面积不变,所以体积减少的部分的形状也是圆柱;根据圆柱的体积=底面积×高,代入数据,即可求出减少的体积。据此解答。
【解析】底面周长:12.56÷2=6.28(厘米)
减少的体积:
(6.28÷3.14÷2)2×3.14×2
=12×3.14×2
=1×3.14×2
=6.28(立方厘米)
这个圆柱形橡皮泥的底面周长是6.28厘米,体积减少了6.28立方厘米。
80.4.5216
【分析】先计算出一分钟每个出水管喷出水的体积,利用圆柱的体积=底面积×高;用出水管的底面积乘一分钟喷出水的长度;一分钟喷出水的长度=速度×时间,代入相应数值计算;再用每个出水管喷出水的体积乘48,求出一分钟一共会喷出水的体积,最后用水的体积乘每立方米水的质量,求出水的总质量,据此解答。
【解析】1分=60秒
2厘米=0.02米
3.14×(0.02÷2)2×(5×60)
=3.14×0.012×300
=3.14×0.0001×300
=0.0942(立方米)
48×0.0942=4.5216(立方米)
4.5216×1=4.5216(吨)
因此一分钟会浪费4.5216吨水。
81.3 9 9 27
【分析】设圆柱的底面半径是1,高是1,变化后的底面半径是3,高是3,根据C=2πr,S=πr2,S侧=2πrh,V=πr2h,用变化后的底面周长、底面积、侧面积、体积结果,除以变化前的结果就是扩大的倍数,据此解答。
【解析】设圆柱的底面半径是1,高是1,变化后的底面半径是3,高是3,
底面周长:(2π×3)÷(2π×1)=6π÷2π=3
底面积:(π×32)÷(π×12)=9π÷π=9
侧面积:(2π×3×3)÷(2π×1×1)=18π÷2π=9
体积:(π×32×3)÷(π×12×1)=(π×9×3)÷(π×1×1)=27π÷π=27
因此底面周长扩大到原来的3倍,底面积扩大到原来的9倍,侧面积扩大到原来的9倍,体积扩大到原来的27倍。
82.0.4∶2=3∶15
【分析】根据比例的基本性质:内项积=外项积,内项积是6,其中有一个外项是0.4,即用除法得出另外一个外项是15,内项两个质数相乘,6=2×3,则内项是2和3,写出相应的比例(答案不唯一)。
【解析】6÷0.4=15
6=2×3
这个比例可以写成0.4∶2=3∶15(答案不唯一)
83.正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解析】y=8x,则y∶x=8(一定),x和y成正比例;
x=,则xy=5(一定),x和y成反比例。
如果y=8x,那么x和y乘正比例;如果x=,那么x和y成反比例。
84.2∶3 2∶3 能 4∶9 不能
【分析】(1)两数相除又叫两个数的比,正方形周长=边长×4,据此写出甲、乙两个正方形的边长之比和周长之比,化简,并求出比值,根据表示两个比相等的式子叫比例,确定能否组成比例;
(2)正方形面积=边长×边长,写出甲、乙两个正方形的面积之比,并求出比值,根据比例的意义,确定面积之比和边长之比能否组成比例。
【解析】(1)边长之比:4∶6=(4÷2)∶(6÷2)=2∶3=2÷3=
周长之比:(4×4)∶(6×4)=16∶24=(16÷8)∶(24÷8)=2∶3=
图中甲、乙两个正方形的边长之比是2∶3,周长之比是2∶3,这两个比能组成比例。
(2)面积之比:(4×4)∶(6×6)=16∶36=(16÷4)∶(36÷4)=4∶9=4÷9=
甲、乙两个正方形的面积之比是4∶9,这个比和边长之比不能组成比例。
85.反 2
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(2)根据所成比例,进行解答。
【解析】(1)2.5×48=120
4×30=120
6×20=120
10×12=120
2.5×48=4×30=6×20=10×12=120(一定),所以货车的载质量与所需货车的数量成反比例。
(2)2.5×48÷60
=120÷60
=2(节)
如果改用每节车厢载质量为60吨的火车运输,需要2节这样的车厢。
86.反 正
【分析】由正比例与反比例的意义可知:两个相关联的量,当它们的比值(商)一定时,这两个量成正比例;当它们的乘积一定时,这两个量成反比例。
【解析】六年级同学排队做广播操,每行人数×排成的行数=六年级总人数(一定),所以每行人数和排成的行数成反比例;
圆锥的底面半径一定,即圆锥的底面积一定。根据圆锥的体积公式可知,圆锥的体积÷高=×底面积,圆锥的底面积一定,则圆锥的体积和高成正比例。
87.①③ ②⑥ ④⑤
【分析】第①个,每千米耗油量一定,路程越大,耗油总量越多,耗油总量除以路程,得到每千米耗油量,结果是定值,正比例关系;
第②个,圆锥体的体积一定,它的底面积和高乘积是定值,反比例关系;
第③个,出油率一定,花生油的质量和花生的质量的比值是定值,正比例关系;
第④个,已读的页数与未读的页数的乘积和比值都在变化,不是定值,不存在比例关系;
第⑤个,用正方形的面积S除以边长a,结果是变量,所以不构成正比例,而边长变大,面积变大,更不可能是反比例,所以二者不构成比例关系;
第⑥个,剪成同样长的小段,每段的长度越长,段数就越少,且每段的长度与剪成的段数的乘积是总长,是定值,典型的反比例关系。
【解析】成正比例的有①③,成反比例的有②⑥,既不成正比例也不成反比例的有④⑤。
88.成反比例 不成比例 成正比例 不成比例
【分析】x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析。
【解析】(1)每盒装的个数×需要的盒数=总个数,乒乓球总个数一定,每盒装的个数和需要的盒数。成反比例
(2)男生人数+女生人数=总人数,全班人数一定,男生人数和女生人数。不成比例
(3)织布总米数÷时间=每小时织布米数,每小时织布的米数一定,织布的总米数和时间。成正比例
(4)长+宽=长方形的周长÷2,长方形的周长一定,长方形的长和宽。不成比例
89.3
【分析】把5分钟看作单位“1”,根据百分数乘法的意义,用5×1%即可求出用5G下载的时间,再把单位换算成秒。
【解析】5×1%=0.05(分钟)
0.05×60=3(秒)
只需3秒。
90.96% 750
【分析】发芽路=发芽种子数÷种子总数×100%,据此求出发芽率;将种子总数看作单位“1”,发芽种子数÷发芽率=种子总数,据此列式计算。
【解析】48÷(48+2)×100%
=48÷50×100%
=0.96×100%
=96%
720÷96%=720÷0.96=750(粒)
这批种子的发芽率是96%。照这样计算,要想保证有720粒种子发芽,至少要种750粒。
91.17.1 19
【分析】由题目可知,每100克鸡蛋中含蛋白质14克,每100克面粉中含蛋白质10.1克,那么50克鸡蛋中含蛋白质的重量就是(14÷2)克,用50克鸡蛋和100克面条中含蛋白质的重量相加即可求出这顿饭淘气一共摄入蛋白质多少克;再用这顿饭淘气一共摄入蛋白质重量除以一个儿童每天需要的蛋白质重量,即可求出大约占一天所需蛋白质总量的百分之几。
【解析】(14÷2)+10.1
=7+10.1
=17.1(克)
17.1÷90×100%
=0.19×100%
=19%
这顿饭淘气一共摄入蛋白质17.1克,大约占一天所需蛋白质总量的19%。
92.85 115
【分析】把原价看作单位“1”,八五折就是现价是原价的85%。一成五就是15%,把去年的玉米的产量看作单位“1”,今年是去年的1+15%,据此解答。
【解析】八五折就是现价是原价的85%。
一成五就是15%。
1+15%=115%
“妇女节”期间游乐园门票八五折优惠,现价是原价的85%,今年的玉米产量比去年增产一成五,今年产量是去年的115%。
93.40 60 50 33.3
【分析】用这袋面粉用去的重量+剩下的重量,求出这袋面粉的总重量,再用用去面粉的重量÷这袋面粉的总重量×100%,求出用去这袋面粉的百分比;
把这袋面粉的总重量看作单位“1”,用1减去用去面粉占总重量的百分比,求出剩下面粉占总重量的百分比;
用用去面粉的重量与剩下面粉的重量差,除以用去面粉的重量,再乘100%,求出剩下的比用去的多的百分之几;
用用去面粉的重量与剩下面粉的重量差,除以剩下面粉的重量,再乘100%,求出用去的比剩下的少百分之几,据此解答。
【解析】10÷(10+15)×100%
=10÷25×100%
=0.4×100%
=40%
1-40%=60%
(15-10)÷10×100%
=5÷10×100%
=0.5×100%
=50%
(15-10)÷15×100%
=5÷15×100%
≈0.333×100%
=33.3%
一袋面粉,用去10千克,还剩15千克,用去这袋面粉的40%,还剩这袋面粉的60%,剩下的比用去的多50%,用去的比剩下的少33.3%
94.25
【分析】求张华滑完全场所用的时间比莉莉多百分之几,用张华滑完全场比莉莉多用的时间除以莉莉滑完全场用的时间,结果用百分数表示,据此解答。
【解析】
张华滑完全场所用的时间比莉莉多25%。
95.20;32;40;75;七成五
【分析】小数化成分数,两位小数先化成分母为100的分数,再化简成最简分数;
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号;
根据成数的意义,百分之几十几就是几成几。
【解析】0.75==
==,=15÷20
==
==,=30∶40
0.75=75%
75%=七成五
即15÷20=0.75==30∶40=75%=七成五。
96.85 10
【分析】把原价看作单位“1”,打八五折就是现价是原价的85%,打九折就是现价是原价的90%,节省了(1-90%),据此解答。
【解析】游乐园门票八五折优惠,也就是现价是原价的85%;学习用品一律打九折出售,也就是现价是原价的90%。
1-90%=10%,所以节省了10%。
因此“儿童节”期间游乐园门票八五折优惠,现价是原价的85%;儿童文具店所有学习用品一律打九折出售,节省10%。
97.5275
【分析】存入银行的钱叫做本金;取款时银行多支付的钱叫做利息;单位时间(如1年、1月、1日等)的利息与本金的比值叫做利率。根据利息=本金×年利率×年数,本金+利息即到期后能取回的钱数,据此解答。
【解析】5000×2.75%×2+5000
=5000×2×2.75%+5000
=275+5000
=5275(元)
到期后共可取回5275元。
98.50
【分析】已知2022年、2023年一年级新生入学人数,根据新生入学增长率=(2023年一年级新生入学人数-2022年一年级新生入学人数)÷2022年一年级新生入学人数×100%,据此计算得出答案。
【解析】一年级新生入学增长率约为:
99.8
【分析】设买了x支圆珠笔,则买了(10-x)支钢笔,根据圆珠笔单价×圆珠笔数量+钢笔单价×钢笔数量=花的总钱数,列出方程求出x的值即可。
【解析】解:设买了x支圆珠笔。
3.5x+7.5×(10-x)=43
3.5x+75-7.5x=43
75-4x=43
75-4x+4x=43+4x
43+4x=75
43+4x-43=75-43
4x=32
4x÷4=32÷4
x=8
买了8支圆珠笔。
100.6
【分析】根据等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,圆锥部分的高÷3=倒入圆柱部分的高,再加上圆柱部分原来的高即可。
【解析】12÷3+2
=4+2
=6(厘米)
细沙的高度是6厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
