(期末考点培优)专题06 解答题 2024-2025学年六年级数学下册期末复习专项青岛版(六三制)(含答案解析)
文档属性
| 名称 | (期末考点培优)专题06 解答题 2024-2025学年六年级数学下册期末复习专项青岛版(六三制)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 10:51:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项青岛版(六三制)
(期末考点培优)专题06 解答题
学校:___________姓名:___________班级:___________考号:___________
1.联合国教科文组织自1995年起,把4月23日定为“世界阅读日”,希望借助这个重要的日子,向大家推广阅读和写作。
(1)据有关资料统计,世界上平均每人每年读书量最多的民族是犹太族,我国的人均阅读量比犹太族少92%。已知我国人均阅读量是每年4.8本,犹太族的人均阅读量是每年多少本?
(2)这天各网站推出了购书优惠活动:A网站可享“每满300元减100元”B网站可享“折上折”,即先打七折再打九折。王老师为充实班级图书角,打算购买一套原价1200元的图书,在哪个网站购书更优惠?
2.我国的高铁建设技术在世界位于领先地位。目前正在修建的高铁梅龙路段,计划每天铺设轨道5公里,将用19.2天完成铺设任务,实际每天铺设6公里,铺完这段轨道实际需要多少天?(用比例知识解答)
3.从古代到近代,匠人们打铁时,用火将铁烧红变软,然后用锤子击打成想要的形状,最后放到凉水里迅速冷却,以增加铁的硬度,这就是“淬(cuì)火”。铁匠将长方体铁块击打成底面半径是2分米,高为6分米的圆锥,然后完全浸没入一个底面半径是5分米的圆柱体容器里淬火,此时圆柱容器里面的水面将会上升多少分米?(损耗忽略不计)。
4.王明从家骑自行车去少年宫,先走上坡路到达A,再走平路到达B。
(1)请结合两图相关信息,算一算,并把图补充完整。
(2)下坡比上坡每分钟多行多少米?
5.某天下午4时,同学们在操场同时测得竹杆的高度和影子的长度,同时还测得教学楼的影长,具体数据如下图:
(1)观察两组数据,你有什么发现?
(2)利用你的发现,求这座教学大楼的高度。估计这幢教学楼是几层?
6.为解决家长上下班接送孩子难问题,武城县每个学校开展了课后延时服务活动,课后延时服务的内容丰富多彩,各种社团百花齐放。足球社团李老师要准备60个足球,现有甲、乙、丙三个商店可以选择。三个商店里足球的单价都是50元,但各个商店的优惠方法不同。
甲店:买10个足球免费赠送2个,不足10个不赠送。 乙店:每个足球打八五折。 丙店:购物每满200元返还现金30元。为了节省费用,李老师应到哪个商店购买?为什么?
7.一根圆柱形木料,如果截成两个小圆柱,它的表面积增加15.7平方分米,如果沿着底面直径截成两个半圆柱,它的表面积将增加80平方分米,这根圆柱形木料的表面积是多少?
8.周末张乐和爸爸去沙滩游玩,爸爸堆了一个近似圆锥的沙堆,沙堆占地面积6平方米,高1.6米,张乐的爸爸准备把这堆沙滩铺到一条宽4米的路上,铺5厘米厚,可以铺多少米?
9.小芳想测量出一块儿鹅卵石的体积,按如下步骤进行了实验。
步骤一:在底面直径是8厘米的圆柱体容器中盛10厘米深的水。
步骤二:将鹅卵石浸没在水中,水面比原来上升了2厘米。
(1)容器中装了多少毫升水?
(2)这块鹅卵石的体积是多少立方厘米?
10.某居民小区的房价原来每平方米6000元,现在下降了一成。
(1)现在房子的售价是每平方米多少元?
(2)李明家打算买该小区一套105平方米的房子,选择一次性付清房款,可以享受九五折的优惠,优惠后李明家实际购买这套房子共付房款多少元?
(3)李明的爸爸三年前将60万元钱存入银行,年利率是2.75%,为买房子,爸爸将这批钱取出,他的爸爸一共可以取出多少元钱?
11.阅读经典,与书同行。读书节活动中。赵老师推荐同学们阅读《骑鹅旅行记》和《鲁滨逊漂流记》这两本书。
(1)张乐打算先阅读《骑鹅旅行记》这本书,如果每天读30页,8天可以读完,张乐想6天读完。他平均每天要多读多少页?(用比例知识解答)
(2)赵老师想买24本《鲁滨逊漂流记》充实班级图书角,周末她走访了甲、乙两家书店,两家书店标价都是50元,但促销方式各不相同,赵老师只带了1000元,你会建议他到哪家店购买?
甲店 乙店
买十送二 打八折
12.河南省的滑县木版年画是国家级非物质文化遗产之一。王爷爷将卖年画所得的2万元存入银行,定期为三年,年利率是1.65%,到期后将本金和利息全部取出,王爷爷能取出多少元钱?
13.一辆邮政车按导航提示从上海出发去德州市运送快递,早上6:00出发,8:00到达第一个收费站时已经行了160千米,照这样的速度,几个小时能到达德州市?
14.2023年受台风“杜苏芮”影响,河北省涿州市遭受到罕见的特大暴雨洪水灾害,全国各地时刻关注灾情发展,伸出援助之手。张叔叔负责驾车从德州到河北运送物资,通过导航系统查得行程信息如图。
(1)德州到涿州实际距离有多远?
(2)张叔叔驾驶的货车出发了2小时一共行驶了140千米。照这样的速度,张叔叔还要行驶多长时间能到达河北省涿州市?(结果用分数表示)
15.有一张长方形铁皮(如图),剪下图中两个圆及一个长方形,正好可以做成一个圆柱,已知圆柱的底面直径为8厘米。
(1)原来长方形铁皮的面积是多少?
(2)这个圆柱的体积是多少?
16.聊城财金热力去年12月份运进一堆煤,原计划每天烧3吨。可以烧96天,由于改造锅炉,每天可以节约0.6吨,改造锅炉后,这堆煤可以烧多少天?(用比例解答)
17.在比例尺是1∶4000000的地图上,量得甲、乙两地的距离是30厘米。两列火车同时从甲、乙两地相对开出,甲车每小时行65千米,乙车每小时行55千米。几小时后两车才能相遇?
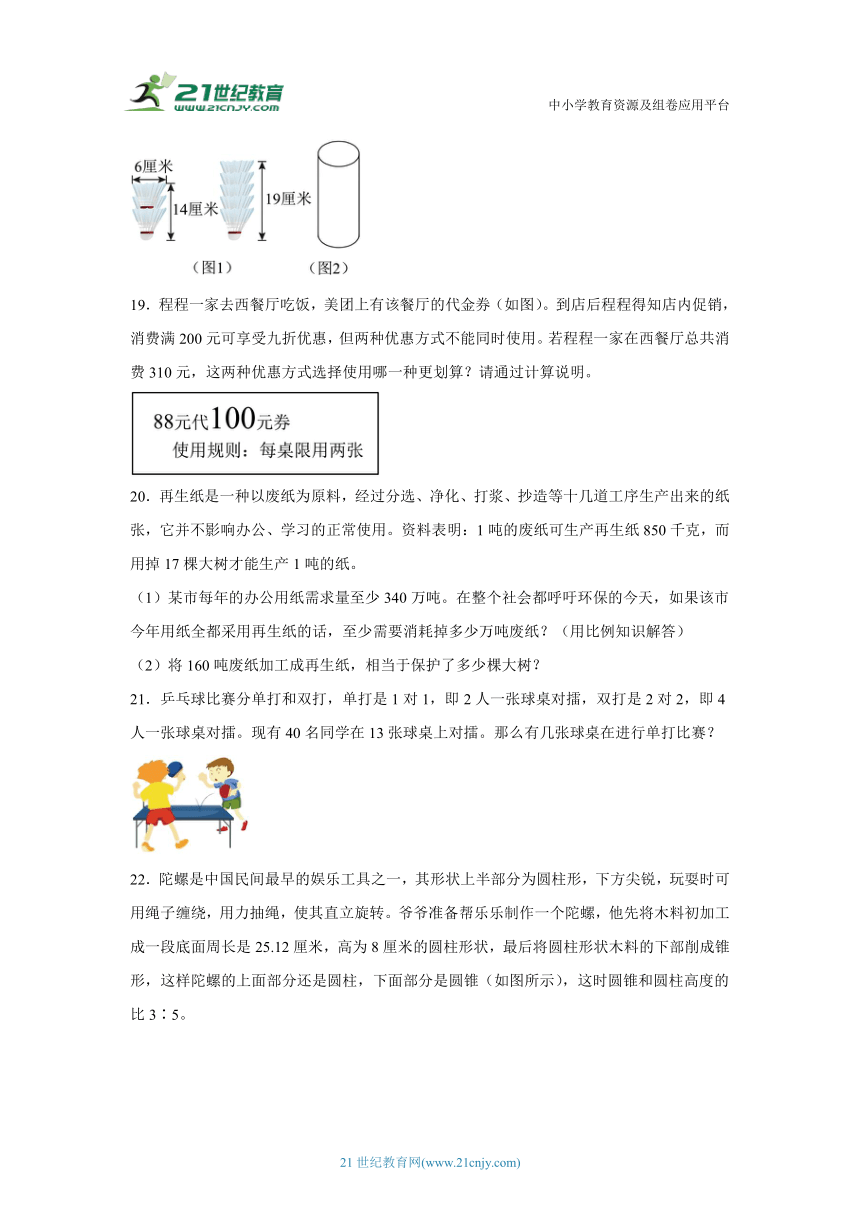
18.羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
19.程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
20.再生纸是一种以废纸为原料,经过分选、净化、打浆、抄造等十几道工序生产出来的纸张,它并不影响办公、学习的正常使用。资料表明:1吨的废纸可生产再生纸850千克,而用掉17棵大树才能生产1吨的纸。
(1)某市每年的办公用纸需求量至少340万吨。在整个社会都呼吁环保的今天,如果该市今年用纸全都采用再生纸的话,至少需要消耗掉多少万吨废纸?(用比例知识解答)
(2)将160吨废纸加工成再生纸,相当于保护了多少棵大树?
21.乒乓球比赛分单打和双打,单打是1对1,即2人一张球桌对擂,双打是2对2,即4人一张球桌对擂。现有40名同学在13张球桌上对擂。那么有几张球桌在进行单打比赛?
22.陀螺是中国民间最早的娱乐工具之一,其形状上半部分为圆柱形,下方尖锐,玩耍时可用绳子缠绕,用力抽绳,使其直立旋转。爷爷准备帮乐乐制作一个陀螺,他先将木料初加工成一段底面周长是25.12厘米,高为8厘米的圆柱形状,最后将圆柱形状木料的下部削成锥形,这样陀螺的上面部分还是圆柱,下面部分是圆锥(如图所示),这时圆锥和圆柱高度的比3∶5。
(1)陀螺的体积是多少立方厘米?
(2)奶奶说要把陀螺上面圆柱部分刷上红色油漆,如图圆锥部分刷黄色油漆,刷红色油漆部分的面积是多少平方厘米?
23.小明在某个晴天的上午利用卷尺和2米长的竹竿测量学校旗杆的高度,他将竹竿直立在学校旗杆的旁边,量得竹竿的影长是1.6米,同一时刻测得旗杆的影长是9.6米,求旗杆的高度。(用比例解答)
24.3月12日植树节,树人小学组织同学们到劳动基地栽一批果树苗。如果每行栽18棵,恰好可以栽40行。如果每行栽15棵,这些树苗要栽多少行?(用比例的方法解答)
25.我们学习圆柱表面积时得出:圆柱的表面积=侧面积+底面积×2=2πrh+2πr2,圆圆在研究中又发现了如下方法,如图所示“圆柱的表面展开图是一个长方形和两个圆,把圆柱的两个底面转化成两个近似的长方形,平移后,与圆柱侧面展开成的长方形合并从而得到一个大的长方形,就可以推导出圆柱的表面积公式”。
(1)分析:拼成的长方形的长相当于圆柱的 ,宽相当于圆柱的 。
(2)归纳:圆柱的表面积就等于拼成的长方形的面积=长×宽= × 。(用含字母的式子表示)
(3)应用:当r=4cm,h=10cm时,用上面的方法计算圆柱的表面积是 平方厘米。
26.光明小学六年级一班全体同学参加最喜欢的运动项目调查活动(每人只能选一项),同学们正在将调查的结果绘制成下面两幅统计图,你能按要求帮他们完成统计表中剩余的部分,并回答出下列问题吗?相信你能细心的完成!
(1)六年级一班一共有学生________人。
(2)喜欢踢毽子的人数占全班总人数的_______%。
(3)全班喜欢乒乓球的比喜欢跳绳的多_______人。
(4)在图1中分别画出乒乓球和跳绳项目的条形图。
27.操场上,同学们正在阳光下测量竹竿高度以及它们影子的长度,测量数据如表。
竹竿 实际高度/m 影子长度/m
竹竿1 1.2 0.4
竹竿2 2.1 0.7
如果这时同学们测出旗杆的影子长度是5.6米,那么旗杆的实际高度是多少米?(用比例解答)
28.实际应用。
在比例尺是1∶3000000的地图上,量得甲、乙两地的距离是20厘米,现一辆客车和一辆货车分别从甲、乙两地同时出发,相向而行,经过4小时相遇。若客车的速度是55千米/时,则货车的速度是多少?
29.等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6厘米的圆柱体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
30.数据分析。
吕剧是国家级非物质文化遗产,中国八大戏曲剧种之一,山东最具代表性的地方剧种。滨州博兴作为吕剧艺术的发源地,创排了一批群众喜闻乐见、脍炙人口的优秀吕剧作品,在全国戏曲评比和展演中屡获佳绩。其中,并绘制了下面两幅不完整的统计图。
(1)该吕剧团共有多少人?
(2)把条形统计图中的人数和扇形统计图中的百分数补充完整。
31.如图是小明坐出租车去展览馆的路线图。已知出租车在3千米以内(含3千米)按起步价8元计算,以后每增加1千米车费就增加1.4元。请你按图中提供的信息算一算,小明完成这次参观(单程)一共要花多少元出租车费?
32.五一期间,商店进行优惠大酬宾活动,所有商品一律按照盈利30%定价,然后打八折出售,已知一件商品最终售价为208元,求这件商品的进价是多少钱?
33.如图,同学们在阳光下分别测量出两根直立竹竿的长度和它们的影子长度,同时,测量出大树的影子长度为8.1米,请你通过计算得出大树的实际高度。(用比例知识解决问题)
34.用铁度制一个圆柱形油桶,底面的周长是6.28分米,高4分米。
①制这个油桶至少需要铁皮多少平方分米?(进一法取近似值,得数保留整平方分米)
②这个油桶大约能装汽油多少千克?(1升汽油0.68千克,得数用四舍五入法保留整数)
35.为了铺垫运动场,学校运来一批沙,堆成圆锥形沙堆。这个沙堆的底面半径是2米,高是1.2米,每立方米的沙堆约重1.7吨,这堆沙约重多少吨?(得数保留整数)
36.某市学生和儿童在三级医院住院就医,医疗费用支付方法如表。
标准 支付方法
一年内 650元以内(含650元) 个人支付全部费用
650元以上部分 个人支付25%,剩余75%由医疗保险基金支付
(1)明明做了一个小手术,住院医疗费用一共是3650元,按上面的方法计算,他本次住院需要个人支付多少钱?
(2)红红今年住院,按上面的方法计算,医疗费用由医疗保险基金支付了1800元。红红本次住院的医疗费用一共是多少钱?
37.我国风能资源丰富,风力发电架随处可见。数学实践小组测得一座风力发电架在阳光下的影长是64米。同时把一根长2米的竹竿直立在地上,测得在阳光下的影长是1.6米,风力发电架高多少米?(用比例知识解答问题)
38.根据《人类血型遗传学》的调查,中国大陆各民族血型百分比如下图。如果按照这样的百分比推算,某县2024级小学毕业生中AB型血的约有442人,那么O型血的有多少人?(得数保留整数)
39.乐乐在数学实践活动中做了一个沙漏。如图,圆锥形容器(装满沙子)的沙子一点点漏入下面的长方体木盒中,若沙子漏完了,那么在长方体木盒中会平铺上大约多少厘米高的沙子?(n取3计算)
40.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解决下面的问题)
(1)12只羊可以换多少把斧头?
(2)一位铁匠,想要制造一批斧头去换小山羊,原计划每天制造2把,24天完成。实际每天比计划多制造50%,实际提前几天完成?
41.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不懈追求的航天梦。经过几代人的不懈奋斗。我国的航天事业取得了辉煌成就。长征五号系列(简称CZ-5)运载火箭实现数字工程化应用,大大推动了航天产品数字化的进程。
(1)长征五号B型火箭在太空绕地球转了102圈。已知绕地球5圈大约需要7.5小时,那么长征五号B型火箭在太空大约运行了多长时间?(用比例解答)
(2)整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。如图是某型号运载火箭整流罩的简约示意图,整流罩本身的厚度不计,该整流罩的容积是多少?
42.我国民间常用生姜、红糖和水煎服以防感冒(俗称“姜汤”)。小明妈妈一般把生姜、红糖和水按2∶5∶75的质量比配好后,煎20分钟左右,做成姜汤,分给全家四口人喝。这天,小明妈妈准备了40克生姜。
(1)她需要准备红糖多少克?
(2)小明家有一个容量为2升的壶,用来煎这天的姜汤,壶够大吗?(1升水的质量为1千克)
(3)根据经验,妈妈估计姜汤煎好后蒸发掉的水量在60%左右,这天煎好后的姜汤大约有多少克?
43.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
44.高科技给我们的生活带来便利的同时,也给一些不法分子提供了可乘之机,他们的电信诈骗手段越来越难以防范。为了防止人们上当受骗,某公司开展了“经历最多的诈骗方式”的调查活动。经过整理分析后,绘制成了两个统计图。
(1)根据图中的信息可知,经历虚假中奖诈骗的有( )人;经历电话欠费诈骗的人数占调查总人数的( )%,有( )人。
(2)把上面的两个统计图补充完整。
(3)为了防止诈骗,你想对身边的人说些什么?
45.中国四大毛笔之乡有:浙江湖笔之乡、安徽宣笔之乡、河北侯笔之乡和山东齐笔之乡。某生产商将每支毛笔按商店定价的七折批发给商店,商店将定价降低10%卖给消费者。如果商店中每支毛笔的现在定价是7.2元,那么商店售出一支这种毛笔盈利多少元?
46.一个零食加工厂需要完成一批零食,每天加工零食的数量与需要的时间如下表。请你根据表格中数据,先填空,再解决问题。
每天加工的数量/袋 600 800 1000 1200
需要加工的时间/天 4 3 2.4 2
(1)因为( )一定,所以( )和( )成( )比例关系。
(2)如果每天加工480袋零食,加工完这批零件需要多少天?(用比例知识解答)
47.一个圆柱形茶叶罐,底面直径是10厘米,高是12厘米,将4个这样的茶叶罐按如图所示的方式紧密地放入纸盒中。
(1)这个纸盒内部的长( )厘米,宽( )厘米,高( )厘米。
(2)这个纸盒中还有空隙吗?如果有,请你算一算空隙有多大。
48.“中国科学制图学之父”裴秀所作的《禹贡地域图》18篇,是按“一分为十里,一寸为百里”的比例绘制而成的。将裴秀绘制地图的制图标准转化为现在国际通用的比例尺,大约相当于今天的1∶1500000。试着来解决下面的实际距离问题吧!
如果在一幅《禹贡地域图》上测得两城的直线距离是4厘米,请你计算两城的实际直线距离是多少千米?(列方程解答)
49.观察下面左图,把罐头盒的商标纸如下图所示沿高剪开,再展开。
(1)把圆柱侧面展开后,得到( )(填图形名称);这个图形的各边与圆柱有什么关系?其中运用什么数学思想方法?
(2)观察上面右图,圆柱的表面是由哪几部分组成的?
(3)圆柱的表面积计算公式是: 。(写字母表达式)
50.中国66号公路,又称为“草原天路”。公路沿线景观奇峻,是中国十大最美公路之一,限速30千米/时。在一幅比例尺是千米的地图上,量得这条公路的长度是4.5厘米。甲、乙两辆车分别从公路两端同时相对开出,经过3小时相遇。已知甲车平均每小时行驶22千米,乙车平均每小时行驶多少千米?
51.网上购物,已经成为人们日常生活的一部分。聪聪妈妈是网购达人,她想在网上购买一款破壁机。店铺活动信息和订单信息如下:
①店内所有商品按八折出售,并有礼品赠送;订单编号:1485987****
②“十一”当天前5分钟之内付款的顾客还能在原来折扣的基础上再享受九折优惠。
付款时间:2023-10-01-00:02:32
付款金额:720元
你能计算出这款破壁机的原价是多少元吗?
52.甲、乙两堆货物共重5.1吨,现在从甲堆中取出0.4吨货物放入乙堆,这时甲堆货物质量的40%等于乙堆货物质量的。乙堆货物原来有多少吨?
53.一个底面半径是9厘米,高是4厘米的圆柱形容器中装满了水,现在把水倒入一个底面半径是6厘米的圆锥形容器中,刚好装满,圆锥形容器的高是多少厘米?
54.探究底面半径为r,高为h的圆柱表面积时,有同学想到了这样的方法:先将两个底面转化成一个近似的长方形,然后与侧面展开后的长方形拼起来成为一个更大的长方形。
因为:圆柱表面积=整个长方形的面积
= 长 × 宽
所以:圆柱表面积S=( )×( )(用含有字母的式子表示)
若h=5厘米,r=2厘米,试着用以上方法求解圆柱的表面积。
55.妈妈给丽丽买了一个圆柱形玩具,玩具的底面直径是30厘米,高是50厘米。
(1)这个圆柱的占地面积是多少?
(2)这个圆柱在制作时至少需要多少平方厘米的皮革材料?(底面也用皮革)
56.动手实践。
测量1枚硬币的体积。
(1)上图是小丽的设计方法:把40枚硬币叠放在一起,先测量40枚硬币的体积(保留一位小数),再算出1枚硬币的体积。请你根据图中测量的尺寸,计算1枚硬币的体积。
(2)你还有其它的测量计算方法吗?请写下来。
57.如图,一个底面直径是20厘米的圆柱形容器,里面浸没着一个底面半径是5厘米的圆锥形铅锤。取出铅锤后,容器中的水面下降了0.5厘米,这个铅锤的高是多少厘米?
58.铺路基一般为包含石子、黏土、沙土等材料的混合材料。一个近似圆锥形的混合材料堆,底面半径5米,高2.4米。将这堆材料铺在长40米,宽10米的路面上,能铺多厚?
59.在比例尺为1∶200的地图上,小明家的客厅长为3厘米,宽为2厘米,爸爸在装修时想用一种浅白色的方砖铺地面,经询问商店,这种方砖铺18平方米需要618块,那么请你计算一下,在不浪费的情况下,爸爸买多少块这种方砖正好够用?
60.把一个底面半径是2厘米的圆锥形铅坠浸入一个装满水的圆柱形玻璃瓶中,玻璃瓶的底面半径是4厘米,将铅坠取出后瓶中水面下降了2厘米,这个铅坠的高是多少?(玻璃瓶壁的厚度忽略不计)
61.黄河流域是中华民族的重要发祥地之一,许多古代文明遗址和历史文化名城都分布在这里。为了更好地了解黄河,小齐买了一幅比例尺为1∶68300000的地图,在图上量得黄河的长度是8厘米,黄河的实际长度是多少千米?
62.在一幅比例尺是1∶500000的地图上量得A、B两地的距离是6.8cm,如果把A、B两地画在比例尺为1∶250000的新地图上,则A、B两地在新地图上的距离是多少厘米?
63.在一幅比例尺是1∶4000000的地图上,量得甲乙两地相距25厘米。一列火车从甲地开往乙地,2小时行驶了200千米,照这样的速度,还要多少小时才能到达乙地?
64.春季为防止流感病毒,放学后学校统一给教室地面和桌椅消毒,桶里有8.7升水,根据下面的说明,需要加入多少升84消毒剂?
84消毒剂的普通用具的使用方法: 1.一般物体 表面和公共场所环境下,用原液按1∶29的体积比兑水,浸泡20分钟。用抹布、拖把擦洗,或用塑料壶喷洒。 2.1∶25进行配比,主要是针对于医用垃圾和传染病病人的呕吐物、分泌物、排泄物,以及马桶等容器进行消毒。
65.丽丽和芳芳攒了一些零用钱,她们所积攒的钱数比是7∶5。在献爱心活动中,丽丽捐了48元,芳芳捐了20元,这时她们剩下的钱数相等。丽丽和芳芳原来各有多少钱?
66.蛋糕上涂抹的一层奶油是由淡奶油和糖粉打发而成的,淡奶油与糖粉的比是10∶3。妈妈买了一盒225克的淡奶油,要打发这盒淡奶油,需要加糖粉多少克?(用比例知识解答)
67.妈妈买回一瓶消毒液,瓶子上有这样的使用说明(见图)。乐乐要将衣物进行消毒,他倒出5克消毒液,需要加水多少克?(用比例解)
消毒清洗对象 消毒液∶水 衣物、物体表面 1∶300 瓜果、家具、厨房用品 1∶500
68.在今年的植树节活动中,为了增强学生爱护树木的意识,提高学生团结协作的能力,某校开展了以“种一棵小树,绿一方净土”为主题的植树活动。其中六年级植树55棵,六年级植树的棵数比五年级多10%,五年级植树多少棵?(画图分析数量关系并解答)
69.为了喜迎国庆,人民广场进行部分路面整修,如果用面积为9平方分米的方砖铺一部分路面,需要800块,如果改用边长为6分米的方砖铺这部分路面,需要多少块?(用比例解)
70.近两年,银行存款利率一降再降。2023年4月份,多家国有银行迎来新一波人民币存款利率下调,下表是本次调息前后某银行整存整取年利率变化表,如果同样是本金10万元定存三年,利息减少多少元?
银行调息前后存款利率表(部分)
整存整取 存期 年利率%(2024年3月) 年利率%(2024年4月)
一年 1.65 1.60
二年 2.05 1.90
三年 2.45 2.35
五年 2.50 2.40
71.育英小学举办演讲比赛,一等奖占参赛人数的10%,二等奖占参赛人数的30%,已知二等奖的人数比一等奖多6人,那么共有多少人参加比赛?
72.牙膏出口处半径为6毫米,蓝蓝每次刷牙都挤出1厘米长的牙膏,这支牙膏可用30次。如果将出口处半径改为5毫米,蓝蓝还是习惯每次挤1厘米长的牙膏。
73.市政府在“世界读书日”期间开展了“龙城读书节”活动,向广大市民发放图书消费券,活动如下图。2023年4月23日,新华书店所有书籍8折优惠。聪聪通过支付宝抢到了消费券,他想购买一本85元的图书,通过计算说明怎样购买便宜?(书店打折活动和消费券不能同时使用)
74.一个圆柱形零件,高是12厘米,底面半径是4厘米,零件的上端有一个圆柱形的孔,孔的直径是6厘米,深是7厘米。如果将这个零件接触空气部分的表面涂上防锈漆,一共需要涂多少平方厘米?
75.某书店在元旦这一天开展促销活动,推出购书优惠卡,顾客买一张优惠卡需付40元,凭此卡购买可打八折。李老师要为电脑兴趣小组的同学购买标价为48元的电脑书20本,要想花费最少,他应该选择优惠卡购买,还是原价购买?请计算说明。
76.一辆汽车从甲地开往乙地,第一小时行了全程的35%,第二小时行了全程的30%,第一小时比第二小时多行了18千米。甲、乙两地相距多少千米?
77.2工人师傅安装一批电线杆,计划每天安装12根,30天完成。由于改进了安装技术,实际每天比计划多安装6根。这批电线杆实际安装了多少天?(用比例知识解答)
78.恩格尔系数是根据恩格尔定律而得出的比例数。其主要内容是指一个家庭或个人收入越少,用于购买生存性的食物的支出在家庭或个人收入中所占的比重就越大。对一个国家而言,一个国家越穷,每个国民的平均支出中用来购买食物的费用所占比例就越大。恩格尔系数则由食物支出金额在总支出金额中所占的比重来最后决定。恩格尔系数达59%以上为贫困,50~59%为温饱,40~50%为小康,30~40%为富裕,低于30%为最富裕。贝贝一家三口人,本月计划支出5600元,其中文化支出为2240元,食物支出比文化支出少37.5%,其余的为其他支出。
(1)贝贝家食物支出是多少元?
(2)按照恩格尔系数计算,贝贝家处于什么水平?
79.一辆汽车,分期付款购买要多加价7%,如果现金购买可按九五折优惠。淘气的爸爸算了算,发现分期付款比现金购买多付7200元,请你算一算这辆车原价是多少元?
80.小刚进行测量土豆体积的实验,步骤如下:
准备一个底面直径10厘米的圆柱形玻璃容器,注入了9厘米深的水(如图①);放入土豆,浸没在水中,水面上升到11厘米处,此时水面距离容器口是1厘米(如图②);再放入土豆,此时有部分水溢出(如图③);取出土豆,这时水面距离容器口4厘米(如图④)。
图① 图② 图③ 图④
根据实验情况,请你解决以下问题:
(1)请求出土豆的体积。
(2)放入土豆后,溢出了多少毫升水?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.(1)60本;(2)B网站
【分析】(1)把犹太族每年人均阅读量看作单位“1”,我国的人均阅读量是犹太族的(1-92%),已知我国人均阅读量是每年4.8本,根据已知一个数的百分之几是多少,求这个数,用除法计算,据此求出未知的单位“1”;
(2)A网站可享“每满300元减100元”,算出1200里面有几个300,售价就需要减去几个100元;
打几折就是按照原价的百分之几十出售,B网站先打七折再打九折,售价=原价×70%×90%;
分别计算出两个网站的价格再比较。
【解析】(1)4.8÷(1-92%)
=4.8÷8%
=60(本)
(2)A网站:1200÷300=4
1200-4×100
=1200-400
=800(元)
B网站:
1200×70%×90%
=840×90%
=756(元)
756<800
答:在B网站购书更优惠。
2.16天
【分析】因为工作总量=工作效率×工作时间,工作总量一定,工作效率和工作时间成反比例,设实际每天铺x公里,列出反比例方程解答。
【解析】解:设铺完这段轨道实际需要x天。
6x=5×19.2
6x=96
6x÷6=96÷6
x=16
答:铺完这段轨道实际需要16天。
3.0.32分米
【分析】已知圆锥底面半径是2分米,高为6分米,根据圆锥的体积公式计算出圆锥的体积,也就是上升的水的体积;已知圆柱体容器的底面半径是5分米,根据圆的面积公式计算出圆柱的底面积,最后用上升的水的体积除以圆柱底面积就是上升的水的高度。
【解析】×3.14×22×6
=×3.14×4×6
=3.14×4×2
=12.56×2
=25.12(立方分米)
3.14×52
=3.14×25
=78.5(平方分米)
25.12÷78.5=0.32(分米)
答:此时圆柱容器里面的水面将会上升0.32分米。
4.(1)见详解;
(2)100米
【分析】(1)全程有三段组成,上坡路段、平路路段、下坡路段,把行全程所用时间看作单位“1”,减去上坡、下坡时间所占全程时间的百分比就是平路占全程时间的百分比。由图可知上坡路段所用时间是8分,占全程时间40%,根据已知一个数的百分之几是多少求一个数的方法,求出行全程所用时间,据此补充两图;
(2)根据图示可知上坡8分行800米,下坡时间是全程时间减去13分钟,下坡路程是(2950-1550)米,根据速度=路程÷时间,分别计算上下坡的速度,据此解答。
【解析】(1)1-(35%+40%)
=1-75%
=25%
8÷40%=8÷0.4=20(分)
如下图所示:
(2)上坡速度:800÷8=100(米/分)
下坡速度:(2950-1550)÷(20-13)
=1400÷7
=200(米/分)
200-100=100(米/分)
答:下坡比上坡每分钟多行100米。
5.(1)我发现:影子长度和实际高度的比值一定,所以影子长度和实际高度成正比例;
(2)教学大楼的高度是9米;这幢教学楼大约是3层
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系,用式子表示为:=k;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系,用式子表示为:xy=k;据此解答;
(2)分析题目,设这座大楼的高度是x米,根据大楼的影子长度∶大楼的高度=竹竿的影子长度∶影子的实际高度列出方程12∶x=2∶1.5,进一步解出方程即可求出教学大楼的高度,再根据“一层楼的实际高度是2.8米”,用教学大楼的高度除以2.8即可求出这幢教学楼是几层。
【解析】(1)3.2米∶2.4米
=3.2∶2.4
=(3.2÷0.8)∶(2.4÷0.8)
=4∶3
=4÷3
=
2米∶1.5米
=2∶1.5
=(2÷0.5)∶(1.5÷0.5)
=4∶3
=4÷3
=
我发现:两组数据中,影子长度∶实际高度=(一定),即影子长度和实际高度的比值是一定的,所以影子长度和实际高度成正比例。
(2)解:设这座大楼的高度是x米。
12∶x=2∶1.5
2x=12×1.5
2x=18
2x÷2=18÷2
x=9
9÷2.8≈3(层)
答:这座教学大楼的高度是9米。这幢教学楼大约是3层。
6.甲店;理由见解析
【分析】分别得出三个店买足球的钱,找出最便宜的。
甲店:买10个足球免费赠送2个,也就是得到12个球,60个足球里面每12个一组有5组,每组里面有10个球是买的,有2个球是送的,即甲店买60个足球只需付50个足球的钱;
乙店:每个足球打八五折,就是现价是原价的85%,先得出每个足球的现价再乘60即可。
丙店:根据总价=单价×数量,得出一共需要3000元,购物每满200元返还现金30元,3000元里面有15个200,一个200返现30元,则15个200返现450元,则最后付的钱=需要的钱-返现的钱。
【解析】甲店:60÷(10+2)
=60÷12
=5(组)
5×10×50
=50×50
=2500(元)
乙店:50×85%×60
=3000×85%
=2550(元)
丙店:60×50=3000(元)
3000÷200=15
3000-15×30
=3000-450
=2550(元)
2500<2550
答:选甲店。
7.141.3平方分米
【分析】一根圆柱形木料在两种截法下表面积增加,需要求原始表面积。第一种截法,把圆柱截成两个小圆柱,截面平行于底面,增加两个横截面(即两个底面),增加的表面积为15.7平方分米,即两个底面积之和;
第二种截法,当沿底面直径截开时,增加两个矩形切面(每个半圆柱一个切面)。矩形切面的长为圆柱的高h,宽为底面直径d,每个矩形面积为h×d,增加的表面积为80平方分米,即两个矩形面积之和:2×(h×d)=80,用除法求出一个矩形的面积;
圆柱的侧面积公式为:圆柱的侧面积=底面周长×高=πdh,圆柱的表面积公式为:圆柱的表面积=两个底面积+侧面积,将数据代入即可求出圆柱形木料的表面积。
【解析】解:设圆柱的底面直径为d分米,高为h分米。
2dh=80(平方分米)
dh=80÷2=40(平方分米)
3.14×40+15.7
=125.6+15.7
=141.3(平方分米)
答:这根圆柱形木料的表面积是141.3平方分米。
8.16米
【分析】这堆沙子的底面积和高已知,先利用圆锥的体积公式:圆锥体积=×底面积×高,求出这堆沙子的体积;铺成的路面实际上就是一个长方体,再依据沙子的体积不变,利用长方体的体积公式:长方体体积=长×宽×高(厚度),即可求出路面的长度。
【解析】5厘米=0.05米
×6×1.6=3.2(立方米)
3.2÷4÷0.05=16(米)
答:可以铺16米。
9.(1)502.4毫升;(2)100.48立方厘米
【分析】(1)水的体积就是圆柱的体积,根据圆柱的体积,代入数据计算即可,最后根据1立方厘米=1毫升计算换算单位即可。
(2)水面比原来上升了2厘米的体积就是鹅卵石的体积,即高是2厘米,根据圆柱的体积公式计算即可。
【解析】(1)8÷2=4(厘米)
3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
答:容器中装了502.4毫升水。
(2)3.14×42×2
=3.14×16×2
=100.48(立方厘米)
答:这块鹅卵石的体积是100.48立方厘米。
10.(1)5400元
(2)538650元
(3)649500元
【分析】(1)把原来房子每平方米的售价看作单位“1”,现在下降了一成,即现在房子每平方米的售价是原来的(1-10%),单位“1”已知,用原价乘(1-10%),求出现在房子每平方米的售价。
(2)把原来房子每平方米的售价看作单位“1”,选择一次性付清房款,可以享受九五折的优惠,即优惠后房子每平方米的售价是原来的95%,单位“1”已知,用原价乘95%,求出优惠后房子每平方米的售价,再乘房子的面积,即可求出优惠后实际需付的房款。
(3)先根据“利息=本金×利率×存期”,求出到期时可得到的利息,再加上本金,即是到期时一共可以取出的钱数。
【解析】(1)一成=10%
6000×(1-10%)
=6000×0.9
=5400(元)
答:现在房子的售价是每平方米5400元。
(2)5400×95%×105
=5400×0.95×105
=5130×105
=538650(元)
答:优惠后李明家实际购买这套房子共付房款538650元。
(3)60万元=600000元
600000×2.75%×3+600000
=600000×0.0275×3+600000
=49500+600000
=649500(元)
答:他的爸爸一共可以取出649500元钱。
11.(1)10页
(2)乙店
【分析】(1)设他平均每天要多读x页,根据每天读的页数×天数=这本书的总页数,列出反比例算式解答即可;
(2)分别计算出两家书店的实际钱数,比较即可。甲店:买十本实际得12本,求出24里面包含几个12,就买几个10本,再根据单价×数量=总价,求出实际钱数;乙店:根据单价×数量=总价,求出应付钱数,将应付钱数看作单位“1”,几折就是百分之几十,应付钱数×折扣=实际钱数。
【解析】(1)解:设他平均每天要多读x页。
(30+x)×6=30×8
(30+x)×6÷6=240÷6
30+x=40
30+x-30=40-30
x=10
答:他平均每天要多读10页。
(2)甲店:24÷12×10×50
=20×50
=1000(元)
乙店:50×24×80%
=1200×0.8
=960(元)
960<1000
答:建议他到乙店购买。
12.20990元
【分析】先根据“利息=本金×利率×存期”,求出到期时可得到的利息,再加上本金,即是到期时可取回的总钱数。
【解析】2万元=20000元
20000×1.65%×3+20000
=20000×0.0165×3+20000
=990+20000
=20990(元)
答:王爷爷能取出20990元。
13.6个小时
【分析】先用到达时间减出发时间得到经过时间,再根据,求出速度,再量出上海线 到德州的图上距离是4厘米(以实际测量为准),根据实际距离=图上距离÷比例尺,代入数据计算可得路程,把单位厘米转化为千米,再根据,代入数据计算即可。
【解析】(小时)
(千米/时)
量得上海线 到德州的图上距离是4厘米
(小时)
答:6个小时能到达德州市。
14.(1)310千米
(2)小时
【分析】(1)根据实际距离=图上距离÷比例尺,代入数据,求德州到涿州的实际距离,注意单位名数的换算。
(2)根据速度=路程÷时间,用140÷2,求出货车的速度,再根据时间=路程÷速度,用德州到涿州的路程÷货车的速度,求出德州到涿州需要的时间,再减去已行的2小时,即可解答。
【解析】(1)3.1÷
=3.1×10000000
=31000000(厘米)
31000000厘米=310千米
答:德州到涿州实际距离有310千米。
(2)310÷(140÷2)-2
=310÷70-2
=-2
=(小时)
答:张叔叔还要行驶小时能到达河北省涿州市。
15.(1)328.96平方厘米
(2)401.92立方厘米
【分析】(1)由题意可知,原来长方形的长等于圆柱的底面周长加上两个底面直径的长,原来长方形的宽等于8厘米,根据圆的周长=×直径求出底面周长,再加上2个8厘米求出原来长方形的长,最后根据长方形的面积=长×宽解答。
(2)圆柱的直径是8厘米,则半径是8÷2=4厘米,高是8厘米,根据圆柱的体积=×半径的平方×高,代入数据解答。
【解析】(1)(3.14×8+8×2)×8
=(25.12+16)×8
=41.12×8
=328.96(平方厘米)
答:原来长方形铁皮的面积是328.96平方厘米。
(2)3.14×(8÷2)2×8
=3.14××8
=3.14×16×8
=50.24×8
=401.92(立方厘米)
答:这个圆柱的体积是401.92立方厘米。
16.120天
【分析】每天烧煤的重量×可以烧的天数=这堆煤的重量,由于这堆煤的重量不变,所以每天烧煤的重量与可以烧的天数成反比例。原计划每天烧3吨,由于改造锅炉,每天可以节约0.6吨,实际每天烧(3-0.6)吨,根据原计划每天烧煤的重量×原计划烧的天数=实际每天烧煤的重量×实际烧的天数,设改造锅炉后,这堆煤可以烧x天,列方程:3×96=(3-0.6)x,解方程,即可解答。
【解析】解:设改造锅炉后,这堆煤可以烧x天。
3×96=(3-0.6)x
2.4x=288
x=288÷2.4
x=120
答:改造锅炉后,这堆煤可以烧120天。
17.10小时
【分析】由“比例尺=图上距离∶实际距离”可知,实际距离=图上距离÷比例尺,先求出甲、乙两地的实际距离,再根据“相遇时间=总路程÷速度和”求出两列火车的相遇时间,据此解答。
【解析】30÷
=30×4000000
=120000000(厘米)
120000000厘米=1200千米
1200÷(65+55)
=1200÷120
=10(小时)
答:10小时后两车才能相遇。
18.(1)31.5厘米
(2)649.98平方厘米
(3)890.19立方厘米
【分析】(1)因为3个羽毛球叠起来高14厘米,5个羽毛球叠起来高19厘米,即5-3=2个羽毛球叠起的高度是19-14=5厘米,那么一个叠起的羽毛球的高度为5÷2=2.5厘米;
用3个羽毛球叠起来的高度减去2个叠起的羽毛球的高度,求出一个羽毛球的高度。
把10个这样的羽毛球摞好装在一个圆柱形的包装盒内,那么10个这样的羽毛球的高度等于一个羽毛球的高度加上(10-1)个叠起的羽毛球的高度,据此求出包装盒的高度。
(2)求这个包装盒所用的包装材料至少的面积,就是求圆柱的表面积,根据圆柱的表面积=侧面积+底面积×2,其中S侧=πdh,S底=πr2,代入数据计算即可。
(3)根据圆柱的体积公式:V=πr2h,代入数据计算求出这个包装盒的体积。
【解析】(1)(19-14)÷2
=5÷2
=2.5(厘米)
14-2×2.5
=14-5
=9(厘米)
9+(10-1)×2.5
=9+9×2.5
=9+22.5
=31.5(厘米)
答:这个包装盒的高度至少是31.5厘米。
(2)3.14×6×31.5+3.14×(6÷2)2×2
=18.84×31.5+3.14×32×2
=593.46+3.14×9×2
=593.46+56.52
=649.98(平方厘米)
答:这个包装盒所用的包装材料至少是649.98平方厘米。
(3)3.14×(6÷2)2×31.5
=3.14×32×31.5
=3.14×9×31.5
=28.26×31.5
=890.19(立方厘米)
答:这个包装盒的体积至少是890.19立方厘米。
19.选择使用满200元九折优惠更划算。
【分析】美团代金券是88元代100元,且每桌限用两张,这意味着使用两张代金券时,实际支付给美团的金额是固定的,即88×2=176元;程程一家消费310元,使用两张100元的代金券后,从总消费金额中减去代金券抵扣的200元,还剩下需要支付的金额为310-2×100=110元;将购买代金券的花费与抵扣后还需支付的金额相加,得到使用美团代金券的总花费为176+110=286元。
店内促销是消费满200元可享受九折优惠,九折在数学上表示为90%,意味着实际支付金额是消费金额的90% ;程程一家消费310元满足九折优惠条件,那么按照九折优惠计算实际花费,就是用消费总额乘折扣,列式即为310×90%=279元。
通过前面的计算,得到使用美团代金券花费286元,店内九折花费279元;因为286>279,所以从花费金额的角度来看,店内九折优惠方式能让程程一家支付更少的钱,这种优惠方式更划算。
【解析】使用两张代金券:
310-100×2+88×2
=310-200+176
=110+176
=286(元)
使用满200元九折优惠:
310×90%=310×0.9=279(元)
286>279
答:选择使用满200元九折优惠更划算。
20.(1)400万吨
(2)2312棵
【分析】(1)根据题意可知,废纸的质量和可生产的再生纸的质量比值一定,则废纸的质量和可生产的再生纸的质量成正比例关系,据此列出正比例方程,并求解。
(2)已知1吨的废纸可生产再生纸850千克(即0.85吨),用160×0.85求出160吨废纸可以生产再生纸的吨数,再乘17,求出相当于保护大树的棵数。
【解析】(1)850千克=0.85吨
解:设至少需要消耗万吨废纸。
∶340=1∶0.85
0.85=340×1
0.85=340
=340÷0.85
=400
答:至少需要消耗掉400万吨废纸。
(2)160×0.85×17
=136×17
=2312(棵)
答:相当于保护了2312棵大树。
21.6张
【分析】假设13张乒乓球桌上都是双打比赛,这样得到的人数就比实际人数多,多的人数就是每张单打桌上多出了2人,用多的人数除以每张桌上多的人数,就得单打的桌数。
【解析】4×13=52(人)
52-40=12(人)
4-2=2(人)
12÷2=6(张)
答:有6张球桌在进行单打比赛。
22.(1)301.44立方厘米;(2)175.84平方厘米
【分析】(1)求陀螺的体积。
求圆柱底面半径:已知圆柱底面周长C=25.12厘米,根据圆的周长公式:C=2πr,可得半径r=C÷2π=25.12÷(2×3.14)=25.12÷6.28=4厘米。
求圆柱和圆锥的高:已知圆柱和圆锥总高8厘米,且圆锥和圆柱高度比是3∶5,那么圆柱的高h柱=8×=8×=5厘米,圆锥的高h锥=8-5=3厘米。
分别求圆柱和圆锥体积并求和:根据圆柱体积公式V柱=πr2h柱,圆锥体积公式V锥=πr2h锥,
可得V柱=3.14×42×5=3.14×16×5=50.24×5=251.2立方厘米,
V锥=×3.14×42×3=50.24立方厘米,陀螺体积
V=V柱+V锥=251.2+50.24=301.44立方厘米
(2)求刷红色油漆部分的面积
刷红色油漆部分是圆柱的侧面积和一个底面积。圆柱侧面积公式为S侧=ch(C是底面周长,h是圆柱高),底面积公式为S底=πr2。
已知C=25.12厘米,h=5厘米,r=4厘米,可得S侧=25.12×5=125.6平方厘米,S底=3.14×42=50.24平方厘米,那么刷红色油漆部分面积S=S侧+S底=125.6+50.24=175.84平方厘米。
【解析】(1)求底面半径
R=25.12÷(2×3.14)
=25.12÷6.28
=4(厘米)
求圆柱和圆锥的高
圆柱的高h柱=8×=5(厘米)
圆锥的高h椎=8-5=3(厘米)
求体积
V柱=3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方厘米)
251.2(立方厘米)
V锥=×3.14×42×3
=×3.14×16×3
=×50.24×3
=×150.72
=50.24(立方厘米)
V=V柱+V锥=251.2+50.24=301.44立方厘米。
答:陀螺的体积是301.44立方厘米。
(2)3.14×42+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:刷红色油漆部分的面积是175.84平方厘米。
23.12米
【分析】根据同一时刻、同一地点物体的实际长度与它的影长的比值一定,那么物体的实际长度与影长成正比例关系,据此列出正比例方程,并求解。
【解析】解:设旗杆的高度米。
2∶1.6=∶9.6
1.6=2×9.6
1.6=19.2
=19.2÷1.6
=12
答:旗杆的高度12米。
24.48行
【分析】判断数量关系:树苗的总棵数是固定不变的。因为“每行栽的棵数×行数=树苗总棵数”,当总棵数一定时,每行栽的棵数越多,行数就越少;每行栽的棵数越少,行数就越多,所以每行栽的棵数和行数成反比例关系。设未知数并列出比例式:设如果每行栽15棵,这些树苗要栽x行。根据反比例关系两种量相对应的数的乘积相等,可列出方程15x=18×40。求解方程:通过解方程15x=18×40,求出x的值,也就是当每行栽15棵时树苗要栽的行数。
【解析】解:设这些树苗要栽x行。
15x=18×40
15x÷15=720÷15
15x×=720×
x=48
答:这些树苗要种48行。
25.(1) 底面周长 (高+半径)
(2) 2πr (h+r)
(3)351.68
【分析】(1)通过观察图形可知,把圆柱展开后,再把两个底面剪拼成近似长方形,然后通过平移与侧面展开图拼在一起拼成一个大长方形。这个大长方形的长等于圆柱的底面周长,大长方形的宽等于圆柱的高加上底面半径。
(2)由此可以推导出圆柱的表面积就等于拼成的长方形的面积=长×宽=2πr×(h+r)。
(3)把数据代入推导出的公式解答即可。
【解析】(1)由分析得:拼成的长方形的长相当于圆柱的底面周长,宽相当于圆柱的(高+半径)。
(2)圆柱的表面积就等于拼成的长方形的面积=长×宽=2πr×(h+r)。
(3)2×3.14×4×(10+4)
=25.12×14
=351.68(平方厘米)
所以这个圆柱的表面积是351.68平方厘米。
26.(1)40
(2)15
(3)7
(4)见详解
【分析】(1)求六年级一班总人数从扇形统计图可知喜欢篮球的人数占全班总人数的20%,从条形统计图可知喜欢篮球的人数是8人。根据 “已知一个数的百分之几是多少,求这个数用除法”,用喜欢篮球的人数除以其占比,即8÷20%=40人,可求出全班总人数。
(2)求喜欢踢毽子的人数占全班总人数的百分比已知喜欢踢毽子的人数是6人,全班总人数是40人。根据 “求一个数是另一个数的百分之几用除法”,用喜欢踢毽子的人数除以全班总人数再乘以100%,即6÷40%×100%=15% 。
(3)求全班喜欢乒乓球的比喜欢跳绳的多的人数。
从扇形统计图可知喜欢乒乓球的人数占全班总人数的30%,喜欢跳绳的人数占全班总人数的12.5%。先分别算出喜欢乒乓球和跳绳的人数,喜欢乒乓球的人数为40×30%=12人,喜欢跳绳的人数为40×12.5%=5人 。再用喜欢乒乓球的人数减去喜欢跳绳的人数,12-5=7人
(4)绘制条形统计图。
已求出喜欢乒乓球的人数是12人,喜欢跳绳的人数是5人。在图1中,根据纵轴上的刻度,在乒乓球项目对应的位置画出高度为12对应的直条,在跳绳项目对应的位置画出高度为5对应的直条。
【解析】(1)8÷20%=40(人)
六年级一班一共有学生40人。
(2)6÷40×100%
=0.15×100%
=15%
喜欢踢毽子的人数占全班总人数的15%。
(3)40×(30%-12.5%)
=40×17.5%
=40×0.175
=7(人)
全班喜欢乒乓球的比喜欢跳绳的多7人。
(4)乒乓球:40×30%=12(人)
跳绳:40×12.5%=5(人)
如下图所示:
27.16.8米
【分析】在同一时刻,物体的实际高度与影长的比值相同,即物体的实际高度与影长成正比例,据此设旗杆的实际高度是x米,根据正比例关系列比例解答即可。
【解析】解:设旗杆的实际高度是x米。
1.2∶0.4=x∶5.6
0.4x=1.2×5.6
0.4x=6.72
0.4x÷0.4=6.72÷0.4
x=16.8
答:旗杆的实际高度是16.8米。
28.95千米/时
【分析】根据“实际距离=图上距离÷比例尺”代入数值计算出甲、乙两地的实际距离;再除以相遇时间,求出两辆车的速度和;最后用两辆车的速度和减去客车的速度,即可求出货车的速度,据此解答。
【解析】20÷
=20×3000000
=60000000(厘米)
=600(千米)
600÷4-55
=150-55
=95(千米/时)
答:货车的速度是95千米/时。
29.(1)56.52立方厘米
(2)14.13立方厘米
(3)6.5厘米
【分析】(1)从图1和图2可知,把一个大球完全浸没在有水的圆柱体容器中,水面上升了(6-4)厘米,那么水上升部分的体积就是大球的体积,根据圆柱的体积公式V=πr2h,求出大球的体积。
(2)图2放入一个大球与图3放入4个小球后,水面上升的高度是一样的,说明大球的体积等于4个小球的体积,用大球的体积除以4,即可求出一个小球的体积。
(3)图4放入了一个大球和一个小球,那么水上升部分的体积等于大球与小球的体积之和;根据h=V÷S,求出水上升的高度,再加上原有水的高度4厘米,即可求出图4中水的高度。
【解析】圆柱体容器的半径:6÷2=3(厘米)
(1)3.14×32×(6-4)
=3.14×9×2
=56.52(立方厘米)
答:大球的体积是56.52立方厘米。
(2)56.52÷4=14.13(立方厘米)
答:小球的体积是14.13立方厘米。
(3)水面升高了:
(56.52+14.13)÷(3.14×32)
=70.65÷(3.14×9)
=70.65÷28.26
=2.5(厘米)
水的高度:2.5+4=6.5(厘米)
答:图4中水的高度是6.5厘米。
30.(1)50人
(2)见详解
【分析】(1)从两幅图中可知,19~40岁的人数占总人数48%,把总人数看作单位“1”,单位“1”未知,用19~40岁的人数除以48%,求出总人数。
(2)用总人数减去18岁及以下、19~40岁、60岁以上的人数,即是41~60岁的人数,据此把条形统计图补充完整。
用18岁及以下、60岁以上的人数除以总人数,求出18岁及以下、60岁以上的人数分别占总人数的百分比;据此把扇形统计图补充完整。
【解析】(1)24÷48%
=24÷0.48
=50(人)
答:吕剧团共有50人。
(2)41~60岁的人数:50-4-24-6=16(人)
18岁及以下的人数占总人数的:
4÷50×100%
=0.08×100%
=8%
60岁以上的人数占总人数的:
6÷50×100%
=0.12×100%
=12%
31.45.8元
【分析】先用“4+8”求出小明从家到文化馆再到展览馆的图上距离,然后根据“图上距离÷比例尺=实际距离”,代入数值,计算出小明从家到展览馆的实际距离;用“小明从家到展览馆的实际距离-3”求出超过3千米的路程,根据“单价×数量=总价”求出超出3千米增加的车费,然后后根据“起步价+增加的车费=租车总费用”,由此解答即可。
【解析】(4+8)÷
=12×250000
=3000000(厘米)
3000000厘米=30千米
8+1.4×(30-3)
=8+1.4×27
=8+37.8
=45.8(元)
答:小明完成这次参观(单程)一共要花45.8元出租车费。
32.200元
【分析】把这件商品的进价看作单位“1”,按照盈利30%定价,那么定价是进价的(1+30%),用进价乘(1+30%),即是定价;
然后打八折出售,是把定价看作单位“1”,那么售价是定价的80%,用定价乘80%,即是售价;
据此得出等量关系:进价×(1+30%)×80%=售价,根据等量关系列出方程,并求解。
【解析】解:设这件商品的进价是元。
(1+30%)×80%=208
1.3×0.8=208
1.04=208
=208÷1.04
=200
答:这件商品的进价是200元。
33.4.5米
【分析】根据同一时间、同一地点物体的实际长度与它的影长的比值一定,那么物体的实际长度与影长成正比例关系,据此列出正比例方程,并求解。
【解析】解:设大树的实际高度是米。
1.8∶1=8.1∶
1.8=8.1×1
=8.1÷1.8
=4.5
答:大树的实际高度是4.5米。
34.①32平方分米
②9千克
【分析】①首先要明确求做成这个油桶需要铁皮多少平方分米,是求圆柱的表面积。圆柱的表面积=侧面积+底面积×2;圆柱的侧面积=底面周长×高,底面积公式:S=π,最后用进一法保留整数。据此解答。
②根据圆柱的体积=底面积×高,求出圆柱的体积是多少立方分米,再把立方分米化成升,最后再乘1升汽油的质量,用四舍五入法保留整数,要看十分位上的数是几,根据四舍五入法保留整数即可。
【解析】①6.28÷3.14÷2
=2÷2
=1(分米)
6.28×4+3.14××2
=6.28×4+3.14×1×2
=25.12+6.28
≈32(平方分米)
答:制这个油桶至少需要铁皮32平方分米。
②由①知:圆柱的底面积半径是1分米;
3.14××4
=3.14×1×4
=12.56(立方分米)
12.56立方分米=12.56升
12.56×0.68=8.5408(千克)
8.5408千克≈9千克
答:这个油桶大约能装汽油9千克。
35.9吨
【分析】根据圆锥的体积公式,再用圆锥的体积乘1.7,再根据四舍五入法:按需要截取到指定的数位后,如果尾数的最高位上的数比5小,就把尾数都舍去(四舍);如果尾数的最高位上的数大于或等于5,把尾数都舍去后,再向它的前一位进一(五入)。
【解析】
(吨)
答:这堆沙约重9吨。
36.(1)1400元;
(2)3050元
【分析】(1)根据表格中的支付方法,超过650元以上的部分,个人支付超过部分的25%,求一个数的百分之几用乘法得个人支付的钱,最后要加上650元即是明明本次住院需要个人支付的钱。
(2)医疗保险基金支付了1800元,也就是占了超过650元以上部分的75%。已知一个数的百分之几用除法,得出超出650部分的钱,最后加上650即可。
【解析】(1)(3650-650)×25%
=3000×25%
=750(元)
750+650=1400(元)
答:他本次住院需要个人支付1400元。
(2)1800÷75%=2400(元)
2400+650=3050(元)
答:红红本次住院的医疗费用一共是3050元。
37.80米
【分析】分析题目,设风力发电架的高是x米,根据风力发电架的影长∶风力发电架的实际高度=竹竿的影长∶竹竿的实际高度列出比例64∶x=1.6∶2,最后解出比例即可。
【解析】解:设风力发电架的高是x米。
64∶x=1.6∶2
1.6x=64×2
1.6x=128
x=128÷1.6
x=80
答:风力发电架的高是80米。
38.1789人
【分析】已知某县2024级小学毕业生中AB型血的约有442人,占总人数的8.5%,把总人数看作单位“1”,单位“1”未知,用AB型血的人数除以8.5%,求出总人数。
从图中可知,O型血的人数占总人数的34.4%,单位“1”未知,用总人数乘34.4%,求出O型血的人数。
【解析】442÷8.5%
=442÷0.085
=5200(人)
5200×34.4%
=5200×0.344
≈1789(人)
答:O型血的有1789人。
39.1.8厘米
【分析】根据题意可知,先求出圆锥形沙漏里装的沙子体积,用公式:V=,当沙子漏到长方体木盒中时,长方体木盒里沙子的体积不变,用长方体木盒里沙子的体积÷长方体木盒的底面积=沙子的高度,据此列式解答。
【解析】×3×(12÷2)2×9÷(15×12)
=×3×62×9÷180
=36×9÷180
=324÷180
≈1.8(厘米)
答:在长方体木盒中会平铺上大约1.8厘米高的沙子。
40.(1)18把
(2)8天
【分析】(1)两数相除又叫两个数的比,根据比的意义,可以确定羊和斧头的比是4∶6,用比例解决问题只要比例两边的比统一即可,设12只羊可以换x把斧头,根据羊的数量∶斧头的数量=4∶6,列出比例解答即可;
(2)将原计划每天制造数量看作单位“1”,实际每天制造数量是原计划每天制造数量的(1+50%),原计划每天制造数量×实际对应百分率=实际每天制造数量,设实际提前x天完成,则实际(24-x)天完成,根据每天制造数量×天数=总数量(一定),列出反比例算式解答即可。
【解析】(1)解:设12只羊可以换x把斧头。
12∶x=4∶6
4x=12×6
4x÷4=72÷4
x=18
答:12只羊可以换18把斧头。
(2)2×(1+50%)
=2×1.5
=3(把)
解:设实际提前x天完成。
(24-x)×3=2×24
72-3x=48
72-3x+3x =48+3x
48+3x=72
48+3x-48=72-48
3x=24
3x÷3=24÷3
x=8
答:实际提前8天完成。
41.(1)153小时
(2)150.72立方米
【分析】(1)根据题意可知,长征五号B型火箭绕地球的圈数∶转的时间=长征五号B型火箭每小时转的圈数(一定),比值一定,那么长征五号B型火箭绕地球的圈数与转的时间成正比例关系,据此列出正比例方程,并求解。
(2)观察图形可知,该整流罩的容积=圆柱的容积+圆锥的容积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【解析】(1)解:设长征五号B型火箭在太空大约运行了小时。
5∶7.5=102∶
5=102×7.5
5=765
=765÷5
=153
答:长征五号B型火箭在太空大约运行了153小时。
(2)底面半径:4÷2=2(米)
3.14×22×10+×3.14×22×(16-10)
=3.14×4×10+×3.14×4×6
=125.6+25.12
=150.72(立方米)
答:整流罩的容积是150.72立方米。
42.(1)100克
(2)壶够大
(3)740克
【分析】(1)已知生姜、红糖和水按2∶5∶75的质量比配成姜汤,即生姜占2份,红糖占5份,水占75份;用生姜的质量除以生姜的份数,求出一份数,再用一份数乘红糖的份数,即是红糖的质量。
(2)把姜汤的质量看作单位“1”,由生姜、红糖和水的质量比是2∶5∶75,可知生姜的质量占姜汤质量的,单位“1”未知,用生姜的质量除以,求出姜汤的质量,再根据进率“1千克=1000克”以及1升水的质量为1千克,得出姜汤的体积,与壶的容量进行比较,得出壶是否够大。
(3)由生姜、红糖和水按2∶5∶75的质量比配成姜汤,用生姜的质量除以2,求出一份数,再用一份数乘75,求出原来的水量;
把原来的水量看作单位“1”,蒸发掉的水量占原来水量的60%,则还剩下的水量占原来水量的(1-60%),单位“1”已知,用原来的水量乘60%,求出剩下的水量,再加上生姜、红糖的质量,即是煎好后的姜汤的质量。
【解析】(1)40÷2×5
=20×5
=100(克)
答:她需要准备红糖100克。
(2)40÷
=40÷
=40×41
=1640(克)
1640克=1.64千克
1.64÷1=1.64升
2升>1.64升
答:壶够大。
(3)40÷2×75
=20×75
=1500(克)
1500×(1-60%)
=1500×(1-0.6)
=1500×0.4
=600(克)
600+40+100=740(克)
答:这天煎好后的姜汤大约有740克。
43.(1)36分钟
(2)见详解
【分析】(1)先根据圆锥的体积公式:V=πr2h,代入数据计算,求出圆锥的体积,再根据水的流速是1.57立方厘米/分钟,用圆锥的体积除以1.57,即可求出圆锥内漏完水需要的时间;
(2)当圆锥内的水全部流入圆柱时,水的体积不变,且圆锥的底面积和圆柱的底面积相等,在等体积等面积的情况下,圆柱中水的高度是圆锥的高度的,根据分数乘法的意义,用6×,即可求出此时圆柱内水的高度。从圆柱的底面开始,沿着圆柱的高向上取2厘米的高度,将这部分圆柱内的区域用阴影填充,表示此时圆柱内的水,据此解答。
【解析】(1)3.14×32×6÷1.57
=3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)6×=2(厘米)
圆柱容器内水深2厘米。
作图如下:
44.(1)50;20;40
(2)见详解
(3)见详解
【分析】(1)从两幅统计图中可知,经历QQ诈骗的有20人,占调查总人数的10%,把调查总人数看作单位“1”,单位“1”未知,用经历QQ诈骗的人数除以10%,求出调查总人数;
从扇形统计图中可知,经历虚假中奖诈骗的占调查总人数的25%,单位“1”已知,用总人数乘25%,求出经历虚假中奖诈骗的人数;
用上当受骗总人数减去经历微信诈骗、虚假中奖诈骗、QQ诈骗的人数,即是经历电话欠费诈骗的人数;
用经历电话欠费诈骗的人数除以调查总人数,求出经历电话欠费诈骗的人数占调查总人数的百分之几。
(2)把调查总人数看作单位“1”,根据减法的意义,用“1”减去经历QQ诈骗、虚假中奖、电话欠费的人数占调查总人数的百分比,即是经历微信诈骗的人数占调查总人数的百分之几;据此把两个统计图补充完整。
(3)为了防止诈骗,结合统计图中的信息,写出自己的想法,合理即可。
【解析】(1)总人数:
20÷10%
=20÷0.1
=200(人)
200×25%
=200×0.25
=50(人)
200-90-50-20=40(人)
40÷200×100%
=0.2×100%
=20%
经历虚假中奖诈骗的有(50)人;经历电话欠费诈骗的人数占调查总人数的(20)%,有(40)人。
(2)1-10%-25%-20%=45%
统计图如下:
(3)为了防止诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电。(答案不唯一)
45.1.6元
【分析】把原来每支毛笔的定价看作单位“1”,现在的定价是7.2元,比原来的定价降低10%,原来的定价=现在的定价÷(1-10%),每支毛笔的进价=原来每支毛笔的定价×70%,每支毛笔的利润=现在每支毛笔的定价-每支毛笔的进价,据此解答。
【解析】七折=70%
7.2÷(1-10%)
=7.2÷0.9
=8(元)
8×70%=5.6(元)
7.2-5.6=1.6(元)
答:商店售出一支这种毛笔盈利1.6元。
46.(1)生产的零食总数;每天加工的数量;需要加工的天数;反
(2)5天
【分析】(1)根据每天加工的数量×需要加工的天数=生产的零食总数,根据反比例的意义进行辨识,两个相关联的量,一个变化另一个随着变化,无论怎么变化,积一定,这两个量是反比例关系;
(2)设加工完这批零件需要x天,根据每天加工的数量×需要加工的天数=生产的零食总数(一定),列出反比例算式,解答即可。
【解析】(1)因为生产的零食总数一定,所以每天加工的数量和需要加工的天数成反比例关系。
(2)解:设加工完这批零件需要x天,
480x=600×4
480x=2400
480x÷480=2400÷480
x=5
答:加工完这批零件需要5天。
47.
(1)20;20;12
(2)有空隙;1032立方厘米。
【分析】(1)观察可知,纸盒的长和宽都是圆柱形茶叶罐的直径的2倍,高是圆柱形茶叶罐的高。
(2)根据,代入数据计算纸盒的体积,用圆柱的底面直径除以2,求出底面半径,再根据圆柱的体积公式,求出圆柱形茶叶罐的体积,最后用纸盒体积减4个圆柱的体积,即可得解。
【解析】(1)(厘米)
这个纸盒内部的长20厘米,宽20厘米,高12厘米。
(2)纸盒体积:
(立方厘米)
圆柱形茶叶罐体积:
(立方厘米)
(立方厘米)
答:这个纸盒中还有空隙,空隙有1032立方厘米。
48.60千米
【分析】设两城的实际直线距离是x厘米,根据图上距离∶实际距离=比例尺,列方程解答,再根据1千米=100000厘米,把单位厘米转化为千米。
【解析】解:设两城的实际直线距离是x厘米,
4∶x=1∶1500000
1x=4×1500000
x=6000000
6000000厘米=60千米
答:两城的实际直线距离是60千米。
49.(1)长方形;长方形的长等于圆柱的底面周长,宽等于圆柱的高;转化
(2)圆柱的表面是有2个底面和一个侧面组成的
(3)S=或S=或S=+ch或S=S侧+S底×2
【分析】(1)圆柱侧面沿高展开是个长方形,长方形的长=圆柱的底面周长,宽=圆柱的高;这是一种转化数学思想方法;
(2)圆柱的表面积包括2个底面和一个侧面,据此分析;
(3)要求圆柱的表面积就是求2个底面和一个侧面的面积和,底面积=圆周率×半径的平方,侧面积=底面周长×高,据此写圆柱表面积公式。
【解析】(1)把圆柱侧面展开后,得到长方形;长方形的长等于圆柱的底面周长,宽等于圆柱的高,其中运用转化数学思想方法。
(2)圆柱的表面是有2个底面和一个侧面组成的。
(3)S=或S=或S=+ch或S=S侧+S底×2。
50.23千米
【分析】根据图,线段比例尺1厘米表示实际距离30千米,两个城市之间的距离是4.5厘米,求实际距离,用30×4.5即可求出这条公路的实际长度;
根据速度×时间=路程,用甲车的速度乘3小时,可得甲车相遇时已经行驶的路程,用总的路程减去甲车行驶的路程可得乙车行驶的路程,再根据速度=路程÷时间,代入数据,可求出乙车的速度。
【解析】由分析可得:
30×4.5=135(千米)
(135-22×3)÷3
=(135-66)÷3
=69÷3
=23(千米)
答:乙车平均每小时行驶23千米。
51.1000元
【分析】根据付款时间可知,符合在原来折扣的基础上再享受九折优惠。几折就是百分之几十,将按八折出售的价格看作单位“1”,付款金额÷90%=按八折出售的价格,再将原价看作单位“1”,按八折出售的价格÷80%=原价,据此列式解答。
【解析】720÷90%÷80%
=720÷0.9÷0.8
=1000(元)
答:这款破壁机的原价是1000元。
52.1.3吨
【分析】设乙堆货物现在有x吨,则甲堆货物现在有(5.1-x)吨,求一个数的几分之几或百分之几是多少用乘法,根据甲堆货物现在吨数×40%=乙堆货物现在吨数×,列出方程求出x的值,是乙堆货物现在吨数,乙堆货物现在吨数-放入的0.4吨=乙堆货物原来吨数。
【解析】解:设乙堆货物现在有x吨。
(5.1-x)×40%=x
(5.1-x)×0.4=x
2.04-0.4x=0.8x
2.04-0.4x+0.4x =0.8x+0.4x
1.2x=2.04
1.2x÷1.2=2.04÷1.2
x=1.7
1.7-0.4=1.3(吨)
答:乙堆货物原来有1.3吨。
53.27厘米
【分析】根据圆柱体积=底面积×高,求出圆柱形容器的容积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【解析】3.14××4×3÷(3.14×)
=3.14×81×4×3÷(3.14×36)
=3052.08÷113.04
=27(厘米)
答:圆锥形容器的高是27厘米。
54.2πr;r+h;87.92平方厘米
【分析】根据图可知:将圆柱的两个底面的圆切分并拼成近似的长方形,拼成的小长方形的长即为底面圆周长,宽为圆柱的底面半径加上圆柱的高,与侧面展开的长方形拼成的大长方形面积即为圆柱表面积,得出圆柱表面积=底面周长×(h+r)。再求出若h=5厘米,r=2厘米圆柱的表面积。
【解析】长方形的长:2πr;
长方形的宽是:h+r;
长方形的面积=(2πr)×(h+r)
圆柱的表面积=(2πr)×(h+r)
h=5厘米,r=2厘米:
(2×3.14×2)×(5+2)
=(6.28×2)×7
=12.56×7
=87.92(平方厘米)
圆柱表面积S=(2πr)×(h+r)。
圆柱的表面积是87.92平方厘米。
55.(1)706.5平方厘米(2)6123平方厘米
【分析】(1)要求这个圆柱的占地面积,也就是求圆柱的底面积,根据圆的面积=πr2,代入相应数值计算即可解答;
(2)要求至少需要多少平方厘米的皮革材料,也就是求圆柱的表面积;根据圆柱的表面积=圆柱的侧面积+2个底面的面积;圆柱的侧面积=底面周长×高,代入相应数值计算即可解答。
【解析】(1)3.14×(30÷2)2
=3.14×152
=3.14×225
=706.5(平方厘米)
答:这个圆柱的占地面积是706.5平方厘米。
(2)3.14×30×50+706.5×2
=3.14×1500+1413
=4710+1413
=6123(平方厘米)
答:这个圆柱在制作时至少需要6123平方厘米的皮革材料。
56.(1)0.9立方厘米
(2)见详解
【分析】(1)根据圆柱体积=底面积×高,先求出40枚硬币的体积,再除以40,即可算出1枚硬币的体积,据此列式解答;
(2)方法不唯一,也可以用排水法进行测量或直接测量1枚硬币的底面直径和高,再根据圆柱体积公式计算出1枚硬币的体积。
【解析】(1)3.14×(2.5÷2)2×7.4÷40
=3.14×1.252×7.4÷40
=3.14×1.5625×7.4÷40
=4.90625×7.4÷40
≈36÷40
=0.9(立方厘米)
答:1枚硬币的体积是0.9立方厘米。
(2)将10枚1元硬币放入装满水的水杯中,溢出水的体积就是10枚1元硬币的体积,除以10,即可计算出1枚硬币的体积;也可以直接测量1枚硬币的底面直径和高,根据圆柱体积=底面积×高,计算出体积。
57.6厘米
【分析】根据题意可知,水面下降部分的体积等于圆锥形铅锤的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,求出水面下降部分的体积,也就是圆锥形铅锤的体积;再根据圆锥的体积公式:体积=底面积×高×,高=体积÷底面积÷,代入数据,即可解答。
【解析】3.14×(20÷2)2×0.5÷(3.14×52)÷
=3.14×102×0.5÷(3.14×25)×3
=3.14×100×0.5÷78.5×3
=314×0.5÷78.5×3
=157÷78.5×3
=2×3
=6(厘米)
答:这个铅锤的高是6厘米。
58.0.157米
【分析】根据圆锥的体积=×底面积×高,代入数值计算出这堆近似圆锥形的混合材料的体积;这堆材料的体积与铺在路面上的材料体积相等,把路面铺的材料近似看作长方体;根据长方体的体积=长×宽×高,用所求的体积除以(长×宽),所得结果即为能铺的厚度。
【解析】
(立方米)
62.8÷(40×10)
=62.8÷400
=0.157(米)
答:能铺0.157米。
59.824块
【分析】根据实际距离=图上距离÷比例尺,换算出客厅实际长和宽,长方形面积=长×宽,据此求出客厅面积,铺的面积÷用的方砖块数=每块方砖面积,客厅面积÷每块方砖面积=方砖块数,据此列式解答。
【解析】3÷=3×200=600(厘米)=6(米)
2÷=2×200=400(厘米)=4(米)
6×4÷(18÷618)
=24÷
=24×
=824(块)
答:爸爸买824块这种方砖正好够用。
60.24厘米
【分析】已知将铅坠取出后瓶中水面下降了2厘米,则圆柱形桶里“减少的那部分水的体积”就是圆锥形铅锤的体积,“减少的那部分水”是一个底面半径4厘米,高2厘米的圆柱体;根据圆柱的体积V=πr2h,代入数据求出圆锥形铅锺的体积,再根据圆锥的高=V×3÷π÷r2,代入数据解答即可。
【解析】3.14×42×2
=3.14×16×2
=50.24×2
=100.48(立方厘米)
100.48×3÷3.14÷22
=301.44÷3.14÷4
=96÷4
=24(厘米)
答:这个铅坠的高是24厘米。
61.5464千米
【分析】已知地图的比例尺和图上黄河的长度,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出黄河的实际长度。
【解析】8÷
=8×68300000
=546400000(厘米)
546400000厘米=5464千米
答:黄河的实际长度是5464千米。
62.13.6厘米
【分析】图上距离与实际距离的比就是这幅图的比例尺;比例尺是1∶500000,也就是实际距离是图上距离的500000倍,所以实际距离为6.8×500000=3400000(厘米),如果把A、B两地画在比例尺为1∶250000的新地图上,也就是现在实际距离是图上距离的250000倍,所以此时图上距离为3400000÷250000=13.6(厘米),据此解答。
【解析】6.8×500000=3400000(厘米)
3400000÷250000=13.6(厘米)
答:A、B两地在新地图上的距离是13.6厘米。
63.8小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲乙两地的实际距离;再根据速度=路程÷时间,用200÷2,求出火车的速度;再根据时间=路程÷速度,用甲乙两地的路程÷火车的速度,求出火车从甲地到乙地需要的时间,再减去2小时,即可解答,注意单位名数的统一。
【解析】25÷
=25×4000000
=100000000(厘米)
100000000厘米=1000千米
1000÷(200÷2)-2
=1000÷100-2
=10-2
=8(小时)
答:还要8小时才能到达乙地。
64.0.3升
【分析】根据题意可知,教室消毒按照说明第1条,用原液按1∶29的体积比兑水即可,设8.7升水需要加入升84消毒剂,则,据此解答。
【解析】解:设需要加入升84消毒剂,
答:需要加入0.3升84消毒剂。
65.丽丽98元;芳芳70元
【分析】设她们剩下的钱数相等均为x元,则丽丽原来的钱数是()元,芳芳原来的钱数是(),根据丽丽和芳芳所积攒的钱数比是7∶5,列出比例,解比例即可解答。
【解析】解:设她们所剩下的钱数为x元,则丽丽原来有()元,芳芳原来有()元。
丽丽原来的钱数:50+48=98(元)
芳芳原来的钱数:50+20=70(元)
答:丽丽原来有98元,芳芳原来有70元。
66.67.5克
【分析】用比例解决问题只要比例两边的比统一即可。设需要加糖粉x克,根据淡奶油∶糖粉=10∶3,列出比例解答即可。
【解析】解:设需要加糖粉x克。
225∶x=10∶3
10x=225×3
10x=675
10x÷10=675÷10
x=67.5
答:需要加糖粉67.5克。
67.1500克
【分析】乐乐要将衣物进行消毒,消毒液和水的比是1∶300,用比例解决问题只要比例两边的比统一即可,设需要加水x克,根据消毒液质量∶需要的水的质量=1∶300,列出比例解答即可。
【解析】解:设需要加水x克。
5∶x=1∶300
x=5×300
x=1500
答:需要加水1500克。
68.图见详解;五年级植树棵数×(1+10%)=六年级植树棵数;50棵
【分析】把五年级植树棵数看作单位“1” 用一条线段表示,用六年级植树的棵数比五年级多10%,相当于五年级的(1+10%),把表示五年级棵数的线段平均分成10份,取其中的11份,即为六年级的棵数。再根据已知一个数的几分之几是多少,求这个数用除法计算,求出五年级的植树棵数。
【解析】
数量关系:五年级植树棵数×(1+10%)=六年级植树棵数
55÷(1+10%)
=55÷1.1
=50(棵)
答:五年级植树50棵。
69.200块
【分析】正方形面积=边长×边长,设需要x块,根据方砖面积×需要的块数=总面积(一定),列出反比例算式解答即可。
【解析】解:设需要x块。
答:需要200块。
70.300元
【分析】根据利息=本金×利率×存期,分别求出年利率变化前后的10万元定存三年的利息,求差即可。
【解析】10万=100000
100000×2.45%×3-10×2.35%×3
=100000×3×(0.0245-0.0235)
=300000×0.001
=300(元)
答:利息减少300元。
71.30人
【分析】把参赛的总人数看作单位“1”,一等奖、二等奖分别占参赛人数的10%、30%,那么二等奖比一等奖多的6人占参赛人数的(30%-10%),单位“1”未知,用多的人数除以(30%-10%),即可求出参赛的总人数。
【解析】6÷(30%-10%)
=6÷(0.3-0.1)
=6÷0.2
=30(人)
答:共有30人参加比赛。
72.43次
【分析】将挤出来的牙膏看作一个圆柱,根据圆柱的体积公式,计算出原来每次挤牙膏的体积,再乘30即可算出这支牙膏的总体积,这支牙膏的总体积除以口径改小以后每次挤出牙膏的体积,即可算出这支牙膏能挤几次。商的小数部分表示不够挤一次的量,故结果采取去尾法,保留整数即可。
【解析】1厘米=10毫米
(次)
答:这支牙膏最多能用43次。
73.使用消费券
【分析】分别计算使用图书消费券和打折购买哪种价格最少。85>78,可以使用20元的消费券,直接用78减20;8折就是80%,用原价85乘80%。最后比较大小即可解答。
【解析】消费券:85-20=65(元)
打折:85×80%=68(元)
65<68
答:使用图书消费券购买便宜。
74.533.8平方厘米
【分析】圆柱形孔的下底面恰好填补了圆柱形零件上底面被挖空的部分面积,因此这个零件接触空气部分的表面积=圆柱形零件的侧面积+圆柱形零件的2个底面积+圆柱形孔的侧面积;根据圆柱的侧面积=底面周长×高,代入相应的数值计算,所得结果即为需要涂漆部分的面积。
【解析】2×3.14×4×12+3.14×42×2+3.14×6×7
=3.14×8×12+3.14×16×2+3.14×42
=3.14×96+3.14×32+3.14×42
=3.14×(96+32+42)
=3.14×170
=533.8(平方厘米)
答:一共需要涂533.8平方厘米。
75.优惠卡购买;理由见详解
【分析】分别计算出按优惠卡购买需要支付的总价和按原价购买需要支付的总价,选择总价最少的方式购买花费最少。
原价购买:根据总价=单价×数量,代入相应数值计算;
优惠卡购买:打八折,即现价是原价的80%,先计算出以单价48元购买20本电脑书的总价钱,再用总价钱乘80%,所得结果再加上购买优惠卡40元,即为按优惠卡购买需付的钱数。
【解析】原价购买:48×20=960(元)
优惠卡购买:48×20×80%+40
=960×0.8+40
=768+40
=808(元)
因为808<960,所以按优惠卡购买需要支付的费用最少,因此选择按优惠卡购买。
76.360千米
【分析】总量=分量÷分率,先用35%-30%求出18千米占总长度的百分之几,也就是18千米对应的分率,再用18除以所对应的分率即可。
【解析】18÷(35%-30%)
=18÷5%
=18÷0.05
=360(千米)
答:甲、乙两地相距360千米。
77.20天
【分析】由于安装的电线杆数是一定的,所以每天安装的根数与工作的天数成反比例。设实际安装了天,据此列比例并解比例。
【解析】解:设实际安装了天
答:这批电线杆实际安装了20天。
78.(1)1400元
(2)最富裕
【分析】(1)把文化支出看作单位“1”,食物支出是文化支出的(1-37.5%),用文化支出的钱数×(1-37.5%),即可求出食物支出的钱数;
(2)再用食物支出的钱数÷计划支出的钱数×100%,求出食物支出占总支出的百分比,再进行比较,即可解答。
【解析】(1)2240×(1-37.5%)
=2240×0.625
=1400(元)
答:贝贝家食物支出是1400元。
(2)1400÷5600×100%
=0.25×100%
=25%
25%<30%,贝贝家处于最富裕。
答:贝贝家处于最富裕。
79.60000元
【分析】可设这辆车的原价是x元,则分期付款需要付的钱是元,现金购买打九五折即按原价的95%购买,价格为元,两者的差值是7200元,可列出方程解出答案。
【解析】解:设这辆车的原价是x元,则可列出方程:
答:这辆车的原价为60000元。
80.(1)157立方厘米
(2)235.5毫升
【分析】(1)水面上升的体积就是土豆A的体积,圆柱形玻璃容器的底面积×水面上升的高度=土豆A的体积,据此列式解答。
(2)土豆B的体积等于把土豆B取出后下降部分水的体积,溢出水的体积=土豆B 的体积-图②中无水部分的体积。
【解析】(1)3.14×(10÷2)2×(11-9)
=3.14×52×2
=3.14×25×2
=157(立方厘米)
答:土豆的体积是157立方厘米。
(2)3.14×(10÷2)2×4-3.14×(10÷2)2×1
=3.14×(10÷2)2×(4-1)
=3.14×52×3
=3.14×25×3
=235.5(立方厘米)
=235.5(毫升)
答:溢出了235.5毫升水。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项青岛版(六三制)
(期末考点培优)专题06 解答题
学校:___________姓名:___________班级:___________考号:___________
1.联合国教科文组织自1995年起,把4月23日定为“世界阅读日”,希望借助这个重要的日子,向大家推广阅读和写作。
(1)据有关资料统计,世界上平均每人每年读书量最多的民族是犹太族,我国的人均阅读量比犹太族少92%。已知我国人均阅读量是每年4.8本,犹太族的人均阅读量是每年多少本?
(2)这天各网站推出了购书优惠活动:A网站可享“每满300元减100元”B网站可享“折上折”,即先打七折再打九折。王老师为充实班级图书角,打算购买一套原价1200元的图书,在哪个网站购书更优惠?
2.我国的高铁建设技术在世界位于领先地位。目前正在修建的高铁梅龙路段,计划每天铺设轨道5公里,将用19.2天完成铺设任务,实际每天铺设6公里,铺完这段轨道实际需要多少天?(用比例知识解答)
3.从古代到近代,匠人们打铁时,用火将铁烧红变软,然后用锤子击打成想要的形状,最后放到凉水里迅速冷却,以增加铁的硬度,这就是“淬(cuì)火”。铁匠将长方体铁块击打成底面半径是2分米,高为6分米的圆锥,然后完全浸没入一个底面半径是5分米的圆柱体容器里淬火,此时圆柱容器里面的水面将会上升多少分米?(损耗忽略不计)。
4.王明从家骑自行车去少年宫,先走上坡路到达A,再走平路到达B。
(1)请结合两图相关信息,算一算,并把图补充完整。
(2)下坡比上坡每分钟多行多少米?
5.某天下午4时,同学们在操场同时测得竹杆的高度和影子的长度,同时还测得教学楼的影长,具体数据如下图:
(1)观察两组数据,你有什么发现?
(2)利用你的发现,求这座教学大楼的高度。估计这幢教学楼是几层?
6.为解决家长上下班接送孩子难问题,武城县每个学校开展了课后延时服务活动,课后延时服务的内容丰富多彩,各种社团百花齐放。足球社团李老师要准备60个足球,现有甲、乙、丙三个商店可以选择。三个商店里足球的单价都是50元,但各个商店的优惠方法不同。
甲店:买10个足球免费赠送2个,不足10个不赠送。 乙店:每个足球打八五折。 丙店:购物每满200元返还现金30元。为了节省费用,李老师应到哪个商店购买?为什么?
7.一根圆柱形木料,如果截成两个小圆柱,它的表面积增加15.7平方分米,如果沿着底面直径截成两个半圆柱,它的表面积将增加80平方分米,这根圆柱形木料的表面积是多少?
8.周末张乐和爸爸去沙滩游玩,爸爸堆了一个近似圆锥的沙堆,沙堆占地面积6平方米,高1.6米,张乐的爸爸准备把这堆沙滩铺到一条宽4米的路上,铺5厘米厚,可以铺多少米?
9.小芳想测量出一块儿鹅卵石的体积,按如下步骤进行了实验。
步骤一:在底面直径是8厘米的圆柱体容器中盛10厘米深的水。
步骤二:将鹅卵石浸没在水中,水面比原来上升了2厘米。
(1)容器中装了多少毫升水?
(2)这块鹅卵石的体积是多少立方厘米?
10.某居民小区的房价原来每平方米6000元,现在下降了一成。
(1)现在房子的售价是每平方米多少元?
(2)李明家打算买该小区一套105平方米的房子,选择一次性付清房款,可以享受九五折的优惠,优惠后李明家实际购买这套房子共付房款多少元?
(3)李明的爸爸三年前将60万元钱存入银行,年利率是2.75%,为买房子,爸爸将这批钱取出,他的爸爸一共可以取出多少元钱?
11.阅读经典,与书同行。读书节活动中。赵老师推荐同学们阅读《骑鹅旅行记》和《鲁滨逊漂流记》这两本书。
(1)张乐打算先阅读《骑鹅旅行记》这本书,如果每天读30页,8天可以读完,张乐想6天读完。他平均每天要多读多少页?(用比例知识解答)
(2)赵老师想买24本《鲁滨逊漂流记》充实班级图书角,周末她走访了甲、乙两家书店,两家书店标价都是50元,但促销方式各不相同,赵老师只带了1000元,你会建议他到哪家店购买?
甲店 乙店
买十送二 打八折
12.河南省的滑县木版年画是国家级非物质文化遗产之一。王爷爷将卖年画所得的2万元存入银行,定期为三年,年利率是1.65%,到期后将本金和利息全部取出,王爷爷能取出多少元钱?
13.一辆邮政车按导航提示从上海出发去德州市运送快递,早上6:00出发,8:00到达第一个收费站时已经行了160千米,照这样的速度,几个小时能到达德州市?
14.2023年受台风“杜苏芮”影响,河北省涿州市遭受到罕见的特大暴雨洪水灾害,全国各地时刻关注灾情发展,伸出援助之手。张叔叔负责驾车从德州到河北运送物资,通过导航系统查得行程信息如图。
(1)德州到涿州实际距离有多远?
(2)张叔叔驾驶的货车出发了2小时一共行驶了140千米。照这样的速度,张叔叔还要行驶多长时间能到达河北省涿州市?(结果用分数表示)
15.有一张长方形铁皮(如图),剪下图中两个圆及一个长方形,正好可以做成一个圆柱,已知圆柱的底面直径为8厘米。
(1)原来长方形铁皮的面积是多少?
(2)这个圆柱的体积是多少?
16.聊城财金热力去年12月份运进一堆煤,原计划每天烧3吨。可以烧96天,由于改造锅炉,每天可以节约0.6吨,改造锅炉后,这堆煤可以烧多少天?(用比例解答)
17.在比例尺是1∶4000000的地图上,量得甲、乙两地的距离是30厘米。两列火车同时从甲、乙两地相对开出,甲车每小时行65千米,乙车每小时行55千米。几小时后两车才能相遇?
18.羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
19.程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
20.再生纸是一种以废纸为原料,经过分选、净化、打浆、抄造等十几道工序生产出来的纸张,它并不影响办公、学习的正常使用。资料表明:1吨的废纸可生产再生纸850千克,而用掉17棵大树才能生产1吨的纸。
(1)某市每年的办公用纸需求量至少340万吨。在整个社会都呼吁环保的今天,如果该市今年用纸全都采用再生纸的话,至少需要消耗掉多少万吨废纸?(用比例知识解答)
(2)将160吨废纸加工成再生纸,相当于保护了多少棵大树?
21.乒乓球比赛分单打和双打,单打是1对1,即2人一张球桌对擂,双打是2对2,即4人一张球桌对擂。现有40名同学在13张球桌上对擂。那么有几张球桌在进行单打比赛?
22.陀螺是中国民间最早的娱乐工具之一,其形状上半部分为圆柱形,下方尖锐,玩耍时可用绳子缠绕,用力抽绳,使其直立旋转。爷爷准备帮乐乐制作一个陀螺,他先将木料初加工成一段底面周长是25.12厘米,高为8厘米的圆柱形状,最后将圆柱形状木料的下部削成锥形,这样陀螺的上面部分还是圆柱,下面部分是圆锥(如图所示),这时圆锥和圆柱高度的比3∶5。
(1)陀螺的体积是多少立方厘米?
(2)奶奶说要把陀螺上面圆柱部分刷上红色油漆,如图圆锥部分刷黄色油漆,刷红色油漆部分的面积是多少平方厘米?
23.小明在某个晴天的上午利用卷尺和2米长的竹竿测量学校旗杆的高度,他将竹竿直立在学校旗杆的旁边,量得竹竿的影长是1.6米,同一时刻测得旗杆的影长是9.6米,求旗杆的高度。(用比例解答)
24.3月12日植树节,树人小学组织同学们到劳动基地栽一批果树苗。如果每行栽18棵,恰好可以栽40行。如果每行栽15棵,这些树苗要栽多少行?(用比例的方法解答)
25.我们学习圆柱表面积时得出:圆柱的表面积=侧面积+底面积×2=2πrh+2πr2,圆圆在研究中又发现了如下方法,如图所示“圆柱的表面展开图是一个长方形和两个圆,把圆柱的两个底面转化成两个近似的长方形,平移后,与圆柱侧面展开成的长方形合并从而得到一个大的长方形,就可以推导出圆柱的表面积公式”。
(1)分析:拼成的长方形的长相当于圆柱的 ,宽相当于圆柱的 。
(2)归纳:圆柱的表面积就等于拼成的长方形的面积=长×宽= × 。(用含字母的式子表示)
(3)应用:当r=4cm,h=10cm时,用上面的方法计算圆柱的表面积是 平方厘米。
26.光明小学六年级一班全体同学参加最喜欢的运动项目调查活动(每人只能选一项),同学们正在将调查的结果绘制成下面两幅统计图,你能按要求帮他们完成统计表中剩余的部分,并回答出下列问题吗?相信你能细心的完成!
(1)六年级一班一共有学生________人。
(2)喜欢踢毽子的人数占全班总人数的_______%。
(3)全班喜欢乒乓球的比喜欢跳绳的多_______人。
(4)在图1中分别画出乒乓球和跳绳项目的条形图。
27.操场上,同学们正在阳光下测量竹竿高度以及它们影子的长度,测量数据如表。
竹竿 实际高度/m 影子长度/m
竹竿1 1.2 0.4
竹竿2 2.1 0.7
如果这时同学们测出旗杆的影子长度是5.6米,那么旗杆的实际高度是多少米?(用比例解答)
28.实际应用。
在比例尺是1∶3000000的地图上,量得甲、乙两地的距离是20厘米,现一辆客车和一辆货车分别从甲、乙两地同时出发,相向而行,经过4小时相遇。若客车的速度是55千米/时,则货车的速度是多少?
29.等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6厘米的圆柱体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
30.数据分析。
吕剧是国家级非物质文化遗产,中国八大戏曲剧种之一,山东最具代表性的地方剧种。滨州博兴作为吕剧艺术的发源地,创排了一批群众喜闻乐见、脍炙人口的优秀吕剧作品,在全国戏曲评比和展演中屡获佳绩。其中,并绘制了下面两幅不完整的统计图。
(1)该吕剧团共有多少人?
(2)把条形统计图中的人数和扇形统计图中的百分数补充完整。
31.如图是小明坐出租车去展览馆的路线图。已知出租车在3千米以内(含3千米)按起步价8元计算,以后每增加1千米车费就增加1.4元。请你按图中提供的信息算一算,小明完成这次参观(单程)一共要花多少元出租车费?
32.五一期间,商店进行优惠大酬宾活动,所有商品一律按照盈利30%定价,然后打八折出售,已知一件商品最终售价为208元,求这件商品的进价是多少钱?
33.如图,同学们在阳光下分别测量出两根直立竹竿的长度和它们的影子长度,同时,测量出大树的影子长度为8.1米,请你通过计算得出大树的实际高度。(用比例知识解决问题)
34.用铁度制一个圆柱形油桶,底面的周长是6.28分米,高4分米。
①制这个油桶至少需要铁皮多少平方分米?(进一法取近似值,得数保留整平方分米)
②这个油桶大约能装汽油多少千克?(1升汽油0.68千克,得数用四舍五入法保留整数)
35.为了铺垫运动场,学校运来一批沙,堆成圆锥形沙堆。这个沙堆的底面半径是2米,高是1.2米,每立方米的沙堆约重1.7吨,这堆沙约重多少吨?(得数保留整数)
36.某市学生和儿童在三级医院住院就医,医疗费用支付方法如表。
标准 支付方法
一年内 650元以内(含650元) 个人支付全部费用
650元以上部分 个人支付25%,剩余75%由医疗保险基金支付
(1)明明做了一个小手术,住院医疗费用一共是3650元,按上面的方法计算,他本次住院需要个人支付多少钱?
(2)红红今年住院,按上面的方法计算,医疗费用由医疗保险基金支付了1800元。红红本次住院的医疗费用一共是多少钱?
37.我国风能资源丰富,风力发电架随处可见。数学实践小组测得一座风力发电架在阳光下的影长是64米。同时把一根长2米的竹竿直立在地上,测得在阳光下的影长是1.6米,风力发电架高多少米?(用比例知识解答问题)
38.根据《人类血型遗传学》的调查,中国大陆各民族血型百分比如下图。如果按照这样的百分比推算,某县2024级小学毕业生中AB型血的约有442人,那么O型血的有多少人?(得数保留整数)
39.乐乐在数学实践活动中做了一个沙漏。如图,圆锥形容器(装满沙子)的沙子一点点漏入下面的长方体木盒中,若沙子漏完了,那么在长方体木盒中会平铺上大约多少厘米高的沙子?(n取3计算)
40.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解决下面的问题)
(1)12只羊可以换多少把斧头?
(2)一位铁匠,想要制造一批斧头去换小山羊,原计划每天制造2把,24天完成。实际每天比计划多制造50%,实际提前几天完成?
41.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不懈追求的航天梦。经过几代人的不懈奋斗。我国的航天事业取得了辉煌成就。长征五号系列(简称CZ-5)运载火箭实现数字工程化应用,大大推动了航天产品数字化的进程。
(1)长征五号B型火箭在太空绕地球转了102圈。已知绕地球5圈大约需要7.5小时,那么长征五号B型火箭在太空大约运行了多长时间?(用比例解答)
(2)整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。如图是某型号运载火箭整流罩的简约示意图,整流罩本身的厚度不计,该整流罩的容积是多少?
42.我国民间常用生姜、红糖和水煎服以防感冒(俗称“姜汤”)。小明妈妈一般把生姜、红糖和水按2∶5∶75的质量比配好后,煎20分钟左右,做成姜汤,分给全家四口人喝。这天,小明妈妈准备了40克生姜。
(1)她需要准备红糖多少克?
(2)小明家有一个容量为2升的壶,用来煎这天的姜汤,壶够大吗?(1升水的质量为1千克)
(3)根据经验,妈妈估计姜汤煎好后蒸发掉的水量在60%左右,这天煎好后的姜汤大约有多少克?
43.如图1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图2中用阴影表示出此时圆柱内的水。
44.高科技给我们的生活带来便利的同时,也给一些不法分子提供了可乘之机,他们的电信诈骗手段越来越难以防范。为了防止人们上当受骗,某公司开展了“经历最多的诈骗方式”的调查活动。经过整理分析后,绘制成了两个统计图。
(1)根据图中的信息可知,经历虚假中奖诈骗的有( )人;经历电话欠费诈骗的人数占调查总人数的( )%,有( )人。
(2)把上面的两个统计图补充完整。
(3)为了防止诈骗,你想对身边的人说些什么?
45.中国四大毛笔之乡有:浙江湖笔之乡、安徽宣笔之乡、河北侯笔之乡和山东齐笔之乡。某生产商将每支毛笔按商店定价的七折批发给商店,商店将定价降低10%卖给消费者。如果商店中每支毛笔的现在定价是7.2元,那么商店售出一支这种毛笔盈利多少元?
46.一个零食加工厂需要完成一批零食,每天加工零食的数量与需要的时间如下表。请你根据表格中数据,先填空,再解决问题。
每天加工的数量/袋 600 800 1000 1200
需要加工的时间/天 4 3 2.4 2
(1)因为( )一定,所以( )和( )成( )比例关系。
(2)如果每天加工480袋零食,加工完这批零件需要多少天?(用比例知识解答)
47.一个圆柱形茶叶罐,底面直径是10厘米,高是12厘米,将4个这样的茶叶罐按如图所示的方式紧密地放入纸盒中。
(1)这个纸盒内部的长( )厘米,宽( )厘米,高( )厘米。
(2)这个纸盒中还有空隙吗?如果有,请你算一算空隙有多大。
48.“中国科学制图学之父”裴秀所作的《禹贡地域图》18篇,是按“一分为十里,一寸为百里”的比例绘制而成的。将裴秀绘制地图的制图标准转化为现在国际通用的比例尺,大约相当于今天的1∶1500000。试着来解决下面的实际距离问题吧!
如果在一幅《禹贡地域图》上测得两城的直线距离是4厘米,请你计算两城的实际直线距离是多少千米?(列方程解答)
49.观察下面左图,把罐头盒的商标纸如下图所示沿高剪开,再展开。
(1)把圆柱侧面展开后,得到( )(填图形名称);这个图形的各边与圆柱有什么关系?其中运用什么数学思想方法?
(2)观察上面右图,圆柱的表面是由哪几部分组成的?
(3)圆柱的表面积计算公式是: 。(写字母表达式)
50.中国66号公路,又称为“草原天路”。公路沿线景观奇峻,是中国十大最美公路之一,限速30千米/时。在一幅比例尺是千米的地图上,量得这条公路的长度是4.5厘米。甲、乙两辆车分别从公路两端同时相对开出,经过3小时相遇。已知甲车平均每小时行驶22千米,乙车平均每小时行驶多少千米?
51.网上购物,已经成为人们日常生活的一部分。聪聪妈妈是网购达人,她想在网上购买一款破壁机。店铺活动信息和订单信息如下:
①店内所有商品按八折出售,并有礼品赠送;订单编号:1485987****
②“十一”当天前5分钟之内付款的顾客还能在原来折扣的基础上再享受九折优惠。
付款时间:2023-10-01-00:02:32
付款金额:720元
你能计算出这款破壁机的原价是多少元吗?
52.甲、乙两堆货物共重5.1吨,现在从甲堆中取出0.4吨货物放入乙堆,这时甲堆货物质量的40%等于乙堆货物质量的。乙堆货物原来有多少吨?
53.一个底面半径是9厘米,高是4厘米的圆柱形容器中装满了水,现在把水倒入一个底面半径是6厘米的圆锥形容器中,刚好装满,圆锥形容器的高是多少厘米?
54.探究底面半径为r,高为h的圆柱表面积时,有同学想到了这样的方法:先将两个底面转化成一个近似的长方形,然后与侧面展开后的长方形拼起来成为一个更大的长方形。
因为:圆柱表面积=整个长方形的面积
= 长 × 宽
所以:圆柱表面积S=( )×( )(用含有字母的式子表示)
若h=5厘米,r=2厘米,试着用以上方法求解圆柱的表面积。
55.妈妈给丽丽买了一个圆柱形玩具,玩具的底面直径是30厘米,高是50厘米。
(1)这个圆柱的占地面积是多少?
(2)这个圆柱在制作时至少需要多少平方厘米的皮革材料?(底面也用皮革)
56.动手实践。
测量1枚硬币的体积。
(1)上图是小丽的设计方法:把40枚硬币叠放在一起,先测量40枚硬币的体积(保留一位小数),再算出1枚硬币的体积。请你根据图中测量的尺寸,计算1枚硬币的体积。
(2)你还有其它的测量计算方法吗?请写下来。
57.如图,一个底面直径是20厘米的圆柱形容器,里面浸没着一个底面半径是5厘米的圆锥形铅锤。取出铅锤后,容器中的水面下降了0.5厘米,这个铅锤的高是多少厘米?
58.铺路基一般为包含石子、黏土、沙土等材料的混合材料。一个近似圆锥形的混合材料堆,底面半径5米,高2.4米。将这堆材料铺在长40米,宽10米的路面上,能铺多厚?
59.在比例尺为1∶200的地图上,小明家的客厅长为3厘米,宽为2厘米,爸爸在装修时想用一种浅白色的方砖铺地面,经询问商店,这种方砖铺18平方米需要618块,那么请你计算一下,在不浪费的情况下,爸爸买多少块这种方砖正好够用?
60.把一个底面半径是2厘米的圆锥形铅坠浸入一个装满水的圆柱形玻璃瓶中,玻璃瓶的底面半径是4厘米,将铅坠取出后瓶中水面下降了2厘米,这个铅坠的高是多少?(玻璃瓶壁的厚度忽略不计)
61.黄河流域是中华民族的重要发祥地之一,许多古代文明遗址和历史文化名城都分布在这里。为了更好地了解黄河,小齐买了一幅比例尺为1∶68300000的地图,在图上量得黄河的长度是8厘米,黄河的实际长度是多少千米?
62.在一幅比例尺是1∶500000的地图上量得A、B两地的距离是6.8cm,如果把A、B两地画在比例尺为1∶250000的新地图上,则A、B两地在新地图上的距离是多少厘米?
63.在一幅比例尺是1∶4000000的地图上,量得甲乙两地相距25厘米。一列火车从甲地开往乙地,2小时行驶了200千米,照这样的速度,还要多少小时才能到达乙地?
64.春季为防止流感病毒,放学后学校统一给教室地面和桌椅消毒,桶里有8.7升水,根据下面的说明,需要加入多少升84消毒剂?
84消毒剂的普通用具的使用方法: 1.一般物体 表面和公共场所环境下,用原液按1∶29的体积比兑水,浸泡20分钟。用抹布、拖把擦洗,或用塑料壶喷洒。 2.1∶25进行配比,主要是针对于医用垃圾和传染病病人的呕吐物、分泌物、排泄物,以及马桶等容器进行消毒。
65.丽丽和芳芳攒了一些零用钱,她们所积攒的钱数比是7∶5。在献爱心活动中,丽丽捐了48元,芳芳捐了20元,这时她们剩下的钱数相等。丽丽和芳芳原来各有多少钱?
66.蛋糕上涂抹的一层奶油是由淡奶油和糖粉打发而成的,淡奶油与糖粉的比是10∶3。妈妈买了一盒225克的淡奶油,要打发这盒淡奶油,需要加糖粉多少克?(用比例知识解答)
67.妈妈买回一瓶消毒液,瓶子上有这样的使用说明(见图)。乐乐要将衣物进行消毒,他倒出5克消毒液,需要加水多少克?(用比例解)
消毒清洗对象 消毒液∶水 衣物、物体表面 1∶300 瓜果、家具、厨房用品 1∶500
68.在今年的植树节活动中,为了增强学生爱护树木的意识,提高学生团结协作的能力,某校开展了以“种一棵小树,绿一方净土”为主题的植树活动。其中六年级植树55棵,六年级植树的棵数比五年级多10%,五年级植树多少棵?(画图分析数量关系并解答)
69.为了喜迎国庆,人民广场进行部分路面整修,如果用面积为9平方分米的方砖铺一部分路面,需要800块,如果改用边长为6分米的方砖铺这部分路面,需要多少块?(用比例解)
70.近两年,银行存款利率一降再降。2023年4月份,多家国有银行迎来新一波人民币存款利率下调,下表是本次调息前后某银行整存整取年利率变化表,如果同样是本金10万元定存三年,利息减少多少元?
银行调息前后存款利率表(部分)
整存整取 存期 年利率%(2024年3月) 年利率%(2024年4月)
一年 1.65 1.60
二年 2.05 1.90
三年 2.45 2.35
五年 2.50 2.40
71.育英小学举办演讲比赛,一等奖占参赛人数的10%,二等奖占参赛人数的30%,已知二等奖的人数比一等奖多6人,那么共有多少人参加比赛?
72.牙膏出口处半径为6毫米,蓝蓝每次刷牙都挤出1厘米长的牙膏,这支牙膏可用30次。如果将出口处半径改为5毫米,蓝蓝还是习惯每次挤1厘米长的牙膏。
73.市政府在“世界读书日”期间开展了“龙城读书节”活动,向广大市民发放图书消费券,活动如下图。2023年4月23日,新华书店所有书籍8折优惠。聪聪通过支付宝抢到了消费券,他想购买一本85元的图书,通过计算说明怎样购买便宜?(书店打折活动和消费券不能同时使用)
74.一个圆柱形零件,高是12厘米,底面半径是4厘米,零件的上端有一个圆柱形的孔,孔的直径是6厘米,深是7厘米。如果将这个零件接触空气部分的表面涂上防锈漆,一共需要涂多少平方厘米?
75.某书店在元旦这一天开展促销活动,推出购书优惠卡,顾客买一张优惠卡需付40元,凭此卡购买可打八折。李老师要为电脑兴趣小组的同学购买标价为48元的电脑书20本,要想花费最少,他应该选择优惠卡购买,还是原价购买?请计算说明。
76.一辆汽车从甲地开往乙地,第一小时行了全程的35%,第二小时行了全程的30%,第一小时比第二小时多行了18千米。甲、乙两地相距多少千米?
77.2工人师傅安装一批电线杆,计划每天安装12根,30天完成。由于改进了安装技术,实际每天比计划多安装6根。这批电线杆实际安装了多少天?(用比例知识解答)
78.恩格尔系数是根据恩格尔定律而得出的比例数。其主要内容是指一个家庭或个人收入越少,用于购买生存性的食物的支出在家庭或个人收入中所占的比重就越大。对一个国家而言,一个国家越穷,每个国民的平均支出中用来购买食物的费用所占比例就越大。恩格尔系数则由食物支出金额在总支出金额中所占的比重来最后决定。恩格尔系数达59%以上为贫困,50~59%为温饱,40~50%为小康,30~40%为富裕,低于30%为最富裕。贝贝一家三口人,本月计划支出5600元,其中文化支出为2240元,食物支出比文化支出少37.5%,其余的为其他支出。
(1)贝贝家食物支出是多少元?
(2)按照恩格尔系数计算,贝贝家处于什么水平?
79.一辆汽车,分期付款购买要多加价7%,如果现金购买可按九五折优惠。淘气的爸爸算了算,发现分期付款比现金购买多付7200元,请你算一算这辆车原价是多少元?
80.小刚进行测量土豆体积的实验,步骤如下:
准备一个底面直径10厘米的圆柱形玻璃容器,注入了9厘米深的水(如图①);放入土豆,浸没在水中,水面上升到11厘米处,此时水面距离容器口是1厘米(如图②);再放入土豆,此时有部分水溢出(如图③);取出土豆,这时水面距离容器口4厘米(如图④)。
图① 图② 图③ 图④
根据实验情况,请你解决以下问题:
(1)请求出土豆的体积。
(2)放入土豆后,溢出了多少毫升水?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.(1)60本;(2)B网站
【分析】(1)把犹太族每年人均阅读量看作单位“1”,我国的人均阅读量是犹太族的(1-92%),已知我国人均阅读量是每年4.8本,根据已知一个数的百分之几是多少,求这个数,用除法计算,据此求出未知的单位“1”;
(2)A网站可享“每满300元减100元”,算出1200里面有几个300,售价就需要减去几个100元;
打几折就是按照原价的百分之几十出售,B网站先打七折再打九折,售价=原价×70%×90%;
分别计算出两个网站的价格再比较。
【解析】(1)4.8÷(1-92%)
=4.8÷8%
=60(本)
(2)A网站:1200÷300=4
1200-4×100
=1200-400
=800(元)
B网站:
1200×70%×90%
=840×90%
=756(元)
756<800
答:在B网站购书更优惠。
2.16天
【分析】因为工作总量=工作效率×工作时间,工作总量一定,工作效率和工作时间成反比例,设实际每天铺x公里,列出反比例方程解答。
【解析】解:设铺完这段轨道实际需要x天。
6x=5×19.2
6x=96
6x÷6=96÷6
x=16
答:铺完这段轨道实际需要16天。
3.0.32分米
【分析】已知圆锥底面半径是2分米,高为6分米,根据圆锥的体积公式计算出圆锥的体积,也就是上升的水的体积;已知圆柱体容器的底面半径是5分米,根据圆的面积公式计算出圆柱的底面积,最后用上升的水的体积除以圆柱底面积就是上升的水的高度。
【解析】×3.14×22×6
=×3.14×4×6
=3.14×4×2
=12.56×2
=25.12(立方分米)
3.14×52
=3.14×25
=78.5(平方分米)
25.12÷78.5=0.32(分米)
答:此时圆柱容器里面的水面将会上升0.32分米。
4.(1)见详解;
(2)100米
【分析】(1)全程有三段组成,上坡路段、平路路段、下坡路段,把行全程所用时间看作单位“1”,减去上坡、下坡时间所占全程时间的百分比就是平路占全程时间的百分比。由图可知上坡路段所用时间是8分,占全程时间40%,根据已知一个数的百分之几是多少求一个数的方法,求出行全程所用时间,据此补充两图;
(2)根据图示可知上坡8分行800米,下坡时间是全程时间减去13分钟,下坡路程是(2950-1550)米,根据速度=路程÷时间,分别计算上下坡的速度,据此解答。
【解析】(1)1-(35%+40%)
=1-75%
=25%
8÷40%=8÷0.4=20(分)
如下图所示:
(2)上坡速度:800÷8=100(米/分)
下坡速度:(2950-1550)÷(20-13)
=1400÷7
=200(米/分)
200-100=100(米/分)
答:下坡比上坡每分钟多行100米。
5.(1)我发现:影子长度和实际高度的比值一定,所以影子长度和实际高度成正比例;
(2)教学大楼的高度是9米;这幢教学楼大约是3层
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系,用式子表示为:=k;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系,用式子表示为:xy=k;据此解答;
(2)分析题目,设这座大楼的高度是x米,根据大楼的影子长度∶大楼的高度=竹竿的影子长度∶影子的实际高度列出方程12∶x=2∶1.5,进一步解出方程即可求出教学大楼的高度,再根据“一层楼的实际高度是2.8米”,用教学大楼的高度除以2.8即可求出这幢教学楼是几层。
【解析】(1)3.2米∶2.4米
=3.2∶2.4
=(3.2÷0.8)∶(2.4÷0.8)
=4∶3
=4÷3
=
2米∶1.5米
=2∶1.5
=(2÷0.5)∶(1.5÷0.5)
=4∶3
=4÷3
=
我发现:两组数据中,影子长度∶实际高度=(一定),即影子长度和实际高度的比值是一定的,所以影子长度和实际高度成正比例。
(2)解:设这座大楼的高度是x米。
12∶x=2∶1.5
2x=12×1.5
2x=18
2x÷2=18÷2
x=9
9÷2.8≈3(层)
答:这座教学大楼的高度是9米。这幢教学楼大约是3层。
6.甲店;理由见解析
【分析】分别得出三个店买足球的钱,找出最便宜的。
甲店:买10个足球免费赠送2个,也就是得到12个球,60个足球里面每12个一组有5组,每组里面有10个球是买的,有2个球是送的,即甲店买60个足球只需付50个足球的钱;
乙店:每个足球打八五折,就是现价是原价的85%,先得出每个足球的现价再乘60即可。
丙店:根据总价=单价×数量,得出一共需要3000元,购物每满200元返还现金30元,3000元里面有15个200,一个200返现30元,则15个200返现450元,则最后付的钱=需要的钱-返现的钱。
【解析】甲店:60÷(10+2)
=60÷12
=5(组)
5×10×50
=50×50
=2500(元)
乙店:50×85%×60
=3000×85%
=2550(元)
丙店:60×50=3000(元)
3000÷200=15
3000-15×30
=3000-450
=2550(元)
2500<2550
答:选甲店。
7.141.3平方分米
【分析】一根圆柱形木料在两种截法下表面积增加,需要求原始表面积。第一种截法,把圆柱截成两个小圆柱,截面平行于底面,增加两个横截面(即两个底面),增加的表面积为15.7平方分米,即两个底面积之和;
第二种截法,当沿底面直径截开时,增加两个矩形切面(每个半圆柱一个切面)。矩形切面的长为圆柱的高h,宽为底面直径d,每个矩形面积为h×d,增加的表面积为80平方分米,即两个矩形面积之和:2×(h×d)=80,用除法求出一个矩形的面积;
圆柱的侧面积公式为:圆柱的侧面积=底面周长×高=πdh,圆柱的表面积公式为:圆柱的表面积=两个底面积+侧面积,将数据代入即可求出圆柱形木料的表面积。
【解析】解:设圆柱的底面直径为d分米,高为h分米。
2dh=80(平方分米)
dh=80÷2=40(平方分米)
3.14×40+15.7
=125.6+15.7
=141.3(平方分米)
答:这根圆柱形木料的表面积是141.3平方分米。
8.16米
【分析】这堆沙子的底面积和高已知,先利用圆锥的体积公式:圆锥体积=×底面积×高,求出这堆沙子的体积;铺成的路面实际上就是一个长方体,再依据沙子的体积不变,利用长方体的体积公式:长方体体积=长×宽×高(厚度),即可求出路面的长度。
【解析】5厘米=0.05米
×6×1.6=3.2(立方米)
3.2÷4÷0.05=16(米)
答:可以铺16米。
9.(1)502.4毫升;(2)100.48立方厘米
【分析】(1)水的体积就是圆柱的体积,根据圆柱的体积,代入数据计算即可,最后根据1立方厘米=1毫升计算换算单位即可。
(2)水面比原来上升了2厘米的体积就是鹅卵石的体积,即高是2厘米,根据圆柱的体积公式计算即可。
【解析】(1)8÷2=4(厘米)
3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
答:容器中装了502.4毫升水。
(2)3.14×42×2
=3.14×16×2
=100.48(立方厘米)
答:这块鹅卵石的体积是100.48立方厘米。
10.(1)5400元
(2)538650元
(3)649500元
【分析】(1)把原来房子每平方米的售价看作单位“1”,现在下降了一成,即现在房子每平方米的售价是原来的(1-10%),单位“1”已知,用原价乘(1-10%),求出现在房子每平方米的售价。
(2)把原来房子每平方米的售价看作单位“1”,选择一次性付清房款,可以享受九五折的优惠,即优惠后房子每平方米的售价是原来的95%,单位“1”已知,用原价乘95%,求出优惠后房子每平方米的售价,再乘房子的面积,即可求出优惠后实际需付的房款。
(3)先根据“利息=本金×利率×存期”,求出到期时可得到的利息,再加上本金,即是到期时一共可以取出的钱数。
【解析】(1)一成=10%
6000×(1-10%)
=6000×0.9
=5400(元)
答:现在房子的售价是每平方米5400元。
(2)5400×95%×105
=5400×0.95×105
=5130×105
=538650(元)
答:优惠后李明家实际购买这套房子共付房款538650元。
(3)60万元=600000元
600000×2.75%×3+600000
=600000×0.0275×3+600000
=49500+600000
=649500(元)
答:他的爸爸一共可以取出649500元钱。
11.(1)10页
(2)乙店
【分析】(1)设他平均每天要多读x页,根据每天读的页数×天数=这本书的总页数,列出反比例算式解答即可;
(2)分别计算出两家书店的实际钱数,比较即可。甲店:买十本实际得12本,求出24里面包含几个12,就买几个10本,再根据单价×数量=总价,求出实际钱数;乙店:根据单价×数量=总价,求出应付钱数,将应付钱数看作单位“1”,几折就是百分之几十,应付钱数×折扣=实际钱数。
【解析】(1)解:设他平均每天要多读x页。
(30+x)×6=30×8
(30+x)×6÷6=240÷6
30+x=40
30+x-30=40-30
x=10
答:他平均每天要多读10页。
(2)甲店:24÷12×10×50
=20×50
=1000(元)
乙店:50×24×80%
=1200×0.8
=960(元)
960<1000
答:建议他到乙店购买。
12.20990元
【分析】先根据“利息=本金×利率×存期”,求出到期时可得到的利息,再加上本金,即是到期时可取回的总钱数。
【解析】2万元=20000元
20000×1.65%×3+20000
=20000×0.0165×3+20000
=990+20000
=20990(元)
答:王爷爷能取出20990元。
13.6个小时
【分析】先用到达时间减出发时间得到经过时间,再根据,求出速度,再量出上海线 到德州的图上距离是4厘米(以实际测量为准),根据实际距离=图上距离÷比例尺,代入数据计算可得路程,把单位厘米转化为千米,再根据,代入数据计算即可。
【解析】(小时)
(千米/时)
量得上海线 到德州的图上距离是4厘米
(小时)
答:6个小时能到达德州市。
14.(1)310千米
(2)小时
【分析】(1)根据实际距离=图上距离÷比例尺,代入数据,求德州到涿州的实际距离,注意单位名数的换算。
(2)根据速度=路程÷时间,用140÷2,求出货车的速度,再根据时间=路程÷速度,用德州到涿州的路程÷货车的速度,求出德州到涿州需要的时间,再减去已行的2小时,即可解答。
【解析】(1)3.1÷
=3.1×10000000
=31000000(厘米)
31000000厘米=310千米
答:德州到涿州实际距离有310千米。
(2)310÷(140÷2)-2
=310÷70-2
=-2
=(小时)
答:张叔叔还要行驶小时能到达河北省涿州市。
15.(1)328.96平方厘米
(2)401.92立方厘米
【分析】(1)由题意可知,原来长方形的长等于圆柱的底面周长加上两个底面直径的长,原来长方形的宽等于8厘米,根据圆的周长=×直径求出底面周长,再加上2个8厘米求出原来长方形的长,最后根据长方形的面积=长×宽解答。
(2)圆柱的直径是8厘米,则半径是8÷2=4厘米,高是8厘米,根据圆柱的体积=×半径的平方×高,代入数据解答。
【解析】(1)(3.14×8+8×2)×8
=(25.12+16)×8
=41.12×8
=328.96(平方厘米)
答:原来长方形铁皮的面积是328.96平方厘米。
(2)3.14×(8÷2)2×8
=3.14××8
=3.14×16×8
=50.24×8
=401.92(立方厘米)
答:这个圆柱的体积是401.92立方厘米。
16.120天
【分析】每天烧煤的重量×可以烧的天数=这堆煤的重量,由于这堆煤的重量不变,所以每天烧煤的重量与可以烧的天数成反比例。原计划每天烧3吨,由于改造锅炉,每天可以节约0.6吨,实际每天烧(3-0.6)吨,根据原计划每天烧煤的重量×原计划烧的天数=实际每天烧煤的重量×实际烧的天数,设改造锅炉后,这堆煤可以烧x天,列方程:3×96=(3-0.6)x,解方程,即可解答。
【解析】解:设改造锅炉后,这堆煤可以烧x天。
3×96=(3-0.6)x
2.4x=288
x=288÷2.4
x=120
答:改造锅炉后,这堆煤可以烧120天。
17.10小时
【分析】由“比例尺=图上距离∶实际距离”可知,实际距离=图上距离÷比例尺,先求出甲、乙两地的实际距离,再根据“相遇时间=总路程÷速度和”求出两列火车的相遇时间,据此解答。
【解析】30÷
=30×4000000
=120000000(厘米)
120000000厘米=1200千米
1200÷(65+55)
=1200÷120
=10(小时)
答:10小时后两车才能相遇。
18.(1)31.5厘米
(2)649.98平方厘米
(3)890.19立方厘米
【分析】(1)因为3个羽毛球叠起来高14厘米,5个羽毛球叠起来高19厘米,即5-3=2个羽毛球叠起的高度是19-14=5厘米,那么一个叠起的羽毛球的高度为5÷2=2.5厘米;
用3个羽毛球叠起来的高度减去2个叠起的羽毛球的高度,求出一个羽毛球的高度。
把10个这样的羽毛球摞好装在一个圆柱形的包装盒内,那么10个这样的羽毛球的高度等于一个羽毛球的高度加上(10-1)个叠起的羽毛球的高度,据此求出包装盒的高度。
(2)求这个包装盒所用的包装材料至少的面积,就是求圆柱的表面积,根据圆柱的表面积=侧面积+底面积×2,其中S侧=πdh,S底=πr2,代入数据计算即可。
(3)根据圆柱的体积公式:V=πr2h,代入数据计算求出这个包装盒的体积。
【解析】(1)(19-14)÷2
=5÷2
=2.5(厘米)
14-2×2.5
=14-5
=9(厘米)
9+(10-1)×2.5
=9+9×2.5
=9+22.5
=31.5(厘米)
答:这个包装盒的高度至少是31.5厘米。
(2)3.14×6×31.5+3.14×(6÷2)2×2
=18.84×31.5+3.14×32×2
=593.46+3.14×9×2
=593.46+56.52
=649.98(平方厘米)
答:这个包装盒所用的包装材料至少是649.98平方厘米。
(3)3.14×(6÷2)2×31.5
=3.14×32×31.5
=3.14×9×31.5
=28.26×31.5
=890.19(立方厘米)
答:这个包装盒的体积至少是890.19立方厘米。
19.选择使用满200元九折优惠更划算。
【分析】美团代金券是88元代100元,且每桌限用两张,这意味着使用两张代金券时,实际支付给美团的金额是固定的,即88×2=176元;程程一家消费310元,使用两张100元的代金券后,从总消费金额中减去代金券抵扣的200元,还剩下需要支付的金额为310-2×100=110元;将购买代金券的花费与抵扣后还需支付的金额相加,得到使用美团代金券的总花费为176+110=286元。
店内促销是消费满200元可享受九折优惠,九折在数学上表示为90%,意味着实际支付金额是消费金额的90% ;程程一家消费310元满足九折优惠条件,那么按照九折优惠计算实际花费,就是用消费总额乘折扣,列式即为310×90%=279元。
通过前面的计算,得到使用美团代金券花费286元,店内九折花费279元;因为286>279,所以从花费金额的角度来看,店内九折优惠方式能让程程一家支付更少的钱,这种优惠方式更划算。
【解析】使用两张代金券:
310-100×2+88×2
=310-200+176
=110+176
=286(元)
使用满200元九折优惠:
310×90%=310×0.9=279(元)
286>279
答:选择使用满200元九折优惠更划算。
20.(1)400万吨
(2)2312棵
【分析】(1)根据题意可知,废纸的质量和可生产的再生纸的质量比值一定,则废纸的质量和可生产的再生纸的质量成正比例关系,据此列出正比例方程,并求解。
(2)已知1吨的废纸可生产再生纸850千克(即0.85吨),用160×0.85求出160吨废纸可以生产再生纸的吨数,再乘17,求出相当于保护大树的棵数。
【解析】(1)850千克=0.85吨
解:设至少需要消耗万吨废纸。
∶340=1∶0.85
0.85=340×1
0.85=340
=340÷0.85
=400
答:至少需要消耗掉400万吨废纸。
(2)160×0.85×17
=136×17
=2312(棵)
答:相当于保护了2312棵大树。
21.6张
【分析】假设13张乒乓球桌上都是双打比赛,这样得到的人数就比实际人数多,多的人数就是每张单打桌上多出了2人,用多的人数除以每张桌上多的人数,就得单打的桌数。
【解析】4×13=52(人)
52-40=12(人)
4-2=2(人)
12÷2=6(张)
答:有6张球桌在进行单打比赛。
22.(1)301.44立方厘米;(2)175.84平方厘米
【分析】(1)求陀螺的体积。
求圆柱底面半径:已知圆柱底面周长C=25.12厘米,根据圆的周长公式:C=2πr,可得半径r=C÷2π=25.12÷(2×3.14)=25.12÷6.28=4厘米。
求圆柱和圆锥的高:已知圆柱和圆锥总高8厘米,且圆锥和圆柱高度比是3∶5,那么圆柱的高h柱=8×=8×=5厘米,圆锥的高h锥=8-5=3厘米。
分别求圆柱和圆锥体积并求和:根据圆柱体积公式V柱=πr2h柱,圆锥体积公式V锥=πr2h锥,
可得V柱=3.14×42×5=3.14×16×5=50.24×5=251.2立方厘米,
V锥=×3.14×42×3=50.24立方厘米,陀螺体积
V=V柱+V锥=251.2+50.24=301.44立方厘米
(2)求刷红色油漆部分的面积
刷红色油漆部分是圆柱的侧面积和一个底面积。圆柱侧面积公式为S侧=ch(C是底面周长,h是圆柱高),底面积公式为S底=πr2。
已知C=25.12厘米,h=5厘米,r=4厘米,可得S侧=25.12×5=125.6平方厘米,S底=3.14×42=50.24平方厘米,那么刷红色油漆部分面积S=S侧+S底=125.6+50.24=175.84平方厘米。
【解析】(1)求底面半径
R=25.12÷(2×3.14)
=25.12÷6.28
=4(厘米)
求圆柱和圆锥的高
圆柱的高h柱=8×=5(厘米)
圆锥的高h椎=8-5=3(厘米)
求体积
V柱=3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方厘米)
251.2(立方厘米)
V锥=×3.14×42×3
=×3.14×16×3
=×50.24×3
=×150.72
=50.24(立方厘米)
V=V柱+V锥=251.2+50.24=301.44立方厘米。
答:陀螺的体积是301.44立方厘米。
(2)3.14×42+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:刷红色油漆部分的面积是175.84平方厘米。
23.12米
【分析】根据同一时刻、同一地点物体的实际长度与它的影长的比值一定,那么物体的实际长度与影长成正比例关系,据此列出正比例方程,并求解。
【解析】解:设旗杆的高度米。
2∶1.6=∶9.6
1.6=2×9.6
1.6=19.2
=19.2÷1.6
=12
答:旗杆的高度12米。
24.48行
【分析】判断数量关系:树苗的总棵数是固定不变的。因为“每行栽的棵数×行数=树苗总棵数”,当总棵数一定时,每行栽的棵数越多,行数就越少;每行栽的棵数越少,行数就越多,所以每行栽的棵数和行数成反比例关系。设未知数并列出比例式:设如果每行栽15棵,这些树苗要栽x行。根据反比例关系两种量相对应的数的乘积相等,可列出方程15x=18×40。求解方程:通过解方程15x=18×40,求出x的值,也就是当每行栽15棵时树苗要栽的行数。
【解析】解:设这些树苗要栽x行。
15x=18×40
15x÷15=720÷15
15x×=720×
x=48
答:这些树苗要种48行。
25.(1) 底面周长 (高+半径)
(2) 2πr (h+r)
(3)351.68
【分析】(1)通过观察图形可知,把圆柱展开后,再把两个底面剪拼成近似长方形,然后通过平移与侧面展开图拼在一起拼成一个大长方形。这个大长方形的长等于圆柱的底面周长,大长方形的宽等于圆柱的高加上底面半径。
(2)由此可以推导出圆柱的表面积就等于拼成的长方形的面积=长×宽=2πr×(h+r)。
(3)把数据代入推导出的公式解答即可。
【解析】(1)由分析得:拼成的长方形的长相当于圆柱的底面周长,宽相当于圆柱的(高+半径)。
(2)圆柱的表面积就等于拼成的长方形的面积=长×宽=2πr×(h+r)。
(3)2×3.14×4×(10+4)
=25.12×14
=351.68(平方厘米)
所以这个圆柱的表面积是351.68平方厘米。
26.(1)40
(2)15
(3)7
(4)见详解
【分析】(1)求六年级一班总人数从扇形统计图可知喜欢篮球的人数占全班总人数的20%,从条形统计图可知喜欢篮球的人数是8人。根据 “已知一个数的百分之几是多少,求这个数用除法”,用喜欢篮球的人数除以其占比,即8÷20%=40人,可求出全班总人数。
(2)求喜欢踢毽子的人数占全班总人数的百分比已知喜欢踢毽子的人数是6人,全班总人数是40人。根据 “求一个数是另一个数的百分之几用除法”,用喜欢踢毽子的人数除以全班总人数再乘以100%,即6÷40%×100%=15% 。
(3)求全班喜欢乒乓球的比喜欢跳绳的多的人数。
从扇形统计图可知喜欢乒乓球的人数占全班总人数的30%,喜欢跳绳的人数占全班总人数的12.5%。先分别算出喜欢乒乓球和跳绳的人数,喜欢乒乓球的人数为40×30%=12人,喜欢跳绳的人数为40×12.5%=5人 。再用喜欢乒乓球的人数减去喜欢跳绳的人数,12-5=7人
(4)绘制条形统计图。
已求出喜欢乒乓球的人数是12人,喜欢跳绳的人数是5人。在图1中,根据纵轴上的刻度,在乒乓球项目对应的位置画出高度为12对应的直条,在跳绳项目对应的位置画出高度为5对应的直条。
【解析】(1)8÷20%=40(人)
六年级一班一共有学生40人。
(2)6÷40×100%
=0.15×100%
=15%
喜欢踢毽子的人数占全班总人数的15%。
(3)40×(30%-12.5%)
=40×17.5%
=40×0.175
=7(人)
全班喜欢乒乓球的比喜欢跳绳的多7人。
(4)乒乓球:40×30%=12(人)
跳绳:40×12.5%=5(人)
如下图所示:
27.16.8米
【分析】在同一时刻,物体的实际高度与影长的比值相同,即物体的实际高度与影长成正比例,据此设旗杆的实际高度是x米,根据正比例关系列比例解答即可。
【解析】解:设旗杆的实际高度是x米。
1.2∶0.4=x∶5.6
0.4x=1.2×5.6
0.4x=6.72
0.4x÷0.4=6.72÷0.4
x=16.8
答:旗杆的实际高度是16.8米。
28.95千米/时
【分析】根据“实际距离=图上距离÷比例尺”代入数值计算出甲、乙两地的实际距离;再除以相遇时间,求出两辆车的速度和;最后用两辆车的速度和减去客车的速度,即可求出货车的速度,据此解答。
【解析】20÷
=20×3000000
=60000000(厘米)
=600(千米)
600÷4-55
=150-55
=95(千米/时)
答:货车的速度是95千米/时。
29.(1)56.52立方厘米
(2)14.13立方厘米
(3)6.5厘米
【分析】(1)从图1和图2可知,把一个大球完全浸没在有水的圆柱体容器中,水面上升了(6-4)厘米,那么水上升部分的体积就是大球的体积,根据圆柱的体积公式V=πr2h,求出大球的体积。
(2)图2放入一个大球与图3放入4个小球后,水面上升的高度是一样的,说明大球的体积等于4个小球的体积,用大球的体积除以4,即可求出一个小球的体积。
(3)图4放入了一个大球和一个小球,那么水上升部分的体积等于大球与小球的体积之和;根据h=V÷S,求出水上升的高度,再加上原有水的高度4厘米,即可求出图4中水的高度。
【解析】圆柱体容器的半径:6÷2=3(厘米)
(1)3.14×32×(6-4)
=3.14×9×2
=56.52(立方厘米)
答:大球的体积是56.52立方厘米。
(2)56.52÷4=14.13(立方厘米)
答:小球的体积是14.13立方厘米。
(3)水面升高了:
(56.52+14.13)÷(3.14×32)
=70.65÷(3.14×9)
=70.65÷28.26
=2.5(厘米)
水的高度:2.5+4=6.5(厘米)
答:图4中水的高度是6.5厘米。
30.(1)50人
(2)见详解
【分析】(1)从两幅图中可知,19~40岁的人数占总人数48%,把总人数看作单位“1”,单位“1”未知,用19~40岁的人数除以48%,求出总人数。
(2)用总人数减去18岁及以下、19~40岁、60岁以上的人数,即是41~60岁的人数,据此把条形统计图补充完整。
用18岁及以下、60岁以上的人数除以总人数,求出18岁及以下、60岁以上的人数分别占总人数的百分比;据此把扇形统计图补充完整。
【解析】(1)24÷48%
=24÷0.48
=50(人)
答:吕剧团共有50人。
(2)41~60岁的人数:50-4-24-6=16(人)
18岁及以下的人数占总人数的:
4÷50×100%
=0.08×100%
=8%
60岁以上的人数占总人数的:
6÷50×100%
=0.12×100%
=12%
31.45.8元
【分析】先用“4+8”求出小明从家到文化馆再到展览馆的图上距离,然后根据“图上距离÷比例尺=实际距离”,代入数值,计算出小明从家到展览馆的实际距离;用“小明从家到展览馆的实际距离-3”求出超过3千米的路程,根据“单价×数量=总价”求出超出3千米增加的车费,然后后根据“起步价+增加的车费=租车总费用”,由此解答即可。
【解析】(4+8)÷
=12×250000
=3000000(厘米)
3000000厘米=30千米
8+1.4×(30-3)
=8+1.4×27
=8+37.8
=45.8(元)
答:小明完成这次参观(单程)一共要花45.8元出租车费。
32.200元
【分析】把这件商品的进价看作单位“1”,按照盈利30%定价,那么定价是进价的(1+30%),用进价乘(1+30%),即是定价;
然后打八折出售,是把定价看作单位“1”,那么售价是定价的80%,用定价乘80%,即是售价;
据此得出等量关系:进价×(1+30%)×80%=售价,根据等量关系列出方程,并求解。
【解析】解:设这件商品的进价是元。
(1+30%)×80%=208
1.3×0.8=208
1.04=208
=208÷1.04
=200
答:这件商品的进价是200元。
33.4.5米
【分析】根据同一时间、同一地点物体的实际长度与它的影长的比值一定,那么物体的实际长度与影长成正比例关系,据此列出正比例方程,并求解。
【解析】解:设大树的实际高度是米。
1.8∶1=8.1∶
1.8=8.1×1
=8.1÷1.8
=4.5
答:大树的实际高度是4.5米。
34.①32平方分米
②9千克
【分析】①首先要明确求做成这个油桶需要铁皮多少平方分米,是求圆柱的表面积。圆柱的表面积=侧面积+底面积×2;圆柱的侧面积=底面周长×高,底面积公式:S=π,最后用进一法保留整数。据此解答。
②根据圆柱的体积=底面积×高,求出圆柱的体积是多少立方分米,再把立方分米化成升,最后再乘1升汽油的质量,用四舍五入法保留整数,要看十分位上的数是几,根据四舍五入法保留整数即可。
【解析】①6.28÷3.14÷2
=2÷2
=1(分米)
6.28×4+3.14××2
=6.28×4+3.14×1×2
=25.12+6.28
≈32(平方分米)
答:制这个油桶至少需要铁皮32平方分米。
②由①知:圆柱的底面积半径是1分米;
3.14××4
=3.14×1×4
=12.56(立方分米)
12.56立方分米=12.56升
12.56×0.68=8.5408(千克)
8.5408千克≈9千克
答:这个油桶大约能装汽油9千克。
35.9吨
【分析】根据圆锥的体积公式,再用圆锥的体积乘1.7,再根据四舍五入法:按需要截取到指定的数位后,如果尾数的最高位上的数比5小,就把尾数都舍去(四舍);如果尾数的最高位上的数大于或等于5,把尾数都舍去后,再向它的前一位进一(五入)。
【解析】
(吨)
答:这堆沙约重9吨。
36.(1)1400元;
(2)3050元
【分析】(1)根据表格中的支付方法,超过650元以上的部分,个人支付超过部分的25%,求一个数的百分之几用乘法得个人支付的钱,最后要加上650元即是明明本次住院需要个人支付的钱。
(2)医疗保险基金支付了1800元,也就是占了超过650元以上部分的75%。已知一个数的百分之几用除法,得出超出650部分的钱,最后加上650即可。
【解析】(1)(3650-650)×25%
=3000×25%
=750(元)
750+650=1400(元)
答:他本次住院需要个人支付1400元。
(2)1800÷75%=2400(元)
2400+650=3050(元)
答:红红本次住院的医疗费用一共是3050元。
37.80米
【分析】分析题目,设风力发电架的高是x米,根据风力发电架的影长∶风力发电架的实际高度=竹竿的影长∶竹竿的实际高度列出比例64∶x=1.6∶2,最后解出比例即可。
【解析】解:设风力发电架的高是x米。
64∶x=1.6∶2
1.6x=64×2
1.6x=128
x=128÷1.6
x=80
答:风力发电架的高是80米。
38.1789人
【分析】已知某县2024级小学毕业生中AB型血的约有442人,占总人数的8.5%,把总人数看作单位“1”,单位“1”未知,用AB型血的人数除以8.5%,求出总人数。
从图中可知,O型血的人数占总人数的34.4%,单位“1”未知,用总人数乘34.4%,求出O型血的人数。
【解析】442÷8.5%
=442÷0.085
=5200(人)
5200×34.4%
=5200×0.344
≈1789(人)
答:O型血的有1789人。
39.1.8厘米
【分析】根据题意可知,先求出圆锥形沙漏里装的沙子体积,用公式:V=,当沙子漏到长方体木盒中时,长方体木盒里沙子的体积不变,用长方体木盒里沙子的体积÷长方体木盒的底面积=沙子的高度,据此列式解答。
【解析】×3×(12÷2)2×9÷(15×12)
=×3×62×9÷180
=36×9÷180
=324÷180
≈1.8(厘米)
答:在长方体木盒中会平铺上大约1.8厘米高的沙子。
40.(1)18把
(2)8天
【分析】(1)两数相除又叫两个数的比,根据比的意义,可以确定羊和斧头的比是4∶6,用比例解决问题只要比例两边的比统一即可,设12只羊可以换x把斧头,根据羊的数量∶斧头的数量=4∶6,列出比例解答即可;
(2)将原计划每天制造数量看作单位“1”,实际每天制造数量是原计划每天制造数量的(1+50%),原计划每天制造数量×实际对应百分率=实际每天制造数量,设实际提前x天完成,则实际(24-x)天完成,根据每天制造数量×天数=总数量(一定),列出反比例算式解答即可。
【解析】(1)解:设12只羊可以换x把斧头。
12∶x=4∶6
4x=12×6
4x÷4=72÷4
x=18
答:12只羊可以换18把斧头。
(2)2×(1+50%)
=2×1.5
=3(把)
解:设实际提前x天完成。
(24-x)×3=2×24
72-3x=48
72-3x+3x =48+3x
48+3x=72
48+3x-48=72-48
3x=24
3x÷3=24÷3
x=8
答:实际提前8天完成。
41.(1)153小时
(2)150.72立方米
【分析】(1)根据题意可知,长征五号B型火箭绕地球的圈数∶转的时间=长征五号B型火箭每小时转的圈数(一定),比值一定,那么长征五号B型火箭绕地球的圈数与转的时间成正比例关系,据此列出正比例方程,并求解。
(2)观察图形可知,该整流罩的容积=圆柱的容积+圆锥的容积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【解析】(1)解:设长征五号B型火箭在太空大约运行了小时。
5∶7.5=102∶
5=102×7.5
5=765
=765÷5
=153
答:长征五号B型火箭在太空大约运行了153小时。
(2)底面半径:4÷2=2(米)
3.14×22×10+×3.14×22×(16-10)
=3.14×4×10+×3.14×4×6
=125.6+25.12
=150.72(立方米)
答:整流罩的容积是150.72立方米。
42.(1)100克
(2)壶够大
(3)740克
【分析】(1)已知生姜、红糖和水按2∶5∶75的质量比配成姜汤,即生姜占2份,红糖占5份,水占75份;用生姜的质量除以生姜的份数,求出一份数,再用一份数乘红糖的份数,即是红糖的质量。
(2)把姜汤的质量看作单位“1”,由生姜、红糖和水的质量比是2∶5∶75,可知生姜的质量占姜汤质量的,单位“1”未知,用生姜的质量除以,求出姜汤的质量,再根据进率“1千克=1000克”以及1升水的质量为1千克,得出姜汤的体积,与壶的容量进行比较,得出壶是否够大。
(3)由生姜、红糖和水按2∶5∶75的质量比配成姜汤,用生姜的质量除以2,求出一份数,再用一份数乘75,求出原来的水量;
把原来的水量看作单位“1”,蒸发掉的水量占原来水量的60%,则还剩下的水量占原来水量的(1-60%),单位“1”已知,用原来的水量乘60%,求出剩下的水量,再加上生姜、红糖的质量,即是煎好后的姜汤的质量。
【解析】(1)40÷2×5
=20×5
=100(克)
答:她需要准备红糖100克。
(2)40÷
=40÷
=40×41
=1640(克)
1640克=1.64千克
1.64÷1=1.64升
2升>1.64升
答:壶够大。
(3)40÷2×75
=20×75
=1500(克)
1500×(1-60%)
=1500×(1-0.6)
=1500×0.4
=600(克)
600+40+100=740(克)
答:这天煎好后的姜汤大约有740克。
43.(1)36分钟
(2)见详解
【分析】(1)先根据圆锥的体积公式:V=πr2h,代入数据计算,求出圆锥的体积,再根据水的流速是1.57立方厘米/分钟,用圆锥的体积除以1.57,即可求出圆锥内漏完水需要的时间;
(2)当圆锥内的水全部流入圆柱时,水的体积不变,且圆锥的底面积和圆柱的底面积相等,在等体积等面积的情况下,圆柱中水的高度是圆锥的高度的,根据分数乘法的意义,用6×,即可求出此时圆柱内水的高度。从圆柱的底面开始,沿着圆柱的高向上取2厘米的高度,将这部分圆柱内的区域用阴影填充,表示此时圆柱内的水,据此解答。
【解析】(1)3.14×32×6÷1.57
=3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)6×=2(厘米)
圆柱容器内水深2厘米。
作图如下:
44.(1)50;20;40
(2)见详解
(3)见详解
【分析】(1)从两幅统计图中可知,经历QQ诈骗的有20人,占调查总人数的10%,把调查总人数看作单位“1”,单位“1”未知,用经历QQ诈骗的人数除以10%,求出调查总人数;
从扇形统计图中可知,经历虚假中奖诈骗的占调查总人数的25%,单位“1”已知,用总人数乘25%,求出经历虚假中奖诈骗的人数;
用上当受骗总人数减去经历微信诈骗、虚假中奖诈骗、QQ诈骗的人数,即是经历电话欠费诈骗的人数;
用经历电话欠费诈骗的人数除以调查总人数,求出经历电话欠费诈骗的人数占调查总人数的百分之几。
(2)把调查总人数看作单位“1”,根据减法的意义,用“1”减去经历QQ诈骗、虚假中奖、电话欠费的人数占调查总人数的百分比,即是经历微信诈骗的人数占调查总人数的百分之几;据此把两个统计图补充完整。
(3)为了防止诈骗,结合统计图中的信息,写出自己的想法,合理即可。
【解析】(1)总人数:
20÷10%
=20÷0.1
=200(人)
200×25%
=200×0.25
=50(人)
200-90-50-20=40(人)
40÷200×100%
=0.2×100%
=20%
经历虚假中奖诈骗的有(50)人;经历电话欠费诈骗的人数占调查总人数的(20)%,有(40)人。
(2)1-10%-25%-20%=45%
统计图如下:
(3)为了防止诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电。(答案不唯一)
45.1.6元
【分析】把原来每支毛笔的定价看作单位“1”,现在的定价是7.2元,比原来的定价降低10%,原来的定价=现在的定价÷(1-10%),每支毛笔的进价=原来每支毛笔的定价×70%,每支毛笔的利润=现在每支毛笔的定价-每支毛笔的进价,据此解答。
【解析】七折=70%
7.2÷(1-10%)
=7.2÷0.9
=8(元)
8×70%=5.6(元)
7.2-5.6=1.6(元)
答:商店售出一支这种毛笔盈利1.6元。
46.(1)生产的零食总数;每天加工的数量;需要加工的天数;反
(2)5天
【分析】(1)根据每天加工的数量×需要加工的天数=生产的零食总数,根据反比例的意义进行辨识,两个相关联的量,一个变化另一个随着变化,无论怎么变化,积一定,这两个量是反比例关系;
(2)设加工完这批零件需要x天,根据每天加工的数量×需要加工的天数=生产的零食总数(一定),列出反比例算式,解答即可。
【解析】(1)因为生产的零食总数一定,所以每天加工的数量和需要加工的天数成反比例关系。
(2)解:设加工完这批零件需要x天,
480x=600×4
480x=2400
480x÷480=2400÷480
x=5
答:加工完这批零件需要5天。
47.
(1)20;20;12
(2)有空隙;1032立方厘米。
【分析】(1)观察可知,纸盒的长和宽都是圆柱形茶叶罐的直径的2倍,高是圆柱形茶叶罐的高。
(2)根据,代入数据计算纸盒的体积,用圆柱的底面直径除以2,求出底面半径,再根据圆柱的体积公式,求出圆柱形茶叶罐的体积,最后用纸盒体积减4个圆柱的体积,即可得解。
【解析】(1)(厘米)
这个纸盒内部的长20厘米,宽20厘米,高12厘米。
(2)纸盒体积:
(立方厘米)
圆柱形茶叶罐体积:
(立方厘米)
(立方厘米)
答:这个纸盒中还有空隙,空隙有1032立方厘米。
48.60千米
【分析】设两城的实际直线距离是x厘米,根据图上距离∶实际距离=比例尺,列方程解答,再根据1千米=100000厘米,把单位厘米转化为千米。
【解析】解:设两城的实际直线距离是x厘米,
4∶x=1∶1500000
1x=4×1500000
x=6000000
6000000厘米=60千米
答:两城的实际直线距离是60千米。
49.(1)长方形;长方形的长等于圆柱的底面周长,宽等于圆柱的高;转化
(2)圆柱的表面是有2个底面和一个侧面组成的
(3)S=或S=或S=+ch或S=S侧+S底×2
【分析】(1)圆柱侧面沿高展开是个长方形,长方形的长=圆柱的底面周长,宽=圆柱的高;这是一种转化数学思想方法;
(2)圆柱的表面积包括2个底面和一个侧面,据此分析;
(3)要求圆柱的表面积就是求2个底面和一个侧面的面积和,底面积=圆周率×半径的平方,侧面积=底面周长×高,据此写圆柱表面积公式。
【解析】(1)把圆柱侧面展开后,得到长方形;长方形的长等于圆柱的底面周长,宽等于圆柱的高,其中运用转化数学思想方法。
(2)圆柱的表面是有2个底面和一个侧面组成的。
(3)S=或S=或S=+ch或S=S侧+S底×2。
50.23千米
【分析】根据图,线段比例尺1厘米表示实际距离30千米,两个城市之间的距离是4.5厘米,求实际距离,用30×4.5即可求出这条公路的实际长度;
根据速度×时间=路程,用甲车的速度乘3小时,可得甲车相遇时已经行驶的路程,用总的路程减去甲车行驶的路程可得乙车行驶的路程,再根据速度=路程÷时间,代入数据,可求出乙车的速度。
【解析】由分析可得:
30×4.5=135(千米)
(135-22×3)÷3
=(135-66)÷3
=69÷3
=23(千米)
答:乙车平均每小时行驶23千米。
51.1000元
【分析】根据付款时间可知,符合在原来折扣的基础上再享受九折优惠。几折就是百分之几十,将按八折出售的价格看作单位“1”,付款金额÷90%=按八折出售的价格,再将原价看作单位“1”,按八折出售的价格÷80%=原价,据此列式解答。
【解析】720÷90%÷80%
=720÷0.9÷0.8
=1000(元)
答:这款破壁机的原价是1000元。
52.1.3吨
【分析】设乙堆货物现在有x吨,则甲堆货物现在有(5.1-x)吨,求一个数的几分之几或百分之几是多少用乘法,根据甲堆货物现在吨数×40%=乙堆货物现在吨数×,列出方程求出x的值,是乙堆货物现在吨数,乙堆货物现在吨数-放入的0.4吨=乙堆货物原来吨数。
【解析】解:设乙堆货物现在有x吨。
(5.1-x)×40%=x
(5.1-x)×0.4=x
2.04-0.4x=0.8x
2.04-0.4x+0.4x =0.8x+0.4x
1.2x=2.04
1.2x÷1.2=2.04÷1.2
x=1.7
1.7-0.4=1.3(吨)
答:乙堆货物原来有1.3吨。
53.27厘米
【分析】根据圆柱体积=底面积×高,求出圆柱形容器的容积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【解析】3.14××4×3÷(3.14×)
=3.14×81×4×3÷(3.14×36)
=3052.08÷113.04
=27(厘米)
答:圆锥形容器的高是27厘米。
54.2πr;r+h;87.92平方厘米
【分析】根据图可知:将圆柱的两个底面的圆切分并拼成近似的长方形,拼成的小长方形的长即为底面圆周长,宽为圆柱的底面半径加上圆柱的高,与侧面展开的长方形拼成的大长方形面积即为圆柱表面积,得出圆柱表面积=底面周长×(h+r)。再求出若h=5厘米,r=2厘米圆柱的表面积。
【解析】长方形的长:2πr;
长方形的宽是:h+r;
长方形的面积=(2πr)×(h+r)
圆柱的表面积=(2πr)×(h+r)
h=5厘米,r=2厘米:
(2×3.14×2)×(5+2)
=(6.28×2)×7
=12.56×7
=87.92(平方厘米)
圆柱表面积S=(2πr)×(h+r)。
圆柱的表面积是87.92平方厘米。
55.(1)706.5平方厘米(2)6123平方厘米
【分析】(1)要求这个圆柱的占地面积,也就是求圆柱的底面积,根据圆的面积=πr2,代入相应数值计算即可解答;
(2)要求至少需要多少平方厘米的皮革材料,也就是求圆柱的表面积;根据圆柱的表面积=圆柱的侧面积+2个底面的面积;圆柱的侧面积=底面周长×高,代入相应数值计算即可解答。
【解析】(1)3.14×(30÷2)2
=3.14×152
=3.14×225
=706.5(平方厘米)
答:这个圆柱的占地面积是706.5平方厘米。
(2)3.14×30×50+706.5×2
=3.14×1500+1413
=4710+1413
=6123(平方厘米)
答:这个圆柱在制作时至少需要6123平方厘米的皮革材料。
56.(1)0.9立方厘米
(2)见详解
【分析】(1)根据圆柱体积=底面积×高,先求出40枚硬币的体积,再除以40,即可算出1枚硬币的体积,据此列式解答;
(2)方法不唯一,也可以用排水法进行测量或直接测量1枚硬币的底面直径和高,再根据圆柱体积公式计算出1枚硬币的体积。
【解析】(1)3.14×(2.5÷2)2×7.4÷40
=3.14×1.252×7.4÷40
=3.14×1.5625×7.4÷40
=4.90625×7.4÷40
≈36÷40
=0.9(立方厘米)
答:1枚硬币的体积是0.9立方厘米。
(2)将10枚1元硬币放入装满水的水杯中,溢出水的体积就是10枚1元硬币的体积,除以10,即可计算出1枚硬币的体积;也可以直接测量1枚硬币的底面直径和高,根据圆柱体积=底面积×高,计算出体积。
57.6厘米
【分析】根据题意可知,水面下降部分的体积等于圆锥形铅锤的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,求出水面下降部分的体积,也就是圆锥形铅锤的体积;再根据圆锥的体积公式:体积=底面积×高×,高=体积÷底面积÷,代入数据,即可解答。
【解析】3.14×(20÷2)2×0.5÷(3.14×52)÷
=3.14×102×0.5÷(3.14×25)×3
=3.14×100×0.5÷78.5×3
=314×0.5÷78.5×3
=157÷78.5×3
=2×3
=6(厘米)
答:这个铅锤的高是6厘米。
58.0.157米
【分析】根据圆锥的体积=×底面积×高,代入数值计算出这堆近似圆锥形的混合材料的体积;这堆材料的体积与铺在路面上的材料体积相等,把路面铺的材料近似看作长方体;根据长方体的体积=长×宽×高,用所求的体积除以(长×宽),所得结果即为能铺的厚度。
【解析】
(立方米)
62.8÷(40×10)
=62.8÷400
=0.157(米)
答:能铺0.157米。
59.824块
【分析】根据实际距离=图上距离÷比例尺,换算出客厅实际长和宽,长方形面积=长×宽,据此求出客厅面积,铺的面积÷用的方砖块数=每块方砖面积,客厅面积÷每块方砖面积=方砖块数,据此列式解答。
【解析】3÷=3×200=600(厘米)=6(米)
2÷=2×200=400(厘米)=4(米)
6×4÷(18÷618)
=24÷
=24×
=824(块)
答:爸爸买824块这种方砖正好够用。
60.24厘米
【分析】已知将铅坠取出后瓶中水面下降了2厘米,则圆柱形桶里“减少的那部分水的体积”就是圆锥形铅锤的体积,“减少的那部分水”是一个底面半径4厘米,高2厘米的圆柱体;根据圆柱的体积V=πr2h,代入数据求出圆锥形铅锺的体积,再根据圆锥的高=V×3÷π÷r2,代入数据解答即可。
【解析】3.14×42×2
=3.14×16×2
=50.24×2
=100.48(立方厘米)
100.48×3÷3.14÷22
=301.44÷3.14÷4
=96÷4
=24(厘米)
答:这个铅坠的高是24厘米。
61.5464千米
【分析】已知地图的比例尺和图上黄河的长度,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出黄河的实际长度。
【解析】8÷
=8×68300000
=546400000(厘米)
546400000厘米=5464千米
答:黄河的实际长度是5464千米。
62.13.6厘米
【分析】图上距离与实际距离的比就是这幅图的比例尺;比例尺是1∶500000,也就是实际距离是图上距离的500000倍,所以实际距离为6.8×500000=3400000(厘米),如果把A、B两地画在比例尺为1∶250000的新地图上,也就是现在实际距离是图上距离的250000倍,所以此时图上距离为3400000÷250000=13.6(厘米),据此解答。
【解析】6.8×500000=3400000(厘米)
3400000÷250000=13.6(厘米)
答:A、B两地在新地图上的距离是13.6厘米。
63.8小时
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲乙两地的实际距离;再根据速度=路程÷时间,用200÷2,求出火车的速度;再根据时间=路程÷速度,用甲乙两地的路程÷火车的速度,求出火车从甲地到乙地需要的时间,再减去2小时,即可解答,注意单位名数的统一。
【解析】25÷
=25×4000000
=100000000(厘米)
100000000厘米=1000千米
1000÷(200÷2)-2
=1000÷100-2
=10-2
=8(小时)
答:还要8小时才能到达乙地。
64.0.3升
【分析】根据题意可知,教室消毒按照说明第1条,用原液按1∶29的体积比兑水即可,设8.7升水需要加入升84消毒剂,则,据此解答。
【解析】解:设需要加入升84消毒剂,
答:需要加入0.3升84消毒剂。
65.丽丽98元;芳芳70元
【分析】设她们剩下的钱数相等均为x元,则丽丽原来的钱数是()元,芳芳原来的钱数是(),根据丽丽和芳芳所积攒的钱数比是7∶5,列出比例,解比例即可解答。
【解析】解:设她们所剩下的钱数为x元,则丽丽原来有()元,芳芳原来有()元。
丽丽原来的钱数:50+48=98(元)
芳芳原来的钱数:50+20=70(元)
答:丽丽原来有98元,芳芳原来有70元。
66.67.5克
【分析】用比例解决问题只要比例两边的比统一即可。设需要加糖粉x克,根据淡奶油∶糖粉=10∶3,列出比例解答即可。
【解析】解:设需要加糖粉x克。
225∶x=10∶3
10x=225×3
10x=675
10x÷10=675÷10
x=67.5
答:需要加糖粉67.5克。
67.1500克
【分析】乐乐要将衣物进行消毒,消毒液和水的比是1∶300,用比例解决问题只要比例两边的比统一即可,设需要加水x克,根据消毒液质量∶需要的水的质量=1∶300,列出比例解答即可。
【解析】解:设需要加水x克。
5∶x=1∶300
x=5×300
x=1500
答:需要加水1500克。
68.图见详解;五年级植树棵数×(1+10%)=六年级植树棵数;50棵
【分析】把五年级植树棵数看作单位“1” 用一条线段表示,用六年级植树的棵数比五年级多10%,相当于五年级的(1+10%),把表示五年级棵数的线段平均分成10份,取其中的11份,即为六年级的棵数。再根据已知一个数的几分之几是多少,求这个数用除法计算,求出五年级的植树棵数。
【解析】
数量关系:五年级植树棵数×(1+10%)=六年级植树棵数
55÷(1+10%)
=55÷1.1
=50(棵)
答:五年级植树50棵。
69.200块
【分析】正方形面积=边长×边长,设需要x块,根据方砖面积×需要的块数=总面积(一定),列出反比例算式解答即可。
【解析】解:设需要x块。
答:需要200块。
70.300元
【分析】根据利息=本金×利率×存期,分别求出年利率变化前后的10万元定存三年的利息,求差即可。
【解析】10万=100000
100000×2.45%×3-10×2.35%×3
=100000×3×(0.0245-0.0235)
=300000×0.001
=300(元)
答:利息减少300元。
71.30人
【分析】把参赛的总人数看作单位“1”,一等奖、二等奖分别占参赛人数的10%、30%,那么二等奖比一等奖多的6人占参赛人数的(30%-10%),单位“1”未知,用多的人数除以(30%-10%),即可求出参赛的总人数。
【解析】6÷(30%-10%)
=6÷(0.3-0.1)
=6÷0.2
=30(人)
答:共有30人参加比赛。
72.43次
【分析】将挤出来的牙膏看作一个圆柱,根据圆柱的体积公式,计算出原来每次挤牙膏的体积,再乘30即可算出这支牙膏的总体积,这支牙膏的总体积除以口径改小以后每次挤出牙膏的体积,即可算出这支牙膏能挤几次。商的小数部分表示不够挤一次的量,故结果采取去尾法,保留整数即可。
【解析】1厘米=10毫米
(次)
答:这支牙膏最多能用43次。
73.使用消费券
【分析】分别计算使用图书消费券和打折购买哪种价格最少。85>78,可以使用20元的消费券,直接用78减20;8折就是80%,用原价85乘80%。最后比较大小即可解答。
【解析】消费券:85-20=65(元)
打折:85×80%=68(元)
65<68
答:使用图书消费券购买便宜。
74.533.8平方厘米
【分析】圆柱形孔的下底面恰好填补了圆柱形零件上底面被挖空的部分面积,因此这个零件接触空气部分的表面积=圆柱形零件的侧面积+圆柱形零件的2个底面积+圆柱形孔的侧面积;根据圆柱的侧面积=底面周长×高,代入相应的数值计算,所得结果即为需要涂漆部分的面积。
【解析】2×3.14×4×12+3.14×42×2+3.14×6×7
=3.14×8×12+3.14×16×2+3.14×42
=3.14×96+3.14×32+3.14×42
=3.14×(96+32+42)
=3.14×170
=533.8(平方厘米)
答:一共需要涂533.8平方厘米。
75.优惠卡购买;理由见详解
【分析】分别计算出按优惠卡购买需要支付的总价和按原价购买需要支付的总价,选择总价最少的方式购买花费最少。
原价购买:根据总价=单价×数量,代入相应数值计算;
优惠卡购买:打八折,即现价是原价的80%,先计算出以单价48元购买20本电脑书的总价钱,再用总价钱乘80%,所得结果再加上购买优惠卡40元,即为按优惠卡购买需付的钱数。
【解析】原价购买:48×20=960(元)
优惠卡购买:48×20×80%+40
=960×0.8+40
=768+40
=808(元)
因为808<960,所以按优惠卡购买需要支付的费用最少,因此选择按优惠卡购买。
76.360千米
【分析】总量=分量÷分率,先用35%-30%求出18千米占总长度的百分之几,也就是18千米对应的分率,再用18除以所对应的分率即可。
【解析】18÷(35%-30%)
=18÷5%
=18÷0.05
=360(千米)
答:甲、乙两地相距360千米。
77.20天
【分析】由于安装的电线杆数是一定的,所以每天安装的根数与工作的天数成反比例。设实际安装了天,据此列比例并解比例。
【解析】解:设实际安装了天
答:这批电线杆实际安装了20天。
78.(1)1400元
(2)最富裕
【分析】(1)把文化支出看作单位“1”,食物支出是文化支出的(1-37.5%),用文化支出的钱数×(1-37.5%),即可求出食物支出的钱数;
(2)再用食物支出的钱数÷计划支出的钱数×100%,求出食物支出占总支出的百分比,再进行比较,即可解答。
【解析】(1)2240×(1-37.5%)
=2240×0.625
=1400(元)
答:贝贝家食物支出是1400元。
(2)1400÷5600×100%
=0.25×100%
=25%
25%<30%,贝贝家处于最富裕。
答:贝贝家处于最富裕。
79.60000元
【分析】可设这辆车的原价是x元,则分期付款需要付的钱是元,现金购买打九五折即按原价的95%购买,价格为元,两者的差值是7200元,可列出方程解出答案。
【解析】解:设这辆车的原价是x元,则可列出方程:
答:这辆车的原价为60000元。
80.(1)157立方厘米
(2)235.5毫升
【分析】(1)水面上升的体积就是土豆A的体积,圆柱形玻璃容器的底面积×水面上升的高度=土豆A的体积,据此列式解答。
(2)土豆B的体积等于把土豆B取出后下降部分水的体积,溢出水的体积=土豆B 的体积-图②中无水部分的体积。
【解析】(1)3.14×(10÷2)2×(11-9)
=3.14×52×2
=3.14×25×2
=157(立方厘米)
答:土豆的体积是157立方厘米。
(2)3.14×(10÷2)2×4-3.14×(10÷2)2×1
=3.14×(10÷2)2×(4-1)
=3.14×52×3
=3.14×25×3
=235.5(立方厘米)
=235.5(毫升)
答:溢出了235.5毫升水。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
