内蒙古包头市昆区2025届九年级下学期中考二模数学试卷(含详解)
文档属性
| 名称 | 内蒙古包头市昆区2025届九年级下学期中考二模数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 13:05:08 | ||
图片预览


文档简介
2025年内蒙古自治区包头市昆区中考二模数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
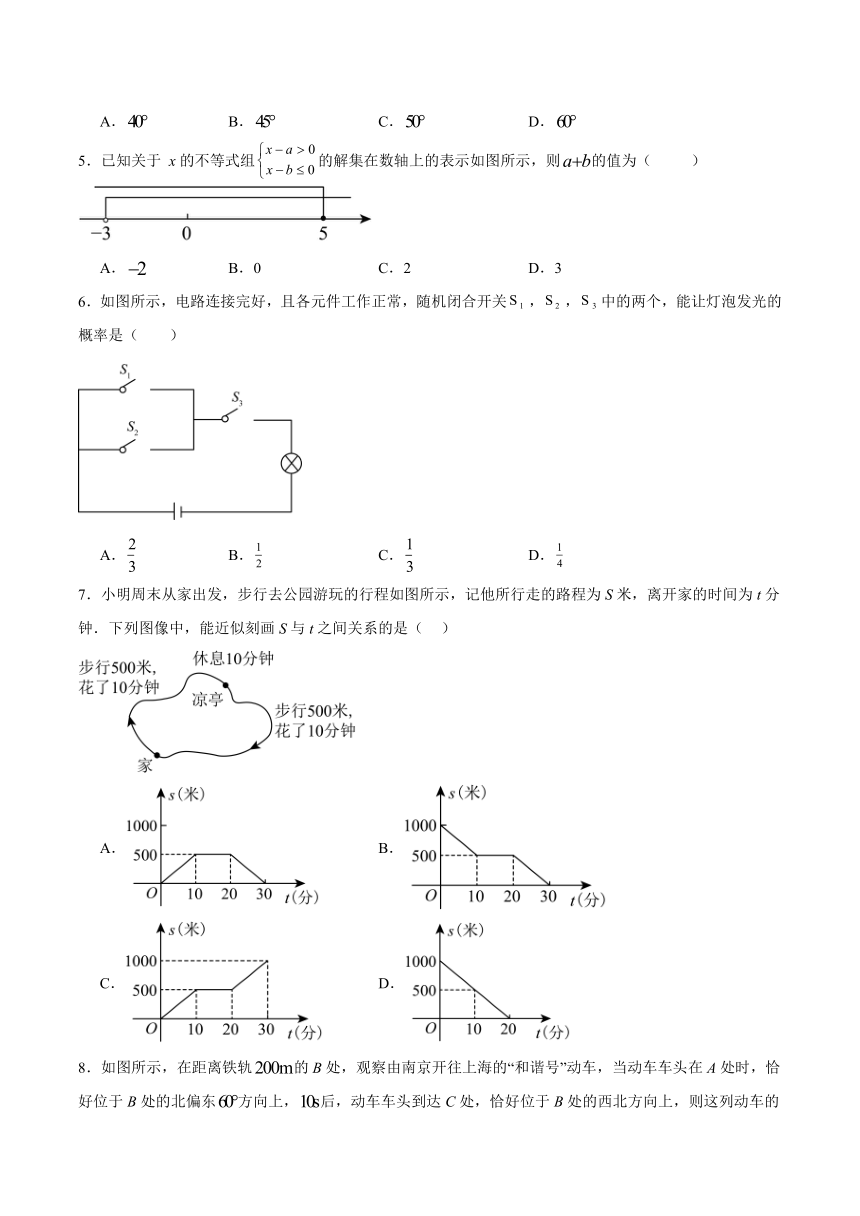
1.紫砂壶,被誉为中国非物质文化遗产的瑰宝,以其独特的成型工艺和多样的造型式样著称,陶器所散发的古朴典雅之色更是引人入胜.如图所展示的是一把精湛工艺紫砂壶“景舟石瓢”,下面四幅图是此紫砂壶的俯视图的是( )
A. B.
C. D.
2.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
A. B. C. D.
3.下列运算正确的是( )
A.=﹣3 B.a2 a4=a6 C.(2a2)3=2a6 D.(a+2)2=a2+4
4.如图,将三角尺的直角顶点放在直尺的一边上,,则的度数等于( )
A. B. C. D.
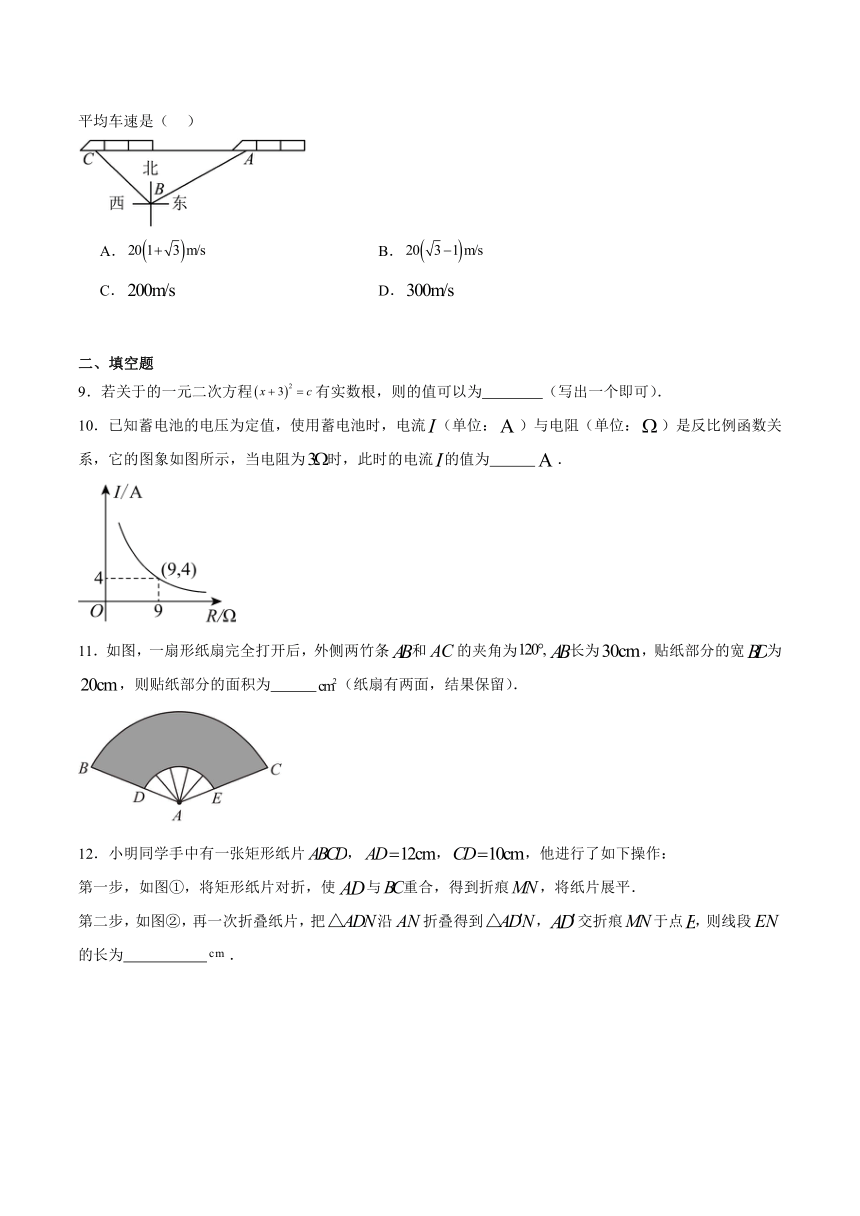
5.已知关于 x的不等式组的解集在数轴上的表示如图所示,则的值为( )
A. B.0 C.2 D.3
6.如图所示,电路连接完好,且各元件工作正常,随机闭合开关,,中的两个,能让灯泡发光的概率是( )
A. B. C. D.
7.小明周末从家出发,步行去公园游玩的行程如图所示,记他所行走的路程为S米,离开家的时间为t分钟.下列图像中,能近似刻画S与t之间关系的是( )
A. B.
C. D.
8.如图所示,在距离铁轨的B处,观察由南京开往上海的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东方向上,后,动车车头到达C处,恰好位于B处的西北方向上,则这列动车的平均车速是( )
A. B.
C. D.
二、填空题
9.若关于的一元二次方程有实数根,则的值可以为 (写出一个即可).
10.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,当电阻为时,此时的电流的值为 .
11.如图,一扇形纸扇完全打开后,外侧两竹条和的夹角为长为,贴纸部分的宽为,则贴纸部分的面积为 (纸扇有两面,结果保留).
12.小明同学手中有一张矩形纸片,,,他进行了如下操作:
第一步,如图①,将矩形纸片对折,使与重合,得到折痕,将纸片展平.
第二步,如图②,再一次折叠纸片,把沿折叠得到,交折痕于点,则线段的长为 .
三、解答题
13.计算:
(1)
(2)
14.某学校举办的“青春飞扬”主题演讲比赛,比赛由10名教师评委和10名学生评委给每位选手打分(百分制),对评委给某位选手的打分进行整理、描述和分析,下面给出了部分信息.
a.教师评委打分:86 88 90 91 91 91 91 92 92 98
b.学生评委打分:85 87 89 90 90 90 90 90 91 98
c.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91
学生评委 90 90
根据以上信息,回答下列问题:
(1)直接写出、的值;
(2)若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为,则______91(填“>”“=”或“<”);
(3)对于学生评委的打分,如果去掉一个最高分和一个最低分,则表中平均数、中位数和众数这三个数据中,哪些数据没有发生变化,说明理由.
15.为了响应国家提倡的“节能环保”号召,某共享电动车公司准备投入资金购买、两种电动车,若购买种电动车25辆、种电动车80辆,需投入资金30.5万元;若购买种电动车60辆、种电动车120辆,需投入资金48万元.已知这两种电动车的单价不变.
(1)求、两种电动车的单价分别是多少元?
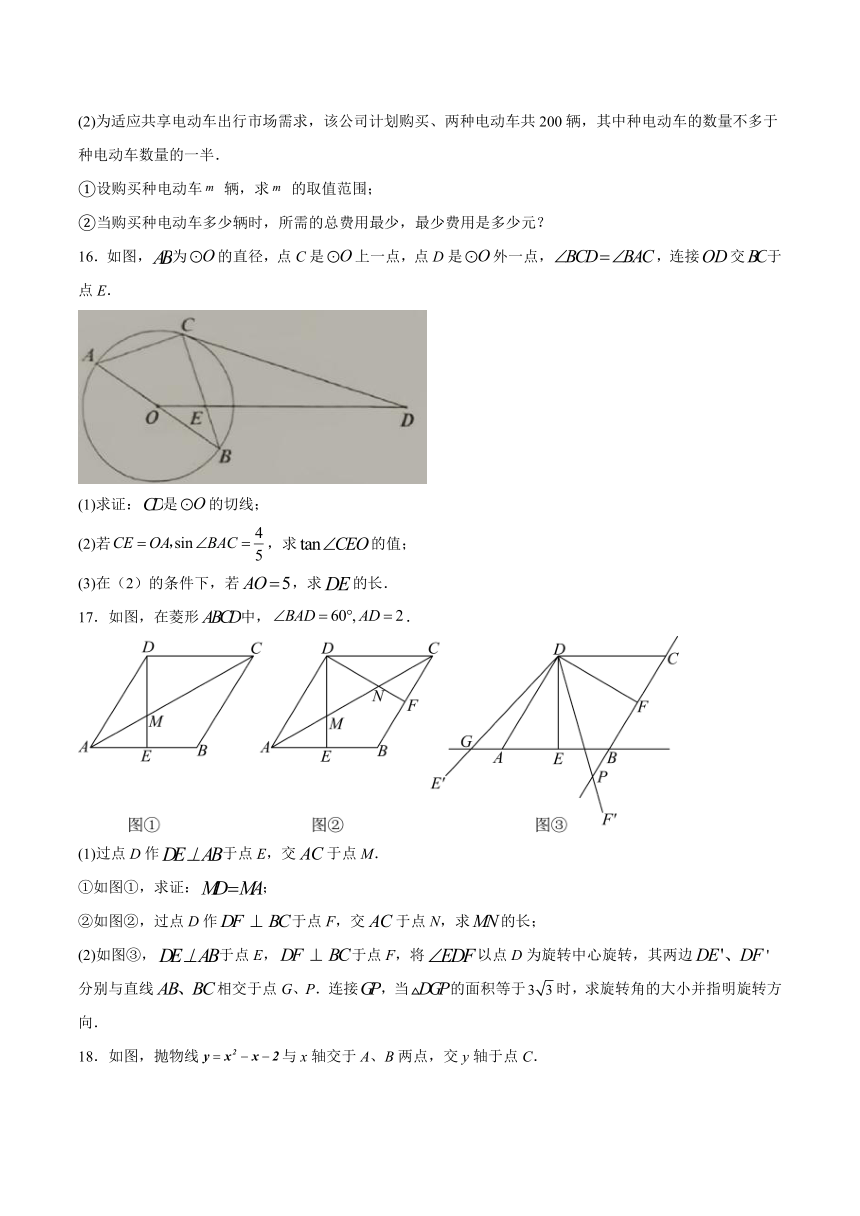
(2)为适应共享电动车出行市场需求,该公司计划购买、两种电动车共200辆,其中种电动车的数量不多于种电动车数量的一半.
①设购买种电动车辆,求的取值范围;
②当购买种电动车多少辆时,所需的总费用最少,最少费用是多少元?
16.如图,为的直径,点C是上一点,点D是外一点,,连接交于点E.
(1)求证:是的切线;
(2)若,求的值;
(3)在(2)的条件下,若,求的长.
17.如图,在菱形中,.
(1)过点D作于点E,交于点M.
①如图①,求证:;
②如图②,过点D作于点F,交于点N,求的长;
(2)如图③,于点E,于点F,将以点D为旋转中心旋转,其两边'分别与直线相交于点G、P.连接,当的面积等于时,求旋转角的大小并指明旋转方向.
18.如图,抛物线与x轴交于A、B两点,交y轴于点C.
(1)求点A、B、C的坐标,并直接写出的度数;
(2)若点D是和线段垂直平分线的交点,则与的周长之比为多少?
(3)在满足(2)的条件下,试探究抛物线上是否存在一点P,使得?若存在,求出点P的坐标;若不存在,请说明理由.
《2025年内蒙古自治区包头市昆区中考二模数学试题 》参考答案
1.D
解:根据俯视图的定义,选项D中的图形符合题意,
故选:D.
2.D
解:,,,,且.
离标准最近.
故选:D.
3.B
A、=3,故错误:
B、正确;
C、(2a2)3=8a6,故正确;
D、(a+2)2=a2+4a+4,故错误;
故选B.
4.C
解:如图:
,
,
,
,
故选:C.
5.C
解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
由数轴可知,不等式组的解集为,
∴,
∴,
故选:C.
6.A
解:列表如下:
共有6种等可能的情况,必须闭合开关灯泡才亮,能让灯泡发光的有4种情况,
则能让灯泡发光的概率是.
故选:A.
7.C
解:开始出发时,他所行走的路程从0米开始增加,故选项B、D不合题意;
步行到达公园游玩的过程中,他所行走的路程不变,在公园回家过程中,路程随时间的增加而增大,故选项A不合题意,选项C符合题意.
故选:C.
8.A
解:过点B作于点M,
∴,
∵当动车车头在A处时,恰好位于B处的北偏东方向上,后,动车车头到达C处,恰好位于B处的西北方向上,
∴,
∴,
∴,
∴,
∴,
∴这列动车的平均车速为.
故答案为:A.
9.5(答案不唯一,只有即可)
解:一元二次方程化为x2+6x+9-c=0,
∵△=36-4(9-c)=4c≥0,
解上式得c≥0.
故答为5(答案不唯一,只有c≥0即可).
10.12
解:设反比例函数的解析式为,把代入得
,
故,
当时,.
故答案为:12.
11.
解:∵,
∴,
∴贴纸部分的面积为;
故答案为:.
12./
解:∵四边形是矩形,
∴,
由折叠可得:,,,,
∴四边形是矩形,
∴,,
∴,
∴,
∴,
设,则,
在中,根据勾股定理可得:,
即,
解得:,
即,
故答案为:.
13.(1)7
(2)
(1)解:
.
(2)
.
14.(1),
(2)
(3)中位数,众数,见解析
(1)解:依题意,出现4次,且出现次数最多
∴,
∵有10名学生评委,
∴中位数排在第和位,
结合数据,排在第和位的数分别是,
则
∴,.
(2)解:依题意,
故答案为:
(3)解:∵学生评委的打分,如果去掉一个最高分和一个最低分,
∴数据是87,89,90,90,90,90,90,91,
此时中位数排在第和位
∴中位数仍为,
90出现的次数最多,即众数仍为,
∴去掉一个最高分和一个最低分对中位数和众数没有影响,
此时平均数,
∴去掉一个最高分和一个最低分对平均数有影响.
15.(1)A、B两种电动车的单价分别为1000元、3500元
(2)①;②当购买A种电动车66辆时所需的总费用最少,最少费用为535000元
(1)解:设A、B两种电动车的单价分别为x元、y元,
由题意得,
解得:,
答:A、B两种电动车的单价分别为1000元、3500元;
(2)解:①设购买A种电动车m辆,则购买B种电动车辆,
∵,
∴;
②设所需购买总费用为w元,
则,
∵,
∴随着的增大而减小,
∵m取正整数,
∴时,最少,
∴(元),
答:当购买A种电动车66辆时所需的总费用最少,最少费用为535000元.
16.(1)见解析
(2)3
(3)
(1)证明:连接,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是的切线.
(2)解:过点O作于F,如图,
∵,
∴设,则,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,,
∴为的中位线,
∴,
∴.
(3)解:连接,如图,
∵,,
∴,
∴,
∴ ,
由(1)可知,,
在中,,
∵,
∴,
∴.
在(2)的条件下,,
∴.
∴,.
∴在中, ,
∴.
17.(1)①见解析;②
(2)顺时针或逆时针旋转60度
(1)解:①证明:∵,
∴,
∵中,,
∴,
∵菱形,
∴,.
∵,
∴,
∴,
∴,
∴;
②∵,
∴,
在菱形中,,
∴,
∵中,,
∵,
∴,
∴.
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴为等边三角形,
∴.
∵中,,
∴,
∴,
∵,
∴,
∵中,,
∴,
∴,
∴.
(2)解:∵,,
∴,又,
∴,
当顺时针旋转时,
由旋转的性质可知,,
,,
在和中,
,
∴,
∴,
∴为等边三角形,
∴的面积,解得,,
则,
∴,
∴当顺时针旋转时,的面积等于,
同理可得,当逆时针旋转时,的面积也等于,
综上所述,将以点D为旋转中心,
顺时针或逆时针旋转时,的面积等于.
18.(1),,,
(2)
(3)存在,或
(1)解:令,则,
解得:,,
,,
,
令,则,
,
,
,
又,
是等腰直角三角形,,
综上所述,,,,.
(2)解:,,,
,,
,
点D是和线段垂直平分线的交点,
点D是的外心,
,,
是等腰直角三角形,
由(1)得,是等腰直角三角形,
,
与的周长之比等于相似比,
与的周长之比为.
(3)解:存在.理由如下:
作点关于抛物线的对称轴的对称点,连接,
则,
,
由抛物线的对称性可得,
四边形是等腰梯形,
,
由(2)得,、是等腰直角三角形,
,
,即,
当点与点重合时满足条件,
;
作点关于直线的对称点,
,
,
由对称性得,,,
,,
当点在直线上时满足条件,
设直线的解析式为,
代入和得,,
解得:,
直线的解析式为,
联立,
解得:或
综上所述,点P的坐标为或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.紫砂壶,被誉为中国非物质文化遗产的瑰宝,以其独特的成型工艺和多样的造型式样著称,陶器所散发的古朴典雅之色更是引人入胜.如图所展示的是一把精湛工艺紫砂壶“景舟石瓢”,下面四幅图是此紫砂壶的俯视图的是( )
A. B.
C. D.
2.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
A. B. C. D.
3.下列运算正确的是( )
A.=﹣3 B.a2 a4=a6 C.(2a2)3=2a6 D.(a+2)2=a2+4
4.如图,将三角尺的直角顶点放在直尺的一边上,,则的度数等于( )
A. B. C. D.
5.已知关于 x的不等式组的解集在数轴上的表示如图所示,则的值为( )
A. B.0 C.2 D.3
6.如图所示,电路连接完好,且各元件工作正常,随机闭合开关,,中的两个,能让灯泡发光的概率是( )
A. B. C. D.
7.小明周末从家出发,步行去公园游玩的行程如图所示,记他所行走的路程为S米,离开家的时间为t分钟.下列图像中,能近似刻画S与t之间关系的是( )
A. B.
C. D.
8.如图所示,在距离铁轨的B处,观察由南京开往上海的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东方向上,后,动车车头到达C处,恰好位于B处的西北方向上,则这列动车的平均车速是( )
A. B.
C. D.
二、填空题
9.若关于的一元二次方程有实数根,则的值可以为 (写出一个即可).
10.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,当电阻为时,此时的电流的值为 .
11.如图,一扇形纸扇完全打开后,外侧两竹条和的夹角为长为,贴纸部分的宽为,则贴纸部分的面积为 (纸扇有两面,结果保留).
12.小明同学手中有一张矩形纸片,,,他进行了如下操作:
第一步,如图①,将矩形纸片对折,使与重合,得到折痕,将纸片展平.
第二步,如图②,再一次折叠纸片,把沿折叠得到,交折痕于点,则线段的长为 .
三、解答题
13.计算:
(1)
(2)
14.某学校举办的“青春飞扬”主题演讲比赛,比赛由10名教师评委和10名学生评委给每位选手打分(百分制),对评委给某位选手的打分进行整理、描述和分析,下面给出了部分信息.
a.教师评委打分:86 88 90 91 91 91 91 92 92 98
b.学生评委打分:85 87 89 90 90 90 90 90 91 98
c.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91
学生评委 90 90
根据以上信息,回答下列问题:
(1)直接写出、的值;
(2)若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为,则______91(填“>”“=”或“<”);
(3)对于学生评委的打分,如果去掉一个最高分和一个最低分,则表中平均数、中位数和众数这三个数据中,哪些数据没有发生变化,说明理由.
15.为了响应国家提倡的“节能环保”号召,某共享电动车公司准备投入资金购买、两种电动车,若购买种电动车25辆、种电动车80辆,需投入资金30.5万元;若购买种电动车60辆、种电动车120辆,需投入资金48万元.已知这两种电动车的单价不变.
(1)求、两种电动车的单价分别是多少元?
(2)为适应共享电动车出行市场需求,该公司计划购买、两种电动车共200辆,其中种电动车的数量不多于种电动车数量的一半.
①设购买种电动车辆,求的取值范围;
②当购买种电动车多少辆时,所需的总费用最少,最少费用是多少元?
16.如图,为的直径,点C是上一点,点D是外一点,,连接交于点E.
(1)求证:是的切线;
(2)若,求的值;
(3)在(2)的条件下,若,求的长.
17.如图,在菱形中,.
(1)过点D作于点E,交于点M.
①如图①,求证:;
②如图②,过点D作于点F,交于点N,求的长;
(2)如图③,于点E,于点F,将以点D为旋转中心旋转,其两边'分别与直线相交于点G、P.连接,当的面积等于时,求旋转角的大小并指明旋转方向.
18.如图,抛物线与x轴交于A、B两点,交y轴于点C.
(1)求点A、B、C的坐标,并直接写出的度数;
(2)若点D是和线段垂直平分线的交点,则与的周长之比为多少?
(3)在满足(2)的条件下,试探究抛物线上是否存在一点P,使得?若存在,求出点P的坐标;若不存在,请说明理由.
《2025年内蒙古自治区包头市昆区中考二模数学试题 》参考答案
1.D
解:根据俯视图的定义,选项D中的图形符合题意,
故选:D.
2.D
解:,,,,且.
离标准最近.
故选:D.
3.B
A、=3,故错误:
B、正确;
C、(2a2)3=8a6,故正确;
D、(a+2)2=a2+4a+4,故错误;
故选B.
4.C
解:如图:
,
,
,
,
故选:C.
5.C
解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
由数轴可知,不等式组的解集为,
∴,
∴,
故选:C.
6.A
解:列表如下:
共有6种等可能的情况,必须闭合开关灯泡才亮,能让灯泡发光的有4种情况,
则能让灯泡发光的概率是.
故选:A.
7.C
解:开始出发时,他所行走的路程从0米开始增加,故选项B、D不合题意;
步行到达公园游玩的过程中,他所行走的路程不变,在公园回家过程中,路程随时间的增加而增大,故选项A不合题意,选项C符合题意.
故选:C.
8.A
解:过点B作于点M,
∴,
∵当动车车头在A处时,恰好位于B处的北偏东方向上,后,动车车头到达C处,恰好位于B处的西北方向上,
∴,
∴,
∴,
∴,
∴,
∴这列动车的平均车速为.
故答案为:A.
9.5(答案不唯一,只有即可)
解:一元二次方程化为x2+6x+9-c=0,
∵△=36-4(9-c)=4c≥0,
解上式得c≥0.
故答为5(答案不唯一,只有c≥0即可).
10.12
解:设反比例函数的解析式为,把代入得
,
故,
当时,.
故答案为:12.
11.
解:∵,
∴,
∴贴纸部分的面积为;
故答案为:.
12./
解:∵四边形是矩形,
∴,
由折叠可得:,,,,
∴四边形是矩形,
∴,,
∴,
∴,
∴,
设,则,
在中,根据勾股定理可得:,
即,
解得:,
即,
故答案为:.
13.(1)7
(2)
(1)解:
.
(2)
.
14.(1),
(2)
(3)中位数,众数,见解析
(1)解:依题意,出现4次,且出现次数最多
∴,
∵有10名学生评委,
∴中位数排在第和位,
结合数据,排在第和位的数分别是,
则
∴,.
(2)解:依题意,
故答案为:
(3)解:∵学生评委的打分,如果去掉一个最高分和一个最低分,
∴数据是87,89,90,90,90,90,90,91,
此时中位数排在第和位
∴中位数仍为,
90出现的次数最多,即众数仍为,
∴去掉一个最高分和一个最低分对中位数和众数没有影响,
此时平均数,
∴去掉一个最高分和一个最低分对平均数有影响.
15.(1)A、B两种电动车的单价分别为1000元、3500元
(2)①;②当购买A种电动车66辆时所需的总费用最少,最少费用为535000元
(1)解:设A、B两种电动车的单价分别为x元、y元,
由题意得,
解得:,
答:A、B两种电动车的单价分别为1000元、3500元;
(2)解:①设购买A种电动车m辆,则购买B种电动车辆,
∵,
∴;
②设所需购买总费用为w元,
则,
∵,
∴随着的增大而减小,
∵m取正整数,
∴时,最少,
∴(元),
答:当购买A种电动车66辆时所需的总费用最少,最少费用为535000元.
16.(1)见解析
(2)3
(3)
(1)证明:连接,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是的切线.
(2)解:过点O作于F,如图,
∵,
∴设,则,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,,
∴为的中位线,
∴,
∴.
(3)解:连接,如图,
∵,,
∴,
∴,
∴ ,
由(1)可知,,
在中,,
∵,
∴,
∴.
在(2)的条件下,,
∴.
∴,.
∴在中, ,
∴.
17.(1)①见解析;②
(2)顺时针或逆时针旋转60度
(1)解:①证明:∵,
∴,
∵中,,
∴,
∵菱形,
∴,.
∵,
∴,
∴,
∴,
∴;
②∵,
∴,
在菱形中,,
∴,
∵中,,
∵,
∴,
∴.
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴为等边三角形,
∴.
∵中,,
∴,
∴,
∵,
∴,
∵中,,
∴,
∴,
∴.
(2)解:∵,,
∴,又,
∴,
当顺时针旋转时,
由旋转的性质可知,,
,,
在和中,
,
∴,
∴,
∴为等边三角形,
∴的面积,解得,,
则,
∴,
∴当顺时针旋转时,的面积等于,
同理可得,当逆时针旋转时,的面积也等于,
综上所述,将以点D为旋转中心,
顺时针或逆时针旋转时,的面积等于.
18.(1),,,
(2)
(3)存在,或
(1)解:令,则,
解得:,,
,,
,
令,则,
,
,
,
又,
是等腰直角三角形,,
综上所述,,,,.
(2)解:,,,
,,
,
点D是和线段垂直平分线的交点,
点D是的外心,
,,
是等腰直角三角形,
由(1)得,是等腰直角三角形,
,
与的周长之比等于相似比,
与的周长之比为.
(3)解:存在.理由如下:
作点关于抛物线的对称轴的对称点,连接,
则,
,
由抛物线的对称性可得,
四边形是等腰梯形,
,
由(2)得,、是等腰直角三角形,
,
,即,
当点与点重合时满足条件,
;
作点关于直线的对称点,
,
,
由对称性得,,,
,,
当点在直线上时满足条件,
设直线的解析式为,
代入和得,,
解得:,
直线的解析式为,
联立,
解得:或
综上所述,点P的坐标为或.
同课章节目录
