第14章 统计 章末复习【含答案】
文档属性
| 名称 | 第14章 统计 章末复习【含答案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 409.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 11:28:27 | ||
图片预览


文档简介
第14章 统计章末复习
[A 基础达标]
1.某防疫站对学生进行身体健康调查,欲采用分层抽样的方法抽取样本.某中学共有学生2 000名,从中抽取了一个容量为200的样本,其中男生103名,则该中学共有女生的人数为( )
A.1 030名 B.97名
C.950名 D.970名
2.交通管理部门为了了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查,假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员100人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为10,6,5,4,则这四个社区驾驶员的总人数N为( )
A.1 000 B.625
C.250 D.500
3.某商场在五一促销活动中,对5月1日9时至14时的销售额进行统计,其频率直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
A.6万元 B.8万元
C.10万元 D.12万元
4.已知一组数据6,7,8,x,y的平均数是7,则这组数据的中位数是( )
A.6 B.7
C.8 D.不确定
5.一个学生期末数学的平时成绩为B的标准为“平时的五次成绩均不小于80分”.根据甲、乙、丙、丁四位同学五次平时成绩的记录数据(记录数据都是正整数),平时成绩一定为B的是( )
A.甲同学:中位数为85,总体均值为82
B.乙同学:众数为83,总体均值为82
C.丙同学:总体均值为84,总体方差为6
D.丁同学:中位数为83,总体方差为6
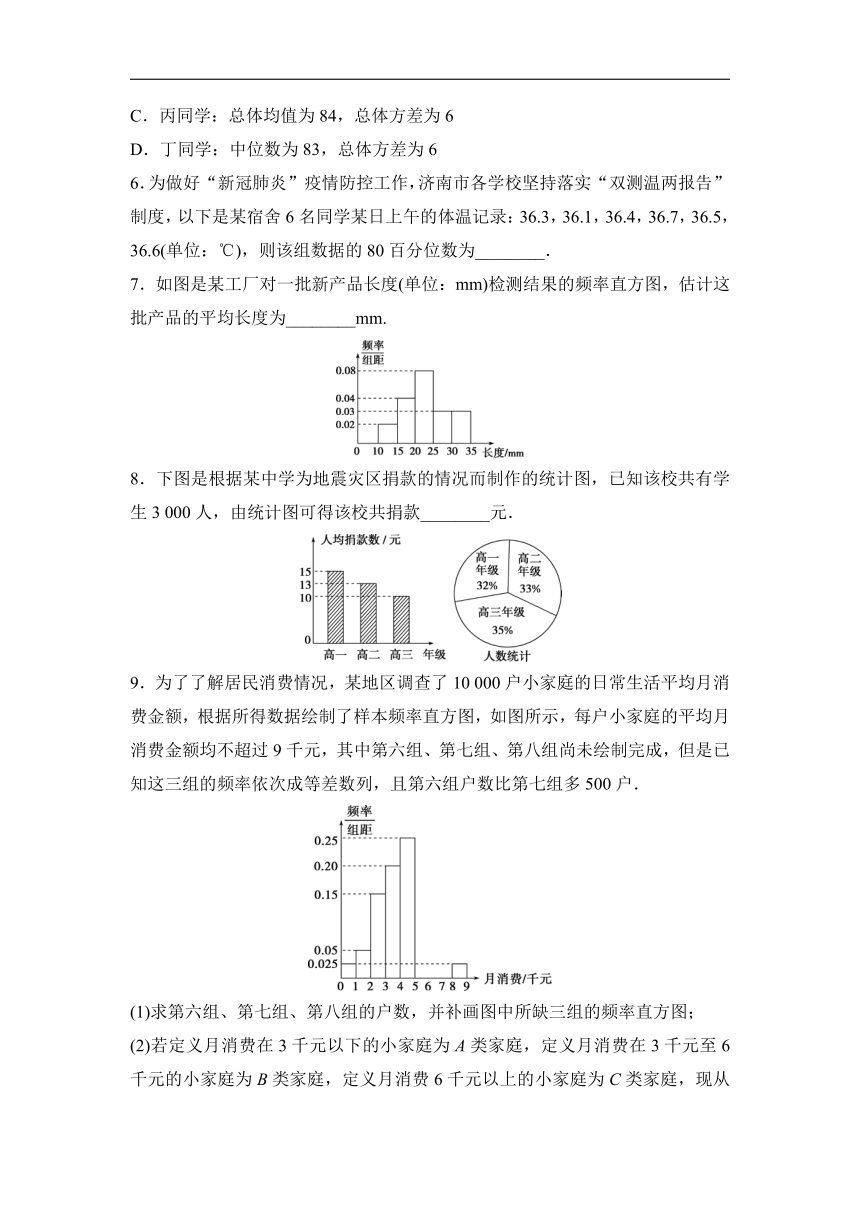
6.为做好“新冠肺炎”疫情防控工作,济南市各学校坚持落实“双测温两报告”制度,以下是某宿舍6名同学某日上午的体温记录:36.3,36.1,36.4,36.7,36.5,36.6(单位:℃),则该组数据的80百分位数为________.
7.如图是某工厂对一批新产品长度(单位:mm)检测结果的频率直方图,估计这批产品的平均长度为________mm.
8.下图是根据某中学为地震灾区捐款的情况而制作的统计图,已知该校共有学生3 000人,由统计图可得该校共捐款________元.
9.为了了解居民消费情况,某地区调查了10 000户小家庭的日常生活平均月消费金额,根据所得数据绘制了样本频率直方图,如图所示,每户小家庭的平均月消费金额均不超过9千元,其中第六组、第七组、第八组尚未绘制完成,但是已知这三组的频率依次成等差数列,且第六组户数比第七组多500户.
(1)求第六组、第七组、第八组的户数,并补画图中所缺三组的频率直方图;
(2)若定义月消费在3千元以下的小家庭为A类家庭,定义月消费在3千元至6千元的小家庭为B类家庭,定义月消费6千元以上的小家庭为C类家庭,现从这10 000户家庭中按分层抽样的方法抽取80户家庭召开座谈会,问A,B,C各层抽取的户数分别是多少?
10.为了了解某市家庭用电量的情况,该市统计部门随机调查了200户居民去年一年的月均用电量(单位:kW·h),并将得到数据按如下方式分为9组:[0,40),[40,80),…,[320,360],绘制得到如下的频率直方图:
(1)试估计抽查样本中用电量在[160,200)的用户数量;
(2)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定第二档月均用电量的范围.(计算百分位数时,结果四舍五入取整数:范围用左开右闭区间表示)
[B 能力提升]
11.(多选)某地区一周的最低气温随时间变化的图象如图所示,根据图中的信息,下列有关该地区这一周最低气温的判断,正确的有( )
A.前六天一直保持上升趋势
B.相邻两天的差最大为3
C.众数为0
D.最大值与最小值的差为7
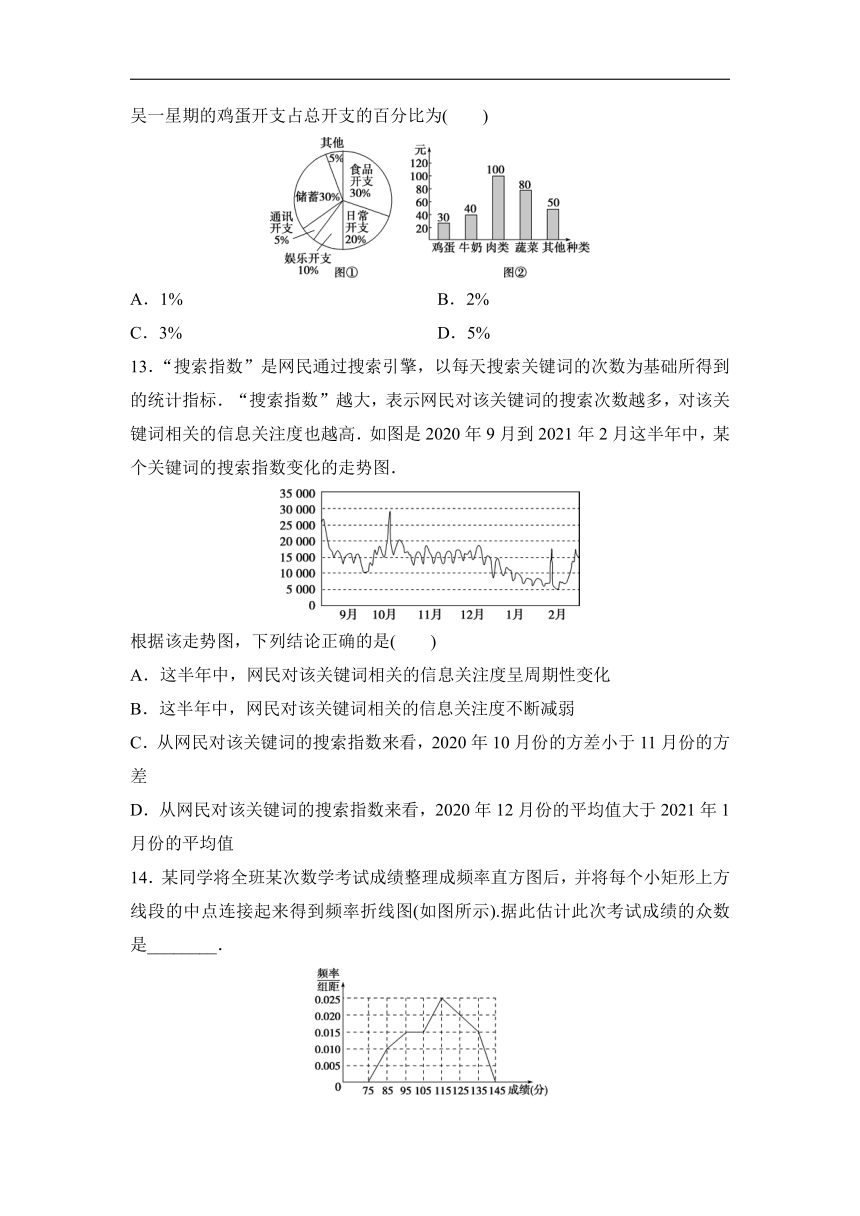
12.小吴一星期的总开支分布如图①所示,一星期的食品开支如图②所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
A.1% B.2%
C.3% D.5%
13.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.如图是2020年9月到2021年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,2020年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,2020年12月份的平均值大于2021年1月份的平均值
14.某同学将全班某次数学考试成绩整理成频率直方图后,并将每个小矩形上方线段的中点连接起来得到频率折线图(如图所示).据此估计此次考试成绩的众数是________.
[C 拓展探究]
15.某制造商为运动会生产一批直径为40 mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
40.02 40.00 39.98 40.00 39.99
40.00 39.98 40.01 39.98 39.99
40.00 39.99 39.95 40.01 40.02
39.98 40.00 39.99 40.00 39.96
(1)完成下面的频率分布表,并画出频率直方图;
分组 频数 频率
[39.95,39.97)
[39.97,39.99)
[39.99,40.01)
[40.01,40.03]
合计
(2)假定乒乓球的直径误差不超过0.02 mm为合格品,若这批乒乓球的总数为10 000只,试根据抽样检查结果估计这批产品的合格数.
参考答案
[A 基础达标]
1.解析:选D.由题意,知该中学共有女生2 000×=970(名),故选D.
2.解析:选C.因为在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为10,6,5,4,所以这四个社区驾驶员的总人数N=(10+6+5+4)×=250,故选C.
3.解析:选C.设11时至12时的销售额为x万元,由于频率直方图中各小组的组距相同,故各小矩形的高度之比等于频率之比,也等于销售额之比,所以9时至10时的销售额与11时至12时的销售额的比为=,
所以有=,解得x=10,故选C.
4.解析:选B.因为==7,得x+y=14,若x<7,则y>7,此时中位数为7,
若x=y=7,则中位数为7,综上所述,这组数据的中位数为7.
5.解析:选C.对于A.甲同学:中位数为85,总体均值为82,可以找到很多反例,如74,80,85,85,86,故A不正确;
对于B.乙同学:众数为83,总体均值为82,可以找到很多反例,如79,80,83,83,85,故B不正确;
对于D.丁同学:中位数为83,总体方差为6,比如反例,78,78,83,83,83,故D不正确;故选C.
6.解析:将6名同学某日上午的体温记录从小到大排列为36.1,36.3, 36.4,36.5,36.6,36.7,因为80%×6=4.8,所以该组数据的80百分位数为36.6,故答案为36.6.
答案:36.6
7.解析:根据频率直方图,估计这批产品的平均长度为(12.5×0.02+17.5×0.04+22.5×0.08+27.5×0.03+32.5×0.03)×5=22.75(mm).
答案:22.75
8.解析:由扇形统计图可知,该中学高一、高二、高三年级分别有学生960人、990人、1 050人,由条形统计图知,该中学高一、高二、高三年级人均捐款分别为15元、13元、10元,所以共捐款15×960+13×990+10×1 050=37 770(元).
答案:37 770
9.解:(1)设第六、七、八组的户数分别是x,y,z,
它们的频率之和为1-(0.025×2+0.05+0.15+0.20+0.25)=0.30,
所以这三组的户数之和为10 000×0.3=3 000.
由于这三组的频率依次成等差数列,所以x,y,z也成等差数列,2y=x+z,又x+y+z=3 000,x-y=500,解得x=1 500,y=1 000,z=500.
所以第六、七、八组的小矩形高度分别为=0.15,=0.10,=0.05.
补全频率直方图.(需注明第七组的小矩形高度为0.10,第六、八两组分别用虚线对应0.15和0.05.)
(2)A类家庭的频率之和为0.025+0.05+0.15=0.225;
B类家庭的频率之和为0.20+0.25+0.15=0.60;
C类家庭的频率之和为0.10+0.05+0.025=0.175.
故A,B,C类家庭分别抽取的户数为80×0.225=18,80×0.6=48,80×0.175=14.
10.解:(1)由频率直方图可得,样本落在[0,40),[40,80),[80,120),[120,160)的频率分别为0.02,0.15,0.27,0.23,落在[200,240),[240,280),[280,320),[320,360]的频率分别为0.09,0.06,0.04,0.01.
因此,样本落在[160,200)的频率为
1-(0.02+0.15+0.27+0.23+0.09+0.06+0.04+0.01)=0.13,
样本中用电量在[160,200)的用户数为200×0.13=26.
(2)因为0.02+0.15+0.27+0.23=0.67,0.02+0.15+0.27+0.23+0.13=0.8,
为了使75%的居民缴费在第一档,只需75%对应的用电量位于[160,200)内,
于是160+40×≈185,
又0.02+0.15+0.27+0.23+0.13+0.09+0.06=0.95,
所以95%对应的用电量为280.
所以第二档的范围可确定为(185,280].
[B 能力提升]
11.解析:选CD.周三到周四,最低气温下降了,所以A项错误;周六与周日的最低气温之差为4 ℃,故B项错误;0 ℃ 出现了2次,而其他的值只出现1次,故众数为0,C项正确;最小值为周一的-3 ℃,最大值为周六的4 ℃,二者差为7 ℃,D项正确.故选CD.
12.解析:选C.由题图①所示,食品开支占总开支的30%.由题图②所示,鸡蛋开支占食品开支的=,所以鸡蛋开支占总开支的百分比为30%×=3%.故选C.
13.解析:选D.对于A,不呈周期变化,故A错;
对于B,并不是不断减弱,中间有增强,故B错;
对于C,10月份的波动大小大于11月份,所以方差要大,故C错;
对于D,由题图可知,2020年12月起到2021年1月份有下降的趋势,所以2020年12月份的平均值大于2021年1月份的平均值,故D正确,故选D.
14.解析:众数是一组数据出现次数最多的数,结合题中频率折线图可以看出,数据“115”对应的纵坐标最大,所以相应的频率最大,频数最大,据此估计此次考试成绩的众数是115.
答案:115
[C 拓展探究]
15.解:(1)频率分布表:
分组 频数 频率
[39.95,39.97) 2 0.10 5
[39.97,39.99) 4 0.20 10
[39.99,40.01) 10 0.50 25
[40.01,40.03] 4 0.20 10
合计 20 1.00
频率直方图:
(2)因为抽样的20只产品中在[39.98,40.02]范围内有18只,所以合格率为×100%=90%,
所以10 000×90%=9 000(只).
即根据抽样检查结果,可以估计这批产品的合格数为9 000只.
[A 基础达标]
1.某防疫站对学生进行身体健康调查,欲采用分层抽样的方法抽取样本.某中学共有学生2 000名,从中抽取了一个容量为200的样本,其中男生103名,则该中学共有女生的人数为( )
A.1 030名 B.97名
C.950名 D.970名
2.交通管理部门为了了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查,假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员100人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为10,6,5,4,则这四个社区驾驶员的总人数N为( )
A.1 000 B.625
C.250 D.500
3.某商场在五一促销活动中,对5月1日9时至14时的销售额进行统计,其频率直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
A.6万元 B.8万元
C.10万元 D.12万元
4.已知一组数据6,7,8,x,y的平均数是7,则这组数据的中位数是( )
A.6 B.7
C.8 D.不确定
5.一个学生期末数学的平时成绩为B的标准为“平时的五次成绩均不小于80分”.根据甲、乙、丙、丁四位同学五次平时成绩的记录数据(记录数据都是正整数),平时成绩一定为B的是( )
A.甲同学:中位数为85,总体均值为82
B.乙同学:众数为83,总体均值为82
C.丙同学:总体均值为84,总体方差为6
D.丁同学:中位数为83,总体方差为6
6.为做好“新冠肺炎”疫情防控工作,济南市各学校坚持落实“双测温两报告”制度,以下是某宿舍6名同学某日上午的体温记录:36.3,36.1,36.4,36.7,36.5,36.6(单位:℃),则该组数据的80百分位数为________.
7.如图是某工厂对一批新产品长度(单位:mm)检测结果的频率直方图,估计这批产品的平均长度为________mm.
8.下图是根据某中学为地震灾区捐款的情况而制作的统计图,已知该校共有学生3 000人,由统计图可得该校共捐款________元.
9.为了了解居民消费情况,某地区调查了10 000户小家庭的日常生活平均月消费金额,根据所得数据绘制了样本频率直方图,如图所示,每户小家庭的平均月消费金额均不超过9千元,其中第六组、第七组、第八组尚未绘制完成,但是已知这三组的频率依次成等差数列,且第六组户数比第七组多500户.
(1)求第六组、第七组、第八组的户数,并补画图中所缺三组的频率直方图;
(2)若定义月消费在3千元以下的小家庭为A类家庭,定义月消费在3千元至6千元的小家庭为B类家庭,定义月消费6千元以上的小家庭为C类家庭,现从这10 000户家庭中按分层抽样的方法抽取80户家庭召开座谈会,问A,B,C各层抽取的户数分别是多少?
10.为了了解某市家庭用电量的情况,该市统计部门随机调查了200户居民去年一年的月均用电量(单位:kW·h),并将得到数据按如下方式分为9组:[0,40),[40,80),…,[320,360],绘制得到如下的频率直方图:
(1)试估计抽查样本中用电量在[160,200)的用户数量;
(2)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定第二档月均用电量的范围.(计算百分位数时,结果四舍五入取整数:范围用左开右闭区间表示)
[B 能力提升]
11.(多选)某地区一周的最低气温随时间变化的图象如图所示,根据图中的信息,下列有关该地区这一周最低气温的判断,正确的有( )
A.前六天一直保持上升趋势
B.相邻两天的差最大为3
C.众数为0
D.最大值与最小值的差为7
12.小吴一星期的总开支分布如图①所示,一星期的食品开支如图②所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
A.1% B.2%
C.3% D.5%
13.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.如图是2020年9月到2021年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,2020年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,2020年12月份的平均值大于2021年1月份的平均值
14.某同学将全班某次数学考试成绩整理成频率直方图后,并将每个小矩形上方线段的中点连接起来得到频率折线图(如图所示).据此估计此次考试成绩的众数是________.
[C 拓展探究]
15.某制造商为运动会生产一批直径为40 mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
40.02 40.00 39.98 40.00 39.99
40.00 39.98 40.01 39.98 39.99
40.00 39.99 39.95 40.01 40.02
39.98 40.00 39.99 40.00 39.96
(1)完成下面的频率分布表,并画出频率直方图;
分组 频数 频率
[39.95,39.97)
[39.97,39.99)
[39.99,40.01)
[40.01,40.03]
合计
(2)假定乒乓球的直径误差不超过0.02 mm为合格品,若这批乒乓球的总数为10 000只,试根据抽样检查结果估计这批产品的合格数.
参考答案
[A 基础达标]
1.解析:选D.由题意,知该中学共有女生2 000×=970(名),故选D.
2.解析:选C.因为在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为10,6,5,4,所以这四个社区驾驶员的总人数N=(10+6+5+4)×=250,故选C.
3.解析:选C.设11时至12时的销售额为x万元,由于频率直方图中各小组的组距相同,故各小矩形的高度之比等于频率之比,也等于销售额之比,所以9时至10时的销售额与11时至12时的销售额的比为=,
所以有=,解得x=10,故选C.
4.解析:选B.因为==7,得x+y=14,若x<7,则y>7,此时中位数为7,
若x=y=7,则中位数为7,综上所述,这组数据的中位数为7.
5.解析:选C.对于A.甲同学:中位数为85,总体均值为82,可以找到很多反例,如74,80,85,85,86,故A不正确;
对于B.乙同学:众数为83,总体均值为82,可以找到很多反例,如79,80,83,83,85,故B不正确;
对于D.丁同学:中位数为83,总体方差为6,比如反例,78,78,83,83,83,故D不正确;故选C.
6.解析:将6名同学某日上午的体温记录从小到大排列为36.1,36.3, 36.4,36.5,36.6,36.7,因为80%×6=4.8,所以该组数据的80百分位数为36.6,故答案为36.6.
答案:36.6
7.解析:根据频率直方图,估计这批产品的平均长度为(12.5×0.02+17.5×0.04+22.5×0.08+27.5×0.03+32.5×0.03)×5=22.75(mm).
答案:22.75
8.解析:由扇形统计图可知,该中学高一、高二、高三年级分别有学生960人、990人、1 050人,由条形统计图知,该中学高一、高二、高三年级人均捐款分别为15元、13元、10元,所以共捐款15×960+13×990+10×1 050=37 770(元).
答案:37 770
9.解:(1)设第六、七、八组的户数分别是x,y,z,
它们的频率之和为1-(0.025×2+0.05+0.15+0.20+0.25)=0.30,
所以这三组的户数之和为10 000×0.3=3 000.
由于这三组的频率依次成等差数列,所以x,y,z也成等差数列,2y=x+z,又x+y+z=3 000,x-y=500,解得x=1 500,y=1 000,z=500.
所以第六、七、八组的小矩形高度分别为=0.15,=0.10,=0.05.
补全频率直方图.(需注明第七组的小矩形高度为0.10,第六、八两组分别用虚线对应0.15和0.05.)
(2)A类家庭的频率之和为0.025+0.05+0.15=0.225;
B类家庭的频率之和为0.20+0.25+0.15=0.60;
C类家庭的频率之和为0.10+0.05+0.025=0.175.
故A,B,C类家庭分别抽取的户数为80×0.225=18,80×0.6=48,80×0.175=14.
10.解:(1)由频率直方图可得,样本落在[0,40),[40,80),[80,120),[120,160)的频率分别为0.02,0.15,0.27,0.23,落在[200,240),[240,280),[280,320),[320,360]的频率分别为0.09,0.06,0.04,0.01.
因此,样本落在[160,200)的频率为
1-(0.02+0.15+0.27+0.23+0.09+0.06+0.04+0.01)=0.13,
样本中用电量在[160,200)的用户数为200×0.13=26.
(2)因为0.02+0.15+0.27+0.23=0.67,0.02+0.15+0.27+0.23+0.13=0.8,
为了使75%的居民缴费在第一档,只需75%对应的用电量位于[160,200)内,
于是160+40×≈185,
又0.02+0.15+0.27+0.23+0.13+0.09+0.06=0.95,
所以95%对应的用电量为280.
所以第二档的范围可确定为(185,280].
[B 能力提升]
11.解析:选CD.周三到周四,最低气温下降了,所以A项错误;周六与周日的最低气温之差为4 ℃,故B项错误;0 ℃ 出现了2次,而其他的值只出现1次,故众数为0,C项正确;最小值为周一的-3 ℃,最大值为周六的4 ℃,二者差为7 ℃,D项正确.故选CD.
12.解析:选C.由题图①所示,食品开支占总开支的30%.由题图②所示,鸡蛋开支占食品开支的=,所以鸡蛋开支占总开支的百分比为30%×=3%.故选C.
13.解析:选D.对于A,不呈周期变化,故A错;
对于B,并不是不断减弱,中间有增强,故B错;
对于C,10月份的波动大小大于11月份,所以方差要大,故C错;
对于D,由题图可知,2020年12月起到2021年1月份有下降的趋势,所以2020年12月份的平均值大于2021年1月份的平均值,故D正确,故选D.
14.解析:众数是一组数据出现次数最多的数,结合题中频率折线图可以看出,数据“115”对应的纵坐标最大,所以相应的频率最大,频数最大,据此估计此次考试成绩的众数是115.
答案:115
[C 拓展探究]
15.解:(1)频率分布表:
分组 频数 频率
[39.95,39.97) 2 0.10 5
[39.97,39.99) 4 0.20 10
[39.99,40.01) 10 0.50 25
[40.01,40.03] 4 0.20 10
合计 20 1.00
频率直方图:
(2)因为抽样的20只产品中在[39.98,40.02]范围内有18只,所以合格率为×100%=90%,
所以10 000×90%=9 000(只).
即根据抽样检查结果,可以估计这批产品的合格数为9 000只.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
