(期末考点培优)专题06 解答题-2024-2025学年五年级数学下册期末复习专项青岛版(六三制)(含解析)
文档属性
| 名称 | (期末考点培优)专题06 解答题-2024-2025学年五年级数学下册期末复习专项青岛版(六三制)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 11:47:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级数学下册期末复习专项青岛(六三制)
(期末考点培优)专题06 解答题
学校:___________姓名:___________班级:___________考号:___________
1.学校表彰“优秀志愿者”准备了49本科技书和29支钢笔,平均分给评选出来的“优秀志愿者”,结果科技书多出4本,钢笔少了1支,这次最多评选了多少名“优秀志愿者”?
2.为庆祝教师节,五(1)班的学生正在礼堂里挂气球。按照2个蓝气球、3个红气球、2个黄气球的顺序循环排列,一共挂了50个气球。三种颜色的气球分别占总数的几分之几?
3.有两根绸带,一根长20米,另一根长28米。把它们截成若干段同样长的小段,而且没有剩余,截成的小段最长是多少米?一共可以截成多少段?
4.在“爱阅读爱数学”活动中,王老师帮乐乐录制了一段4.5分钟的短视频。其中的时间他在讲数学故事,的时间在介绍自己喜欢的数学读物:张景中院士的《帮你学数学》,剩下的时间在和同学互动。乐乐和同学互动的时间占这个短视频的几分之几?
5.某公交车站的始发站每6分钟发出一辆5路车,每8分钟发出一辆7路车,如果这两路公交车早上6:00同时从始发站发车,那么这两路公交车的第二次共同发车时间是6:48,你同意吗?请写出你的判断理由。
6.学校为古诗词大赛中表现优异的同学准备了47支中性笔和31个笔记本作为奖品,每名同学得到的奖品种类和数量完全相同,最后余下了2支中性笔和1个笔记本,最多有几名同学得到奖品?
7.中国农历中“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的白天时间是15小时,这一天北京黑夜时间是一天总时间的几分之几?
8.【新颖材料】济南别称泉城,素有“四面荷花三面柳,一城山色半城湖”的美誉。通过调查统计,趵突泉暑假期间旅客的购票情况:人工售票口购票约占,网上购票约占,其余为自动售票机购票,自动售票机购票占总售票数的几分之几?
9.两根铁丝,一根长12米,另一根长18米,要把它们截成整米的同样长的小段没有剩余,每段最长多少米?这两根铁丝一共可以截成多少段?
10.一个长方体水箱,从里面量长24厘米,宽18厘米,深15厘米。给里面加入10厘米深的水,妙妙把一个土豆放入水中后(土豆完全浸没在水中),水面上升到12.5厘米,土豆的体积是多少立方厘米?
11.张明为过生日的妈妈买了一件礼物,他准备用彩带捆扎礼盒(如图),已知礼盒的长是35厘米,宽是20厘米,盒高15厘米,彩带接头处需35厘米。捆扎这个礼盒至少需要多长的彩带?
12.谷雨是春季的最后一个节气,这时雨水充沛,适合播种。实验小学的同学们把学校劳动教育基地划分为“花圃区”和“农耕园”两个区域进行花草和蔬菜种植,其中花圃区面积是23平方米,农耕园面积是35平方米,花圃区的面积是农耕园的几分之几?花圃区的面积占学校劳动实践基地的几分之几?
13.一块长23厘米、宽20厘米的长方形铁皮(如图),从四个角各切掉一个边长为4厘米的正方形,然后做成一个无盖长方体盒子,这个盒子的容积是多少?
14.在古代建筑中,汉砖被广泛应用于宫殿、寺庙等建筑的建造,也多用于道路的铺设和修建,一个长30厘米、宽2分米、高18厘米的汉砖,它的体积是多少立方厘米?合多少立方分米?
15.淄博是齐文化的发源地,琉璃文化源远流长,底蕴深厚,淄博琉璃始于汉代,兴于元代,盛于清朝,逐步发展成为世界琉璃产销中心,业界素有“世界琉璃看中国,中国琉璃看淄博”之说。假期,明明去淄博旅游,带回一个漂亮的琉璃镇尺,他想测量出这个镇尺的体积,于是他找来一个棱长10厘米的正方体容器,里面装有一些水,将这个高8厘米的长方体镇尺竖直放入水中(镇尺底面与容器底面平行),镇尺浸没6厘米时,水就满了。这个镇尺的体积是多少?(容器厚度忽略不计)
16.登山是一种很好的有氧运动,周末小李和爸爸去登山,先用小时走了全程的,又用半小时走了全程的一半。
(1)已经走了多少小时?
(2)还剩全程的几分之几没有走?
17.2024年4月23日是第29个世界读书日,实验小学开展“阅读嘉年华”活动。琳琳去学校图书馆选了一本《生活中的数学》,共360页,第一天看了80页,第二天看了全书的。
(1)琳琳第一天看了全书的几分之几?
(2)还剩下这本书的几分之几没有看?
18.将一块长14厘米、宽10厘米、高3厘米的长方体铁块完全浸没在一个长方体的油箱中,取出铁块后,油面的高度下降了2.1厘米。这个长方体油箱的底面积是多少平方厘米?
19.手工课上,王丽用边长16厘米的正方形卡纸,从四个角上剪掉边长为4厘米的正方形,做成一个无盖的盒子。
(1)做这个盒子用了多少平方厘米的铁皮?
(2)这个盒子的容积是多少立方厘米?
20.小芳在父亲生日这天给爸爸准备了一份礼物,并且用包装盒进行了精美的装饰,包装如下图所示,已知包装盒的长宽高分别是4分米、3分米、1分米,制作这个包装盒需要多少平方分米硬纸板?用彩带捆扎包装盒至少需要多少分米的彩带?(打结处用了2.5分米)
21.端午节与春节、清明节、中秋节并称为中国汉族的四大传统节日,自古以来端午节便有划龙舟及食粽等节日活动。小明和小宇为迎端午学习包粽子,妈妈为他们准备了千克糯米,小明用了其中的,小宇用了其中的,这些糯米还剩下几分之几?
22.小亮想测量出一块鹅卵石的体积,进行了如下操作:
步骤一:在长4分米,宽3分米、高2分米的玻璃容器中盛8厘米深的水。
步骤二:将鹅卵石浸没在水中,此时测得水面高度为12厘米。
(1)你能根据她的实验求出这块鹅卵石的体积?
(2)利用这种操作方法求鹅卵石的体积,运用了数学上的( )思想,学习( )也用了这种思想。
23.小明准备把三根分别长30厘米、48厘米、66厘米的木棒截成一些长度相等的小木棒(最后没有剩余),截成的小木棒最长是多少厘米?一共能截成多少段这样的小木棒?
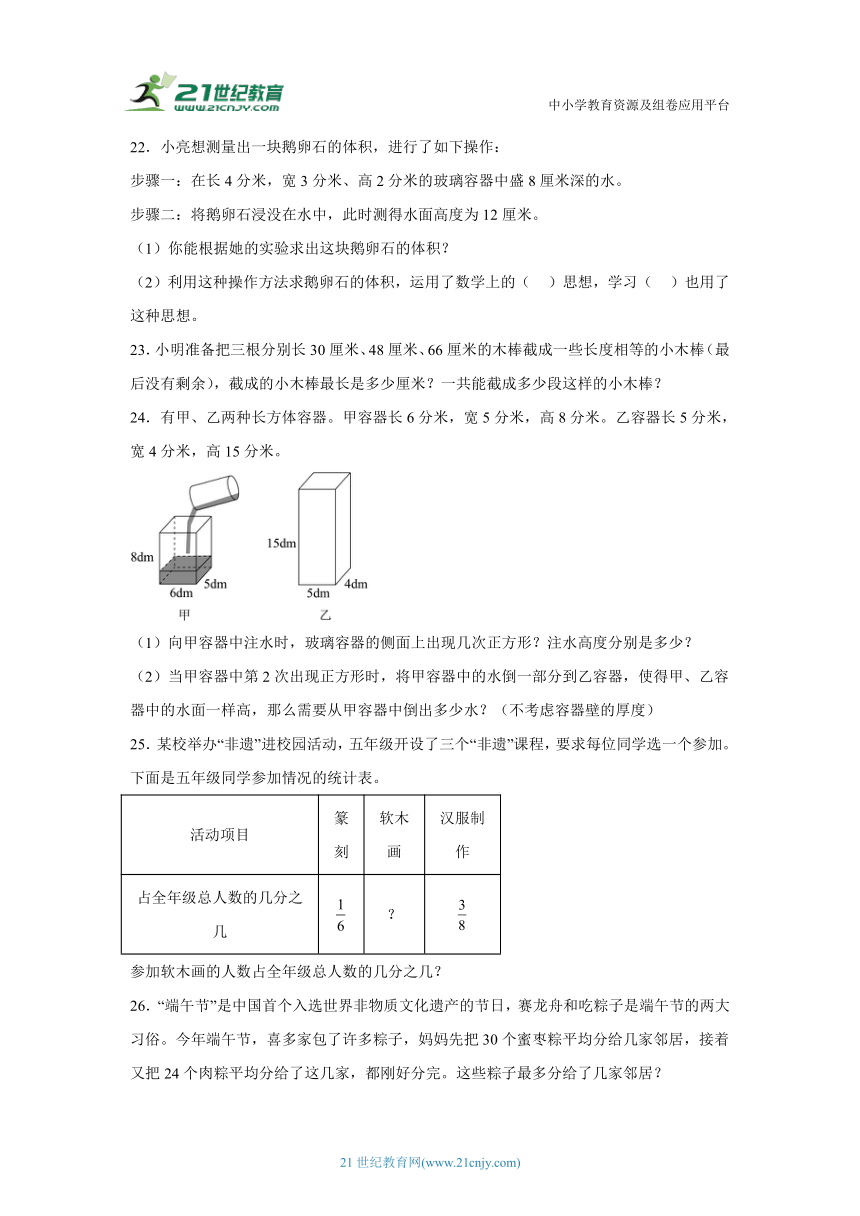
24.有甲、乙两种长方体容器。甲容器长6分米,宽5分米,高8分米。乙容器长5分米,宽4分米,高15分米。
(1)向甲容器中注水时,玻璃容器的侧面上出现几次正方形?注水高度分别是多少?
(2)当甲容器中第2次出现正方形时,将甲容器中的水倒一部分到乙容器,使得甲、乙容器中的水面一样高,那么需要从甲容器中倒出多少水?(不考虑容器壁的厚度)
25.某校举办“非遗”进校园活动,五年级开设了三个“非遗”课程,要求每位同学选一个参加。下面是五年级同学参加情况的统计表。
活动项目 篆刻 软木画 汉服制作
占全年级总人数的几分之几 ?
参加软木画的人数占全年级总人数的几分之几?
26.“端午节”是中国首个入选世界非物质文化遗产的节日,赛龙舟和吃粽子是端午节的两大习俗。今年端午节,喜多家包了许多粽子,妈妈先把30个蜜枣粽平均分给几家邻居,接着又把24个肉粽平均分给了这几家,都刚好分完。这些粽子最多分给了几家邻居?
27.在中国传统文化中,龙、凤、鹤被称为吉祥三宝。龙和风现只留存在传说中,而鹤就是被冠之为“一品鸟”的丹顶鹤,是现今人世间可以看到的国宝。世界上丹顶鹤野生群种的个体总数约为3000只,目前,生活在我国的丹顶鹤野生群种的个体总数约为1800只,请问生活在我国的丹顶鹤野生群种的个体总数占世界的几分之几?
28.根据气象部门统计,2021年是干旱的一年。在青岛年降水总量中,夏季降雨量占,比春季降雨量多,春季降雨量占全年的几分之几?春夏两季的降水量比秋冬两季多几分之几?
29.回答问题。
①这是一个正方体的水槽;
②三块石子的体积分别是1号137立方厘米,2号358立方厘米,3号450立方厘米;
③乌鸦只能够到水槽的最上沿。乌鸦怎样才能喝到水?
30.
停车点 起点站 中间第1站 中间第2站 中间第3站 中间第4站 终点站
上下车人数 ﹢24 ﹣5 ﹢1 0 ﹢3 ﹣5 0 ﹣11 ﹢9 ﹣16
一辆汽车从起点开出后,这中经过4个停车点,最后到达终点站。下表记录了该客车的载客数量的变化情况。
(1)中间4站哪个站没有人上车?哪个站没有人下车?
(2)汽车从中间第1站开往中间第2站时,车上有多少人?
(3)从表中你还知道了什么?
31.张师傅计划今天加工80个零件,实际上午加工了计划任务的,下午加工了计划任务的,晚上还加工了20个。他今天完成计划任务了吗?
32.欢欢和果果看同一本书,欢欢计划36天看完,每天看相同的页数;果果计划30天看完,每天也看相同的页数。现在两人各看了6天,他们分别看了这本书的几分之几?
33.把一根长彩带剪成长度相等的几段,如果剪成4分米一段的,那么少1分米;如果剪成6分米一段的,那么少1分米;如果剪成8分米一段的,也少1分米。这个长彩带的长度至少是多少分米?
34.同学们在用一些小棒和橡皮泥拼搭一个长方体框架。
(1)上图是已经拼搭好的部分,还需要( )根2厘米长的小棒、( )根4厘米长的小棒、( )根7厘米长的小棒。
(2)如果给这个长方体框架的每个面都铺上彩纸,至少需要多少平方厘米彩纸?
35.植树节到了,学校在操场的四周每隔4米种1棵树,种到21棵后发现树苗不够了,于是决定重新种,改为每隔5米种1棵,这样重新种时,有多少棵树苗不必拔掉?
36.整理图书时,管理员李老师发现科技类图书占图书总数的,文学类图书占图书总数的,工具类图书占图书总数的。
(1)工具类图书比科技类图书少的部分占图书总数的几分之几?
(2)你觉得李老师统计完所有的图书种类了吗?请说明理由。
37.杨家埠木版年画是一种传统民间版画。一批木版年画的长是24cm,宽是16cm,要用这种规格的年画布置成正方形展板,边长最短可以是多少厘米?需要多少块木版年画?
38.黄河是中华文明主要的发源地,中国人称其为“母亲河”。黄河每年都会生产16亿吨泥沙,其中有12亿吨流入大海,剩下的泥沙常年留在黄河下游,形成冲积平原,有利于种植。每年泥沙总量的几分之几会流入大海?剩余泥沙占总量的几分之几?
39.兴趣小组要用一根绳子编制中国结,小阳用去了米,欢欢用去了米,还剩下米。
(1)欢欢比小阳少用多少米?
(2)这根绳子原来长多少米?
40.幸福超市运回42块肥皂和36盒牙膏,现在要把肥皂和牙膏捆一起做奖品,要求每份奖品的肥皂一样多,牙膏也一样多(正好用完,没有剩余)。这些东西最多能捆多少个这样的奖品?
41.端午节吃粽子是中国人的传统习俗。芳芳和林林学习包粽子,妈妈准备了千克糯米,芳芳用了其中的,林林用了其中的,这些糯米还剩下几分之几?
42.李阿姨把一个西瓜分给甲、乙、丙三个人吃,甲和乙一共吃了这个西瓜的,乙和丙一共吃了这个西瓜的,请你算出三个人分别吃了这个西瓜的几分之几?
43.实验学校为一间长5米、宽4.5米的微机室地面铺方砖,应选择边长是多少分米的正方形方砖比较合适?铺完这间微机室至少需要多少块这样的方砖?
44.有同样大小的红、绿、蓝三种颜色的彩旗54个,将它们按照2个红旗、1个绿旗、3个蓝旗的顺序排列。三种颜色的彩旗各占总数的几分之几?
45.元宵节非常热闹,小涵到街上看花灯,花灯闪烁着光芒。小涵绕着花灯走了几圈,只估摸着大概有55~65盏花灯。你知道一共有多少盏花灯吗?
46.为了庆祝六一儿童节,学校举行书画展,展区已经布置了三种作品,你认为展区还有地方展示其他作品吗?用你喜欢的方式进行说明。
书法作品占展区的 油画作品占展区的 素描作品占展区的
47.2023年5月10日,天舟六号货运飞船发射成功,标志着中国空间站建设迈出重要一步。飞船运输物资总质量约是5800千克,其中约有70千克的新鲜水果。此次运输,新鲜水果的质量约占运输物资总质量的几分之几?
48.学校开展劳动教育活动,为五年级开辟了一块面积为340平方米的长方形菜地,其中西红柿占,辣椒占,剩下的全部种黄瓜。
(1)辣椒比西红柿多占菜地几分之几?
(2)黄瓜占整块菜地的几分之几?
(3)蔬菜成长一段时间之后需要喷洒农药除虫,学校购买的农药50克药片需要放入1.5千克水中,那么配制好的药水中,药的质量占药水的质量的几分之几?
49.芳芳调查了全班最喜欢阅读的三种读物情况:最喜欢阅读文史类和科普类的人数占全班人数的,最喜欢文学类和科普类的人数占全班总数的。请问最喜欢科普书的人占全班人数的几分之几?(先用画图的方法分析,再列式解答。)
50.垃圾分为可回收垃圾和不可回收垃圾,其中不可回收垃圾包括厨余垃圾、有害垃圾和其他垃圾。某小区一年产生的不可回收垃圾中的厨余垃圾占,其他垃圾占。有害垃圾占不可回收垃圾的几分之几?
51.我国是受荒漠化危害最严重的国家之一。在荒漠化总面积中,轻度荒漠化面积约占。中度荒漠化面积约占,其余的是重度荒漠化,
(1)重度荒漠化的面积约占荒漠化总面积的几分之几?
(2)重度荒漠化的面积所占比例比轻度和中度荒漠化面积所占比例的和少几分之几?
52.第十三届“中国青年女作家”将评审委员会由32位评委组成,经过严格的评审,10位女科学家获奖者从110个单位提名的235位有效候选人中脱颖而出,本届获奖的女科学家占被提名的女科学家的几分之几?
53.在“亲子共度一本书”活动中,阳阳和妈妈、爸爸一起阅读《中华历史故事》。一周内,妈妈看了这本书的,阳阳看了这本书的,爸爸比妈妈多看了这本书的。
(1)爸爸看了这本书的几分之几?
(2)阳阳比妈妈多看了这本书的几分之几?
54.大课间时同学们玩“抱团”游戏,人数在20和30之间。同学们发现当抱团口令为3,4或6时,每个人都可以抱团成功。有多少人在玩游戏?
“抱团”游戏的规则
当听到口令中所报的数后,相应人数的同学迅速抱在一起,算作成功。
55.一块砖底面长12厘米,宽10厘米,要铺成一个正方形图案,这个正方形的边长最小是多少厘米?铺这样的一个正方形图案需要多少块砖?
56.在太阳系的八大行星中,只有金星和天王星的自转方向和公转方向不一致。金星的自转方向与公转方向相反,天王星则是与公转轨道呈97°角地“躺着”旋转的。自转方向和公转方向不一致的行星占行星总数的几分之几?
57.五年级一班的学生进行队列表演,每行16人或12人都正好是整行。已知这个班的学生人数不超过50人,你能算出这个班有多少人参加队列表演吗?
58.一个长方体水槽内部长6分米,宽4分米,深3分米,水面离槽口有5厘米,如果放入一块棱长为3分米的正方体铁块,此时水槽的水是否会溢出?如果会,会溢出多少升水?
59.美术小组的同学要将一张长72厘米、宽48厘米的长方形卡纸裁成大小相等的正方形,裁好后正好没有剩余,裁成的正方形的边长最长是多少厘米?可以裁成多少个正方形?
60.学校开展劳动教育活动,五年级开辟了一块面积为公顷的长方形菜地,其中西红柿占,辣椒占,剩下的全部种油菜花。
(1)将下边的长方形看做这块菜地,请在图中用不同的阴影面积表示出西红柿和辣椒的情况。
(2)油菜花占整块菜地的几分之几?
61.2023年3月21日是第21个“世界睡眠日”,人的一生中有的时间是在睡眠中度过。根据教育部“睡眠管理”的有关规定,小学生每天的睡眠时间应该达到10小时,小明每天晚上8时睡觉,第二天早上7时起床,他每天睡觉的时间是全天的几分之几?
62.手工课上,刘鹏将一张长36厘米、宽27厘米的长方形卡纸剪成若干张同样大小的正方形卡片,纸张不能有剩余。正方形卡片边长最大是多少厘米?可以剪出几张这样的正方形卡片?
63.第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事。中国冰雪健儿敢于追梦,最终取得了9金4银2铜共15枚奖牌的好成绩。
(1)中国取得的金牌数占所获奖牌总数的几分之几?
(2)银牌和铜牌共占所获奖牌总数的几分之几?
(3)请根据所给出的数学信息提出一个数问题并解答。
64.把一个体积为3.6立方分米的铁球浸没在棱长为3分米的正方体容器中,这时水面刚好升至玻璃缸口,如果取出铁球,容器里的水深是多少分米?
65.如图,一个正方体玻璃容器(无盖)的棱长是2分米。向容器中倒入5升水,再把一个土豆没入水中。这时量得容器内水深14厘米。土豆的体积是多少?(玻璃的厚度忽略不计)
66.外卖给我们的生活带来了很大的便利,这种便利离不开外卖人员的辛苦付出。淘气的叔叔是一个外卖骑手,下图是他的外卖保温包的示意图,做一个这样的保温包至少需要多少平方厘米的材料?(重叠部分忽略不计)
67.十一假期,小丽一家开车到离家约160千米的趵突泉景区游玩。汽车油箱里有19.5升汽油,每升汽油可供汽车行驶8.5千米,他们到趵突泉中途还需要加油吗?
68.“水立方”位于北京奥林匹克公园内,它与一墙之隔的“鸟巢”一起被称为2008年北京奥运会两大标志性建筑物。你知道吗?在水立方内有一个国际标准的长方体游泳池,它的长是50米,宽是25米,深是3米。
(1)在内壁沿池底向上2米处画一条水位线。它的全长是多少米?
(2)如果用瓷砖贴水池的四周和底面,贴瓷砖的面积是多少平方米?
(3)如果池内水深2米,这个游泳池内的水有多少吨?(1立方米水重1吨)
69.“龟兔赛跑”是我们非常熟悉的故事,大意是乌龟和兔子赛跑,开跑不久兔子就超过乌龟很远,于是兔子就在路边睡了一觉,而乌龟一直往目的地奔跑,最终乌龟获得了胜利。
如果兔子跑完全程用了12分钟,乌龟跑完全程用了10分钟,那么乌龟所用时间是兔子的几分之几?
70.王叔叔要用长3分米、宽2分米的瓷砖铺一个正方形图案。如果都用整块的瓷砖,铺成的图案边长至少是多少分米?把你的想法用你喜欢的方法表达出来(可以写一写,可以算一算,也可以画图说一说)。
71.一次晚会上共有三种饮料。餐后统计,这三种饮料一共饮用了78瓶,平均每2人饮用一瓶A饮料,每3人饮用一瓶B饮料,每4人饮用一瓶C饮料。参加晚会的总人数是多少?
72.一次晚会供有三种饮料,餐后统计,三种饮料共用了78瓶;平均每2人饮用1瓶饮料,每3人饮用一瓶B饮料,每4人饮用一瓶C饮料,参加晚会的总人数是多少?
73.实验小学五年级学生参加绘画兴趣班的人数是40~50人,如果按8人一组分正好分完,如果按12人一组分也正好分完。五年级参加绘画兴趣班的学生有多少人?
74.李奶奶和王奶奶经常去同一个公园锻炼身体,李奶奶每4天去一次,王奶奶每5天去一次。6月10日她们刚一起在公园参加了活动,下一次她们在公园相遇是几月几日?
75.如图所示包装盒的长宽高分别是3分米、2分米、1分米,制作这个包装盒需要多少平方分米硬纸板?用彩带捆扎包装盒至少需要多少分米的彩带?(打结处用了2.5分米)
76.如图为了美化鱼缸,在鱼缸底部放入几块小石头,放入前水面高度是22厘米,放入后水面高度是24厘米,放入石头的体积是多少立方厘米?
77.母亲节这天,欢欢用零花钱的给妈妈买了一束鲜花,同时,她用零花钱的买了一条领带,父亲节时送给了爸爸。
(1)母亲节礼物比父亲节礼物多用去欢欢零花钱的几分之几?
(2)欢欢的零花钱还能剩下几分之几?
78.王老师买了一个长方体鱼缸,如图所示,为了提高观赏性,王老师在鱼缸里放了一块假山。水面高度由原来的10厘米上升到12.5厘米。这块假山的体积是多少立方厘米?
79.数学课上,同学们策划设计用一块长24厘米,宽16厘米的长方形铁皮,在四个角上各剪去一个小正方形(如图所示),做成一个无盖的长方体储物盒。林林和小强分别设计了不同的方案,林林选择边长为3厘米,小强选择边长为4厘米。他们两个谁的方案做成的长方体储物盒容积最大?
80.为落实“双减”政策,丰富同学们延时期间的校园生活。实验小学开设了足球、篮球、游泳、创客等独具特色的社团。五年级二班的同学都参加了社团。其中的同学参加了足球社团,的同学参加了游泳社团,的同学参加了创客社团,参加足球、游泳、创客社团的一共占本班学生的几分之几?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.15名
【分析】科技书多出4本,钢笔少了1支,说明“优秀志愿者”的人数最多是(49-4)和(29+1)的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【解析】49-4=45(本)
29+1=30(本)
45=3×3×5
30=2×3×5
3×5=15(名)
答:这次最多评选了15名“优秀志愿者”。
2.蓝气球:;红气球:;黄气球:
【分析】一组即一个周期有(2+3+2)个气球,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个,据此可以确定有7组余1个,且余下的一个是蓝气球,蓝气球×组数+1=蓝气球个数,红气球和黄气球个数分别乘组数,可以求出红气球和蓝气球个数。用三种颜色的气球分别÷总数,即可求出三种颜色的气球分别占总数的几分之几。
【解析】50÷(2+3+2)
=50÷7
=7(组)……1(个)
蓝气球:2×7+1
=14+1
=15(个)
15÷50==
红气球:3×7=21(个)
21÷50=
黄气球:2×7=14(个)
14÷50==
答:三种颜色的气球分别占总数的、、。
3.4米,12段
【分析】要把两根不同长度的绸带截成同样长且无剩余的小段,每小段的长度就是两根绸带长度的公因数,而要求最长的小段长度,就是求它们的最大公因数;求出最大公因数后,再用两根绸带的长分别除以它们的最大公因数,分别计算出两根绸带按此长度能截成的段数,最后相加得到总段数。
【解析】20=2×2×5
28=2×2×7
所以20和28的最大公因数是:2×2=4,即截成的小段最长是4米。
20÷4+28÷4
=5+7
=12(段)
答:截成的小段最长是4米,一共可以截成12段。
4.
【分析】把录制的短视频的总时间看作单位“1”,把讲数学故事占的总时间的与介绍自己喜欢的数学读物占的相加,求出讲数学故事和介绍自己喜欢的数学读物占单位“1”的分率,再用1减去这个分率即可求出乐乐和同学互动的时间占这个短视频的几分之几。
【解析】1-(+)
=1-(+)
=1-
=
答:乐乐和同学互动的时间占这个短视频的。
5.不同意;理由见详解
【分析】每隔6的倍数分钟,5路车发车;每隔8的倍数分钟,7路车发车。所以每隔6和8的公倍数分钟,两车同时发车,第二次共同发车应是隔6和8的最小公倍数分钟,再发车,即用6和8的最小公倍数分钟加发到时间即可得解,据此解答。
【解析】
第一次发车与第二次发车经过的时间(分钟)
答:不同意。因为6和8的最小公倍数是24,这两路公交车的第二次共同发车时间应该是6:24。
6.15名
【分析】根据题意,如果中性笔有47-2=45支,笔记本有31-1=30个,就正好平均分完,每名同学分得的奖品种类和数量完全相同,那么最多得到奖品的人数就是45和30的最大公因数。
把45、30分解质因数后,把公有的相同质因数乘起来就是最大公因数,即可得解。
【解析】47-2=45(支)
31-1=30(个)
45=3×3×5
30=2×3×5
45和30的最大公因数是:3×5=15
即最多有15名同学得到奖品。
答:最多有15名同学得到奖品。
7.
【分析】分析题目,先根据1天=24小时,用24减去白天的时间即可得到黑夜的时间,求一个数是另一个数的几分之几用除法,再用黑夜的时间除以一天的总时间,即可得到黑夜时间是一天总时间的几分之几。
【解析】(24-15)÷24
=9÷24
=
=
答:这一天北京黑夜时间是一天总时间的。
8.
【分析】把总售票数看作单位“1”,根据减法的意义,用“1”减去人工售票口购票、网上购票约占总售票数的几分之几,即是自动售票机购票占总售票数的几分之几。
【解析】
答:自动售票机购票占总售票数的。
9.6米;5段
【分析】截成同样长的几段且没有剩余,说明每段铁丝是12和18的公因数,求每段最长是多少米,则是求12和18的最大公因数,再用12除以最大公因数的商加上18除以最大公因数的商,即是一共截成的段数,据此解答。
【解析】12=2×2×3
18=2×3×3
12和18的最大公因数是2×3=6,每段最长是6米。
(12÷6)+(18÷6)
=2+3
=5(段)
答:每段最长6米,这两根铁丝一共可以截成5段。
10.1080立方厘米
【分析】根据题意,土豆的体积是水上升的体积,结合长方体的体积公式V=abh,解答即可。
【解析】24×18×(12.5-10)
=432×2.5
=1080(立方厘米)
答:土豆的体积是1080立方厘米。
11.205厘米
【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等。由图形可知:需要彩带的长度等于2条长+4条高+2条宽+打结用的长度,代入数据计算即可求解。
【解析】35×2+20×2+15×4+35
=70+40+60+35
=205(厘米)
答:捆扎这个礼盒至少需要205厘米的彩带。
12.;
【分析】由题意可知,学校实践基地面积是平方米,根据求一个数是另一个数的几分之几用除法计算,分别用花圃区的面积除以农耕园面积,用花圃区的面积除以学校劳动实践基地面积,计算即可。
【解析】23÷35=
23÷(23+35)
=23÷58
=
答:花圃区的面积是农耕园的;花圃区的面积占学校劳动实践基地的。
13.720毫升
【分析】做成长方体盒子的长是(23-4×2)厘米,宽是(20-4×2)厘米,高是4厘米,根据长方体体积公式,再把体积单位转化为容积单位即可。
【解析】(23-4×2)×(20-4×2)×4
=15×12×4
=180×4
=720(立方厘米)
720立方厘米=720毫升
答:这个盒子的容积是720毫升。
14.10800立方厘米;10.8立方分米
【分析】先统一单位为厘米,然后根据长方体体积=长×宽×高,求出汉砖的体积,再根据1立方分米=1000立方厘米进行单位换算即可。
【解析】2分米=20厘米
30×20×18
=600×18
=10800(立方厘米)
10800立方厘米=10.8立方分米
答:它的体积是10800立方厘米,合10.8立方分米。
15.400立方厘米
【分析】根据正方体体积=棱长×棱长×棱长,求出正方体容器的容积,正方体容器的底面积×水面高度=水的体积,正方体容器的容积-水的体积=高6厘米的镇尺体积。高6厘米的镇尺体积÷6=镇尺底面积,镇尺底面积×镇尺高=镇尺体积,据此列式解答。
【解析】10×10×10-10×10×7
=1000-700
=300(立方厘米)
300÷6=50(平方厘米)
50×8=400(立方厘米)
答:这个镇尺的体积是400立方厘米。
【点评】关键是先求出镇尺底面积,掌握并灵活运用长方体和正方体体积公式。
16.(1)小时
(2)
【分析】(1)半小时是小时,先用的时间+又用的时间=已经走的时间,据此列式解答;
(2)将全程看作单位“1”,全程的一半是,1-先走了全程的几分之几-有走了全程的几分之几=还剩全程的几分之几,据此列式解答。
【解析】(1)+=+=(小时)
答:已经走了小时。
(2)1--
=-
=-
=
答:还剩全程的没有走。
17.(1);
(2)
【分析】(1)将全书页数看作单位“1”,第一天看的页数÷全书页数=第一天看了全书的几分之几;
(2)将全书页数看作单位“1”,1-第一天看了全书的几分之几-第二天看了全书的几分之几=还剩下这本书的几分之几没有看。
【解析】(1)80÷360==
答:琳琳第一天看了全书的。
(2)1--
=-
=-
=
答:还剩下这本书的没有看。
18.200平方厘米
【分析】油面下降的体积等于长方体铁块的体积,根据长方体体积=长×宽×高,求出长方体铁块的体积,再根据长方体底面积=体积÷高,求出长方体油箱的底面积,据此列式解答。
【解析】14×10×3÷2.1
=420÷2.1
=200(平方厘米)
答:这个长方体油箱的底面积是200平方厘米。
19.(1)192平方厘米;
(2)256立方厘米
【分析】(1)这个盒子所用的铁皮的面积=原来正方形的面积-四个小正方形的面积。正方形的面积=边长×边长,将数据代入计算即可。
(2)按照题意,画出如下的示意图,得出这个无盖的盒子是个长为8厘米,宽为8厘米,高为4厘米的长方体。根据得出这个盒子的容积。
【解析】(1)16×16-4×4×4
=256-64
=192(平方厘米)
答:做这个盒子用了192平方厘米。
(2)16-2×4
=16-8
=8(厘米)
8×8×4=256(立方厘米)
答:这个盒子的容积是256立方厘米。
20.38平方分米;20.5分米
【分析】求制作这个包装盒硬纸板的面积,就是求长方体的表面积,根据,代入数据计算即可;观察可知,求彩带的长度,即把2条长,2条宽,4条高及打结的长度加起来,即可得解。
【解析】
(平方分米)
(分米)
答:制作这个包装盒需要38平方分米硬纸板;用彩带捆扎包装盒至少需要20.5分米的彩带。
21.
【分析】把妈妈为他们准备的糯米的重量看作单位“1”,用1减去小明用去的占总重量的分率,减去小宇用去的占总重量的分率,即可解答。
【解析】1--
=-
=
答:这些糯米还剩下。
22.(1)4.8立方分米
(2)转化;平行四边形面积(答案不唯一)
【分析】(1)这块鹅卵石的体积等于上升的水的体积,用长方体的体积公式底面积乘高(即上升的厘米数)即可,计算统一单位;
(2)在求鹅卵石体积时是把鹅卵石的体积转化为上升部分水的体积,在学习一种平行四边形的面积时,也是把平行四边形进行割补,转化为长方形,从而推导出平等行四边形的面积,也是用这种方法解答。
【解析】(1)12-8=4(厘米)
4厘米=0.4分米
4×3×0.4
=12×0.4
=4.8(立方分米)
答:这块鹅卵石的体积是4.8立方分米。
(2)利用这种操作方法求鹅卵石的体积,运用了数学上的转化思想,学习平行四边形面积也用了这种思想(答案不唯一)。
23.6厘米;24段
【分析】把三根分别长30厘米、48厘米、66厘米的木棒截成一些长度相等的小木棒(最后没有剩余),截成的小木棒最长的长度就是30、48和66的最大公因数;再用三根木棒的长度分别除以它们的最大公因数求出商,最后再相加即可求出一共能截成多少段这样的小木棒。
【解析】
2×3=6(厘米)
30÷6+48÷6+66÷6
=5+8+11
=13+11
=24(段)
答:截成的小木棒最长是6厘米,一共能截成24段这样的小木棒。
24.(1)两次;5分米,6分米;
(2)72立方分米。
【分析】(1)根据题意可知,甲容器的侧面出现正方形的条件是注水高度等于容器的长或宽。所以甲容器的长为6分米,宽为5分米,当注水高度为5分米或者6分米时,出现正方形。
(2)根据题意,结合长方形的体积公式:长×宽×高,求出甲容器的水的体积,要使甲、乙两个容器的水面一样高,需要计算出甲、乙两个容器的底面积之和,再用总体积除以底面积之和,即为乙容器中水的高度,再根据长方体的体积公式求出答案即可。
【解析】(1)答:出现两次正方形;一次是5分米,一次是6分米。
(2)体积:6×5×6
=30×6
=180(立方分米)
底面积之和:6×5+5×4
=30+20
=50(立方分米)
高:180÷50=3.6(分米)
水的体积:3.6×5×4
=18×4
=72(立方分米)
答:需要从甲容器中倒出72立方分米的水。
25.
【分析】把全年级总人数看作单位“1”,用单位“1”减去篆刻占全年级总人数的分率,减去汉服制作占全年级总人数的分率,即可求出参加软木画的人数占全年级总人数的分率,据此解答。
【解析】1--
=-
=-
=
答:参加软木画的人数占全年级总人数的。
26.6家
【分析】根据题意,把30个蜜枣粽、24个肉粽平均分给几家邻居都刚好分完,说明邻居的数量是30和24的公因数。求这些粽子最多分给了几家邻居,就是求30和24的最大公因数。把30和24分解质因数后,把它们公有的质因数乘起来就是最大公因数,即可求解。
【解析】30=2×3×5
24=2×2×2×3
30和24的最大公因数是:2×3=6
即最多分给了6家邻居。
答:这些粽子最多分给了6家邻居。
27.
【分析】根据求一个数占另一个数的几分之几,用一个数÷另一个数,结果用分数表示即可,即用生活在我国的丹顶鹤野生群种的个体总数÷世界上丹顶鹤野生群种的个体总数,即可解答。
【解析】1800÷3000=
答:生活在我国的丹顶鹤野生群种的个体总数占世界的。
28.;
【分析】(1)根据题意,求的是春季降水量占全年的几分之几,夏季降雨量比春季降水量多,则可用夏季降雨量 =春季降雨量占全年的几分之几,据此解答。
(2)根据题意,求的是春夏两季的降水量比秋冬两季多几分之几?把全年的降水量看作为“1”,则可列出算式:(春季降雨量+夏季降雨量) (1 春季降雨量 夏季降雨量)=春夏两季的降水量比秋冬两季多的降水量,据此解答。
【解析】 =
(+) (1 )
= ( )
=
=
答:春季降水量占全年的,春、夏两季的降水量比秋、冬两季多全年降水量的。
29.见详解
【分析】根据题意,要使乌鸦喝到水,需要把石子放入水槽,使水面上升到水槽的最上沿或溢出水槽。要使水面上升到水槽的最上沿,根据长方体体积=长×宽×高,上升的水的体积应是20×20×(20-18)。而2号和3号石子的体积之和是358+450=808(立方厘米),大于800毫升,即可以把2号和3号石子放入水槽,乌鸦就能喝到水。也可以把三块石头都放入水槽,水更会溢出水槽,乌鸦也可以喝到水。
【解析】20×20×(20-18)
=20×20×2
=800(毫升)
第一种方法:2号和3号石子一起放入
358+450=808(立方厘米)
808立方厘米=808毫升
808毫升>800毫升
第二种方法:1号、2号、3号石子一起放入
137+358+450=945(立方厘米)
945立方厘米=945毫升
945毫升>800毫升
答:把2号和3号石子放入水槽或把1号、2号和3号石子放入水槽,乌鸦就能喝到水。
30.(1)中间第3站;中间第2站;
(2)23人
(3)见详解
【分析】(1)上车和下车是两个相反意义的量,可以用正负数表示。正数表示上车的人数,负数表示下车的人数;0表示既不上车也不下车。
(2)从中间第1站开往中间第2站时,车上的人数应该加上上车的人数,再减去下车的人数。
(3)根据正负数的意义,读取表中数据,即可解答。
【解析】(1)中间第3站上下车人数是﹣5和0,说明这一站下车5人,没有人上车。
中间第2站上下车人数是0和﹢3,说明这一站没有人下车,上车3人。
答:中间4站第3站没有人上车,第2站没有人下车。
(2)24-5+1=20(人)
20+3=23(人)
答:车上有23人。
(3)中间第1站,下车5人,上车1人,中间第4站,下车11人,上车9人。
答:中间第2站和第4站,下车人数比上车人数多。(答案不唯一合理即可)
31.没完成
【分析】把计划要加工的零件总个数看作单位“1”,先根据求一个数是另一个数的几分之几,用20除以80,求出晚上加工的20个零件占总个数的几分之几;
再把上午、下午、晚上分别加工零件的个数占总个数的分率相加,即是今天一共完成总个数的几分之几,再与1比较大小,如果超过或等于1,则完成了计划任务;如果小于1,则没有完成计划任务。
【解析】
答:他今天没完成计划任务。
32.欢欢:;果果:
【分析】从题意可知,每天看的页数相同,欢欢计划36天看完,她已看了6天,6天占36天的几分之几,即欢欢看了这本书的几分之几。果果计划30天看完,她已看了6天,6天占30天的几分之几,即果果看了这本书的几分之几。根据求一个数是另一个数的几分之几,用除法计算。据此解答。
【解析】6÷36
=
=
6÷30
=
=
答:欢欢6天看了这本书的,果果6天看了这本书的。
33.23分米
【分析】从题意可知:剪成4分米、6分米或8分米都少1分米,这根彩带的长度比4、6、8的公倍数都少1,从“至少”可知,求最小公倍数。用分解质因数的方法求出4、6和8的全部公有的质因数和各自独立的质因数,它们连乘的积就是4、6和8的最小公倍数。最后用最小公倍数减去1就是这根彩带的长度。据此解答。
【解析】4=2×2
6=2×3
8=2×2×2
4、6和8的最小公倍数:2×2×2×3=24
24-1=23(分米)
答:这个长彩带的长度至少是23分米。
34.(1)2;3;1;(2)100平方厘米
【分析】(1)根据长方体的特征,要搭成长方体框架,则需要4条长、4条宽、4条高。已经有2条2厘米长的木棒,1条4厘米长的木棒,3条7厘米长的木棒,则还需要2条2厘米长的木棒,3条4厘米长的木棒,1条7厘米长的木棒;
(2)根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据即可求出彩纸的面积。
【解析】(1)还需要2根2厘米长的小棒、3根4厘米长的小棒、1根7厘米长的小棒。
(2)(7×2+7×4+2×4)×2
=(14+28+8)×2
=50×2
=100(平方厘米)
答:至少需要100平方厘米彩纸。
35.5棵
【分析】21棵树有20个间隔,每个间隔长4米,一共植树长度为20×4=80(米)。由每隔4米改成每隔5米,需要求出4和5的最小公倍数,看看已经植树的米数里有几个4和5的最小公倍数,再加上1,就是不必要拔掉的树的棵数。据此解答即可。
【解析】4×(21-1)
=4×20
=80(米)
4和5的最小公倍数是20
80÷20=4(个)
4+1=5(棵)
答:有5棵树苗不必拔掉。
【点评】明确原间隔数和新的间隔数,求出两者的公倍数,确定有多少棵树无需移动。
36.(1)
(2)没有;理由见详解
【分析】(1)用科技类图书占图书总数的分率-工具类图书占图书种类的分率,即可求出工具类图书比科技类图书少的部分占图书总数的分率。
(2)把图书种类看作单位“1”,用科技书占图书总数的分率加上文学类占图书总数的分率加上工具书图书占总数的分率,如果结果等于1,说明李老师统计完所有的图书种类;如果小于1,说明李老师没有统计完所有的图书种类;据此解答。
【解析】(1)-=
答:工具类图书比科技类图书少的部分占图书总数的。
(2)++
=+
=
<1,李老师没有统计完所有的图书种类。
答:李老师没有统计完所有的图书种类。
37.48厘米;6块
【分析】先找出24和16的最小公倍数,得出边长最短的长度是多少,然后再求出需要多少块木版年画。
【解析】
所以24和16的最小公倍数为:
48÷24=2
48÷16=3
2×3=6(块)
答:边长最短是48厘米,需要6块木板年画。
38.;
【分析】用流入大海的泥沙除以泥沙总量,求出每年泥沙总量的几分之几会流入大海;再把泥沙总量看作单位“1”,用单位“1”减去流入大海的泥沙占总泥沙的分率,就是剩余泥沙占总量的分率。
【解析】12÷16=
1-=
答:每年泥沙总量的会流入大海,剩余泥沙占总量的。
39.(1)米(2)米
【分析】(1)小阳用去了米,欢欢用去了米,要求欢欢比小阳少用多少米,用()计算;
(2)小阳用去的长度加上欢欢用去的长度,再加上剩下的长度,所得结果即为这条绳子原来的长度。
【解析】(1)(米)
答:欢欢比小阳少用米。
(2)(米)
答:这根绳子原来长米。
40.6个
【分析】根据题目要求,香皂的块数42和牙膏的盒数36应该同时能被奖品的份数整除,求份数最大可以是几份,求出42和36的最大公因数即可,据此解答。
【解析】42=2×3×7
36=2×3×6
所以42和36的最大公因数是2×3=6
故这些东西最多能捆6个这样的奖品。
41.
【分析】把这些糯米的总重量看作单位“1”,用1分别减去芳芳用去其中的和林林用去其中的,所得结果即为这些糯米还剩下几分之几,据此解答。
【解析】
答:这些糯米还剩下。
42.甲吃了,乙吃了,丙吃了
【分析】把整个西瓜看作单位“1”, 乙和丙一共吃了这个西瓜的,用1减去即可求出甲吃了这个西瓜的几分之几;甲和乙一共吃了这个西瓜的,用1减去可以求出丙吃了这个西瓜的几分之几;用1减去甲和丙吃的分率,即可求出乙吃了西瓜的几分之几。
【解析】甲:
丙:
乙:
=1-
=
答:甲吃了这个西瓜的,乙吃了这个西瓜的,丙吃了这个西瓜的。
43.5分米;90块
【分析】先将微机室的长和宽的单位换算成分米,求出长和宽的最大公因数,就在正方形方砖的边长;再用微机室的长除以方砖的边长,求出方砖行数,用微机室的宽除以方砖的边长,求出方砖的列数,再用行数×列数,即可求出方砖的块数。
【解析】5米=50分米;4.5米=45分米
50=2×5×5
45=3×3×5
50和45的最大公因数是5;方砖的边长为5分米。
(50÷5)×(45÷5)
=10×9
=90(块)
答:应选择边长是5分米的正方形方砖比较合适,铺完这间微机室至少需要90块这样的方砖。
44.;;
【分析】以2个红旗、1个绿旗、3个蓝旗为1个周期。每个周期一共有(2+1+3=6)个旗子,用54÷6即可求出有9个周期,据此分别用2×9、1×9和3×9求出红旗、绿旗和蓝旗的个数,最后根据求一个数占另一个数的几分之几,用一个数除以另一个数,分别用三种颜色的旗子的数量除以旗子的总数,即可求出三种颜色的旗子各占总数的几分之几。
【解析】2+1+3
=3+3
=6(个)
54÷6=9(组)
红旗:2×9÷54
=18÷54
=
绿旗:1×9÷54=
蓝旗:3×9÷54
=27÷54
=
答:红旗各占总数的,绿旗各占总数的,蓝旗各占总数的。
45.61盏
【分析】读题可知,花灯的数量比2、3、5的公倍数多1,先求出2、3、5的最小公倍数,再用最小公倍数分别乘1、乘2、乘3……找到55~65之间的公倍数,加1即可。
【解析】2×3×5=30
30×2=60(盏)
60+1=61(盏)
答:一共有61盏花灯。
46.展区有地方展示其他作品。
【分析】将展区面积看作单位“1”,其中书法占,油画作品占,素描作品占,运用分数减法得出剩余区域所占的分数,据此可得出答案。
【解析】将画展展区面积看作单位“1”,则除了书法作品、油画作品、素描作品所占面积外,剩下的区域占比为:
即其他作品的展区占了画展展区的,即还有地方展示其他作品。
答:展区还有地方展示其他作品。
47.
【分析】求新鲜水果的质量约占运输物资总质量的几分之几,用新鲜水果的质量除以运输物资总质量,结果能约分的要约成最简分数。
【解析】70÷5800=
答:新鲜水果的质量约占运输物资总质量的。
48.(1)
(2)
(3)
【分析】(1)西红柿、辣椒占地面积,都是以长方形菜地面积为单位“1”,用辣椒面积占总面积分率减去西红柿占总面积分率,求出辣椒比西红柿多占菜地几分之几即可;
(2)长方形菜地面积为单位“1”,用单位“1”减去辣椒面积占总面积分率与西红柿占总面积分率,求出黄瓜占整块菜地的几分之几即可;
(3)药水的质量等于药与水的质量之和,用药的质量除以药水质量,求出药的质量占药水的质量的几分之几,注意单位换算。
【解析】(1)
答:辣椒比西红柿多占菜地。
(2)
答:黄瓜占整块菜地的。
(3)1.5千克=1500克
答:药的质量占药水的质量的。
【点评】本题考查分数加减法、分数与除法的关系,解答本题的关键是掌握题中的数量关系。
49.画图见详解,
【分析】由题意可知,将全班人数看作单位“1”,然后平均分成9份。最喜欢阅读文史类和科普类的人数占全班人数的,则最喜欢文学类的人数占全班人数的1-=。最喜欢文学类和科普类的人数占全班总数的,则最喜欢文史类的人数占全班人数的1-=。最喜欢科普类的人数占全班人数的1--=。据此解答。
【解析】根据分析画图如下:
文学类:1-=
文史类:1-=
科普类:1--=
答:最喜欢科普书的人数占全班人数的。
50.
【分析】将不可回收垃圾看成单位“1”,用单位“1”减去厨余垃圾、其他垃圾所占的分率即可求出有害垃圾所占的分率,据此解答。
【解析】1--
=-
=
答:有害垃圾占不可回收垃圾的。
51.(1)
(2)
【分析】(1)以荒漠化总面积为单位“1”,用1减去轻度荒漠化的分率,减去中度荒漠化的分率,即可求出重度荒漠化的分率。
(2)用轻度荒漠化的分率加上中度荒漠化的分率,再减去重度荒漠化的分率,即可求解。
【解析】(1)
答:重度荒漠化的面积约占荒漠化总面积的。
(2)
答:重度荒漠化的面积所占比例比轻度和中度荒漠化面积所占比例的和少。
52.
【分析】求一个数占另一个数的几分之几,用除法,用获奖女科学家人数除以女科学家候选人数,即可解答。
【解析】10÷235=
答:本届获奖的女科学家占被提名的女科学家的。
53.(1)
(2)
【分析】(1)用妈妈看了这本书的分率+爸爸比妈妈多看了这本书的,就是爸爸看了这本书的几分之几。
(2)用阳阳看了这本书的分率-妈妈看了这本书的分率,即可求出阳阳比妈妈多看了这本书的几分之几。
【解析】(1)+=
答:爸爸看了这本书的。
(2)-=
答:阳阳比妈妈多看了这本书的。
54.24人
【分析】根据题意,口令为3,4或6时,每个人都可以抱团成功,所以人数应该是3、4和6的公倍数,同时该公倍数应该在20和30之间,据此解答即可。
【解析】由分析可得:
3=1×3
4=2×2
6=2×3
3、4或6的最小公倍数是:2×2×3=12;
则3、4或6的公倍数有:12、24、36、48、60…
三个数的公倍数在20和30之间的为:24,所以有24人。
答:有24人在玩游戏。
55.60厘米;30块
【分析】由题意可知求出12厘米与10厘米的最小公倍数即可求出拼成的正方形的边长,因为是密铺,所以用拼成的正方形的面积除以长方形的地砖的面积,即可求出需要的块数。
【解析】12=2×2×3
10=2×5
所以12和10的最小公倍数是:2×2×3×5=60
即正方形的边长最小是60厘米,
60×60÷(12×10)
=3600÷120
=30(块)
答:这个正方形的边长最小是60厘米,铺这样的一个正方形图案需要30块砖。
56.
【分析】根据题意,求金星和天王星是八大行星的几分之几,用2除以8即可解答。
【解析】2÷8=
答:自转方向和公转方向不一致的行星占行星总数的。
【点评】此题考查了分数与除法的关系,要求学生掌握。
57.48人
【分析】求这个班有多少人参加队列表演,就是求16和12的公倍数,且小于50;根据求最小公倍数的方法:两个数的公有质因数的连乘积,就是这两个数的最小公倍数,据此解答。
【解析】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48,这个班有48人参加队列表演。
答:这个班有48人参加队列表演
58.会;15升
【分析】根据正方体体积=棱长×棱长×棱长,求出铁块体积,水槽长×宽×水面离槽口高度=水槽内剩余容积,比较铁块体积和水槽内剩余容积,确定是否会溢出,正方体铁块体积-水槽内剩余容积=溢出的水的体积,注意统一单位。
【解析】3×3×3=27(立方厘米)
5厘米=0.5分米
6×4×0.5=12(立方厘米)
27>12
27-12=15(立方分米)=15(升)
答:此时水槽的水会溢出,会溢出15升水。
59.24厘米;6个
【分析】裁成若干个同样大小的正方形,且没有剩余,裁成的正方形的最大边长就是长方形的长和宽的最大公因数,根据分解质因数的方法,把72和48分别分解质因数,这两个数的公有质因数的乘积就是它们的最大公因数;再根据长方形面积公式:面积=长×宽;正方形面积公式:面积=边长×边长,代入数据,求出长方形卡纸的面积和裁成的正方形面积,再用长方形面积÷正方形面积,即可求出可以裁成几个正方形。
【解析】72=2×2×2×3×3
48=2×2×2×2×3
72和48的最大公因数是:2×2×2×3=24
正方形的边长最长是24厘米。
72×48÷(24×24)
=3456÷576
=6(个)
答:裁成的正方形的边长最长是24厘米,可以裁成6个正方形。
60.(1)图见详解
(2)
【分析】(1)把这块菜地看作单位“1”,平均分成4份,取其中1份,即把长方形平均切割成4份,其中l份涂上颜色即可表示种植西红柿的面积占这块菜地的分率;同理,把这块菜地看作单位“1”,平均分成8份,取其中3份,即把长方形平均切割成8份,其中3份涂上颜色即可表示种植辣椒的面积占这块菜地的分率。
(2)根据分数的意义,把这块菜地看作单位“1”,用l减去种植西红柿的面积占这块菜地的分率和种植辣椒的面积占这块菜地的分率,即可求出种植油菜花的面积所占的分率。
【解析】(1)作图如下:
西红柿 辣椒
(2)1--
=-
=
答:油菜花占整块菜地的。
61.
【分析】求得晚上8时到第二天早上7时共睡觉的时间,以全天24小时为单位“1”,根据分数的意义,用睡觉的时间除以24,即得到睡觉的时间是全天的几分之几,据此解答。
【解析】晚八时到第二天早上七时共睡觉的时间:
12:00-8:00=4(小时)
7:00-0:00=7(小时)
7+4=11(小时)
11÷24=
答:他每天睡觉的时间是全天的。
62.9厘米;12个
【分析】求出长和宽的最大公因数就是剪成的最大正方形的边长,用长方形面积÷正方形面积=剪出的个数。
【解析】36和27的最大公因数是9,所以最大正方形的边长是9厘米;
36×27÷(9×9)
=972÷81
=12(张)
答: 正方形卡片边长最大是9厘米,可以剪出12张这样的正方形卡片。
63.(1)
(2)
(3)银牌数占所获奖牌总数的几分之几?
【分析】(1)中国取得的金牌数÷所获奖牌总数=中国取得的金牌数占所获奖牌总数的几分之几。
(2)(银牌数+铜牌数)÷所获奖牌总数=银牌和铜牌共占所获奖牌总数的几分之。
(3)答案不唯一,如银牌数占所获奖牌总数的几分之几?银牌数÷所获奖牌总数=银牌数占所获奖牌总数的几分之几。
【解析】(1)9÷15==
答:中国取得的金牌数占所获奖牌总数的。
(2)(4+2)÷15
=6÷15
=
=
答:银牌和铜牌共占所获奖牌总数的。
(3)银牌数占所获奖牌总数的几分之几?
4÷15=
答:银牌数占所获奖牌总数的。
64.2.6分米
【分析】正方体体积=棱长×棱长×棱长,据此求出正方体容器的容积,正方体容器的容积-铁球体积=水的体积,根据长方体的高=体积÷底面积,即可求出水深。
【解析】3×3×3-3.6
=27-3.6
=23.4(立方分米)
23.4÷(3×3)
=23.4÷9
=2.6(分米)
答:容器里的水深是2.6分米。
65.0.6立方分米
【分析】5升=5立方分米,14厘米=1.4分米,根据长方体的体积=长×宽×高,用2×2×1.4即可求出水和土豆的体积和,再减去水的体积,即可求出土豆的体积。
【解析】5升=5立方分米
14厘米=1.4分米
2×2×1.4-5
=5.6-5
=0.6(立方分米)
答:土豆的体积是0.6立方分米。
66.10138平方厘米
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(50×37+50×37+37×37)×2即可求出做一个这样的保温包至少需要的材料面积。
【解析】(50×37+50×37+37×37)×2
=(1850+1850+1369)×2
=5069×2
=10138(平方厘米)
答:做一个这样的保温包至少需要10138平方厘米的材料。
67.不需要
【分析】油箱里的汽油升数×每升汽油行驶距离=这箱汽油可行驶距离,与到趵突泉景区的距离比较即可。
【解析】19.5×8.5=165.75(千米)
165.75>160
答:他们到趵突泉中途不需要加油。
68.(1)150米
(2)1700平方米
(3)2500吨
【分析】(1)水位线的全长就是长方体底面周长,根据长方形周长=(长+宽)×2,列式解答即可;
(2)贴瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(3)根据长方体体积=长×宽×高,求出水的体积,水的体积×1立方米水的吨数=游泳池内水的吨数,列式解答即可。
【解析】(1)
(米)
答:它的全长是150米。
(2)
(平方米)
答:贴瓷砖的面积是1700平方米。
(3)(吨)
答:这个游泳池内的水有2500吨。
69.
【分析】根据题意,求一个数是另一个数的几分之几用除法计算,即10÷12。
【解析】
答:那么乌龟所用时间是兔子的。
70.6分米
【分析】根据题意,用长3分米、宽2分米的长方形瓷砖铺成一个正方形图案,那么正方形的边长是3和2的公倍数;求铺成的正方形图案最小的边长,就是求3和2的最小公倍数。
3和2是互质数,那么它们的最小公倍数是它俩的乘积,据此解答。
【解析】如图:
3和2的最小公倍数是:3×2=6
即正方形的边长至少是6分米。
答:铺成的图案边长至少是6分米。
【点评】本题考查最小公倍数的实际应用,利用求两个数的最小公倍数的方法解决问题。
71.72人
【分析】根据题意可知参加晚会的人数是不变的,一定是2、3、4的公倍数,那就先求出2、3、4的最小公倍数是:2×3×4=12,若安排12人一桌,那么一桌共需要饮料:12÷2+12÷3+12÷4=13瓶,而三种饮料共用了78瓶,所以一共有:78÷13=6桌,用一桌的12人乘6即得参加晚会的人数;据此解答。
【解析】2、3、4的最小公倍数是2×3×4=12。
12÷2+12÷3+12÷4
=6+4+3
=13(瓶)
12×(78÷13)
=12×6
=72(人)
答:参加晚会的总人数是72人。
【点评】此题主要是考查对公倍数的应用,先明白此题关键是参加会餐的人数是不变的,一定是2、3、4的公倍数。
72.72人
【解析】思路点拨:由题意可知参加晚会人数应是2、3、4的公倍数。
解:2、3、4的最小公倍数为12。
(瓶)
(人)
答:参加晚会的总人数是72人。
73.48人
【分析】如果按8人一组分正好分完,如果按12人一组分也正好分完。说明参加绘画兴趣班的学生数量正好是8和12的公倍数,先根据求一个数的倍数的方法,分别求出8和12的倍数,再找出这两个数的公倍数,并且这个公倍数的大小要满足在40~50之间。据此解答。
【解析】8的倍数:8、16、24、32、40、48…
12的倍数:12、24、36、48…
8和12的公倍数:24、48…
因为48介于40到50之间,所以参加绘画兴趣班的学生有48人。
答:五年级参加绘画兴趣班的学生有48人。
【点评】此题的解题关键是根据求两个数的公倍数的方法解决实际的问题。
74.6月30日
【分析】李奶奶每4天去一次,王奶奶每5天去一次,则她们再次在公园相遇需要经过的天数是4和5的最小公倍数。4和5的最小公倍数是20,则从6月10日经过20天后的日期就是她们再次在公园相遇的时间。
【解析】4和5是互质数,所以4和5的最小公倍数是4×5=20。
即经过20天她们会再次在公园相遇。
6月10日+20天=6月30日
答:下一次她们在公园相遇是6月30日。
【点评】本题考查了最小公倍数的灵活运用以及日期的推算。
75.22平方分米;16.5分米
【分析】把长方体的长、宽、高的数据代入到长方体的表面积公式:S=(a×b+a×h+b×h)×2中,计算出长方体的表面积,即是制作这个包装盒需要的硬纸板面积。根据长方体的特征,12条棱分为3组,每组4条棱的长度相等,由图形可知,所需彩带的长度等于两条长+两条宽+4条高再加上打结用的2.5分米,据此解答。
【解析】(3×2+2×1+3×1)×2
=(6+2+3)×2
=11×2
=22(平方分米)
3×2+2×2+1×4+2.5
=6+4+4+2.5
=16.5(分米)
答:制作这个包装盒需要22平方分米硬纸板,用彩带捆扎包装盒至少需要16.5分米的彩带。
【点评】此题考查的目的是理解掌握长方体的特征和长方体表面积的实际应用,关键是弄清如何捆扎的,确定是求哪几条棱的长度和;在计算时要分清需要计算几个长方形面的面积。
76.1800立方厘米
【分析】石头完全浸没在水里后,石头的体积=水面上升的体积,水面上升的体积可看作长为45厘米,宽为20厘米,高为(24-22)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【解析】45×20×(24-22)
=45×20×2
=900×2
=1800(立方厘米)
答:放入石头的体积是1800立方厘米。
【点评】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
77.(1)
(2)
【分析】(1)用母亲节礼物占零花钱的分率减父亲节礼物占零花钱的分率即可。
(2)把欢欢的零花钱总数看作单位“1”,用减法计算即可得欢欢的零花钱还能剩下几分之几。
【解析】(1)
=
=
答:母亲节礼物比父亲节礼物多用去欢欢零花钱的。
(2)
=
=
=
=
答:欢欢的零花钱还能剩下。
【点评】本题主要考查了分数加减法应用题,要细心计算。
78.750立方厘米
【分析】假山完全浸没在水里后,假山的体积=水面上升的体积,水面上升的体积可看作长为25厘米,宽为12厘米,高为(12.5-10)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【解析】25×12×(12.5-10)
=25×12×2.5
=300×2.5
=750(立方厘米)
答:这块假山的体积是750立方厘米。
【点评】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
79.林林
【分析】通过观察图形可知:折成的无盖长方体储物盒的长是(24-小正方形的边长×2)厘米,宽是(16-小正方形的边长×2)厘米,高是小正方形的边长。把储物盒的长、宽、高相乘,即可求出储物盒的容积。据此分别求出林林和小强设计的储物盒的容积,再比较大小即可。
【解析】林林:(24-3×2)×(16-3×2)×3
=(24-6)×(16-6)×3
=18×10×3
=540(立方厘米)
小强:(24-4×2)×(16-4×2)×4
=(24-8)×(16-8)×4
=16×8×4
=512(立方厘米)
540>512
答:林林的方案做成的长方体储物盒容积最大。
【点评】用长方形铁皮或正方形铁皮制成盒子(四个角上分别去掉一个相同的小正方形),盒子的长和宽要在铁皮的长和宽中去掉两个小正方形的边长,盒子的高是铁皮四个角去掉的小正方形的边长。
80.
【分析】把参加足球、游泳、创客社团的人数占五年级二班人数的分率相加,即可得解。
【解析】++
=
=
答:参加足球、游泳、创客社团的一共占本班学生的。
【点评】本题主要考查了分数加法应用题,要细心计算。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级数学下册期末复习专项青岛(六三制)
(期末考点培优)专题06 解答题
学校:___________姓名:___________班级:___________考号:___________
1.学校表彰“优秀志愿者”准备了49本科技书和29支钢笔,平均分给评选出来的“优秀志愿者”,结果科技书多出4本,钢笔少了1支,这次最多评选了多少名“优秀志愿者”?
2.为庆祝教师节,五(1)班的学生正在礼堂里挂气球。按照2个蓝气球、3个红气球、2个黄气球的顺序循环排列,一共挂了50个气球。三种颜色的气球分别占总数的几分之几?
3.有两根绸带,一根长20米,另一根长28米。把它们截成若干段同样长的小段,而且没有剩余,截成的小段最长是多少米?一共可以截成多少段?
4.在“爱阅读爱数学”活动中,王老师帮乐乐录制了一段4.5分钟的短视频。其中的时间他在讲数学故事,的时间在介绍自己喜欢的数学读物:张景中院士的《帮你学数学》,剩下的时间在和同学互动。乐乐和同学互动的时间占这个短视频的几分之几?
5.某公交车站的始发站每6分钟发出一辆5路车,每8分钟发出一辆7路车,如果这两路公交车早上6:00同时从始发站发车,那么这两路公交车的第二次共同发车时间是6:48,你同意吗?请写出你的判断理由。
6.学校为古诗词大赛中表现优异的同学准备了47支中性笔和31个笔记本作为奖品,每名同学得到的奖品种类和数量完全相同,最后余下了2支中性笔和1个笔记本,最多有几名同学得到奖品?
7.中国农历中“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的白天时间是15小时,这一天北京黑夜时间是一天总时间的几分之几?
8.【新颖材料】济南别称泉城,素有“四面荷花三面柳,一城山色半城湖”的美誉。通过调查统计,趵突泉暑假期间旅客的购票情况:人工售票口购票约占,网上购票约占,其余为自动售票机购票,自动售票机购票占总售票数的几分之几?
9.两根铁丝,一根长12米,另一根长18米,要把它们截成整米的同样长的小段没有剩余,每段最长多少米?这两根铁丝一共可以截成多少段?
10.一个长方体水箱,从里面量长24厘米,宽18厘米,深15厘米。给里面加入10厘米深的水,妙妙把一个土豆放入水中后(土豆完全浸没在水中),水面上升到12.5厘米,土豆的体积是多少立方厘米?
11.张明为过生日的妈妈买了一件礼物,他准备用彩带捆扎礼盒(如图),已知礼盒的长是35厘米,宽是20厘米,盒高15厘米,彩带接头处需35厘米。捆扎这个礼盒至少需要多长的彩带?
12.谷雨是春季的最后一个节气,这时雨水充沛,适合播种。实验小学的同学们把学校劳动教育基地划分为“花圃区”和“农耕园”两个区域进行花草和蔬菜种植,其中花圃区面积是23平方米,农耕园面积是35平方米,花圃区的面积是农耕园的几分之几?花圃区的面积占学校劳动实践基地的几分之几?
13.一块长23厘米、宽20厘米的长方形铁皮(如图),从四个角各切掉一个边长为4厘米的正方形,然后做成一个无盖长方体盒子,这个盒子的容积是多少?
14.在古代建筑中,汉砖被广泛应用于宫殿、寺庙等建筑的建造,也多用于道路的铺设和修建,一个长30厘米、宽2分米、高18厘米的汉砖,它的体积是多少立方厘米?合多少立方分米?
15.淄博是齐文化的发源地,琉璃文化源远流长,底蕴深厚,淄博琉璃始于汉代,兴于元代,盛于清朝,逐步发展成为世界琉璃产销中心,业界素有“世界琉璃看中国,中国琉璃看淄博”之说。假期,明明去淄博旅游,带回一个漂亮的琉璃镇尺,他想测量出这个镇尺的体积,于是他找来一个棱长10厘米的正方体容器,里面装有一些水,将这个高8厘米的长方体镇尺竖直放入水中(镇尺底面与容器底面平行),镇尺浸没6厘米时,水就满了。这个镇尺的体积是多少?(容器厚度忽略不计)
16.登山是一种很好的有氧运动,周末小李和爸爸去登山,先用小时走了全程的,又用半小时走了全程的一半。
(1)已经走了多少小时?
(2)还剩全程的几分之几没有走?
17.2024年4月23日是第29个世界读书日,实验小学开展“阅读嘉年华”活动。琳琳去学校图书馆选了一本《生活中的数学》,共360页,第一天看了80页,第二天看了全书的。
(1)琳琳第一天看了全书的几分之几?
(2)还剩下这本书的几分之几没有看?
18.将一块长14厘米、宽10厘米、高3厘米的长方体铁块完全浸没在一个长方体的油箱中,取出铁块后,油面的高度下降了2.1厘米。这个长方体油箱的底面积是多少平方厘米?
19.手工课上,王丽用边长16厘米的正方形卡纸,从四个角上剪掉边长为4厘米的正方形,做成一个无盖的盒子。
(1)做这个盒子用了多少平方厘米的铁皮?
(2)这个盒子的容积是多少立方厘米?
20.小芳在父亲生日这天给爸爸准备了一份礼物,并且用包装盒进行了精美的装饰,包装如下图所示,已知包装盒的长宽高分别是4分米、3分米、1分米,制作这个包装盒需要多少平方分米硬纸板?用彩带捆扎包装盒至少需要多少分米的彩带?(打结处用了2.5分米)
21.端午节与春节、清明节、中秋节并称为中国汉族的四大传统节日,自古以来端午节便有划龙舟及食粽等节日活动。小明和小宇为迎端午学习包粽子,妈妈为他们准备了千克糯米,小明用了其中的,小宇用了其中的,这些糯米还剩下几分之几?
22.小亮想测量出一块鹅卵石的体积,进行了如下操作:
步骤一:在长4分米,宽3分米、高2分米的玻璃容器中盛8厘米深的水。
步骤二:将鹅卵石浸没在水中,此时测得水面高度为12厘米。
(1)你能根据她的实验求出这块鹅卵石的体积?
(2)利用这种操作方法求鹅卵石的体积,运用了数学上的( )思想,学习( )也用了这种思想。
23.小明准备把三根分别长30厘米、48厘米、66厘米的木棒截成一些长度相等的小木棒(最后没有剩余),截成的小木棒最长是多少厘米?一共能截成多少段这样的小木棒?
24.有甲、乙两种长方体容器。甲容器长6分米,宽5分米,高8分米。乙容器长5分米,宽4分米,高15分米。
(1)向甲容器中注水时,玻璃容器的侧面上出现几次正方形?注水高度分别是多少?
(2)当甲容器中第2次出现正方形时,将甲容器中的水倒一部分到乙容器,使得甲、乙容器中的水面一样高,那么需要从甲容器中倒出多少水?(不考虑容器壁的厚度)
25.某校举办“非遗”进校园活动,五年级开设了三个“非遗”课程,要求每位同学选一个参加。下面是五年级同学参加情况的统计表。
活动项目 篆刻 软木画 汉服制作
占全年级总人数的几分之几 ?
参加软木画的人数占全年级总人数的几分之几?
26.“端午节”是中国首个入选世界非物质文化遗产的节日,赛龙舟和吃粽子是端午节的两大习俗。今年端午节,喜多家包了许多粽子,妈妈先把30个蜜枣粽平均分给几家邻居,接着又把24个肉粽平均分给了这几家,都刚好分完。这些粽子最多分给了几家邻居?
27.在中国传统文化中,龙、凤、鹤被称为吉祥三宝。龙和风现只留存在传说中,而鹤就是被冠之为“一品鸟”的丹顶鹤,是现今人世间可以看到的国宝。世界上丹顶鹤野生群种的个体总数约为3000只,目前,生活在我国的丹顶鹤野生群种的个体总数约为1800只,请问生活在我国的丹顶鹤野生群种的个体总数占世界的几分之几?
28.根据气象部门统计,2021年是干旱的一年。在青岛年降水总量中,夏季降雨量占,比春季降雨量多,春季降雨量占全年的几分之几?春夏两季的降水量比秋冬两季多几分之几?
29.回答问题。
①这是一个正方体的水槽;
②三块石子的体积分别是1号137立方厘米,2号358立方厘米,3号450立方厘米;
③乌鸦只能够到水槽的最上沿。乌鸦怎样才能喝到水?
30.
停车点 起点站 中间第1站 中间第2站 中间第3站 中间第4站 终点站
上下车人数 ﹢24 ﹣5 ﹢1 0 ﹢3 ﹣5 0 ﹣11 ﹢9 ﹣16
一辆汽车从起点开出后,这中经过4个停车点,最后到达终点站。下表记录了该客车的载客数量的变化情况。
(1)中间4站哪个站没有人上车?哪个站没有人下车?
(2)汽车从中间第1站开往中间第2站时,车上有多少人?
(3)从表中你还知道了什么?
31.张师傅计划今天加工80个零件,实际上午加工了计划任务的,下午加工了计划任务的,晚上还加工了20个。他今天完成计划任务了吗?
32.欢欢和果果看同一本书,欢欢计划36天看完,每天看相同的页数;果果计划30天看完,每天也看相同的页数。现在两人各看了6天,他们分别看了这本书的几分之几?
33.把一根长彩带剪成长度相等的几段,如果剪成4分米一段的,那么少1分米;如果剪成6分米一段的,那么少1分米;如果剪成8分米一段的,也少1分米。这个长彩带的长度至少是多少分米?
34.同学们在用一些小棒和橡皮泥拼搭一个长方体框架。
(1)上图是已经拼搭好的部分,还需要( )根2厘米长的小棒、( )根4厘米长的小棒、( )根7厘米长的小棒。
(2)如果给这个长方体框架的每个面都铺上彩纸,至少需要多少平方厘米彩纸?
35.植树节到了,学校在操场的四周每隔4米种1棵树,种到21棵后发现树苗不够了,于是决定重新种,改为每隔5米种1棵,这样重新种时,有多少棵树苗不必拔掉?
36.整理图书时,管理员李老师发现科技类图书占图书总数的,文学类图书占图书总数的,工具类图书占图书总数的。
(1)工具类图书比科技类图书少的部分占图书总数的几分之几?
(2)你觉得李老师统计完所有的图书种类了吗?请说明理由。
37.杨家埠木版年画是一种传统民间版画。一批木版年画的长是24cm,宽是16cm,要用这种规格的年画布置成正方形展板,边长最短可以是多少厘米?需要多少块木版年画?
38.黄河是中华文明主要的发源地,中国人称其为“母亲河”。黄河每年都会生产16亿吨泥沙,其中有12亿吨流入大海,剩下的泥沙常年留在黄河下游,形成冲积平原,有利于种植。每年泥沙总量的几分之几会流入大海?剩余泥沙占总量的几分之几?
39.兴趣小组要用一根绳子编制中国结,小阳用去了米,欢欢用去了米,还剩下米。
(1)欢欢比小阳少用多少米?
(2)这根绳子原来长多少米?
40.幸福超市运回42块肥皂和36盒牙膏,现在要把肥皂和牙膏捆一起做奖品,要求每份奖品的肥皂一样多,牙膏也一样多(正好用完,没有剩余)。这些东西最多能捆多少个这样的奖品?
41.端午节吃粽子是中国人的传统习俗。芳芳和林林学习包粽子,妈妈准备了千克糯米,芳芳用了其中的,林林用了其中的,这些糯米还剩下几分之几?
42.李阿姨把一个西瓜分给甲、乙、丙三个人吃,甲和乙一共吃了这个西瓜的,乙和丙一共吃了这个西瓜的,请你算出三个人分别吃了这个西瓜的几分之几?
43.实验学校为一间长5米、宽4.5米的微机室地面铺方砖,应选择边长是多少分米的正方形方砖比较合适?铺完这间微机室至少需要多少块这样的方砖?
44.有同样大小的红、绿、蓝三种颜色的彩旗54个,将它们按照2个红旗、1个绿旗、3个蓝旗的顺序排列。三种颜色的彩旗各占总数的几分之几?
45.元宵节非常热闹,小涵到街上看花灯,花灯闪烁着光芒。小涵绕着花灯走了几圈,只估摸着大概有55~65盏花灯。你知道一共有多少盏花灯吗?
46.为了庆祝六一儿童节,学校举行书画展,展区已经布置了三种作品,你认为展区还有地方展示其他作品吗?用你喜欢的方式进行说明。
书法作品占展区的 油画作品占展区的 素描作品占展区的
47.2023年5月10日,天舟六号货运飞船发射成功,标志着中国空间站建设迈出重要一步。飞船运输物资总质量约是5800千克,其中约有70千克的新鲜水果。此次运输,新鲜水果的质量约占运输物资总质量的几分之几?
48.学校开展劳动教育活动,为五年级开辟了一块面积为340平方米的长方形菜地,其中西红柿占,辣椒占,剩下的全部种黄瓜。
(1)辣椒比西红柿多占菜地几分之几?
(2)黄瓜占整块菜地的几分之几?
(3)蔬菜成长一段时间之后需要喷洒农药除虫,学校购买的农药50克药片需要放入1.5千克水中,那么配制好的药水中,药的质量占药水的质量的几分之几?
49.芳芳调查了全班最喜欢阅读的三种读物情况:最喜欢阅读文史类和科普类的人数占全班人数的,最喜欢文学类和科普类的人数占全班总数的。请问最喜欢科普书的人占全班人数的几分之几?(先用画图的方法分析,再列式解答。)
50.垃圾分为可回收垃圾和不可回收垃圾,其中不可回收垃圾包括厨余垃圾、有害垃圾和其他垃圾。某小区一年产生的不可回收垃圾中的厨余垃圾占,其他垃圾占。有害垃圾占不可回收垃圾的几分之几?
51.我国是受荒漠化危害最严重的国家之一。在荒漠化总面积中,轻度荒漠化面积约占。中度荒漠化面积约占,其余的是重度荒漠化,
(1)重度荒漠化的面积约占荒漠化总面积的几分之几?
(2)重度荒漠化的面积所占比例比轻度和中度荒漠化面积所占比例的和少几分之几?
52.第十三届“中国青年女作家”将评审委员会由32位评委组成,经过严格的评审,10位女科学家获奖者从110个单位提名的235位有效候选人中脱颖而出,本届获奖的女科学家占被提名的女科学家的几分之几?
53.在“亲子共度一本书”活动中,阳阳和妈妈、爸爸一起阅读《中华历史故事》。一周内,妈妈看了这本书的,阳阳看了这本书的,爸爸比妈妈多看了这本书的。
(1)爸爸看了这本书的几分之几?
(2)阳阳比妈妈多看了这本书的几分之几?
54.大课间时同学们玩“抱团”游戏,人数在20和30之间。同学们发现当抱团口令为3,4或6时,每个人都可以抱团成功。有多少人在玩游戏?
“抱团”游戏的规则
当听到口令中所报的数后,相应人数的同学迅速抱在一起,算作成功。
55.一块砖底面长12厘米,宽10厘米,要铺成一个正方形图案,这个正方形的边长最小是多少厘米?铺这样的一个正方形图案需要多少块砖?
56.在太阳系的八大行星中,只有金星和天王星的自转方向和公转方向不一致。金星的自转方向与公转方向相反,天王星则是与公转轨道呈97°角地“躺着”旋转的。自转方向和公转方向不一致的行星占行星总数的几分之几?
57.五年级一班的学生进行队列表演,每行16人或12人都正好是整行。已知这个班的学生人数不超过50人,你能算出这个班有多少人参加队列表演吗?
58.一个长方体水槽内部长6分米,宽4分米,深3分米,水面离槽口有5厘米,如果放入一块棱长为3分米的正方体铁块,此时水槽的水是否会溢出?如果会,会溢出多少升水?
59.美术小组的同学要将一张长72厘米、宽48厘米的长方形卡纸裁成大小相等的正方形,裁好后正好没有剩余,裁成的正方形的边长最长是多少厘米?可以裁成多少个正方形?
60.学校开展劳动教育活动,五年级开辟了一块面积为公顷的长方形菜地,其中西红柿占,辣椒占,剩下的全部种油菜花。
(1)将下边的长方形看做这块菜地,请在图中用不同的阴影面积表示出西红柿和辣椒的情况。
(2)油菜花占整块菜地的几分之几?
61.2023年3月21日是第21个“世界睡眠日”,人的一生中有的时间是在睡眠中度过。根据教育部“睡眠管理”的有关规定,小学生每天的睡眠时间应该达到10小时,小明每天晚上8时睡觉,第二天早上7时起床,他每天睡觉的时间是全天的几分之几?
62.手工课上,刘鹏将一张长36厘米、宽27厘米的长方形卡纸剪成若干张同样大小的正方形卡片,纸张不能有剩余。正方形卡片边长最大是多少厘米?可以剪出几张这样的正方形卡片?
63.第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事。中国冰雪健儿敢于追梦,最终取得了9金4银2铜共15枚奖牌的好成绩。
(1)中国取得的金牌数占所获奖牌总数的几分之几?
(2)银牌和铜牌共占所获奖牌总数的几分之几?
(3)请根据所给出的数学信息提出一个数问题并解答。
64.把一个体积为3.6立方分米的铁球浸没在棱长为3分米的正方体容器中,这时水面刚好升至玻璃缸口,如果取出铁球,容器里的水深是多少分米?
65.如图,一个正方体玻璃容器(无盖)的棱长是2分米。向容器中倒入5升水,再把一个土豆没入水中。这时量得容器内水深14厘米。土豆的体积是多少?(玻璃的厚度忽略不计)
66.外卖给我们的生活带来了很大的便利,这种便利离不开外卖人员的辛苦付出。淘气的叔叔是一个外卖骑手,下图是他的外卖保温包的示意图,做一个这样的保温包至少需要多少平方厘米的材料?(重叠部分忽略不计)
67.十一假期,小丽一家开车到离家约160千米的趵突泉景区游玩。汽车油箱里有19.5升汽油,每升汽油可供汽车行驶8.5千米,他们到趵突泉中途还需要加油吗?
68.“水立方”位于北京奥林匹克公园内,它与一墙之隔的“鸟巢”一起被称为2008年北京奥运会两大标志性建筑物。你知道吗?在水立方内有一个国际标准的长方体游泳池,它的长是50米,宽是25米,深是3米。
(1)在内壁沿池底向上2米处画一条水位线。它的全长是多少米?
(2)如果用瓷砖贴水池的四周和底面,贴瓷砖的面积是多少平方米?
(3)如果池内水深2米,这个游泳池内的水有多少吨?(1立方米水重1吨)
69.“龟兔赛跑”是我们非常熟悉的故事,大意是乌龟和兔子赛跑,开跑不久兔子就超过乌龟很远,于是兔子就在路边睡了一觉,而乌龟一直往目的地奔跑,最终乌龟获得了胜利。
如果兔子跑完全程用了12分钟,乌龟跑完全程用了10分钟,那么乌龟所用时间是兔子的几分之几?
70.王叔叔要用长3分米、宽2分米的瓷砖铺一个正方形图案。如果都用整块的瓷砖,铺成的图案边长至少是多少分米?把你的想法用你喜欢的方法表达出来(可以写一写,可以算一算,也可以画图说一说)。
71.一次晚会上共有三种饮料。餐后统计,这三种饮料一共饮用了78瓶,平均每2人饮用一瓶A饮料,每3人饮用一瓶B饮料,每4人饮用一瓶C饮料。参加晚会的总人数是多少?
72.一次晚会供有三种饮料,餐后统计,三种饮料共用了78瓶;平均每2人饮用1瓶饮料,每3人饮用一瓶B饮料,每4人饮用一瓶C饮料,参加晚会的总人数是多少?
73.实验小学五年级学生参加绘画兴趣班的人数是40~50人,如果按8人一组分正好分完,如果按12人一组分也正好分完。五年级参加绘画兴趣班的学生有多少人?
74.李奶奶和王奶奶经常去同一个公园锻炼身体,李奶奶每4天去一次,王奶奶每5天去一次。6月10日她们刚一起在公园参加了活动,下一次她们在公园相遇是几月几日?
75.如图所示包装盒的长宽高分别是3分米、2分米、1分米,制作这个包装盒需要多少平方分米硬纸板?用彩带捆扎包装盒至少需要多少分米的彩带?(打结处用了2.5分米)
76.如图为了美化鱼缸,在鱼缸底部放入几块小石头,放入前水面高度是22厘米,放入后水面高度是24厘米,放入石头的体积是多少立方厘米?
77.母亲节这天,欢欢用零花钱的给妈妈买了一束鲜花,同时,她用零花钱的买了一条领带,父亲节时送给了爸爸。
(1)母亲节礼物比父亲节礼物多用去欢欢零花钱的几分之几?
(2)欢欢的零花钱还能剩下几分之几?
78.王老师买了一个长方体鱼缸,如图所示,为了提高观赏性,王老师在鱼缸里放了一块假山。水面高度由原来的10厘米上升到12.5厘米。这块假山的体积是多少立方厘米?
79.数学课上,同学们策划设计用一块长24厘米,宽16厘米的长方形铁皮,在四个角上各剪去一个小正方形(如图所示),做成一个无盖的长方体储物盒。林林和小强分别设计了不同的方案,林林选择边长为3厘米,小强选择边长为4厘米。他们两个谁的方案做成的长方体储物盒容积最大?
80.为落实“双减”政策,丰富同学们延时期间的校园生活。实验小学开设了足球、篮球、游泳、创客等独具特色的社团。五年级二班的同学都参加了社团。其中的同学参加了足球社团,的同学参加了游泳社团,的同学参加了创客社团,参加足球、游泳、创客社团的一共占本班学生的几分之几?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.15名
【分析】科技书多出4本,钢笔少了1支,说明“优秀志愿者”的人数最多是(49-4)和(29+1)的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【解析】49-4=45(本)
29+1=30(本)
45=3×3×5
30=2×3×5
3×5=15(名)
答:这次最多评选了15名“优秀志愿者”。
2.蓝气球:;红气球:;黄气球:
【分析】一组即一个周期有(2+3+2)个气球,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个,据此可以确定有7组余1个,且余下的一个是蓝气球,蓝气球×组数+1=蓝气球个数,红气球和黄气球个数分别乘组数,可以求出红气球和蓝气球个数。用三种颜色的气球分别÷总数,即可求出三种颜色的气球分别占总数的几分之几。
【解析】50÷(2+3+2)
=50÷7
=7(组)……1(个)
蓝气球:2×7+1
=14+1
=15(个)
15÷50==
红气球:3×7=21(个)
21÷50=
黄气球:2×7=14(个)
14÷50==
答:三种颜色的气球分别占总数的、、。
3.4米,12段
【分析】要把两根不同长度的绸带截成同样长且无剩余的小段,每小段的长度就是两根绸带长度的公因数,而要求最长的小段长度,就是求它们的最大公因数;求出最大公因数后,再用两根绸带的长分别除以它们的最大公因数,分别计算出两根绸带按此长度能截成的段数,最后相加得到总段数。
【解析】20=2×2×5
28=2×2×7
所以20和28的最大公因数是:2×2=4,即截成的小段最长是4米。
20÷4+28÷4
=5+7
=12(段)
答:截成的小段最长是4米,一共可以截成12段。
4.
【分析】把录制的短视频的总时间看作单位“1”,把讲数学故事占的总时间的与介绍自己喜欢的数学读物占的相加,求出讲数学故事和介绍自己喜欢的数学读物占单位“1”的分率,再用1减去这个分率即可求出乐乐和同学互动的时间占这个短视频的几分之几。
【解析】1-(+)
=1-(+)
=1-
=
答:乐乐和同学互动的时间占这个短视频的。
5.不同意;理由见详解
【分析】每隔6的倍数分钟,5路车发车;每隔8的倍数分钟,7路车发车。所以每隔6和8的公倍数分钟,两车同时发车,第二次共同发车应是隔6和8的最小公倍数分钟,再发车,即用6和8的最小公倍数分钟加发到时间即可得解,据此解答。
【解析】
第一次发车与第二次发车经过的时间(分钟)
答:不同意。因为6和8的最小公倍数是24,这两路公交车的第二次共同发车时间应该是6:24。
6.15名
【分析】根据题意,如果中性笔有47-2=45支,笔记本有31-1=30个,就正好平均分完,每名同学分得的奖品种类和数量完全相同,那么最多得到奖品的人数就是45和30的最大公因数。
把45、30分解质因数后,把公有的相同质因数乘起来就是最大公因数,即可得解。
【解析】47-2=45(支)
31-1=30(个)
45=3×3×5
30=2×3×5
45和30的最大公因数是:3×5=15
即最多有15名同学得到奖品。
答:最多有15名同学得到奖品。
7.
【分析】分析题目,先根据1天=24小时,用24减去白天的时间即可得到黑夜的时间,求一个数是另一个数的几分之几用除法,再用黑夜的时间除以一天的总时间,即可得到黑夜时间是一天总时间的几分之几。
【解析】(24-15)÷24
=9÷24
=
=
答:这一天北京黑夜时间是一天总时间的。
8.
【分析】把总售票数看作单位“1”,根据减法的意义,用“1”减去人工售票口购票、网上购票约占总售票数的几分之几,即是自动售票机购票占总售票数的几分之几。
【解析】
答:自动售票机购票占总售票数的。
9.6米;5段
【分析】截成同样长的几段且没有剩余,说明每段铁丝是12和18的公因数,求每段最长是多少米,则是求12和18的最大公因数,再用12除以最大公因数的商加上18除以最大公因数的商,即是一共截成的段数,据此解答。
【解析】12=2×2×3
18=2×3×3
12和18的最大公因数是2×3=6,每段最长是6米。
(12÷6)+(18÷6)
=2+3
=5(段)
答:每段最长6米,这两根铁丝一共可以截成5段。
10.1080立方厘米
【分析】根据题意,土豆的体积是水上升的体积,结合长方体的体积公式V=abh,解答即可。
【解析】24×18×(12.5-10)
=432×2.5
=1080(立方厘米)
答:土豆的体积是1080立方厘米。
11.205厘米
【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等。由图形可知:需要彩带的长度等于2条长+4条高+2条宽+打结用的长度,代入数据计算即可求解。
【解析】35×2+20×2+15×4+35
=70+40+60+35
=205(厘米)
答:捆扎这个礼盒至少需要205厘米的彩带。
12.;
【分析】由题意可知,学校实践基地面积是平方米,根据求一个数是另一个数的几分之几用除法计算,分别用花圃区的面积除以农耕园面积,用花圃区的面积除以学校劳动实践基地面积,计算即可。
【解析】23÷35=
23÷(23+35)
=23÷58
=
答:花圃区的面积是农耕园的;花圃区的面积占学校劳动实践基地的。
13.720毫升
【分析】做成长方体盒子的长是(23-4×2)厘米,宽是(20-4×2)厘米,高是4厘米,根据长方体体积公式,再把体积单位转化为容积单位即可。
【解析】(23-4×2)×(20-4×2)×4
=15×12×4
=180×4
=720(立方厘米)
720立方厘米=720毫升
答:这个盒子的容积是720毫升。
14.10800立方厘米;10.8立方分米
【分析】先统一单位为厘米,然后根据长方体体积=长×宽×高,求出汉砖的体积,再根据1立方分米=1000立方厘米进行单位换算即可。
【解析】2分米=20厘米
30×20×18
=600×18
=10800(立方厘米)
10800立方厘米=10.8立方分米
答:它的体积是10800立方厘米,合10.8立方分米。
15.400立方厘米
【分析】根据正方体体积=棱长×棱长×棱长,求出正方体容器的容积,正方体容器的底面积×水面高度=水的体积,正方体容器的容积-水的体积=高6厘米的镇尺体积。高6厘米的镇尺体积÷6=镇尺底面积,镇尺底面积×镇尺高=镇尺体积,据此列式解答。
【解析】10×10×10-10×10×7
=1000-700
=300(立方厘米)
300÷6=50(平方厘米)
50×8=400(立方厘米)
答:这个镇尺的体积是400立方厘米。
【点评】关键是先求出镇尺底面积,掌握并灵活运用长方体和正方体体积公式。
16.(1)小时
(2)
【分析】(1)半小时是小时,先用的时间+又用的时间=已经走的时间,据此列式解答;
(2)将全程看作单位“1”,全程的一半是,1-先走了全程的几分之几-有走了全程的几分之几=还剩全程的几分之几,据此列式解答。
【解析】(1)+=+=(小时)
答:已经走了小时。
(2)1--
=-
=-
=
答:还剩全程的没有走。
17.(1);
(2)
【分析】(1)将全书页数看作单位“1”,第一天看的页数÷全书页数=第一天看了全书的几分之几;
(2)将全书页数看作单位“1”,1-第一天看了全书的几分之几-第二天看了全书的几分之几=还剩下这本书的几分之几没有看。
【解析】(1)80÷360==
答:琳琳第一天看了全书的。
(2)1--
=-
=-
=
答:还剩下这本书的没有看。
18.200平方厘米
【分析】油面下降的体积等于长方体铁块的体积,根据长方体体积=长×宽×高,求出长方体铁块的体积,再根据长方体底面积=体积÷高,求出长方体油箱的底面积,据此列式解答。
【解析】14×10×3÷2.1
=420÷2.1
=200(平方厘米)
答:这个长方体油箱的底面积是200平方厘米。
19.(1)192平方厘米;
(2)256立方厘米
【分析】(1)这个盒子所用的铁皮的面积=原来正方形的面积-四个小正方形的面积。正方形的面积=边长×边长,将数据代入计算即可。
(2)按照题意,画出如下的示意图,得出这个无盖的盒子是个长为8厘米,宽为8厘米,高为4厘米的长方体。根据得出这个盒子的容积。
【解析】(1)16×16-4×4×4
=256-64
=192(平方厘米)
答:做这个盒子用了192平方厘米。
(2)16-2×4
=16-8
=8(厘米)
8×8×4=256(立方厘米)
答:这个盒子的容积是256立方厘米。
20.38平方分米;20.5分米
【分析】求制作这个包装盒硬纸板的面积,就是求长方体的表面积,根据,代入数据计算即可;观察可知,求彩带的长度,即把2条长,2条宽,4条高及打结的长度加起来,即可得解。
【解析】
(平方分米)
(分米)
答:制作这个包装盒需要38平方分米硬纸板;用彩带捆扎包装盒至少需要20.5分米的彩带。
21.
【分析】把妈妈为他们准备的糯米的重量看作单位“1”,用1减去小明用去的占总重量的分率,减去小宇用去的占总重量的分率,即可解答。
【解析】1--
=-
=
答:这些糯米还剩下。
22.(1)4.8立方分米
(2)转化;平行四边形面积(答案不唯一)
【分析】(1)这块鹅卵石的体积等于上升的水的体积,用长方体的体积公式底面积乘高(即上升的厘米数)即可,计算统一单位;
(2)在求鹅卵石体积时是把鹅卵石的体积转化为上升部分水的体积,在学习一种平行四边形的面积时,也是把平行四边形进行割补,转化为长方形,从而推导出平等行四边形的面积,也是用这种方法解答。
【解析】(1)12-8=4(厘米)
4厘米=0.4分米
4×3×0.4
=12×0.4
=4.8(立方分米)
答:这块鹅卵石的体积是4.8立方分米。
(2)利用这种操作方法求鹅卵石的体积,运用了数学上的转化思想,学习平行四边形面积也用了这种思想(答案不唯一)。
23.6厘米;24段
【分析】把三根分别长30厘米、48厘米、66厘米的木棒截成一些长度相等的小木棒(最后没有剩余),截成的小木棒最长的长度就是30、48和66的最大公因数;再用三根木棒的长度分别除以它们的最大公因数求出商,最后再相加即可求出一共能截成多少段这样的小木棒。
【解析】
2×3=6(厘米)
30÷6+48÷6+66÷6
=5+8+11
=13+11
=24(段)
答:截成的小木棒最长是6厘米,一共能截成24段这样的小木棒。
24.(1)两次;5分米,6分米;
(2)72立方分米。
【分析】(1)根据题意可知,甲容器的侧面出现正方形的条件是注水高度等于容器的长或宽。所以甲容器的长为6分米,宽为5分米,当注水高度为5分米或者6分米时,出现正方形。
(2)根据题意,结合长方形的体积公式:长×宽×高,求出甲容器的水的体积,要使甲、乙两个容器的水面一样高,需要计算出甲、乙两个容器的底面积之和,再用总体积除以底面积之和,即为乙容器中水的高度,再根据长方体的体积公式求出答案即可。
【解析】(1)答:出现两次正方形;一次是5分米,一次是6分米。
(2)体积:6×5×6
=30×6
=180(立方分米)
底面积之和:6×5+5×4
=30+20
=50(立方分米)
高:180÷50=3.6(分米)
水的体积:3.6×5×4
=18×4
=72(立方分米)
答:需要从甲容器中倒出72立方分米的水。
25.
【分析】把全年级总人数看作单位“1”,用单位“1”减去篆刻占全年级总人数的分率,减去汉服制作占全年级总人数的分率,即可求出参加软木画的人数占全年级总人数的分率,据此解答。
【解析】1--
=-
=-
=
答:参加软木画的人数占全年级总人数的。
26.6家
【分析】根据题意,把30个蜜枣粽、24个肉粽平均分给几家邻居都刚好分完,说明邻居的数量是30和24的公因数。求这些粽子最多分给了几家邻居,就是求30和24的最大公因数。把30和24分解质因数后,把它们公有的质因数乘起来就是最大公因数,即可求解。
【解析】30=2×3×5
24=2×2×2×3
30和24的最大公因数是:2×3=6
即最多分给了6家邻居。
答:这些粽子最多分给了6家邻居。
27.
【分析】根据求一个数占另一个数的几分之几,用一个数÷另一个数,结果用分数表示即可,即用生活在我国的丹顶鹤野生群种的个体总数÷世界上丹顶鹤野生群种的个体总数,即可解答。
【解析】1800÷3000=
答:生活在我国的丹顶鹤野生群种的个体总数占世界的。
28.;
【分析】(1)根据题意,求的是春季降水量占全年的几分之几,夏季降雨量比春季降水量多,则可用夏季降雨量 =春季降雨量占全年的几分之几,据此解答。
(2)根据题意,求的是春夏两季的降水量比秋冬两季多几分之几?把全年的降水量看作为“1”,则可列出算式:(春季降雨量+夏季降雨量) (1 春季降雨量 夏季降雨量)=春夏两季的降水量比秋冬两季多的降水量,据此解答。
【解析】 =
(+) (1 )
= ( )
=
=
答:春季降水量占全年的,春、夏两季的降水量比秋、冬两季多全年降水量的。
29.见详解
【分析】根据题意,要使乌鸦喝到水,需要把石子放入水槽,使水面上升到水槽的最上沿或溢出水槽。要使水面上升到水槽的最上沿,根据长方体体积=长×宽×高,上升的水的体积应是20×20×(20-18)。而2号和3号石子的体积之和是358+450=808(立方厘米),大于800毫升,即可以把2号和3号石子放入水槽,乌鸦就能喝到水。也可以把三块石头都放入水槽,水更会溢出水槽,乌鸦也可以喝到水。
【解析】20×20×(20-18)
=20×20×2
=800(毫升)
第一种方法:2号和3号石子一起放入
358+450=808(立方厘米)
808立方厘米=808毫升
808毫升>800毫升
第二种方法:1号、2号、3号石子一起放入
137+358+450=945(立方厘米)
945立方厘米=945毫升
945毫升>800毫升
答:把2号和3号石子放入水槽或把1号、2号和3号石子放入水槽,乌鸦就能喝到水。
30.(1)中间第3站;中间第2站;
(2)23人
(3)见详解
【分析】(1)上车和下车是两个相反意义的量,可以用正负数表示。正数表示上车的人数,负数表示下车的人数;0表示既不上车也不下车。
(2)从中间第1站开往中间第2站时,车上的人数应该加上上车的人数,再减去下车的人数。
(3)根据正负数的意义,读取表中数据,即可解答。
【解析】(1)中间第3站上下车人数是﹣5和0,说明这一站下车5人,没有人上车。
中间第2站上下车人数是0和﹢3,说明这一站没有人下车,上车3人。
答:中间4站第3站没有人上车,第2站没有人下车。
(2)24-5+1=20(人)
20+3=23(人)
答:车上有23人。
(3)中间第1站,下车5人,上车1人,中间第4站,下车11人,上车9人。
答:中间第2站和第4站,下车人数比上车人数多。(答案不唯一合理即可)
31.没完成
【分析】把计划要加工的零件总个数看作单位“1”,先根据求一个数是另一个数的几分之几,用20除以80,求出晚上加工的20个零件占总个数的几分之几;
再把上午、下午、晚上分别加工零件的个数占总个数的分率相加,即是今天一共完成总个数的几分之几,再与1比较大小,如果超过或等于1,则完成了计划任务;如果小于1,则没有完成计划任务。
【解析】
答:他今天没完成计划任务。
32.欢欢:;果果:
【分析】从题意可知,每天看的页数相同,欢欢计划36天看完,她已看了6天,6天占36天的几分之几,即欢欢看了这本书的几分之几。果果计划30天看完,她已看了6天,6天占30天的几分之几,即果果看了这本书的几分之几。根据求一个数是另一个数的几分之几,用除法计算。据此解答。
【解析】6÷36
=
=
6÷30
=
=
答:欢欢6天看了这本书的,果果6天看了这本书的。
33.23分米
【分析】从题意可知:剪成4分米、6分米或8分米都少1分米,这根彩带的长度比4、6、8的公倍数都少1,从“至少”可知,求最小公倍数。用分解质因数的方法求出4、6和8的全部公有的质因数和各自独立的质因数,它们连乘的积就是4、6和8的最小公倍数。最后用最小公倍数减去1就是这根彩带的长度。据此解答。
【解析】4=2×2
6=2×3
8=2×2×2
4、6和8的最小公倍数:2×2×2×3=24
24-1=23(分米)
答:这个长彩带的长度至少是23分米。
34.(1)2;3;1;(2)100平方厘米
【分析】(1)根据长方体的特征,要搭成长方体框架,则需要4条长、4条宽、4条高。已经有2条2厘米长的木棒,1条4厘米长的木棒,3条7厘米长的木棒,则还需要2条2厘米长的木棒,3条4厘米长的木棒,1条7厘米长的木棒;
(2)根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据即可求出彩纸的面积。
【解析】(1)还需要2根2厘米长的小棒、3根4厘米长的小棒、1根7厘米长的小棒。
(2)(7×2+7×4+2×4)×2
=(14+28+8)×2
=50×2
=100(平方厘米)
答:至少需要100平方厘米彩纸。
35.5棵
【分析】21棵树有20个间隔,每个间隔长4米,一共植树长度为20×4=80(米)。由每隔4米改成每隔5米,需要求出4和5的最小公倍数,看看已经植树的米数里有几个4和5的最小公倍数,再加上1,就是不必要拔掉的树的棵数。据此解答即可。
【解析】4×(21-1)
=4×20
=80(米)
4和5的最小公倍数是20
80÷20=4(个)
4+1=5(棵)
答:有5棵树苗不必拔掉。
【点评】明确原间隔数和新的间隔数,求出两者的公倍数,确定有多少棵树无需移动。
36.(1)
(2)没有;理由见详解
【分析】(1)用科技类图书占图书总数的分率-工具类图书占图书种类的分率,即可求出工具类图书比科技类图书少的部分占图书总数的分率。
(2)把图书种类看作单位“1”,用科技书占图书总数的分率加上文学类占图书总数的分率加上工具书图书占总数的分率,如果结果等于1,说明李老师统计完所有的图书种类;如果小于1,说明李老师没有统计完所有的图书种类;据此解答。
【解析】(1)-=
答:工具类图书比科技类图书少的部分占图书总数的。
(2)++
=+
=
<1,李老师没有统计完所有的图书种类。
答:李老师没有统计完所有的图书种类。
37.48厘米;6块
【分析】先找出24和16的最小公倍数,得出边长最短的长度是多少,然后再求出需要多少块木版年画。
【解析】
所以24和16的最小公倍数为:
48÷24=2
48÷16=3
2×3=6(块)
答:边长最短是48厘米,需要6块木板年画。
38.;
【分析】用流入大海的泥沙除以泥沙总量,求出每年泥沙总量的几分之几会流入大海;再把泥沙总量看作单位“1”,用单位“1”减去流入大海的泥沙占总泥沙的分率,就是剩余泥沙占总量的分率。
【解析】12÷16=
1-=
答:每年泥沙总量的会流入大海,剩余泥沙占总量的。
39.(1)米(2)米
【分析】(1)小阳用去了米,欢欢用去了米,要求欢欢比小阳少用多少米,用()计算;
(2)小阳用去的长度加上欢欢用去的长度,再加上剩下的长度,所得结果即为这条绳子原来的长度。
【解析】(1)(米)
答:欢欢比小阳少用米。
(2)(米)
答:这根绳子原来长米。
40.6个
【分析】根据题目要求,香皂的块数42和牙膏的盒数36应该同时能被奖品的份数整除,求份数最大可以是几份,求出42和36的最大公因数即可,据此解答。
【解析】42=2×3×7
36=2×3×6
所以42和36的最大公因数是2×3=6
故这些东西最多能捆6个这样的奖品。
41.
【分析】把这些糯米的总重量看作单位“1”,用1分别减去芳芳用去其中的和林林用去其中的,所得结果即为这些糯米还剩下几分之几,据此解答。
【解析】
答:这些糯米还剩下。
42.甲吃了,乙吃了,丙吃了
【分析】把整个西瓜看作单位“1”, 乙和丙一共吃了这个西瓜的,用1减去即可求出甲吃了这个西瓜的几分之几;甲和乙一共吃了这个西瓜的,用1减去可以求出丙吃了这个西瓜的几分之几;用1减去甲和丙吃的分率,即可求出乙吃了西瓜的几分之几。
【解析】甲:
丙:
乙:
=1-
=
答:甲吃了这个西瓜的,乙吃了这个西瓜的,丙吃了这个西瓜的。
43.5分米;90块
【分析】先将微机室的长和宽的单位换算成分米,求出长和宽的最大公因数,就在正方形方砖的边长;再用微机室的长除以方砖的边长,求出方砖行数,用微机室的宽除以方砖的边长,求出方砖的列数,再用行数×列数,即可求出方砖的块数。
【解析】5米=50分米;4.5米=45分米
50=2×5×5
45=3×3×5
50和45的最大公因数是5;方砖的边长为5分米。
(50÷5)×(45÷5)
=10×9
=90(块)
答:应选择边长是5分米的正方形方砖比较合适,铺完这间微机室至少需要90块这样的方砖。
44.;;
【分析】以2个红旗、1个绿旗、3个蓝旗为1个周期。每个周期一共有(2+1+3=6)个旗子,用54÷6即可求出有9个周期,据此分别用2×9、1×9和3×9求出红旗、绿旗和蓝旗的个数,最后根据求一个数占另一个数的几分之几,用一个数除以另一个数,分别用三种颜色的旗子的数量除以旗子的总数,即可求出三种颜色的旗子各占总数的几分之几。
【解析】2+1+3
=3+3
=6(个)
54÷6=9(组)
红旗:2×9÷54
=18÷54
=
绿旗:1×9÷54=
蓝旗:3×9÷54
=27÷54
=
答:红旗各占总数的,绿旗各占总数的,蓝旗各占总数的。
45.61盏
【分析】读题可知,花灯的数量比2、3、5的公倍数多1,先求出2、3、5的最小公倍数,再用最小公倍数分别乘1、乘2、乘3……找到55~65之间的公倍数,加1即可。
【解析】2×3×5=30
30×2=60(盏)
60+1=61(盏)
答:一共有61盏花灯。
46.展区有地方展示其他作品。
【分析】将展区面积看作单位“1”,其中书法占,油画作品占,素描作品占,运用分数减法得出剩余区域所占的分数,据此可得出答案。
【解析】将画展展区面积看作单位“1”,则除了书法作品、油画作品、素描作品所占面积外,剩下的区域占比为:
即其他作品的展区占了画展展区的,即还有地方展示其他作品。
答:展区还有地方展示其他作品。
47.
【分析】求新鲜水果的质量约占运输物资总质量的几分之几,用新鲜水果的质量除以运输物资总质量,结果能约分的要约成最简分数。
【解析】70÷5800=
答:新鲜水果的质量约占运输物资总质量的。
48.(1)
(2)
(3)
【分析】(1)西红柿、辣椒占地面积,都是以长方形菜地面积为单位“1”,用辣椒面积占总面积分率减去西红柿占总面积分率,求出辣椒比西红柿多占菜地几分之几即可;
(2)长方形菜地面积为单位“1”,用单位“1”减去辣椒面积占总面积分率与西红柿占总面积分率,求出黄瓜占整块菜地的几分之几即可;
(3)药水的质量等于药与水的质量之和,用药的质量除以药水质量,求出药的质量占药水的质量的几分之几,注意单位换算。
【解析】(1)
答:辣椒比西红柿多占菜地。
(2)
答:黄瓜占整块菜地的。
(3)1.5千克=1500克
答:药的质量占药水的质量的。
【点评】本题考查分数加减法、分数与除法的关系,解答本题的关键是掌握题中的数量关系。
49.画图见详解,
【分析】由题意可知,将全班人数看作单位“1”,然后平均分成9份。最喜欢阅读文史类和科普类的人数占全班人数的,则最喜欢文学类的人数占全班人数的1-=。最喜欢文学类和科普类的人数占全班总数的,则最喜欢文史类的人数占全班人数的1-=。最喜欢科普类的人数占全班人数的1--=。据此解答。
【解析】根据分析画图如下:
文学类:1-=
文史类:1-=
科普类:1--=
答:最喜欢科普书的人数占全班人数的。
50.
【分析】将不可回收垃圾看成单位“1”,用单位“1”减去厨余垃圾、其他垃圾所占的分率即可求出有害垃圾所占的分率,据此解答。
【解析】1--
=-
=
答:有害垃圾占不可回收垃圾的。
51.(1)
(2)
【分析】(1)以荒漠化总面积为单位“1”,用1减去轻度荒漠化的分率,减去中度荒漠化的分率,即可求出重度荒漠化的分率。
(2)用轻度荒漠化的分率加上中度荒漠化的分率,再减去重度荒漠化的分率,即可求解。
【解析】(1)
答:重度荒漠化的面积约占荒漠化总面积的。
(2)
答:重度荒漠化的面积所占比例比轻度和中度荒漠化面积所占比例的和少。
52.
【分析】求一个数占另一个数的几分之几,用除法,用获奖女科学家人数除以女科学家候选人数,即可解答。
【解析】10÷235=
答:本届获奖的女科学家占被提名的女科学家的。
53.(1)
(2)
【分析】(1)用妈妈看了这本书的分率+爸爸比妈妈多看了这本书的,就是爸爸看了这本书的几分之几。
(2)用阳阳看了这本书的分率-妈妈看了这本书的分率,即可求出阳阳比妈妈多看了这本书的几分之几。
【解析】(1)+=
答:爸爸看了这本书的。
(2)-=
答:阳阳比妈妈多看了这本书的。
54.24人
【分析】根据题意,口令为3,4或6时,每个人都可以抱团成功,所以人数应该是3、4和6的公倍数,同时该公倍数应该在20和30之间,据此解答即可。
【解析】由分析可得:
3=1×3
4=2×2
6=2×3
3、4或6的最小公倍数是:2×2×3=12;
则3、4或6的公倍数有:12、24、36、48、60…
三个数的公倍数在20和30之间的为:24,所以有24人。
答:有24人在玩游戏。
55.60厘米;30块
【分析】由题意可知求出12厘米与10厘米的最小公倍数即可求出拼成的正方形的边长,因为是密铺,所以用拼成的正方形的面积除以长方形的地砖的面积,即可求出需要的块数。
【解析】12=2×2×3
10=2×5
所以12和10的最小公倍数是:2×2×3×5=60
即正方形的边长最小是60厘米,
60×60÷(12×10)
=3600÷120
=30(块)
答:这个正方形的边长最小是60厘米,铺这样的一个正方形图案需要30块砖。
56.
【分析】根据题意,求金星和天王星是八大行星的几分之几,用2除以8即可解答。
【解析】2÷8=
答:自转方向和公转方向不一致的行星占行星总数的。
【点评】此题考查了分数与除法的关系,要求学生掌握。
57.48人
【分析】求这个班有多少人参加队列表演,就是求16和12的公倍数,且小于50;根据求最小公倍数的方法:两个数的公有质因数的连乘积,就是这两个数的最小公倍数,据此解答。
【解析】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48,这个班有48人参加队列表演。
答:这个班有48人参加队列表演
58.会;15升
【分析】根据正方体体积=棱长×棱长×棱长,求出铁块体积,水槽长×宽×水面离槽口高度=水槽内剩余容积,比较铁块体积和水槽内剩余容积,确定是否会溢出,正方体铁块体积-水槽内剩余容积=溢出的水的体积,注意统一单位。
【解析】3×3×3=27(立方厘米)
5厘米=0.5分米
6×4×0.5=12(立方厘米)
27>12
27-12=15(立方分米)=15(升)
答:此时水槽的水会溢出,会溢出15升水。
59.24厘米;6个
【分析】裁成若干个同样大小的正方形,且没有剩余,裁成的正方形的最大边长就是长方形的长和宽的最大公因数,根据分解质因数的方法,把72和48分别分解质因数,这两个数的公有质因数的乘积就是它们的最大公因数;再根据长方形面积公式:面积=长×宽;正方形面积公式:面积=边长×边长,代入数据,求出长方形卡纸的面积和裁成的正方形面积,再用长方形面积÷正方形面积,即可求出可以裁成几个正方形。
【解析】72=2×2×2×3×3
48=2×2×2×2×3
72和48的最大公因数是:2×2×2×3=24
正方形的边长最长是24厘米。
72×48÷(24×24)
=3456÷576
=6(个)
答:裁成的正方形的边长最长是24厘米,可以裁成6个正方形。
60.(1)图见详解
(2)
【分析】(1)把这块菜地看作单位“1”,平均分成4份,取其中1份,即把长方形平均切割成4份,其中l份涂上颜色即可表示种植西红柿的面积占这块菜地的分率;同理,把这块菜地看作单位“1”,平均分成8份,取其中3份,即把长方形平均切割成8份,其中3份涂上颜色即可表示种植辣椒的面积占这块菜地的分率。
(2)根据分数的意义,把这块菜地看作单位“1”,用l减去种植西红柿的面积占这块菜地的分率和种植辣椒的面积占这块菜地的分率,即可求出种植油菜花的面积所占的分率。
【解析】(1)作图如下:
西红柿 辣椒
(2)1--
=-
=
答:油菜花占整块菜地的。
61.
【分析】求得晚上8时到第二天早上7时共睡觉的时间,以全天24小时为单位“1”,根据分数的意义,用睡觉的时间除以24,即得到睡觉的时间是全天的几分之几,据此解答。
【解析】晚八时到第二天早上七时共睡觉的时间:
12:00-8:00=4(小时)
7:00-0:00=7(小时)
7+4=11(小时)
11÷24=
答:他每天睡觉的时间是全天的。
62.9厘米;12个
【分析】求出长和宽的最大公因数就是剪成的最大正方形的边长,用长方形面积÷正方形面积=剪出的个数。
【解析】36和27的最大公因数是9,所以最大正方形的边长是9厘米;
36×27÷(9×9)
=972÷81
=12(张)
答: 正方形卡片边长最大是9厘米,可以剪出12张这样的正方形卡片。
63.(1)
(2)
(3)银牌数占所获奖牌总数的几分之几?
【分析】(1)中国取得的金牌数÷所获奖牌总数=中国取得的金牌数占所获奖牌总数的几分之几。
(2)(银牌数+铜牌数)÷所获奖牌总数=银牌和铜牌共占所获奖牌总数的几分之。
(3)答案不唯一,如银牌数占所获奖牌总数的几分之几?银牌数÷所获奖牌总数=银牌数占所获奖牌总数的几分之几。
【解析】(1)9÷15==
答:中国取得的金牌数占所获奖牌总数的。
(2)(4+2)÷15
=6÷15
=
=
答:银牌和铜牌共占所获奖牌总数的。
(3)银牌数占所获奖牌总数的几分之几?
4÷15=
答:银牌数占所获奖牌总数的。
64.2.6分米
【分析】正方体体积=棱长×棱长×棱长,据此求出正方体容器的容积,正方体容器的容积-铁球体积=水的体积,根据长方体的高=体积÷底面积,即可求出水深。
【解析】3×3×3-3.6
=27-3.6
=23.4(立方分米)
23.4÷(3×3)
=23.4÷9
=2.6(分米)
答:容器里的水深是2.6分米。
65.0.6立方分米
【分析】5升=5立方分米,14厘米=1.4分米,根据长方体的体积=长×宽×高,用2×2×1.4即可求出水和土豆的体积和,再减去水的体积,即可求出土豆的体积。
【解析】5升=5立方分米
14厘米=1.4分米
2×2×1.4-5
=5.6-5
=0.6(立方分米)
答:土豆的体积是0.6立方分米。
66.10138平方厘米
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(50×37+50×37+37×37)×2即可求出做一个这样的保温包至少需要的材料面积。
【解析】(50×37+50×37+37×37)×2
=(1850+1850+1369)×2
=5069×2
=10138(平方厘米)
答:做一个这样的保温包至少需要10138平方厘米的材料。
67.不需要
【分析】油箱里的汽油升数×每升汽油行驶距离=这箱汽油可行驶距离,与到趵突泉景区的距离比较即可。
【解析】19.5×8.5=165.75(千米)
165.75>160
答:他们到趵突泉中途不需要加油。
68.(1)150米
(2)1700平方米
(3)2500吨
【分析】(1)水位线的全长就是长方体底面周长,根据长方形周长=(长+宽)×2,列式解答即可;
(2)贴瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(3)根据长方体体积=长×宽×高,求出水的体积,水的体积×1立方米水的吨数=游泳池内水的吨数,列式解答即可。
【解析】(1)
(米)
答:它的全长是150米。
(2)
(平方米)
答:贴瓷砖的面积是1700平方米。
(3)(吨)
答:这个游泳池内的水有2500吨。
69.
【分析】根据题意,求一个数是另一个数的几分之几用除法计算,即10÷12。
【解析】
答:那么乌龟所用时间是兔子的。
70.6分米
【分析】根据题意,用长3分米、宽2分米的长方形瓷砖铺成一个正方形图案,那么正方形的边长是3和2的公倍数;求铺成的正方形图案最小的边长,就是求3和2的最小公倍数。
3和2是互质数,那么它们的最小公倍数是它俩的乘积,据此解答。
【解析】如图:
3和2的最小公倍数是:3×2=6
即正方形的边长至少是6分米。
答:铺成的图案边长至少是6分米。
【点评】本题考查最小公倍数的实际应用,利用求两个数的最小公倍数的方法解决问题。
71.72人
【分析】根据题意可知参加晚会的人数是不变的,一定是2、3、4的公倍数,那就先求出2、3、4的最小公倍数是:2×3×4=12,若安排12人一桌,那么一桌共需要饮料:12÷2+12÷3+12÷4=13瓶,而三种饮料共用了78瓶,所以一共有:78÷13=6桌,用一桌的12人乘6即得参加晚会的人数;据此解答。
【解析】2、3、4的最小公倍数是2×3×4=12。
12÷2+12÷3+12÷4
=6+4+3
=13(瓶)
12×(78÷13)
=12×6
=72(人)
答:参加晚会的总人数是72人。
【点评】此题主要是考查对公倍数的应用,先明白此题关键是参加会餐的人数是不变的,一定是2、3、4的公倍数。
72.72人
【解析】思路点拨:由题意可知参加晚会人数应是2、3、4的公倍数。
解:2、3、4的最小公倍数为12。
(瓶)
(人)
答:参加晚会的总人数是72人。
73.48人
【分析】如果按8人一组分正好分完,如果按12人一组分也正好分完。说明参加绘画兴趣班的学生数量正好是8和12的公倍数,先根据求一个数的倍数的方法,分别求出8和12的倍数,再找出这两个数的公倍数,并且这个公倍数的大小要满足在40~50之间。据此解答。
【解析】8的倍数:8、16、24、32、40、48…
12的倍数:12、24、36、48…
8和12的公倍数:24、48…
因为48介于40到50之间,所以参加绘画兴趣班的学生有48人。
答:五年级参加绘画兴趣班的学生有48人。
【点评】此题的解题关键是根据求两个数的公倍数的方法解决实际的问题。
74.6月30日
【分析】李奶奶每4天去一次,王奶奶每5天去一次,则她们再次在公园相遇需要经过的天数是4和5的最小公倍数。4和5的最小公倍数是20,则从6月10日经过20天后的日期就是她们再次在公园相遇的时间。
【解析】4和5是互质数,所以4和5的最小公倍数是4×5=20。
即经过20天她们会再次在公园相遇。
6月10日+20天=6月30日
答:下一次她们在公园相遇是6月30日。
【点评】本题考查了最小公倍数的灵活运用以及日期的推算。
75.22平方分米;16.5分米
【分析】把长方体的长、宽、高的数据代入到长方体的表面积公式:S=(a×b+a×h+b×h)×2中,计算出长方体的表面积,即是制作这个包装盒需要的硬纸板面积。根据长方体的特征,12条棱分为3组,每组4条棱的长度相等,由图形可知,所需彩带的长度等于两条长+两条宽+4条高再加上打结用的2.5分米,据此解答。
【解析】(3×2+2×1+3×1)×2
=(6+2+3)×2
=11×2
=22(平方分米)
3×2+2×2+1×4+2.5
=6+4+4+2.5
=16.5(分米)
答:制作这个包装盒需要22平方分米硬纸板,用彩带捆扎包装盒至少需要16.5分米的彩带。
【点评】此题考查的目的是理解掌握长方体的特征和长方体表面积的实际应用,关键是弄清如何捆扎的,确定是求哪几条棱的长度和;在计算时要分清需要计算几个长方形面的面积。
76.1800立方厘米
【分析】石头完全浸没在水里后,石头的体积=水面上升的体积,水面上升的体积可看作长为45厘米,宽为20厘米,高为(24-22)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【解析】45×20×(24-22)
=45×20×2
=900×2
=1800(立方厘米)
答:放入石头的体积是1800立方厘米。
【点评】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
77.(1)
(2)
【分析】(1)用母亲节礼物占零花钱的分率减父亲节礼物占零花钱的分率即可。
(2)把欢欢的零花钱总数看作单位“1”,用减法计算即可得欢欢的零花钱还能剩下几分之几。
【解析】(1)
=
=
答:母亲节礼物比父亲节礼物多用去欢欢零花钱的。
(2)
=
=
=
=
答:欢欢的零花钱还能剩下。
【点评】本题主要考查了分数加减法应用题,要细心计算。
78.750立方厘米
【分析】假山完全浸没在水里后,假山的体积=水面上升的体积,水面上升的体积可看作长为25厘米,宽为12厘米,高为(12.5-10)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【解析】25×12×(12.5-10)
=25×12×2.5
=300×2.5
=750(立方厘米)
答:这块假山的体积是750立方厘米。
【点评】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
79.林林
【分析】通过观察图形可知:折成的无盖长方体储物盒的长是(24-小正方形的边长×2)厘米,宽是(16-小正方形的边长×2)厘米,高是小正方形的边长。把储物盒的长、宽、高相乘,即可求出储物盒的容积。据此分别求出林林和小强设计的储物盒的容积,再比较大小即可。
【解析】林林:(24-3×2)×(16-3×2)×3
=(24-6)×(16-6)×3
=18×10×3
=540(立方厘米)
小强:(24-4×2)×(16-4×2)×4
=(24-8)×(16-8)×4
=16×8×4
=512(立方厘米)
540>512
答:林林的方案做成的长方体储物盒容积最大。
【点评】用长方形铁皮或正方形铁皮制成盒子(四个角上分别去掉一个相同的小正方形),盒子的长和宽要在铁皮的长和宽中去掉两个小正方形的边长,盒子的高是铁皮四个角去掉的小正方形的边长。
80.
【分析】把参加足球、游泳、创客社团的人数占五年级二班人数的分率相加,即可得解。
【解析】++
=
=
答:参加足球、游泳、创客社团的一共占本班学生的。
【点评】本题主要考查了分数加法应用题,要细心计算。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
