2024-2025学年浙江省杭州市拱墅区八年级下册数学期末模拟练习(含答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州市拱墅区八年级下册数学期末模拟练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 653.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 22:51:25 | ||
图片预览



文档简介
2024-2025学年浙江省杭州市拱墅区八年级下册数学期末模拟练习
一、选择题(共10小题,每小题3分,共30分)
1.能使有意义的x的取值范围是( )
A. B. C. D.
2.已知一个菱形的两条对角线长分别是12,,则这个菱形的面积为( )
A. B. C. D.36
3.一元二次方程的解为( )
A. B. C. D.
4.如图,在中,点M是AB延长线上的一点,若,则的度数是( )
A. B. C. D.
5.下列各式计算正确的是( )
A. B. C. D.
6. 若点A(-3,y1),B(-2,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y3<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
7.中国明代数学家程大位编写的数学名著<算法统宗>中记载道:“平地秋千未起,路板一尺离地:送行二步与人齐,五尺人高曾记:仕女佳人争蹴,终朝笑语欢姐;良工高士素好奇,算出索长有几?”其大意是:“秋千静止的时候,踏板离地1尺,将它往前推送两步(约为10尺)时,此时踏板升高,离地5尺,秋千的绳累始终拉的很直,问秋干绳索有多长?”如图,若设秋千的绳索OA长为x尺,可列方程为( )
A. B.
C. D.
8.黑板上有一个计算方差的算式:,根据上式的信息.下列结论不正确的是( )
A.平均数为8 B.添加一个数8后方差不变
C.添加一个数8后标准差变小 D.
9.将正方形①②③按如图所示的方式摆放,若正方形①②的面积分别是81和144,则正方形③的边长为( ).
A.225 B.63 C.50 D.15
10.已知关于的方程有两个相等实数根.若在直角坐标系中,点在直线l:y上,点在直线下方,则PQ的最小值为( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.比较大小: (填“”、“”或“”)
12.若函数的图象经过点和,则的值为 .
13. 小芳参加校艺术节独唱比赛,其中唱功、表情、动作三个方面的得分分别为90分,80分,95分,综合成绩中唱功占,表情占,动作占,则小芳的综合成绩为 分.
14.若a是方程2x2﹣x﹣5=0的一个根,则代数式2a﹣4a2+1的值是 .
15.门窗是中国古代木构架建筑上的重要组成部分.如图①所示是一款冰裂纹窗格,图②是窗格中的部分图案.其中是五边形的4个外角,若,则的度数是 °.
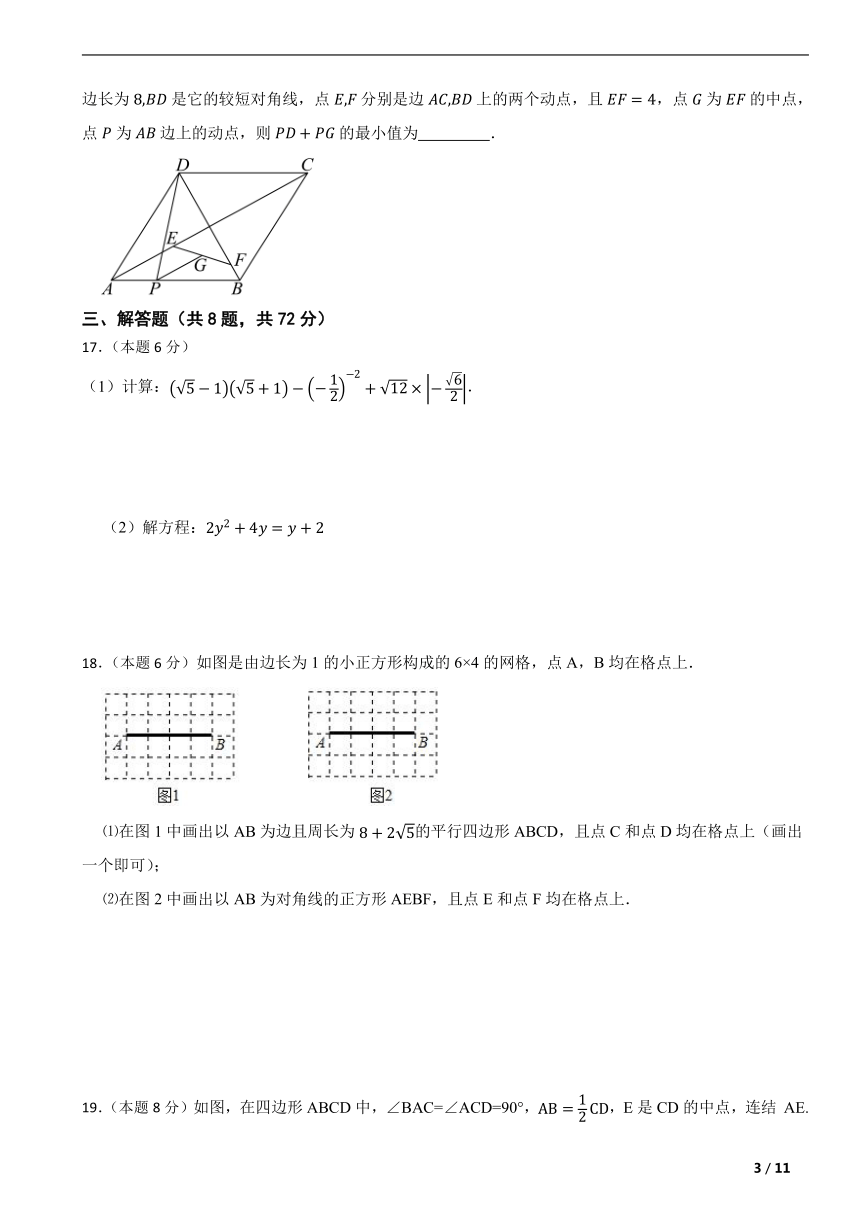
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
三、解答题(共8题,共72分)
17.(本题6分)
(1)计算:.
(2)解方程:
18.(本题6分)如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.
⑴在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);
⑵在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.
19.(本题8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,,E是CD的中点,连结 AE.
(1)求证:四边形ABCE 是平行四边形.
(2)若AC=4,AD=4,求四边形 ABCE 的面积.
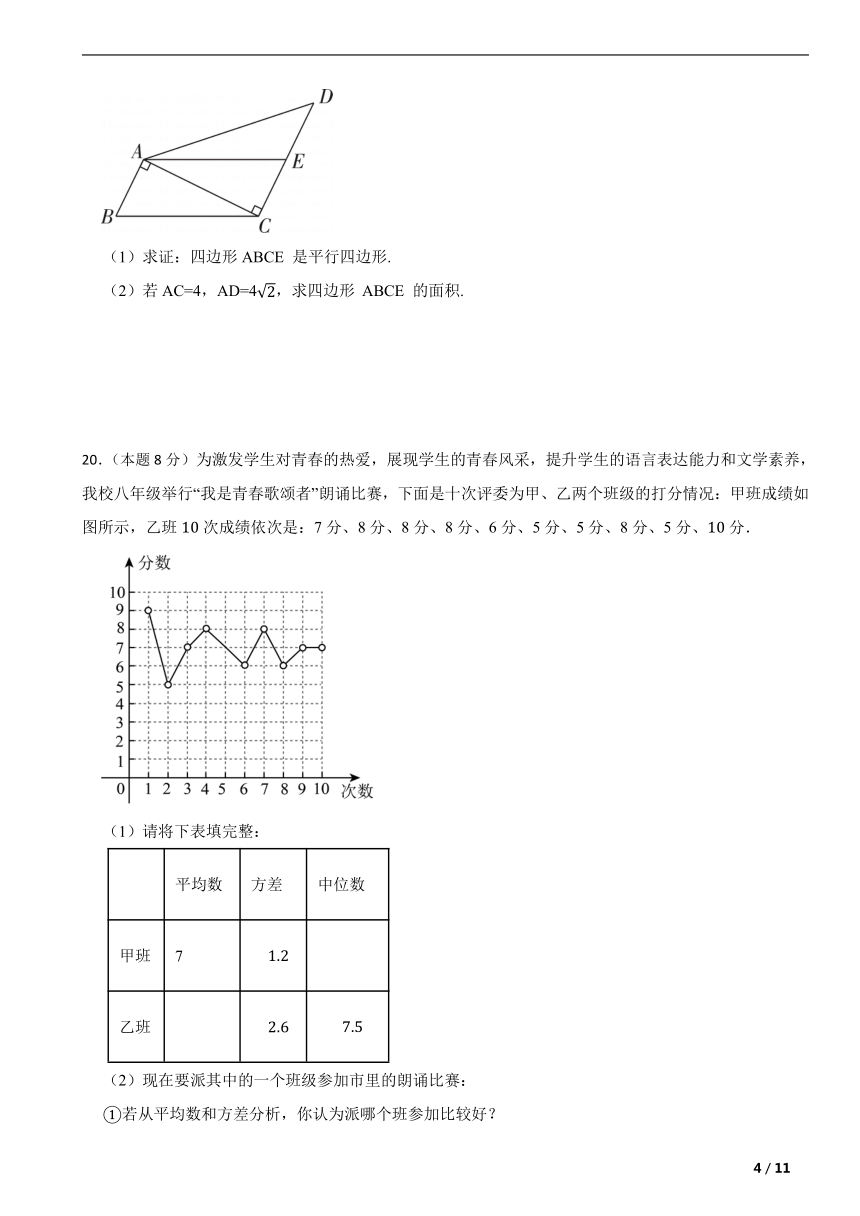
20.(本题8分)为激发学生对青春的热爱,展现学生的青春风采,提升学生的语言表达能力和文学素养,我校八年级举行“我是青春歌颂者”朗诵比赛,下面是十次评委为甲、乙两个班级的打分情况:甲班成绩如图所示,乙班次成绩依次是:7分、8分、8分、8分、6分、5分、5分、8分、5分、分.
(1)请将下表填完整:
平均数 方差 中位数
甲班 7
乙班
(2)现在要派其中的一个班级参加市里的朗诵比赛:
若从平均数和方差分析,你认为派哪个班参加比较好?
若从平均数和中位数分析,你认为派哪个班参加比较好?
21(本题10分)设函数,函数(,,b是常数,;
(1)若函数和函数的图象交于,两点.
①求函数,的表达式.
②当时,比较与的大小(直接写出结果).
(2)若点在函数的图象上,点C先向下平移3个单位,再向左平移6个单位,得到点D,点D恰好落在函数的图象上,求n的值.
22.(本题10分)
背景 今年的春节动画电影“哪吒2”火爆影院,吸引了大量市民观影,各大影院积极推送.
素材1 某影院正月初一的票房收入费用为6万元,随着观影人数的不断增多,正月初三的票房收入达到8.64万元.
素材2 随着电影的爆火,某商家生产了一批“哪吒”手办进行销售,已知一个“哪吒”手办的生产成本为30元,经销一段时间后发现:当该款手办售价定为65元/个时,平均每天售出30个;售价每降低1元,平均每天多售出3个,该店计划下调售价使平均每天的销售利润为1500元.
问题解决
任务1 求从正月初一到正月初三该影院票房收入的天平均增长率.
任务2 根据素材2,为了推广该款“哪吒”手办,且尽可能多的减少库存,求下调后每个手办的售价.
任务3 根据素材2,平均每天能否获利2100元?若能,请求出每个手办应降价多少元;若不能,请说明理由.
23.(本题12分)已知反比例函数.
(1)若反比例函数的图象经过点,求的值.
(2)若点,在函数的图象上,比较,,的大小.
(3)反比例函数,如果,且,函数的最大值比函数的最大值大,函数的最小值比函数的最小值大,试证明.
24.(本题12分)综合与实践
折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为完美矩形.
(1)操作发现:
如图①,将纸片按所示折叠成完美矩形,若的面积为,,则此完美矩形的边长 ,面积为 .
(2)类比探究:
如图②,将平行四边形纸片按所示折叠成完美矩形,若平行四边形的面积为,,则完美矩形的周长为 .
(3)拓展延伸:
如图③,将平行四边形纸片按所示折叠成完美矩形,若,,求此完美矩形的周长为多少.
参考答案
1.B
2.B
3.C
4.D
5.C
6.C
7.D
8.B
9.D
10.A
11.
12.2
13.90
14.-9
15.
16.
17.(1);(2)
18.解:⑴如图1中,四边形ABCD即为所求;
⑵如图2中,正方形AEBF即为所求.
19.(1)证明:∵∠BAC=∠ACD=90°
∴AB∥CE
∵AB=CD,点E是CD的中点
∴AB=CE
∴四边形ABCE是平行四边形
(2)解:∵∠ACD=90°,AC=4,AD=
∴CD==4
∴S△ACD=×4×4=8
∵点E是CD的中点
∴S△ACE=S△AED
∵四边形ABCE是平行四边形,AC是其对角线
∴S△ABC=S△ACE
∴S四边形ABCE=2S△ACE=S△ACD=8
20.(1)答:补全表格如下:
平均数 方差 中位数
甲班 7 7
乙班 7
(2)解:从平均数和方差分析,甲乙的平均数一样,但甲的方差较小,较稳定;故派甲班参加比较好;
从平均数和中位数分析,甲乙的平均数一样,但乙班的中位数较大,故派乙班参加比较好;
21.(1)解:①把点代入,
,
解得:,
∴函数的表达式为,
把点代入,解得,
把点,点代入,
,
解得,
∴函数的表达式为;
②<
(2)解:由平移,可得点D坐标为,
∴,
解得:
22.任务1:从正月初一到正月初三该影院票房收入的天平均增长率为;任务2:下调后每个手办的售价为50元;任务3:不能
23.(1)解:将点坐标代入得:,
解得:,
(2)解:中,
反比例函数图象分布在第一三象限,随的增大而减小,
,
,,,
;
(3)证明:反比例函数,如果,且,
随的增大而增大,则的最大值为,最小值为,
反比例函数如果,且,
随的增大而减小,则的最大值为,最小值为,
函数的最大值比函数的最大值大,函数的最小值比函数的最小值大,
,,
,,
得:,
.
24.(1);
(2)16
(3)解:连接,如图所示:
由折叠可得:点E和G分别是AB和CD的中点,
∴AE=DG,AE∥DG,
∴四边形AEGD是平行四边形,
∴AD=EG=HF,
∵EF:EH=3:4,
∴设,则,
∴在中,,
∴,
解得:,
∴,,
∴矩形的周长.
1 / 1
一、选择题(共10小题,每小题3分,共30分)
1.能使有意义的x的取值范围是( )
A. B. C. D.
2.已知一个菱形的两条对角线长分别是12,,则这个菱形的面积为( )
A. B. C. D.36
3.一元二次方程的解为( )
A. B. C. D.
4.如图,在中,点M是AB延长线上的一点,若,则的度数是( )
A. B. C. D.
5.下列各式计算正确的是( )
A. B. C. D.
6. 若点A(-3,y1),B(-2,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y3<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
7.中国明代数学家程大位编写的数学名著<算法统宗>中记载道:“平地秋千未起,路板一尺离地:送行二步与人齐,五尺人高曾记:仕女佳人争蹴,终朝笑语欢姐;良工高士素好奇,算出索长有几?”其大意是:“秋千静止的时候,踏板离地1尺,将它往前推送两步(约为10尺)时,此时踏板升高,离地5尺,秋千的绳累始终拉的很直,问秋干绳索有多长?”如图,若设秋千的绳索OA长为x尺,可列方程为( )
A. B.
C. D.
8.黑板上有一个计算方差的算式:,根据上式的信息.下列结论不正确的是( )
A.平均数为8 B.添加一个数8后方差不变
C.添加一个数8后标准差变小 D.
9.将正方形①②③按如图所示的方式摆放,若正方形①②的面积分别是81和144,则正方形③的边长为( ).
A.225 B.63 C.50 D.15
10.已知关于的方程有两个相等实数根.若在直角坐标系中,点在直线l:y上,点在直线下方,则PQ的最小值为( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.比较大小: (填“”、“”或“”)
12.若函数的图象经过点和,则的值为 .
13. 小芳参加校艺术节独唱比赛,其中唱功、表情、动作三个方面的得分分别为90分,80分,95分,综合成绩中唱功占,表情占,动作占,则小芳的综合成绩为 分.
14.若a是方程2x2﹣x﹣5=0的一个根,则代数式2a﹣4a2+1的值是 .
15.门窗是中国古代木构架建筑上的重要组成部分.如图①所示是一款冰裂纹窗格,图②是窗格中的部分图案.其中是五边形的4个外角,若,则的度数是 °.
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
三、解答题(共8题,共72分)
17.(本题6分)
(1)计算:.
(2)解方程:
18.(本题6分)如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.
⑴在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);
⑵在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.
19.(本题8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,,E是CD的中点,连结 AE.
(1)求证:四边形ABCE 是平行四边形.
(2)若AC=4,AD=4,求四边形 ABCE 的面积.
20.(本题8分)为激发学生对青春的热爱,展现学生的青春风采,提升学生的语言表达能力和文学素养,我校八年级举行“我是青春歌颂者”朗诵比赛,下面是十次评委为甲、乙两个班级的打分情况:甲班成绩如图所示,乙班次成绩依次是:7分、8分、8分、8分、6分、5分、5分、8分、5分、分.
(1)请将下表填完整:
平均数 方差 中位数
甲班 7
乙班
(2)现在要派其中的一个班级参加市里的朗诵比赛:
若从平均数和方差分析,你认为派哪个班参加比较好?
若从平均数和中位数分析,你认为派哪个班参加比较好?
21(本题10分)设函数,函数(,,b是常数,;
(1)若函数和函数的图象交于,两点.
①求函数,的表达式.
②当时,比较与的大小(直接写出结果).
(2)若点在函数的图象上,点C先向下平移3个单位,再向左平移6个单位,得到点D,点D恰好落在函数的图象上,求n的值.
22.(本题10分)
背景 今年的春节动画电影“哪吒2”火爆影院,吸引了大量市民观影,各大影院积极推送.
素材1 某影院正月初一的票房收入费用为6万元,随着观影人数的不断增多,正月初三的票房收入达到8.64万元.
素材2 随着电影的爆火,某商家生产了一批“哪吒”手办进行销售,已知一个“哪吒”手办的生产成本为30元,经销一段时间后发现:当该款手办售价定为65元/个时,平均每天售出30个;售价每降低1元,平均每天多售出3个,该店计划下调售价使平均每天的销售利润为1500元.
问题解决
任务1 求从正月初一到正月初三该影院票房收入的天平均增长率.
任务2 根据素材2,为了推广该款“哪吒”手办,且尽可能多的减少库存,求下调后每个手办的售价.
任务3 根据素材2,平均每天能否获利2100元?若能,请求出每个手办应降价多少元;若不能,请说明理由.
23.(本题12分)已知反比例函数.
(1)若反比例函数的图象经过点,求的值.
(2)若点,在函数的图象上,比较,,的大小.
(3)反比例函数,如果,且,函数的最大值比函数的最大值大,函数的最小值比函数的最小值大,试证明.
24.(本题12分)综合与实践
折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为完美矩形.
(1)操作发现:
如图①,将纸片按所示折叠成完美矩形,若的面积为,,则此完美矩形的边长 ,面积为 .
(2)类比探究:
如图②,将平行四边形纸片按所示折叠成完美矩形,若平行四边形的面积为,,则完美矩形的周长为 .
(3)拓展延伸:
如图③,将平行四边形纸片按所示折叠成完美矩形,若,,求此完美矩形的周长为多少.
参考答案
1.B
2.B
3.C
4.D
5.C
6.C
7.D
8.B
9.D
10.A
11.
12.2
13.90
14.-9
15.
16.
17.(1);(2)
18.解:⑴如图1中,四边形ABCD即为所求;
⑵如图2中,正方形AEBF即为所求.
19.(1)证明:∵∠BAC=∠ACD=90°
∴AB∥CE
∵AB=CD,点E是CD的中点
∴AB=CE
∴四边形ABCE是平行四边形
(2)解:∵∠ACD=90°,AC=4,AD=
∴CD==4
∴S△ACD=×4×4=8
∵点E是CD的中点
∴S△ACE=S△AED
∵四边形ABCE是平行四边形,AC是其对角线
∴S△ABC=S△ACE
∴S四边形ABCE=2S△ACE=S△ACD=8
20.(1)答:补全表格如下:
平均数 方差 中位数
甲班 7 7
乙班 7
(2)解:从平均数和方差分析,甲乙的平均数一样,但甲的方差较小,较稳定;故派甲班参加比较好;
从平均数和中位数分析,甲乙的平均数一样,但乙班的中位数较大,故派乙班参加比较好;
21.(1)解:①把点代入,
,
解得:,
∴函数的表达式为,
把点代入,解得,
把点,点代入,
,
解得,
∴函数的表达式为;
②<
(2)解:由平移,可得点D坐标为,
∴,
解得:
22.任务1:从正月初一到正月初三该影院票房收入的天平均增长率为;任务2:下调后每个手办的售价为50元;任务3:不能
23.(1)解:将点坐标代入得:,
解得:,
(2)解:中,
反比例函数图象分布在第一三象限,随的增大而减小,
,
,,,
;
(3)证明:反比例函数,如果,且,
随的增大而增大,则的最大值为,最小值为,
反比例函数如果,且,
随的增大而减小,则的最大值为,最小值为,
函数的最大值比函数的最大值大,函数的最小值比函数的最小值大,
,,
,,
得:,
.
24.(1);
(2)16
(3)解:连接,如图所示:
由折叠可得:点E和G分别是AB和CD的中点,
∴AE=DG,AE∥DG,
∴四边形AEGD是平行四边形,
∴AD=EG=HF,
∵EF:EH=3:4,
∴设,则,
∴在中,,
∴,
解得:,
∴,,
∴矩形的周长.
1 / 1
同课章节目录
