小升初《圆与扇形》专项训练(含解析)
文档属性
| 名称 | 小升初《圆与扇形》专项训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 13:50:19 | ||
图片预览



文档简介
登录二一教育在线组卷平台 助您教考全无忧
小升初《圆与扇形》专项训练
一、单选题
1.圆的大小与圆的( )无关。
A.半径 B.直径 C.圆心
2.在一个边长是4dm的正方形内画一个最大的圆,这个圆的周长是( )dm。
A.12.56 B.6.28 C.10.28 D.25.12
3. ( P19第7题变式)如图是马戏团表演时用的独轮车,车轴安装在车轮的圆心处,车才能平稳运行,这是利用了( )。
A.圆是轴对称图形 B.圆的半径都相等 C.圆心决定圆的位置
4.画一个周长为 18.84 厘米的圆,则圆规两脚问的距离是( )厘米。
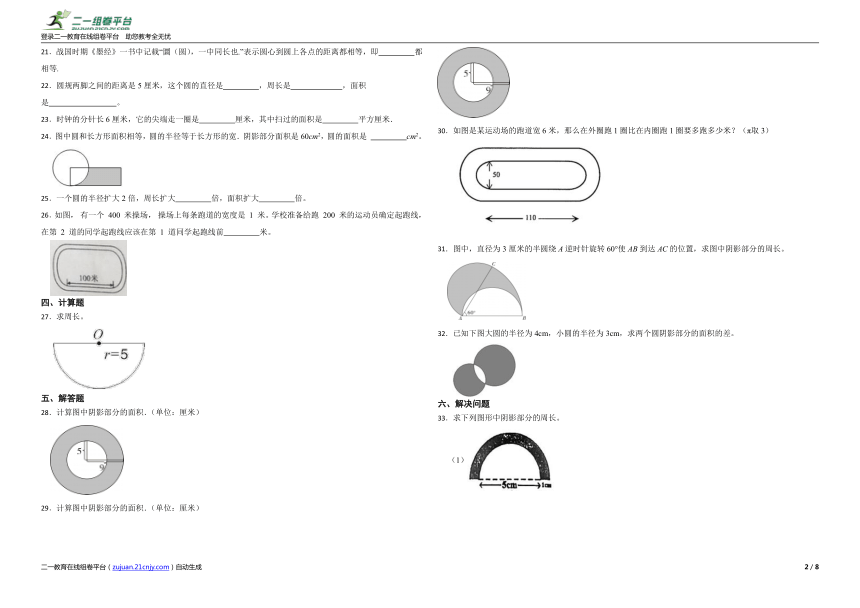
A.2 B.3 C.4 D.6
5.如果圆的半径是6厘米,那么它的面积是( )平方厘米.
A.6π B.12π C.36π D.24π
6.大圆内有两个小圆(如图),大圆的周长与两个小圆的周长之和相比( )。
A.大圆的周长长
B.同样长
C.两个小圆的周长之和长
7.用一个长5厘米,宽3厘米的长方形纸片剪一个最大的圆,这个圆的周长是( )
A.9.42厘米 B.15.7厘米
C.4.71厘米 D.9.42平方厘米
8.淘气在探索圆的面积计算公式时,把一个圆剪拼成一个长3.14厘米的近似长方形,这个圆的半径和面积是( )。
A.1厘米;3.14平方厘米 B.1厘米;6.28平方厘米
C.2厘米;12.56平方厘米 D.3厘米;9.42平方厘米
9.下面图( )中的阴影部分可能是圆心角为100°的扇形.
A. B.
C. D.
10.用四根同样长的绳子围成等边三角形、长方形、正方形和圆形,( )的面积最大。
A.等边三角形 B.长方形 C.正方形 D.圆形
二、判断题
11.圆的半径从6dm增加到9dm,圆的面积增加了45dm2。( )
12.小圆直径等于大圆的半径,大圆的周长是小圆的周长2倍,面积是小圆的4倍。( )
13.半径为2cm的圆的周长和面积相等。( )
14.半圆的周长可以用πr+2r=(π+2)r计算。( )
15.在同一平面内,任意两个圆都成轴对称。( )
16.一个半圆的周长是20.56分米,这个半圆的面积是41.12平方分米。( )
三、填空题
17.画圆时,圆规两脚尖之间的距离是3cm,所画成的圆周长是 厘米.
18.正方形的边长是10㎝,在它之中画一个最大的圆,圆的半径是 ㎝。
19.如图所示,将一个半径为r的圆分成若干等份,可以拼成一个近似的平行四边形。
圆周长的一半等于平行四边形的 。
平行四边形的高等于圆的 。
平行四边形的面积=底×高= × 。
圆的面积= 。
20.用圆规画一个圆,圆规两脚间的距离是4厘米,这个圆的周长是 厘米,面积是 平方厘米。
21.战国时期《墨经》一书中记载“圜(圆),一中同长也.”表示圆心到圆上各点的距离都相等,即 都相等.
22.圆规两脚之间的距离是5厘米,这个圆的直径是 ,周长是 ,面积是 。
23.时钟的分针长6厘米,它的尖端走一圈是 厘米,其中扫过的面积是 平方厘米.
24.图中圆和长方形面积相等,圆的半径等于长方形的宽.阴影部分面积是60cm2,圆的面积是 cm2。
25.一个圆的半径扩大2倍,周长扩大 倍,面积扩大 倍。
26.如图, 有一个 400 米操场, 操场上每条跑道的宽度是 1 米。学校准备给跑 200 米的运动员确定起跑线,在第 2 道的同学起跑线应该在第 1 道同学起跑线前 米。
四、计算题
27.求周长。
五、解答题
28.计算图中阴影部分的面积.(单位:厘米)
29.计算图中阴影部分的面积.(单位:厘米)
30.如图是某运动场的跑道宽6米,那么在外圈跑1圈比在内圈跑1圈要多跑多少米?(π取3)
31.图中,直径为3厘米的半圆绕A逆时针旋转60°使AB到达AC的位置,求图中阴影部分的周长。
32.已知下图大圆的半径为4cm,小圆的半径为3cm,求两个圆阴影部分的面积的差。
六、解决问题
33.求下列图形中阴影部分的周长。
(1)
(2)
34.一辆自行车轮胎的外半径是0.36米,如果每分钟转100周,通过一座1千米长的大桥需要几分钟?(得数保留一位小数)
35.一块长方形草地的一个角上有一根木桩,木桩上拴着一只羊,如果拴羊的绳子长4 m,这只羊无法吃到的草地面积是多少平方米?
七、口算与估算
36.直接写得数。(π取3.14)
5π= 25π=
8π= 6π=
9π= 20π= 7π= 36π=
八、图形计算
37.某款车上安装的雨刷是在一个摆臂上安装胶条,如下图所示,雨刷摆臂的长度是60cm,胶条的长度是45cm,摆动角度是180°,那么这种雨刷能刷到的面积是多少
答案解析部分
1.【答案】C
【解析】【解答】解:圆的大小与圆的圆心无关。
故答案为:C
【分析】圆心决定圆的位置,圆的直径或半径长度决定圆的大小。
2.【答案】A
【解析】【解答】解:3.14×4=12.56(分米)
故答案为:A。
【分析】这个圆的周长=π×直径;其中,直径=正方形的边长。
3.【答案】B
【解析】【解答】解:车轴安装在车轮的圆心处,车才能平稳运行,这是因为圆的半径都相等,当车轴在圆心时,车轮上各点到车轴的距离相等,能保证车轮平稳转动。
故答案为:B。
【分析】明确圆的基本性质,圆的半径是从圆心到圆上任意一点的距离,车轴在圆心时,车轮滚动过程中,车轮上各个点到车轴的距离始终保持不变,这样就能使车平稳运行,因此B选项正确。
4.【答案】B
【解析】【解答】解:18.84÷3.14÷2=6÷2=3(厘米);
故答案为:B。
【分析】 圆规两脚问的距离是指所画圆的半径,利用题目给出圆的周长,根据圆的周长=2πr,可以求出圆的半径r。
5.【答案】C
【解析】【解答】6×6×π=36π
故答案为:C
【分析】圆的面积=圆周率×半径×半径.
6.【答案】B
【解析】【解答】解:设大圆直径是2,则小圆直径是1。
大圆周长:3.14×2=6.28;
两个小圆周长:3.14×1×2=6.28;
所以大圆的周长与两个小圆的周长之和相等。
故答案为:B。
【分析】圆周长公式:C=πd。两个小圆的直径和等于大圆的直径,所以大圆周长与两个小圆周长之和相等。
7.【答案】A
【解析】【解答】解:3.14×3=9.42(厘米),
答:这个圆的周长是9.42厘米.
故选:A.
【分析】如图所示,所剪的最大圆的直径等于长方形的宽,长方形的宽已知,从而可以求出其周长.
8.【答案】A
【解析】【解答】解:半径:3.14×3.14=1(厘米),
面积:3.14×12=3.14(平方厘米)。
故答案为:A。
【分析】拼成近似长方形的长相当于圆周长的一半,所以用长方形的长除以3.14即可求出半径,然后根据圆面积公式计算面积。圆面积公式:S=πr2。
9.【答案】A
【解析】【解答】A、这个阴影部分可能是圆心角为100°的扇形;
B、这个圆心角接近一个平角,故不可能是圆心角为100°的扇形;
C、这个圆心角小于直角,故不可能是圆心角为100°的扇形;
D、这个角不是圆心角。
故答案为:A。
【分析】圆心角是指以顶点为圆心,以两条半径为边的角。这个圆心角与它所对的弧围成的图形就是扇形。根据这个定义结合各选项看哪个图形的圆心角可能是100°。
10.【答案】D
【解析】【解答】设这根绳子的长度为8,则
等边三角形:
8÷3≈2.7
等边三角形的面积一定小于与它等底等高的平行四边形的面积的一半,与它等底等高的平行四边形的面积的一半一定小于2.7×2.7÷2=7.29÷2=3.645.
长方形:
8÷2=4
当长方形的长与宽都取整数时,它的长与宽分别是3和1、2和2,当长与宽都是2时变成正方形。
3×1=3
2×2=4
圆:
8÷3.14÷2≈1.3
3.14×1.32 =5.3066
综合各种图形的面积可知,用同样长的绳子围成的上述各种图形中,圆的面积最大。
故答案为:D。
【分析】设这根绳子的长为一个定值,根据各种图形的周长公式与面积公式,分别计算它们的面积,最后比较大小即可。
11.【答案】错误
【解析】【解答】解:3.14×9×9-3.14×6×6
=254.34-113.04
=141.3(平方分米)
故答案为:错误。
【分析】π×9的平方=增加后的面积;π×6的平方=增加前的面积;增加后的面积-增加前的面积=增加的面积。
12.【答案】正确
【解析】【解答】解:小圆直径等于大圆的半径,大圆的周长是小圆的周长2倍,面积是小圆的4倍,原题干说法正确。
故答案为:正确。
【分析】在同圆或等圆中,圆的直径=半径×2,圆的周长=π×半径×2,圆的面积=π×半径2,所以大圆的周长是小圆的周长2倍,面积是小圆的4倍。
13.【答案】错误
【解析】【解答】解:圆的周长和面积无法比较大小,原题说法错误.
故答案为:错误
【分析】周长是围成圆一周曲线的长度,面积是指圆的大小,周长和面积的意义不同,无法比较大小.
14.【答案】正确
【解析】【解答】解:半圆的周长可以用πr+2r=(π+2)r计算。原题说法正确。
故答案为:正确。
【分析】πr表示圆周长的一半,2r是直径,半圆的周长就包括圆周长的一半和一条直径的长度。
15.【答案】错误
【解析】【解答】两个圆成轴对称,这两个圆必须完全相同.任意两个圆,它们的半径并不一定相等。半径不等,这两个圆就不可能成轴对称.
【分析】在同一平面内,不相同的两个圆不能成轴对称,只有等圆才可能成轴对称.
16.【答案】错误
【解析】【解答】解:设这个半圆的半径是x分米,
3.14×2x÷2+2x=20.56
3.14x+2x=20.56
5.14x=20.56
x=20.56÷5.14
x=4
面积:3.14×42÷2
=3.14×16÷2
=25.12(平方分米)
原题计算错误。
故答案为:错误
【分析】半圆的周长包括所在圆的周长的一半和直径的长度,设半径是x分米,根据周长包括的长度列出方程,解方程求出半径,然后根据圆面积公式计算半圆的面积。
17.【答案】18.84
【解析】【解答】解:3.14×(3×2)
=3.14×6
=18.84(厘米)
故答案为:18.84。
【分析】画圆时,圆规两脚尖之间的距离就等于所画圆的半径,根据圆的周长公式:C=2πr,把数据代入公式解答即可求出圆的周长。
18.【答案】5
【解析】【解答】10÷2=5(cm).
故答案为:5.
【分析】在一个正方形之中画一个最大的圆,圆的半径是正方形边长的一半,据此列式解答.
19.【答案】底;半径;πr;r;πr2
【解析】【解答】解:圆周长的一半等于平行四边形的底。平行四边形的高等于圆的半径。平行四边形的面积=底×高=πr×r。圆的面积=πr2。
故答案为:底;半径;πr;r;πr2。
【分析】从图上可以看出,将一个半径为r的圆分成若干等份,可以拼成一个近似的平行四边形,此时平行四边形的底就是圆周长的一半,高就是圆的半径;根据平行四边形面积计算公式“ 平行四边形的面积=底×高 ”,因此根据图中信息可以延伸为πr×r,即圆的面积=πr2。
20.【答案】25.12;50.24
【解析】【解答】解:周长:4×2×3.14
=8×3.14
=25.12(厘米);
42×3.14
=16×3.14
=50.24(平方厘米);
故答案为:25.12;50.24。
【分析】圆规两脚之间的距离就是圆的半径,圆周长=半径×2×π,圆面积=半径2×π,据此代入数值计算即可。
21.【答案】半径
【解析】【解答】解:表示圆心到圆上各点的距离都相等,即半径都相等。
故答案为:半径。
【分析】根据半径的定义作答即可。
22.【答案】10厘米;31.4厘米;78.5平方厘米
【解析】【解答】解:5×2=10(厘米)
3.14×10=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)。
故答案为:10厘米;31.4厘米;78.5平方厘米。
【分析】圆的直径=半径×2,圆的周长=π×直径;圆的面积=π×半径2。
23.【答案】37.68;113.04
【解析】【解答】解:2×3.14×6=37.68(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
答:它的尖端走一圈是37.68厘米,其中扫过的面积是113.04平方厘米.
故答案为:37.68;113.04.
【分析】分针一小时正好走一圈,针尖走过的路线正好画成了一个圆,求尖端走了一圈的长度,实际是求半径是6厘米的圆的周长是多少,它走一圈扫过的面积就是半径为6厘米的圆的面积,可利用圆的周长公式、圆的面积公式解答即可.
24.【答案】80
【解析】【解答】解:60÷3×4
=20×4
=80(cm2)
故答案为:80。
【分析】从图中可以看出,圆剩下的面积=长方形中的阴影部分面积,那么长方形和圆重合部分的面积=阴影部分的面积÷3,所以圆的面积=长方形和圆重合部分的面积×4,据此作答即可。
25.【答案】2;4
【解析】【解答】 一个圆的半径扩大2倍,周长扩大2倍,面积扩大4倍.
故答案为:2;4.
【分析】根据圆的周长公式:C=2πr,当半径扩大a倍,周长也扩大a倍;根据圆的面积公式:S=πr2,当半径扩大a倍,面积扩大a2倍,据此解答.
26.【答案】3.14
【解析】【解答】解:3.14×1=3.14(米)
故答案为:3.14。
【分析】首先,明确赛跑距离是在直道与弯道共同构成的200米。对于200米的赛跑,由于是在环形跑道上,实际上涉及到的跑道部分是半圈,即两个半径为R的半圆和两段直道组成;
对于第1道,弯道部分的周长是基于跑道的内圈半径R计算,而第2道弯道部分的周长则基于R+1米计算,因为跑道宽度为1米,所以每向外一圈半径增加1米。
27.【答案】3.14×5×2÷2+5×2
=15.7×2÷2+10
=15.7+10
=25.7(cm)
答:这个图形的周长是25.7cm。
【解析】【分析】观察图可知,这是一个半圆,要求半圆的周长,圆的周长÷2+直径=半圆的周长,据此列式解答。
28.【答案】解:3.14×(92-52)
=3.14×(81-25)
=3.14×56
=175.84(平方厘米)
答:阴影部分的面积是175.84平方厘米。
【解析】【分析】 阴影部分的图形的一个圆环,圆环的面积=大圆的面积-小圆的面积 ,用字母表示S环=S大-S小=π(R2-r2),将大圆半径和小圆半径代入公式即可求出答案。
29.【答案】解:3.14×(92-52)
=3.14×(81-25)
=3.14×56
=175.84(平方厘米)
答:阴影部分的面积是175.84平方厘米。
【解析】【分析】 阴影部分的图形的一个圆环,圆环的面积=大圆的面积-小圆的面积 ,用字母表示S环=S大-S小=π(R2-r2),将大圆半径和小圆半径代入公式即可求出答案。
30.【答案】解:内跑道周长=πd+110×2
=3×50+110×2
=150+220
=370(米)
外跑道周长=π(d+6+6)+110×2
=3×(50+6+6)+110×2
=3×62+220
=186+220
=406(米)
406-370=36(米)
答:在外圈跑圈比在内圈要多跑36米.
【解析】【分析】根据图可知,这个跑道宽6米,两头是直径50米的两个半圆,中间是一个长110米,宽50米的长方形,内跑道周长=内半圆周长×2+长方形的两条长边;外跑道周长=外半圆周长×2+长方形的两条长边.内外侧跑道之差就是在外圈跑圈比在内圈要多跑的米数.列式解答即可.
31.【答案】解:3.14×3+3.14×3×2×
=9.42+3.14
=12.56(厘米)
答:阴影部分的周长是12.56厘米。
【解析】【分析】由图可知,阴影部分外圈的弧长等于直径为3厘米的圆周长的一半加半径为3厘米的圆周长的,内圈的弧长等于直径为3厘米的圆周长的一半,即阴影部分周长=直径为3厘米的圆周长+半径为3厘米的圆周长的,据此解答。
32.【答案】解:3.14×42 3.14×32
=3.14×16 3.14×9
=3.14×(16-9)
=3.14×7
=21.98(平方厘米)
答:两个圆阴影部分的面积的差是21.98平方厘米.
【解析】【分析】观察图形可知,空白处是两个圆的公共部分,所以两个圆的阴影部分的面积的差,就是这两个圆的面积之差,据此利用圆的面积公式计算即可解答问题.
33.【答案】(1)解:5×3.14÷2
=15.7÷2
=7.85(厘米)
(5+1+1)×3.14÷2
=7×3.14÷2
=10.99(厘米)
7.85+10.99+1×2=20.84(厘米)
答:阴影部分的周长是20.84厘米。
(2)解:8×3.14=25.12(分米)
25.12+8×2
=25.12+16
=41.12(分米)
答:阴影部分的周长是41.12厘米。
【解析】【分析】(1)从图中可以看出,内圆的周长÷2+半圆的周长÷2+阴影部分的宽×2=阴影部分的周长,其中内圆的周长=内圆的直径×π,外圆的周长=(内圆的直径+阴影部分的宽+阴影部分的宽)×π,据此作答即可;
(2)从图中可以看出,阴影部分的直径=正方形的边长×2+直径为8分米的圆的周长,其中直径为8分米的圆的周长=直径×π,据此作答即可。
34.【答案】解:1千米=1000米
1000÷(2×3.14×0.36×100)
=1000÷226.08
≈4.4(分钟)
答:通过一座1千米长的大桥需要4.4分钟。
【解析】【分析】根据圆周长公式计算出车轮的周长,再乘100就是自行车每分钟走的长度,然后用大桥的长度除以自行车每分钟走的长度即可求出需要的时间。1千米=1000米。
35.【答案】解:10×6-4×4×3.14×
=60-12.56
=47.44(平方米)
答:这只羊无法吃到的草地面积是47.44平方米。
【解析】【分析】如图:,阴影部分即为这只羊无法吃到的草地面积,为:长方形的面积-半径是4米的圆面积的,根据长方形面积=长×宽、圆面积=半径×半径×π,代入数值进行解答即可。
36.【答案】5π=15.7;25π=78.5;8π=25.12;6π=18.84;
9π=28.26;20π=62.8;7π=21.98;36π=113.04。
【解析】【分析】将π=3.14代入式子中计算即可。
37.【答案】解:60-45=15(cm)
3.14×602÷2
=3.144×3600÷2
=11304÷2
=5652(cm2)
3.14×152÷2
=3.14×225÷2
=706.5÷2
=353.25(cm2)
5652-353.25=5298.75(cm2)
答:这种雨刷能刷到的面积是5298.75cm2。
【解析】【分析】先求出胶条长度与雨刷摆臂长度相差的长度,由图可知,雨刷转的面积为圆的面积的一半,再根据圆的面积公式”S=πr2“分别求出雨刷摆臂能转动的面积和雨刷胶条无法转动到的面积,然后用雨刷摆臂能转动的面积减去雨刷胶条无法转动到的面积,即可求出雨刷能刷到的面积 。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
小升初《圆与扇形》专项训练
一、单选题
1.圆的大小与圆的( )无关。
A.半径 B.直径 C.圆心
2.在一个边长是4dm的正方形内画一个最大的圆,这个圆的周长是( )dm。
A.12.56 B.6.28 C.10.28 D.25.12
3. ( P19第7题变式)如图是马戏团表演时用的独轮车,车轴安装在车轮的圆心处,车才能平稳运行,这是利用了( )。
A.圆是轴对称图形 B.圆的半径都相等 C.圆心决定圆的位置
4.画一个周长为 18.84 厘米的圆,则圆规两脚问的距离是( )厘米。
A.2 B.3 C.4 D.6
5.如果圆的半径是6厘米,那么它的面积是( )平方厘米.
A.6π B.12π C.36π D.24π
6.大圆内有两个小圆(如图),大圆的周长与两个小圆的周长之和相比( )。
A.大圆的周长长
B.同样长
C.两个小圆的周长之和长
7.用一个长5厘米,宽3厘米的长方形纸片剪一个最大的圆,这个圆的周长是( )
A.9.42厘米 B.15.7厘米
C.4.71厘米 D.9.42平方厘米
8.淘气在探索圆的面积计算公式时,把一个圆剪拼成一个长3.14厘米的近似长方形,这个圆的半径和面积是( )。
A.1厘米;3.14平方厘米 B.1厘米;6.28平方厘米
C.2厘米;12.56平方厘米 D.3厘米;9.42平方厘米
9.下面图( )中的阴影部分可能是圆心角为100°的扇形.
A. B.
C. D.
10.用四根同样长的绳子围成等边三角形、长方形、正方形和圆形,( )的面积最大。
A.等边三角形 B.长方形 C.正方形 D.圆形
二、判断题
11.圆的半径从6dm增加到9dm,圆的面积增加了45dm2。( )
12.小圆直径等于大圆的半径,大圆的周长是小圆的周长2倍,面积是小圆的4倍。( )
13.半径为2cm的圆的周长和面积相等。( )
14.半圆的周长可以用πr+2r=(π+2)r计算。( )
15.在同一平面内,任意两个圆都成轴对称。( )
16.一个半圆的周长是20.56分米,这个半圆的面积是41.12平方分米。( )
三、填空题
17.画圆时,圆规两脚尖之间的距离是3cm,所画成的圆周长是 厘米.
18.正方形的边长是10㎝,在它之中画一个最大的圆,圆的半径是 ㎝。
19.如图所示,将一个半径为r的圆分成若干等份,可以拼成一个近似的平行四边形。
圆周长的一半等于平行四边形的 。
平行四边形的高等于圆的 。
平行四边形的面积=底×高= × 。
圆的面积= 。
20.用圆规画一个圆,圆规两脚间的距离是4厘米,这个圆的周长是 厘米,面积是 平方厘米。
21.战国时期《墨经》一书中记载“圜(圆),一中同长也.”表示圆心到圆上各点的距离都相等,即 都相等.
22.圆规两脚之间的距离是5厘米,这个圆的直径是 ,周长是 ,面积是 。
23.时钟的分针长6厘米,它的尖端走一圈是 厘米,其中扫过的面积是 平方厘米.
24.图中圆和长方形面积相等,圆的半径等于长方形的宽.阴影部分面积是60cm2,圆的面积是 cm2。
25.一个圆的半径扩大2倍,周长扩大 倍,面积扩大 倍。
26.如图, 有一个 400 米操场, 操场上每条跑道的宽度是 1 米。学校准备给跑 200 米的运动员确定起跑线,在第 2 道的同学起跑线应该在第 1 道同学起跑线前 米。
四、计算题
27.求周长。
五、解答题
28.计算图中阴影部分的面积.(单位:厘米)
29.计算图中阴影部分的面积.(单位:厘米)
30.如图是某运动场的跑道宽6米,那么在外圈跑1圈比在内圈跑1圈要多跑多少米?(π取3)
31.图中,直径为3厘米的半圆绕A逆时针旋转60°使AB到达AC的位置,求图中阴影部分的周长。
32.已知下图大圆的半径为4cm,小圆的半径为3cm,求两个圆阴影部分的面积的差。
六、解决问题
33.求下列图形中阴影部分的周长。
(1)
(2)
34.一辆自行车轮胎的外半径是0.36米,如果每分钟转100周,通过一座1千米长的大桥需要几分钟?(得数保留一位小数)
35.一块长方形草地的一个角上有一根木桩,木桩上拴着一只羊,如果拴羊的绳子长4 m,这只羊无法吃到的草地面积是多少平方米?
七、口算与估算
36.直接写得数。(π取3.14)
5π= 25π=
8π= 6π=
9π= 20π= 7π= 36π=
八、图形计算
37.某款车上安装的雨刷是在一个摆臂上安装胶条,如下图所示,雨刷摆臂的长度是60cm,胶条的长度是45cm,摆动角度是180°,那么这种雨刷能刷到的面积是多少
答案解析部分
1.【答案】C
【解析】【解答】解:圆的大小与圆的圆心无关。
故答案为:C
【分析】圆心决定圆的位置,圆的直径或半径长度决定圆的大小。
2.【答案】A
【解析】【解答】解:3.14×4=12.56(分米)
故答案为:A。
【分析】这个圆的周长=π×直径;其中,直径=正方形的边长。
3.【答案】B
【解析】【解答】解:车轴安装在车轮的圆心处,车才能平稳运行,这是因为圆的半径都相等,当车轴在圆心时,车轮上各点到车轴的距离相等,能保证车轮平稳转动。
故答案为:B。
【分析】明确圆的基本性质,圆的半径是从圆心到圆上任意一点的距离,车轴在圆心时,车轮滚动过程中,车轮上各个点到车轴的距离始终保持不变,这样就能使车平稳运行,因此B选项正确。
4.【答案】B
【解析】【解答】解:18.84÷3.14÷2=6÷2=3(厘米);
故答案为:B。
【分析】 圆规两脚问的距离是指所画圆的半径,利用题目给出圆的周长,根据圆的周长=2πr,可以求出圆的半径r。
5.【答案】C
【解析】【解答】6×6×π=36π
故答案为:C
【分析】圆的面积=圆周率×半径×半径.
6.【答案】B
【解析】【解答】解:设大圆直径是2,则小圆直径是1。
大圆周长:3.14×2=6.28;
两个小圆周长:3.14×1×2=6.28;
所以大圆的周长与两个小圆的周长之和相等。
故答案为:B。
【分析】圆周长公式:C=πd。两个小圆的直径和等于大圆的直径,所以大圆周长与两个小圆周长之和相等。
7.【答案】A
【解析】【解答】解:3.14×3=9.42(厘米),
答:这个圆的周长是9.42厘米.
故选:A.
【分析】如图所示,所剪的最大圆的直径等于长方形的宽,长方形的宽已知,从而可以求出其周长.
8.【答案】A
【解析】【解答】解:半径:3.14×3.14=1(厘米),
面积:3.14×12=3.14(平方厘米)。
故答案为:A。
【分析】拼成近似长方形的长相当于圆周长的一半,所以用长方形的长除以3.14即可求出半径,然后根据圆面积公式计算面积。圆面积公式:S=πr2。
9.【答案】A
【解析】【解答】A、这个阴影部分可能是圆心角为100°的扇形;
B、这个圆心角接近一个平角,故不可能是圆心角为100°的扇形;
C、这个圆心角小于直角,故不可能是圆心角为100°的扇形;
D、这个角不是圆心角。
故答案为:A。
【分析】圆心角是指以顶点为圆心,以两条半径为边的角。这个圆心角与它所对的弧围成的图形就是扇形。根据这个定义结合各选项看哪个图形的圆心角可能是100°。
10.【答案】D
【解析】【解答】设这根绳子的长度为8,则
等边三角形:
8÷3≈2.7
等边三角形的面积一定小于与它等底等高的平行四边形的面积的一半,与它等底等高的平行四边形的面积的一半一定小于2.7×2.7÷2=7.29÷2=3.645.
长方形:
8÷2=4
当长方形的长与宽都取整数时,它的长与宽分别是3和1、2和2,当长与宽都是2时变成正方形。
3×1=3
2×2=4
圆:
8÷3.14÷2≈1.3
3.14×1.32 =5.3066
综合各种图形的面积可知,用同样长的绳子围成的上述各种图形中,圆的面积最大。
故答案为:D。
【分析】设这根绳子的长为一个定值,根据各种图形的周长公式与面积公式,分别计算它们的面积,最后比较大小即可。
11.【答案】错误
【解析】【解答】解:3.14×9×9-3.14×6×6
=254.34-113.04
=141.3(平方分米)
故答案为:错误。
【分析】π×9的平方=增加后的面积;π×6的平方=增加前的面积;增加后的面积-增加前的面积=增加的面积。
12.【答案】正确
【解析】【解答】解:小圆直径等于大圆的半径,大圆的周长是小圆的周长2倍,面积是小圆的4倍,原题干说法正确。
故答案为:正确。
【分析】在同圆或等圆中,圆的直径=半径×2,圆的周长=π×半径×2,圆的面积=π×半径2,所以大圆的周长是小圆的周长2倍,面积是小圆的4倍。
13.【答案】错误
【解析】【解答】解:圆的周长和面积无法比较大小,原题说法错误.
故答案为:错误
【分析】周长是围成圆一周曲线的长度,面积是指圆的大小,周长和面积的意义不同,无法比较大小.
14.【答案】正确
【解析】【解答】解:半圆的周长可以用πr+2r=(π+2)r计算。原题说法正确。
故答案为:正确。
【分析】πr表示圆周长的一半,2r是直径,半圆的周长就包括圆周长的一半和一条直径的长度。
15.【答案】错误
【解析】【解答】两个圆成轴对称,这两个圆必须完全相同.任意两个圆,它们的半径并不一定相等。半径不等,这两个圆就不可能成轴对称.
【分析】在同一平面内,不相同的两个圆不能成轴对称,只有等圆才可能成轴对称.
16.【答案】错误
【解析】【解答】解:设这个半圆的半径是x分米,
3.14×2x÷2+2x=20.56
3.14x+2x=20.56
5.14x=20.56
x=20.56÷5.14
x=4
面积:3.14×42÷2
=3.14×16÷2
=25.12(平方分米)
原题计算错误。
故答案为:错误
【分析】半圆的周长包括所在圆的周长的一半和直径的长度,设半径是x分米,根据周长包括的长度列出方程,解方程求出半径,然后根据圆面积公式计算半圆的面积。
17.【答案】18.84
【解析】【解答】解:3.14×(3×2)
=3.14×6
=18.84(厘米)
故答案为:18.84。
【分析】画圆时,圆规两脚尖之间的距离就等于所画圆的半径,根据圆的周长公式:C=2πr,把数据代入公式解答即可求出圆的周长。
18.【答案】5
【解析】【解答】10÷2=5(cm).
故答案为:5.
【分析】在一个正方形之中画一个最大的圆,圆的半径是正方形边长的一半,据此列式解答.
19.【答案】底;半径;πr;r;πr2
【解析】【解答】解:圆周长的一半等于平行四边形的底。平行四边形的高等于圆的半径。平行四边形的面积=底×高=πr×r。圆的面积=πr2。
故答案为:底;半径;πr;r;πr2。
【分析】从图上可以看出,将一个半径为r的圆分成若干等份,可以拼成一个近似的平行四边形,此时平行四边形的底就是圆周长的一半,高就是圆的半径;根据平行四边形面积计算公式“ 平行四边形的面积=底×高 ”,因此根据图中信息可以延伸为πr×r,即圆的面积=πr2。
20.【答案】25.12;50.24
【解析】【解答】解:周长:4×2×3.14
=8×3.14
=25.12(厘米);
42×3.14
=16×3.14
=50.24(平方厘米);
故答案为:25.12;50.24。
【分析】圆规两脚之间的距离就是圆的半径,圆周长=半径×2×π,圆面积=半径2×π,据此代入数值计算即可。
21.【答案】半径
【解析】【解答】解:表示圆心到圆上各点的距离都相等,即半径都相等。
故答案为:半径。
【分析】根据半径的定义作答即可。
22.【答案】10厘米;31.4厘米;78.5平方厘米
【解析】【解答】解:5×2=10(厘米)
3.14×10=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)。
故答案为:10厘米;31.4厘米;78.5平方厘米。
【分析】圆的直径=半径×2,圆的周长=π×直径;圆的面积=π×半径2。
23.【答案】37.68;113.04
【解析】【解答】解:2×3.14×6=37.68(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
答:它的尖端走一圈是37.68厘米,其中扫过的面积是113.04平方厘米.
故答案为:37.68;113.04.
【分析】分针一小时正好走一圈,针尖走过的路线正好画成了一个圆,求尖端走了一圈的长度,实际是求半径是6厘米的圆的周长是多少,它走一圈扫过的面积就是半径为6厘米的圆的面积,可利用圆的周长公式、圆的面积公式解答即可.
24.【答案】80
【解析】【解答】解:60÷3×4
=20×4
=80(cm2)
故答案为:80。
【分析】从图中可以看出,圆剩下的面积=长方形中的阴影部分面积,那么长方形和圆重合部分的面积=阴影部分的面积÷3,所以圆的面积=长方形和圆重合部分的面积×4,据此作答即可。
25.【答案】2;4
【解析】【解答】 一个圆的半径扩大2倍,周长扩大2倍,面积扩大4倍.
故答案为:2;4.
【分析】根据圆的周长公式:C=2πr,当半径扩大a倍,周长也扩大a倍;根据圆的面积公式:S=πr2,当半径扩大a倍,面积扩大a2倍,据此解答.
26.【答案】3.14
【解析】【解答】解:3.14×1=3.14(米)
故答案为:3.14。
【分析】首先,明确赛跑距离是在直道与弯道共同构成的200米。对于200米的赛跑,由于是在环形跑道上,实际上涉及到的跑道部分是半圈,即两个半径为R的半圆和两段直道组成;
对于第1道,弯道部分的周长是基于跑道的内圈半径R计算,而第2道弯道部分的周长则基于R+1米计算,因为跑道宽度为1米,所以每向外一圈半径增加1米。
27.【答案】3.14×5×2÷2+5×2
=15.7×2÷2+10
=15.7+10
=25.7(cm)
答:这个图形的周长是25.7cm。
【解析】【分析】观察图可知,这是一个半圆,要求半圆的周长,圆的周长÷2+直径=半圆的周长,据此列式解答。
28.【答案】解:3.14×(92-52)
=3.14×(81-25)
=3.14×56
=175.84(平方厘米)
答:阴影部分的面积是175.84平方厘米。
【解析】【分析】 阴影部分的图形的一个圆环,圆环的面积=大圆的面积-小圆的面积 ,用字母表示S环=S大-S小=π(R2-r2),将大圆半径和小圆半径代入公式即可求出答案。
29.【答案】解:3.14×(92-52)
=3.14×(81-25)
=3.14×56
=175.84(平方厘米)
答:阴影部分的面积是175.84平方厘米。
【解析】【分析】 阴影部分的图形的一个圆环,圆环的面积=大圆的面积-小圆的面积 ,用字母表示S环=S大-S小=π(R2-r2),将大圆半径和小圆半径代入公式即可求出答案。
30.【答案】解:内跑道周长=πd+110×2
=3×50+110×2
=150+220
=370(米)
外跑道周长=π(d+6+6)+110×2
=3×(50+6+6)+110×2
=3×62+220
=186+220
=406(米)
406-370=36(米)
答:在外圈跑圈比在内圈要多跑36米.
【解析】【分析】根据图可知,这个跑道宽6米,两头是直径50米的两个半圆,中间是一个长110米,宽50米的长方形,内跑道周长=内半圆周长×2+长方形的两条长边;外跑道周长=外半圆周长×2+长方形的两条长边.内外侧跑道之差就是在外圈跑圈比在内圈要多跑的米数.列式解答即可.
31.【答案】解:3.14×3+3.14×3×2×
=9.42+3.14
=12.56(厘米)
答:阴影部分的周长是12.56厘米。
【解析】【分析】由图可知,阴影部分外圈的弧长等于直径为3厘米的圆周长的一半加半径为3厘米的圆周长的,内圈的弧长等于直径为3厘米的圆周长的一半,即阴影部分周长=直径为3厘米的圆周长+半径为3厘米的圆周长的,据此解答。
32.【答案】解:3.14×42 3.14×32
=3.14×16 3.14×9
=3.14×(16-9)
=3.14×7
=21.98(平方厘米)
答:两个圆阴影部分的面积的差是21.98平方厘米.
【解析】【分析】观察图形可知,空白处是两个圆的公共部分,所以两个圆的阴影部分的面积的差,就是这两个圆的面积之差,据此利用圆的面积公式计算即可解答问题.
33.【答案】(1)解:5×3.14÷2
=15.7÷2
=7.85(厘米)
(5+1+1)×3.14÷2
=7×3.14÷2
=10.99(厘米)
7.85+10.99+1×2=20.84(厘米)
答:阴影部分的周长是20.84厘米。
(2)解:8×3.14=25.12(分米)
25.12+8×2
=25.12+16
=41.12(分米)
答:阴影部分的周长是41.12厘米。
【解析】【分析】(1)从图中可以看出,内圆的周长÷2+半圆的周长÷2+阴影部分的宽×2=阴影部分的周长,其中内圆的周长=内圆的直径×π,外圆的周长=(内圆的直径+阴影部分的宽+阴影部分的宽)×π,据此作答即可;
(2)从图中可以看出,阴影部分的直径=正方形的边长×2+直径为8分米的圆的周长,其中直径为8分米的圆的周长=直径×π,据此作答即可。
34.【答案】解:1千米=1000米
1000÷(2×3.14×0.36×100)
=1000÷226.08
≈4.4(分钟)
答:通过一座1千米长的大桥需要4.4分钟。
【解析】【分析】根据圆周长公式计算出车轮的周长,再乘100就是自行车每分钟走的长度,然后用大桥的长度除以自行车每分钟走的长度即可求出需要的时间。1千米=1000米。
35.【答案】解:10×6-4×4×3.14×
=60-12.56
=47.44(平方米)
答:这只羊无法吃到的草地面积是47.44平方米。
【解析】【分析】如图:,阴影部分即为这只羊无法吃到的草地面积,为:长方形的面积-半径是4米的圆面积的,根据长方形面积=长×宽、圆面积=半径×半径×π,代入数值进行解答即可。
36.【答案】5π=15.7;25π=78.5;8π=25.12;6π=18.84;
9π=28.26;20π=62.8;7π=21.98;36π=113.04。
【解析】【分析】将π=3.14代入式子中计算即可。
37.【答案】解:60-45=15(cm)
3.14×602÷2
=3.144×3600÷2
=11304÷2
=5652(cm2)
3.14×152÷2
=3.14×225÷2
=706.5÷2
=353.25(cm2)
5652-353.25=5298.75(cm2)
答:这种雨刷能刷到的面积是5298.75cm2。
【解析】【分析】先求出胶条长度与雨刷摆臂长度相差的长度,由图可知,雨刷转的面积为圆的面积的一半,再根据圆的面积公式”S=πr2“分别求出雨刷摆臂能转动的面积和雨刷胶条无法转动到的面积,然后用雨刷摆臂能转动的面积减去雨刷胶条无法转动到的面积,即可求出雨刷能刷到的面积 。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
