云南省昭通市绥江县2025届九年级下学期中考二模数学试卷(含详解)
文档属性
| 名称 | 云南省昭通市绥江县2025届九年级下学期中考二模数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 839.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 06:44:25 | ||
图片预览

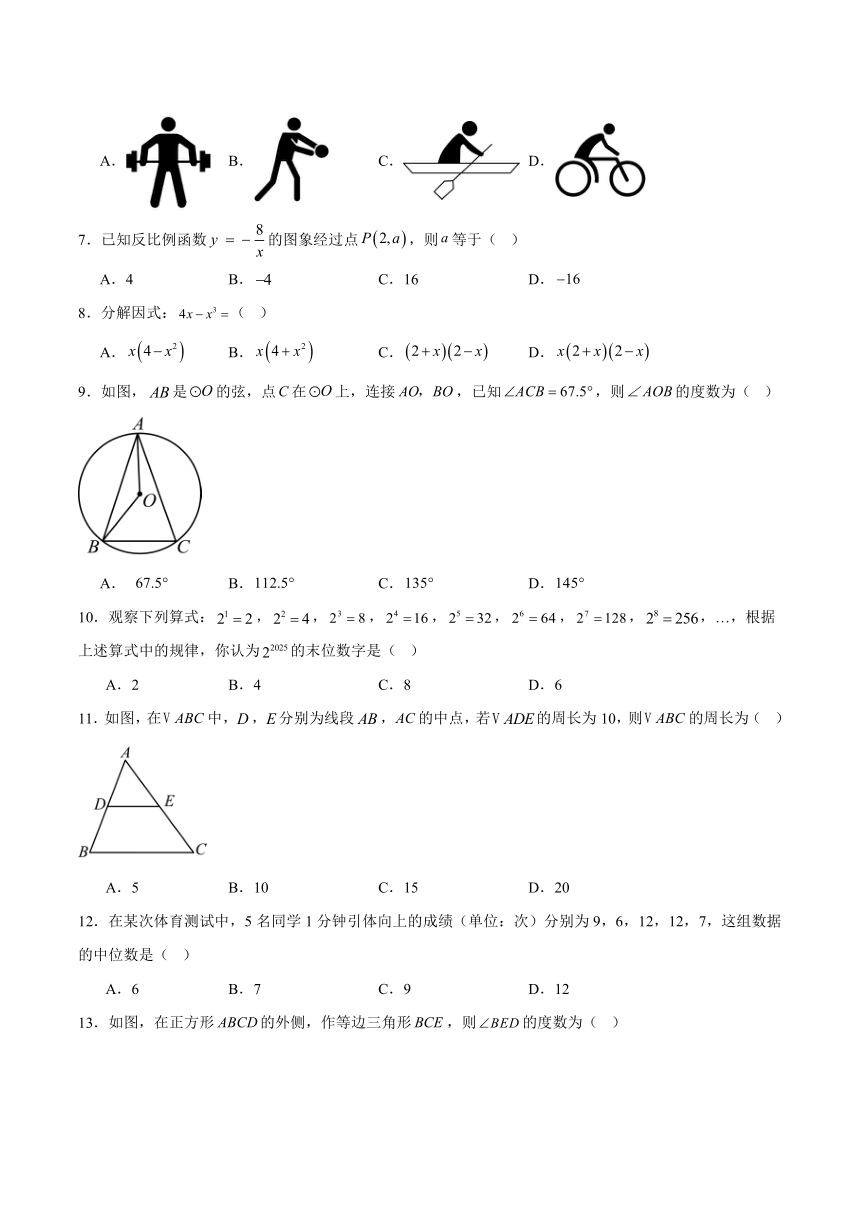



文档简介
云南省昭通市绥江县2025年5月初中学业水平考试模拟(二)数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.毛主席在《沁园春·雪》一诗中写道:“惜秦皇汉武,略输文采;唐宗宋祖,稍逊风骚.”秦始皇于公元前221年攻灭齐国,完成统一中国之大业,建立皇帝制度,号称“始皇帝”;唐太宗于公元630年攻灭东突厥,收伏西域诸国,获尊“天可汗”称号.若将公元前221年记为年,则公元630年可记为( )
A.年 B.年 C.409年 D.年
2.下列图形中,不是长方体展开图的是( )
A. B. C. D.
3.河口口岸是中越边境云南段最大的陆路口岸,据统计,年月,从河口口岸入境开启中国之行的越南旅游团中,持用护照进入内地旅游的团队达个,共人次,同比分别上升和.用科学记数法可以表示为( )
A. B. C. D.
4.如图,直线与直线a,b都相交.若,,则( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.每天运动一小时,健康生活一辈子.下列关于体育运动的图标中,可以看作轴对称图形的是( )
A. B. C. D.
7.已知反比例函数的图象经过点,则等于( )
A.4 B. C.16 D.
8.分解因式:( )
A. B. C. D.
9.如图,是的弦,点在上,连接,已知,则的度数为( )
A. B. C. D.
10.观察下列算式:,,,,,,,,…,根据上述算式中的规律,你认为的末位数字是( )
A.2 B.4 C.8 D.6
11.如图,在中,,分别为线段,的中点,若的周长为10,则的周长为( )
A.5 B.10 C.15 D.20
12.在某次体育测试中,5名同学1分钟引体向上的成绩(单位:次)分别为9,6,12,12,7,这组数据的中位数是( )
A.6 B.7 C.9 D.12
13.如图,在正方形的外侧,作等边三角形,则的度数为( )
A. B. C. D.
14.某水果商店2023年售出1000箱蓝莓,2025年售出1440箱蓝莓,若将这两年销售蓝莓箱数的平均增长率设为,根据题意,下列方程正确的是( )
A. B.
C. D.
15.将一个底面半径为的圆锥的侧面展开后得到一个圆心角为的扇形,这个圆锥的母线长为( )
A. B. C. D.
二、填空题
16.若在实数范围内有意义,则实数x的取值范围是 .
17.一个七边形的内角和等于 .
18.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .
19.某校近期准备开展数学美育专题讲座,分别讲解数学美育的五个层次.层次1:数学知识中的数学美;层次2:数学文化中的数学美;层次3:数学应用中的创新之美;层次4:数学教学互动中的感染之美;层次5:数学德育中的心灵之美.为了解学生喜好,学校随机抽取了该校部分学生进行问卷调查(要求每人必选且只能选一个最想听的数学美育层次讲座),对数据进行整理,绘制了两个不完整的统计图,如图所示:
若该校有2000名学生,根据图中信息,最想听数学美育层次1的学生约有 人.
三、解答题
20.计算:.
21.如图,,.求证:.
22.我省民族众多,民族服饰更是支系繁多,各具特色,但都承载着厚重的民族文化.某剧院购进A,B两款民族服饰以供演出使用,用1800元购进的款服饰的数量和用1400购进的款服饰的数量相同,每套款服饰的价格比每套款服饰的价格贵40元,分别求A,B两款服饰每套的价格.
23.大理(记为),丽江(记为)和西双版纳(记为)是云南省内著名的旅游胜地.甲、乙两名同学准备在端午节假期前往云南省游玩,各自随机选择大理,丽江,西双版纳三个地方中的一个,二人选择哪个地方不受任何因素影响,每一个地方被选到的可能性相同.记甲同学的选择为,乙同学的选择为.
(1)请用列表法或画树状图法中的一种方法,求所有可能出现的结果总数;
(2)求甲和乙至少有一人去丽江游玩的概率.
24.如图,菱形的对角线与相交于点,延长至点,使.分别以D,E为圆心,以大于的长为半径画弧,两弧在内部相交于点,作射线交于点.
(1)求证:四边形是矩形;
(2)若,,连接,求的长.
25.绿化树种具有过滤和滞纳大气污染颗粒物的能力,因此成为城市绿化的常用树种,其中榆树和白蜡树因其生长迅速,枝叶繁茂而被广泛种植.已知3棵榆树和2棵白蜡树的滞尘总量为23千克,5棵榆树和4棵白蜡树的滞尘总量为41千克.
(1)每棵榆树和白蜡树的滞尘量分别是多少千克?
(2)一条新建的城市道路需要种植这两种树,一棵榆树的种植成本是400元,一棵白蜡树的种植成本是200元,种植两种树木的总棵数为60棵,要求滞尘总量不少于280千克,且种植总成本尽可能低,应该怎样种植这两种树才能使种植总成本最低?求出该费用.
26.在平面直角坐标系中,已知抛物线(为常数).当时,随的增大而减小;当时,随的增大而增大,实数是抛物线与轴交点的横坐标,且,.
(1)求的值;
(2)请你猜想与的大小关系,并说明理由.
27.如图,内接于,是的直径,半径交弦于点,交弦于点,过点作交的延长线于点,,过点作于点,交于点.
(1)求证:是的切线;
(2)若点是弦的中点,,,求图中阴影部分的面积;
(3)若,将绕点顺时针旋转得到,点恰好在线段上,试探究线段与的数量关系.
《云南省昭通市绥江县2025年5月初中学业水平考试模拟(二)数学试题》参考答案
1.A
解:将公元前221年记为年,则公元630年可记为年,
故选:A.
2.B
解:由长方体展开图的特点可知,A、C、D中展开图都是长方体的展开图,B中展开图不是长方体展开图,
故选:B.
3.B
解:,
故选:B.
4.D
解:如图,
∵,
∴,
∵,
∴,
故选:D.
5.C
解:A、,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、与不是同类二次根式,不能合并,原式计算错误,不符合题意;
故选:C.
6.A
解:A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意;
故选A.
7.B
解:∵反比例函数的图象经过点,
∴,
故选:B.
8.D
解:
,
故选:D.
9.C
解:,
,
故选:C.
10.A
解:因为,,,,,,,,…,
通过观察发现末尾数字以2,4,8,6,这4个数字为循环,
所以,
所以末位数字是2.
故选A.
11.D
解:∵,分别为线段,的中点,
∴是的中位线,
∴,
∴,
∴的周长:的周长,
∵的周长为10,
∴的周长为20,
故选:D.
12.C
解:从小到大排序为6,7,9,12,12,最中间的数是9,
∴中位数是9,
故选:C.
13.C
解:∵四边形是正方形,是等边三角形,
∴,
∴,
∴,
∴,
故选:C.
14.A
解:若将这两年销售蓝莓箱数的平均增长率设为,根据题意,,
故选:A.
15.B
解:设圆锥的母线长为,
由题意得,,
解得,
故选:.
16.
解:由题意可得,
,
,
故答案为:.
17.900
解:,
故答案为:900.
18.
解:根据题意得,
解得.
故答案为:.
19.120
解:人,
∴这次一共调查了200人,
∴样本中最想听数学美育层次1的人数为人,
人,
∴该校有2000名学生,最想听数学美育层次1的学生约有120人,
故答案为:120.
20.2
解:原式
.
21.见解析
证明:,,
,即.
在和中,
,
.
22.每套款服饰的价格是140元,每套款服饰的价格是180元
解:设每套款服饰的售价是元,则每套款服饰的售价是元.
由题意得.
由得,即.
.
经检验,是原分式方程的解,且符合题目要求,此时.
答:每套款服饰的价格是140元,每套款服饰的价格是180元.
23.(1)所有可能出现的结果总数有9种
(2)甲和乙至少有一人去丽江游玩的概率为
(1)解:由题意列表如下:
由表可知,共有9种等可能出现的结果
(2)解:由(1)可知,甲和乙至少有一人去丽江游玩的有,,,,共5种结果,
概率为.
24.(1)见解析
(2)的长为
(1)证明:在菱形中,,
,,
是菱形的对角线,
.
由题知,,则,
结合作图可得:平分,
,
,则.
,
.
是菱形的对角线,
.
,则.
∴四边形是平行四边形.
菱形的对角线与相交于点,
,
四边形是矩形.
(2)解:由(1)知,,.
在菱形中,,
,则.
在Rt中,,
.
四边形是矩形,
.
在Rt中,.
25.(1)每棵榆树的滞尘量为5千克,每棵白蜡树的滞尘量为4千克
(2)种植40棵榆树,20棵白蜡树,种植总成本最低,为20000元
(1)解;设每棵榆树的滞尘量为千克,每棵白蜡树的滞尘量为千克.
由题意得,,
解得.
答:每棵榆树的滞尘量为5千克,每棵白蜡树的滞尘量为4千克.
(2)解:设种植棵榆树,种植棵白蜡树.
由题意得,,
解得,.
设种植总成本为元.
由题意得,
,
随的增大而增大.
当时,取得最小值,最小值为,
此时.
答:种植40棵榆树,20棵白蜡树,种植总成本最低,为20000元.
26.(1)
(2)当时,;当时,.理由见解析
(1)解:∵当时,随的增大而减小;当时,随的增大而增大,
抛物线的对称轴为直线,
,
;
(2)解:由(1)知,抛物线的解析式为,
实数是抛物线与轴交点的横坐标,
,则,
,,
,
解得,,
,
①当时,
,
,即,
②当时,
,
,即.
27.(1)见解析
(2)图中阴影部分的面积为
(3)
(1)证明:是的直径,点在上,
,
则,
,
,
,
,
,即,
是的半径,
是的切线;
(2)解:,,
,
半径交弦于点,点是弦的中点,
,,
,,
,
,则,
(负值舍去),
在中,,
,则,
,
是等边三角形,
;
(3)解:如图,分别过点,作的垂线,,垂足为,,
由旋转可得,,,
,
,
,
,
,,
是的直径,
,
,
,
,
,
,
,
,
,
,
,,
,
.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.毛主席在《沁园春·雪》一诗中写道:“惜秦皇汉武,略输文采;唐宗宋祖,稍逊风骚.”秦始皇于公元前221年攻灭齐国,完成统一中国之大业,建立皇帝制度,号称“始皇帝”;唐太宗于公元630年攻灭东突厥,收伏西域诸国,获尊“天可汗”称号.若将公元前221年记为年,则公元630年可记为( )
A.年 B.年 C.409年 D.年
2.下列图形中,不是长方体展开图的是( )
A. B. C. D.
3.河口口岸是中越边境云南段最大的陆路口岸,据统计,年月,从河口口岸入境开启中国之行的越南旅游团中,持用护照进入内地旅游的团队达个,共人次,同比分别上升和.用科学记数法可以表示为( )
A. B. C. D.
4.如图,直线与直线a,b都相交.若,,则( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.每天运动一小时,健康生活一辈子.下列关于体育运动的图标中,可以看作轴对称图形的是( )
A. B. C. D.
7.已知反比例函数的图象经过点,则等于( )
A.4 B. C.16 D.
8.分解因式:( )
A. B. C. D.
9.如图,是的弦,点在上,连接,已知,则的度数为( )
A. B. C. D.
10.观察下列算式:,,,,,,,,…,根据上述算式中的规律,你认为的末位数字是( )
A.2 B.4 C.8 D.6
11.如图,在中,,分别为线段,的中点,若的周长为10,则的周长为( )
A.5 B.10 C.15 D.20
12.在某次体育测试中,5名同学1分钟引体向上的成绩(单位:次)分别为9,6,12,12,7,这组数据的中位数是( )
A.6 B.7 C.9 D.12
13.如图,在正方形的外侧,作等边三角形,则的度数为( )
A. B. C. D.
14.某水果商店2023年售出1000箱蓝莓,2025年售出1440箱蓝莓,若将这两年销售蓝莓箱数的平均增长率设为,根据题意,下列方程正确的是( )
A. B.
C. D.
15.将一个底面半径为的圆锥的侧面展开后得到一个圆心角为的扇形,这个圆锥的母线长为( )
A. B. C. D.
二、填空题
16.若在实数范围内有意义,则实数x的取值范围是 .
17.一个七边形的内角和等于 .
18.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .
19.某校近期准备开展数学美育专题讲座,分别讲解数学美育的五个层次.层次1:数学知识中的数学美;层次2:数学文化中的数学美;层次3:数学应用中的创新之美;层次4:数学教学互动中的感染之美;层次5:数学德育中的心灵之美.为了解学生喜好,学校随机抽取了该校部分学生进行问卷调查(要求每人必选且只能选一个最想听的数学美育层次讲座),对数据进行整理,绘制了两个不完整的统计图,如图所示:
若该校有2000名学生,根据图中信息,最想听数学美育层次1的学生约有 人.
三、解答题
20.计算:.
21.如图,,.求证:.
22.我省民族众多,民族服饰更是支系繁多,各具特色,但都承载着厚重的民族文化.某剧院购进A,B两款民族服饰以供演出使用,用1800元购进的款服饰的数量和用1400购进的款服饰的数量相同,每套款服饰的价格比每套款服饰的价格贵40元,分别求A,B两款服饰每套的价格.
23.大理(记为),丽江(记为)和西双版纳(记为)是云南省内著名的旅游胜地.甲、乙两名同学准备在端午节假期前往云南省游玩,各自随机选择大理,丽江,西双版纳三个地方中的一个,二人选择哪个地方不受任何因素影响,每一个地方被选到的可能性相同.记甲同学的选择为,乙同学的选择为.
(1)请用列表法或画树状图法中的一种方法,求所有可能出现的结果总数;
(2)求甲和乙至少有一人去丽江游玩的概率.
24.如图,菱形的对角线与相交于点,延长至点,使.分别以D,E为圆心,以大于的长为半径画弧,两弧在内部相交于点,作射线交于点.
(1)求证:四边形是矩形;
(2)若,,连接,求的长.
25.绿化树种具有过滤和滞纳大气污染颗粒物的能力,因此成为城市绿化的常用树种,其中榆树和白蜡树因其生长迅速,枝叶繁茂而被广泛种植.已知3棵榆树和2棵白蜡树的滞尘总量为23千克,5棵榆树和4棵白蜡树的滞尘总量为41千克.
(1)每棵榆树和白蜡树的滞尘量分别是多少千克?
(2)一条新建的城市道路需要种植这两种树,一棵榆树的种植成本是400元,一棵白蜡树的种植成本是200元,种植两种树木的总棵数为60棵,要求滞尘总量不少于280千克,且种植总成本尽可能低,应该怎样种植这两种树才能使种植总成本最低?求出该费用.
26.在平面直角坐标系中,已知抛物线(为常数).当时,随的增大而减小;当时,随的增大而增大,实数是抛物线与轴交点的横坐标,且,.
(1)求的值;
(2)请你猜想与的大小关系,并说明理由.
27.如图,内接于,是的直径,半径交弦于点,交弦于点,过点作交的延长线于点,,过点作于点,交于点.
(1)求证:是的切线;
(2)若点是弦的中点,,,求图中阴影部分的面积;
(3)若,将绕点顺时针旋转得到,点恰好在线段上,试探究线段与的数量关系.
《云南省昭通市绥江县2025年5月初中学业水平考试模拟(二)数学试题》参考答案
1.A
解:将公元前221年记为年,则公元630年可记为年,
故选:A.
2.B
解:由长方体展开图的特点可知,A、C、D中展开图都是长方体的展开图,B中展开图不是长方体展开图,
故选:B.
3.B
解:,
故选:B.
4.D
解:如图,
∵,
∴,
∵,
∴,
故选:D.
5.C
解:A、,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、与不是同类二次根式,不能合并,原式计算错误,不符合题意;
故选:C.
6.A
解:A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意;
故选A.
7.B
解:∵反比例函数的图象经过点,
∴,
故选:B.
8.D
解:
,
故选:D.
9.C
解:,
,
故选:C.
10.A
解:因为,,,,,,,,…,
通过观察发现末尾数字以2,4,8,6,这4个数字为循环,
所以,
所以末位数字是2.
故选A.
11.D
解:∵,分别为线段,的中点,
∴是的中位线,
∴,
∴,
∴的周长:的周长,
∵的周长为10,
∴的周长为20,
故选:D.
12.C
解:从小到大排序为6,7,9,12,12,最中间的数是9,
∴中位数是9,
故选:C.
13.C
解:∵四边形是正方形,是等边三角形,
∴,
∴,
∴,
∴,
故选:C.
14.A
解:若将这两年销售蓝莓箱数的平均增长率设为,根据题意,,
故选:A.
15.B
解:设圆锥的母线长为,
由题意得,,
解得,
故选:.
16.
解:由题意可得,
,
,
故答案为:.
17.900
解:,
故答案为:900.
18.
解:根据题意得,
解得.
故答案为:.
19.120
解:人,
∴这次一共调查了200人,
∴样本中最想听数学美育层次1的人数为人,
人,
∴该校有2000名学生,最想听数学美育层次1的学生约有120人,
故答案为:120.
20.2
解:原式
.
21.见解析
证明:,,
,即.
在和中,
,
.
22.每套款服饰的价格是140元,每套款服饰的价格是180元
解:设每套款服饰的售价是元,则每套款服饰的售价是元.
由题意得.
由得,即.
.
经检验,是原分式方程的解,且符合题目要求,此时.
答:每套款服饰的价格是140元,每套款服饰的价格是180元.
23.(1)所有可能出现的结果总数有9种
(2)甲和乙至少有一人去丽江游玩的概率为
(1)解:由题意列表如下:
由表可知,共有9种等可能出现的结果
(2)解:由(1)可知,甲和乙至少有一人去丽江游玩的有,,,,共5种结果,
概率为.
24.(1)见解析
(2)的长为
(1)证明:在菱形中,,
,,
是菱形的对角线,
.
由题知,,则,
结合作图可得:平分,
,
,则.
,
.
是菱形的对角线,
.
,则.
∴四边形是平行四边形.
菱形的对角线与相交于点,
,
四边形是矩形.
(2)解:由(1)知,,.
在菱形中,,
,则.
在Rt中,,
.
四边形是矩形,
.
在Rt中,.
25.(1)每棵榆树的滞尘量为5千克,每棵白蜡树的滞尘量为4千克
(2)种植40棵榆树,20棵白蜡树,种植总成本最低,为20000元
(1)解;设每棵榆树的滞尘量为千克,每棵白蜡树的滞尘量为千克.
由题意得,,
解得.
答:每棵榆树的滞尘量为5千克,每棵白蜡树的滞尘量为4千克.
(2)解:设种植棵榆树,种植棵白蜡树.
由题意得,,
解得,.
设种植总成本为元.
由题意得,
,
随的增大而增大.
当时,取得最小值,最小值为,
此时.
答:种植40棵榆树,20棵白蜡树,种植总成本最低,为20000元.
26.(1)
(2)当时,;当时,.理由见解析
(1)解:∵当时,随的增大而减小;当时,随的增大而增大,
抛物线的对称轴为直线,
,
;
(2)解:由(1)知,抛物线的解析式为,
实数是抛物线与轴交点的横坐标,
,则,
,,
,
解得,,
,
①当时,
,
,即,
②当时,
,
,即.
27.(1)见解析
(2)图中阴影部分的面积为
(3)
(1)证明:是的直径,点在上,
,
则,
,
,
,
,
,即,
是的半径,
是的切线;
(2)解:,,
,
半径交弦于点,点是弦的中点,
,,
,,
,
,则,
(负值舍去),
在中,,
,则,
,
是等边三角形,
;
(3)解:如图,分别过点,作的垂线,,垂足为,,
由旋转可得,,,
,
,
,
,
,,
是的直径,
,
,
,
,
,
,
,
,
,
,
,,
,
.
同课章节目录
