【期末押题卷】2024-2025学年数学八年级下册苏科版(含解析)
文档属性
| 名称 | 【期末押题卷】2024-2025学年数学八年级下册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 20:54:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【期末押题卷】2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2023秋 沈丘县期末)商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
2.(2024秋 澄迈县期末)若分式有意义,则a的取值范围是( )
A.a≠0 B.a≠3 C.a<3 D.a≥3
3.(2024秋 天津期末)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.(2025春 锦江区校级期末)已知分式P,Q,其中n为任意正整数,则P,Q的大小关系为( )
A.P<Q
B.P=Q
C.P>Q
D.P,Q的大小关系与n的取值有关
5.(2024秋 南关区校级期末)实数a,b在数轴上的位置如图所示,化简|a﹣b|的结果是( )
A.a B.﹣a C.a﹣2b D.﹣a+2b
6.(2024秋 水城区期末)菱形ABCD的边长为3cm,那么菱形的周长是( )
A.9cm B.15cm C.12cm D.18cm
7.(2024秋 渠县期末)已知反比例函数的图象上有点A(x1,y1),B(x2,y2),C(x3,y3),且x1>x2>0>x3,则关于y1,y2,y3大小关系正确的是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
8.(2025春 锦江区校级期末)如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接AE.若AE∥BD,则∠CAD的度数为( )
A.100° B.90° C.70° D.60°
二.填空题(共8小题)
9.(2024秋 荔湾区期末)若分式有意义,则x的取值范围是 .
10.(2024秋 太原期末)已知,四边形ABCD是平行四边形,对角线AC,BD交于点O.若增加一个条件,将它边的数量关系特殊化,可使AC⊥BD,则增加的一个条件可以是 .(写出一个即可)
11.(2017秋 简阳市期末)已知实数x,y满足条件y3,则xy= .
12.(2020秋 开州区期末)如图,在矩形ABCD中,AB=4,BC=7,EA平分∠BAD交BC于点E,连接DE,将矩形ABCD沿DE翻折,翻折后点D与点D'点对应,再将所得△C'D'E绕着点E旋转,线段C'D'与线段ED交于点P.当PD=PC'时,则DC'的长为 .
13.(2024秋 阳谷县期末)若关于x的分式方程有增根,则m的值为 .
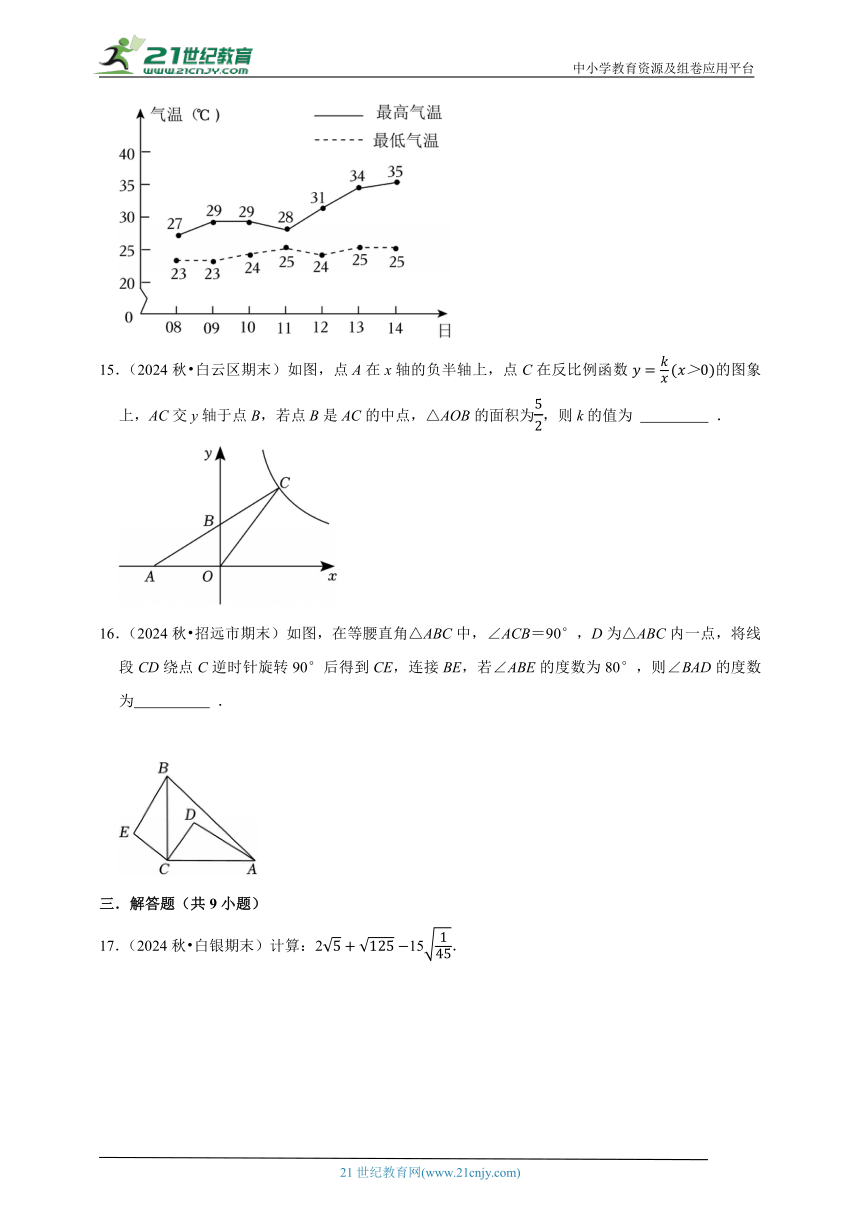
14.(2024秋 太康县期末)某地区6月8日~14日的气温折线统计图如图所示,则这一周中温差最大的日期是 .
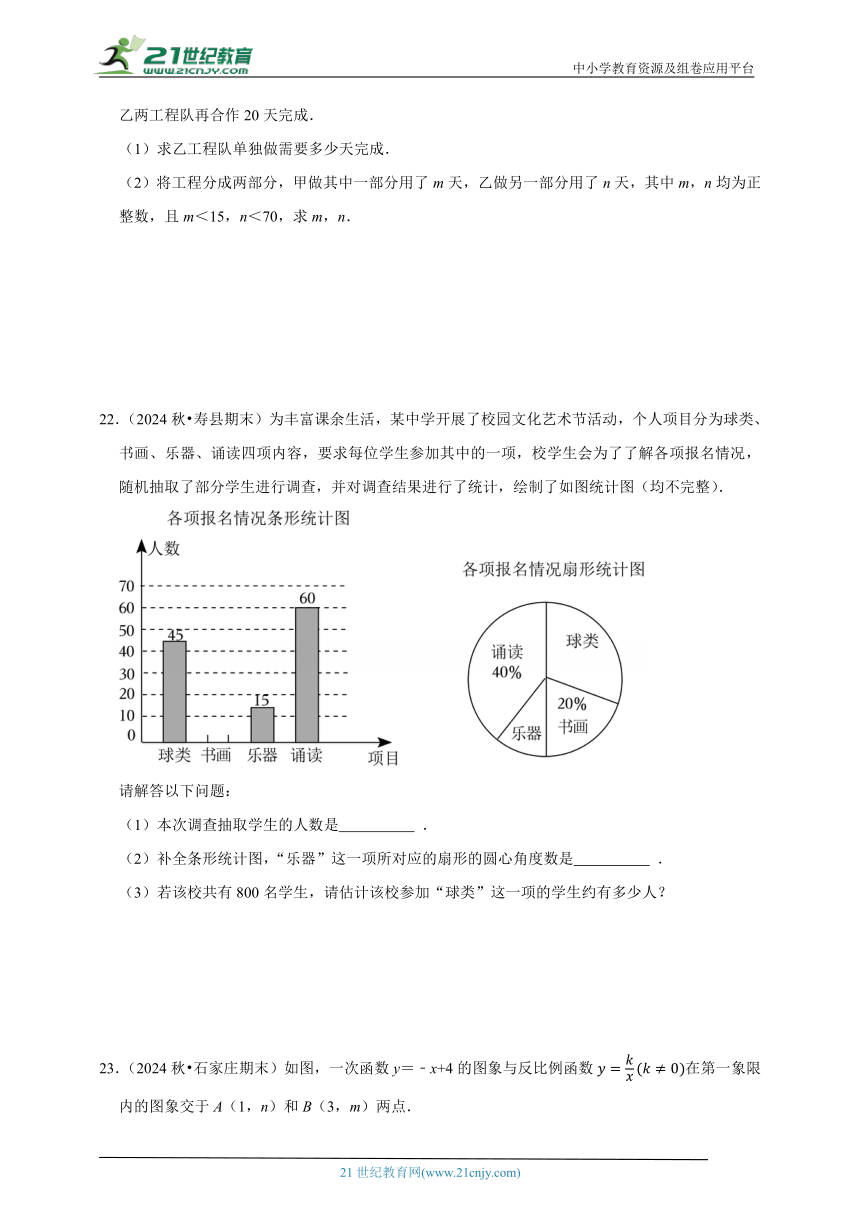
15.(2024秋 白云区期末)如图,点A在x轴的负半轴上,点C在反比例函数的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 .
16.(2024秋 招远市期末)如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠ABE的度数为80°,则∠BAD的度数为 .
三.解答题(共9小题)
17.(2024秋 白银期末)计算:215.
18.(2024秋 城关区校级期末)解分式方程:.
19.(2024秋 郏县期末)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)填空:①当△ABC满足条件∠BAC=90°时,四边形AFBD是 形;
②当△ABC满足条件 时,四边形AFBD是正方形.
20.(2024秋 渠县校级期末)已知x,y,求下列各式的值.
(1);
(2)x2﹣3xy+y2.
21.(2024秋 安定区期末)一项工程,甲工程队单独做40天完成.若乙工程队单独做30天后,甲、乙两工程队再合作20天完成.
(1)求乙工程队单独做需要多少天完成.
(2)将工程分成两部分,甲做其中一部分用了m天,乙做另一部分用了n天,其中m,n均为正整数,且m<15,n<70,求m,n.
22.(2024秋 寿县期末)为丰富课余生活,某中学开展了校园文化艺术节活动,个人项目分为球类、书画、乐器、诵读四项内容,要求每位学生参加其中的一项,校学生会为了了解各项报名情况,随机抽取了部分学生进行调查,并对调查结果进行了统计,绘制了如图统计图(均不完整).
请解答以下问题:
(1)本次调查抽取学生的人数是 .
(2)补全条形统计图,“乐器”这一项所对应的扇形的圆心角度数是 .
(3)若该校共有800名学生,请估计该校参加“球类”这一项的学生约有多少人?
23.(2024秋 石家庄期末)如图,一次函数y=﹣x+4的图象与反比例函数在第一象限内的图象交于A(1,n)和B(3,m)两点.
(1)求反比例函数的表达式;
(2)求△AOB面积;
(3)在第一象限内,当一次函数y=﹣x+4的值大于反比例函数的值时,直接写出自变量x的取值范围.
24.(2024秋 涟源市期末)已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1)AE∥FB;
(2)四边形CFDE是平行四边形.
25.(2024秋 绵阳期末)如图,在直角坐标系中,面积为18的矩形ABCD的AB边在y轴上,点D的坐标为(2,6),双曲线经过点C.
(1)求双曲线的解析式;
(2)连接OD,若将矩形ABCD沿着x轴的负方向平移t个单位时,线段OD与双曲线恰有两个公共点,求t的取值范围.
【期末押题卷】2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C B D C C C D D
一.选择题(共8小题)
1.(2023秋 沈丘县期末)商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
【解答】解:根据概率的意义可得“抽到一等奖的概率为0.1”就是说抽10次可能抽到一等奖,也可能没有抽到一等奖,
故选:C.
2.(2024秋 澄迈县期末)若分式有意义,则a的取值范围是( )
A.a≠0 B.a≠3 C.a<3 D.a≥3
【解答】解:∵分式有意义,
∴a﹣3≠0,解得a≠3,
故选:B.
3.(2024秋 天津期末)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不符合题意
B.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
D.是轴对称图形,又是中心对称图形,故此选项符合题意.
故选:D.
4.(2025春 锦江区校级期末)已知分式P,Q,其中n为任意正整数,则P,Q的大小关系为( )
A.P<Q
B.P=Q
C.P>Q
D.P,Q的大小关系与n的取值有关
【解答】解:P﹣Q
,
∵n为任意正整数,
∴n(n+1)>0,
∴0,
∴P>Q,
故选:C.
5.(2024秋 南关区校级期末)实数a,b在数轴上的位置如图所示,化简|a﹣b|的结果是( )
A.a B.﹣a C.a﹣2b D.﹣a+2b
【解答】解:∵由图可知,b<0<a,|b|>a,
∴a﹣b>0,
∴原式=a﹣b﹣b=a﹣2b.
故选:C.
6.(2024秋 水城区期末)菱形ABCD的边长为3cm,那么菱形的周长是( )
A.9cm B.15cm C.12cm D.18cm
【解答】解:∵四边形ABCD是菱形,
∴菱形ABCD的周长=4×3=12(cm),
故选:C.
7.(2024秋 渠县期末)已知反比例函数的图象上有点A(x1,y1),B(x2,y2),C(x3,y3),且x1>x2>0>x3,则关于y1,y2,y3大小关系正确的是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
【解答】解:由条件可知反比例函数的图象在二,四象限,在每个象限内,y随x的增大而增大,
又∵x1>x2>0>x3,
∴y3>y1>y2.
故选:D.
8.(2025春 锦江区校级期末)如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接AE.若AE∥BD,则∠CAD的度数为( )
A.100° B.90° C.70° D.60°
【解答】解:由旋转变换的性质可知:AB=AD,∠BAD=100°,
∴∠ABD=∠ADB(180°﹣100°)=40°,
∵AE∥BD,
∴∠EAD=∠ADB=40°,
∵∠CAE=∠BAD=100°,
∴∠CAD=∠CAE﹣∠EAD=60°.
故选:D.
二.填空题(共8小题)
9.(2024秋 荔湾区期末)若分式有意义,则x的取值范围是 x≠2 .
【解答】解:根据题意得x﹣2≠0,
∴x≠2,
故答案为:x≠2
10.(2024秋 太原期末)已知,四边形ABCD是平行四边形,对角线AC,BD交于点O.若增加一个条件,将它边的数量关系特殊化,可使AC⊥BD,则增加的一个条件可以是 AB=BC(答案不唯一) .(写出一个即可)
【解答】解:当AB=BC时, ABCD为菱形,
此时AC⊥BD.
∴增加的一个条件可以是AB=BC.
故答案为:AB=BC(答案不唯一).
11.(2017秋 简阳市期末)已知实数x,y满足条件y3,则xy= 8 .
【解答】解:由题意,得
,
解得x=2,
y=3.
xy=23=8,
故答案为:8.
12.(2020秋 开州区期末)如图,在矩形ABCD中,AB=4,BC=7,EA平分∠BAD交BC于点E,连接DE,将矩形ABCD沿DE翻折,翻折后点D与点D'点对应,再将所得△C'D'E绕着点E旋转,线段C'D'与线段ED交于点P.当PD=PC'时,则DC'的长为 .
【解答】解:∵四边形ABCD是矩形,
∴AB=CD=4,∠BAD=∠C=∠B=90°,
∵EA平分∠BAD交BC于点E,
∴∠BAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=BE=4,
∴EC=BC﹣BE=3,
∴DE5,
∵将矩形ABCD沿DE翻折,
∴CE=C'E=3,
如图,
设C′P=x,则DP=x,PE=DE﹣DP=5﹣x,
在Rt△EC′P中,(5﹣x)2=x2+32,
∴x,
∴C'P=DP,
∴EP=5,
∵sin∠C'EP,
∴,
∴C'H,
∵cos∠C'EP,
∴,
∴EH,
∴DH=DE﹣EH,
∴C'D,
故答案为.
13.(2024秋 阳谷县期末)若关于x的分式方程有增根,则m的值为 ﹣2 .
【解答】解:,
x﹣1=m﹣2(x+1),
解得:x,
∵分式方程有增根,
∴x+1=0,
∴x=﹣1,
把x=﹣1代入x中得:1,
解得:m=﹣2,
故答案为:﹣2.
14.(2024秋 太康县期末)某地区6月8日~14日的气温折线统计图如图所示,则这一周中温差最大的日期是 6月14日 .
【解答】解:6月8日的温差为:27﹣23=4;6月9日的温差为:29﹣23=6;
6月10日的温差为:29﹣24=5;6月11日的温差为:28﹣25=3;
6月12日的温差为:31﹣24=7;6月13日的温差为:34﹣25=9;
6月14日的温差为:35﹣25=10;
且3<4<5<6<7<9<10.
故答案为:6月14日.
15.(2024秋 白云区期末)如图,点A在x轴的负半轴上,点C在反比例函数的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 10 .
【解答】解:如图,过点C作CD⊥y轴于D,
∴∠CDB=∠AOB=90°,
∵点B是AC的中点,
∴AB=CB,
在△ABO和△BCD中,
,
∴△CDB≌△AOB(AAS),
∴BD=OB,
∴S△CDB=S△AOB=S△BCO,
∴S△COD=5,
∴|k|=S△COD=5,
∴|k|=10,
∵k>0,
∴k=10.
故答案为:10.
16.(2024秋 招远市期末)如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠ABE的度数为80°,则∠BAD的度数为 10° .
【解答】解:∵△ABC是等腰直角三角形,
∴BC=AC,
∠ABC=∠BAC=45°,
∵∠ABE=80°,
∴∠EBC=∠ABE﹣∠ABC=80°﹣45°=35°,
∵∠BCE+∠BCD=∠ECD=90°,
∠BCD+∠ACD=∠BCA=90°,
∴∠BCE=∠ACD,
由题意得,CE=CD,
在△BEC和△ADC中,
,
∴△BEC≌△ADC(SAS),
∴∠DAC=∠EBC=35°,
∴∠BAD=∠BAC﹣∠DAC=45°﹣35°=10°,
故答案为:10°.
三.解答题(共9小题)
17.(2024秋 白银期末)计算:215.
【解答】解:原式=25
=6.
18.(2024秋 城关区校级期末)解分式方程:.
【解答】解:原方程去分母得:x+1﹣(2x﹣1)=x2﹣1,
整理得:x2+x﹣3=0,
∵a=1,b=1,c=﹣3,
∴Δ=12﹣4×1×(﹣3)=13>0,
则x,
即x1,x2,
经检验,x1,x2都是原方程的解.
19.(2024秋 郏县期末)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)填空:①当△ABC满足条件∠BAC=90°时,四边形AFBD是 菱 形;
②当△ABC满足条件 ∠BAC=90°,AB=AC 时,四边形AFBD是正方形.
【解答】(1)证明:∵E为AD的中点,D为BC中点,
∴AE=DE,BD=CD,
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
在△AFE和△DCE中,
,
∴△AFE≌△DCE(AAS),
∴AF=CD,
∴AF=BD,
∵AF∥BD
∴四边形AFBD为平行四边形;
(2)解:①当△ABC满足条件∠BAC=90°时,四边形AFBD是菱形,理由为:
∵E为AD的中点,D为BC中点,
∴AE=DE,BD=CD,
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
在△AFE和△DCE中,
,
∴△AFE≌△DCE(AAS),
∴AF=CD,
∴AF=BD,
∵AF∥BD
∴四边形AFBD为平行四边形;
∵∠BAC=90°,D是BC的中点,
∴
∵四边形AFBD为平行四边形,AD=BD;
∴四边形AFBD为菱形;
故答案为:菱形;
②当△ABC满足条件∠BAC=90°,AB=AC时,四边形AFBD是正方形,理由为:
由①知当△ABC满足条件∠BAC=90°时,四边形AFBD是菱形,
∵AB=AC,D为BC中点,
∴AD为BC边上的中线,
∴AD⊥BC,即∠ADB=90°,
∵四边形AFBD是菱形,∠ADB=90°
∴四边形AFBD为正方形.
故答案为:∠BAC=90°,AB=AC.
20.(2024秋 渠县校级期末)已知x,y,求下列各式的值.
(1);
(2)x2﹣3xy+y2.
【解答】解:(1)∵x(2)2=7﹣4,y(2)2=7+4,
∴;
(2)x2﹣3xy+y2=(x﹣y)2﹣xy
=(7﹣47﹣4)2﹣(7﹣4)(7+4)
=192﹣(49﹣48)
=191.
21.(2024秋 安定区期末)一项工程,甲工程队单独做40天完成.若乙工程队单独做30天后,甲、乙两工程队再合作20天完成.
(1)求乙工程队单独做需要多少天完成.
(2)将工程分成两部分,甲做其中一部分用了m天,乙做另一部分用了n天,其中m,n均为正整数,且m<15,n<70,求m,n.
【解答】解:(1)设乙工程队单独做需要x天完成,
根据题意得:1,
解得:x=100,
经检验,x=100是所列方程的解,且符合题意.
答:乙工程队单独做需要100天完成;
(2)根据题意得:1,
∴n=100m,
又∵m,n均为正整数,且m<15,n<70,
∴.
答:m的值为14,n的值为65.
22.(2024秋 寿县期末)为丰富课余生活,某中学开展了校园文化艺术节活动,个人项目分为球类、书画、乐器、诵读四项内容,要求每位学生参加其中的一项,校学生会为了了解各项报名情况,随机抽取了部分学生进行调查,并对调查结果进行了统计,绘制了如图统计图(均不完整).
请解答以下问题:
(1)本次调查抽取学生的人数是 150 .
(2)补全条形统计图,“乐器”这一项所对应的扇形的圆心角度数是 36° .
(3)若该校共有800名学生,请估计该校参加“球类”这一项的学生约有多少人?
【解答】解:(1)由条形图可知,参加诵读活动的人数为60人,
由扇形图可知,参加诵读活动的人数占40%,
则抽取的学生数为:60÷40%=150(人),
故答案为:150;
(2)“书画”的人数是:150×20%=30(人),
补全统计图如下:
“乐器”这一项所对应的扇形的圆心角度数是360°=36°;
故答案为:36°;
(3)根据题意得:800240(人),
答:估计该校参加“球类”这一项的学生约有240人.
23.(2024秋 石家庄期末)如图,一次函数y=﹣x+4的图象与反比例函数在第一象限内的图象交于A(1,n)和B(3,m)两点.
(1)求反比例函数的表达式;
(2)求△AOB面积;
(3)在第一象限内,当一次函数y=﹣x+4的值大于反比例函数的值时,直接写出自变量x的取值范围.
【解答】解:(1)将点A(1,n)代入y=﹣x+4得,
﹣1+4=n,
解得n=3,
所以点A的坐标为(1,3).
将点A坐标代入y得,
k=1×3=3,
所以反比例函数的表达式为y.
(2)两直线AB与y轴和x轴的交点分别为M和N,
将点B坐标代入y=﹣x+4得,
m=1,
所以点B坐标为(3,1).
将x=0代入y=﹣x+4得,
y=4,
所以点M的坐标为(0,4),
同理可得,点N的坐标为(4,0),
所以,,
所以S△AOB=S△MON﹣S△AOM﹣S△BON=8﹣2﹣2=4.
(3)由函数图象可知,
在第一象限内,当1<x<3时,一次函数的图象在反比例函数图象的上方,
所以自变量x的取值范围是1<x<3.
24.(2024秋 涟源市期末)已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1)AE∥FB;
(2)四边形CFDE是平行四边形.
【解答】(1)证明:∵点A,D,C,B在同一条直线上,AD=BC,
∴AD+DC=BC+CD,
即AC=BD,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE∥FB;
(2)证明:∵AD=BC,AE=BF,∠A=∠B,
∴△ADE≌△BCF(SAS),
∴DE=CF,
又∵CE=DF,
∴四边形CFDE是平行四边形.
25.(2024秋 绵阳期末)如图,在直角坐标系中,面积为18的矩形ABCD的AB边在y轴上,点D的坐标为(2,6),双曲线经过点C.
(1)求双曲线的解析式;
(2)连接OD,若将矩形ABCD沿着x轴的负方向平移t个单位时,线段OD与双曲线恰有两个公共点,求t的取值范围.
【解答】解:(1)由条件可得点C和点D的横坐标相等,
设点C(2,yc),
∴BC=2,CD=﹣yc+6,
∴S ABCD=BC CD=2×(﹣yc+6)=18,
解得:yc=﹣3,
∴C(2,﹣3),
把C(2,﹣3)代入双曲线,
解得:k=﹣6,
∴双曲线;
(2)设直线OD的解析式为y=k1x(k1≠0),
∵点D的坐标为(2,6),
∴k1=3,
∴直线OD的解析式为y=3x,
平移后的直线OD的解析式为y=3(x+t),
∴,
化简得:x2+tx+2=0,
∵平移后的线段OD与双曲线恰有两个公共点,
∴Δ=b2﹣4ac=t2﹣8=0,
即解得:,
∵t>0,
∴,
∴当时,平移后的线段OD与双曲线有1个公共点,
∴当时,平移后的线段OD与双曲线恰有两个公共点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末押题卷】2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2023秋 沈丘县期末)商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
2.(2024秋 澄迈县期末)若分式有意义,则a的取值范围是( )
A.a≠0 B.a≠3 C.a<3 D.a≥3
3.(2024秋 天津期末)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.(2025春 锦江区校级期末)已知分式P,Q,其中n为任意正整数,则P,Q的大小关系为( )
A.P<Q
B.P=Q
C.P>Q
D.P,Q的大小关系与n的取值有关
5.(2024秋 南关区校级期末)实数a,b在数轴上的位置如图所示,化简|a﹣b|的结果是( )
A.a B.﹣a C.a﹣2b D.﹣a+2b
6.(2024秋 水城区期末)菱形ABCD的边长为3cm,那么菱形的周长是( )
A.9cm B.15cm C.12cm D.18cm
7.(2024秋 渠县期末)已知反比例函数的图象上有点A(x1,y1),B(x2,y2),C(x3,y3),且x1>x2>0>x3,则关于y1,y2,y3大小关系正确的是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
8.(2025春 锦江区校级期末)如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接AE.若AE∥BD,则∠CAD的度数为( )
A.100° B.90° C.70° D.60°
二.填空题(共8小题)
9.(2024秋 荔湾区期末)若分式有意义,则x的取值范围是 .
10.(2024秋 太原期末)已知,四边形ABCD是平行四边形,对角线AC,BD交于点O.若增加一个条件,将它边的数量关系特殊化,可使AC⊥BD,则增加的一个条件可以是 .(写出一个即可)
11.(2017秋 简阳市期末)已知实数x,y满足条件y3,则xy= .
12.(2020秋 开州区期末)如图,在矩形ABCD中,AB=4,BC=7,EA平分∠BAD交BC于点E,连接DE,将矩形ABCD沿DE翻折,翻折后点D与点D'点对应,再将所得△C'D'E绕着点E旋转,线段C'D'与线段ED交于点P.当PD=PC'时,则DC'的长为 .
13.(2024秋 阳谷县期末)若关于x的分式方程有增根,则m的值为 .
14.(2024秋 太康县期末)某地区6月8日~14日的气温折线统计图如图所示,则这一周中温差最大的日期是 .
15.(2024秋 白云区期末)如图,点A在x轴的负半轴上,点C在反比例函数的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 .
16.(2024秋 招远市期末)如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠ABE的度数为80°,则∠BAD的度数为 .
三.解答题(共9小题)
17.(2024秋 白银期末)计算:215.
18.(2024秋 城关区校级期末)解分式方程:.
19.(2024秋 郏县期末)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)填空:①当△ABC满足条件∠BAC=90°时,四边形AFBD是 形;
②当△ABC满足条件 时,四边形AFBD是正方形.
20.(2024秋 渠县校级期末)已知x,y,求下列各式的值.
(1);
(2)x2﹣3xy+y2.
21.(2024秋 安定区期末)一项工程,甲工程队单独做40天完成.若乙工程队单独做30天后,甲、乙两工程队再合作20天完成.
(1)求乙工程队单独做需要多少天完成.
(2)将工程分成两部分,甲做其中一部分用了m天,乙做另一部分用了n天,其中m,n均为正整数,且m<15,n<70,求m,n.
22.(2024秋 寿县期末)为丰富课余生活,某中学开展了校园文化艺术节活动,个人项目分为球类、书画、乐器、诵读四项内容,要求每位学生参加其中的一项,校学生会为了了解各项报名情况,随机抽取了部分学生进行调查,并对调查结果进行了统计,绘制了如图统计图(均不完整).
请解答以下问题:
(1)本次调查抽取学生的人数是 .
(2)补全条形统计图,“乐器”这一项所对应的扇形的圆心角度数是 .
(3)若该校共有800名学生,请估计该校参加“球类”这一项的学生约有多少人?
23.(2024秋 石家庄期末)如图,一次函数y=﹣x+4的图象与反比例函数在第一象限内的图象交于A(1,n)和B(3,m)两点.
(1)求反比例函数的表达式;
(2)求△AOB面积;
(3)在第一象限内,当一次函数y=﹣x+4的值大于反比例函数的值时,直接写出自变量x的取值范围.
24.(2024秋 涟源市期末)已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1)AE∥FB;
(2)四边形CFDE是平行四边形.
25.(2024秋 绵阳期末)如图,在直角坐标系中,面积为18的矩形ABCD的AB边在y轴上,点D的坐标为(2,6),双曲线经过点C.
(1)求双曲线的解析式;
(2)连接OD,若将矩形ABCD沿着x轴的负方向平移t个单位时,线段OD与双曲线恰有两个公共点,求t的取值范围.
【期末押题卷】2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C B D C C C D D
一.选择题(共8小题)
1.(2023秋 沈丘县期末)商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”.下列说法正确的是( )
A.抽10次奖必有一次抽到一等奖
B.抽一次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
【解答】解:根据概率的意义可得“抽到一等奖的概率为0.1”就是说抽10次可能抽到一等奖,也可能没有抽到一等奖,
故选:C.
2.(2024秋 澄迈县期末)若分式有意义,则a的取值范围是( )
A.a≠0 B.a≠3 C.a<3 D.a≥3
【解答】解:∵分式有意义,
∴a﹣3≠0,解得a≠3,
故选:B.
3.(2024秋 天津期末)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不符合题意
B.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
D.是轴对称图形,又是中心对称图形,故此选项符合题意.
故选:D.
4.(2025春 锦江区校级期末)已知分式P,Q,其中n为任意正整数,则P,Q的大小关系为( )
A.P<Q
B.P=Q
C.P>Q
D.P,Q的大小关系与n的取值有关
【解答】解:P﹣Q
,
∵n为任意正整数,
∴n(n+1)>0,
∴0,
∴P>Q,
故选:C.
5.(2024秋 南关区校级期末)实数a,b在数轴上的位置如图所示,化简|a﹣b|的结果是( )
A.a B.﹣a C.a﹣2b D.﹣a+2b
【解答】解:∵由图可知,b<0<a,|b|>a,
∴a﹣b>0,
∴原式=a﹣b﹣b=a﹣2b.
故选:C.
6.(2024秋 水城区期末)菱形ABCD的边长为3cm,那么菱形的周长是( )
A.9cm B.15cm C.12cm D.18cm
【解答】解:∵四边形ABCD是菱形,
∴菱形ABCD的周长=4×3=12(cm),
故选:C.
7.(2024秋 渠县期末)已知反比例函数的图象上有点A(x1,y1),B(x2,y2),C(x3,y3),且x1>x2>0>x3,则关于y1,y2,y3大小关系正确的是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
【解答】解:由条件可知反比例函数的图象在二,四象限,在每个象限内,y随x的增大而增大,
又∵x1>x2>0>x3,
∴y3>y1>y2.
故选:D.
8.(2025春 锦江区校级期末)如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接AE.若AE∥BD,则∠CAD的度数为( )
A.100° B.90° C.70° D.60°
【解答】解:由旋转变换的性质可知:AB=AD,∠BAD=100°,
∴∠ABD=∠ADB(180°﹣100°)=40°,
∵AE∥BD,
∴∠EAD=∠ADB=40°,
∵∠CAE=∠BAD=100°,
∴∠CAD=∠CAE﹣∠EAD=60°.
故选:D.
二.填空题(共8小题)
9.(2024秋 荔湾区期末)若分式有意义,则x的取值范围是 x≠2 .
【解答】解:根据题意得x﹣2≠0,
∴x≠2,
故答案为:x≠2
10.(2024秋 太原期末)已知,四边形ABCD是平行四边形,对角线AC,BD交于点O.若增加一个条件,将它边的数量关系特殊化,可使AC⊥BD,则增加的一个条件可以是 AB=BC(答案不唯一) .(写出一个即可)
【解答】解:当AB=BC时, ABCD为菱形,
此时AC⊥BD.
∴增加的一个条件可以是AB=BC.
故答案为:AB=BC(答案不唯一).
11.(2017秋 简阳市期末)已知实数x,y满足条件y3,则xy= 8 .
【解答】解:由题意,得
,
解得x=2,
y=3.
xy=23=8,
故答案为:8.
12.(2020秋 开州区期末)如图,在矩形ABCD中,AB=4,BC=7,EA平分∠BAD交BC于点E,连接DE,将矩形ABCD沿DE翻折,翻折后点D与点D'点对应,再将所得△C'D'E绕着点E旋转,线段C'D'与线段ED交于点P.当PD=PC'时,则DC'的长为 .
【解答】解:∵四边形ABCD是矩形,
∴AB=CD=4,∠BAD=∠C=∠B=90°,
∵EA平分∠BAD交BC于点E,
∴∠BAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=BE=4,
∴EC=BC﹣BE=3,
∴DE5,
∵将矩形ABCD沿DE翻折,
∴CE=C'E=3,
如图,
设C′P=x,则DP=x,PE=DE﹣DP=5﹣x,
在Rt△EC′P中,(5﹣x)2=x2+32,
∴x,
∴C'P=DP,
∴EP=5,
∵sin∠C'EP,
∴,
∴C'H,
∵cos∠C'EP,
∴,
∴EH,
∴DH=DE﹣EH,
∴C'D,
故答案为.
13.(2024秋 阳谷县期末)若关于x的分式方程有增根,则m的值为 ﹣2 .
【解答】解:,
x﹣1=m﹣2(x+1),
解得:x,
∵分式方程有增根,
∴x+1=0,
∴x=﹣1,
把x=﹣1代入x中得:1,
解得:m=﹣2,
故答案为:﹣2.
14.(2024秋 太康县期末)某地区6月8日~14日的气温折线统计图如图所示,则这一周中温差最大的日期是 6月14日 .
【解答】解:6月8日的温差为:27﹣23=4;6月9日的温差为:29﹣23=6;
6月10日的温差为:29﹣24=5;6月11日的温差为:28﹣25=3;
6月12日的温差为:31﹣24=7;6月13日的温差为:34﹣25=9;
6月14日的温差为:35﹣25=10;
且3<4<5<6<7<9<10.
故答案为:6月14日.
15.(2024秋 白云区期末)如图,点A在x轴的负半轴上,点C在反比例函数的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 10 .
【解答】解:如图,过点C作CD⊥y轴于D,
∴∠CDB=∠AOB=90°,
∵点B是AC的中点,
∴AB=CB,
在△ABO和△BCD中,
,
∴△CDB≌△AOB(AAS),
∴BD=OB,
∴S△CDB=S△AOB=S△BCO,
∴S△COD=5,
∴|k|=S△COD=5,
∴|k|=10,
∵k>0,
∴k=10.
故答案为:10.
16.(2024秋 招远市期末)如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠ABE的度数为80°,则∠BAD的度数为 10° .
【解答】解:∵△ABC是等腰直角三角形,
∴BC=AC,
∠ABC=∠BAC=45°,
∵∠ABE=80°,
∴∠EBC=∠ABE﹣∠ABC=80°﹣45°=35°,
∵∠BCE+∠BCD=∠ECD=90°,
∠BCD+∠ACD=∠BCA=90°,
∴∠BCE=∠ACD,
由题意得,CE=CD,
在△BEC和△ADC中,
,
∴△BEC≌△ADC(SAS),
∴∠DAC=∠EBC=35°,
∴∠BAD=∠BAC﹣∠DAC=45°﹣35°=10°,
故答案为:10°.
三.解答题(共9小题)
17.(2024秋 白银期末)计算:215.
【解答】解:原式=25
=6.
18.(2024秋 城关区校级期末)解分式方程:.
【解答】解:原方程去分母得:x+1﹣(2x﹣1)=x2﹣1,
整理得:x2+x﹣3=0,
∵a=1,b=1,c=﹣3,
∴Δ=12﹣4×1×(﹣3)=13>0,
则x,
即x1,x2,
经检验,x1,x2都是原方程的解.
19.(2024秋 郏县期末)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)填空:①当△ABC满足条件∠BAC=90°时,四边形AFBD是 菱 形;
②当△ABC满足条件 ∠BAC=90°,AB=AC 时,四边形AFBD是正方形.
【解答】(1)证明:∵E为AD的中点,D为BC中点,
∴AE=DE,BD=CD,
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
在△AFE和△DCE中,
,
∴△AFE≌△DCE(AAS),
∴AF=CD,
∴AF=BD,
∵AF∥BD
∴四边形AFBD为平行四边形;
(2)解:①当△ABC满足条件∠BAC=90°时,四边形AFBD是菱形,理由为:
∵E为AD的中点,D为BC中点,
∴AE=DE,BD=CD,
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
在△AFE和△DCE中,
,
∴△AFE≌△DCE(AAS),
∴AF=CD,
∴AF=BD,
∵AF∥BD
∴四边形AFBD为平行四边形;
∵∠BAC=90°,D是BC的中点,
∴
∵四边形AFBD为平行四边形,AD=BD;
∴四边形AFBD为菱形;
故答案为:菱形;
②当△ABC满足条件∠BAC=90°,AB=AC时,四边形AFBD是正方形,理由为:
由①知当△ABC满足条件∠BAC=90°时,四边形AFBD是菱形,
∵AB=AC,D为BC中点,
∴AD为BC边上的中线,
∴AD⊥BC,即∠ADB=90°,
∵四边形AFBD是菱形,∠ADB=90°
∴四边形AFBD为正方形.
故答案为:∠BAC=90°,AB=AC.
20.(2024秋 渠县校级期末)已知x,y,求下列各式的值.
(1);
(2)x2﹣3xy+y2.
【解答】解:(1)∵x(2)2=7﹣4,y(2)2=7+4,
∴;
(2)x2﹣3xy+y2=(x﹣y)2﹣xy
=(7﹣47﹣4)2﹣(7﹣4)(7+4)
=192﹣(49﹣48)
=191.
21.(2024秋 安定区期末)一项工程,甲工程队单独做40天完成.若乙工程队单独做30天后,甲、乙两工程队再合作20天完成.
(1)求乙工程队单独做需要多少天完成.
(2)将工程分成两部分,甲做其中一部分用了m天,乙做另一部分用了n天,其中m,n均为正整数,且m<15,n<70,求m,n.
【解答】解:(1)设乙工程队单独做需要x天完成,
根据题意得:1,
解得:x=100,
经检验,x=100是所列方程的解,且符合题意.
答:乙工程队单独做需要100天完成;
(2)根据题意得:1,
∴n=100m,
又∵m,n均为正整数,且m<15,n<70,
∴.
答:m的值为14,n的值为65.
22.(2024秋 寿县期末)为丰富课余生活,某中学开展了校园文化艺术节活动,个人项目分为球类、书画、乐器、诵读四项内容,要求每位学生参加其中的一项,校学生会为了了解各项报名情况,随机抽取了部分学生进行调查,并对调查结果进行了统计,绘制了如图统计图(均不完整).
请解答以下问题:
(1)本次调查抽取学生的人数是 150 .
(2)补全条形统计图,“乐器”这一项所对应的扇形的圆心角度数是 36° .
(3)若该校共有800名学生,请估计该校参加“球类”这一项的学生约有多少人?
【解答】解:(1)由条形图可知,参加诵读活动的人数为60人,
由扇形图可知,参加诵读活动的人数占40%,
则抽取的学生数为:60÷40%=150(人),
故答案为:150;
(2)“书画”的人数是:150×20%=30(人),
补全统计图如下:
“乐器”这一项所对应的扇形的圆心角度数是360°=36°;
故答案为:36°;
(3)根据题意得:800240(人),
答:估计该校参加“球类”这一项的学生约有240人.
23.(2024秋 石家庄期末)如图,一次函数y=﹣x+4的图象与反比例函数在第一象限内的图象交于A(1,n)和B(3,m)两点.
(1)求反比例函数的表达式;
(2)求△AOB面积;
(3)在第一象限内,当一次函数y=﹣x+4的值大于反比例函数的值时,直接写出自变量x的取值范围.
【解答】解:(1)将点A(1,n)代入y=﹣x+4得,
﹣1+4=n,
解得n=3,
所以点A的坐标为(1,3).
将点A坐标代入y得,
k=1×3=3,
所以反比例函数的表达式为y.
(2)两直线AB与y轴和x轴的交点分别为M和N,
将点B坐标代入y=﹣x+4得,
m=1,
所以点B坐标为(3,1).
将x=0代入y=﹣x+4得,
y=4,
所以点M的坐标为(0,4),
同理可得,点N的坐标为(4,0),
所以,,
所以S△AOB=S△MON﹣S△AOM﹣S△BON=8﹣2﹣2=4.
(3)由函数图象可知,
在第一象限内,当1<x<3时,一次函数的图象在反比例函数图象的上方,
所以自变量x的取值范围是1<x<3.
24.(2024秋 涟源市期末)已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1)AE∥FB;
(2)四边形CFDE是平行四边形.
【解答】(1)证明:∵点A,D,C,B在同一条直线上,AD=BC,
∴AD+DC=BC+CD,
即AC=BD,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE∥FB;
(2)证明:∵AD=BC,AE=BF,∠A=∠B,
∴△ADE≌△BCF(SAS),
∴DE=CF,
又∵CE=DF,
∴四边形CFDE是平行四边形.
25.(2024秋 绵阳期末)如图,在直角坐标系中,面积为18的矩形ABCD的AB边在y轴上,点D的坐标为(2,6),双曲线经过点C.
(1)求双曲线的解析式;
(2)连接OD,若将矩形ABCD沿着x轴的负方向平移t个单位时,线段OD与双曲线恰有两个公共点,求t的取值范围.
【解答】解:(1)由条件可得点C和点D的横坐标相等,
设点C(2,yc),
∴BC=2,CD=﹣yc+6,
∴S ABCD=BC CD=2×(﹣yc+6)=18,
解得:yc=﹣3,
∴C(2,﹣3),
把C(2,﹣3)代入双曲线,
解得:k=﹣6,
∴双曲线;
(2)设直线OD的解析式为y=k1x(k1≠0),
∵点D的坐标为(2,6),
∴k1=3,
∴直线OD的解析式为y=3x,
平移后的直线OD的解析式为y=3(x+t),
∴,
化简得:x2+tx+2=0,
∵平移后的线段OD与双曲线恰有两个公共点,
∴Δ=b2﹣4ac=t2﹣8=0,
即解得:,
∵t>0,
∴,
∴当时,平移后的线段OD与双曲线有1个公共点,
∴当时,平移后的线段OD与双曲线恰有两个公共点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
