【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)(含解析)
文档属性
| 名称 | 【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 20:55:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2024秋 田阳区期末)下列常见的微信表情包中,属于轴对称图形的是( )
A. B. C. D.
2.(2024秋 桐柏县期末)数学课上,老师和同学们做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为2000,则“正面朝上”的频数最接近( )
A.400 B.600 C.1000 D.1600
3.(2024秋 武陟县期末)已知am=6,an=3,则am+n的值为( )
A.9 B.18 C.3 D.2
4.(2024秋 武陟县期末)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
5.(2024秋 顺城区期末)根据下列条件,能画出唯一△ABC的是( )
A.AB=5,AC=6,∠A=50°
B.AB=3,AC=4,∠C=30°
C.∠A=60°,∠B=45°,∠C=75°
D.AB=3,BC=4,AC=8
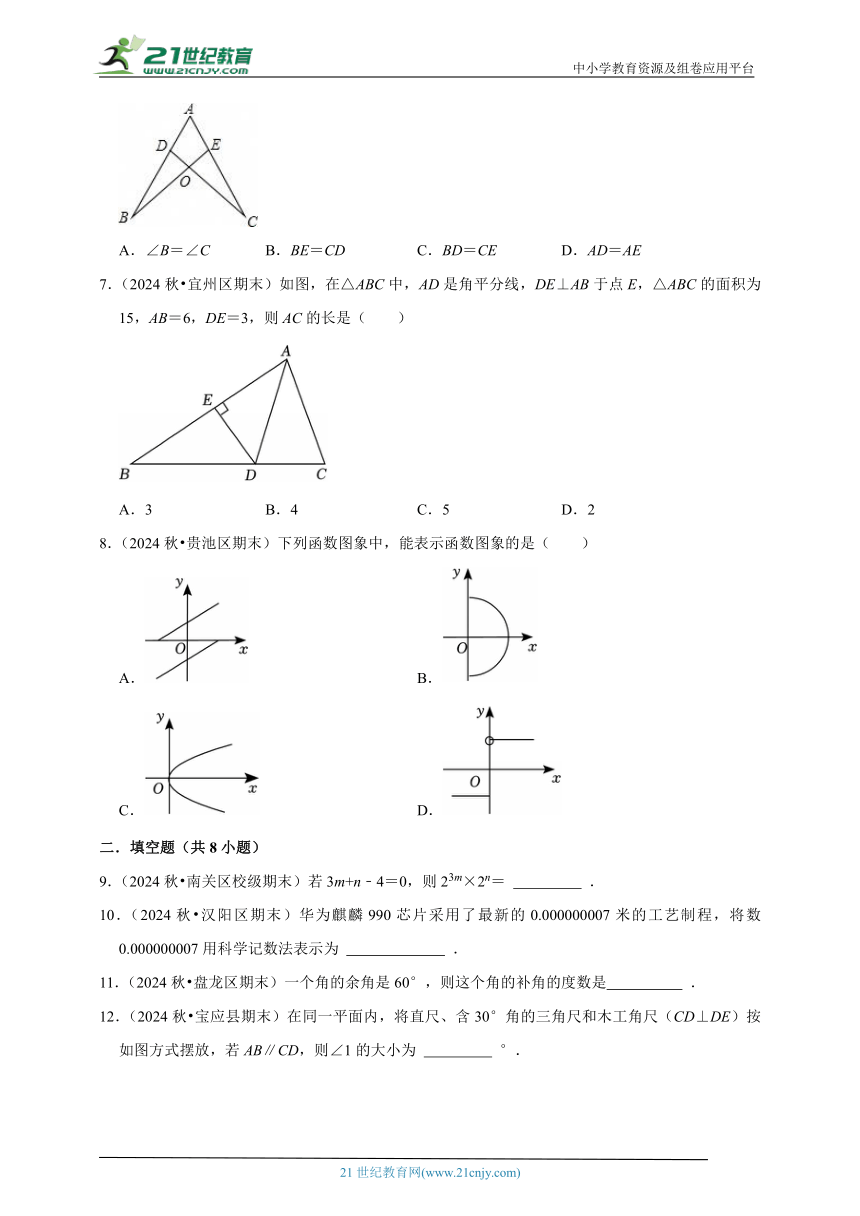
6.(2024秋 泰山区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.BE=CD C.BD=CE D.AD=AE
7.(2024秋 宜州区期末)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC的长是( )
A.3 B.4 C.5 D.2
8.(2024秋 贵池区期末)下列函数图象中,能表示函数图象的是( )
A. B.
C. D.
二.填空题(共8小题)
9.(2024秋 南关区校级期末)若3m+n﹣4=0,则23m×2n= .
10.(2024秋 汉阳区期末)华为麒麟990芯片采用了最新的0.000000007米的工艺制程,将数0.000000007用科学记数法表示为 .
11.(2024秋 盘龙区期末)一个角的余角是60°,则这个角的补角的度数是 .
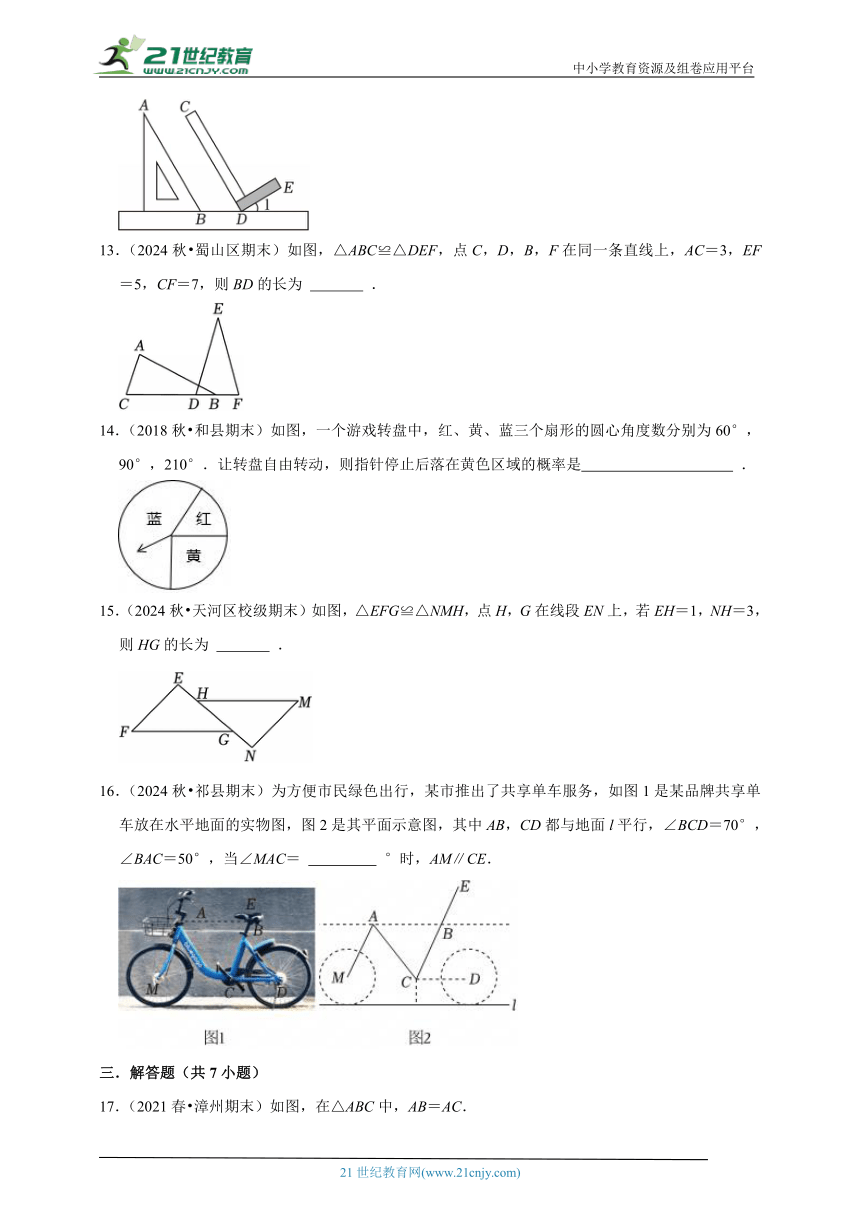
12.(2024秋 宝应县期末)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 °.
13.(2024秋 蜀山区期末)如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 .
14.(2018秋 和县期末)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,则指针停止后落在黄色区域的概率是 .
15.(2024秋 天河区校级期末)如图,△EFG≌△NMH,点H,G在线段EN上,若EH=1,NH=3,则HG的长为 .
16.(2024秋 祁县期末)为方便市民绿色出行,某市推出了共享单车服务,如图1是某品牌共享单车放在水平地面的实物图,图2是其平面示意图,其中AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,当∠MAC= °时,AM∥CE.
三.解答题(共7小题)
17.(2021春 漳州期末)如图,在△ABC中,AB=AC.
(1)利用尺规,作AB边的垂直平分线交AC于点D,交AB于点E.(不写作法,保留作图痕迹)
(2)在(1)中,连接BD,若BC=6,AB=8,求△BDC的周长.
18.(2025春 玉林期中)请将解答过程填写完整:
如图,EF∥AD,∠BAC=70°,若∠1=∠2,求∠AGD的度数.
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
∵∠1=∠2,
∴∠1= .(等量代换)
∴AB∥ .
∴ +∠BAC=180°.(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= .(等式的性质)
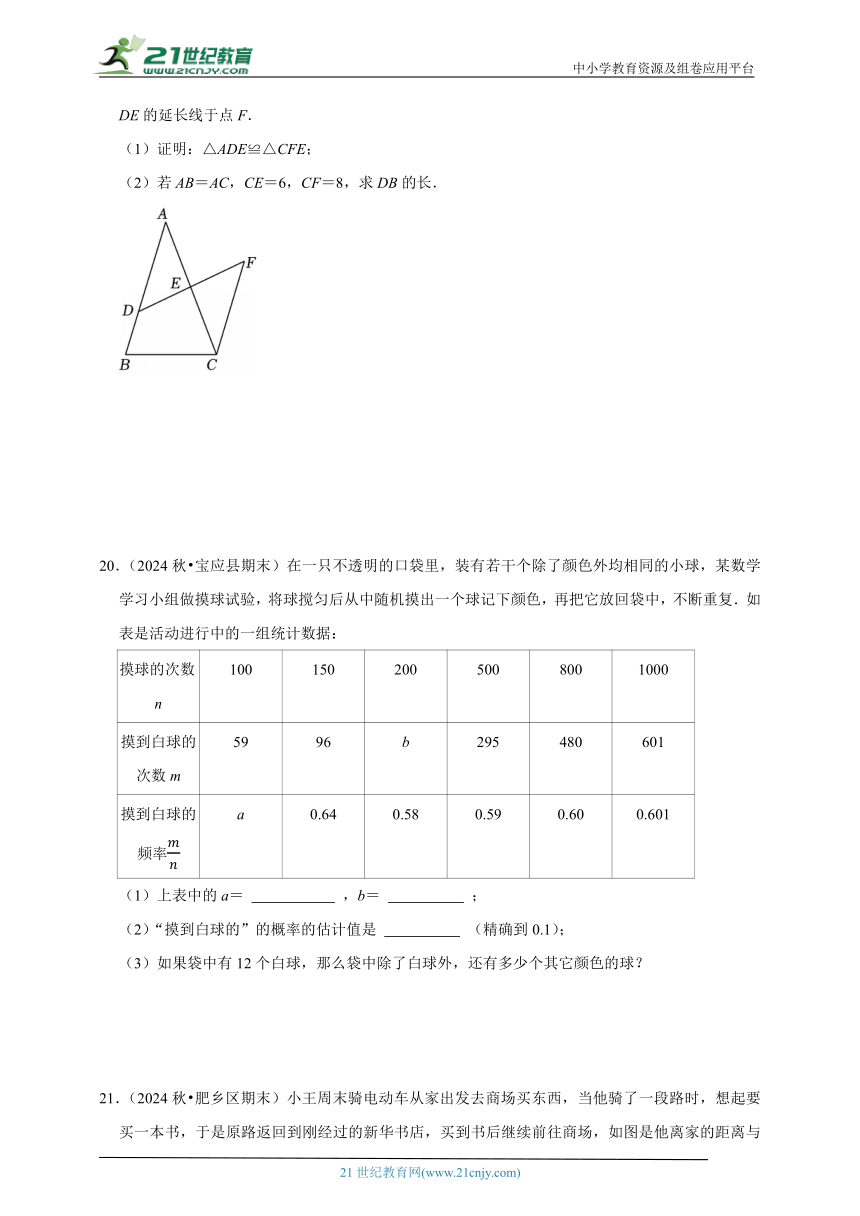
19.(2023秋 昆明期末)如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=6,CF=8,求DB的长.
20.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.(2024秋 肥乡区期末)小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王家距离书店多远?
(2)小王在新华书店停留了多长时间?
(3)新华书店到商场的距离是多少?
22.(2024秋 大名县期末)如图,在△ABC中,BD平分∠ABC,CD平分∠ACB,DE⊥AB于点E,DF⊥BC于点F.
(1)若∠ABC=40°,∠ACB=70°,求∠BDC的度数;
(2)若DE=2,BC=9,求△BCD的面积.
23.(2024秋 靖江市期末)如图1,点F在线段AB上,点E在线段CD上,∠1+∠2=180°,∠A=∠D.
(1)试说明:AB∥CD;
(2)如图2所示,延长AB到M,在∠MBC,∠BCD内部有一点P,连接BP,CP.若∠CBP=3∠MBP,∠BCP=3∠DCP,求∠BPC的度数.
【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C B C A B B D
一.选择题(共8小题)
1.(2024秋 田阳区期末)下列常见的微信表情包中,属于轴对称图形的是( )
A. B. C. D.
【解答】解:A选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,B、C、D选项中的图形都不是轴对称图形.
故选:A.
2.(2024秋 桐柏县期末)数学课上,老师和同学们做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为2000,则“正面朝上”的频数最接近( )
A.400 B.600 C.1000 D.1600
【解答】解:随着实验次数的增加,正面向上的频率逐渐稳定到某个常数附近,
,
观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,
则“正面朝上”的频数最接近2000×0.5=1000次,
故选:C.
3.(2024秋 武陟县期末)已知am=6,an=3,则am+n的值为( )
A.9 B.18 C.3 D.2
【解答】解:∵am=6,an=3,
∴am+n
=am an
=6×3
=18,
∴B符合题意,ACD不符合题意.
故选:B.
4.(2024秋 武陟县期末)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【解答】解:∵要使凉亭到草坪三条边的距离相等,
∴凉亭应在△ABC三条角平分线的交点处.
故选:C.
5.(2024秋 顺城区期末)根据下列条件,能画出唯一△ABC的是( )
A.AB=5,AC=6,∠A=50°
B.AB=3,AC=4,∠C=30°
C.∠A=60°,∠B=45°,∠C=75°
D.AB=3,BC=4,AC=8
【解答】解:A、AB=5,AC=6,∠A=50°,符合“SAS”,所以根据条件能画出唯一△ABC,故此选项符合题意;
B、AB=3,AC=4,∠C=30°,根据两边及一边对角不能判定两三角形全等,即作出的三角形不唯一,故此选项不符合题意;
C、∠A=60°,∠B=45°,∠C=75°,根据三角相等不能判定两三角形全等,即作出的三角形不唯一,故此选项不符合题意;
D、AB=3,BC=4,AC=8,∵3+4<8,∴不满足三角形三边的关系,即三边不能构成三角形,故此选项不符合题意;
故选:A.
6.(2024秋 泰山区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.BE=CD C.BD=CE D.AD=AE
【解答】解:∵AB=AC,∠A为公共角,
A、如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;
B、如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;
C、如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;
D、如添AD=AE,利用SAS即可证明△ABE≌△ACD.
故选:B.
7.(2024秋 宜州区期末)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC的长是( )
A.3 B.4 C.5 D.2
【解答】解:如图,作DF⊥AC于F,
,
∵在△ABC中,AD是角平分线,DE⊥AB于点E,
∴DF=DE=3,
∵△ABC的面积为15,
∴S△ABC=S△ABD+S△ACD=15,即,
∴,
∴AC=4,
所以AC的长为4,
综上所述,只有选项B正确,符合题意,
故选:B.
8.(2024秋 贵池区期末)下列函数图象中,能表示函数图象的是( )
A. B.
C. D.
【解答】解:A、B、C选项中的图象,对一个确定的x的值,有两个y值与之对应,所以不是函数图象;
D选项中的图象,对每一个确定的x的值,都有唯一确定的y值与之对应,所以是函数图象,
故选:D.
二.填空题(共8小题)
9.(2024秋 南关区校级期末)若3m+n﹣4=0,则23m×2n= 16 .
【解答】解:∵3m+n﹣4=0,
∴3m+n=4,
∴23m×2n=23m+n=24=16.
故答案为:16.
10.(2024秋 汉阳区期末)华为麒麟990芯片采用了最新的0.000000007米的工艺制程,将数0.000000007用科学记数法表示为 7×10﹣9 .
【解答】解:0.000000007=7×10﹣9.
故答案为:7×10﹣9.
11.(2024秋 盘龙区期末)一个角的余角是60°,则这个角的补角的度数是 150 .
【解答】解:这个角的余角=90°﹣60°=30°,
这个角的补角=180°﹣30°=150°.
故答案为:150°.
12.(2024秋 宝应县期末)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 30 °.
【解答】解:如图:
∵AB∥CD,
∴∠2=∠CDB=60°,
∵CD⊥DE,
∴∠CDE=90°,
∴∠1=180°﹣∠CDB﹣∠CDE=30°,
故答案为:30.
13.(2024秋 蜀山区期末)如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 1 .
【解答】解:∵△ABC≌△DEF,
∴DF=AC=3,BC=EF=5,
∵CF=7,
∴BF=CF﹣BC=2,
∴BD=DF﹣BF=3﹣2=1.
故答案为:1.
14.(2018秋 和县期末)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,则指针停止后落在黄色区域的概率是 .
【解答】解:∵黄扇形区域的圆心角为90°,
所以黄区域所占的面积比例为,
即转动圆盘一次,指针停在黄区域的概率是,
故答案为:.
15.(2024秋 天河区校级期末)如图,△EFG≌△NMH,点H,G在线段EN上,若EH=1,NH=3,则HG的长为 2 .
【解答】解:∵△EFG≌△NMH,
∴EG=NH=3,
∴HG=EG﹣EH=3﹣1=2,
故答案为:2.
16.(2024秋 祁县期末)为方便市民绿色出行,某市推出了共享单车服务,如图1是某品牌共享单车放在水平地面的实物图,图2是其平面示意图,其中AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,当∠MAC= 60 °时,AM∥CE.
【解答】解:∵共享单车放在水平地面的平面示意图中,AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,
∴AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAC+∠ACB+∠BCD=180°,
∴∠ACB=180°﹣70°﹣50°=60°,
当∠MAC=∠ACB=60°时,AM∥CE,
故答案为:60.
三.解答题(共7小题)
17.(2021春 漳州期末)如图,在△ABC中,AB=AC.
(1)利用尺规,作AB边的垂直平分线交AC于点D,交AB于点E.(不写作法,保留作图痕迹)
(2)在(1)中,连接BD,若BC=6,AB=8,求△BDC的周长.
【解答】解:(1)如图所示,直线DE即为所求;
(2)∵DE垂直平分AB,
∴AD=BD,
∴△BCD的周长为:
BD+CD+BC
=AD+CD+BC
=AC+BC
=8+6
=14.
18.(2025春 玉林期中)请将解答过程填写完整:
如图,EF∥AD,∠BAC=70°,若∠1=∠2,求∠AGD的度数.
解:∵EF∥AD,(已知)
∴∠2=∠3.( 两直线平行,同位角相等 )
∵∠1=∠2,
∴∠1= ∠3 .(等量代换)
∴AB∥ DG .
∴ ∠AGD +∠BAC=180°.(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= 110° .(等式的性质)
【解答】解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG.
∴∠AGD+∠BAC=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°(等式的性质).
故答案为:两直线平行,同位角相等,∠3,DG,∠AGD,110°.
19.(2023秋 昆明期末)如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=6,CF=8,求DB的长.
【解答】(1)证明:∵点E是边AC的中点,
∴AE=CE,
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS);
(2)解:∵△ADE≌△CFE,CF=8,
∴CF=AD=8,
∵AB=AC,点E是边AC的中点,CE=6,
∴AC=2CE=12,
∴AB=12,
∴DB=AB﹣AD=12﹣8=4.
20.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= 0.59 ,b= 116 ;
(2)“摸到白球的”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
21.(2024秋 肥乡区期末)小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王家距离书店多远?
(2)小王在新华书店停留了多长时间?
(3)新华书店到商场的距离是多少?
【解答】解:(1)由函数图象可知,小王家距离书店4000米;
(2)小王在新华书店停留了30﹣20=10(分钟);
(3)新华书店到商场的距离:6250﹣4000=2250(米).
22.(2024秋 大名县期末)如图,在△ABC中,BD平分∠ABC,CD平分∠ACB,DE⊥AB于点E,DF⊥BC于点F.
(1)若∠ABC=40°,∠ACB=70°,求∠BDC的度数;
(2)若DE=2,BC=9,求△BCD的面积.
【解答】解:(1)∵BD平分∠ABC,∠ABC=40°,
∴,
∵CD平分∠ACB,∠ACB=70°,
∴,
∴∠BDC=180°﹣20°﹣35°=125°.
(2)BD平分∠ABC,DE⊥AB,DF⊥BC,DE=2,
∴DF=DE=2.
∵BC=9,
∴.
23.(2024秋 靖江市期末)如图1,点F在线段AB上,点E在线段CD上,∠1+∠2=180°,∠A=∠D.
(1)试说明:AB∥CD;
(2)如图2所示,延长AB到M,在∠MBC,∠BCD内部有一点P,连接BP,CP.若∠CBP=3∠MBP,∠BCP=3∠DCP,求∠BPC的度数.
【解答】解:(1)如图:
∵∠2+∠3=180°,∠1+∠2=180°,
∴∠1=∠3,
∴AE∥DF,
∴∠A=∠BFD,
∵∠A=∠D,
∴∠D=∠BFD,
∴AB∥CD;
(2)∵AM∥CD,
∴∠MBC+∠DCB=180°,
∵∠CBP=3∠MBP,∠BCP=3∠DCP,
∴∠CBP∠MBC,∠BCP∠DCB,
∴∠CBP+∠BCP∠MBC∠DCB=135°,
∴∠BPC=180°﹣(∠CBP+∠BCP)=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2024秋 田阳区期末)下列常见的微信表情包中,属于轴对称图形的是( )
A. B. C. D.
2.(2024秋 桐柏县期末)数学课上,老师和同学们做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为2000,则“正面朝上”的频数最接近( )
A.400 B.600 C.1000 D.1600
3.(2024秋 武陟县期末)已知am=6,an=3,则am+n的值为( )
A.9 B.18 C.3 D.2
4.(2024秋 武陟县期末)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
5.(2024秋 顺城区期末)根据下列条件,能画出唯一△ABC的是( )
A.AB=5,AC=6,∠A=50°
B.AB=3,AC=4,∠C=30°
C.∠A=60°,∠B=45°,∠C=75°
D.AB=3,BC=4,AC=8
6.(2024秋 泰山区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.BE=CD C.BD=CE D.AD=AE
7.(2024秋 宜州区期末)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC的长是( )
A.3 B.4 C.5 D.2
8.(2024秋 贵池区期末)下列函数图象中,能表示函数图象的是( )
A. B.
C. D.
二.填空题(共8小题)
9.(2024秋 南关区校级期末)若3m+n﹣4=0,则23m×2n= .
10.(2024秋 汉阳区期末)华为麒麟990芯片采用了最新的0.000000007米的工艺制程,将数0.000000007用科学记数法表示为 .
11.(2024秋 盘龙区期末)一个角的余角是60°,则这个角的补角的度数是 .
12.(2024秋 宝应县期末)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 °.
13.(2024秋 蜀山区期末)如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 .
14.(2018秋 和县期末)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,则指针停止后落在黄色区域的概率是 .
15.(2024秋 天河区校级期末)如图,△EFG≌△NMH,点H,G在线段EN上,若EH=1,NH=3,则HG的长为 .
16.(2024秋 祁县期末)为方便市民绿色出行,某市推出了共享单车服务,如图1是某品牌共享单车放在水平地面的实物图,图2是其平面示意图,其中AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,当∠MAC= °时,AM∥CE.
三.解答题(共7小题)
17.(2021春 漳州期末)如图,在△ABC中,AB=AC.
(1)利用尺规,作AB边的垂直平分线交AC于点D,交AB于点E.(不写作法,保留作图痕迹)
(2)在(1)中,连接BD,若BC=6,AB=8,求△BDC的周长.
18.(2025春 玉林期中)请将解答过程填写完整:
如图,EF∥AD,∠BAC=70°,若∠1=∠2,求∠AGD的度数.
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
∵∠1=∠2,
∴∠1= .(等量代换)
∴AB∥ .
∴ +∠BAC=180°.(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= .(等式的性质)
19.(2023秋 昆明期末)如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=6,CF=8,求DB的长.
20.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.(2024秋 肥乡区期末)小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王家距离书店多远?
(2)小王在新华书店停留了多长时间?
(3)新华书店到商场的距离是多少?
22.(2024秋 大名县期末)如图,在△ABC中,BD平分∠ABC,CD平分∠ACB,DE⊥AB于点E,DF⊥BC于点F.
(1)若∠ABC=40°,∠ACB=70°,求∠BDC的度数;
(2)若DE=2,BC=9,求△BCD的面积.
23.(2024秋 靖江市期末)如图1,点F在线段AB上,点E在线段CD上,∠1+∠2=180°,∠A=∠D.
(1)试说明:AB∥CD;
(2)如图2所示,延长AB到M,在∠MBC,∠BCD内部有一点P,连接BP,CP.若∠CBP=3∠MBP,∠BCP=3∠DCP,求∠BPC的度数.
【期末押题卷】2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C B C A B B D
一.选择题(共8小题)
1.(2024秋 田阳区期末)下列常见的微信表情包中,属于轴对称图形的是( )
A. B. C. D.
【解答】解:A选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,B、C、D选项中的图形都不是轴对称图形.
故选:A.
2.(2024秋 桐柏县期末)数学课上,老师和同学们做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为2000,则“正面朝上”的频数最接近( )
A.400 B.600 C.1000 D.1600
【解答】解:随着实验次数的增加,正面向上的频率逐渐稳定到某个常数附近,
,
观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,
则“正面朝上”的频数最接近2000×0.5=1000次,
故选:C.
3.(2024秋 武陟县期末)已知am=6,an=3,则am+n的值为( )
A.9 B.18 C.3 D.2
【解答】解:∵am=6,an=3,
∴am+n
=am an
=6×3
=18,
∴B符合题意,ACD不符合题意.
故选:B.
4.(2024秋 武陟县期末)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【解答】解:∵要使凉亭到草坪三条边的距离相等,
∴凉亭应在△ABC三条角平分线的交点处.
故选:C.
5.(2024秋 顺城区期末)根据下列条件,能画出唯一△ABC的是( )
A.AB=5,AC=6,∠A=50°
B.AB=3,AC=4,∠C=30°
C.∠A=60°,∠B=45°,∠C=75°
D.AB=3,BC=4,AC=8
【解答】解:A、AB=5,AC=6,∠A=50°,符合“SAS”,所以根据条件能画出唯一△ABC,故此选项符合题意;
B、AB=3,AC=4,∠C=30°,根据两边及一边对角不能判定两三角形全等,即作出的三角形不唯一,故此选项不符合题意;
C、∠A=60°,∠B=45°,∠C=75°,根据三角相等不能判定两三角形全等,即作出的三角形不唯一,故此选项不符合题意;
D、AB=3,BC=4,AC=8,∵3+4<8,∴不满足三角形三边的关系,即三边不能构成三角形,故此选项不符合题意;
故选:A.
6.(2024秋 泰山区期末)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.BE=CD C.BD=CE D.AD=AE
【解答】解:∵AB=AC,∠A为公共角,
A、如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;
B、如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;
C、如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;
D、如添AD=AE,利用SAS即可证明△ABE≌△ACD.
故选:B.
7.(2024秋 宜州区期末)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC的长是( )
A.3 B.4 C.5 D.2
【解答】解:如图,作DF⊥AC于F,
,
∵在△ABC中,AD是角平分线,DE⊥AB于点E,
∴DF=DE=3,
∵△ABC的面积为15,
∴S△ABC=S△ABD+S△ACD=15,即,
∴,
∴AC=4,
所以AC的长为4,
综上所述,只有选项B正确,符合题意,
故选:B.
8.(2024秋 贵池区期末)下列函数图象中,能表示函数图象的是( )
A. B.
C. D.
【解答】解:A、B、C选项中的图象,对一个确定的x的值,有两个y值与之对应,所以不是函数图象;
D选项中的图象,对每一个确定的x的值,都有唯一确定的y值与之对应,所以是函数图象,
故选:D.
二.填空题(共8小题)
9.(2024秋 南关区校级期末)若3m+n﹣4=0,则23m×2n= 16 .
【解答】解:∵3m+n﹣4=0,
∴3m+n=4,
∴23m×2n=23m+n=24=16.
故答案为:16.
10.(2024秋 汉阳区期末)华为麒麟990芯片采用了最新的0.000000007米的工艺制程,将数0.000000007用科学记数法表示为 7×10﹣9 .
【解答】解:0.000000007=7×10﹣9.
故答案为:7×10﹣9.
11.(2024秋 盘龙区期末)一个角的余角是60°,则这个角的补角的度数是 150 .
【解答】解:这个角的余角=90°﹣60°=30°,
这个角的补角=180°﹣30°=150°.
故答案为:150°.
12.(2024秋 宝应县期末)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 30 °.
【解答】解:如图:
∵AB∥CD,
∴∠2=∠CDB=60°,
∵CD⊥DE,
∴∠CDE=90°,
∴∠1=180°﹣∠CDB﹣∠CDE=30°,
故答案为:30.
13.(2024秋 蜀山区期末)如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 1 .
【解答】解:∵△ABC≌△DEF,
∴DF=AC=3,BC=EF=5,
∵CF=7,
∴BF=CF﹣BC=2,
∴BD=DF﹣BF=3﹣2=1.
故答案为:1.
14.(2018秋 和县期末)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,则指针停止后落在黄色区域的概率是 .
【解答】解:∵黄扇形区域的圆心角为90°,
所以黄区域所占的面积比例为,
即转动圆盘一次,指针停在黄区域的概率是,
故答案为:.
15.(2024秋 天河区校级期末)如图,△EFG≌△NMH,点H,G在线段EN上,若EH=1,NH=3,则HG的长为 2 .
【解答】解:∵△EFG≌△NMH,
∴EG=NH=3,
∴HG=EG﹣EH=3﹣1=2,
故答案为:2.
16.(2024秋 祁县期末)为方便市民绿色出行,某市推出了共享单车服务,如图1是某品牌共享单车放在水平地面的实物图,图2是其平面示意图,其中AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,当∠MAC= 60 °时,AM∥CE.
【解答】解:∵共享单车放在水平地面的平面示意图中,AB,CD都与地面l平行,∠BCD=70°,∠BAC=50°,
∴AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAC+∠ACB+∠BCD=180°,
∴∠ACB=180°﹣70°﹣50°=60°,
当∠MAC=∠ACB=60°时,AM∥CE,
故答案为:60.
三.解答题(共7小题)
17.(2021春 漳州期末)如图,在△ABC中,AB=AC.
(1)利用尺规,作AB边的垂直平分线交AC于点D,交AB于点E.(不写作法,保留作图痕迹)
(2)在(1)中,连接BD,若BC=6,AB=8,求△BDC的周长.
【解答】解:(1)如图所示,直线DE即为所求;
(2)∵DE垂直平分AB,
∴AD=BD,
∴△BCD的周长为:
BD+CD+BC
=AD+CD+BC
=AC+BC
=8+6
=14.
18.(2025春 玉林期中)请将解答过程填写完整:
如图,EF∥AD,∠BAC=70°,若∠1=∠2,求∠AGD的度数.
解:∵EF∥AD,(已知)
∴∠2=∠3.( 两直线平行,同位角相等 )
∵∠1=∠2,
∴∠1= ∠3 .(等量代换)
∴AB∥ DG .
∴ ∠AGD +∠BAC=180°.(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= 110° .(等式的性质)
【解答】解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG.
∴∠AGD+∠BAC=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°(等式的性质).
故答案为:两直线平行,同位角相等,∠3,DG,∠AGD,110°.
19.(2023秋 昆明期末)如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=6,CF=8,求DB的长.
【解答】(1)证明:∵点E是边AC的中点,
∴AE=CE,
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS);
(2)解:∵△ADE≌△CFE,CF=8,
∴CF=AD=8,
∵AB=AC,点E是边AC的中点,CE=6,
∴AC=2CE=12,
∴AB=12,
∴DB=AB﹣AD=12﹣8=4.
20.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= 0.59 ,b= 116 ;
(2)“摸到白球的”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
21.(2024秋 肥乡区期末)小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王家距离书店多远?
(2)小王在新华书店停留了多长时间?
(3)新华书店到商场的距离是多少?
【解答】解:(1)由函数图象可知,小王家距离书店4000米;
(2)小王在新华书店停留了30﹣20=10(分钟);
(3)新华书店到商场的距离:6250﹣4000=2250(米).
22.(2024秋 大名县期末)如图,在△ABC中,BD平分∠ABC,CD平分∠ACB,DE⊥AB于点E,DF⊥BC于点F.
(1)若∠ABC=40°,∠ACB=70°,求∠BDC的度数;
(2)若DE=2,BC=9,求△BCD的面积.
【解答】解:(1)∵BD平分∠ABC,∠ABC=40°,
∴,
∵CD平分∠ACB,∠ACB=70°,
∴,
∴∠BDC=180°﹣20°﹣35°=125°.
(2)BD平分∠ABC,DE⊥AB,DF⊥BC,DE=2,
∴DF=DE=2.
∵BC=9,
∴.
23.(2024秋 靖江市期末)如图1,点F在线段AB上,点E在线段CD上,∠1+∠2=180°,∠A=∠D.
(1)试说明:AB∥CD;
(2)如图2所示,延长AB到M,在∠MBC,∠BCD内部有一点P,连接BP,CP.若∠CBP=3∠MBP,∠BCP=3∠DCP,求∠BPC的度数.
【解答】解:(1)如图:
∵∠2+∠3=180°,∠1+∠2=180°,
∴∠1=∠3,
∴AE∥DF,
∴∠A=∠BFD,
∵∠A=∠D,
∴∠D=∠BFD,
∴AB∥CD;
(2)∵AM∥CD,
∴∠MBC+∠DCB=180°,
∵∠CBP=3∠MBP,∠BCP=3∠DCP,
∴∠CBP∠MBC,∠BCP∠DCB,
∴∠CBP+∠BCP∠MBC∠DCB=135°,
∴∠BPC=180°﹣(∠CBP+∠BCP)=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
