【期末押题卷】2024-2025学年数学七年级下册人教版(2024)(含解析)
文档属性
| 名称 | 【期末押题卷】2024-2025学年数学七年级下册人教版(2024)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 15:26:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末押题卷】2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024春 黔东南州期末)在实数1,﹣1,0,中,最大的数是( )
A.1 B.﹣1 C.0 D.
2.(2024秋 鄞州区期末)若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
3.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
4.(2024秋 龙岗区期末)平面直角坐标系中,在第四象限的点是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
5.(2024秋 扬州期末)如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B+∠BCD=180° D.∠B=∠5
6.(2024秋 张店区期末)若,则m的值在( )
A.0和之间 B.和1之间 C.1和之间 D.和3之间
7.(2024秋 南山区期末)如图,将生活中的竹篱笆局部抽象成几何图形,下列条件中能判断直线a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
8.(2024秋 东台市期末)老师在黑板上画出如图所示的图形,要求学生添加条件,使得AB∥CD,随后抽取了四名学生的答案纸展示如下:
甲:∠B+∠BCD=180°;
乙:∠1=∠2;
丙:∠B=∠DCE;
丁:∠3=∠4.
则不能得到AB∥CD的是( )
A.甲 B.乙 C.丙 D.丁
二.填空题(共8小题)
9.(2024春 清江浦区期末)命题“如果a2>b2,那么a>b”是 命题(填“真”或“假”).
10.(2024春 崇川区期末)已知点P(a,a+2)在x轴上,则点P的坐标是 .
11.(2023春 临泉县期末)写出一个比大且比小的整数 .
12.(2019春 北流市期末)如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
13.(2024秋 巴中期末)为增强学生体质,感受中国的传统文化,我校体育老师提出将国家级非物质文化遗产——“抖空竹”引入体育社团.图1是某同学“抖空竹”时的一个瞬间,小明把它抽象成图2的数学问题:已知AB∥CD,∠E=28°,∠ECD=114°,则∠A的度数是 .
14.(2019秋 日照期末)在实数范围定义运算“*”:a*b=2a+b,则满足x*(x﹣6)=0的实数x是 .
15.(2024秋 凤翔区期末)已知是二元一次方程x+ay=5的一个解,则a的值为 .
16.(2023春 海州区期末)在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若∠B'FB=80°,则∠AEF= °.
三.解答题(共8小题)
17.(2024秋 安顺期末)(1)计算:
(2)从下列三个方程中任选2个组成方程组,并解这个方程组.
①x+y=10;②2x+y=16;③x=y+4.
18.(2024秋 城关区校级期末)解不等式组,并写出这个不等式组的所有整数解.
19.(2024秋 滨江区期末)已知3a+1的两个平方根分别是7﹣m和2﹣2m,9+b的立方根是2.
(1)求m,a,b的值;
(2)求7a﹣b的平方根.
20.(2024秋 定安县期末)如图,直线AB与CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若,求∠BOD的大小.
21.(2024秋 市北区期末)关于x,y的二元一次方程均可以变形为ax+by=c的形式,其中a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c).
(1)二元一次方程4x﹣3y=5的“关联系数”为 ;
(2)已知关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),若为该方程的一组解,且m,n均为正整数,求m,n的值.
22.(2024秋 宜宾期末)如图,已知∠A=110°,∠ABC=70°,BD⊥CD于点D,EF⊥CD于点F,试说明∠1=∠2.请补全说理过程,即在横线处填上结论或理由.
解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥① ,(② ),
∴∠1=∠3(③ ),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(④ ),
∴∠2=∠3(⑤ ),
∴∠1=∠2(等量代换).
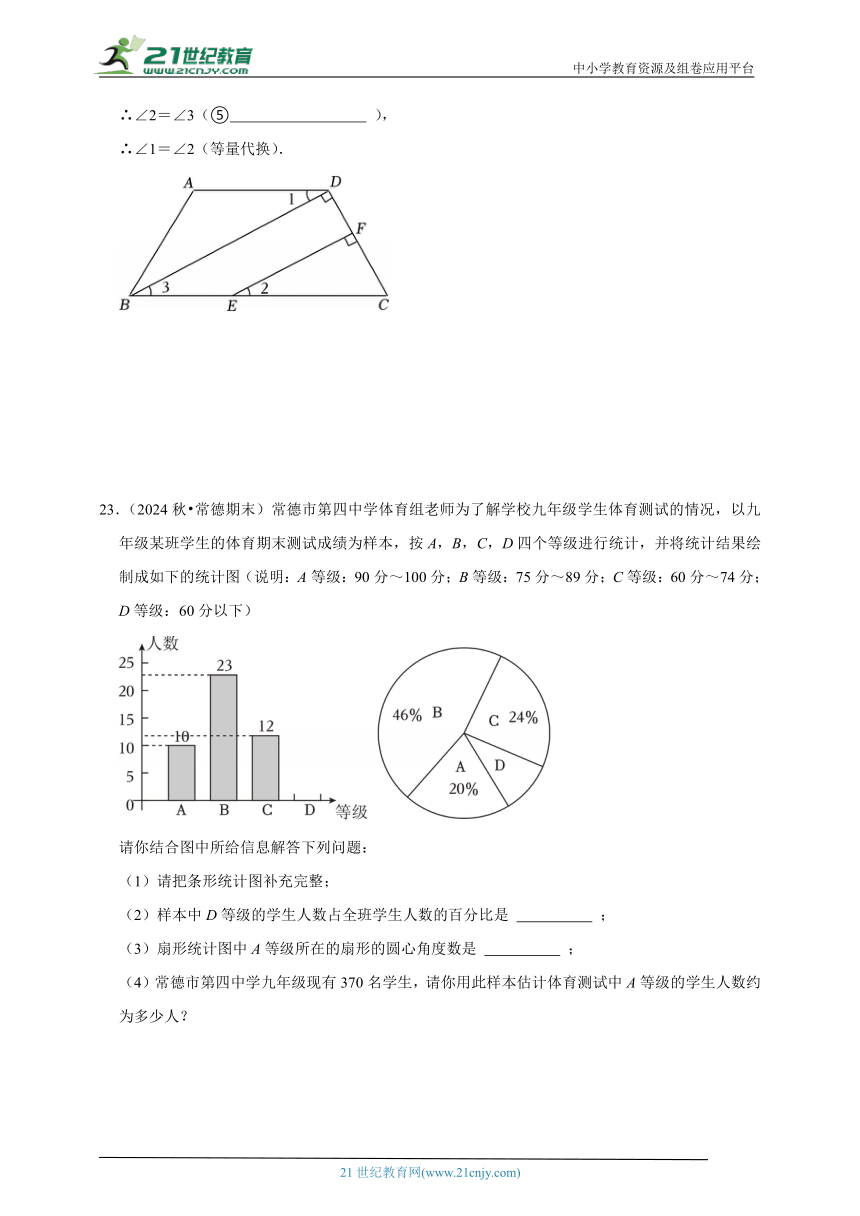
23.(2024秋 常德期末)常德市第四中学体育组老师为了解学校九年级学生体育测试的情况,以九年级某班学生的体育期末测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图(说明:A等级:90分~100分;B等级:75分~89分;C等级:60分~74分;D等级:60分以下)
请你结合图中所给信息解答下列问题:
(1)请把条形统计图补充完整;
(2)样本中D等级的学生人数占全班学生人数的百分比是 ;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)常德市第四中学九年级现有370名学生,请你用此样本估计体育测试中A等级的学生人数约为多少人?
24.(2024秋 海陵区校级期末)已知AB∥CD.
(1)如图1,∠1比∠2的2倍少60°,求∠1的度数;
(2)如图2,若∠A+∠C=180°,求证:∠AEF=∠CFE;
(3)如图3,过E作∠AEP的角平分线EM交FP的延长线于M,∠DFP的角平分线FN交EM的反向延长线于N,若∠M与3∠N互补,试探索直线EP与直线FN的位置关系,并说明理由.
【期末押题卷】2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C D B A B B D
一.选择题(共8小题)
1.(2024春 黔东南州期末)在实数1,﹣1,0,中,最大的数是( )
A.1 B.﹣1 C.0 D.
【解答】解:∵,
∴,
∵,
∴最大的数是,
故选:D.
2.(2024秋 鄞州区期末)若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
【解答】解:A.因为a>b,3a>3b,所以不等式成立,故选项错误,A不符合题意;
B.因为a>b,a﹣1>b﹣2,所以不等式成立,故选项正确,B不符合题意;
C.当a=﹣1,b=﹣2时,满足a>b,但a2>b2不成立,故选项错误,C符合题意;
D.因为a>b,1﹣3a<1﹣3b,所以不等式成立,故选项错误,D不符合题意;
故选:C.
3.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
【解答】解:A、两点之间,线段最短是真命题;
B、对顶角相等是真命题;
C、直角的补角仍然是直角是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补是假命题;
故选:D.
4.(2024秋 龙岗区期末)平面直角坐标系中,在第四象限的点是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
【解答】解:A、(1,2)位于第一象限,故A错误;
B、(1,﹣2)位于第四象限,故B正确;
C、(﹣1,2)位于第二象限,故C错误;
D、(﹣1,﹣2)位于第三象限,故D错误;
故选:B.
5.(2024秋 扬州期末)如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B+∠BCD=180° D.∠B=∠5
【解答】解:A、∵∠1=∠2,∴AD∥BC,故本选项正确;
B、∵∠3=∠4,∴AB∥CD,故本选项错误;
C、∵∠B+∠BCD=180°,∴AB∥CD,故本选项错误;
D、∵∠B=∠5,∴AB∥CD,故本选项错误.
故选:A.
6.(2024秋 张店区期末)若,则m的值在( )
A.0和之间 B.和1之间 C.1和之间 D.和3之间
【解答】解:∵4<5<9,
∴,
∴,即,
∴,
故选:B.
7.(2024秋 南山区期末)如图,将生活中的竹篱笆局部抽象成几何图形,下列条件中能判断直线a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
【解答】解:由∠1=∠2,不能判定a∥b,
故A不符合题意;
∵∠2=∠3,
∴a∥b,
故B符合题意;
由∠3=∠4,不能判定a∥b,
故C不符合题意;
由∠4=∠5,不能判定a∥b,
故D不符合题意;
故选:B.
8.(2024秋 东台市期末)老师在黑板上画出如图所示的图形,要求学生添加条件,使得AB∥CD,随后抽取了四名学生的答案纸展示如下:
甲:∠B+∠BCD=180°;
乙:∠1=∠2;
丙:∠B=∠DCE;
丁:∠3=∠4.
则不能得到AB∥CD的是( )
A.甲 B.乙 C.丙 D.丁
【解答】解:甲、当∠B+∠BCD=180°时,由同旁内角互补,两直线平行得AB∥CD,故不符合题意;
乙、∵∠1=∠2,
∴AB∥CD,故不符合题意;
丙、当∠B=∠DCE时,由同位角相等,两直线平行得AB∥CD,故不符合题意;
丁、当∠3=∠4时,由内错角相等,两直线平行得AD∥BC,故符合题意.
故选:D.
二.填空题(共8小题)
9.(2024春 清江浦区期末)命题“如果a2>b2,那么a>b”是 假 命题(填“真”或“假”).
【解答】解:假设a=﹣3,b=2,则满足a2>b2,
但a<b,
因此,这个命题是假命题.
故答案为:假.
10.(2024春 崇川区期末)已知点P(a,a+2)在x轴上,则点P的坐标是 (﹣2,0) .
【解答】解:因为点P(a,a+2)在x轴上,
所以a+2=0,
解得a=﹣2,
所以点P的坐标为(﹣2,0),
故答案为:(﹣2,0).
11.(2023春 临泉县期末)写出一个比大且比小的整数 3(答案不唯一) .
【解答】解:∵23,45,
∴所有比小且比大的整数有3,4,
∴这个整数可以是3,
故答案为:3(答案不唯一).
12.(2019春 北流市期末)如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 35 °.
【解答】解:如图:
∵∠3=180°﹣∠1=180°﹣55°=125°,
∵直尺两边互相平行,
∴∠2+90°=∠3,
∴∠2=125°﹣90°=35°.
故答案为:35.
13.(2024秋 巴中期末)为增强学生体质,感受中国的传统文化,我校体育老师提出将国家级非物质文化遗产——“抖空竹”引入体育社团.图1是某同学“抖空竹”时的一个瞬间,小明把它抽象成图2的数学问题:已知AB∥CD,∠E=28°,∠ECD=114°,则∠A的度数是 86° .
【解答】解:如图所示:延长DC交AE于点F,
根据题意,∠E=28°,∠ECD=114°,
∴根据三角形的外角的性质得,∠ECD=∠E+∠EFD,即114°=28°+∠EFD,
解得∠EFD=86°,
∵AB∥CD,
∴根据平行线的性质得,∠A=∠EFD=86°,
所以∠A的度数为86°.
故答案为:86°.
14.(2019秋 日照期末)在实数范围定义运算“*”:a*b=2a+b,则满足x*(x﹣6)=0的实数x是 2 .
【解答】解:已知等式化简得:2x+(x﹣6)=0,
去括号得:2x+x﹣6=0,
移项合并得:3x=6,
解得:x=2,
故答案为:2
15.(2024秋 凤翔区期末)已知是二元一次方程x+ay=5的一个解,则a的值为 7 .
【解答】解:二元一次方程x+ay=5的一组解是,
∴﹣2+a=5,
解得:a=7,
故答案为:7.
16.(2023春 海州区期末)在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若∠B'FB=80°,则∠AEF= 40 °.
【解答】解:由题知∠EFB'=∠EFB,AD∥BC,
∵∠EFB'+∠EFB+∠BFB'=360°,∠BFB'=80°,
∴∠EFB'=∠EFB=140°,
∵AD∥BC,
∴∠AEF+∠EFB=180°,
∴∠AEF=180°﹣140°=40°.
故答案为:40.
三.解答题(共8小题)
17.(2024秋 安顺期末)(1)计算:
(2)从下列三个方程中任选2个组成方程组,并解这个方程组.
①x+y=10;②2x+y=16;③x=y+4.
【解答】解:(1)原式
;
(2)选①②得:,
由②﹣①,得x=6,
把x=6代入①,得6+y=10,
解得y=4,
∴原方程组的解是.
18.(2024秋 城关区校级期末)解不等式组,并写出这个不等式组的所有整数解.
【解答】解:,
由①得x≤2,
由②得 x>﹣1,
∴原不等式组的解集为﹣1<x≤2,
∴原不等式组的所有整数解为0,1,2.
19.(2024秋 滨江区期末)已知3a+1的两个平方根分别是7﹣m和2﹣2m,9+b的立方根是2.
(1)求m,a,b的值;
(2)求7a﹣b的平方根.
【解答】解:(1)根据题意可知,3a+1的两个平方根分别是7﹣m和2﹣2m,
∴7﹣m=﹣(2﹣2m),
7﹣m=﹣2+2m,
3m=9,
解得m=3,
∴3a+1=(7﹣m)2=(7﹣3)2=16,
解得a=5,
∵9+b的立方根是2.
∴9+b=23,解得b=﹣1,
故m,a,b的值分别是3,5,﹣1;
(2)∵a=5,b=﹣1,
∴7a﹣b=7×5﹣(﹣1)=36,
又因为36的平方根为±6,
∴7a﹣b的平方根为±6.
20.(2024秋 定安县期末)如图,直线AB与CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若,求∠BOD的大小.
【解答】解:(1)ON⊥CD,理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=∠AOM=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,
即∠COM=90°,
∴ON⊥CD;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵,
∴∠BOC=4∠1,
∵∠BOC=∠1+∠BOM,
∴4∠1=∠1+90°,
解得∠1=30°,
∴∠BOC=120°,
∵∠BOC+∠BOD=180°,
∴∠BOD=180°﹣∠BOC=180°﹣120°=60°,
即∠BOD的度数为60°.
21.(2024秋 市北区期末)关于x,y的二元一次方程均可以变形为ax+by=c的形式,其中a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c).
(1)二元一次方程4x﹣3y=5的“关联系数”为 (4,﹣3,5) ;
(2)已知关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),若为该方程的一组解,且m,n均为正整数,求m,n的值.
【解答】解:(1)∵a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c),
∴二元一次方程4x﹣3y=5的“关联系数”为(4,﹣3,5);
故答案为:(4,﹣3,5);
(2)∵关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),
∴二元一次方程为2x﹣y=1.
∵为该方程的一组解,m,n均为正整数,
∴2(m+n)﹣m﹣5=1,即m+2n=6.
∴或.
22.(2024秋 宜宾期末)如图,已知∠A=110°,∠ABC=70°,BD⊥CD于点D,EF⊥CD于点F,试说明∠1=∠2.请补全说理过程,即在横线处填上结论或理由.
解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥① BC ,(② 同旁内角互补,两直线平行 ),
∴∠1=∠3(③ 两直线平行,内错角相等 ),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(④ 同一平面内,垂直于同一条直线的两条直线互相平行 ),
∴∠2=∠3(⑤ 两直线平行,同位角相等 ),
∴∠1=∠2(等量代换).
【解答】解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
故答案为:BC;同旁内角互补,两直线平行;两直线平行,内错角相等;同一平面内,垂直于同一条直线的两条直线互相平行;两直线平行,同位角相等.
23.(2024秋 常德期末)常德市第四中学体育组老师为了解学校九年级学生体育测试的情况,以九年级某班学生的体育期末测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图(说明:A等级:90分~100分;B等级:75分~89分;C等级:60分~74分;D等级:60分以下)
请你结合图中所给信息解答下列问题:
(1)请把条形统计图补充完整;
(2)样本中D等级的学生人数占全班学生人数的百分比是 10% ;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 72° ;
(4)常德市第四中学九年级现有370名学生,请你用此样本估计体育测试中A等级的学生人数约为多少人?
【解答】解:(1)总人数为10÷20%=50(人),
则样本中D等级的学生人数为:50﹣10﹣23﹣12=5(人),
补全条形统计图:
(2)样本中D等级的学生人数占全班学生人数的百分比为:
,
故答案为:10%;
(3)∵A等级的学生人数占全班学生人数的百分比为20%,
∴扇形统计图中A等级所在的扇形的圆心角度数为:360°×20%=72°,
故答案为:72°;
(4)用370乘以A等级的学生人数占全班学生人数的百分比可得:
370×20%=74(人),
答:估计体育测试中A等级的学生人数约为74人.
24.(2024秋 海陵区校级期末)已知AB∥CD.
(1)如图1,∠1比∠2的2倍少60°,求∠1的度数;
(2)如图2,若∠A+∠C=180°,求证:∠AEF=∠CFE;
(3)如图3,过E作∠AEP的角平分线EM交FP的延长线于M,∠DFP的角平分线FN交EM的反向延长线于N,若∠M与3∠N互补,试探索直线EP与直线FN的位置关系,并说明理由.
【解答】解:(1)∵AB∥CD,由平行线的性质可得:
∠1=∠DFE,∠2=∠DFE,
∴∠1=∠2,
∴∠1=2∠1﹣60°,
∴∠1=60°
(2)证明:延长AE交CD于H,
∵AB∥CD,
∴∠A+∠AHD=180°,
∵∠A+∠C=180°,
∴∠C=∠AHD,
∴CF∥AH,
∴∠AEF=∠CFE;
(3)解:EP∥FN,
过点N作NH∥AB,过点M作MG∥AB,
∵CD∥AB∥MG∥NH,
∴∠HNM=∠AEM=∠GMN,∠3=∠HNF,∠CFM=∠GMF,
∴∠NMF=∠GMN+∠CFM=∠AEM+∠CFM,
∵FN平分∠DFM,
∴∠DFM=2∠3,
∴∠CFM=180°﹣2∠3,
∴∠NMF=∠AEM+180°﹣2∠3,
∴∠NMF=∠AEM+180°﹣2∠HNF
∴∠NMF=∠AEM+180°﹣2∠HNM﹣2∠MNF,
∴∠NMF=180°﹣∠AEM﹣2∠MNF,
∵∠NMF与3∠MNF互补,
∴∠NMF+3∠MNF=180°,
∴∠AEM=∠MNF,
∵ME平分∠AEP,
∴∠MEP=∠AEM=∠MNF,
∴EP∥FN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末押题卷】2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024春 黔东南州期末)在实数1,﹣1,0,中,最大的数是( )
A.1 B.﹣1 C.0 D.
2.(2024秋 鄞州区期末)若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
3.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
4.(2024秋 龙岗区期末)平面直角坐标系中,在第四象限的点是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
5.(2024秋 扬州期末)如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B+∠BCD=180° D.∠B=∠5
6.(2024秋 张店区期末)若,则m的值在( )
A.0和之间 B.和1之间 C.1和之间 D.和3之间
7.(2024秋 南山区期末)如图,将生活中的竹篱笆局部抽象成几何图形,下列条件中能判断直线a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
8.(2024秋 东台市期末)老师在黑板上画出如图所示的图形,要求学生添加条件,使得AB∥CD,随后抽取了四名学生的答案纸展示如下:
甲:∠B+∠BCD=180°;
乙:∠1=∠2;
丙:∠B=∠DCE;
丁:∠3=∠4.
则不能得到AB∥CD的是( )
A.甲 B.乙 C.丙 D.丁
二.填空题(共8小题)
9.(2024春 清江浦区期末)命题“如果a2>b2,那么a>b”是 命题(填“真”或“假”).
10.(2024春 崇川区期末)已知点P(a,a+2)在x轴上,则点P的坐标是 .
11.(2023春 临泉县期末)写出一个比大且比小的整数 .
12.(2019春 北流市期末)如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
13.(2024秋 巴中期末)为增强学生体质,感受中国的传统文化,我校体育老师提出将国家级非物质文化遗产——“抖空竹”引入体育社团.图1是某同学“抖空竹”时的一个瞬间,小明把它抽象成图2的数学问题:已知AB∥CD,∠E=28°,∠ECD=114°,则∠A的度数是 .
14.(2019秋 日照期末)在实数范围定义运算“*”:a*b=2a+b,则满足x*(x﹣6)=0的实数x是 .
15.(2024秋 凤翔区期末)已知是二元一次方程x+ay=5的一个解,则a的值为 .
16.(2023春 海州区期末)在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若∠B'FB=80°,则∠AEF= °.
三.解答题(共8小题)
17.(2024秋 安顺期末)(1)计算:
(2)从下列三个方程中任选2个组成方程组,并解这个方程组.
①x+y=10;②2x+y=16;③x=y+4.
18.(2024秋 城关区校级期末)解不等式组,并写出这个不等式组的所有整数解.
19.(2024秋 滨江区期末)已知3a+1的两个平方根分别是7﹣m和2﹣2m,9+b的立方根是2.
(1)求m,a,b的值;
(2)求7a﹣b的平方根.
20.(2024秋 定安县期末)如图,直线AB与CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若,求∠BOD的大小.
21.(2024秋 市北区期末)关于x,y的二元一次方程均可以变形为ax+by=c的形式,其中a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c).
(1)二元一次方程4x﹣3y=5的“关联系数”为 ;
(2)已知关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),若为该方程的一组解,且m,n均为正整数,求m,n的值.
22.(2024秋 宜宾期末)如图,已知∠A=110°,∠ABC=70°,BD⊥CD于点D,EF⊥CD于点F,试说明∠1=∠2.请补全说理过程,即在横线处填上结论或理由.
解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥① ,(② ),
∴∠1=∠3(③ ),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(④ ),
∴∠2=∠3(⑤ ),
∴∠1=∠2(等量代换).
23.(2024秋 常德期末)常德市第四中学体育组老师为了解学校九年级学生体育测试的情况,以九年级某班学生的体育期末测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图(说明:A等级:90分~100分;B等级:75分~89分;C等级:60分~74分;D等级:60分以下)
请你结合图中所给信息解答下列问题:
(1)请把条形统计图补充完整;
(2)样本中D等级的学生人数占全班学生人数的百分比是 ;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)常德市第四中学九年级现有370名学生,请你用此样本估计体育测试中A等级的学生人数约为多少人?
24.(2024秋 海陵区校级期末)已知AB∥CD.
(1)如图1,∠1比∠2的2倍少60°,求∠1的度数;
(2)如图2,若∠A+∠C=180°,求证:∠AEF=∠CFE;
(3)如图3,过E作∠AEP的角平分线EM交FP的延长线于M,∠DFP的角平分线FN交EM的反向延长线于N,若∠M与3∠N互补,试探索直线EP与直线FN的位置关系,并说明理由.
【期末押题卷】2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C D B A B B D
一.选择题(共8小题)
1.(2024春 黔东南州期末)在实数1,﹣1,0,中,最大的数是( )
A.1 B.﹣1 C.0 D.
【解答】解:∵,
∴,
∵,
∴最大的数是,
故选:D.
2.(2024秋 鄞州区期末)若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
【解答】解:A.因为a>b,3a>3b,所以不等式成立,故选项错误,A不符合题意;
B.因为a>b,a﹣1>b﹣2,所以不等式成立,故选项正确,B不符合题意;
C.当a=﹣1,b=﹣2时,满足a>b,但a2>b2不成立,故选项错误,C符合题意;
D.因为a>b,1﹣3a<1﹣3b,所以不等式成立,故选项错误,D不符合题意;
故选:C.
3.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
【解答】解:A、两点之间,线段最短是真命题;
B、对顶角相等是真命题;
C、直角的补角仍然是直角是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补是假命题;
故选:D.
4.(2024秋 龙岗区期末)平面直角坐标系中,在第四象限的点是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
【解答】解:A、(1,2)位于第一象限,故A错误;
B、(1,﹣2)位于第四象限,故B正确;
C、(﹣1,2)位于第二象限,故C错误;
D、(﹣1,﹣2)位于第三象限,故D错误;
故选:B.
5.(2024秋 扬州期末)如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B+∠BCD=180° D.∠B=∠5
【解答】解:A、∵∠1=∠2,∴AD∥BC,故本选项正确;
B、∵∠3=∠4,∴AB∥CD,故本选项错误;
C、∵∠B+∠BCD=180°,∴AB∥CD,故本选项错误;
D、∵∠B=∠5,∴AB∥CD,故本选项错误.
故选:A.
6.(2024秋 张店区期末)若,则m的值在( )
A.0和之间 B.和1之间 C.1和之间 D.和3之间
【解答】解:∵4<5<9,
∴,
∴,即,
∴,
故选:B.
7.(2024秋 南山区期末)如图,将生活中的竹篱笆局部抽象成几何图形,下列条件中能判断直线a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
【解答】解:由∠1=∠2,不能判定a∥b,
故A不符合题意;
∵∠2=∠3,
∴a∥b,
故B符合题意;
由∠3=∠4,不能判定a∥b,
故C不符合题意;
由∠4=∠5,不能判定a∥b,
故D不符合题意;
故选:B.
8.(2024秋 东台市期末)老师在黑板上画出如图所示的图形,要求学生添加条件,使得AB∥CD,随后抽取了四名学生的答案纸展示如下:
甲:∠B+∠BCD=180°;
乙:∠1=∠2;
丙:∠B=∠DCE;
丁:∠3=∠4.
则不能得到AB∥CD的是( )
A.甲 B.乙 C.丙 D.丁
【解答】解:甲、当∠B+∠BCD=180°时,由同旁内角互补,两直线平行得AB∥CD,故不符合题意;
乙、∵∠1=∠2,
∴AB∥CD,故不符合题意;
丙、当∠B=∠DCE时,由同位角相等,两直线平行得AB∥CD,故不符合题意;
丁、当∠3=∠4时,由内错角相等,两直线平行得AD∥BC,故符合题意.
故选:D.
二.填空题(共8小题)
9.(2024春 清江浦区期末)命题“如果a2>b2,那么a>b”是 假 命题(填“真”或“假”).
【解答】解:假设a=﹣3,b=2,则满足a2>b2,
但a<b,
因此,这个命题是假命题.
故答案为:假.
10.(2024春 崇川区期末)已知点P(a,a+2)在x轴上,则点P的坐标是 (﹣2,0) .
【解答】解:因为点P(a,a+2)在x轴上,
所以a+2=0,
解得a=﹣2,
所以点P的坐标为(﹣2,0),
故答案为:(﹣2,0).
11.(2023春 临泉县期末)写出一个比大且比小的整数 3(答案不唯一) .
【解答】解:∵23,45,
∴所有比小且比大的整数有3,4,
∴这个整数可以是3,
故答案为:3(答案不唯一).
12.(2019春 北流市期末)如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 35 °.
【解答】解:如图:
∵∠3=180°﹣∠1=180°﹣55°=125°,
∵直尺两边互相平行,
∴∠2+90°=∠3,
∴∠2=125°﹣90°=35°.
故答案为:35.
13.(2024秋 巴中期末)为增强学生体质,感受中国的传统文化,我校体育老师提出将国家级非物质文化遗产——“抖空竹”引入体育社团.图1是某同学“抖空竹”时的一个瞬间,小明把它抽象成图2的数学问题:已知AB∥CD,∠E=28°,∠ECD=114°,则∠A的度数是 86° .
【解答】解:如图所示:延长DC交AE于点F,
根据题意,∠E=28°,∠ECD=114°,
∴根据三角形的外角的性质得,∠ECD=∠E+∠EFD,即114°=28°+∠EFD,
解得∠EFD=86°,
∵AB∥CD,
∴根据平行线的性质得,∠A=∠EFD=86°,
所以∠A的度数为86°.
故答案为:86°.
14.(2019秋 日照期末)在实数范围定义运算“*”:a*b=2a+b,则满足x*(x﹣6)=0的实数x是 2 .
【解答】解:已知等式化简得:2x+(x﹣6)=0,
去括号得:2x+x﹣6=0,
移项合并得:3x=6,
解得:x=2,
故答案为:2
15.(2024秋 凤翔区期末)已知是二元一次方程x+ay=5的一个解,则a的值为 7 .
【解答】解:二元一次方程x+ay=5的一组解是,
∴﹣2+a=5,
解得:a=7,
故答案为:7.
16.(2023春 海州区期末)在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若∠B'FB=80°,则∠AEF= 40 °.
【解答】解:由题知∠EFB'=∠EFB,AD∥BC,
∵∠EFB'+∠EFB+∠BFB'=360°,∠BFB'=80°,
∴∠EFB'=∠EFB=140°,
∵AD∥BC,
∴∠AEF+∠EFB=180°,
∴∠AEF=180°﹣140°=40°.
故答案为:40.
三.解答题(共8小题)
17.(2024秋 安顺期末)(1)计算:
(2)从下列三个方程中任选2个组成方程组,并解这个方程组.
①x+y=10;②2x+y=16;③x=y+4.
【解答】解:(1)原式
;
(2)选①②得:,
由②﹣①,得x=6,
把x=6代入①,得6+y=10,
解得y=4,
∴原方程组的解是.
18.(2024秋 城关区校级期末)解不等式组,并写出这个不等式组的所有整数解.
【解答】解:,
由①得x≤2,
由②得 x>﹣1,
∴原不等式组的解集为﹣1<x≤2,
∴原不等式组的所有整数解为0,1,2.
19.(2024秋 滨江区期末)已知3a+1的两个平方根分别是7﹣m和2﹣2m,9+b的立方根是2.
(1)求m,a,b的值;
(2)求7a﹣b的平方根.
【解答】解:(1)根据题意可知,3a+1的两个平方根分别是7﹣m和2﹣2m,
∴7﹣m=﹣(2﹣2m),
7﹣m=﹣2+2m,
3m=9,
解得m=3,
∴3a+1=(7﹣m)2=(7﹣3)2=16,
解得a=5,
∵9+b的立方根是2.
∴9+b=23,解得b=﹣1,
故m,a,b的值分别是3,5,﹣1;
(2)∵a=5,b=﹣1,
∴7a﹣b=7×5﹣(﹣1)=36,
又因为36的平方根为±6,
∴7a﹣b的平方根为±6.
20.(2024秋 定安县期末)如图,直线AB与CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若,求∠BOD的大小.
【解答】解:(1)ON⊥CD,理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=∠AOM=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,
即∠COM=90°,
∴ON⊥CD;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵,
∴∠BOC=4∠1,
∵∠BOC=∠1+∠BOM,
∴4∠1=∠1+90°,
解得∠1=30°,
∴∠BOC=120°,
∵∠BOC+∠BOD=180°,
∴∠BOD=180°﹣∠BOC=180°﹣120°=60°,
即∠BOD的度数为60°.
21.(2024秋 市北区期末)关于x,y的二元一次方程均可以变形为ax+by=c的形式,其中a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c).
(1)二元一次方程4x﹣3y=5的“关联系数”为 (4,﹣3,5) ;
(2)已知关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),若为该方程的一组解,且m,n均为正整数,求m,n的值.
【解答】解:(1)∵a,b,c均为常数且a≠0,b≠0,规定:方程ax+by=c的“关联系数”记为(a,b,c),
∴二元一次方程4x﹣3y=5的“关联系数”为(4,﹣3,5);
故答案为:(4,﹣3,5);
(2)∵关于x,y的二元一次方程的“关联系数”为(2,﹣1,1),
∴二元一次方程为2x﹣y=1.
∵为该方程的一组解,m,n均为正整数,
∴2(m+n)﹣m﹣5=1,即m+2n=6.
∴或.
22.(2024秋 宜宾期末)如图,已知∠A=110°,∠ABC=70°,BD⊥CD于点D,EF⊥CD于点F,试说明∠1=∠2.请补全说理过程,即在横线处填上结论或理由.
解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥① BC ,(② 同旁内角互补,两直线平行 ),
∴∠1=∠3(③ 两直线平行,内错角相等 ),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(④ 同一平面内,垂直于同一条直线的两条直线互相平行 ),
∴∠2=∠3(⑤ 两直线平行,同位角相等 ),
∴∠1=∠2(等量代换).
【解答】解:∵∠A=110°,∠ABC=70°,
∴∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
又∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
故答案为:BC;同旁内角互补,两直线平行;两直线平行,内错角相等;同一平面内,垂直于同一条直线的两条直线互相平行;两直线平行,同位角相等.
23.(2024秋 常德期末)常德市第四中学体育组老师为了解学校九年级学生体育测试的情况,以九年级某班学生的体育期末测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图(说明:A等级:90分~100分;B等级:75分~89分;C等级:60分~74分;D等级:60分以下)
请你结合图中所给信息解答下列问题:
(1)请把条形统计图补充完整;
(2)样本中D等级的学生人数占全班学生人数的百分比是 10% ;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 72° ;
(4)常德市第四中学九年级现有370名学生,请你用此样本估计体育测试中A等级的学生人数约为多少人?
【解答】解:(1)总人数为10÷20%=50(人),
则样本中D等级的学生人数为:50﹣10﹣23﹣12=5(人),
补全条形统计图:
(2)样本中D等级的学生人数占全班学生人数的百分比为:
,
故答案为:10%;
(3)∵A等级的学生人数占全班学生人数的百分比为20%,
∴扇形统计图中A等级所在的扇形的圆心角度数为:360°×20%=72°,
故答案为:72°;
(4)用370乘以A等级的学生人数占全班学生人数的百分比可得:
370×20%=74(人),
答:估计体育测试中A等级的学生人数约为74人.
24.(2024秋 海陵区校级期末)已知AB∥CD.
(1)如图1,∠1比∠2的2倍少60°,求∠1的度数;
(2)如图2,若∠A+∠C=180°,求证:∠AEF=∠CFE;
(3)如图3,过E作∠AEP的角平分线EM交FP的延长线于M,∠DFP的角平分线FN交EM的反向延长线于N,若∠M与3∠N互补,试探索直线EP与直线FN的位置关系,并说明理由.
【解答】解:(1)∵AB∥CD,由平行线的性质可得:
∠1=∠DFE,∠2=∠DFE,
∴∠1=∠2,
∴∠1=2∠1﹣60°,
∴∠1=60°
(2)证明:延长AE交CD于H,
∵AB∥CD,
∴∠A+∠AHD=180°,
∵∠A+∠C=180°,
∴∠C=∠AHD,
∴CF∥AH,
∴∠AEF=∠CFE;
(3)解:EP∥FN,
过点N作NH∥AB,过点M作MG∥AB,
∵CD∥AB∥MG∥NH,
∴∠HNM=∠AEM=∠GMN,∠3=∠HNF,∠CFM=∠GMF,
∴∠NMF=∠GMN+∠CFM=∠AEM+∠CFM,
∵FN平分∠DFM,
∴∠DFM=2∠3,
∴∠CFM=180°﹣2∠3,
∴∠NMF=∠AEM+180°﹣2∠3,
∴∠NMF=∠AEM+180°﹣2∠HNF
∴∠NMF=∠AEM+180°﹣2∠HNM﹣2∠MNF,
∴∠NMF=180°﹣∠AEM﹣2∠MNF,
∵∠NMF与3∠MNF互补,
∴∠NMF+3∠MNF=180°,
∴∠AEM=∠MNF,
∵ME平分∠AEP,
∴∠MEP=∠AEM=∠MNF,
∴EP∥FN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
